Fault Location in H-Type AC Filters Based on Characteristics of Sudden Current Changes
Abstract
1. Introduction
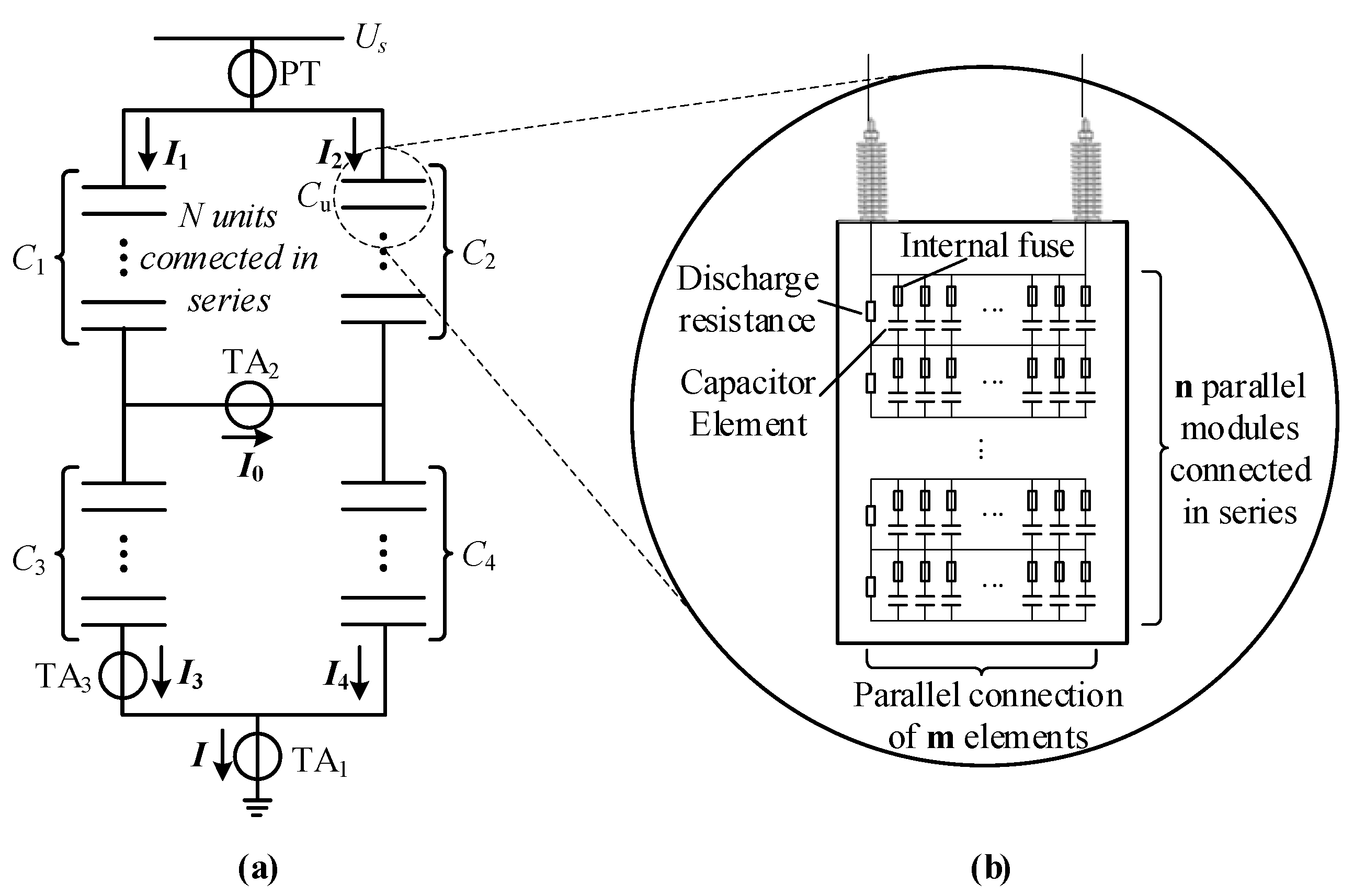
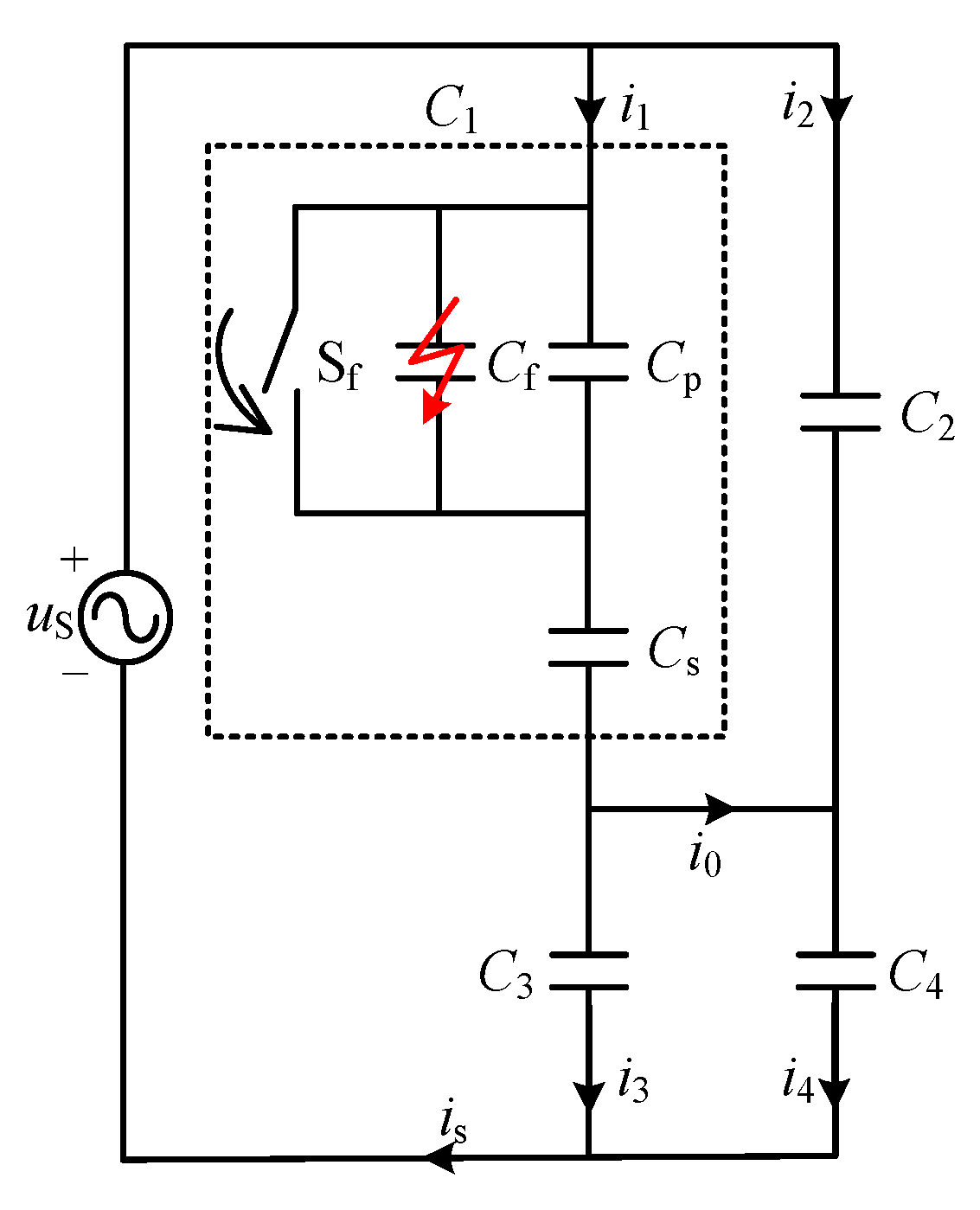
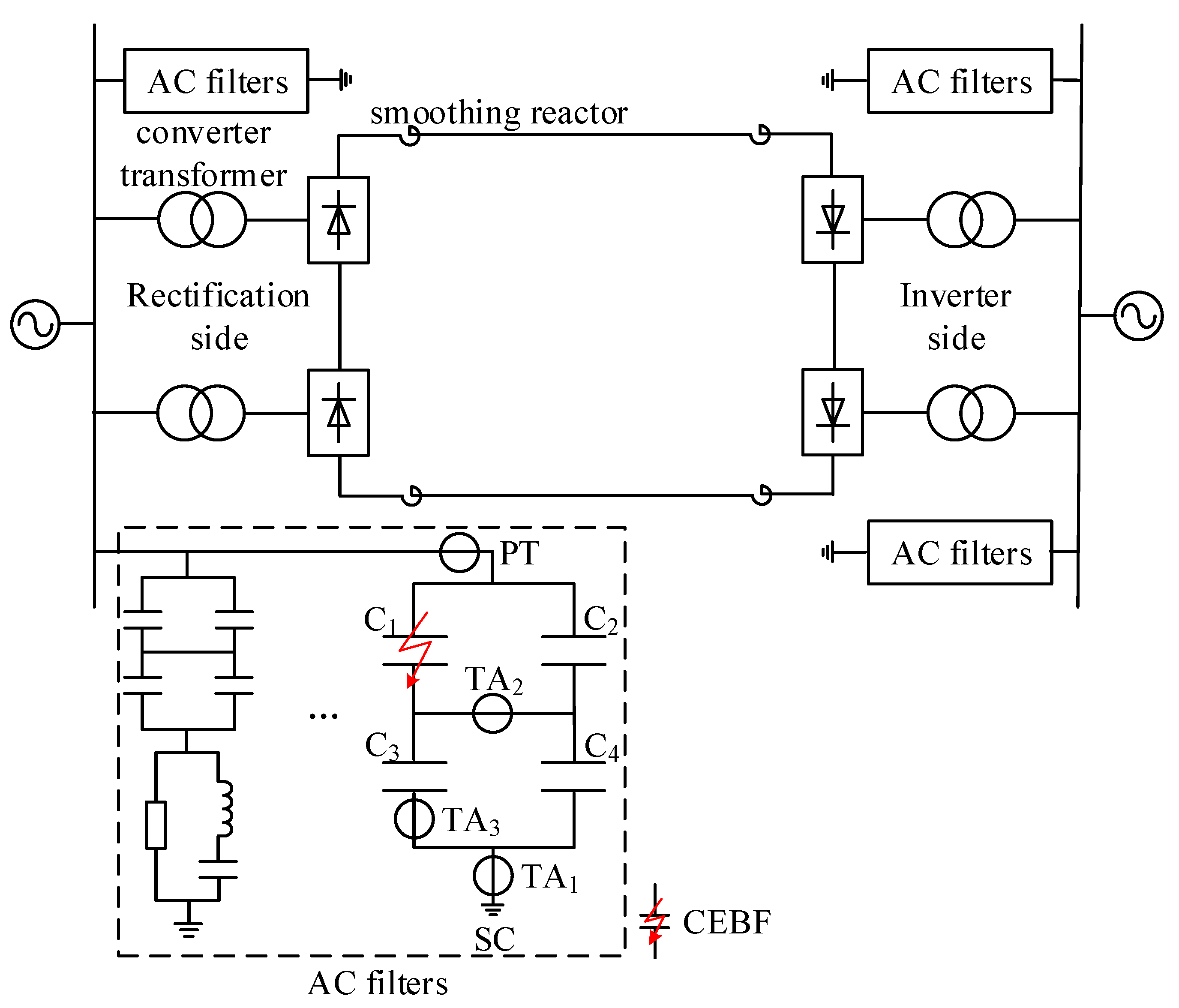
2. Equivalent Circuit and Transient Characteristic Analysis of CEBFs
2.1. Equivalent Circuit of CEBFs
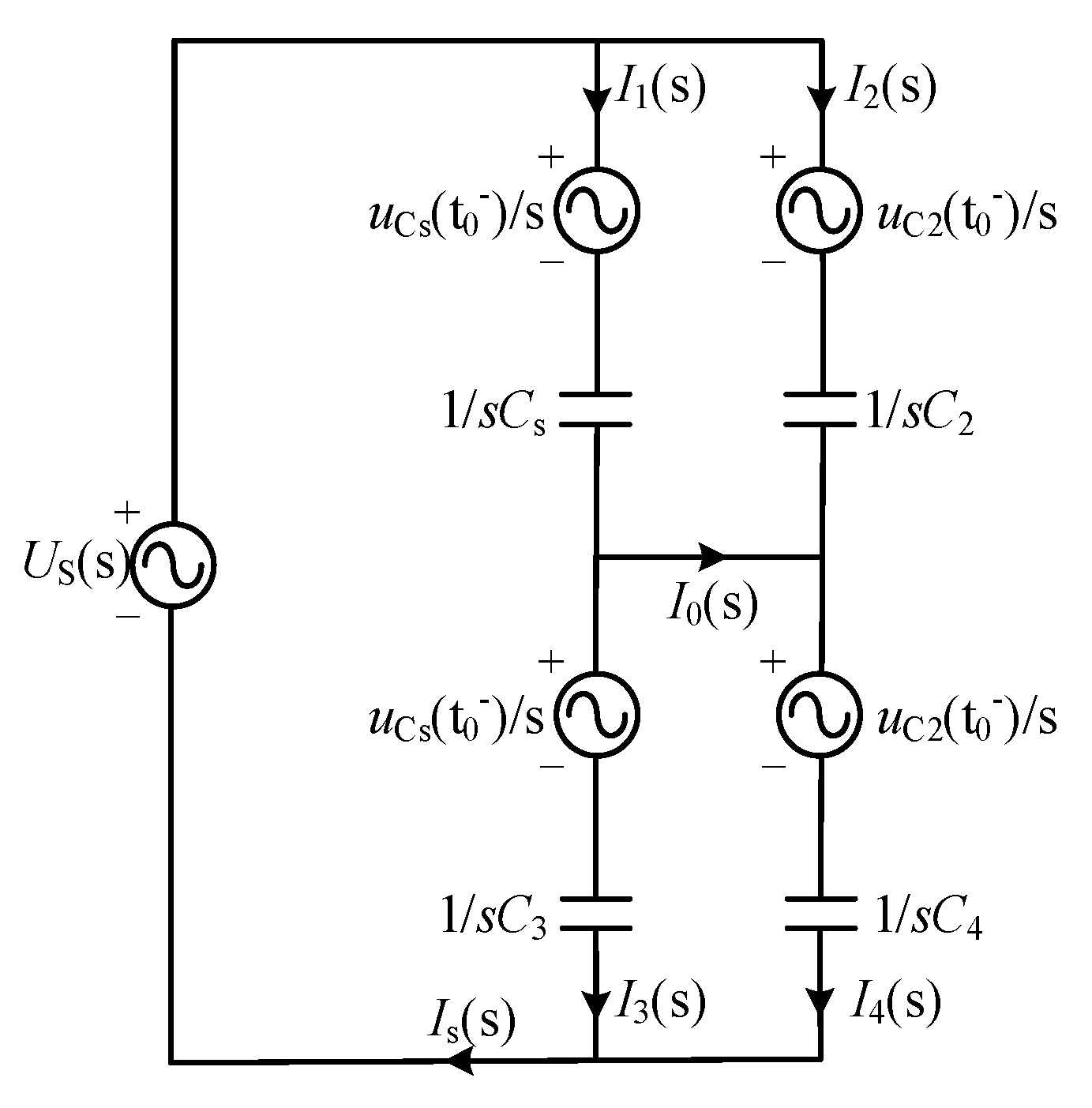
2.2. Transient Characteristic Analysis of CEBFs
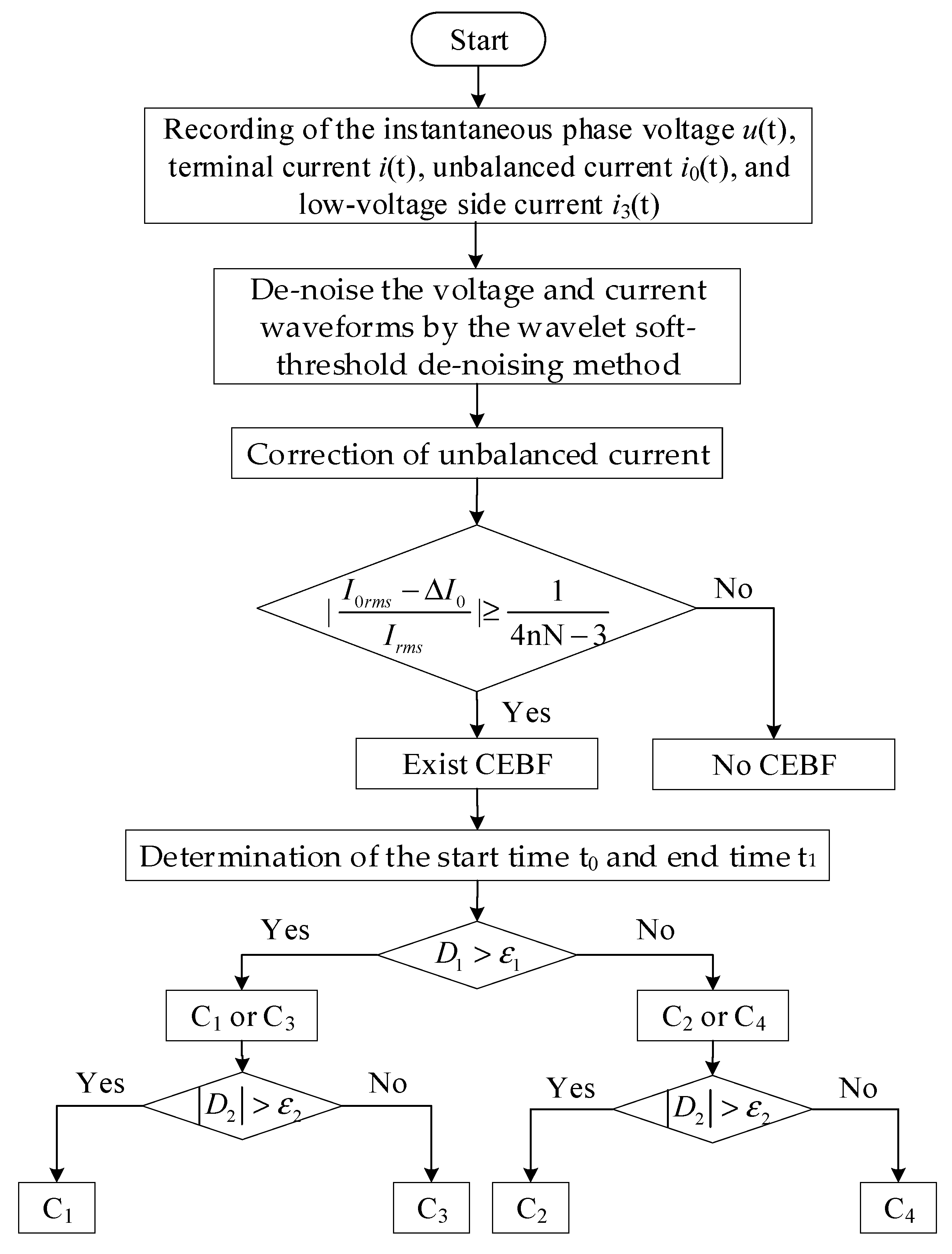
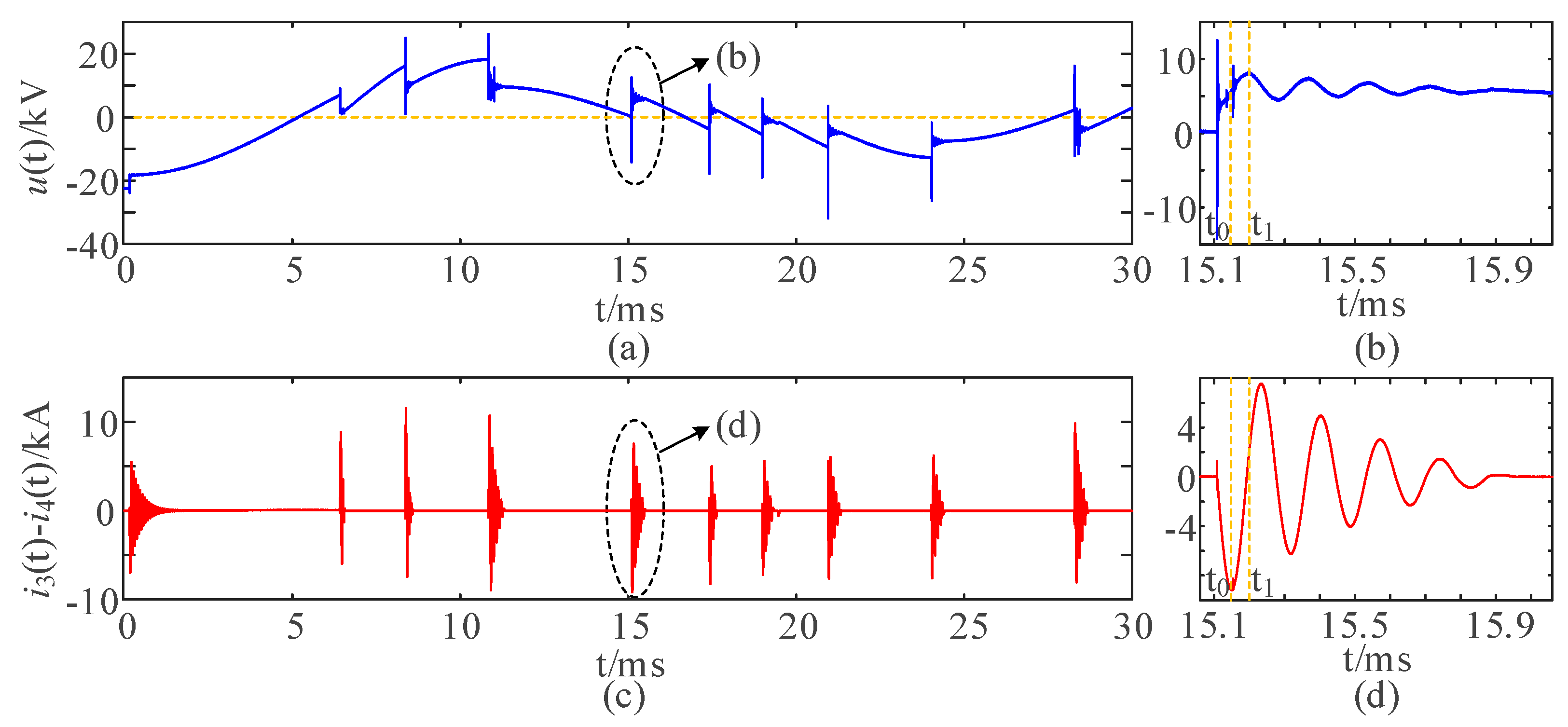
3. Fault Location Based on Characteristics of Sudden Current Changes
- Step 1: CEBF identification.
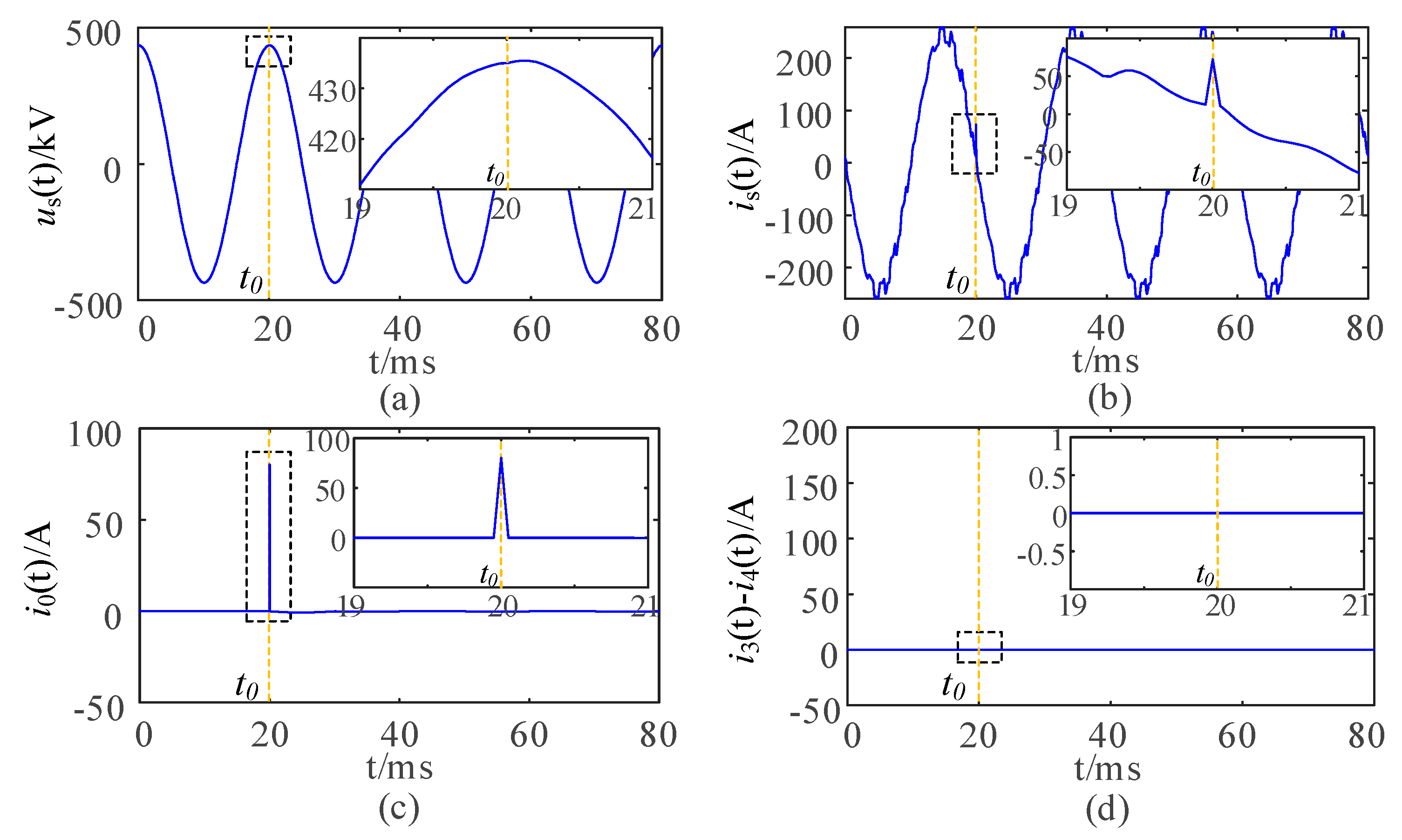
- Step 2: Determination of the start time t0 and end time t1 of the sudden change process.
- Step 3: Localization of the CEBF.
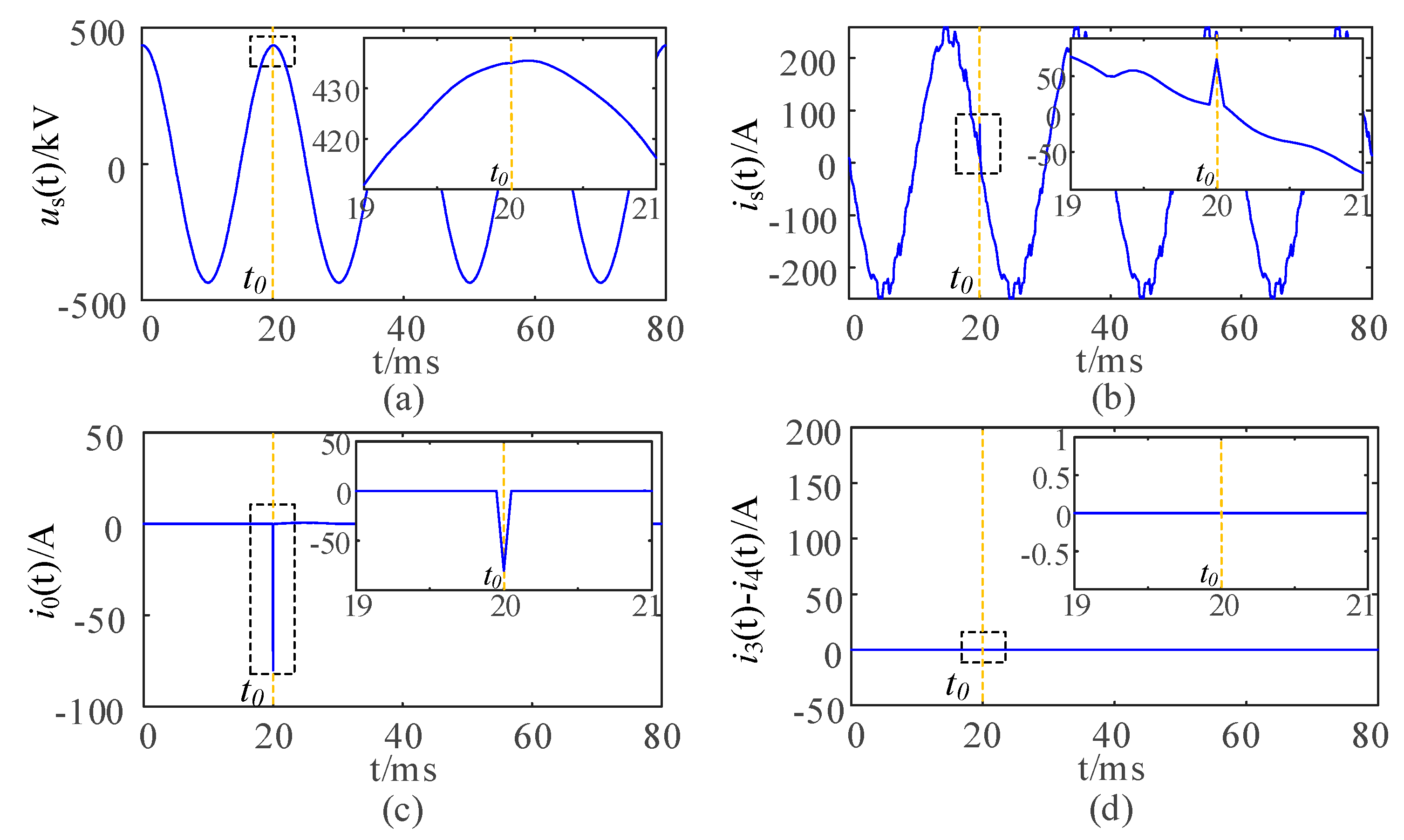
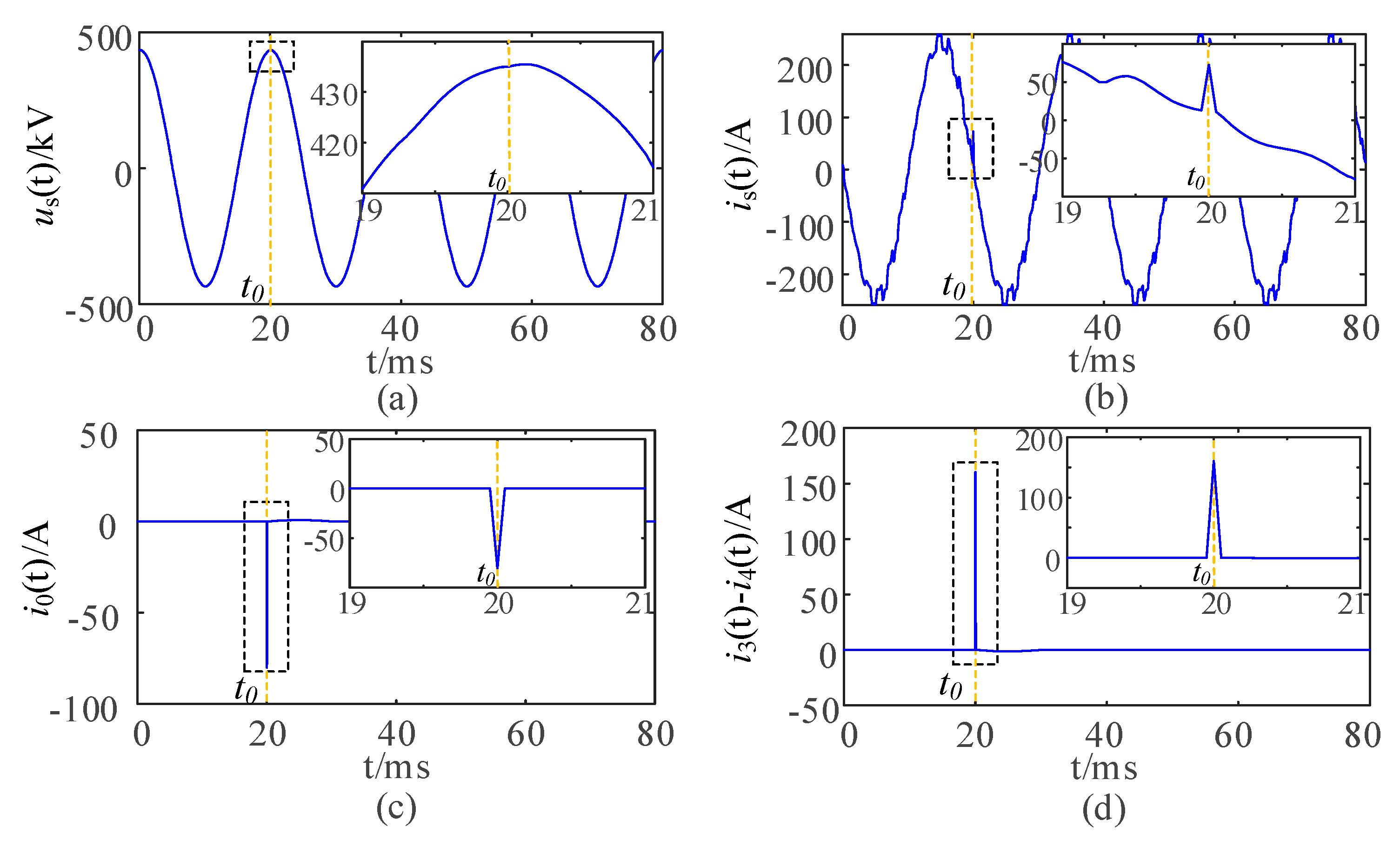
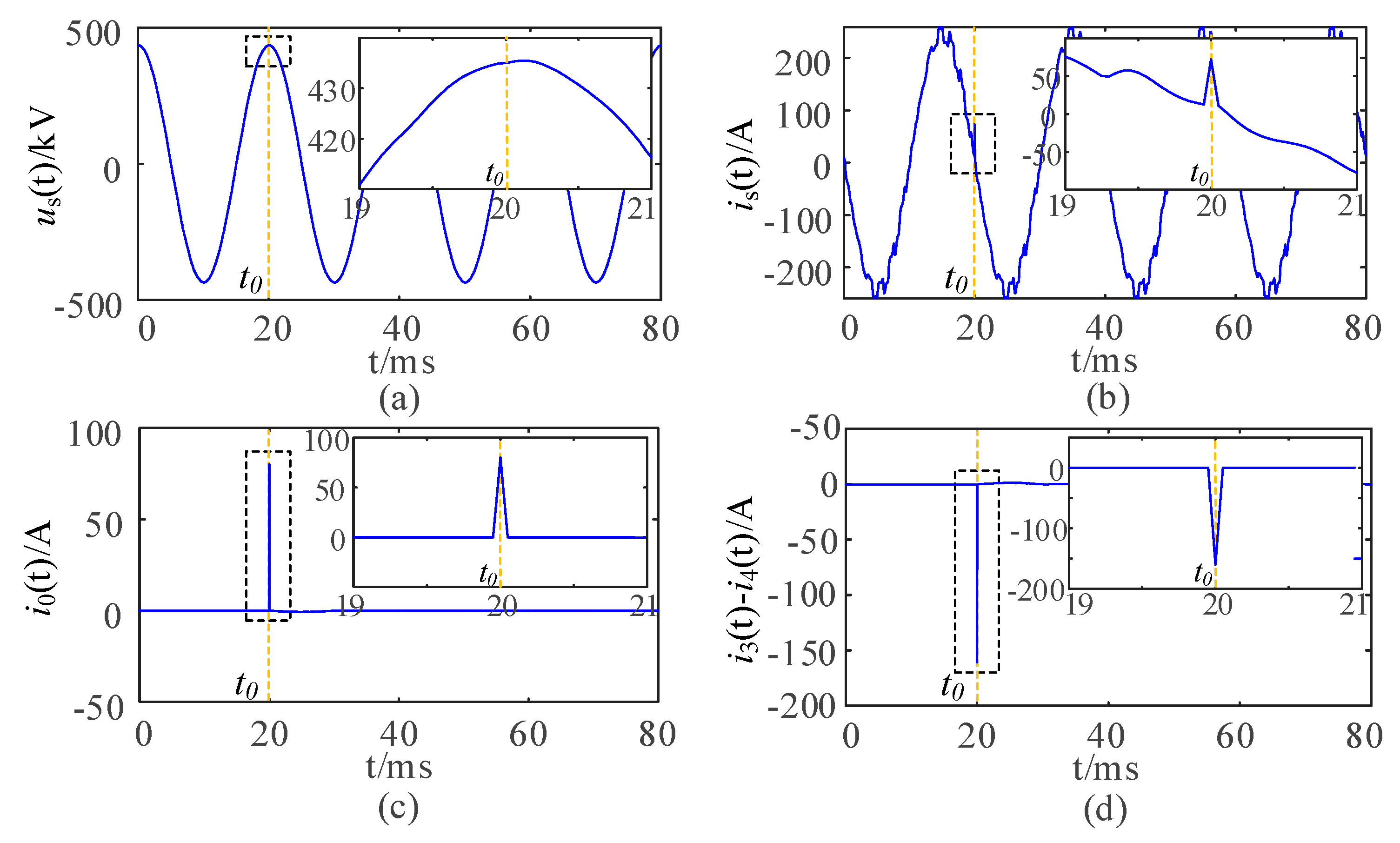
4. Simulation Verification
4.1. Simulation Model
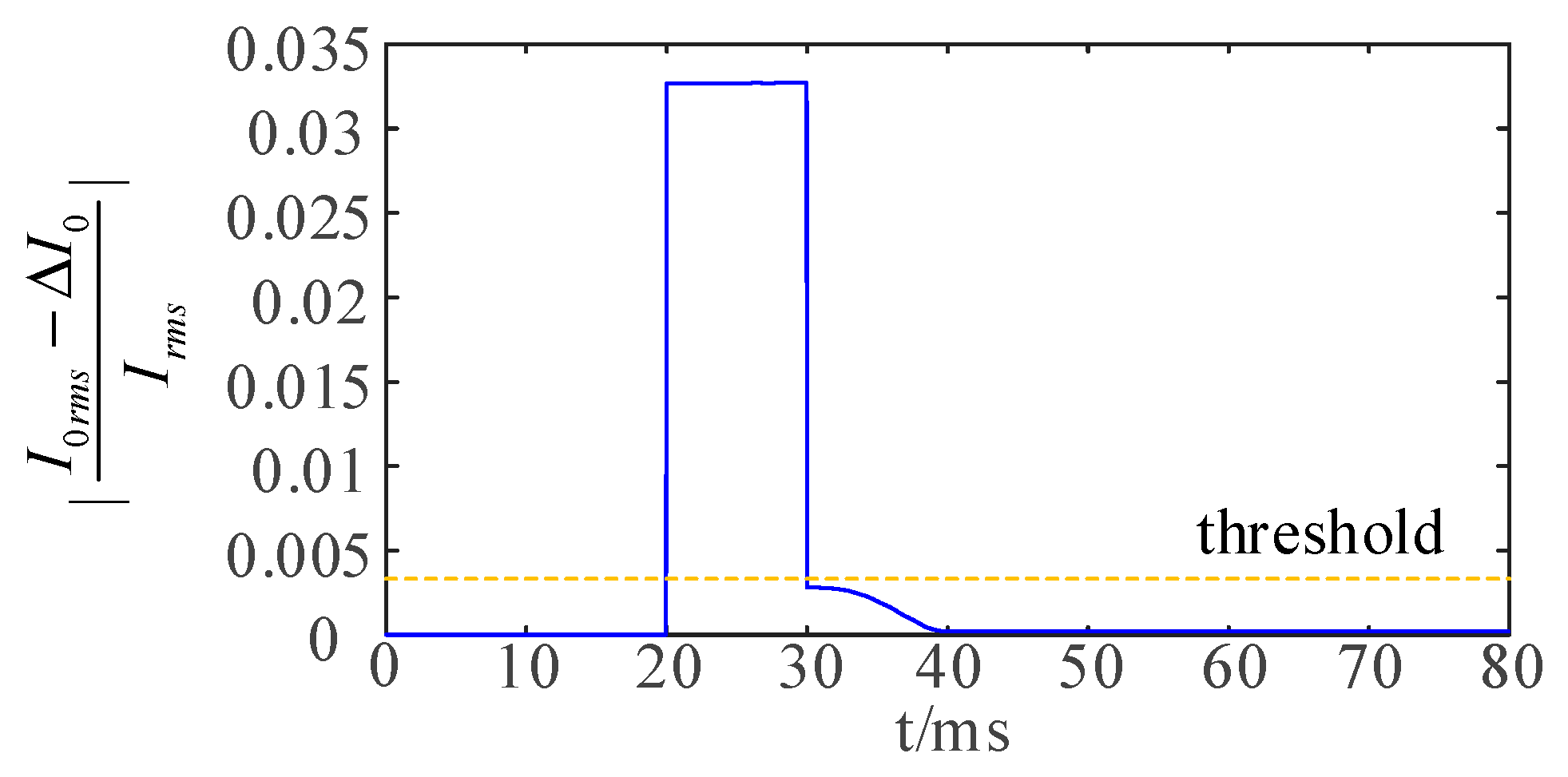
4.2. Simulation Results
4.3. Algorithm Influence Factor Analysis
4.3.1. The Influence of Fault Locations, Sampling Frequencies, Breakdown Times, Fuse Blowout Times, and Signal-to-Noise Ratios
- Sampling frequency: The sampling frequency has a significant impact on the proposed algorithm. Given that this method relies on transient signals for localization, increasing the sampling frequency significantly enhances the accuracy and reliability of the algorithm.
- Breakdown time: The breakdown time has a relatively minor impact on our method. A breakdown occurring near the voltage peak (20 ms and 30 ms) generates more significant transient current signals, while a breakdown near the voltage zero-crossing point (15 ms and 35 ms) results in smaller changes in the transient current signals.
- Fuse blowout time: The fuse blowout time has a minimal impact on the proposed algorithm. The timescale of sudden change in waveform is only 0.05 ms, which is much shorter than the time required for the fuse to blow, and the characteristic quantities used in this paper are the integral values of the sudden changes. Thus, the influence of the fuse blowout time on the algorithm is limited.
- SNR: The SNR has a minor impact on the algorithm. The localization method is based on the transient current signals, the magnitude of which is typically much greater than that of the background noise signals. Therefore, in most cases, the influence of noise on the localization accuracy is limited.
4.3.2. The Influence of Converter Type
4.3.3. The Influence of Transformer Measurement Error
4.3.4. The Influence of Capacitor Bank Configurations
4.4. Comparative Analysis with Existing Methods
4.5. Applicability Analysis of the Proposed Method
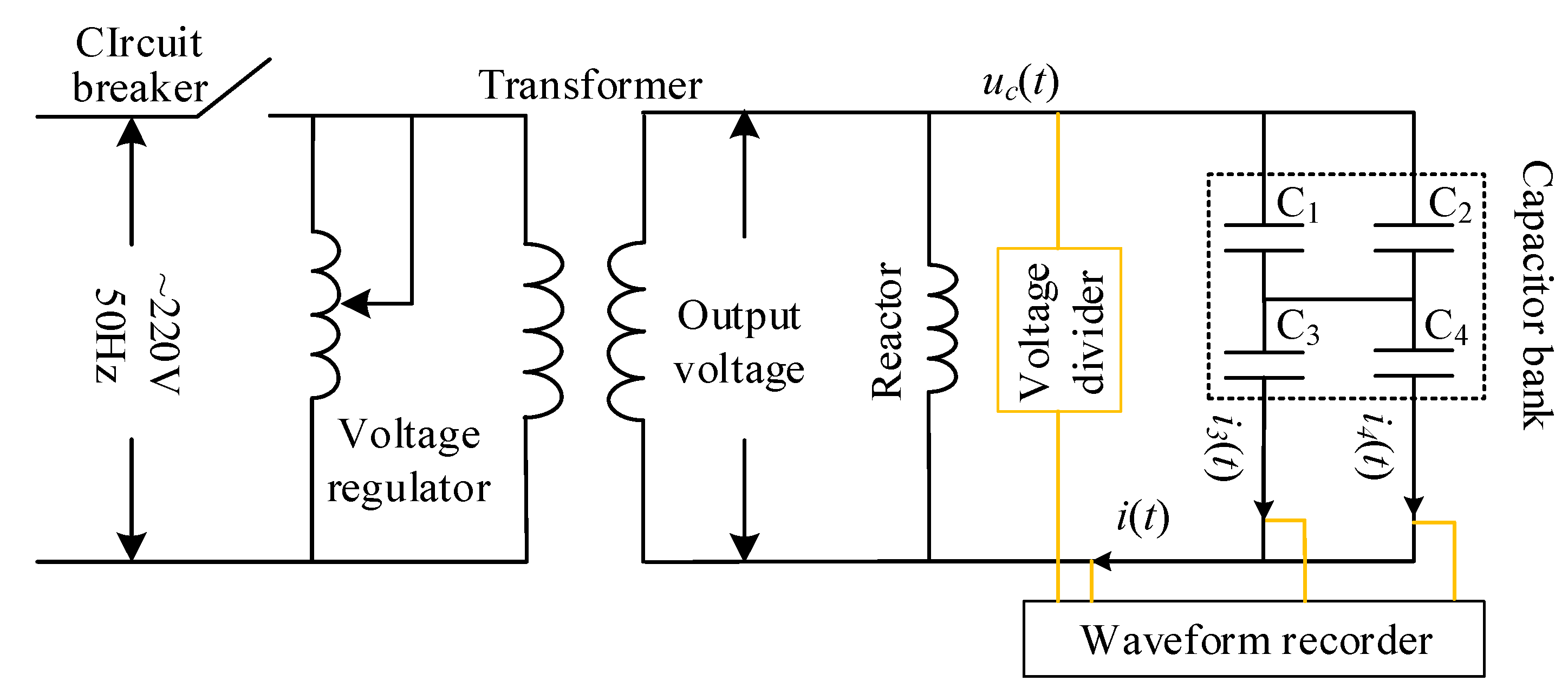
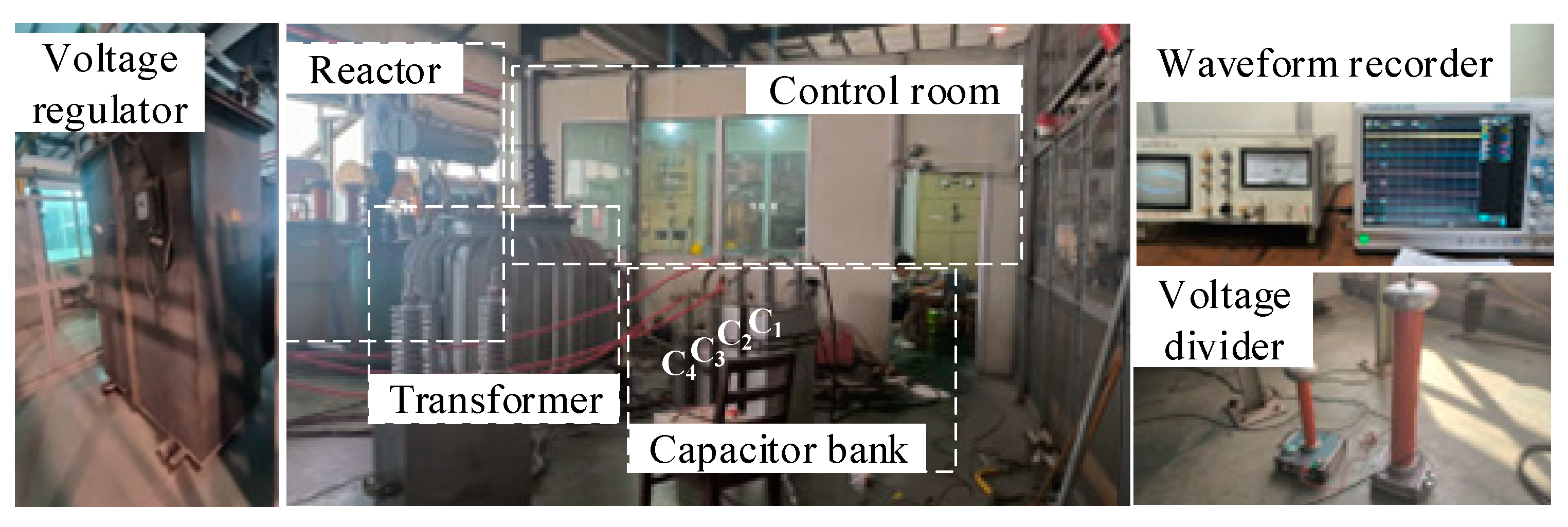
5. Experimental Data Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CEBFs | Capacitor Element Breakdown Faults |
| HVDC | High Voltage Direct Current |
| AC | Alternating Current |
| DC | Direct Current |
| LCC | Line Commutated Converter |
| SC | Shunt Capacitor |
| DWT | Discrete Wavelet Transform |
| SNR | Signal-to-Noise Ratio |
| CCC | Capacitor Commutated Converter |
| CSC | Current Source Converter |
| MMC | Modular Multilevel Converter |
References
- Li, K.; Huang, M.; Zha, X. An Overview of Reliability Analysis Methods for an HVDC Transmission System. Power Syst. Prot. Control. 2024, 52, 174–187. [Google Scholar] [CrossRef]
- Lee, J.-H.; Jung, J.-J.; Sul, S.-K. Suppression of AC Coupling Effects on HVdc Transmission System Based on MMC. IEEE Trans. Power Electron. 2024, 39, 11571–11582. [Google Scholar] [CrossRef]
- Wang, B.; Wei, X.; Xia, Y. An Innovative Arc Fault Model and Detection Method for Circuit Breakers in LCC-HVDC AC Filter Banks. IEEE Trans. Power Deliv. 2023, 38, 3888–3899. [Google Scholar] [CrossRef]
- Ma, X.; Yang, T.; Wang, Y.; Yuan, H.; Liu, Z.; Xu, R. Optimization Method of AC Filter Field Layout Structure in UHV Converter Station. In Proceedings of the 2023 IEEE International Conference on Power Science and Technology (ICPST), Kunming, China, 5 May 2023; pp. 173–180. [Google Scholar]
- Huang, M.; Xiong, W.; Wu, K. Analysis of AC Filter Detuning Characteristics and Improvement Measures in Converter Station. J. Phys. Conf. Ser. 2023, 2728, 012048. [Google Scholar] [CrossRef]
- Fanequiço, L.; Gomes, C.; Van Coller, J. Impacts of AC Filter Tripping at the Songo Rectifier Station in Southern Africa. In Proceedings of the 2024 IEEE PES/IAS PowerAfrica, Johannesburg, South Africa, 7 October 2024; pp. 1–5. [Google Scholar]
- Gao, H. The Characteristics and Suppression Protection Measures of AC Filter Closing Inrush Current Considering Residual Voltage and Residual Charge. Eng. Lett. 2024, 32, 2191–2199. [Google Scholar]
- Santoso, S. On Determining the Relative Location of Switched Capacitor Banks. IEEE Trans. Power Deliv. 2007, 22, 1108–1116. [Google Scholar] [CrossRef]
- Yadav, N.; Tummuru, N.R. Filter Capacitor Current Dynamics-based Frequency-domain Fault Detection Approach for Grid-connected Low-voltage DC Microgrid. IEEE Trans. Ind. Electron. 2023, 70, 12784–12794. [Google Scholar] [CrossRef]
- Chiradeja, P.; Lertwanitrot, P.; Ngaopitakkul, A.; Pothisarn, C. Behaviour Analysis of H-bridge High-voltage Capacitor Banks Fault on 230-kv Substation Using Discrete Wavelet Transform. IET Gener. Trans. Dist. 2023, 17, 4810–4825. [Google Scholar] [CrossRef]
- Lertwanitrot, P.; Ngaopitakkul, A. Application of Magnitude and Phase Angle to Boundary Area-based Algorithm for Unbalance Relay Protection Scheme in 115-kV Capacitor Bank. IEEE Access 2021, 9, 35709–35717. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, L.; Yan, F.; Wu, Y.; Wang, Z.; Ma, Y. Design of the Internal Fuse Dimension for HV Shunt Capacitor in UHV Transmission Projects. IEEE Trans. Plasma Sci. 2024, 52, 2229–2240. [Google Scholar] [CrossRef]
- Chen, X.; Yu, M.; Yin, B.; Zhao, Y.; Zhang, X.; Lv, G. Capacitor Fault Warning and Simulation Based on Harmonic Changes. Electrotech. Electric 2023, 10, 32–35. [Google Scholar]
- Mu, D.; Lin, S.; Lei, Y.; Fang, G. Bridge Arm Fault Location Method for High Voltage Capacitor of DC Filter in HVDC Systems Based on Current Characteristics. In Proceedings of the 2020 IEEE 1st China International Youth Conference on Electrical Engineering (CIYCEE), Wuhan, China, 1 November 2020; pp. 1–7. [Google Scholar]
- Lei, M.; Zhang, S.; Xu, X. Study on Fault Location Method of Bridge Differential Unbalanced Protection Capacitor Bank Based on Relative Current Detection. Power Capacit. React. Power Compens. 2021, 42, 1–5. [Google Scholar]
- Yu, H.; Zhang, J.; Sun, H.; He, Y.; Zhou, H.; Yuan, M.; Yang, L.; Qu, S.; Tang, H.; Li, J. Fault Location Method of H-bridge Capacitor Bank in Converter Station Based on Current Criterion of High Voltage Bridge Arm. In Proceedings of the 2022 IEEE 5th International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 18 November 2022; Volume 2022, pp. 274–277. [Google Scholar]
- Li, Y.; Rao, Z.; Li, Z.; Ding, L. Research on Fault Location Method of Track Circuit Compensation Capacitor Based on Probabilistic Neural Network. Electr. Meas. Instrum. 2023, 60, 48–56. [Google Scholar] [CrossRef]
- Jouybari-Moghaddam, H.; Sidhu, T.S.; Dadash Zadeh, M.R.; Parikh, P.P. Shunt Capacitor Banks Online Monitoring Using a Superimposed Reactance Method. IEEE Trans. Smart Grid 2018, 9, 5554–5563. [Google Scholar] [CrossRef]
- Mohanty, R.; Pradhan, A.K. Time-domain Protection and Fault Location of Wye-connected Shunt Capacitor Banks Using Superimposed Current and Differential Voltage. IEEE Trans. Power Deliv. 2021, 36, 3486–3495. [Google Scholar] [CrossRef]
- Liang, J.; Zhu, K. Distribution Capacitor Health Monitoring Based on the Disturbances of Element Breakdown Faults. IEEE Trans. Power Deliv. 2022, 37, 4064–4072. [Google Scholar] [CrossRef]
- Peng, Y.Z.; Wang, H.Y.; Zhang, W.N. Study on Unbalance Protection Fault of AC Filter Capacitor Bank of UHV Converter Station. Power Capacit. React. Power Compens. 2024, 6–13. [Google Scholar] [CrossRef]
- Liang, J.B. (Shandong University, Jinan, China). Personal communication, 2021.
- Yan, F.; He, H.W.; Wang, Z. Internal Fuse Performance of High Voltage Capacitor Unit. High Volt. Eng. 2016, 42, 1790–1796. [Google Scholar]
- Zhu, T.-X.; Wang, N.-N.; Guo, W.-M. The Application of the Unbalance Current Protection for Capacitor of AC Filter Used in the HVDC System of CSG. Power Syst. Prot. Control. 2010, 38, 102–105. [Google Scholar]
- Xiao, Y.; Zhang, J.Y.; Li, J.P. Criterion and Settings of Unbalanced Current Protection for Filter Capacitor Bank of H Configuration. Power Syst. Prot. Control. 2015, 43, 120–128. [Google Scholar]
- Yan, C.; Yang, H.; Liu, Q.; Zhang, P.; Zhang, B. Impact of Nonlinear AC Fault Arc Resistance on Commutation Failures in LCC-HVDC Systems. IEEE Trans. Power Electron. 2024, 39, 12096–12100. [Google Scholar] [CrossRef]
- Funaki, T.; Matsuura, K. Predictive firing angle calculation for constant effective margin angle control of CCC-HVdc. IEEE Trans. Power Deliv. 2000, 15, 1087–1093. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, L.; Wei, X.; Qi, L.; Gao, C.; He, Z.; Chen, Q. Design and Operation Mode of Based on Controllable Current Source Converter HVDC System. Proc. Chin. Soc. Electr. Eng. 2022, 42, 2532–2541. [Google Scholar] [CrossRef]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular multilevel converters for HVDC applications: Review on converter cells and functionalities. IEEE Trans. Power Electron. 2015, 30, 18–36. [Google Scholar] [CrossRef]

| Method | Advantages | Limitations |
|---|---|---|
| Steady-state variation in current [14] | Simple calculation and easy implementation | Requires additional current transformers on the high-voltage side, increasing costs and safety risks. |
| Relative steady-state current [15] | Simple calculation and low cost | Relies on steady-state analysis; poor performance when there are few failures of capacitor elements. |
| Quantitative relationship [16] | Simple calculation and easy implementation | Requires additional current transformers on the high-voltage side. |
| Probabilistic neural network [17] | Effectively reducing problem complexity and capable of handling complex fault scenarios | Requires additional current transformers on the high-voltage side. Requires a large amount of training data and computing resources. |
| Fault Arm | The Initial Phase Angle of the Fault | The Sudden Change in the Unbalanced Current | The Sudden Change in the Current Difference on the Low-Voltage Side |
|---|---|---|---|
| C1 | + | 0 | |
| − | 0 | ||
| C2 | − | 0 | |
| + | 0 | ||
| C3 | − | + | |
| + | − | ||
| C4 | + | − | |
| − | + |
| Fault Location | D1 | D2 | Localization Result |
|---|---|---|---|
| C1 | 1.9831 | 0 | C1 |
| C2 | −1.9827 | 0 | C2 |
| C3 | 1.9824 | 3.9920 | C3 |
| C4 | −1.9829 | −3.9639 | C4 |
| Fault Setting | Feature Quantities | Localization Result | |||||
|---|---|---|---|---|---|---|---|
| Fault Location | Sampling Frequency (kHz) | Breakdown Time (ms) | Fuse Blowout Time (ms) | SNR (dB) | D1 | D2 | |
| C1 | 15 | 20 | 0.5 | 100 | 1.9898 | 0 | C1 |
| 20 | 1.9819 | 0 | C1 | ||||
| 25 | 1.9691 | 0 | C1 | ||||
| 30 | 1.9617 | 0 | C1 | ||||
| C2 | 20 | 15 | 0.5 | 100 | −0.3039 | 0 | C2 |
| 20 | −1.9819 | 0 | C2 | ||||
| 25 | −0.2599 | 0 | C2 | ||||
| 30 | −1.9817 | 0 | C2 | ||||
| C3 | 20 | 20 | 0.2 | 100 | 2.0059 | 4.0115 | C3 |
| 0.4 | 2.0005 | 4.0011 | C3 | ||||
| 0.6 | 1.9909 | 3.9817 | C3 | ||||
| 0.8 | 1.9786 | 3.9573 | C3 | ||||
| C4 | 20 | 20 | 0.5 | 40 | −2.0059 | −1.0118 | C4 |
| 50 | −2.0060 | −1.0120 | C4 | ||||
| 60 | −2.0060 | −1.0119 | C4 | ||||
| 70 | −2.0058 | −1.0110 | C4 | ||||
| Type of Converter | Harmonic Characteristic | Filter Requirement | Application Scenario |
|---|---|---|---|
| LCC | The 12k ± 1th order characteristic harmonics (k = 1, 2, 3, 4…) | Reactive power compensation and filtering are required | Large capacity, long-distance power transmission |
| CCC | The 12k ± 1th order characteristic harmonics (k = 1, 2, 3, 4…) | Need filtering | Lower requirements for power grid strength |
| CSC | The 12k ± 1th order characteristic harmonics with low content (k = 1, 2, 3, 4…) | Reactive power compensation and filtering are required | High requirements for commutation stability |
| MMC | High frequency harmonics | No need for reactive power compensation and filtering | Small and medium-sized, multi terminal DC transmission |
| Fault Setting | Feature Quantities | Localization Result | |||
|---|---|---|---|---|---|
| Type of Converter | Harmonic Content (%) | Fault Location | D1 | D2 | |
| LCC/CCC | / | C1 | 1.9819 | 0 | C1 |
| C2 | −1.9827 | 0 | C2 | ||
| C3 | 1.9824 | 3.9920 | C3 | ||
| C4 | −1.9829 | −3.9639 | C4 | ||
| CSC | 60% LCC | C1 | 1.9873 | 0 | C1 |
| C2 | −1.9871 | 0 | C2 | ||
| C3 | 1.9881 | 3.9962 | C3 | ||
| C4 | −1.9901 | −3.9845 | C4 | ||
| 20% LCC | C1 | 1.9992 | 0 | C1 | |
| C2 | −1.9985 | 0 | C2 | ||
| C3 | 1.9985 | 3.9990 | C3 | ||
| C4 | −1.9983 | −3.9976 | C4 | ||
| MMC | 0 | C1 | 2.0021 | 0 | C1 |
| C2 | −2.0017 | 0 | C2 | ||
| C3 | 2.0020 | 4.0003 | C3 | ||
| C4 | −2.0014 | −4.0011 | C4 | ||
| Fault Setting | Feature Quantities | Localization Result | ||
|---|---|---|---|---|
| Accuracy Class | Fault Location | D1 | D2 | |
| 1P | C1 | 1.9755 | 0 | C1 |
| C2 | −1.9681 | 0 | C2 | |
| C3 | 1.9722 | 3.9724 | C3 | |
| C4 | −1.9789 | −3.9408 | C4 | |
| 2P | C1 | 1.9558 | 0 | C1 |
| C2 | −1.9450 | 0 | C2 | |
| C3 | 1.9534 | 3.9371 | C3 | |
| C4 | −1.9558 | −3.9003 | C4 | |
| 5P | C1 | 1.9200 | 0 | C1 |
| C2 | −1.8800 | 0 | C2 | |
| C3 | 1.9000 | 3.8594 | C3 | |
| C4 | −1.9115 | −3.8297 | C4 | |
| Fault Setting | Feature Quantities | Localization Result | ||
|---|---|---|---|---|
| The Number of Capacitor Units | Fault Location | D1 | D2 | |
| 30 | C1 | 1.9819 | 0 | C1 |
| C2 | −1.9827 | 0 | C2 | |
| C3 | 1.9824 | 3.9920 | C3 | |
| C4 | −1.9829 | −3.9639 | C4 | |
| 60 | C1 | 0.4970 | 0 | C1 |
| C2 | −0.4957 | 0 | C2 | |
| C3 | 0.4956 | 0.7986 | C3 | |
| C4 | −0.4958 | 0.7928 | C4 | |
| 90 | C1 | 0.2087 | 0 | C1 |
| C2 | −0.1992 | 0 | C2 | |
| C3 | 0.1984 | 0.3593 | C3 | |
| C4 | −0.1998 | 0.3568 | C4 | |
| Localization Algorithm | Accuracy (%) | Average Location Time (s) |
|---|---|---|
| Reference [14] | 85.7 | 0.973 |
| Reference [15] | 80.4 | 0.726 |
| Reference [16] | 87.0 | 1.131 |
| Reference [17] | 91.6 | 119.254 |
| Proposed algorithm | 94.6 | 1.467 |
| Device | Model | Main Function | Key Parameters |
|---|---|---|---|
| Voltage regulator | TDA315 | Smooth voltage regulation | Rated capacity: 315 kVA Input voltage: 380 V Output voltage: 0–650 V |
| Reactor | YDGK-2875/4.57−62.1 | Reactive power compensation | Rated capacity: 2875 kVA SNR < 50 dB Rated frequency: 50 Hz |
| Transformer | EXC-315/4.57~62.1 | Voltage transformation | Rated capacity: 315 kVA Rated frequency: 50 Hz |
| Waveform recorder | DL950 | Waveform capture, data storage, waveform analysis | Number of channels: 8 Sampling Frequency ≤ 200 MHz |
| Voltage divider | NR-FRC-100 kV | High-voltage measurement | Voltage ratio: 100 kV |
| Capacitor | m | n | CN (uF) | C_meas (uF) | C_1st (uF) | C_2nd (uF) |
|---|---|---|---|---|---|---|
| C1 | 21 | 1 | 72 | 73.23 | 73.23 | 73.23 |
| C2 | 21 | 1 | 72 | 72.46 | 72.46 | 72.46 |
| C3 | 8 | 3 | 21.05 | 21.08 | 21.08 | 21.08 |
| C4 | 8 | 3 | 21.05 | 20.18 | 19.02 | open circuit |
| Test Number | D2 | ε2 | Localization Result | |
|---|---|---|---|---|
| 1 | −0.9627 | 0.1732 | 0.0001 | C4 |
| 2 | 0.2272 | −0.3247 | 0.0001 | C4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Xiao, W.; Zhang, S.; Li, Y. Fault Location in H-Type AC Filters Based on Characteristics of Sudden Current Changes. Energies 2025, 18, 1403. https://doi.org/10.3390/en18061403
Zhang W, Xiao W, Zhang S, Li Y. Fault Location in H-Type AC Filters Based on Characteristics of Sudden Current Changes. Energies. 2025; 18(6):1403. https://doi.org/10.3390/en18061403
Chicago/Turabian StyleZhang, Wenhai, Wen Xiao, Shu Zhang, and Yuzhe Li. 2025. "Fault Location in H-Type AC Filters Based on Characteristics of Sudden Current Changes" Energies 18, no. 6: 1403. https://doi.org/10.3390/en18061403
APA StyleZhang, W., Xiao, W., Zhang, S., & Li, Y. (2025). Fault Location in H-Type AC Filters Based on Characteristics of Sudden Current Changes. Energies, 18(6), 1403. https://doi.org/10.3390/en18061403





