Ventilation Air Methane (VAM) Utilisation: Comparison of the Thermal and Catalytic Oxidation Processes
Abstract
1. Introduction
- Catalytic technologies
- Catalytic reverse flow reactor;
- Catalytic monolithic reactor;
- Catalytic lean burn gas turbine.
- Thermal technologies
- Thermal reverse flow reactor;
- Recuperative gas turbine.
- Adsorption technology
- Methane concentrator.
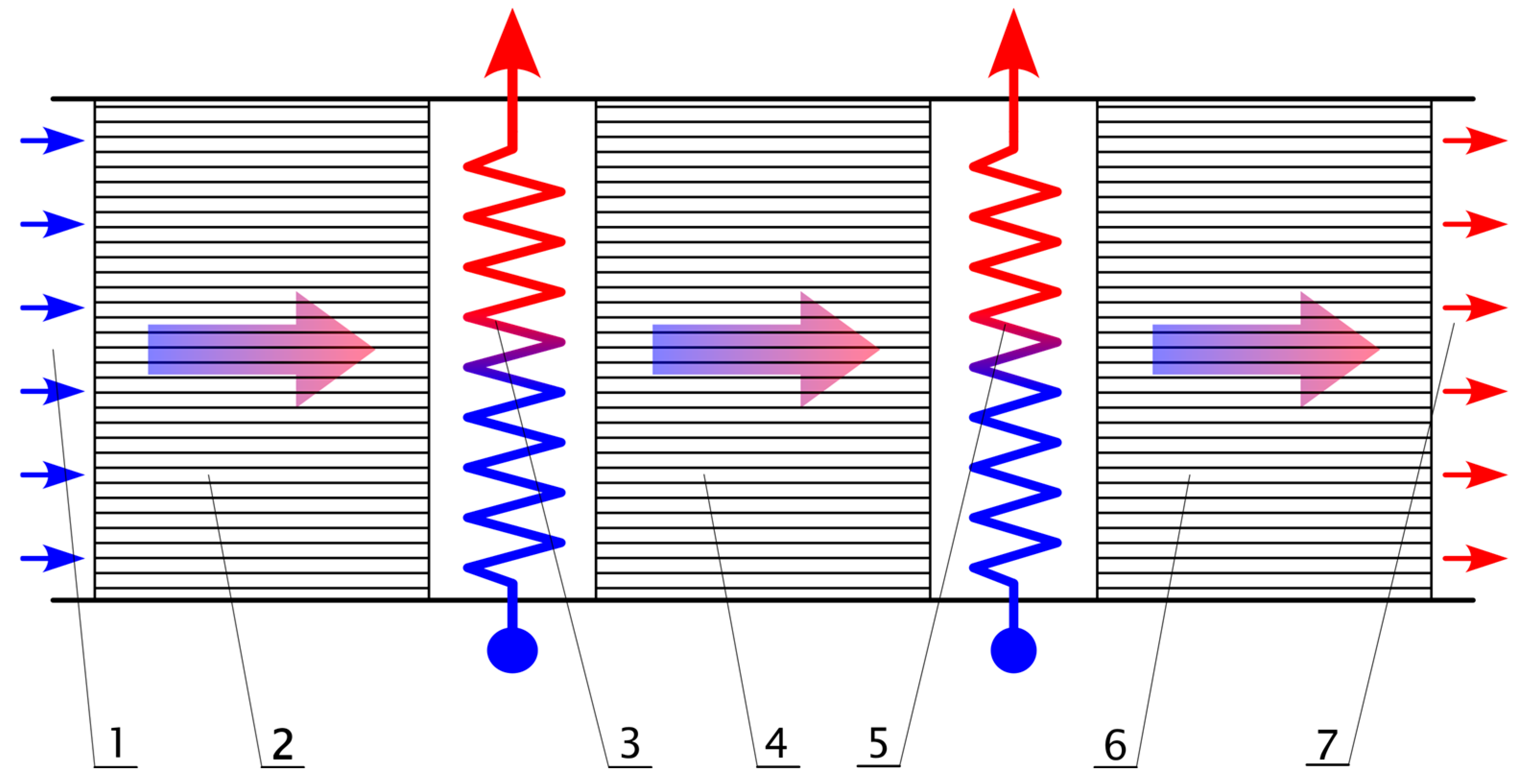
2. Modelling
2.1. Kinetics of the Thermal Oxidation
2.2. Kinetics of the Catalytic Oxidation
2.3. Simulation Assumptions
- Thermal afterburning—700 °C;
- Catalytic afterburning—400 °C.
3. Results and Discussion
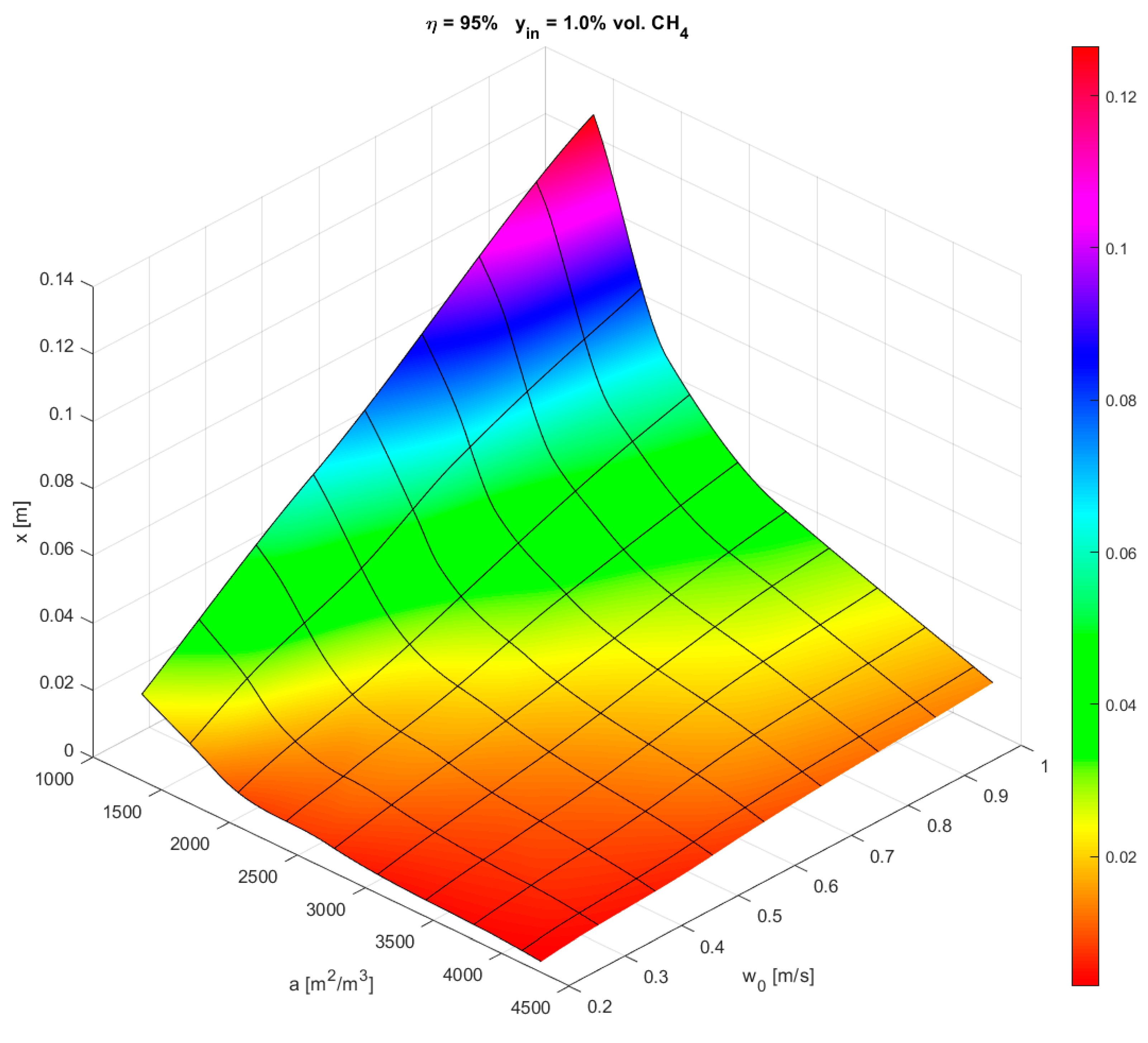
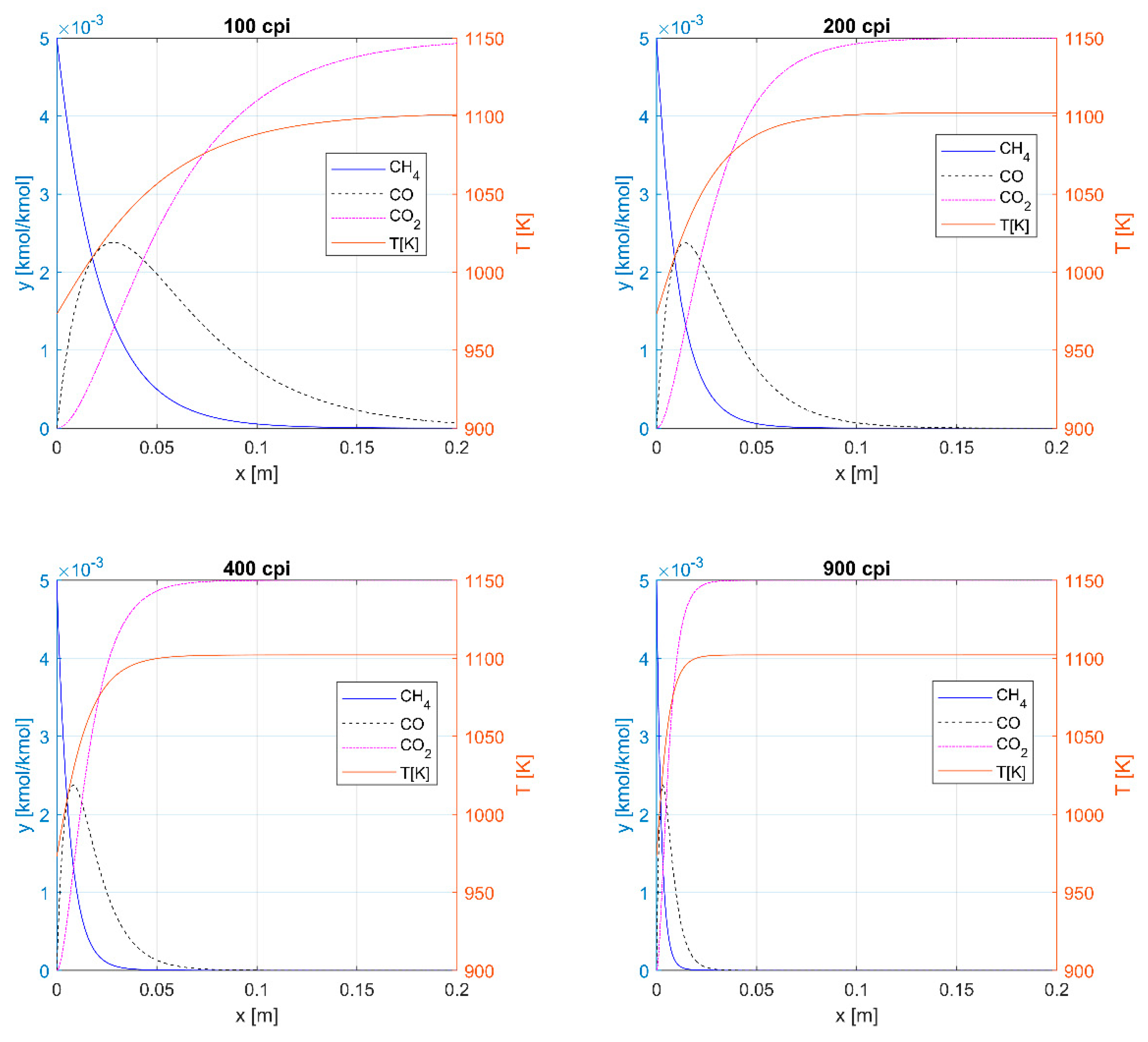
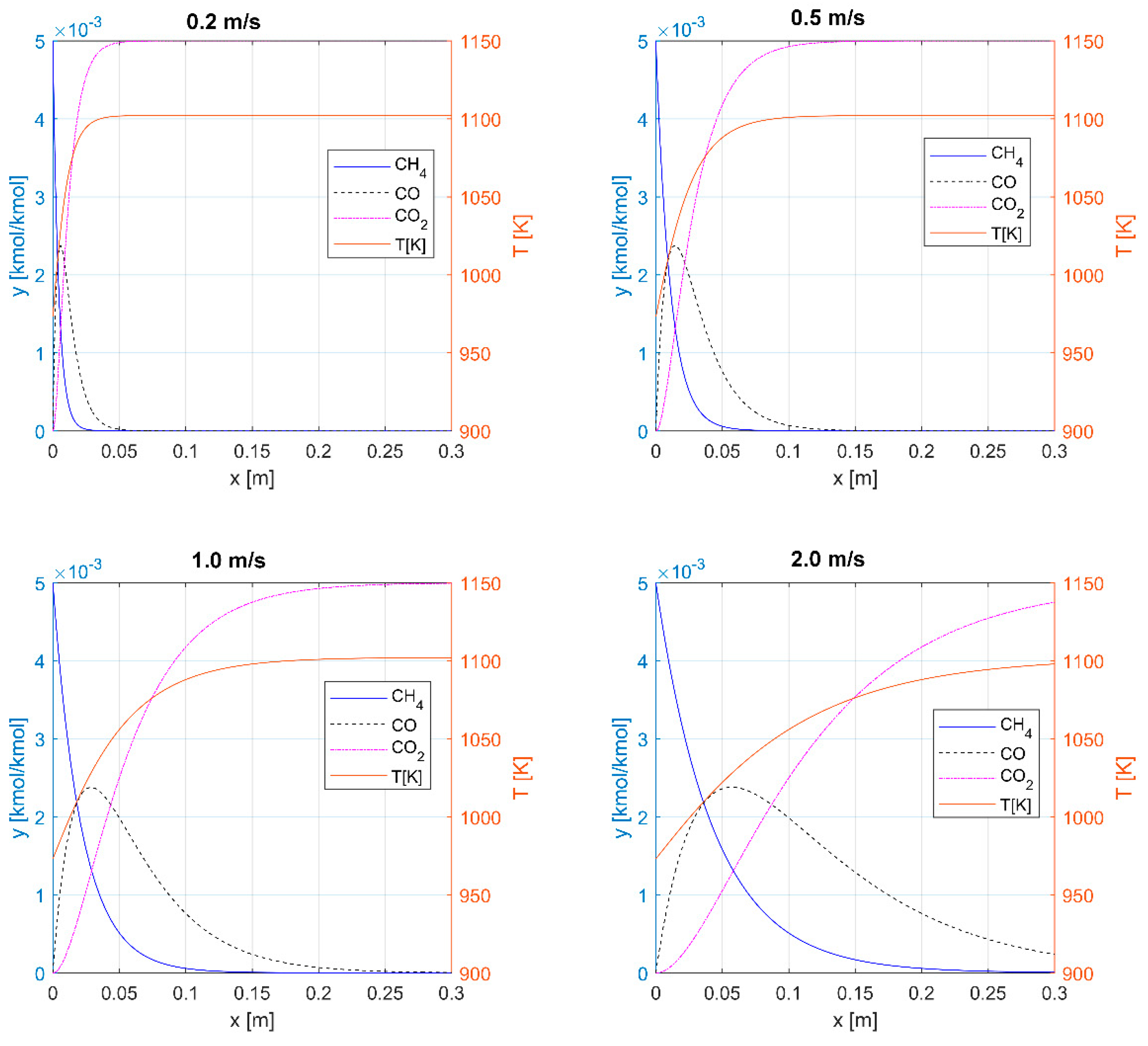
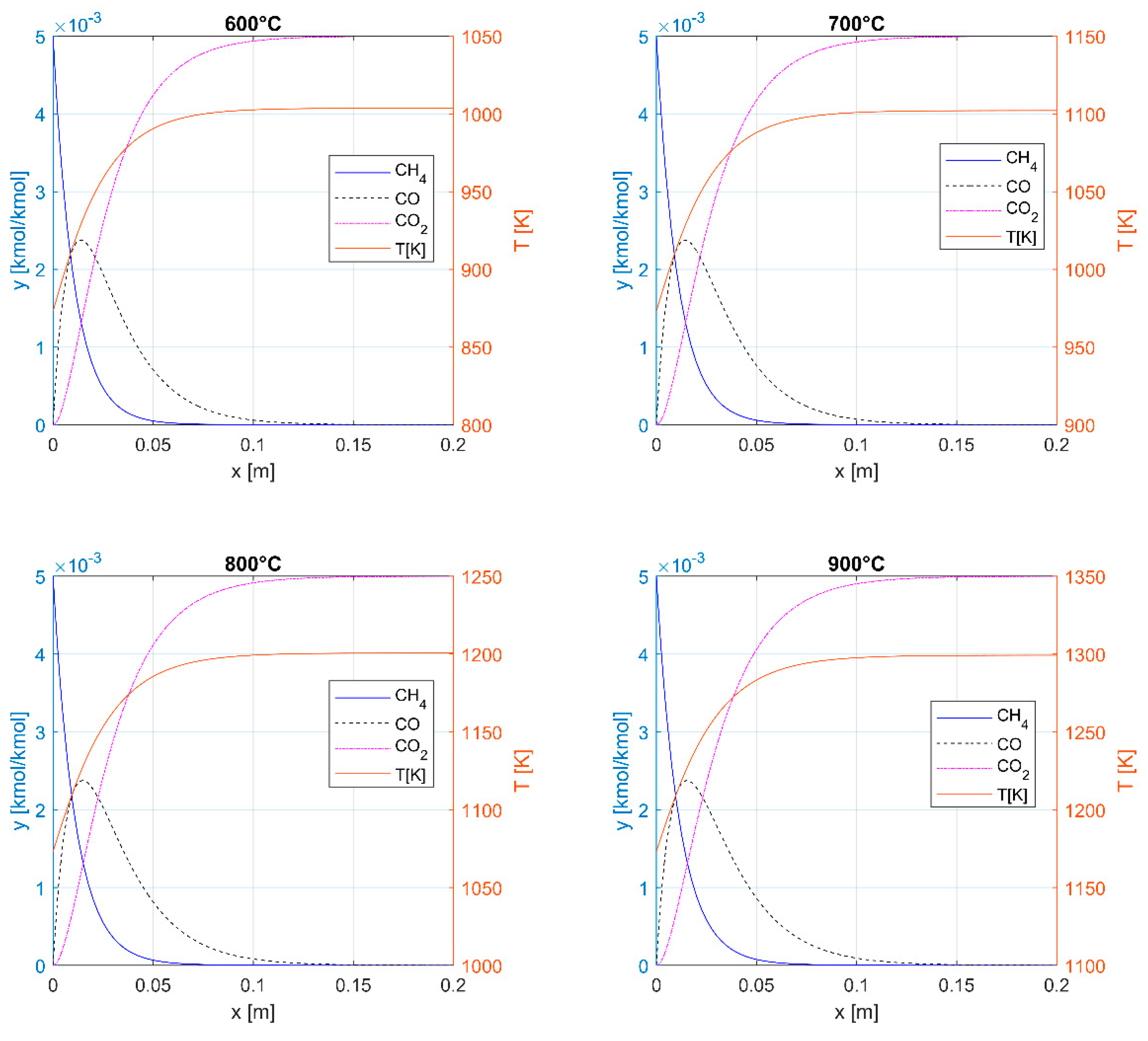
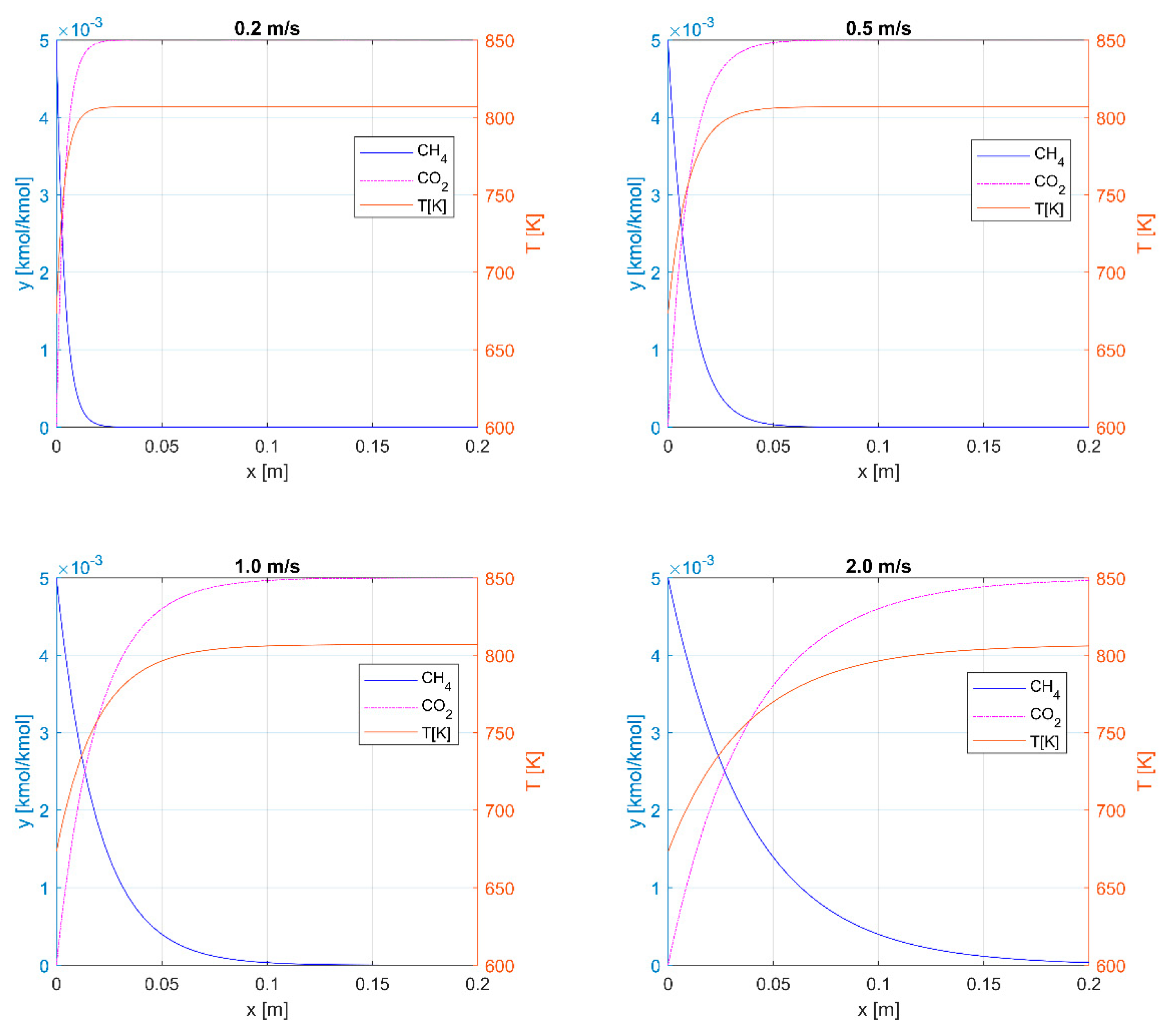
3.1. Thermal Oxidation
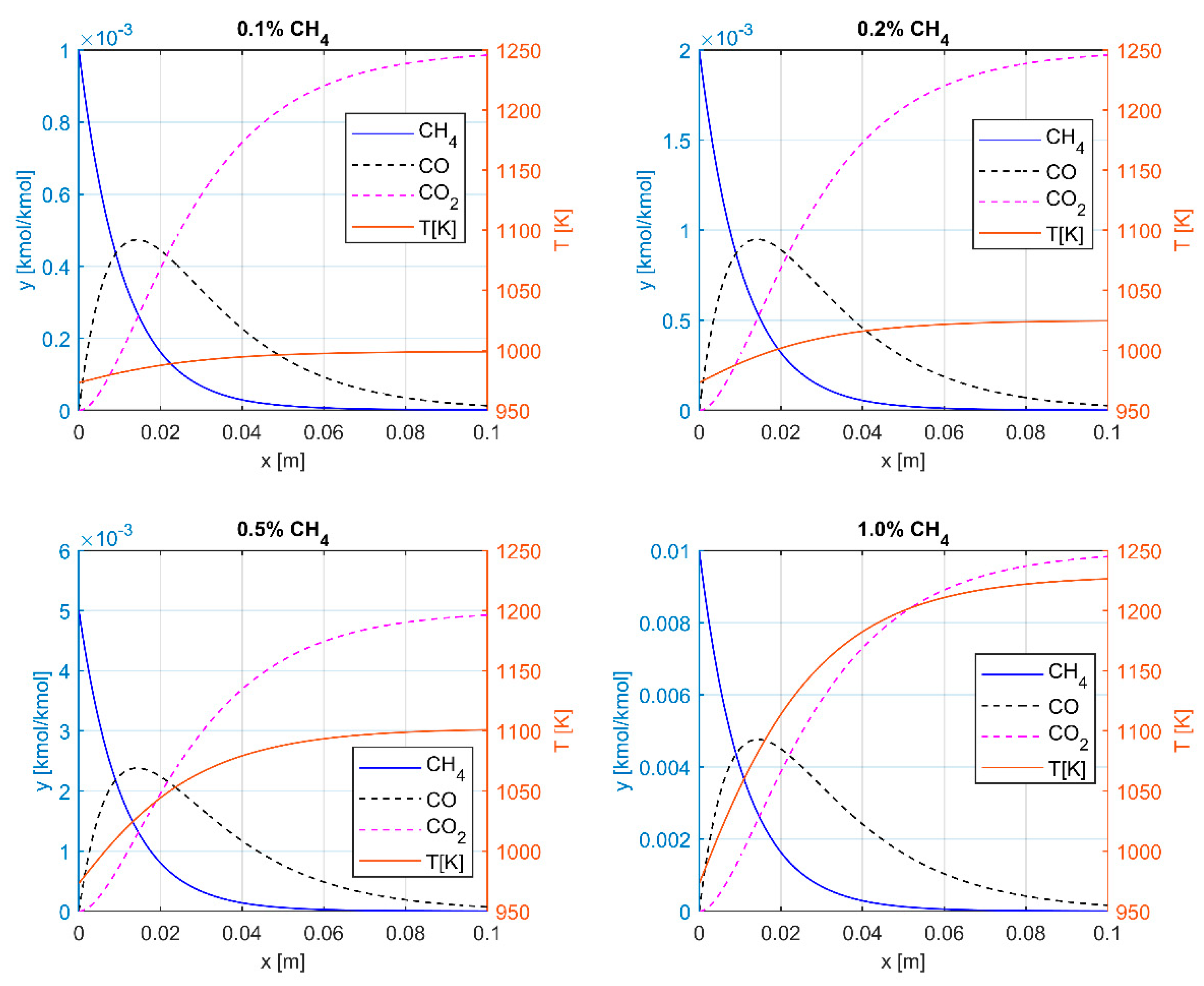
3.2. Catalytic Oxidation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ac | channel cross-sectional surface area, m2 |
| a | monolith specific surface, m2/m3 |
| BQ | exergy, J/kg |
| CA | molar concentration, kmol/m3 |
| cp | specific heat, J/kg K |
| DA | diffusivity, m2/s |
| dH | hydraulic diameter, m |
| kC | mass transfer coefficient, m/s |
| kCr | transfer reaction coefficient, Equation (3), m/s |
| kH | heat losses coefficient, m/s |
| kr | kinetic constant, m/s |
| Nu | Nusselt number |
| P | pressure, Pa |
| Pc | channel perimeter, m |
| Q | heat recovered, J/kg |
| R | gas constant, J/kmol K |
| r | reaction rate, kmol/m2s |
| Sh | Sherwood number |
| T | temperature, K |
| TH | temperature potential of recovered heat, K |
| To | ambient temperature, K |
| w0 | gas superficial velocity, m/s |
| x | axial coordinate, m |
| yA | mole fraction, mol/mol |
| ΔHr | reaction enthalpy, J/kmol |
| α | heat transfer coefficient, W/m2K |
| ε | porosity |
| η | reaction conversion |
| ηC | Carnot efficiency |
| λ | thermal conductivity, W/mK |
| ρ | density, kg/m3 |
| Subscripts | |
| A | methane |
| in | inlet |
| H | external reactor wall |
| S | monolith surface |
| Abbreviations | |
| VAM | ventilation air methane |
| LT | low temperature |
| HT | high temperature |
| LEL | lower explosion limit |
| UEL | upper explosion limit |
| GWP | global warming potential |
| CPSI | channel per square inch |
References
- Regulation of the Polish Minister of Energy 1 of 23 November 2016 on Detailed Requirements for the Operation of Underground Mining Plants (in Polish: Rozporządzenie Ministra Energii 1 z dnia 23 Listopada 2016 r. w Sprawie Szczegółowych Wymagań Dotyczących Prowadzenia Ruchu Podziemnych Zakładów Górniczych), Dz.U.2017.1118. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20170001118 (accessed on 30 January 2025).
- Regulation (EU) 2024/1787 of the European Parliament and of the Council of 13 June 2024 on the Reduction of Methane Emissions in the Energy Sector and Amending Regulation (EU) 2019/942. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32024R1787 (accessed on 30 January 2025).
- Intergovernmental Panel on Climate Change. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report (AR6) of the Intergovernmental Panel on Climate Change. 2021. Available online: https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_FullReport.pdf (accessed on 30 January 2025).
- Zheng, B.; Liu, Y.; Liu, R.; Meng, J.; Mao, M. Experimental Investigation of Flow Resistance in a Coal Mine Ventilation Air Methane Preheated Catalytic Oxidation Reactor. J. Chem. 2015, 2015, 75789. [Google Scholar] [CrossRef]
- Deng, W.; Xiaofeng Xie, X.; Guo, Y.; Hu, G. Breakthroughs in CH4 capture technologies: Key to reducing fugitive methane emissions in the energy sector. Carbon Capture Sci. Technol. 2024, 13, 100316. [Google Scholar] [CrossRef]
- Su, S.; Chen, H.; Teakle, P.; Xue, S. Characteristics of coal mine ventilation air flows. J. Environ. Manag. 2008, 86, 44–62. [Google Scholar] [CrossRef] [PubMed]
- Hinde, P.; Mitchell, I.; Riddell, M. COMET (TM)—A New Ventilation Air Methane (VAM) Abatement Technology. Johns. Matthey Technol. Rev. 2016, 60, 211–221. [Google Scholar] [CrossRef]
- Setiawan, A.; Friggieri, J.; Kennedy, E.M.; Dlugogorski, B.Z.; Stockenhuber, M. Catalytic combustion of ventilation air methane (VAM)—Long term catalyst stability in the presence of water vapour and mine dust. Catal. Sci. Technol. 2014, 4, 1793–1802. [Google Scholar] [CrossRef]
- Yin, J.J.; Su, S.; Yu, X.X.; Bae, J.S.; Jin, Y.G.; Villella, A.; Jara, M.; Ashby, M.; Cunnington, M.; Loney, M. Site Trials and Demonstration of a Novel Pilot Ventilation Air Methane Mitigator. Energy Fuels 2020, 34, 9885–9893. [Google Scholar] [CrossRef]
- Ventilation Air Methane (VAM) Utilization Technologies. Available online: https://www.epa.gov/sites/production/files/2017-01/documents/vam_technologies-1-2017.pdf.pdf (accessed on 30 January 2025).
- Shanxi LuAn Group Gaohe Mine VAM Destruction and Utilization Project. Available online: https://cdm.unfccc.int/Projects/DB/TUEV-RHEIN1352801900.72/view (accessed on 30 January 2025).
- Wang, Z.; Zhou, H.; Peng, X.; Cao, S.; Tang, Z.; Li, K.; Fan, S.; Xue, W.; Yao, G.; Xu, S. A predictive model with time-varying delays employing channel equalization convolutional neural network for NOx emissions in flexible power generation. Energy 2024, 306, 132495. [Google Scholar] [CrossRef]
- Lundberg, D.J.; Kim, J.; Parviz, D.; Strano, M.S. Mitigation of ventilation air methane (VAM) using novel methanotrophic coating materials: A technical analysis. Environ. Res. Lett. 2023, 18, 114039. [Google Scholar] [CrossRef]
- Swolkień, J. Polish underground coal mines as point sources of methane emission to the atmosphere. Int. J. Greenh. Gas Control 2020, 94, 102921. [Google Scholar] [CrossRef]
- Mao, M.M.; Shi, J.R.; Liu, Y.Q.; Gao, M.; Chen, Q. Experimental investigation on control of temperature asymmetry and nonuniformity in a pilot scale thermal flow reversal reactor. Appl. Therm. Eng. 2020, 175, 115375. [Google Scholar] [CrossRef]
- Zheng, B.; Liu, Y.Q.; Sun, P.; Meng, J.; Liu, R.X. Dehydrogenation characteristics of lean methane in a thermal reverse-flow reactor. Int. J. Hydrogen Energy 2019, 44, 5137–5142. [Google Scholar] [CrossRef]
- Gao, P.F.; Gou, X.L. Experimental Research on the Thermal Oxidation of Ventilation Air Methane in a Thermal Reverse Flow Reactor. Acs Omega 2019, 4, 14886–14894. [Google Scholar] [CrossRef] [PubMed]
- Marin, P.; Vega, A.; Diez, F.V.; Ordonez, S. Control of regenerative catalytic oxidisers used in coal mine ventilation air methane exploitation. Process Saf. Environ. Prot. 2020, 134, 333–342. [Google Scholar] [CrossRef]
- Wang, Y.K.; Man, C.B.; Che, D.F. Catalytic Combustion of Ventilation Air Methane in a Reverse-Flow Reactor. Energy Fuels 2010, 24, 4841–4848. [Google Scholar] [CrossRef]
- Salomons, S.; Hayes, R.E.; Poirier, M.; Sapoundjiev, H. Flow reversal reactor for the catalytic combustion of lean methane mixtures. Catal. Today 2003, 83, 59–69. [Google Scholar] [CrossRef]
- Mundra, I.; Lockley, A. Emergent methane mitigation and removal approaches: A review. Atmos. Environ. X 2024, 21, 100223. [Google Scholar] [CrossRef]
- Gosiewski, K.; Pawlaczyk, A. Catalytic or thermal reversed flow combustion of coal mine ventilation air methane: What is better choice and when? Chem. Eng. J. 2014, 238, 78–85. [Google Scholar] [CrossRef]
- Pawlaczyk, A.; Gosiewski, K. Combustion of lean methane-air mixtures in monolith beds: Kinetic studies in low and high temperatures. Chem. Eng. J. 2015, 282, 29–36. [Google Scholar] [CrossRef]
- Gancarczyk, A.; Iwaniszyn, M.; Piątek, M.; Korpyś, M.; Sindera, K.; Jodłowski, P.J.; Łojewska, J.; Kołodziej, A. Catalytic Combustion of Low-Concentration Methane on Structured Catalyst Supports. Ind. Eng. Chem. Res. 2018, 57, 10281–10291. [Google Scholar] [CrossRef]
- Clarke, M.; Seddon, D. Ventilation Air Methane (VAM) Destruction the New Challenge to the Underground Coalmining Industry. 2011. Available online: https://api.semanticscholar.org/CorpusID:201072295 (accessed on 30 January 2025).
- Ordonez, S.; Hurtado, P.; Sastre, H.; Diez, F.V. Methane catalytic combustion over Pd/Al2O3 in presence of sulphur dioxide: Development of a deactivation model. Appl. Catal. A-Gen. 2004, 259, 41–48. [Google Scholar] [CrossRef]
- Shah, K.; Moghtaderi, B.; Doroodchi, E.; Sandford, J. A feasibility study on a novel stone dust looping process for abatement of ventilation air methane. Fuel Process. Technol. 2015, 140, 285–296. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Gao, D.; Sun, T.; Zhang, C.; Wang, S. Influence of metal oxides on the performance of Pd/Al2O3 catalysts for methane combustion under lean-fuel conditions. Fuel Process. Technol. 2013, 111, 55–61. [Google Scholar] [CrossRef]
- Setiawan, A.; Kennedy, E.M.; Dlugogorski, B.Z.; Adesina, A.A.; Stockenhuber, M. The stability of Co3O4, Fe2O3, Au/Co3O4 and Au/Fe2O3 catalysts in the catalytic combustion of lean methane mixtures in the presence of water. Catal. Today 2015, 258, 276–283. [Google Scholar] [CrossRef]
- Haojie, G.; Zhongqing, Y.; Li, Z.; Yunfei, Y.; Mingnv, G. Low-concentration methane combustion over a Cu/g-Al2O3 catalyst: Effects of water. RSC Adv. 2015, 5, 18915–18921. [Google Scholar]
- Hosseiniamoli, H.; Setiawan, A.; Adesina, A.A.; Kennedy, E.M.; Stockenhuber, M. The stability of Pd/TS-1 and Pd/silicalite-1 for catalytic oxidation of methane—Understanding the role of titanium. Catal. Sci. Technol. 2020, 10, 1193–1204. [Google Scholar] [CrossRef]
- Coney, C.; Stere, C.; Millington, P.; Raj, A.; Wilkinson, S.; Caracotsios, M.; McCullough, G.; Hardacre, C.; Morgan, K.; Thompsett, D.; et al. Spatially-resolved investigation of the water inhibition of methane oxidation over palladium. Catal. Sci. Technol. 2020, 10, 1858–1874. [Google Scholar] [CrossRef]
- Fernandez, J.; Marin, P.; Diez, F.V.; Ordonez, S. Experimental demonstration and modelling of an adsorption-enhanced reverse flow reactor for the catalytic combustion of coal mine ventilation air methane. Chem. Eng. J. 2015, 279, 198–206. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering; John Wiley & Sons, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Iwaniszyn, M.; Korpyś, M.; Rotkegel, A.; Ziobrowski, Z.; Kołodziej, A.; Sindera, K.; Suwak, M.; Gancarczyk, A. Innovative Fixed-Bed Reactor Integrated with Heat Transfer System for Lean Methane Mixture Removal. Energies 2024, 17, 4408. [Google Scholar] [CrossRef]
- Kołodziej, A.; Łojewska, J.; Tyczkowski, J.; Jodłowski, P.; Redzynia, W.; Iwaniszyn, M.; Zapotoczny, S.; Kuśtrowski, P. Coupled engineering and chemical approach to the design of a catalytic structured reactor for combustion of VOCs: Cobalt oxide catalyst on knitted wire gauzes. Chem. Eng. J. 2012, 200, 329–337. [Google Scholar] [CrossRef]
- Gancarczyk, A.; Sindera, K.; Iwaniszyn, M.; Piątek, M.; Macek, W.; Jodłowski, P.J.; Wroński, S.; Sitarz, M.; Łojewska, J.; Kołodziej, A. Metal Foams as Novel Catalyst Support in Environmental Processes. Catalysts 2019, 9, 587. [Google Scholar] [CrossRef]
- Cybulski, A.; Moulijn, J.A. Monoliths in heterogeneous catalysis. Catal. Rev. Sci. Eng. 1994, 36, 179–270. [Google Scholar] [CrossRef]
- Williams, J.L. Monolith structures, materials, properties and uses. Catal. Today 2001, 69, 3–9. [Google Scholar] [CrossRef]
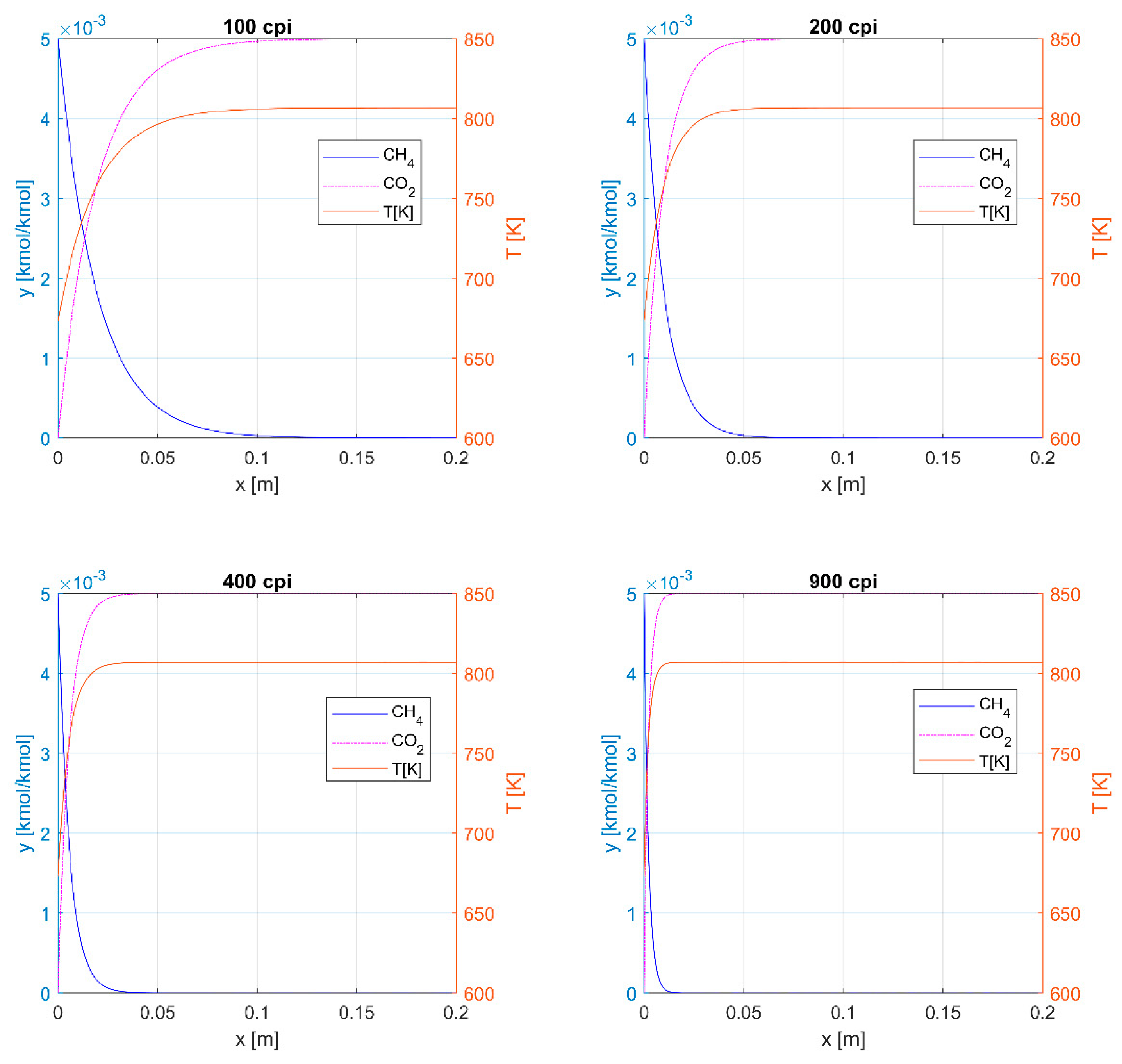
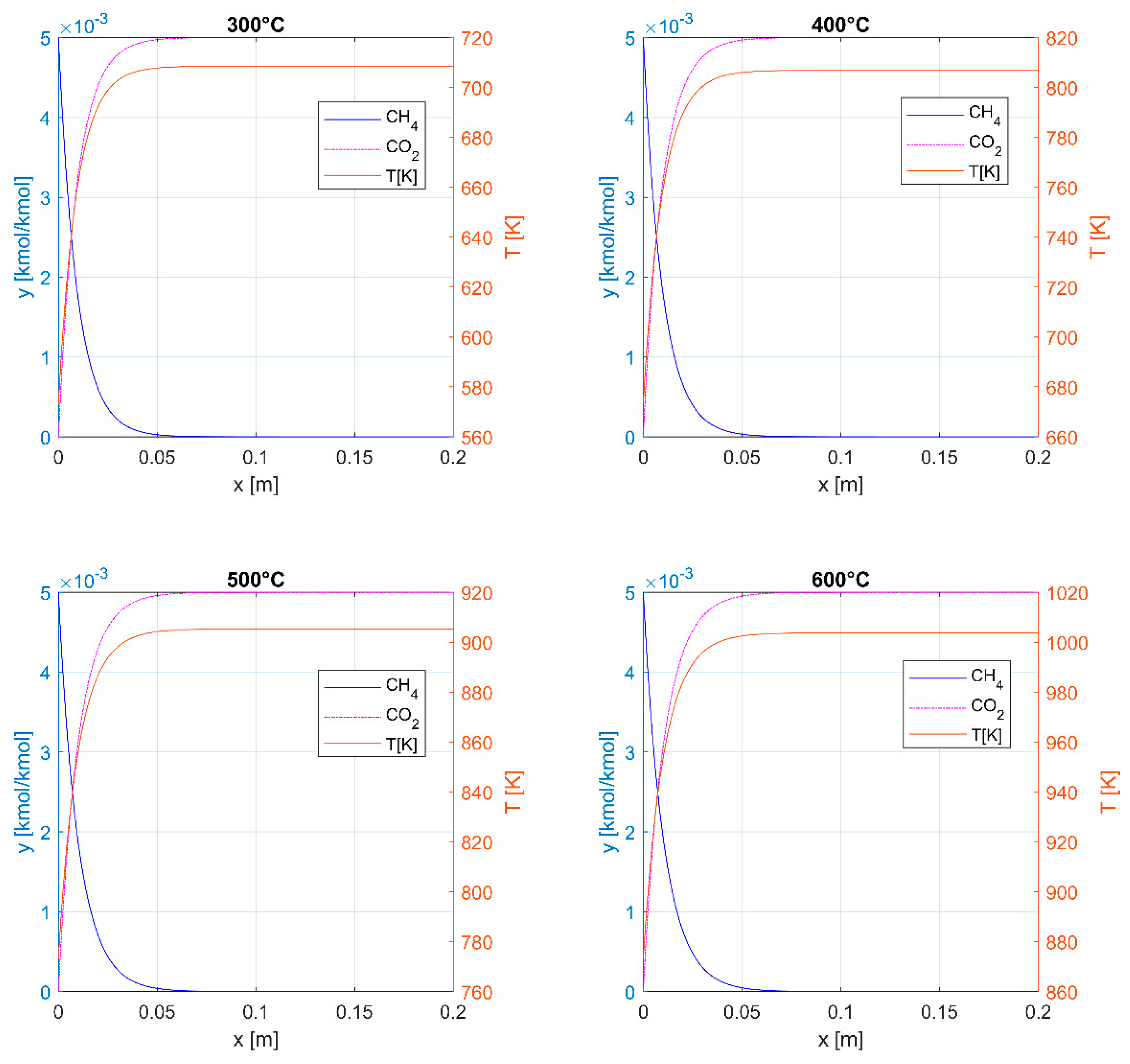
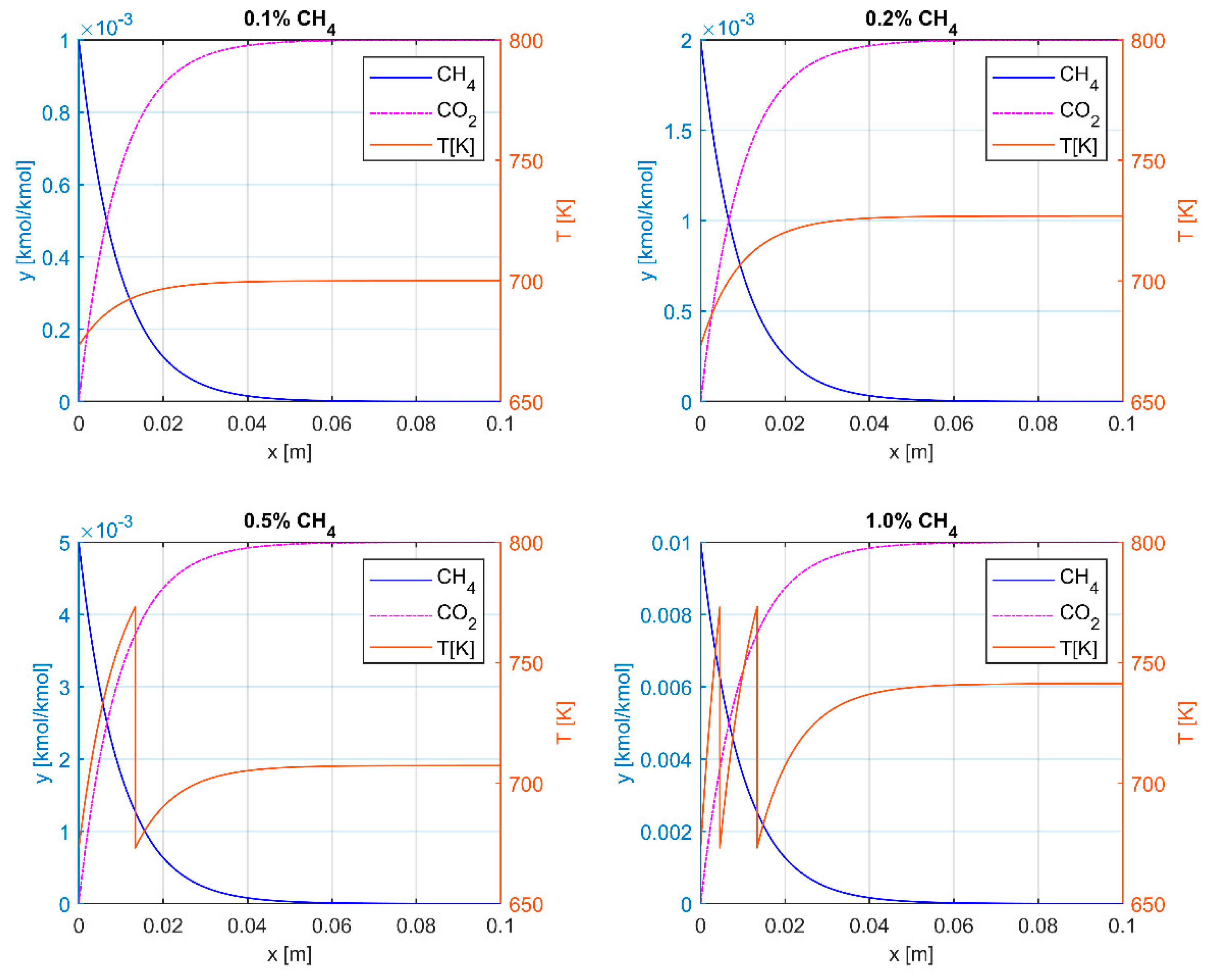
| CPSI | ε | a, m2m−3 | dH, mm |
|---|---|---|---|
| 100 | 0.72 | 1339 | 2.15 |
| 200 | 0.73 | 1898 | 1.54 |
| 400 | 0.85 | 2709 | 1.26 |
| 900 | 0.83 | 4311 | 0.77 |
| yin [% CH4] | TH [K] | Q [kJ/kg] | BQ [kJ/kg] | ηC |
|---|---|---|---|---|
| 0.1 | 999.1 | 28.7 | 20.3 | 0.71 |
| 0.2 | 1025 | 57.4 | 41.0 | 0.71 |
| 0.5 | 1102.2 | 143.2 | 105.1 | 0.73 |
| 1 | 1229.2 | 286.1 | 217.9 | 0.76 |
| Component | Monolith | Method | |||
|---|---|---|---|---|---|
| 100 | 200 | 400 | 900 | ||
| CH4 | 0.12 | 0.06 | 0.04 | 0.02 | Thermal |
| CO | >0.2 | 0.12 | 0.07 | 0.03 | Thermal |
| CH4 | 0.10 | 0.055 | 0.03 | 0.02 | Catalytic |
| CH4 | 0.12 | 0.06 | 0.04 | 0.02 | Thermal |
| yin [% CH4] | TH [K] | Q [kJ/kg] | BQ [kJ/kg] | ηC |
|---|---|---|---|---|
| 0.1 outlet | 700.1 | 28.7 | 16.8 | 0.58 |
| 0.2 outlet | 726.9 | 57.4 | 34.3 | 0.60 |
| 0.5 step 1 | 773 | 106.7 | 66.3 | 0.62 |
| 0.5 outlet | 707.3 | 36.5 | 21.4 | 0.59 |
| 1.0 step 1 | 773 | 106.7 | 66.3 | 0.62 |
| 1.0 step 2 | 773 | 106.7 | 66.3 | 0.62 |
| 1.0 outlet | 741.3 | 72.7 | 44.0 | 0.60 |
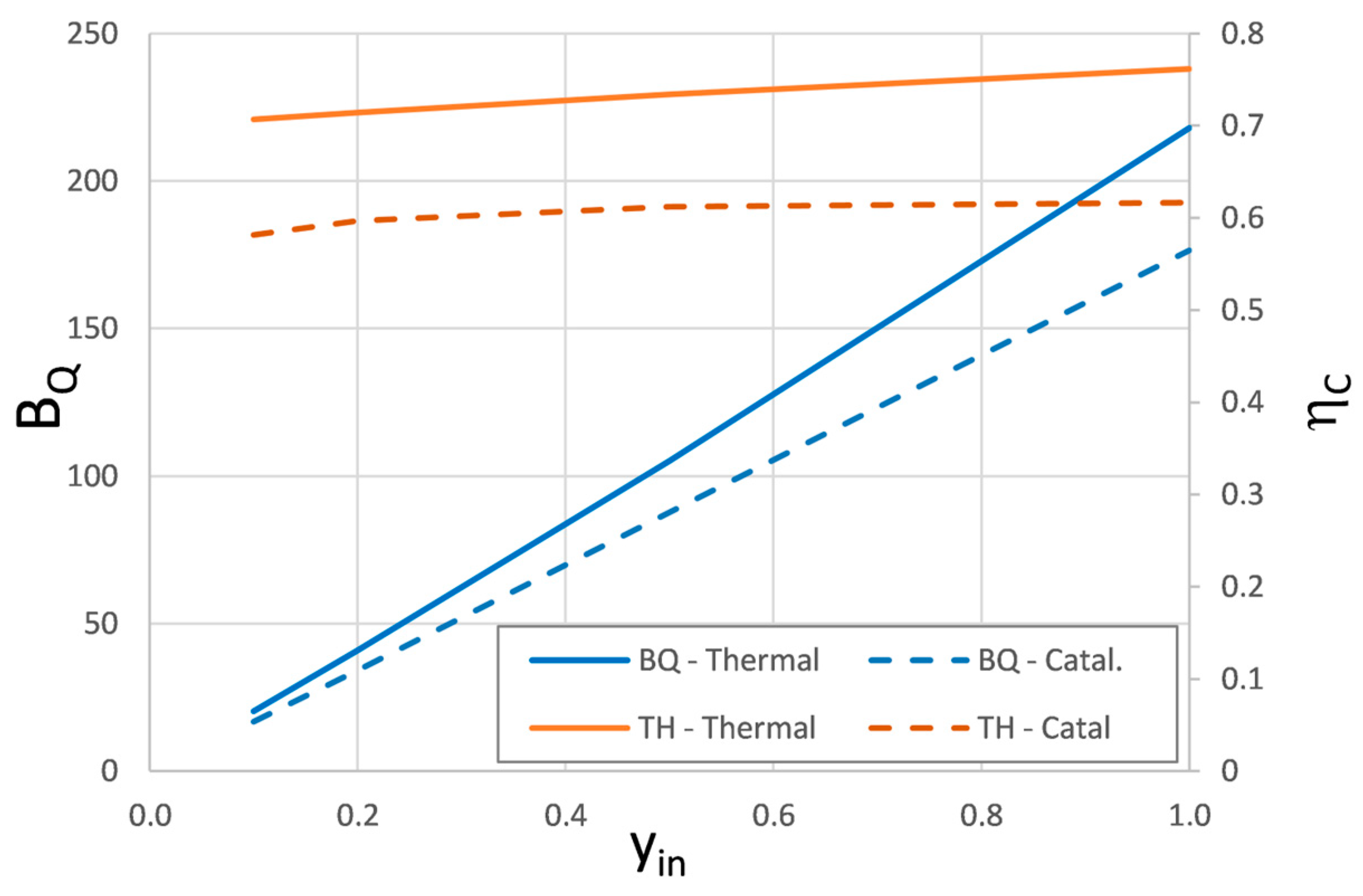
| yin, % | Thermal Process | Catalytic Process | BQ-Therm/BQ-Catal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| TH | Q | BQ | ηC | TH * | Q | BQ | ηC ** | ||
| 0.1 | 999.1 | 28.7 | 20.3 | 0.71 | 700.1 | 28.7 | 16.8 | 0.58 | 1.21 |
| 0.2 | 1025 | 57.4 | 41.0 | 0.71 | 726.9 | 57.4 | 34.3 | 0.60 | 1.20 |
| 0.5 | 1102.2 | 143.2 | 105.1 | 0.73 | 707.3 | 143.2 | 87.7 | 0.61 | 1.20 |
| 1 | 1229.2 | 286.1 | 217.9 | 0.76 | 741.3 | 286.1 | 176.6 | 0.62 | 1.23 |
| Thermal Process | Catalytic Process | |||||||
|---|---|---|---|---|---|---|---|---|
| Monolith, cpsi | 100 | 200 | 400 | 900 | 100 | 200 | 400 | 900 |
| Length [m] to ηCH4 = 95% | 0.12 | 0.06 | 0.04 | 0.02 | 0.10 | 0.055 | 0.03 | 0.02 |
| Length [m] to ηCH4+CO = 99.5% | >0.2 | 0.12 | 0.07 | 0.03 | 0.10 | 0.055 | 0.03 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwaniszyn, M.; Pawlaczyk-Kurek, A.; Kołodziej, A.; Rotkegel, A.; Tańczyk, M.; Skiba, J.; Hildebrandt, R.; Bałaga, D.; Siegmund, M.; Gancarczyk, A. Ventilation Air Methane (VAM) Utilisation: Comparison of the Thermal and Catalytic Oxidation Processes. Energies 2025, 18, 1428. https://doi.org/10.3390/en18061428
Iwaniszyn M, Pawlaczyk-Kurek A, Kołodziej A, Rotkegel A, Tańczyk M, Skiba J, Hildebrandt R, Bałaga D, Siegmund M, Gancarczyk A. Ventilation Air Methane (VAM) Utilisation: Comparison of the Thermal and Catalytic Oxidation Processes. Energies. 2025; 18(6):1428. https://doi.org/10.3390/en18061428
Chicago/Turabian StyleIwaniszyn, Marzena, Anna Pawlaczyk-Kurek, Andrzej Kołodziej, Adam Rotkegel, Marek Tańczyk, Jacek Skiba, Robert Hildebrandt, Dominik Bałaga, Michał Siegmund, and Anna Gancarczyk. 2025. "Ventilation Air Methane (VAM) Utilisation: Comparison of the Thermal and Catalytic Oxidation Processes" Energies 18, no. 6: 1428. https://doi.org/10.3390/en18061428
APA StyleIwaniszyn, M., Pawlaczyk-Kurek, A., Kołodziej, A., Rotkegel, A., Tańczyk, M., Skiba, J., Hildebrandt, R., Bałaga, D., Siegmund, M., & Gancarczyk, A. (2025). Ventilation Air Methane (VAM) Utilisation: Comparison of the Thermal and Catalytic Oxidation Processes. Energies, 18(6), 1428. https://doi.org/10.3390/en18061428







