A Novel FDIA Model for Virtual Power Plant Cyber–Physical Systems Based on Network Topology and DG Outputs
Abstract
:1. Introduction
1.1. Motivation
- How to develop a cyber-attack model that considers the emerging background of PPPNs? How to implement such an attack that considers the coordination between VPPs and the distribution system operator (DSO)?
- How to design the cyber-attack process without being detected by the control center? What are the economic and security impacts of this attack on the joint operation of VPP aggregators and the distribution power system?
1.2. Literature Review
1.2.1. Attack Targets
1.2.2. Solving Strategy of Cyber-Attack Models
1.2.3. Attack Scenarios of PPPNs
- The communication heterogeneity between private power and public VPP networks is always ignored, and the impact analysis is unreasonable and even incorrect when cyberattacks take place on PPPNs.
- Network topology and DG outputs are critical data for VPPs, but existing FDIA models only consider launching cyber-attacks from a single aspect.
- To the best of the authors’ knowledge, there exists no effective optimization framework of FDIA designed for balancing computation accuracy and efficiency.
1.3. Contributions
- Developing a new cyberattack framework considering the scenario of PPPN operations and analyzing the cyber vulnerability of the DSO and VPP aggregators.
- Proposing a topology–DG joint attack model where an attacker compromises the data of DG outputs and network topology information by, respectively, injecting the bad data into the PPPNs.
- Proposing a hybrid optimization framework that realizes the critical solution functions by inner-layer second-order cone programming (SOCP) and outer-layer particle swarm optimizer (PSO).
1.4. Paper Organization
2. Communication, State Estimation, and NTP Assumptions
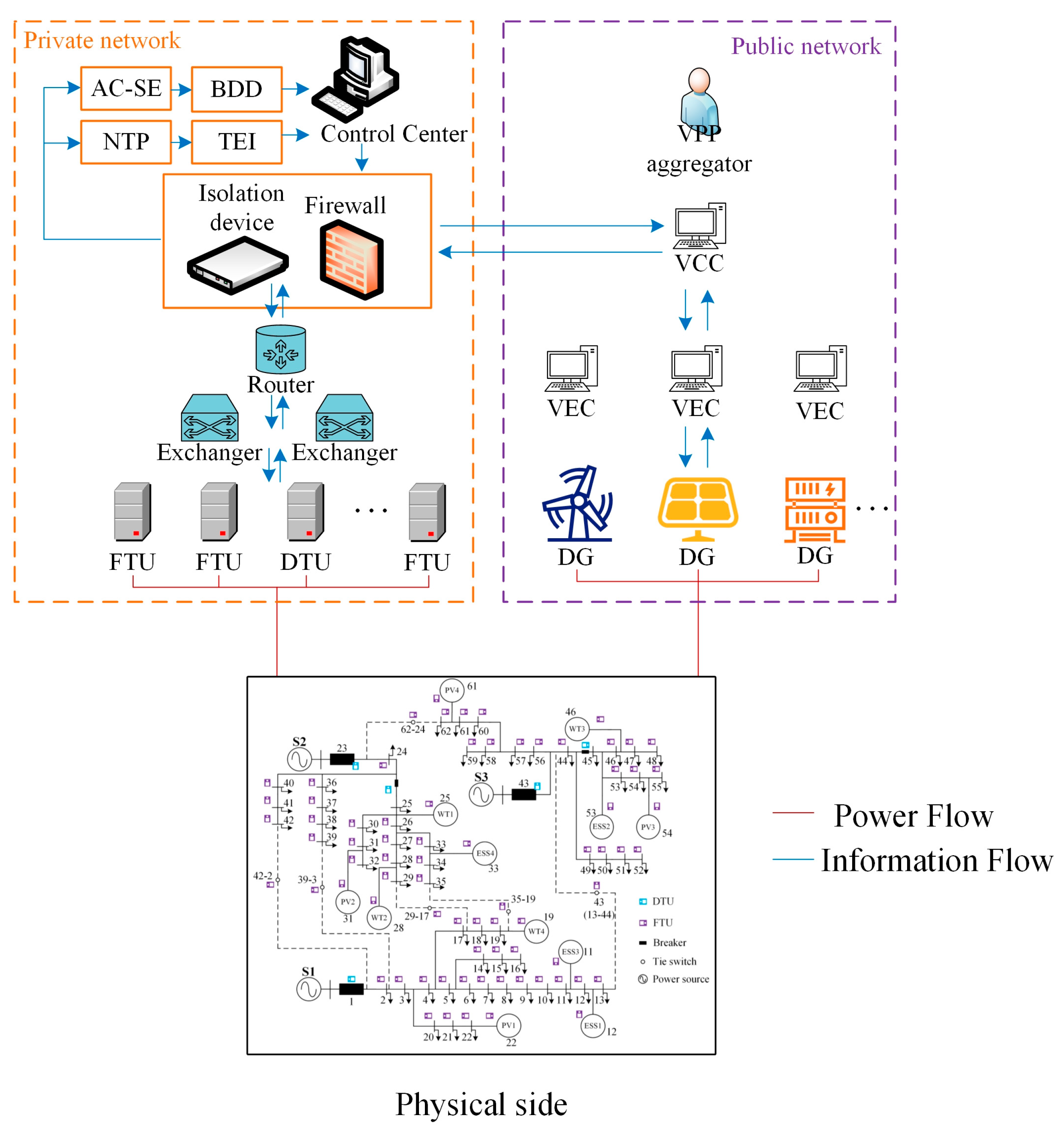
2.1. Communication Architecture
- The attacker masters the principle of operating the power system and has knowledge of the target power grid. Furthermore, the attacker has access to the public–private power network and can manipulate any meter measurement in the target power grid. This assumption is consistent with other studies on FDIAs.
- For the simplicity and clarity of this work, a powerful DSO is created to handle the dispatching of both the power grid and VPP’s submissive DGs. Despite a DSO having no authority to directly give instructions to the DGs within a VPP in practice, both the DSO and the VPP aggregator have the same interests in facing cyber-attacks.
2.2. State Estimation Model and BDD Principle
2.3. NTP and TEI
3. Topology–DG Joint Attack Model of Distribution-VPP CPPS
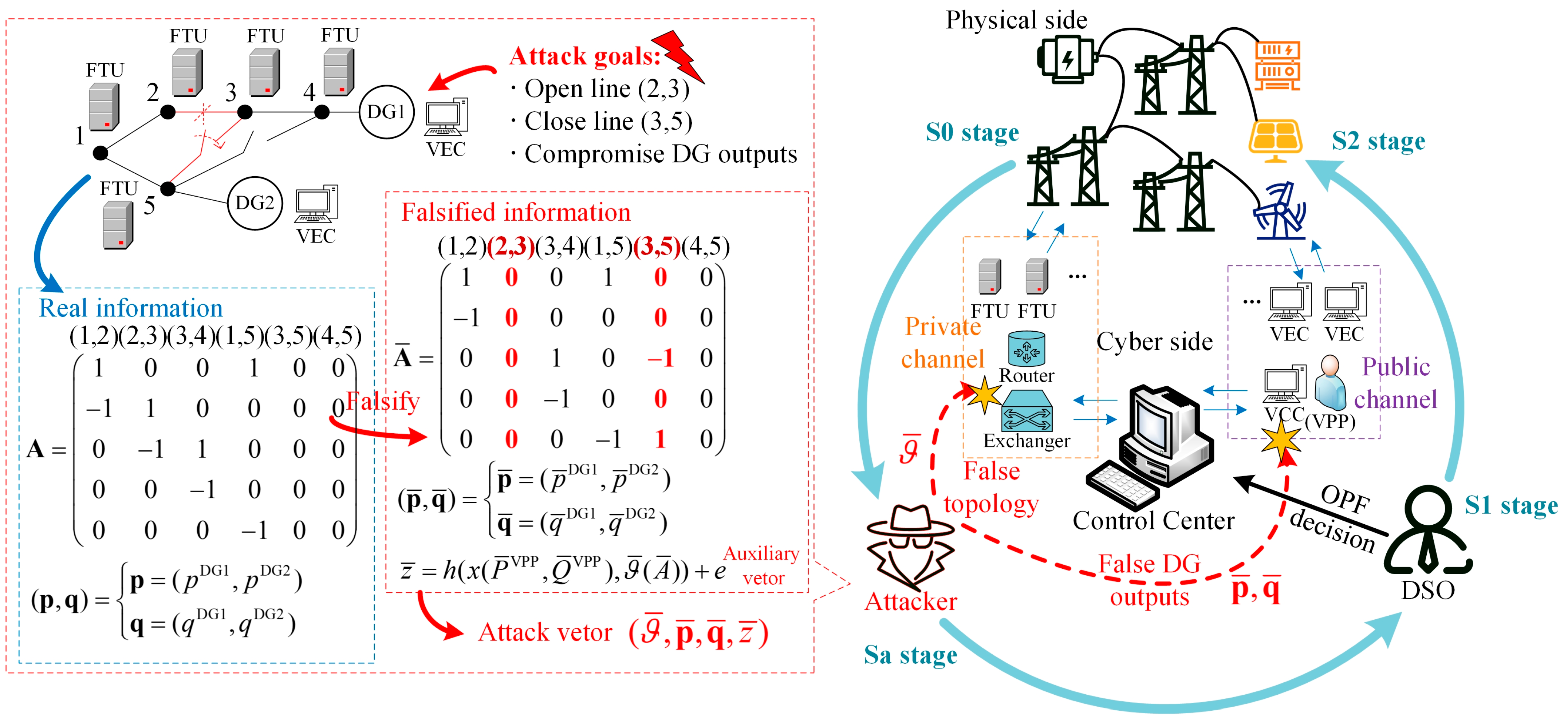
3.1. Launching a Topology–DG Attack
- S0, Pre-attack stage: The distribution system is in the normal operation state following the optimal dispatching order, and only tolerable measurement errors exist between the physical state and the estimated state in cyberspace.
- Sa, Attack stage: The attacker intrudes into VECs with falsified DG output data via the channel in the public network while the connection information and the power flow data from terminal devices are also altered.
- S1, Decision stage: The tampered data bypasses the BDD and TEI, and the incorrect data enter the control center. DSO recalculates the optimal power flow based on the data and sends new instructions to the VPP aggregator.
- S2, Damage stage: the VPP aggregator readjusts the outputs of the submissive DGs according to the new commands, and the distribution system reaches a new operation state after the attack.
3.2. Constructing Attack Vector
3.3. Topology–DG Attack Model
3.3.1. Attack Objectives
3.3.2. Attack Constraints
3.3.3. Optimal Dispatching Model
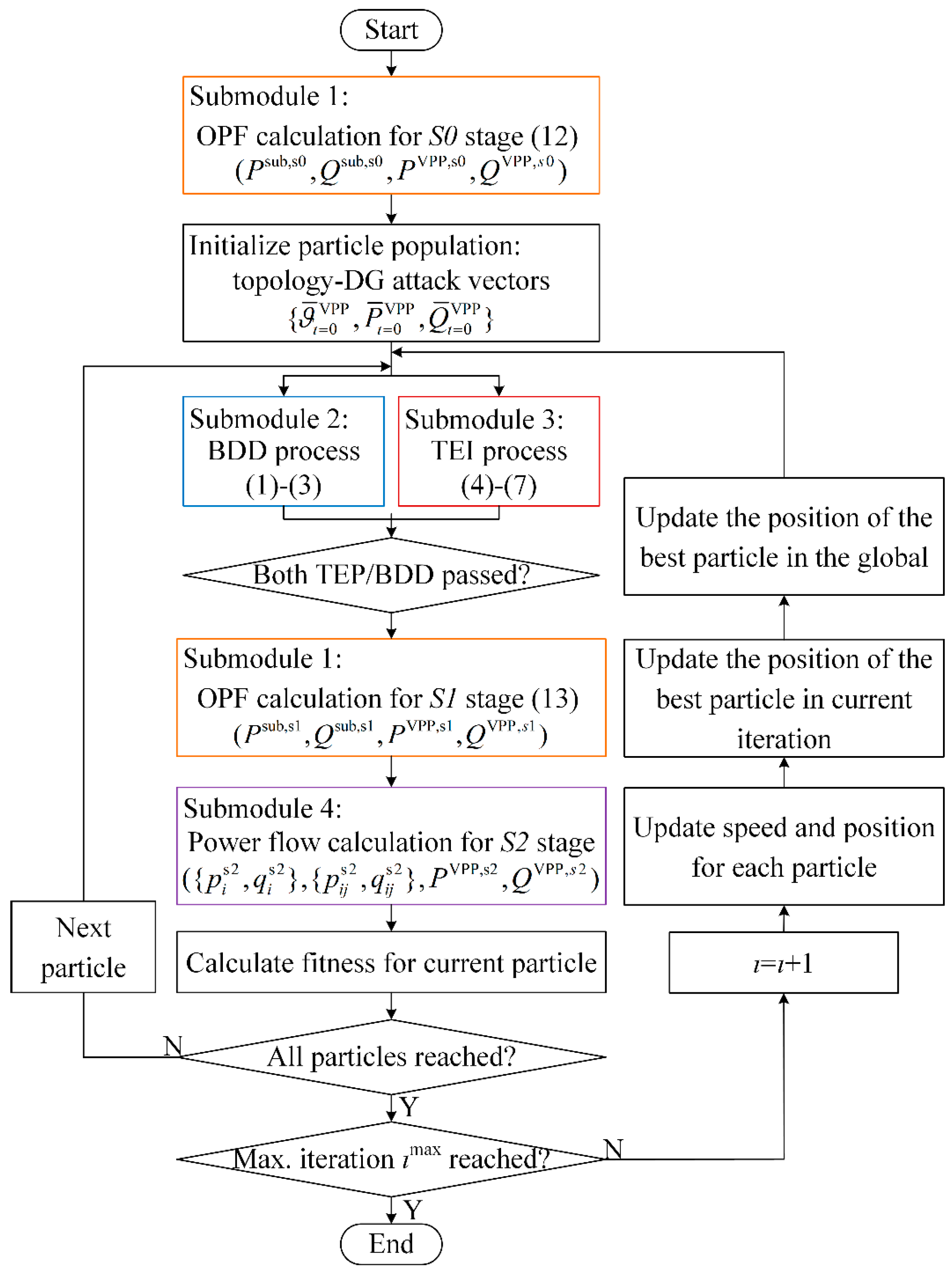
4. Hybrid Solution Method
- Initializing population: Preparing the operation data for stage S0 and initializing the population in the form of an individual set of responses composed of a group of attack variables.
- Bypassing BDD and TEI: Generating noised attack vectors based on each particle’s information. The BDD and the TEI submodules are simulated to decide whether the attack vector of each particle is allowed to enter the control center. If the attack vector passes both detections, then it enters the control center; otherwise, the particle is eliminated.
- Calculating new dispatch instructions: Simulating the dispatch decision for the misguided DSO at stage S1.
- Defining damages on the physical system: Calculating the new power flow for the physical distribution system with the misguided instructions and the fitness of each individual is calculated.
- Updating populations: Updating the position and velocity for each PSO particle and updating the information of the best particle and starting the solving process of the next iteration until the optimization process reaches the maximum iterating number.
5. Case Study
5.1. Performance Evaluation
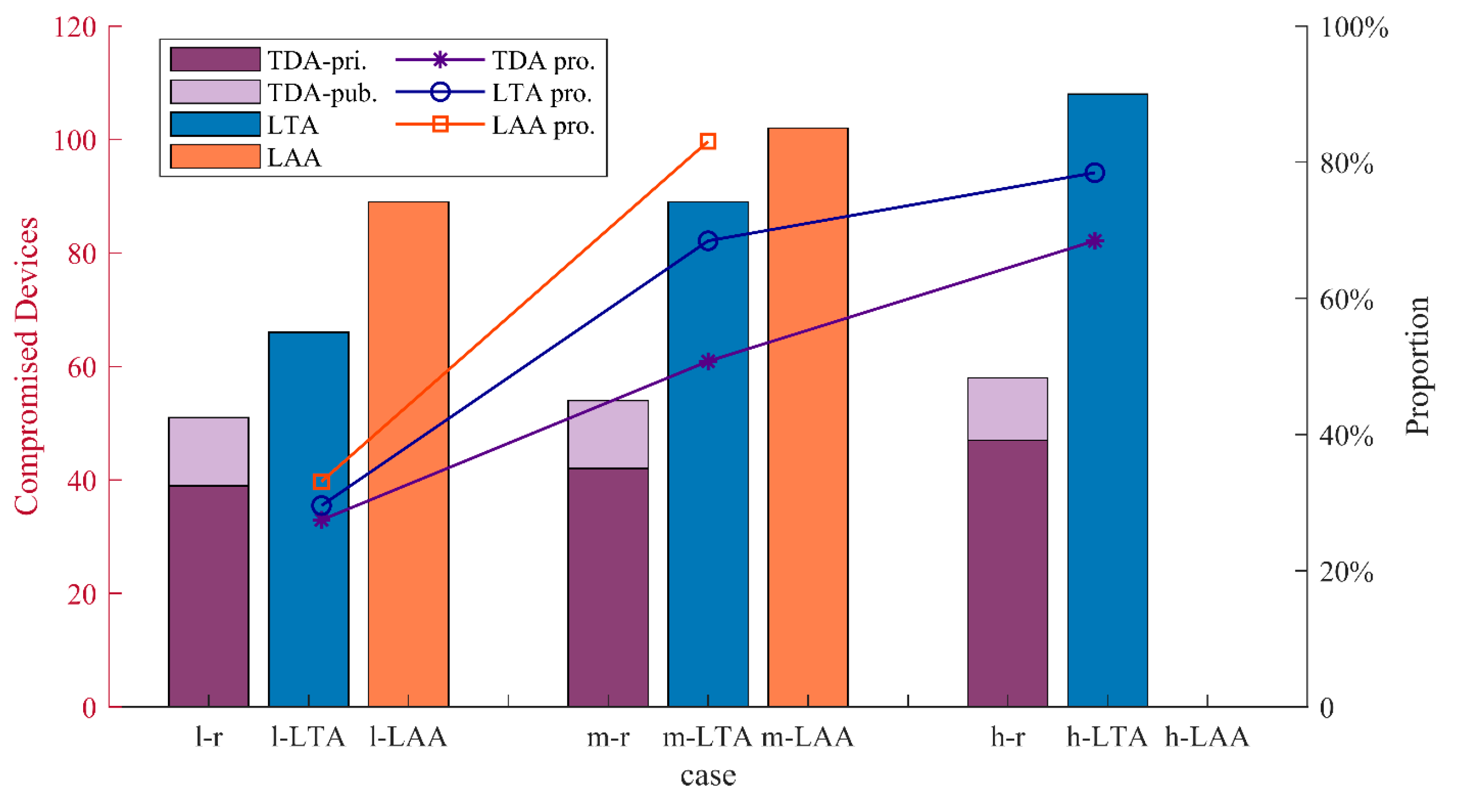
5.1.1. Objective-1: Minimizing the Attack Resource
5.1.2. Objective-2: Minimizing the Revenue of VPP Aggregator
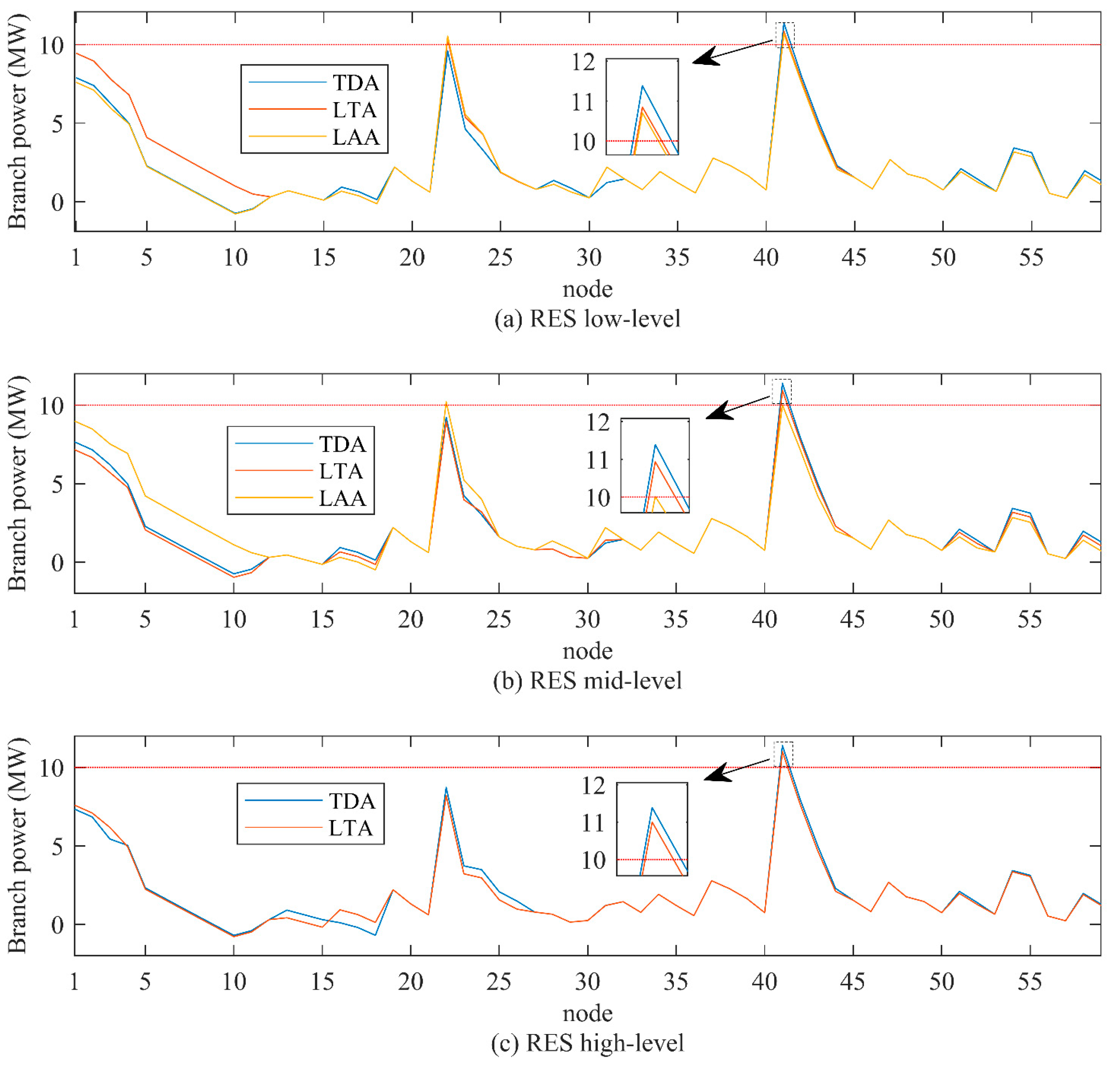
5.1.3. Objective-3: Maximizing the Overload Rate of One Feeder
5.2. Comparative Analysis
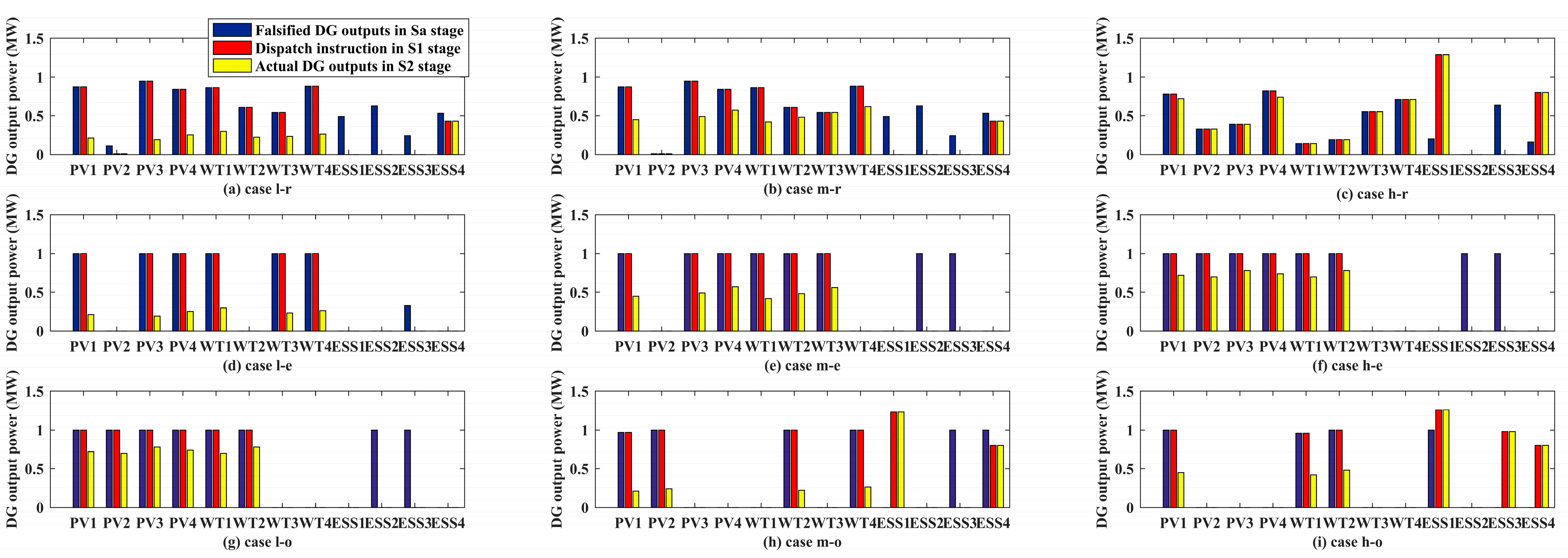
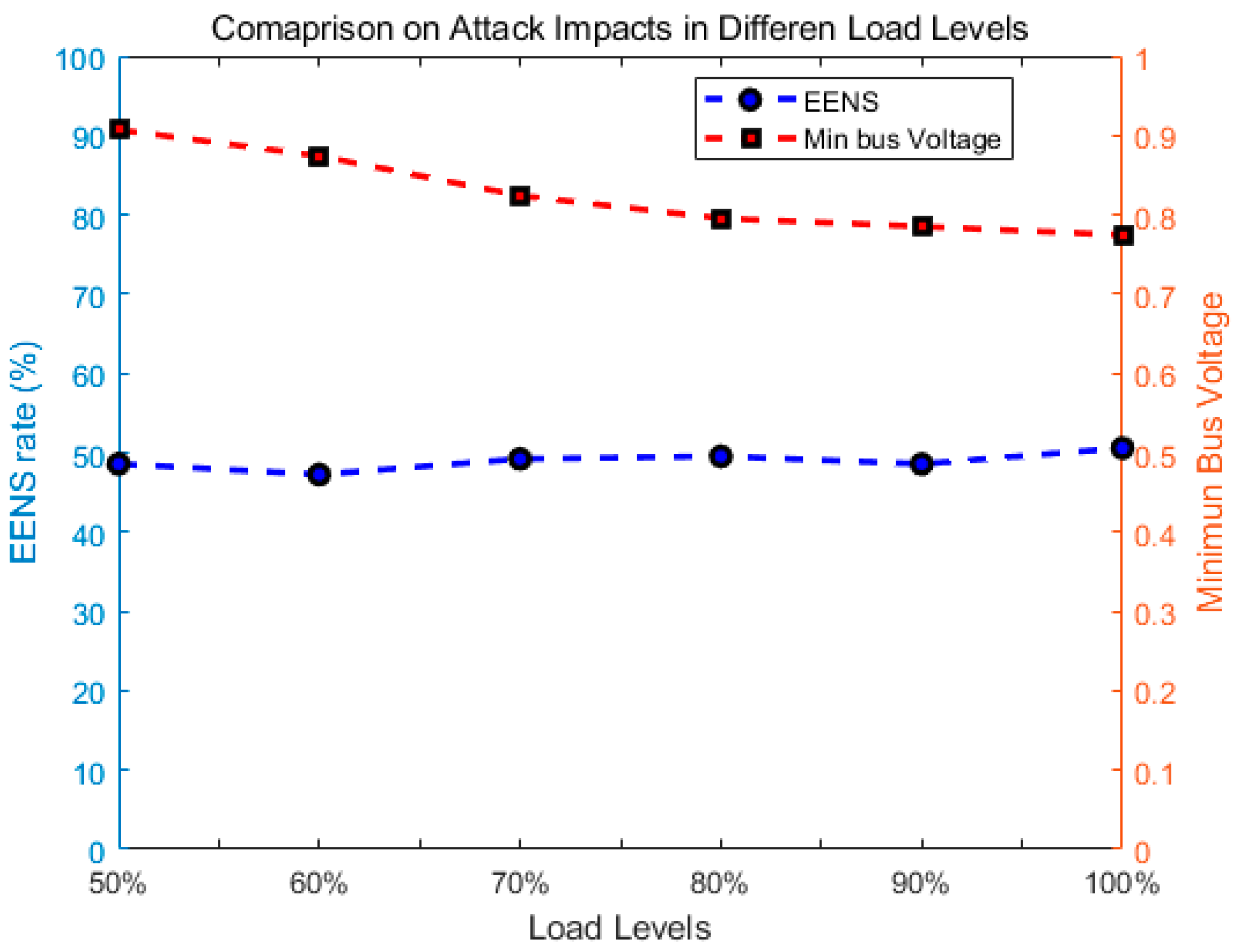
5.3. Robustness Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BDD | Bad Data Detection |
| CPPS | Cyber–Physical Power System |
| DG | Distributed Generator |
| DSO | Distribution System Operator |
| DTU | Distribution Terminal Unit |
| EMS | Energy Management System |
| ESS | Energy Storage System |
| FDIA | False Data Injection Attack |
| FTU | Feeder Terminal Unit |
| TDA | Topology-Distributed-Generator Attack |
| LAA | Load-Altering Attack |
| LTA | Line-Switch Topology Attack |
| MINLP | Mixed Integer Non-Linear Problem |
| MITM | Man-in-the-Middle |
| NTP | Network Topology Processing |
| PPPN | Public–Private Power Network |
| PSO | Particle Swarm Optimizer |
| RES | Renewable Energy Sources |
| SCADA | Supervisory Control and Data Acquisition |
| SOCP | Second-Order Cone Programming |
| TEI | Topology Error Identification |
| VCC | VPP Cloud Service Center |
| VEC | VPP Edge Service Center |
| VPP | Virtual Power Plant |
References
- Wang, Q.; Tai, W.; Tang, Y.; Ni, M. Review of the false data injection attack against the cyber-physical power system. IET Cyber-Phys. Syst. Theory Appl. 2019, 4, 101–107. [Google Scholar]
- Amin, M.; El-Sousy, F.F.M.; Aziz, G.A.A.; Gaber, K.; Mohammed, A. CPS Attacks Mitigation Approaches on Power Electronic Systems with Security Challenges for Smart Grid Applications: A Review. IEEE Access 2021, 9, 38571–38601. [Google Scholar]
- Hasan, M.K.; Habib, A.K.M.A.; Shukur, Z.; Ibrahim, F.; Islam, S.; Razzaque, M.A. Review on cyber-physical and cyber-security system in smart grid: Standards, protocols, constraints, and recommendations. J. Netw. Comput. Appl. 2023, 209, 103540. [Google Scholar]
- Liang, G.; Weller, S.R.; Zhao, J.; Luo, F.; Dong, Z.Y. The 2015 Ukraine Blackout: Implications for False Data Injection Attacks. IEEE Trans. Power Syst. 2017, 32, 3317–3318. [Google Scholar]
- Xin, B.; Li, M.; He, J.; He, J.; Sun, W. Research on Security Defense System of New Power System. Proc. CSEE 2023, 43, 5723–5731. [Google Scholar]
- Chen, J.; Lu, B.; Feng, Y.; Li, X. Value Co-production Model and Mechanism of Regional Energy Internet Ecosystem Under the Concept of Sharing. Proc. CSEE 2022, 42, 8103–8116. [Google Scholar]
- Tuyen, N.D.; Quan, N.S.; Linh, V.B.; Tuyen, V.; Fujita, G. A Comprehensive Review of Cybersecurity in Inverter-Based Smart Power System Amid the Boom of Renewable Energy. IEEE Access 2022, 10, 35846–35875. [Google Scholar]
- Song, Y.; Liu, X.; Li, Z.; Shanhidehpour, M.; Li, Z. Intelligent data attacks against power systems using incomplete network information: A review. J. Mod. Power Syst. Clean Energy 2018, 6, 630–641. [Google Scholar]
- Yang, H.; He, X.; Wang, Z.; Qiu, R.C.; Ai, Q. Blind False Data Injection Attacks Against State Estimation Based on Matrix Reconstruction. IEEE Trans. Smart Grid 2022, 13, 3174–3187. [Google Scholar]
- Reda, H.T.; Anwar, A.; Mahmood, A. Comprehensive survey and taxonomies of false data injection attacks in smart grids: Attack models, targets, and impacts. Renew. Sustain. Energy Rev. 2022, 163, 112423. [Google Scholar] [CrossRef]
- Khan, O.G.M.; El-Saadany, E.F.; Youssef, A.; Shaaban, M.F. Cyber Security of Market-Based Congestion Management Methods in Power Distribution Systems. IEEE Trans. Ind. Inform. 2021, 17, 8142–8153. [Google Scholar] [CrossRef]
- Lu, K.D.; Wu, Z.G. Multi-Objective False Data Injection Attacks of Cyber–Physical Power Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3924–3928. [Google Scholar]
- Tu, H.; Xia, Y.; Chi, K.T.; Chen, X. A Hybrid Cyber Attack Model for Cyber-Physical Power Systems. IEEE Access 2020, 8, 114876–114883. [Google Scholar] [CrossRef]
- Xu, S.; Xia, Y.; Liang, H. Analysis of Malware-Induced Cyber Attacks in Cyber-Physical Power Systems. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3482–3486. [Google Scholar]
- Lu, K.; Wu, Z.; Huang, T. Differential Evolution-Based Three Stage Dynamic Cyber-Attack of Cyber-Physical Power Systems. IEEE/ASME Trans. Mechatron. 2023, 28, 1137–1148. [Google Scholar]
- Kim, J.; Tong, L. On Topology Attack of a Smart Grid: Undetectable Attacks and Countermeasures. IEEE J. Sel. Areas Commun. 2013, 31, 1294–1305. [Google Scholar]
- Liang, G.; Weller, S.R.; Zhao, J.; Luo, F.; Dong, Z.Y. A Framework for Cyber-Topology Attacks: Line-Switching and New Attack Scenarios. IEEE Trans. Smart Grid 2019, 10, 1704–1712. [Google Scholar]
- Liu, C.; He, W.; Deng, R.; Tian, Y.; Du, W. False-Data-Injection-Enabled Network Parameter Modifications in Power Systems: Attack and Detection. IEEE Trans. Ind. Inform. 2023, 19, 177–188. [Google Scholar]
- Ismail, M.; Shaaban, M.F.; Naidu, M.; Serpedin, E. Deep Learning Detection of Electricity Theft Cyber-Attacks in Renewable Distributed Generation. IEEE Trans. Smart Grid 2020, 11, 3428–3437. [Google Scholar] [CrossRef]
- Gu, W.; Ding, S.; Lu, S.; Zhao, P.; Zou, D.; Qiu, Y.; Yu, R.; Sheng, L. Coordinated Heat and Power Cyber-attacks With Time Window Matching Strategy. IEEE Trans. Smart Grid 2023, 14, 2747–2761. [Google Scholar]
- Jhala, K.; Natarajan, B.; Pahwa, A.; Wu, H. Stability of Transactive Energy Market-Based Power Distribution System Under Data Integrity Attack. IEEE Trans. Ind. Inform. 2019, 15, 5541–5550. [Google Scholar] [CrossRef]
- Li, P.; Liu, Y.; Xin, H.; Jiang, X. A Robust Distributed Economic Dispatch Strategy of Virtual Power Plant Under Cyber-Attacks. IEEE Trans. Ind. Inform. 2018, 14, 4343–4352. [Google Scholar]
- Fotis, G.; Vita, V.; Maris, T.I. Risks in the European Transmission System and a Novel Restoration Strategy for a Power System after a Major Blackout. Appl. Sci. 2023, 13, 83. [Google Scholar]
- Hou, J.; Wang, J.; Song, Y.; Sun, W.; Hou, Y. Small-Signal Angle Stability-Oriented False Data Injection Cyber-Attacks on Power Systems. IEEE Trans. Smart Grid 2023, 14, 635–648. [Google Scholar]
- Zhang, H.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Wang, P.; Guo, Q.; Sun, H. A Stochastic Bi-Level Optimal Allocation Approach of Intelligent Buildings Considering Energy Storage Sharing Services. IEEE Trans. Consum. Electron. 2024, 70, 5142–5153. [Google Scholar]
- Palomino, A.; Giraldo, J.; Parvania, M. Graph-Based Interdependent Cyber-Physical Risk Analysis of Power Distribution Networks. IEEE Trans. Power Deliv. 2023, 38, 1510–1520. [Google Scholar]
- Meng, Y.; Zhang, H.; Fan, W. Analysis of the Network Structure Characteristics of Virtual Power Plants Based on a Complex Network. Electr. Power Syst. Res. 2022, 204, 107717. [Google Scholar] [CrossRef]
- Hui, H.; Ding, Y.; Shi, Q.; Li, F.; Yan, J. 5G Network-Based Internet of Things for Demand Response in Smart Grid: A Survey on Application Potential. Appl. Energy 2020, 257, 113972. [Google Scholar] [CrossRef]
- Rahim, S.; Wang, Z.; Ju, P. Overview and Applications of Robust Optimization in the Avant-Garde Energy Grid Infrastructure: A Systematic Review. Applied Energy 2022, 319, 119140. [Google Scholar]
- Li, Q.; Zhang, J.; Zhao, J.; Ye, J.; Song, W.; Li, F. Adaptive Hierarchical Cyber Attack Detection and Localization in Active Distribution Systems. IEEE Trans. Smart Grid 2022, 13, 2369–2380. [Google Scholar] [CrossRef]
- Ye, J.; Giani, A.; Elasser, A.; Mazumder, S.K.; Farnell, C.; Mantooth, H.A.; Kim, T.; Liu, J.; Chen, B.; Seo, G.; et al. A Review of Cyber–Physical Security for Photovoltaic Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4879–4901. [Google Scholar] [CrossRef]
- Yin, H.; Liu, D.; Chen, G. Coordinated Cyber-attack Model and Cross-space Fault Propagation Mechanism for Virtual Power Plant. Autom. Electr. Power Syst. 2023, 47, 34–43. [Google Scholar]
- Jena, P.K.; Ghosh, S.; Koley, E. Design of a coordinated cyber-physical attack in IoT based smart grid under limited intruder accessibility. Int. J. Crit. Infrastruct. Prot. 2021, 35, 100484. [Google Scholar] [CrossRef]
- Jena, P.K.; Ghosh, S.; Koley, E.; Mohanta, D.K.; Kamwa, I. Design of AC state estimation based cyber-physical attack for disrupting electricity market operation under limited sensor information. Electr. Power Syst. Res. 2022, 205, 107732. [Google Scholar] [CrossRef]
- Liang, Y.; Bai, M.; Liu, K.; Liu, D.; Qi, D.; Guo, Q. Cyber-physical Test Case for Distribution Grid Operation and Control. CSEE J. Power Energy Syst. 2023, 9, 707–721. [Google Scholar]
- Zhai, X.; Li, Z.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Jin, X.; Wang, P.; Sun, H. Risk-averse energy management for integrated electricity and heat systems considering building heating vertical imbalance: An asynchronous decentralized approach. Appl. Energy 2025, 383, 125271. [Google Scholar] [CrossRef]

| DGs | Bus | Rated Power (MW) | (¥/MW) | RES Level (MW) | ||
|---|---|---|---|---|---|---|
| Low | Mid | High | ||||
| PV1 | 22 | 1 | 150 | 0.21 | 0.45 | 0.72 |
| PV2 | 31 | 1 | 150 | 0.24 | 0.51 | 0.70 |
| PV3 | 54 | 1 | 150 | 0.19 | 0.49 | 0.78 |
| PV4 | 61 | 1 | 150 | 0.25 | 0.57 | 0.74 |
| WT1 | 25 | 1 | 120 | 0.30 | 0.42 | 0.70 |
| WT2 | 28 | 1 | 120 | 0.22 | 0.48 | 0.78 |
| WT3 | 46 | 1 | 120 | 0.23 | 0.56 | 0.76 |
| WT4 | 19 | 1 | 120 | 0.26 | 0.62 | 0.82 |
| ESS1 | 12 | 1.5 | 180 | \ | \ | \ |
| ESS2 | 53 | 1.5 | 180 | \ | \ | \ |
| ESS3 | 11 | 0.8 | 110 | \ | \ | \ |
| ESS4 | 33 | 1 | 100 | \ | \ | \ |
| Attack Objective | Min Attack Resources (r) | Min VPP Revenue (e) | Max Overload Power (o) | |
|---|---|---|---|---|
| RES Level | ||||
| Low (l) | Case l-r | Case l-e | Case l-o | |
| Mid (m) | Case m-r | Case m-e | Case m-o | |
| High (h) | Case h-r | Case h-e | Case h-o | |
| Case | l-r | m-r | h-r | |
|---|---|---|---|---|
| Sa Stage | Topology attack | 11-12(−), 18-19(−), 13-44(+), 19-35(+) | 11-12(−), 18-19(−), 13-44(+), 19-35(+) | 18-19(−), 19-35(+) |
| Falsified DGs | 12/12 | 12/12 | 11/12 | |
| Falsified branch meters | 35/65 | 38/65 | 45/65 | |
| Total falsified devices | 51/142 | 54/142 | 58/142 | |
| S2 Stage | Overloaded feeder (rate) | 23-24 (105.89%), 43-44 (107.06%) | 23-24 (102.07%) | 23-24 (101.30%) |
| Minimum bus voltage magnitude | 0.8525 | 0.8258 | 0.8974 | |
| Case | l-e | m-e | h-e | |
|---|---|---|---|---|
| Sa stage | Topology attack | 10-11(−), 18–19(−), 28-29(−), 13–44(+), 17-29(+), 19–35(+) | 9-10(−), 26–27(−), 57-60(−), 13–44(+), 17-29(+), 24–62(+) | 12-13(−), 18-19(−), 26-27(−), 13-44(+), 17-29(+), 19-35(+) |
| Falsified DGs | 12/12 | 12/12 | 12/12 | |
| Falsified branch meters | 44/65 | 45/65 | 48/65 | |
| S1 stage | Expected VPP benefit | ¥17,190 | ¥17,190 | ¥17,190 |
| Expected VPP outputs | 6 MW | 6 MW | 6 MW | |
| S2 stage | VPP actual benefit | ¥4127 | ¥8508 | ¥12,641 |
| VPP actual outputs | 1.44 MW | 2.97 MW | 4.42 MW | |
| Minimum bus voltage magnitude | 0.8851 | 0.9015 | 0.9045 | |
| Case | l-o | m-o | h-o | |
|---|---|---|---|---|
| Sa stage | Topology attack | 34-35(−), 36-37(−), 57-60(−), 3-39(+), 19-35(+), 24-62(+) | 12-13(−), 27-28(−), 36-37(−), 57-60(−), 3-39(+), 13-44(+), 17-29(+), 24-62(+) | 12-13(−), 17-18(−), 37-38(−), 57-60(−), 3-39(+), 13-44(+), 19-35(+), 24-62(+) |
| Falsified DGs | 10/12 | 11/12 | 12/12 | |
| Falsified branch meters | 42/65 | 46/65 | 53/65 | |
| S2 stage | VPP actual outputs | 2.96 MW | 4.39 WM | 5.22 WM |
| Overloaded feeder (rate) | 43-44 (113.86%), 23-24 (106.59%) | 43-44 (113.86%) | 43-44 (113.86%) | |
| Minimum bus voltage magnitude | 0.8712 | 0.8964 | 0.9125 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Gong, J.; Xiao, S.; Yang, J.; Su, X. A Novel FDIA Model for Virtual Power Plant Cyber–Physical Systems Based on Network Topology and DG Outputs. Energies 2025, 18, 1597. https://doi.org/10.3390/en18071597
Wu S, Gong J, Xiao S, Yang J, Su X. A Novel FDIA Model for Virtual Power Plant Cyber–Physical Systems Based on Network Topology and DG Outputs. Energies. 2025; 18(7):1597. https://doi.org/10.3390/en18071597
Chicago/Turabian StyleWu, Shuo, Junhao Gong, Shiqu Xiao, Jiajia Yang, and Xiangjing Su. 2025. "A Novel FDIA Model for Virtual Power Plant Cyber–Physical Systems Based on Network Topology and DG Outputs" Energies 18, no. 7: 1597. https://doi.org/10.3390/en18071597
APA StyleWu, S., Gong, J., Xiao, S., Yang, J., & Su, X. (2025). A Novel FDIA Model for Virtual Power Plant Cyber–Physical Systems Based on Network Topology and DG Outputs. Energies, 18(7), 1597. https://doi.org/10.3390/en18071597







