Research on the Quantitative Impact of Power Angle Oscillations on Transient Voltage Stability in AC/DC Receiving-End Power Grids
Abstract
1. Introduction
2. The Instability Issues of the Receiving-End Grid Under Different Generators’ Capacity
2.1. Voltage Instability Characteristics of SW DC Receiving-End Grid
2.2. The Coupling Characteristics Between Generators and Loads
2.3. The Mechanism of Voltage Decline Due to Power Angle Swinging
3. Stability Analysis of the AC/DC Receiving-End Grid
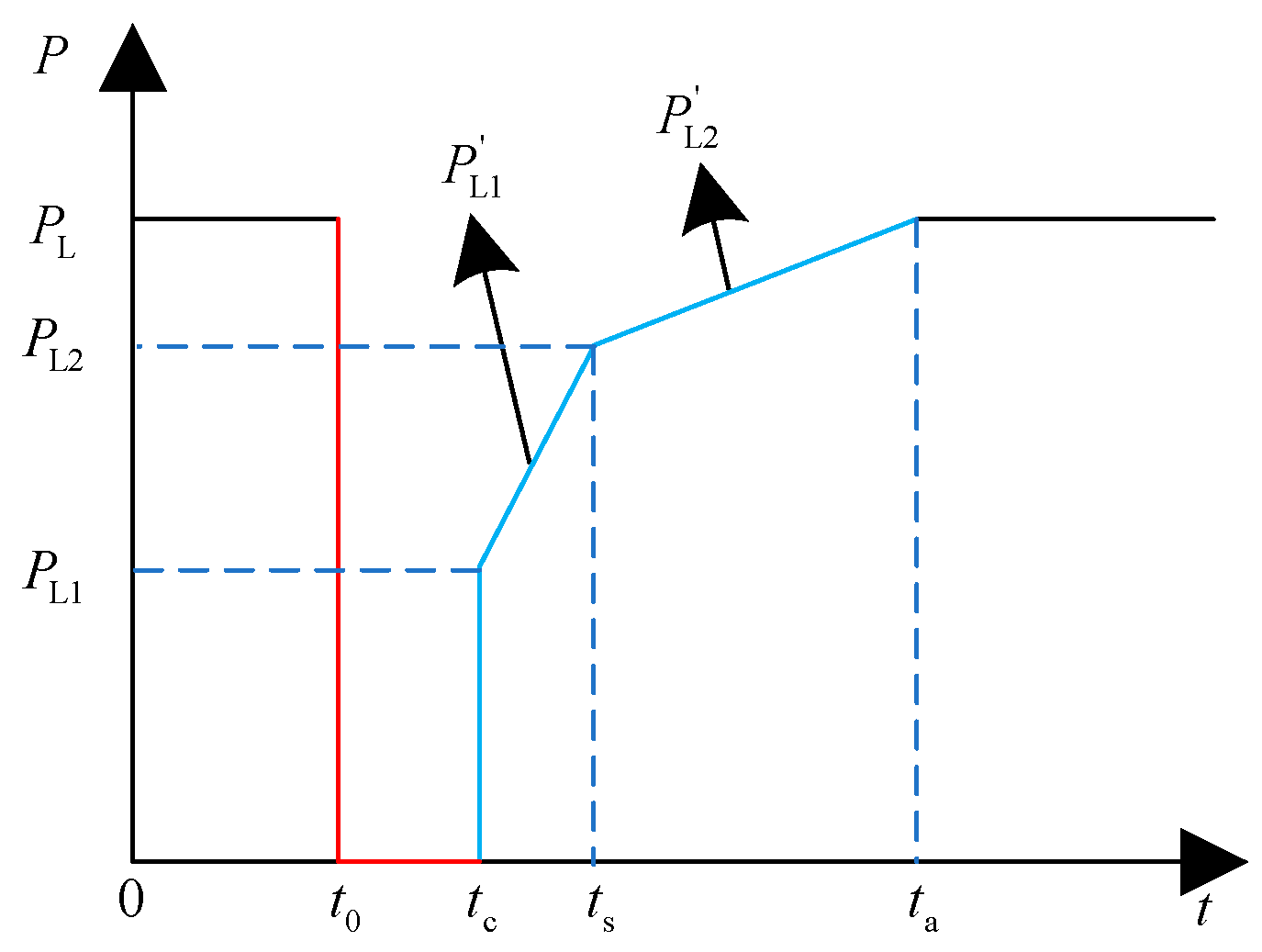
3.1. Load Recovery Characteristics
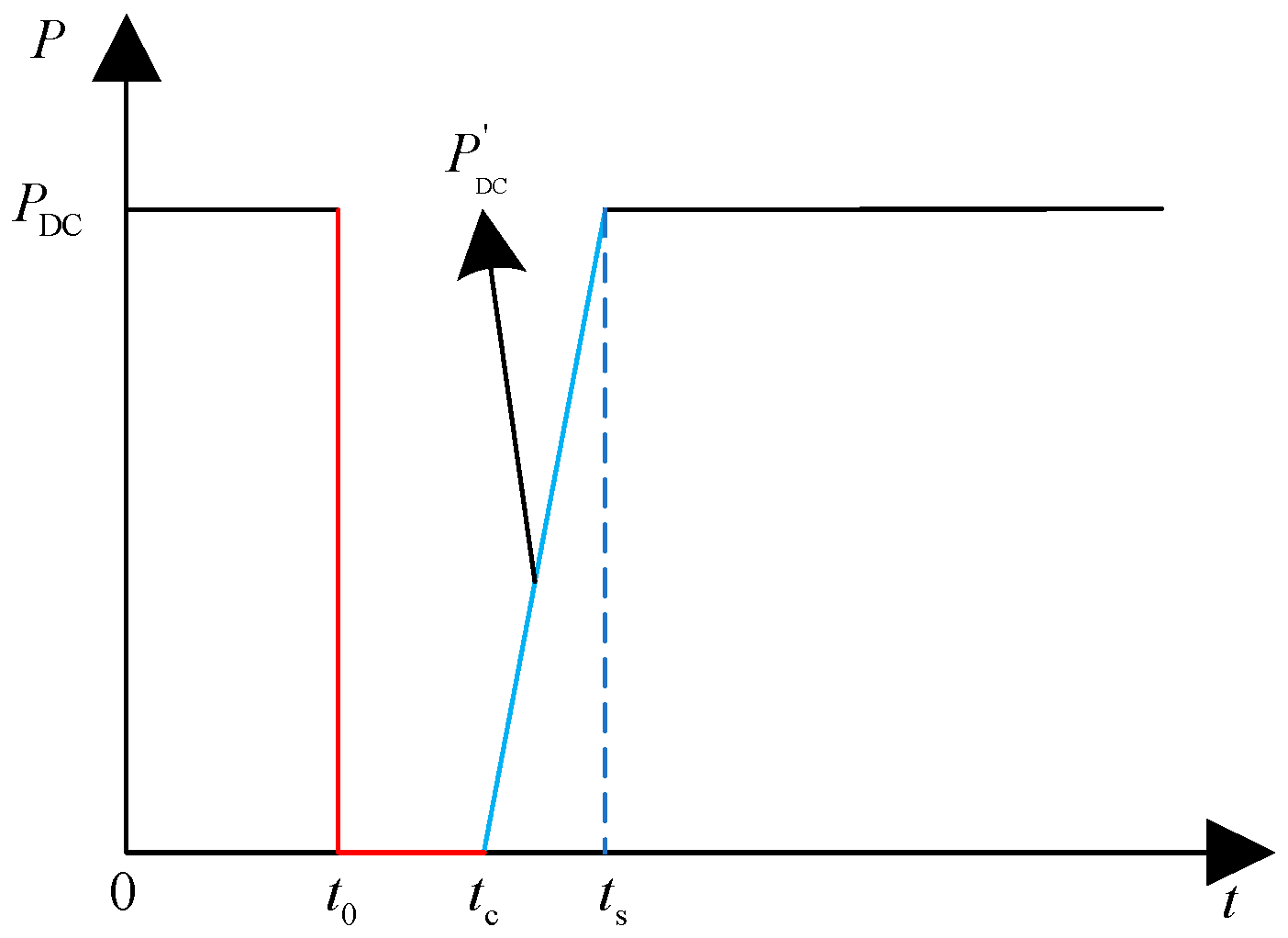
3.2. DC Power Recovery Characteristics
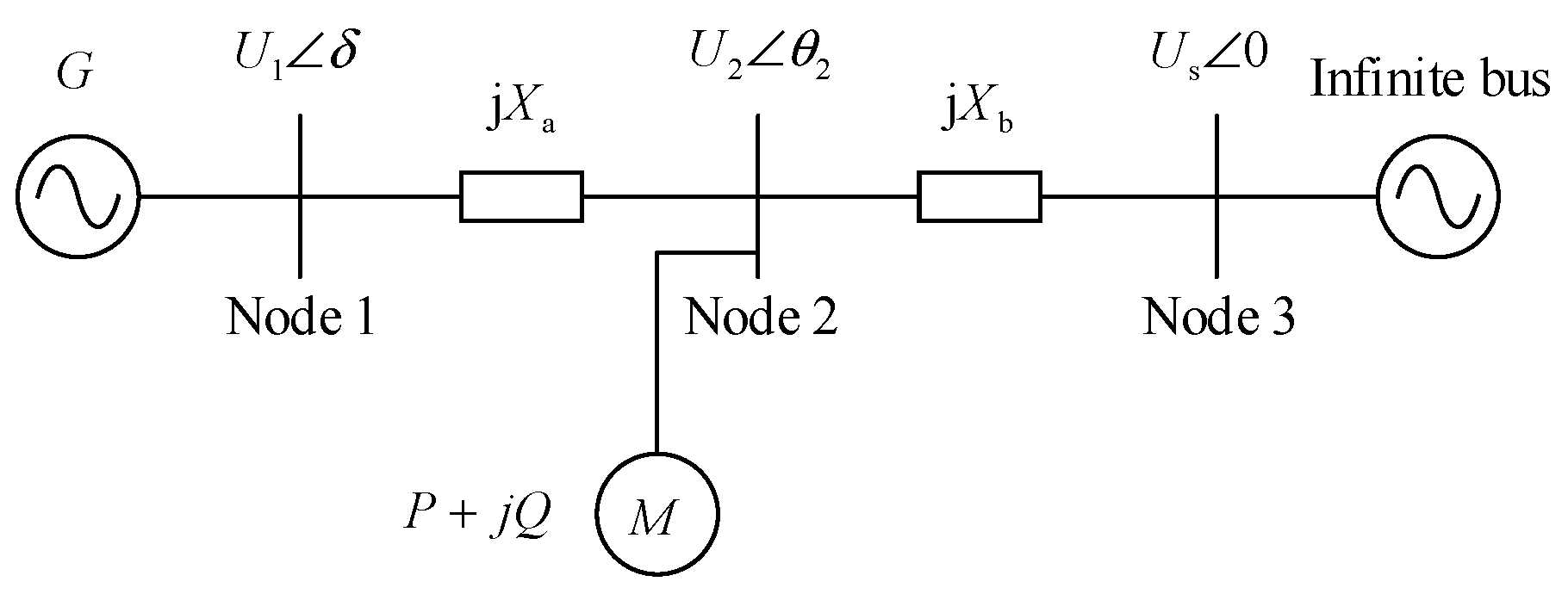
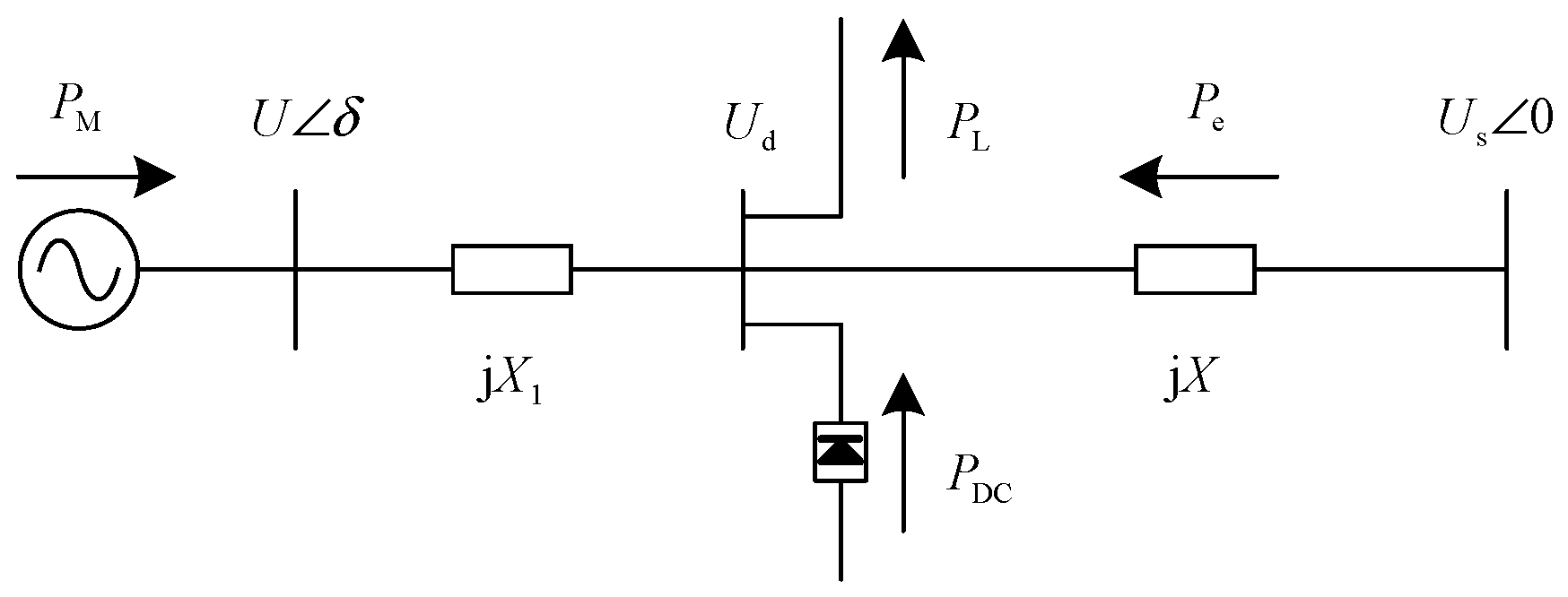
3.3. The Simplified Model of the Receiving-End Grid and Stability Analysis
- (1)
- The first stage corresponds to the period from time tc to time ts, during which the DC power and load power are in their first phase of recovery. The equivalent mechanical power during this stage is denoted as PM + P′DC − P′L1;
- (2)
- The second stage corresponds to the period from time ts to time ta, after the DC power has been restored, during which the load power undergoes its second phase of recovery. The equivalent mechanical power during this stage is denoted as PM + PDC − P′L2;
- (3)
- The third stage corresponds to the period from time ta to time tm, after both DC power and load power have been restored to their initial values. During this stage, the power angle continues to swing to its maximum value. The equivalent mechanical power during this stage is denoted as PM + PDC − PL.
- (1)
- DC and Local Generators Distribution
- (2)
- AC/DC Power Distribution
- (3)
- Local Generators and External AC Intake Distribution
4. Quantitative Analysis of Generators’ Capacity Range Under Transient Stability Constraints
- (1)
- First, write the rotor motion equations for different stages;
- (2)
- Second, integrate to determine the generator’s speed;
- (3)
- Third, integrate to determine the power angle.
5. Case Verification
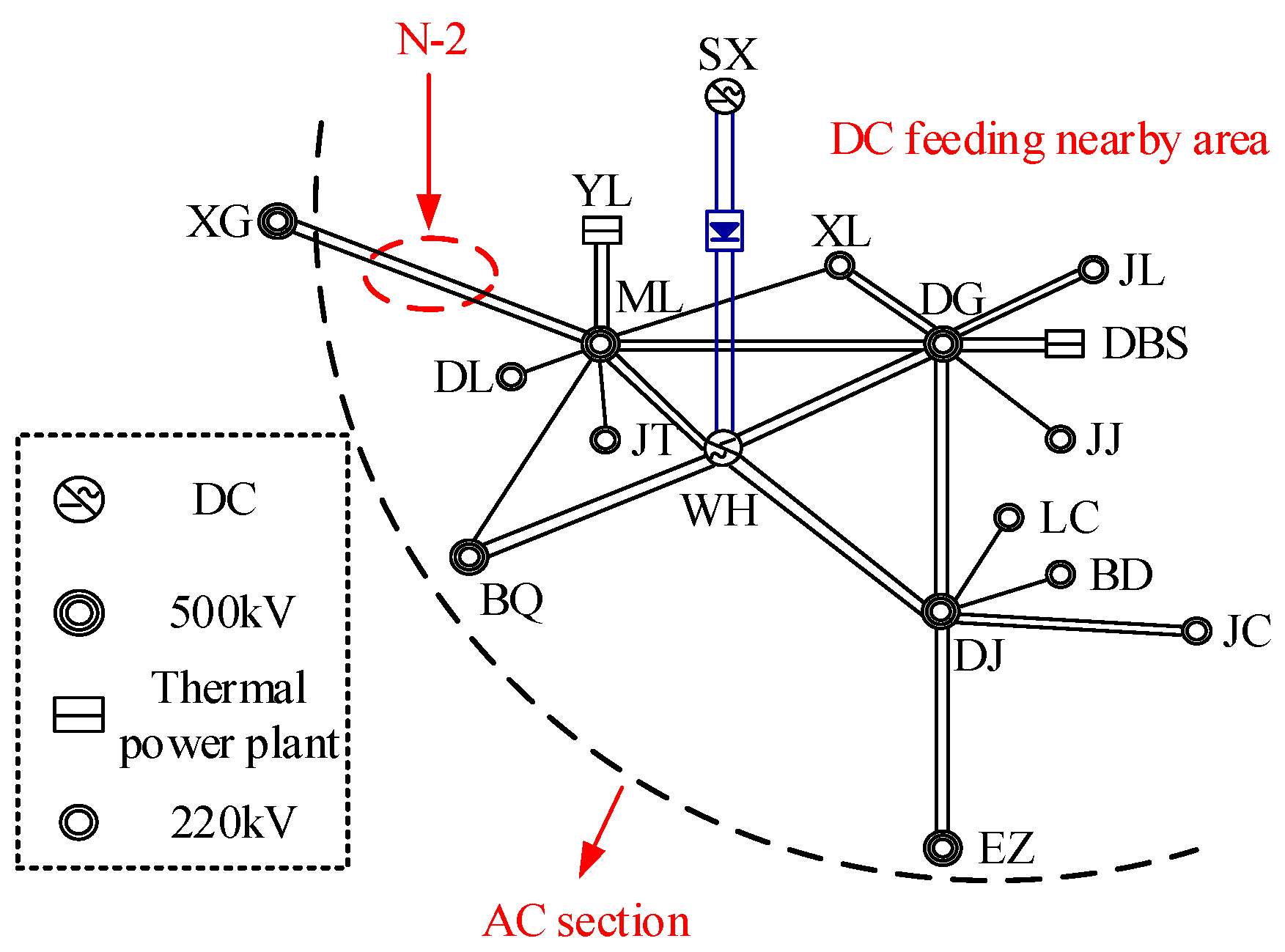
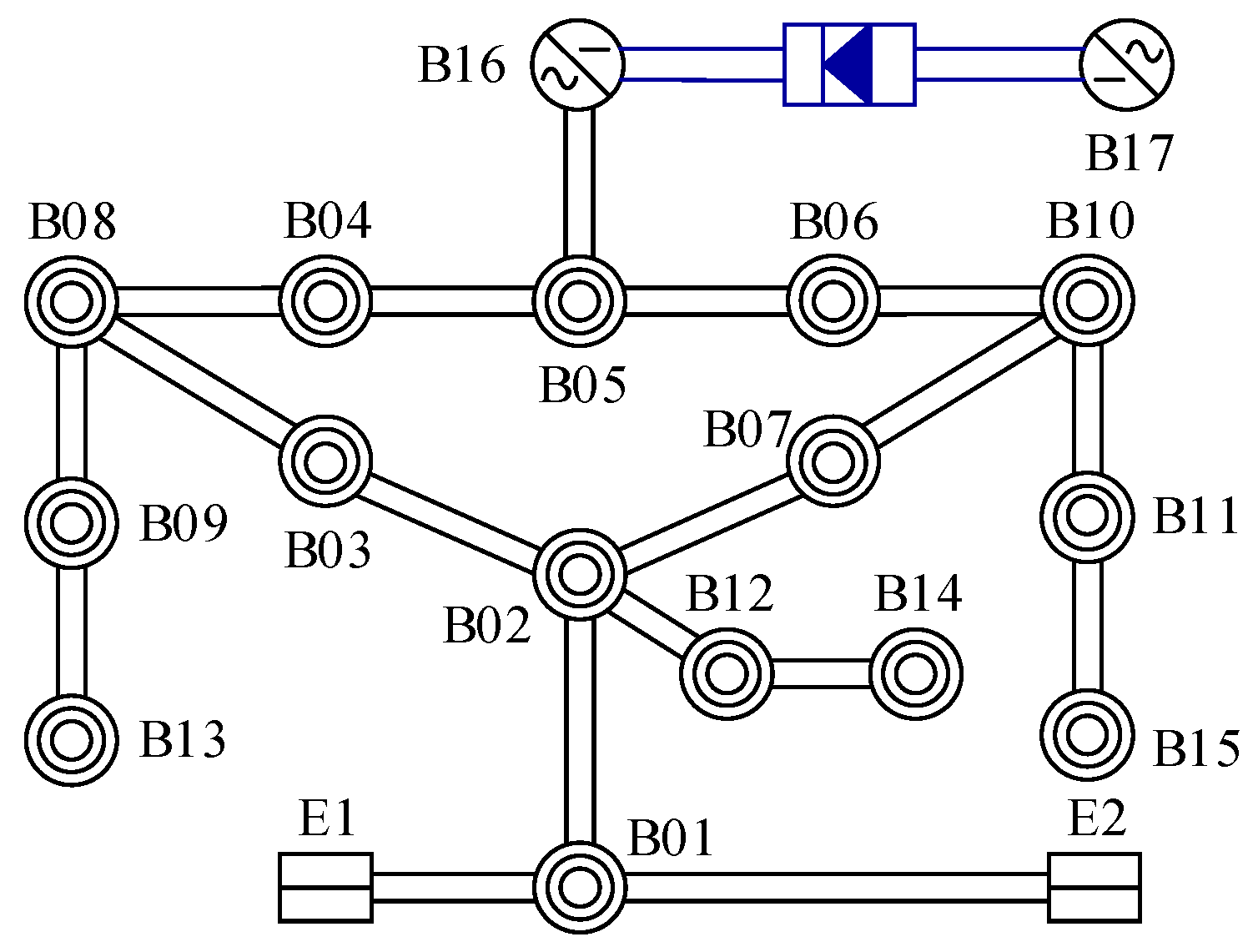
5.1. System Network Structure
5.2. Sensitivity Factor Analysis of Transient Stability
5.2.1. DC and Local Generators Distribution
5.2.2. AC/DC Power Distribution
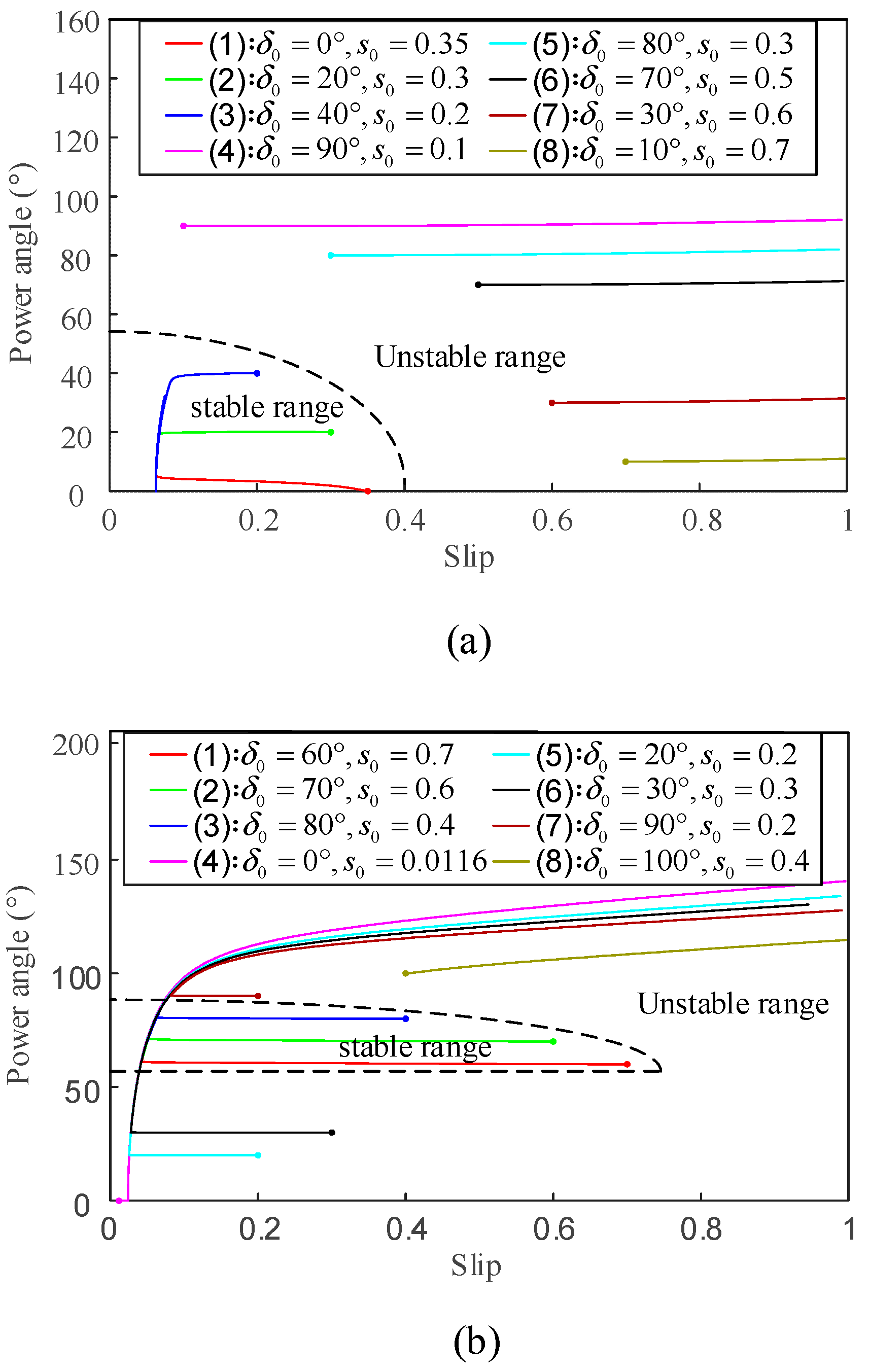
5.2.3. Static Power Angle Stability Limit
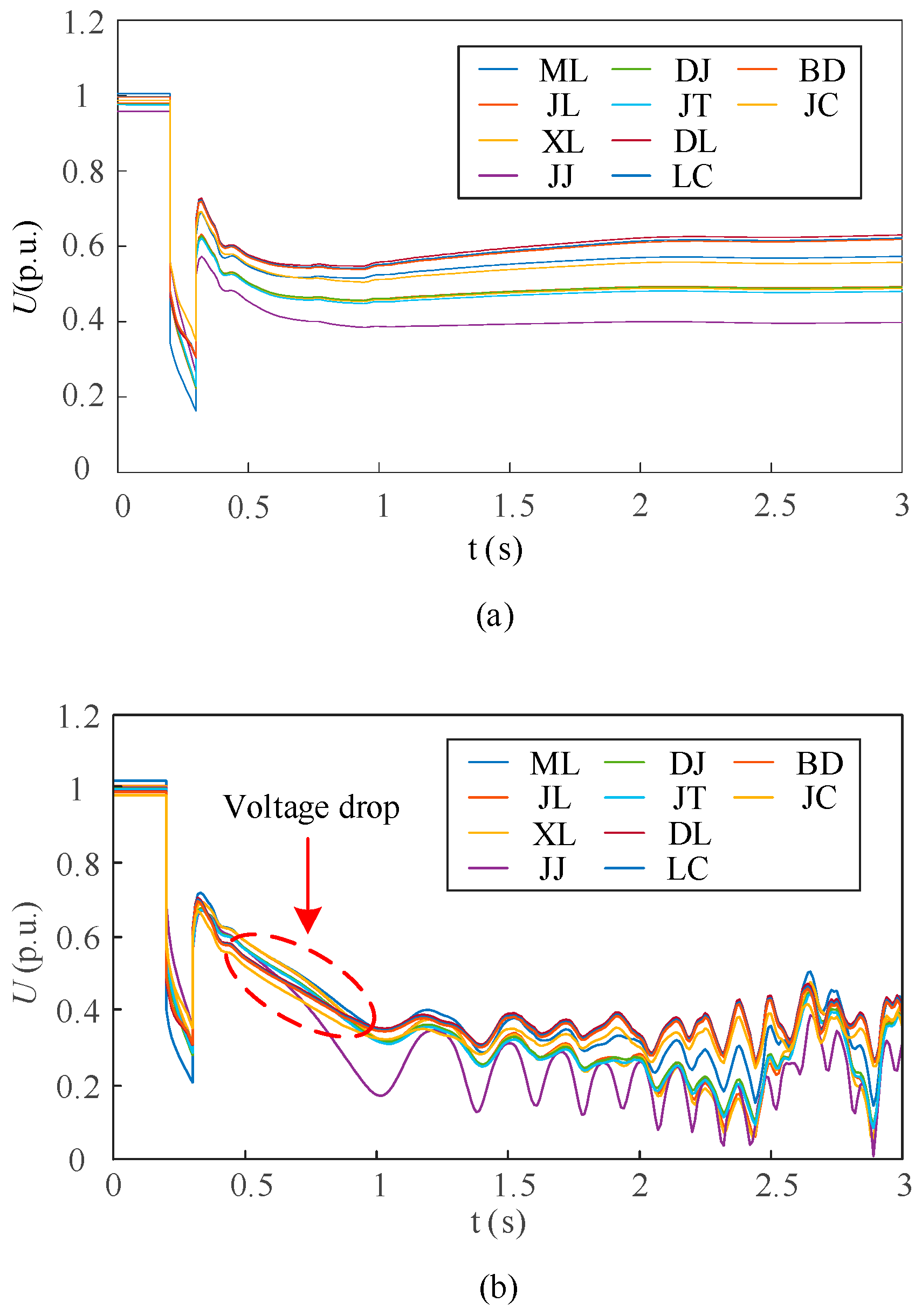
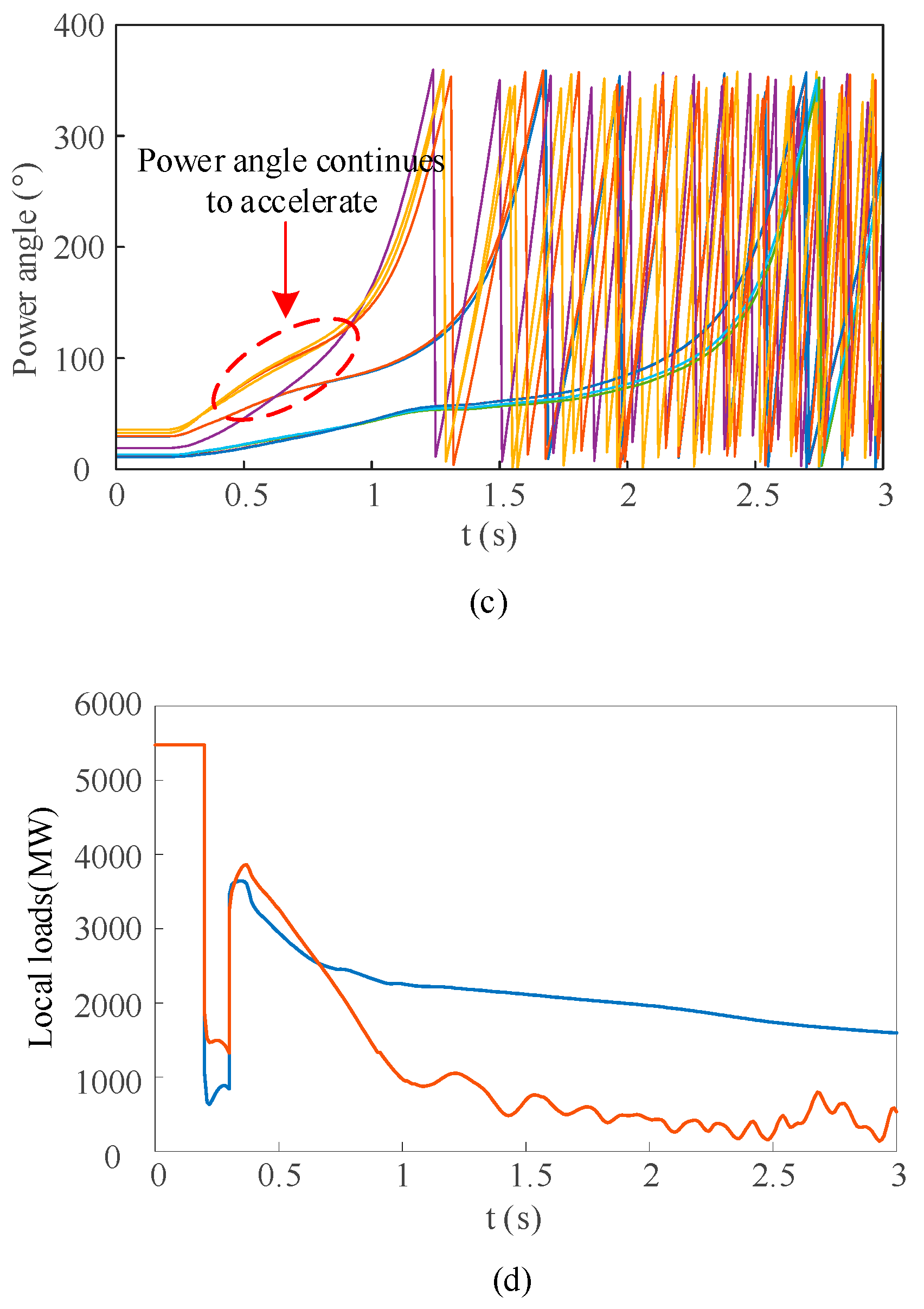
5.3. Simulation Verification of Local Generators’ Capacity Range
6. Conclusions
- (1)
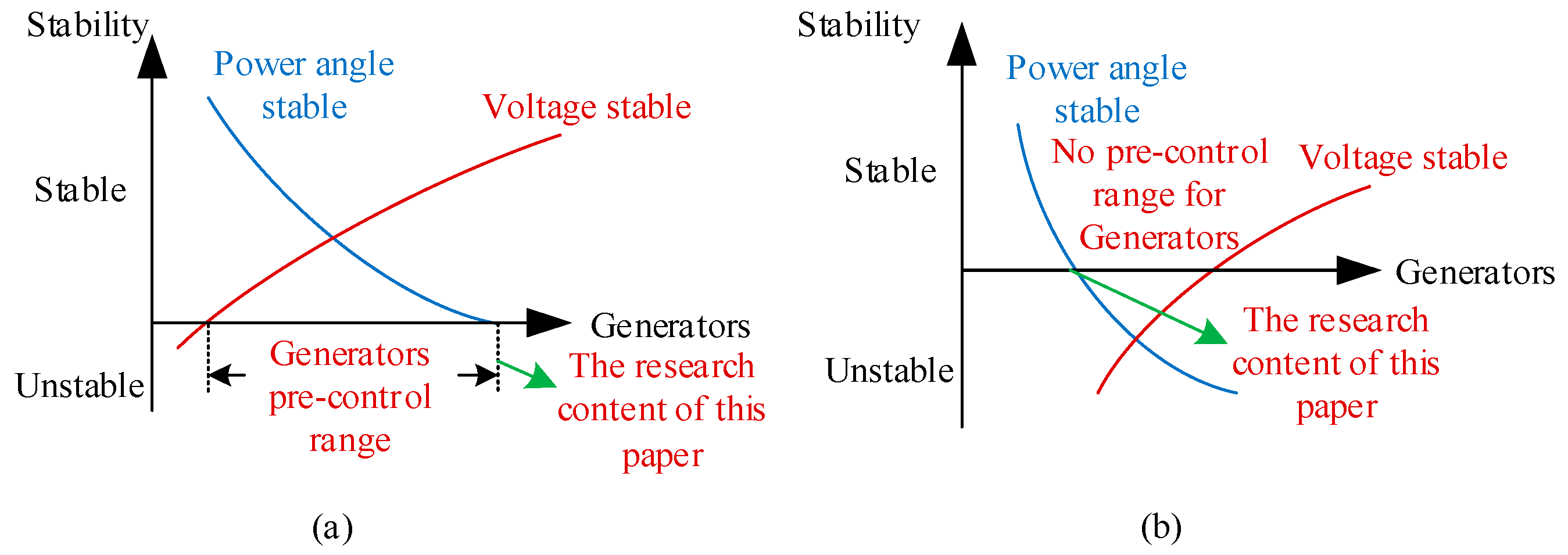
- Increasing the number of local generators’ capacity is an effective measure to address voltage stability issues. However, excessive generators’ capacity can lead to power angle stability problems, resulting in some receiving end grids lacking a stable generators’ capacity pre-control range. Therefore, the generators’ capacity for receiving end grids should be limited;
- (2)
- As the number of local generators’ capacity increases, the grid transitions from a voltage stability issue to a power angle stability issue. A higher number of local generators’ capacity leads to larger power angle swings after faults, which in turn reduces the Thevenin equivalent voltage seen by the load, exacerbating the system voltage drop. In practical power systems, if other factors are not considered, the transition between voltage stability and power angle stability primarily depends on the proportional relationship between the generators’ capacity level and the load level. Traditional stability assessment methods typically analyze the system based on a single constraint condition (either voltage or power angle), without explicitly defining the reasonable range of generators’ capacity or quantifying the induction motor load capacity that the system can withstand. This limitation makes it difficult for existing methods to fully capture the actual stability characteristics of the system;
- (3)
- In the allocation of DC power, local generators, and AC power replacement, the system stability does not change monotonically, and a specific grid analysis is needed;
- (4)
- Considering the two-phase recovery characteristics of DC power and load after a fault, this paper proposes a method for quantifying the maximum generators’ capacity limit, with a calculation error not exceeding 10.25%. Within the calculated range, the generators’ capacity can ensure that the receiving end system does not become unstable due to excessive power angle acceleration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, X.; Tang, Y.; Bu, G. Confronting Problem and Challenge of Large Scale AC-DC Hybrid Power Grid Operation. Proc. CSEE 2019, 39, 3107–3119. [Google Scholar]
- Zhou, X.; Chen, S.; Lu, Z. Technology Features of the New Generation Power System in China. Proc. CSEE 2018, 38, 1893–1904. [Google Scholar]
- Tang, Y. Voltage Stability Analysis of Power System; Beijing Science Press: Beijing, China, 2011. [Google Scholar]
- Kawabe, K.; Tanaka, K. Analytical Method for Short-Term Voltage Stability Using the Stability Boundary in the P-V Plane. IEEE Trans. Power Syst. 2014, 29, 3041–3047. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, X.; Li, R. Influence of Induction Motor Load Parameters on Power System Transient Voltage Stability. Power Syst. Technol. 2005, 29, 1–6. [Google Scholar]
- Li, L.; Lu, C.; Huang, Z. Analytical Assessment of Transient Voltage Stability of Load Bus Considering Induction Motors. Autom. Electr. Power Syst. 2009, 33, 1–5. [Google Scholar]
- He, L.; Li, X.; Xu, M. Assessment of Ransient Voltage Stability of Load Bus Considering the Mechanical Torque of Dynamic Load. Autom. Electr. Power Syst. 2010, 34, 1–5. [Google Scholar]
- Zhang, W.; Zhang, B.; Pan, J. Mechanism Analysis for Transient Voltage Instability Based on Crossfeed Characteristics between Power Network and Load of Induction Motor. Autom. Electr. Power Syst. 2017, 41, 8–14. [Google Scholar]
- Du, W.; Su, G.; Wang, H.; Ji, Y. Dynamic Instability of a Power System Caused by Aggregation of Induction Motor Loads. IEEE Trans. Power Syst. 2019, 34, 4361–4369. [Google Scholar] [CrossRef]
- Yao, R.; Sun, K.; Shi, D.; Zhang, X. Voltage Stability Analysis of Power Systems with Induction Motors Based on Holomorphic Embedding. IEEE Trans. Power Syst. 2019, 34, 1278–1288. [Google Scholar] [CrossRef]
- Aik, D.L.H.; Andersson, G. Power stability analysis of multi-infeed HVDC systems. IEEE Trans. Power Deliv. 1998, 13, 923–931. [Google Scholar] [CrossRef]
- Zhang, F.; Xin, H.-H.; Xu, Q.; Dai, P.; Qin, X.-H. Generalized Short Circuit Ratio for Multi-infeed DC Systems: Influence Factors. Proc. CSEE 2017, 37, 5303–5312. [Google Scholar]
- Xiao, H.; Li, Y.; Shi, D. Integrated Short Circuit Ratio Strength Index for Static Voltage Stability analysis of Multi-infeed LCC-HVDC Systems. Proc. CSEE 2017, 37, 6471–6480. [Google Scholar]
- Li, D.; Sun, M.; Zhao, Y. The Steady-state Voltage Stability Analysis of Multi-infeed LCC-HVDC System Based on Equivalent Operating Short Circuit Ratio. Proc. CSEE 2020, 40, 3847–3857. [Google Scholar]
- Qiu, W.; He, J.; Yu, Z. Transient Voltage Stability Analysis of Hunan Power Grid with Infeed UHVDC. Electr. Power Autom. Equip. 2019, 39, 168–173. [Google Scholar]
- Bian, H.; Pan, X.; Liu, F. Study on Voltage Stability Analysis and Improvement Measures for Henan Province with a Background of Multiple DC Feeding. Power Syst. Prot. Control 2020, 48, 125–131. [Google Scholar]
- Ran, H.; Wang, Z.; Gao, B. Two-stage Transient Voltage Evaluation Suitable for HVDC Receiving Systems. Power Syst. Technol. 2023, 47, 4272–4284. [Google Scholar]
- Zhang, Q.; Feng, Y.; Cui, Y. Overall consideration of peak regulation and voltage stability on scheduling units in Shanghai power grid with multiple HVDC feed-in. Power Syst. Clean Energy 2016, 32, 54–60. [Google Scholar]
- Wang, E.; Liu, H.; Chen, R. Comparative Analysis of Near-Zone Characteristics of Shan-Wu DC Based on Jing-Wu Double Circuit Constraint Fault. Hubei Electr. Power 2022, 46, 42–50. [Google Scholar]
- Deng, H.; Lou, B.; Hua, W. Study on AC/DC hybrid characteristics and generator set optimization in Zhejiang power grid. Shaanxi Electr. Power 2017, 45, 55–59. [Google Scholar]
- Liu, Y.; Li, Z.; Zhang, Z. An Analytical Calculation Method for Total Transfer Capability of Transmission Section Based on Evaluation of System Short Circuit Capability. Electr. Power 2025, 58, 98–107. [Google Scholar]
- Qin, J.; Li, H.; Sun, Y. Optimization method for minimum start-up mode of conventional units considering constraints on the maximum grid connection strength of new energy. Power Syst. Prot. Control 2023, 51, 127–135. [Google Scholar]
- Yao, J.; Chen, Z.; Zhang, W. Minimum Start-up Sequence Method of Receiving Terminal Based on Generator and Load Dynamic Reactive Power Response. Smart Power 2018, 46, 66–71. [Google Scholar]
- Bian, H.; Wang, K.; Huang, C. Analysis of Key Indicators for Transient Voltage Recovery and Their Application in DC Receiving-End Systems. Jiangxi Electr. Power 2022, 46, 17–20+24. [Google Scholar]
- Jia, Q.; Peng, L.; Wang, X. Method for Determining the Minimum Capacity Scale of Generators Under Voltage Stability Constraints. In Proceedings of the 2023 IEEE International Conference on Advanced Power System Automation and Protection (APAP), Xuchang, China, 8–12 October 2023; pp. 119–123. [Google Scholar]
- Van Cutsem, T.; Vouras, C.D. Voltage stability analysis in transient and mid-termtime scales. IEEE Trans. Power Syst. 1996, 11, 146–154. [Google Scholar] [CrossRef]
- Wei, W.; Yong, T.; Huadong, S.; Jian, H.; Weifang, L. The Recognition of Principal Mode between Rotor Angle Instability and Transient Voltage Instability. Proc. CSEE 2014, 34, 5610–5617. [Google Scholar]
- Zheng, C.; Sun, H.; Zhang, A.; Lv, S. Discrimination of Rotor Angle Stability and Voltage Stability Based on Wide-area Branch Response and Emergency Control. Proc. CSEE 2021, 41, 6148–6160. [Google Scholar]
- Gu, Z.; Tang, Y.; Yi, J. Study on Mechanism of Interrelationship between Power System Angle Stability and Induction Motor Stability. Power Syst. Technol. 2017, 41, 2499–2505. [Google Scholar]
- Li, X.; Liu, C.; Xin, S. Coupling Mechanism Analysis and Coupling Strength Evaluation Index of Transient Power Angle Stability and Transient Voltage Stability. Proc. CSEE 2021, 41, 5091–5107. [Google Scholar]
- Shi, Z.; Yao, W.; Huang, Y. Power System Dominant Instability Mode Identification Based on Convolutional Neural Networks with Squeeze and Excitation Block and Simulation Data. Proc. CSEE 2022, 42, 7719–7731. [Google Scholar]
- Zhang, R.; Yao, W.; Shi, Z. Semi-supervised Learning Framework of Dominant Instability Mode Identification Via Fusion of Virtual Adversarial Training and Mean Teacher Model. Proc. CSEE 2022, 42, 7497–7509. [Google Scholar]
- Vournas, C.D.; Sauer, P.W.; Pai, M.A. Relationships between voltage and angle stability of power systems. Int. J. Electr. Power Energy Syst. 1996, 18, 493–500. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, J.; Wang, T. Analysis of Impact of Power Recovery Speed on Transient Stability of Sending-side System after Large Capacity HVDC Commutation Failure. Power Syst. Technol. 2020, 44, 1815–1825. [Google Scholar]
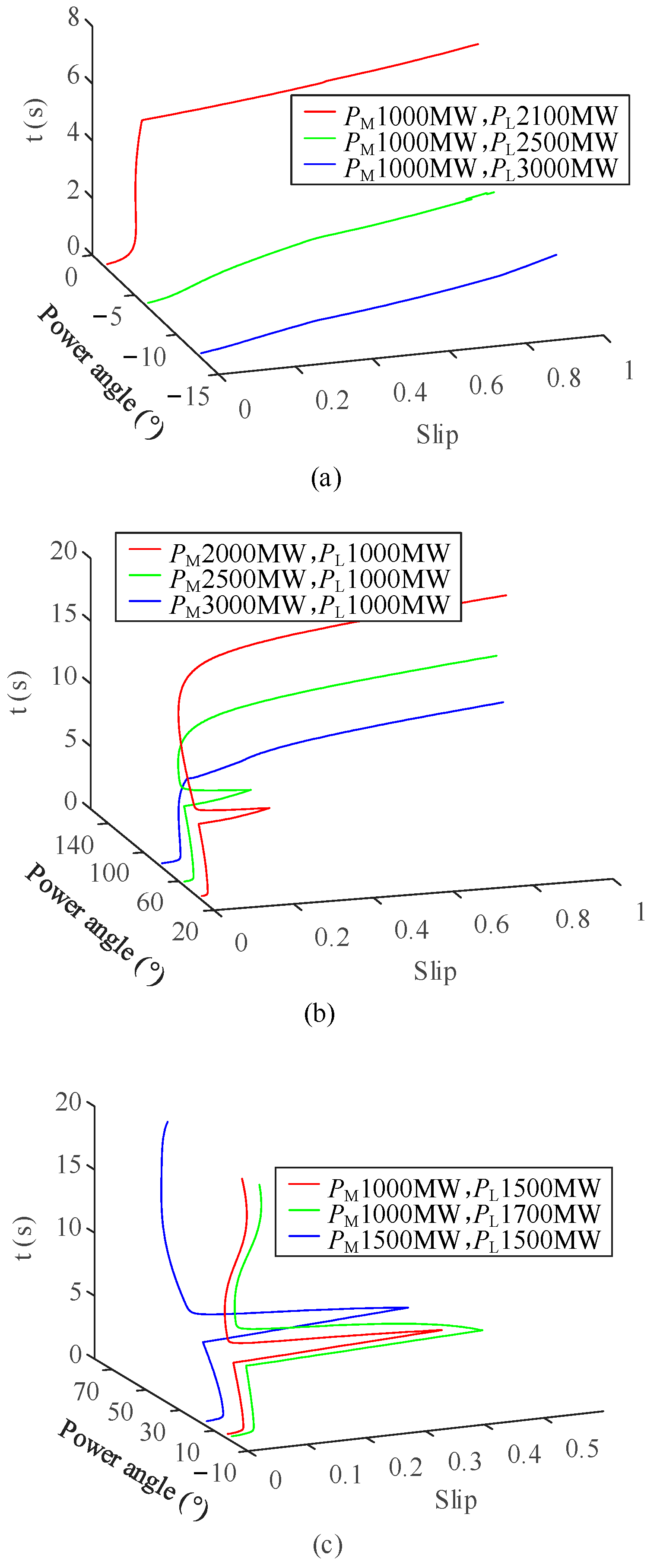
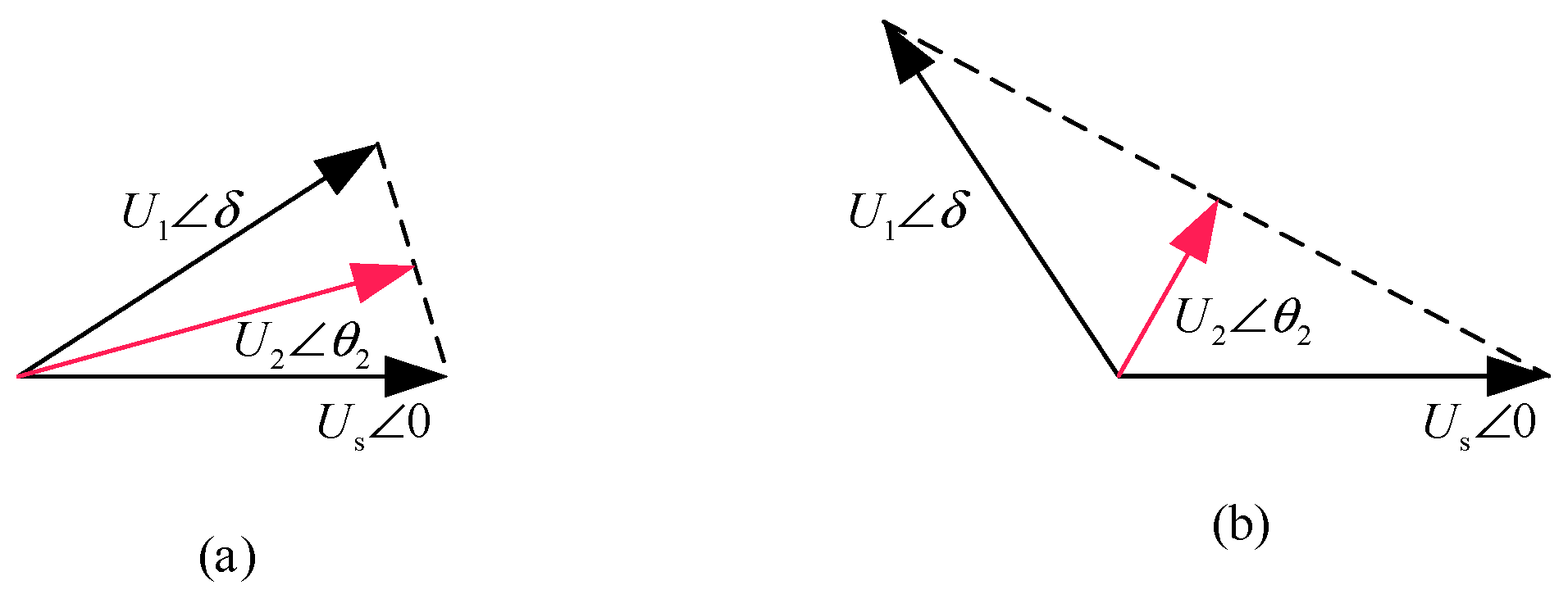


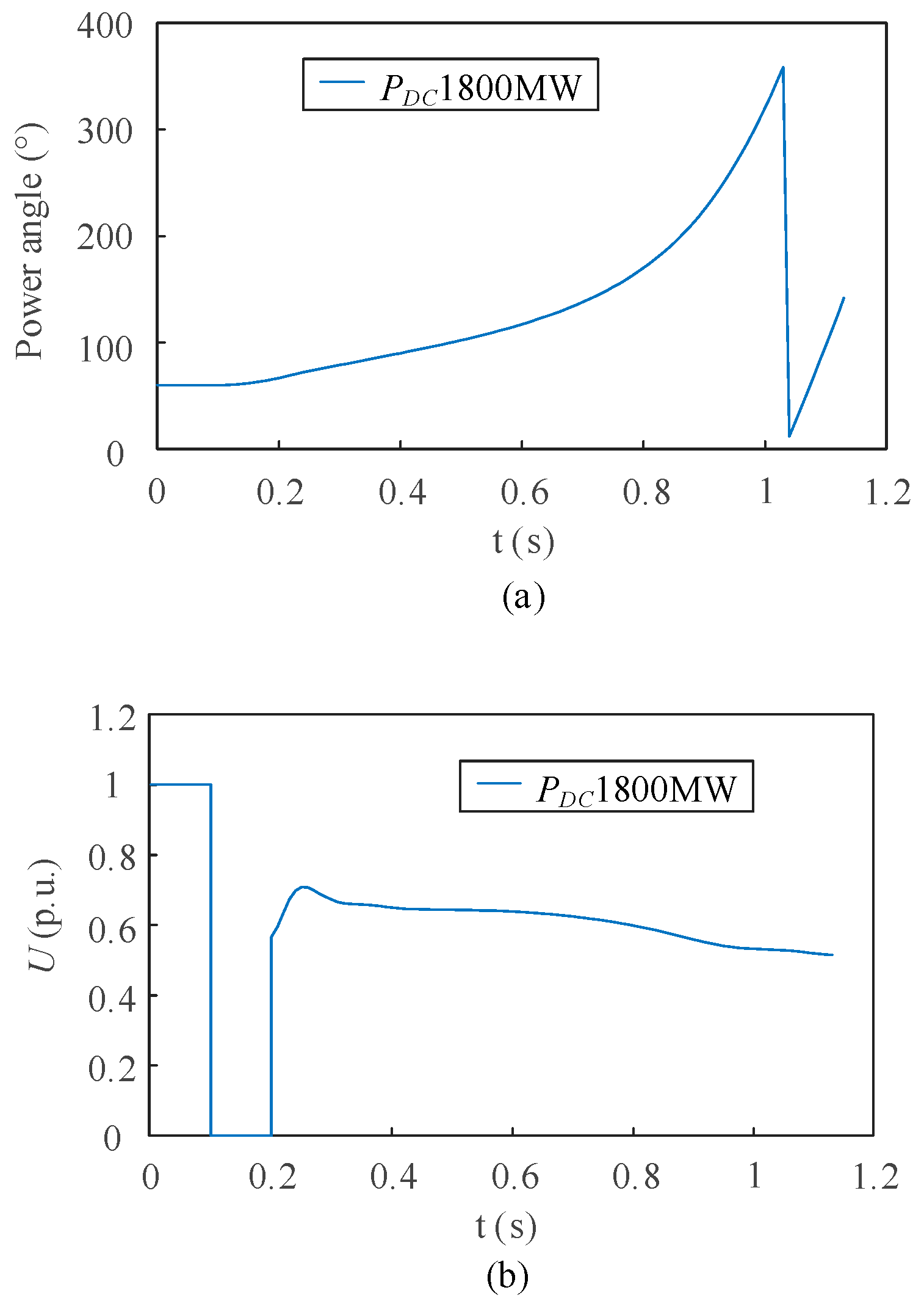
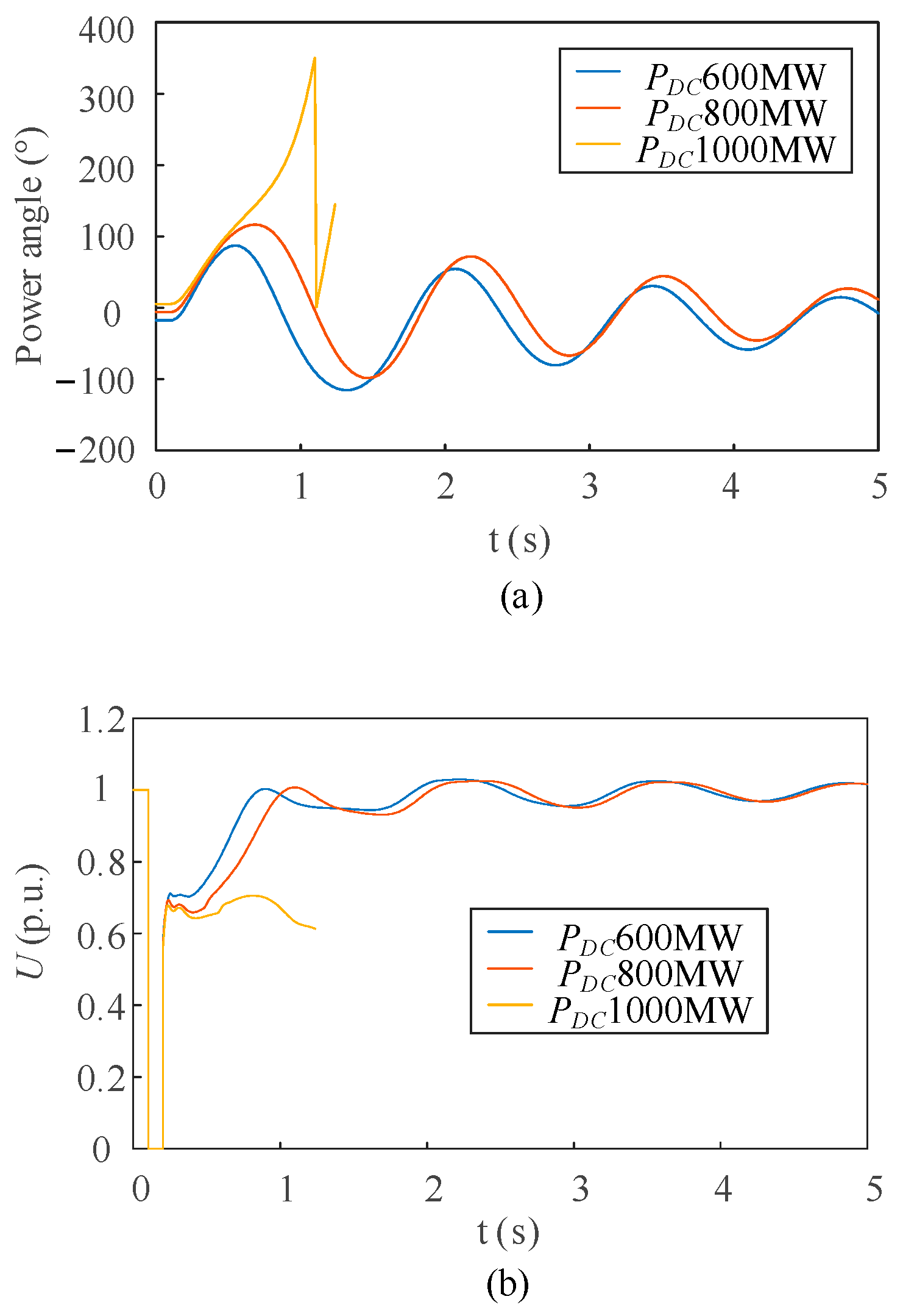
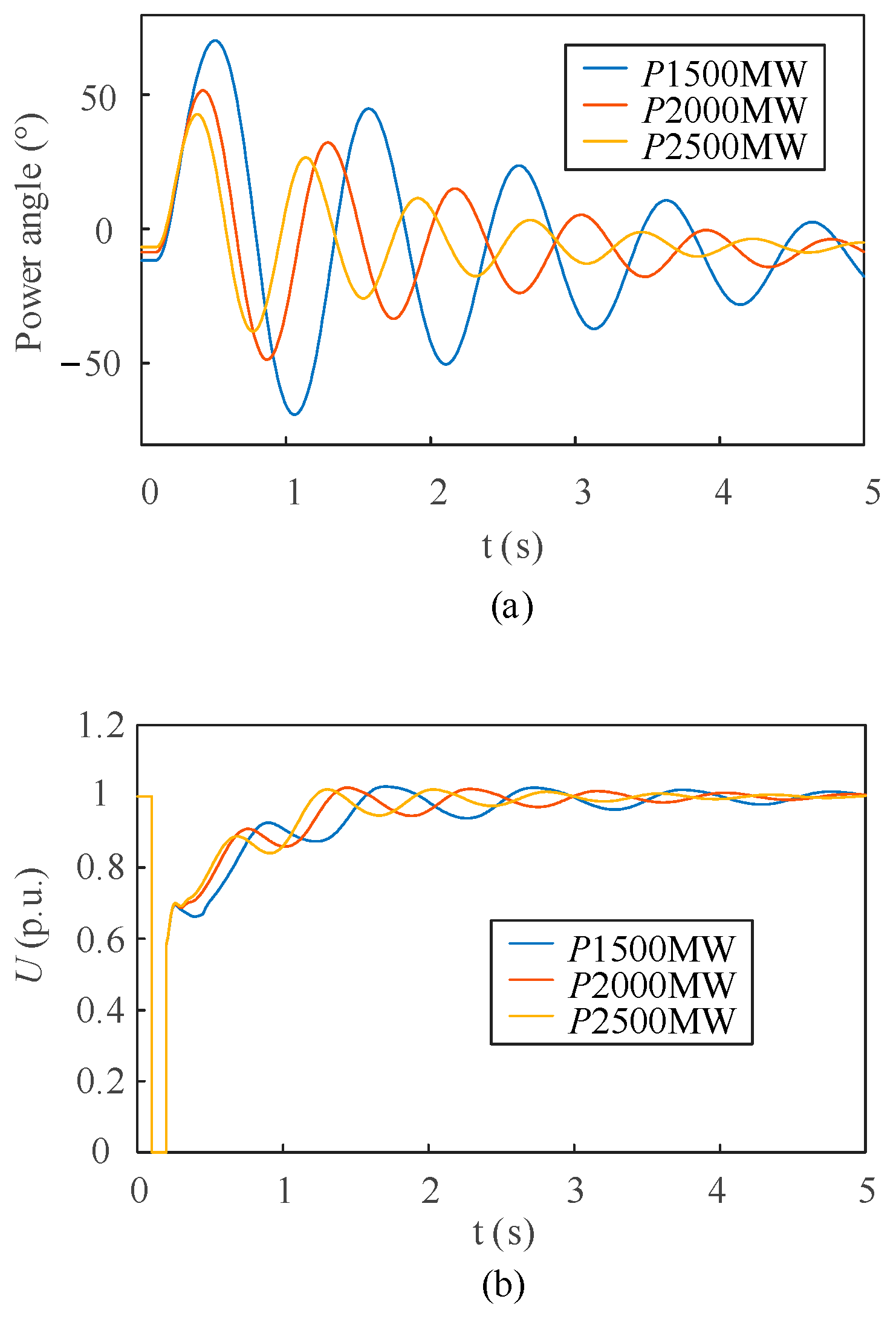
| Different Operating Conditions | Simulation Value | Theoretical Value | Error (%) |
|---|---|---|---|
| DC power 800 MW, Load 2400 MW; | 1895 | 2030 | 7.12 |
| DC power 1000 MW, Load 2600 MW; | 1925 | 2114 | 9.82 |
| DC power 1200 MW, Load 2800 MW; | 1980 | 2183 | 10.25 |
| DC power 1000 MW, Load 2400 MW; | 1725 | 1830 | 6.09 |
| DC power 1200 MW, Load 2400 MW; | 1595 | 1650 | 3.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, L.; Xu, S.; An, Z.; Wang, Y.; Wang, B. Research on the Quantitative Impact of Power Angle Oscillations on Transient Voltage Stability in AC/DC Receiving-End Power Grids. Energies 2025, 18, 1925. https://doi.org/10.3390/en18081925
Peng L, Xu S, An Z, Wang Y, Wang B. Research on the Quantitative Impact of Power Angle Oscillations on Transient Voltage Stability in AC/DC Receiving-End Power Grids. Energies. 2025; 18(8):1925. https://doi.org/10.3390/en18081925
Chicago/Turabian StylePeng, Long, Shiyun Xu, Zeyuan An, Yi Wang, and Bo Wang. 2025. "Research on the Quantitative Impact of Power Angle Oscillations on Transient Voltage Stability in AC/DC Receiving-End Power Grids" Energies 18, no. 8: 1925. https://doi.org/10.3390/en18081925
APA StylePeng, L., Xu, S., An, Z., Wang, Y., & Wang, B. (2025). Research on the Quantitative Impact of Power Angle Oscillations on Transient Voltage Stability in AC/DC Receiving-End Power Grids. Energies, 18(8), 1925. https://doi.org/10.3390/en18081925





