A Multi-Time Scale Optimal Scheduling Strategy for the Electro-Hydrogen Coupling System Based on the Modified TCN-PPO

Abstract

The regional integrated energy system, centered on electro-hydrogen technology, serves as a crucial mechanism for advancing the utilization of a high proportion of renewable energy and achieving the low-carbon transition of the energy system. In this context, a multi-time scale optimization model for distributed electro-hydrogen coupling systems is proposed, utilizing an enhanced deep reinforcement learning (DRL) method. Firstly, considering the comprehensive operation cost and real-time deviations, the optimization model of day-ahead and real-time multi-time scale electro-hydrogen coupling system is constructed. Secondly, A dynamic perception model of environmental information is established based on a time convolutional network (TCN) to achieve multi-time scale feature capture of the coupling system and to improve the ability of the agents to perceive the environment of the coupling system. Then, the proposed optimization model is transformed into the Markov decision process (MDP), and a modified Proximal Policy Optimization (PPO) algorithm is introduced to achieve optimal solutions. Finally, case studies are conducted to analyze the electro-hydrogen coupling system in a specific region. The case studies verify the effectiveness of deep reinforcement learning and the electro-hydrogen coupling system in new energy consumption.

1. Introduction

The carbon peaking and carbon neutrality goals necessitate transformative changes in China’s energy system, rendering the transition to a clean, low-carbon, and efficient energy architecture unavoidable [1]. However, the intermittent and volatile nature of both load demand and renewable energy generation presents significant challenges to the stable and secure operation of the power system [2]. In this context, hydrogen energy, recognized as a clean energy source, has garnered significant attention and emerged as a preferred solution for the integrated development of large-scale wind turbines (WT) and photovoltaic (PV) storage. The electro-hydrogen coupling system is increasingly viewed as a pivotal solution for modern power systems [3,4,5]. Investigating the optimal scheduling strategy of the electro-hydrogen coupling system holds substantial importance for enhancing new energy consumption and achieving the dual-carbon objectives within the power industry.

Currently, the primary methods to address the optimal scheduling of the electro-hydrogen coupling system are categorized into single-stage and two-stage methods. Stochastic programming (SP), a widely adopted single-stage method, involves developing an SP model and employing autoregressive moving average techniques to formulate a day-ahead scheduling model. This method optimizes the operation of the electro-hydrogen coupling system by incorporating uncertainties.

Leveraging autoregressive integrated moving average and forward selection techniques, reference [6] introduces a stochastic day-ahead scheduling model for renewable energy-based microgrids, which enables optimal energy management and dynamic energy balance in microgrids powered exclusively by renewable energy. Reference [7] examines the characteristics and requirements of electro-hydrogen shared energy storage and regional integrated energy systems, proposing an energy-sharing architecture and a hierarchical optimal scheduling method that incorporates hydrogen trading. This method utilizes particle swarm optimization (PSO) and mixed-integer linear programming algorithms, enhancing renewable energy utilization. In reference [8], a nonlinear mixed-integer dynamic optimal scheduling model is developed to minimize economic operating costs, carbon dioxide emissions, and energy consumption. The non-dominated sorting genetic algorithm is employed to derive a negative carbon optimal scheduling scheme for the integrated energy system, resulting in 7.23% reductions in operating cost and 9.94% in energy consumption compared with the conventional triple supply system.

Although SP offers a straightforward solution strategy, it is often impractical to predetermine the probability distributions of distributed energy sources, such as load and wind, in the practical implementation of the electro-hydrogen coupling system. Moreover, particle swarm optimization (PSO) and other heuristic algorithms risk trapping solutions in local optima, while the consistency and reliability of the solution strategy remain challenging to ensure. To address these challenges, reference [9] introduces an integrated energy scheduling strategy based on robust optimization (RO) combined with hydrogen energy, designed to perform effectively across all uncertainties. Reference [10] presents a novel multi-objective robust optimization model for an integrated energy system with hydrogen storage, addressing the source-load uncertainty issues in the electro-hydrogen coupling system. The model demonstrates its effectiveness in reducing cost, carbon emissions, and the abandonment of wind and solar energy. Reference [11] develops a data-driven robust optimization model by addressing the coordinated scheduling challenges in the multi-energy coupling system resulting from the expansion of wind and gas installations. The model demonstrates the effectiveness and superiority in coordinating the scheduling of the multi-energy coupling system. However, the results based on the robust optimization (RO) method tend to be conservative, and their high computational complexity renders them time-consuming and inefficient.

The two-stage optimization strategy typically accounts for prediction error characteristics across various time scales and is extensively employed in the operational methodologies of the electro-hydrogen coupling system. Reference [12] addresses the uncertainties in renewable energy generation and demand by implementing a multi-time scale rolling optimization method. This method constructs a hydrogen-based multi-energy microgrid energy management architecture, incorporating both day-ahead and real-time energy scheduling through model predictive control (MPC). This method aims to reduce microgrid operating costs and enhance system energy utilization efficiency. Authors in Reference [13] introduce a real-time energy management method and an optimal control strategy based on dynamic programming and model predictive control (DP-MPC). This strategy accounts for the characteristics and real-time operational statuses of diverse energy sources in the electro-hydrogen hybrid energy storage microgrid, facilitating effective energy management and optimal scheduling while enhancing system stability and economic performance. Zheng et al. [14] focus on the integrated energy system as their research subject, employing a multi-time scale integrated demand response method. They propose a strategic optimization operation architecture and a corresponding optimization model to achieve efficient, economical operation and equitable energy allocation within the integrated energy system. Reference [15] examines the multi-stage and multi-time scale features of the hydrogen-based integrated energy system. It develops a multi-stage and multi-time scale optimal energy management architecture to ensure efficient operation and optimal scheduling of the hydrogen-based integrated energy system.

The efficacy of model predictive control (MPC) is heavily reliant on the precision of the system model. Inaccurate models or the presence of unmodeled dynamic characteristics can result in control instability. Building on this foundation, References [16,17,18,19] investigate the application of two-stage RO in addressing system uncertainties. Reference [16], based on the regional integrated energy system, employs a two-stage RO method to propose a low-carbon economic scheduling strategy that accounts for the uncertainties of wind power and solar energy. This strategy supports the reliable operation and low-carbon development of the regional integrated energy system. Li et al. [17] examine the small-disturbance stability and dynamic response characteristics of the integrated hydrogen hybrid energy system. It introduces a two-stage RO method incorporating stability constraints and develops an associated optimization model to ensure the system’s economic stability. Leveraging the two-stage distributed RO theory within multi-region integrated energy systems, a two-stage distributed robust optimal control strategy is presented in reference [18]. This strategy optimizes the configuration of the multi-region integrated energy system by addressing the complex coupling relationships and uncertainties across regions. Reference [19] addresses energy sharing and carbon transfer by developing a two-stage distributed RO model for integrated energy system clusters. It introduces an optimal strategy rooted in RO theory to achieve economical and efficient operation of these clusters in uncertain environments.

Although the two-stage RO model offers enhanced flexibility and decision-making capabilities in managing uncertainties, such as fluctuations in wind power output, its solutions often remain overly conservative, failing to achieve an optimal balance between economic efficiency and system safety.

Deep reinforcement learning (DRL) integrates the expressive power of deep learning with the decision-making capabilities of reinforcement learning. Owing to its proficiency in handling complex and uncertain environments, it has garnered significant attention in the realm of electro-hydrogen scheduling applications. References [20,21] concentrate on the energy management of the electro-hydrogen coupling system and isolated hydrogen microgrids, utilizing DRL and predictor-driven stochastic optimal techniques to address challenges such as energy conversion, utilization, and information uncertainty. Yang et al. [22] examine the uncertainties within the electro-hydrogen integrated energy system and introduce a multi-stage stochastic scheduling method along with an associated optimal model to facilitate efficient, economical scheduling and ensure the reliable operation of the electro-hydrogen integrated energy system. In reference [23], the authors implement a day-ahead and real-time two-stage scheduling method, employing the Deep Deterministic Policy Gradient (DDPG) algorithm within DRL for the real-time stage. A data-driven two-stage scheduling strategy coupled with an associated optimal model for the multi-energy system is proposed to achieve efficient and economical scheduling of the system.

Kakodkar et al. [24] propose a DRL-based algorithm for optimal online economic dispatch in virtual power plants (VPPs), which leverages DRL to reduce computational complexity, incorporates the large and continuous state spaces arising from stochastic distributed generation characteristics, and implements an edge computing framework to address the stochasticity and high-dimensional state space challenges inherent in VPP operations.

Reference [25] addresses the challenges posed by operational uncertainties in microgrids with high renewable penetration rates to flexible operation by proposing a DRL-based collaborative energy management framework. This three-stage framework integrates internal pricing mechanism establishment, microgrid dispatch optimization, and VPP energy storage management, with comprehensive simulation experiments conducted using real-world datasets to validate the proposed methodology.

In reference [26], Huang et al. develop a DRL-based multi-scenario optimal dispatch methodology for VPPs. Their approach advances the field by designing renewable generation characteristic indices to quantify operational patterns, leveraging conditional generative adversarial networks for high-fidelity scenario data generation, and formulating a transformed VPP dispatch model that systematically integrates stochastic renewable behaviors. The methodology culminates in the application of the Soft Actor-Critic algorithm to derive robust economic dispatch strategies resilient to multi-source uncertainties. In summary, the existing research has made a great contribution to the modeling and solving of the scheduling of the electro-hydrogen coupling system. However, there are still two significant limitations in the existing literature:

(1)

Model dependency dilemma: Conventional methods frequently rely on a set of rigid assumptions and idealized scenarios, necessitating precise modeling of uncertainties and dynamic behaviors. However, in real-world applications, factors such as system parameters, fluctuations in renewable energy, variations in electro-hydrogen load demand, and other complexities exacerbate the model’s intricacy and the challenges of its resolution, thereby constraining the efficacy of conventional methods in practical settings [24].

(2)

Temporal feature neglect: DRL methods demonstrate significant potential in addressing complex decision-making challenges, relying on agents to perceive environmental states and formulate decisions. Nevertheless, current methods exhibit limited capacity to capture and analyze multi-time scale dynamic characteristics [12], making it challenging to discern precisely the temporal features of the coupling system across varying scales. Consequently, agents may overlook the equilibrium between long-term trends and short-term fluctuations during decision-making.

Unlike conventional approaches constrained by stochastic programming’s dependency on precise probability distributions, robust optimization’s tendency toward conservative strategies, and heuristic algorithms’ susceptibility to local optima, this paper proposes a novel multi-time scale optimal scheduling strategy utilizing DRL for the electro-hydrogen coupling system, which enables autonomous discovery of multi-timescale temporal dynamics through self-supervised feature extraction while achieving self-adaptive policy iteration via dual-mode advantage estimation. Taking into account the operational economy and carbon efficiency of the system, a day-ahead operational model targeting the lowest comprehensive cost, alongside a combined day-ahead and real-time optimal model aiming to minimize real-time deviations, is developed. This research incorporates the TCN model to achieve multi-scale perception and extraction of environmental information within the coupling system. Furthermore, a modified TCN-PPO algorithm is proposed for training and problem-solving, culminating in the formulation of a two-stage operational architecture for the system. This paper presents the following three key contributions:

(1)

This paper proposes a multi-time scale optimal scheduling architecture for the electro-hydrogen coupling system, integrating the modified PPO and TCN algorithms. The temporal characteristics of the coupling system are comprehensively extracted and utilized as model inputs through TCN. Additionally, the optimal paradigm of deep reinforcement learning is employed to address the real-time and stochastic challenges introduced by renewable energy sources and loads. This method not only reduces operational costs but also enhances the utilization of new energy.

(2)

A multi-time scale environmental perception model, leveraging TCN, is developed for the electro-hydrogen coupling system. By analyzing the multi-time scale temporal structure data of the coupling system, which encompasses local patterns and long-term dependencies, the TCN model facilitates a profound exploration of multi-time scale features. This enhances the model’s capacity to perceive and interpret the environmental dynamics of the coupling system.

(3)

To address the limitations of the conventional PPO algorithm, including low training efficiency, poor stability, and weak state perception, the modified PPO algorithm is introduced. By incorporating state feature enhancement, the adaptive clipping rate (ACR), and the prioritized experience replay (PER) mechanism, high-quality solutions for multi-time scale optimal challenges in the coupling system are successfully obtained.

2. Problem Formulation

Figure 1 illustrates the multi-time scale optimal scheduling architecture of the electro-hydrogen coupling system, developed based on the modified TCN-PPO architecture. The upper and lower sections of the diagram depict the system’s optimal scheduling architecture for the day-ahead and real-time stages, respectively. Additionally, the left section of the diagram is divided into a multi-time scale schematic encompassing both day-ahead and real-time stages. In the day-ahead optimization stage, the prediction results of equipment output serve as model inputs to formulate the day-ahead operation plan, whereas, in the real-time optimization stage, the model detects real-time power fluctuations to dynamically adjust the operation plan. Furthermore, the central section of the diagram displays two TCN-based environment sensing modules for the day-ahead and real-time scales, respectively, enabling the agent to acquire deep temporal characteristics of the electrical coupling system. Finally, the right side of the figure presents the policy output module incorporating the modified PPO algorithm, which optimizes model training efficiency through state feature enhancement, the adaptive clipping rate, and the PER mechanism. The optimal mapping between environmental states and scheduling policies is successfully established.

2.1. Multi-Time Scale Optimal Operation Model for Electro-Hydrogen Coupling System

2.1.1. Day-Ahead Optimization

The minimization of the integrated operating cost in the day-ahead optimization stage is set as the optimization objective $F_1$. The objective includes the power purchase cost, the system operation and maintenance cost, and the start–stop cost of the electrolyzer. The optimization model objectives and constraints are as follows:

• objective function

$$\min F_1={\displaystyle \sum _{t=1}^T{C}_t^{\mathrm{buy},\mathrm{long}}+C_t^{\mathrm{op},\mathrm{long}}+C_t^{\mathrm{start},\mathrm{long}}}$$

(1)

$$C_t^{\mathrm{buy},\mathrm{long}}={\mu }_t^{\mathrm{TOU}}{P}_t^{\mathrm{buy},\mathrm{long}}\Delta t$$

(2)

$$\begin{array}{l}{C}_t^{\mathrm{op},\mathrm{long}}={\mu }^{\mathrm{ESS}}{\displaystyle \sum _{i=1}^{N^{\mathrm{ESS}}}\left|P_{i,t}^{\mathrm{ESS},\mathrm{long}}\right|\Delta t}+\\ {\mu }^{\mathrm{EC}}{\displaystyle \sum _{i=1}^{N^{\mathrm{EC}}}{P}_{i,t}^{\mathrm{EC},\mathrm{long}}\Delta t}+{\mu }^{\mathrm{HFC}}{\displaystyle \sum _{i=1}^{N^{\mathrm{HFC}}}{P}_{i,t}^{\mathrm{HFC},\mathrm{long}}\Delta t}\end{array}$$

(3)

$$C_t^{\mathrm{start},\mathrm{long}}={\mu }^{\mathrm{start}}{\displaystyle \sum _{i=1}^{N^{\mathrm{EC}}}{\phi }_{i,t}\left(1-{\phi }_{i,t-1}\right)+{\phi }_{i,t-1}\left(1-{\phi }_{i,t}\right)}$$

(4)

where $C_t^{\mathrm{buy},\mathrm{long}}$, $C_t^{\mathrm{op},\mathrm{long}}$, $C_t^{\mathrm{start},\mathrm{long}}$, $C_t^{\mathrm{pun},\mathrm{long}}$ are the power purchase cost, the system operation and maintenance cost, and the start–stop cost of the electrolyzer, respectively, at time t of the previous day’s planning stage. T is the total time step. ${\mu }_t^{\mathrm{TOU}}$, ${\mu }^{\mathrm{ESS}}$, ${\mu }^{\mathrm{EC}}$, ${\mu }^{\mathrm{HFC}}$, and ${\mu }^{\mathrm{start}}$ are grid industrial time-of-use tariffs, electric storage Operation and Maintenance (O&M) cost factors, electrolyzer O&M cost factors, fuel cell O&M coefficients, and the start–stop cost of the electrolyzer, respectively. $P_t^{\mathrm{buy},\mathrm{long}}$ is the power of the electricity purchased from the main grid. $N^{\mathrm{ESS}}$, $N^{\mathrm{EC}}$, and $N^{\mathrm{HFC}}$ are the number of electrical storage, electrolyzer, and fuel cell, respectively. $P_{i,t}^{\mathrm{ESS},\mathrm{long}}$ is the charge/discharge power of the ith electric energy storage at time t, with a positive value during discharge and a negative value during charging. $P_{i,t}^{\mathrm{EC},\mathrm{long}}$ is the power of the ith electrolyzer at time t. ${\phi }_{i,t}$ is the start/stop status of the ith electrolyzer at time t, where 1 signifies starting and 0 otherwise. $P_{i,t}^{\mathrm{HFC},\mathrm{long}}$ is the discharge power of the ith Hybrid Fuel Cell (HFC) at time t.

2.

Constraints

(1)

Electrical load balance constraints

$$\begin{array}{l}{P}_t^{\mathrm{buy},\mathrm{long}}+{\displaystyle \sum _{i=1}^{N^{\mathrm{PV}}}{P}_{i,t}^{\mathrm{PV},\mathrm{long}}}+{\displaystyle \sum _{i=1}^{N^{\mathrm{WT}}}{P}_{i,t}^{\mathrm{WT},\mathrm{long}}}+{\displaystyle \sum _{i=1}^{N^{\mathrm{ESS}}}{P}_{i,t}^{\mathrm{ESS},\mathrm{long}}}\\ +{\displaystyle \sum _{i=1}^{N^{\mathrm{HFC}}}{P}_{i,t}^{\mathrm{HFC},\mathrm{long}}}=P_t^{\mathrm{load},\mathrm{long}}+{\displaystyle \sum _{i=1}^{N^{\mathrm{EC}}}{P}_{i,t}^{\mathrm{EC},\mathrm{long}}}\end{array}$$

(5)

where $N^{\mathrm{PV}}$, $N^{\mathrm{WT}}$ are the number of photovoltaic and wind power respectively. $P_{i,t}^{\mathrm{PV},\mathrm{L}}$, $P_{i,t}^{\mathrm{WT},\mathrm{L}}$, $P_t^{\mathrm{Load},\mathrm{L}}$ are the output of the ith photovoltaic at time t, the output of the ith wind power at time t, and the size of the electrical load at time t, respectively. All electrical power variables in the equations are expressed in units of kilowatts (kW).

(2)

Hydrogen load balance constraints

$$\begin{array}{l}{\displaystyle \sum _{i=1}^{N^{\mathrm{EC}}}{\eta }^{\mathrm{EC}}{H}_{i,t}^{\mathrm{EC},\mathrm{long}}}+{\displaystyle \sum _{i=1}^{N^{\mathrm{HST}}}{\eta }^{\mathrm{HST},\mathrm{dis},\mathrm{long}}{H}_{i,t}^{\mathrm{HST},\mathrm{dis}}}=\\ H_t^{\mathrm{load},\mathrm{long}}+{\displaystyle \sum _{i=1}^{N^{\mathrm{HFC}}}{H}_{i,t}^{\mathrm{HFC},\mathrm{long}}/{\eta }^{\mathrm{HFC}}}+{\displaystyle \sum _{i=1}^{N^{\mathrm{HST}}}{H}_{i,t}^{\mathrm{HST},\mathrm{ch},\mathrm{long}}/{\eta }^{\mathrm{HST},\mathrm{ch}}}\end{array}$$

(6)

where $H_{i,t}^{\mathrm{EC},\mathrm{L}}$ is the amount of hydrogen produced by the ith electrolyzer at time t. $H_{i,t}^{\mathrm{HST},\mathrm{dis},\mathrm{L}}$ is the amount of hydrogen released from the ith hydrogen storage tank at time t. $H_t^{\mathrm{Load},\mathrm{L}}$ is the hydrogen load size at time t. $H_{i,t}^{\mathrm{HFC},\mathrm{L}}$ is the hydrogen consumption of the ith fuel cell at time t. $H_{i,t}^{\mathrm{HST},\mathrm{ch},\mathrm{L}}$ is the hydrogen filling of the ith hydrogen storage tank at time t. All hydrogen-related variables in the equations are expressed in units of kilograms (kg). ${\eta }^{\mathrm{EC}},{\eta }^{\mathrm{HST},\mathrm{dis}},{\eta }^{\mathrm{HST},\mathrm{ch}},{\eta }^{\mathrm{HFC}}\in (0, 1]$ represent the hydrogen production efficiency of the electrolyzer, the charging/discharging efficiency of the hydrogen storage tank, and the hydrogen utilization efficiency of the fuel cell, respectively.

(3)

Contact line power constraints

$$P_{\min }^{\mathrm{PN}}\le P_t^{\mathrm{buy},\mathrm{long}}\le P_{\max }^{\mathrm{PN}}$$

(7)

where $P_{\min }^{\mathrm{PN}}$, $P_{\max }^{\mathrm{PN}}$ are the lower and upper limits of the power purchased from the main grid contact line, respectively.

(4)

Electrolyzer power constraints

$$\begin{array}{l}\left(1-{\phi }_{i,t}\right)P_{i,t}^{\mathrm{EC},0}+{\phi }_{i,t}{P}_{i,\min }^{\mathrm{EC}}\le P_{i,t}^{\mathrm{EC},\mathrm{long}}\\ \le \left(1-{\phi }_{i,t}\right)P_{i,t}^{\mathrm{EC},0}+{\phi }_{i,t}{P}_{i,\max }^{\mathrm{EC}}\end{array}$$

(8)

where $P_{i,t}^{\mathrm{EC},0}$ is the standby power of the ith electrolyzer at time t. $P_{\min }^{\mathrm{EC}}$, $P_{\max }^{\mathrm{EC}}$ are the minimum and maximum operating power of the electrolyzer, respectively.

(5)

Electrical storage operational constraints

$$\left|P_{i,t}^{\mathrm{ESS},\mathrm{long}}\right|\le P_{i,\max }^{\mathrm{ESS}}$$

(9)

$$S_{i,\min }^{\mathrm{ESS}}\le S_{i,t}^{\mathrm{ESS},\mathrm{long}}\le S_{i,\max }^{\mathrm{ESS}}$$

(10)

where $P_{i,\max }^{\mathrm{ESS}}$ is the maximum charge/discharge power of the ith energy storage system (ESS). $S_{i,t}^{\mathrm{ESS},\mathrm{long}}$ is the SOC of the ith ESS at time t. $S_{i,\min }^{\mathrm{ESS}}$ and $S_{i,\max }^{\mathrm{ESS}}$ are the lower and upper SOC limits of the ith ESS, respectively.

2.1.2. Real-Time Optimization

To reduce the day-ahead and real-time two-stage operational deviation and improve the system’s ability to consume clean energy, the adjustment cost as well as the penalty for wind and solar abandonment are taken as the optimization objective $F_2$ in the real-time optimization.

• Objective function

$$\min F_2=\Delta C_t^{\mathrm{buy},\mathrm{short}}+\Delta C_t^{\mathrm{op},\mathrm{short}}+C_t^{\mathrm{pun},\mathrm{short}}$$

(11)

$$\Delta C_t^{\mathrm{buy},\mathrm{short}}={\lambda }_1^{\mathrm{pun}}\left|\Delta P_t^{\mathrm{buy},\mathrm{short}}\right|\Delta t$$

(12)

$$\Delta C_t^{\mathrm{op},\mathrm{short}}={\lambda }_2^{\mathrm{pun}}\left(\begin{array}{l}{\displaystyle \sum _{i=1}^{N^{\mathrm{ESS}}}\left|\Delta P_{i,t}^{\mathrm{ESS},\mathrm{short}}\right|\Delta t}+\\ {\displaystyle \sum _{i=1}^{N^{\mathrm{EC}}}\left|\Delta P_{i,t}^{\mathrm{EC},\mathrm{short}}\right|\Delta t}+{\displaystyle \sum _{i=1}^{N^{\mathrm{HFC}}}\left|\Delta P_{i,t}^{\mathrm{HFC},\mathrm{short}}\right|\Delta t}\end{array}\right)$$

(13)

$$C_t^{\mathrm{pun},\mathrm{short}}={\lambda }_3^{\mathrm{pun}}\left({\displaystyle \sum _{i=1}^{N^{\mathrm{PV}}}{P}_{i,t}^{\mathrm{PV},\mathrm{cut},\mathrm{short}}\Delta t}+{\displaystyle \sum _{i=1}^{N^{\mathrm{WT}}}{P}_{i,t}^{\mathrm{WT},\mathrm{cut},\mathrm{short}}\Delta t}\right)$$

(14)

where $\Delta C_t^{\mathrm{buy},\mathrm{short}}$, $\Delta C_t^{\mathrm{op},\mathrm{short}}$, $C_t^{\mathrm{pun},\mathrm{short}}$ are the intraday short-time scale power purchase adjustment cost, system operation power adjustment cost, and wind and light abandonment penalty, respectively. ${\lambda }_1^{\mathrm{pun}}$, ${\lambda }_2^{\mathrm{pun}}$, ${\lambda }_3^{\mathrm{pun}}$ are the penalty coefficients. $\Delta P_t^{\mathrm{buy},\mathrm{short}}$ is the power purchase adjustment power at time t. $\Delta P_{i,t}^{\mathrm{ESS},\mathrm{short}}$ is the adjustment power of the ith ESS at time t. $\Delta P_{i,t}^{\mathrm{EC},\mathrm{short}}$ is the adjustment power of the ith EC at time t. $\Delta P_{i,t}^{\mathrm{HFC},\mathrm{short}}$ is the adjustment power of the ith HFC at time t. $P_{i,t}^{\mathrm{PV},\mathrm{cut},\mathrm{short}}$ is the discarded power of the ith PV at time t. $P_{i,t}^{\mathrm{WT},\mathrm{cut},\mathrm{short}}$ is the discarded power of the ith wind power at time t.

2.

Constraints

Short-time scale constraints should be considered for long-time scale scheduling plan constraints. Power adjustments based on the day-ahead power plan lead to an intraday real-time power plan:

$$P_t^{\mathrm{buy},\mathrm{short}}=P_t^{\mathrm{buy},\mathrm{long}}+\Delta P_t^{\mathrm{buy},\mathrm{short}}$$

(15)

$$P_{i,t}^{\mathrm{ESS},\mathrm{short}}=P_{i,t}^{\mathrm{ESS},\mathrm{long}}+\Delta P_{i,t}^{\mathrm{ESS},\mathrm{short}}$$

(16)

$$P_{i,t}^{\mathrm{EC},\mathrm{short}}=P_{i,t}^{\mathrm{EC},\mathrm{long}}+\Delta P_{i,t}^{\mathrm{EC},\mathrm{short}}$$

(17)

$$P_{i,t}^{\mathrm{HFC},\mathrm{short}}=P_{i,t}^{\mathrm{HFC},\mathrm{long}}+\Delta P_{i,t}^{\mathrm{HFC},\mathrm{short}}$$

(18)

where $P_t^{\mathrm{buy},\mathrm{short}}$ is the intraday real-time power purchase. $P_{i,t}^{\mathrm{ESS},\mathrm{short}}$ is the charging and discharging power of the ith ESS at time t. $P_{i,t}^{\mathrm{EC},\mathrm{short}}$ is the power of the ith Electrolytic Cell (EC) at time t. $P_{i,t}^{\mathrm{HFC},\mathrm{short}}$ is the power of the ith HFC at time t.

2.2. TCN-Based Dynamic Sensing Model for Environmental Information

The operational characteristics and temporal features of various devices in the electro-hydrogen coupling system exhibit significant variability. The limited capability of conventional DRL methods to capture temporal features hinders the comprehensive identification of time-dependent and high-dimensional environmental information. Compared with the gradient vanishing issues and sequential computation constraints inherent in traditional recurrent neural networks when modeling long-term temporal dependencies, TCN addresses these limitations through causal convolutions that preserve chronological causality in the temporal dimension. By employing dilated convolutions to construct exponentially expanding receptive fields, TCN effectively captures multi-scale temporal patterns while enabling highly efficient parallel computations. This architecture demonstrates particular suitability for energy system optimization scenarios requiring simultaneous modeling of short-term operational fluctuations and long-term evolutionary trends in equipment behavior. To address this issue, a dynamic environmental sensing model based on TCN is proposed. The proposed model is designed to effectively extract multi-time scale temporal features from the environmental data of the electro-hydrogen hybrid energy storage system and precisely capture system dynamics. The model offers robust support for the development of more accurate and efficient scheduling strategies.

The TCN algorithm processes and analyzes temporal data using convolutional neural networks, effectively capturing both local patterns and long-term dependencies. The algorithm consists of the following three main modules.

2.2.1. Causal Convolution

Causal convolution constitutes a fundamental component of the TCN. This mechanism ensures that the model avoids accessing future information by employing specific convolutional operations, thereby mitigating the issue of information leakage [25]. The equation of causal convolution is as follows:

$$y_t={\displaystyle \sum _{\tau =0}^{T-1}{w}_{\tau }}·x_{\max (t-\tau ,0)}$$

(19)

where $y_t$ is the output. T is the width of the convolution kernel. $w_{\tau }$ is the weight of the convolution kernel at delay τ. $x_{\max (t-\tau ,0)}$ is the input at time point t − τ. τ is the time delay of the convolution kernel. If $t-\tau <0$, then 0 is used instead.

2.2.2. Dilated Convolution

Figure 2 illustrates the schematic representation of dilated convolution. Based on the standard convolution operation, the receptive field of the convolution kernel is extended through the introduction of multiple “holes” between its neighboring elements. This method enables the TCN to substantially broaden its receptive domain and improve its ability to perceive the electro-hydrogen coupling system while maintaining the original size of the convolution kernel. The mathematical expression $F(x_t)$ for the dilated convolution is as follows:

$$F(x_t)={\displaystyle \sum _{i=0}^{k-1}{f}_i}\cdot x_{t-d\cdot i}$$

(20)

where $x_{t-d\cdot i}$ is the input at time point $t-d\cdot i$. f is the filter, and k is the size of the filter. d is the dilation rate, which determines the number of voids in the convolution kernel.

2.2.3. Residual Connection

To mitigate the gradient vanishing issue and accelerate network convergence, the TCN incorporates skip connections via residual blocks, facilitating information flow across layers. This method allows each network layer to focus on learning residual mappings rather than reconstructing the complete transformation from scratch. It substantially enhances the training stability of deep networks and bolsters the model’s expressive capability.

$$y=\sigma (x+G(x))$$

(21)

where $\sigma$ is the activation function. G(x) is the series residual modular transform.

2.3. System Operation Model Based on MDP

Considering the dynamics of environmental information in multi-time scales of the coupling system, we construct the multi-time scale optimal model as an MDP and use DRL to solve it. As a sequential decision-making architecture, the MDP seeks to identify an optimal policy that maximizes the cumulative rewards achieved by the agents. Within this architecture, the operational state of the coupling system is defined as the state space. The potential scheduling strategies constitute the action space, while the reward function is formulated based on the system’s operational objectives and constraints. By integrating the sequential decision-making capabilities of MDP with the high-dimensional state space processing abilities of DRL, the model effectively addresses the dynamic variations of environmental information across multi-time scales in the coupling system. The details of the modeling process are delineated below.

2.3.1. State Space

Based on the operation information of the electro-hydrogen coupling system, the long-time scale state $s_t^{\mathrm{long}}$ and the short-time scale state $s_t^{\mathrm{short}}$ are obtained as follows, respectively:

$$s_t^{\mathrm{long}}=\left\{P_{i,t}^{\mathrm{PV},\mathrm{long}},P_{i,t}^{\mathrm{WT},\mathrm{long}},S_{i,t}^{\mathrm{ESS},\mathrm{long}},P_t^{\mathrm{load},\mathrm{long}},H_t^{\mathrm{load},\mathrm{long}}\right\}$$

(22)

$$s_t^{\mathrm{short}}=\left\{\begin{array}{l}{P}_{i,t}^{\mathrm{PV},\mathrm{short}},P_{i,t}^{\mathrm{WT},\mathrm{short}},S_{i,t}^{\mathrm{ESS},\mathrm{short}},P_t^{\mathrm{load},\mathrm{short}},\\ H_t^{\mathrm{load},\mathrm{short}},P_{i,t}^{\mathrm{ESS},\mathrm{long}},P_{i,t}^{\mathrm{EC},\mathrm{long}},P_{i,t}^{\mathrm{HFC},\mathrm{long}}\end{array}\right\}$$

(23)

where $P_{i,t}^{\mathrm{PV},\mathrm{short}}$ is the real-time output of the ith PV at time t. $P_{i,t}^{\mathrm{WT},\mathrm{short}}$ is the real-time output of the ith wind power at time t. $S_{i,t}^{\mathrm{ESS},\mathrm{short}}$ is the real-time SOC of ith ESS at time t. $P_t^{\mathrm{load},\mathrm{short}}$ is the size of electrical load at time t. $H_t^{\mathrm{load},\mathrm{short}}$ is the electrical load size at time t.

2.3.2. Action Space

Based on the system state information, the agents can select an action strategy and execute it in the action space. The long-time scale and short-time scale actions $a_t^{\mathrm{long}}$ and $a_t^{\mathrm{short}}$ can be described as follows:

$$a_t^{\mathrm{long}}=\left\{P_{i,t}^{\mathrm{ESS},\mathrm{long}},P_{i,t}^{\mathrm{EC},\mathrm{long}},P_{i,t}^{\mathrm{HFC},\mathrm{long}}\right\}$$

(24)

$$a_t^{\mathrm{short}}=\left\{\begin{array}{l}\Delta P_{i,t}^{\mathrm{ESS},\mathrm{short}},\Delta P_{i,t}^{\mathrm{EC},\mathrm{short}},\Delta P_{i,t}^{\mathrm{HFC},\mathrm{short}}\\ ,P_{i,t}^{\mathrm{PV},\mathrm{cut},\mathrm{short}},P_{i,t}^{\mathrm{WT},\mathrm{cut},\mathrm{short}}\end{array}\right\}$$

(25)

2.3.3. Reward Function

The reward is defined as the immediate feedback received by the agent upon executing an action policy, where a higher reward value indicates a more effective strategy. Therefore, the long-time scale and short-time scale reward functions $r_t^{\mathrm{long}}$ and $r_t^{\mathrm{short}}$ can be described as follows:

$$r_t^{\mathrm{long}}=-C_t^{\mathrm{buy},\mathrm{long}}-C_t^{\mathrm{op},\mathrm{long}}-C_t^{\mathrm{start},\mathrm{long}}$$

(26)

$$r_t^{\mathrm{short}}=-\Delta C_t^{\mathrm{buy},\mathrm{short}}-\Delta C_t^{\mathrm{op},\mathrm{short}}-C_t^{\mathrm{pun},\mathrm{short}}$$

(27)

3. Proposed Method Based on the Modified TCN-PPO

3.1. Fundamentals of the PPO Algorithm

When coordinating intermittent renewable energy integration with discrete electrolyzer operations, the PPO algorithm effectively balances the exploration–exploitation trade-off. Compared with deterministic policy methods like Deep Deterministic Policy Gradient (DDPG), PPO’s adaptive clipping mechanism prevents catastrophic policy divergence during hydrogen load transients while maintaining multi-timescale coordination capabilities.

As a DRL algorithm based on Actor–Critic architecture [26], the dominance function ${\widehat{A}}_t(a,s)$ of the PPO algorithm can be expressed as follows:

$$\begin{array}{ll}{\widehat{A}}_t(a,s)=& -V_{\varphi }\left(s_t\right)+r_t+\gamma r_{t+1}+\cdots \\ & +{\gamma }^{K-t+1}{r}_{K-1}+{\gamma }^{K-t}{V}_{\varphi }\left(s_K\right)\end{array}$$

(28)

where $V_{\varphi }\left(s_t\right)$ is the state value function. $\gamma$ is the discount rate. $K$ is the horizon length.

To maximize the desired reward, the objective function L of the PPO algorithm can be expressed as follows:

$$\begin{array}{ll}L& =\max {\mathbb{E}}_t\left[{\displaystyle \frac{{\pi }_{{\theta }^{k+1}}(a|s)}{{\pi }_{{\theta }^k}(a|s)}}{\widehat{A}}_t(a,s)\right]\\ & =\max {\mathbb{E}}_t\left[{\tau }_t{\widehat{A}}_t(a,s)\right]\end{array}$$

(29)

where ${\tau }_t$ is the ratio of old and new policy. ${\pi }_{{\theta }^k}(·)$ is the strategy function of the kth step.

The ratio between the old and new policies is typically constrained during training to maintain process stability. The trimmed objective function $L_{\mathrm{clip}}$ can be expressed as follows:

$$L_{\mathrm{clip}}=\max {\mathbb{E}}_t\left[\min \left({\tau }_t{\widehat{A}}_t,\mathrm{clip}\left({\tau }_t\right){\widehat{A}}_t\right)\right]$$

(30)

$$\mathrm{clip}\left({\tau }_t\right)=\left\{\begin{array}{ll}1-\epsilon ,& {\tau }_t<1-\epsilon \\ {\tau }_t,& 1-\epsilon \le {\tau }_t\le 1+\epsilon \\ 1+\epsilon ,& {\tau }_t>1+\epsilon \end{array}\right.$$

(31)

where clip( ) is the clipping function. $\epsilon$ is the clipping rate clip ratio.

3.2. Modified Mechanisms of the PPO Algorithm

Although the PPO algorithm is widely used for addressing continuous action decision problems, it faces significant limitations, including weak temporal feature perception, limited exploration capability, and poor stability. To address these limitations, we introduce the modified TCN-PPO algorithm, an enhanced version of TCN-PPO. The algorithm’s training performance and solution quality are enhanced through the state feature augmentation, the adaptive clipping rate, and the PER caching mechanism.

3.2.1. State Feature Enhancement

TCN-based multi-time scale environmental information sensing for an electro-hydrogen coupling system to enhance the sensing ability of the agent on the state characteristics of the environment. The state $s_t^{\mathrm{long}}$ of the DRL agent will be expanded to a multi-time step state ${\widehat{s}}_t^{\mathrm{long}}$.

$$\left\{\begin{array}{l}{\widehat{s}}_t^{\mathrm{long}}=\left\{s_{t-{\kappa }_1}^{\mathrm{long}},s_{t-{\kappa }_1+1}^{\mathrm{long}},\cdots ,s_t^{\mathrm{long}}\right\}\\ {\widehat{s}}_t^{\mathrm{short}}=\left\{s_{t-{\kappa }_2}^{\mathrm{short}},s_{t-{\kappa }_2+1}^{\mathrm{short}},\cdots ,s_t^{\mathrm{short}}\right\}\end{array}\right.$$

(32)

where ${\widehat{s}}_t^{\mathrm{long}}$ and ${\widehat{s}}_t^{\mathrm{short}}$ represent the long-time scale states and short-time scale states after the introduction of the TCN, respectively. ${\kappa }_1$ and ${\kappa }_2$ are the information-capturing fields of view of the long-time scale and short-time scale agents, respectively.

3.2.2. Adaptive Clipping Rate

To balance the algorithm’s convergence speed during the pre-training stage and its stability during the post-training stage, the Cosine Decay model is employed to adaptively adjust the hyper-parameter clipping rate $\epsilon$. The clipping rate during training can be calculated by Equation (33).

$$\epsilon ={\displaystyle \frac{1}{2}}{\epsilon }_0\left[1+\cos \left({\displaystyle \frac{n}{N}}\pi \right)\right]$$

(33)

where ${\epsilon }_0$ is the initial clipping rate. n and N represent the current training round and total rounds, respectively.

As shown in Equation (33), during the initial training stage, samples offer substantial learning information and experience, facilitating significant model adjustments to enhance strategy performance. Therefore, a larger clipping rate is set to improve the algorithm update amplitude and training efficiency. During the later training stages, as the model strategy improves, a lower clipping rate is adopted to ensure convergence stability.

3.2.3. Prioritized Experience Replay

In reinforcement learning, a higher loss value indicates a greater contribution of the sample to parameter updates. This signifies a higher intrinsic value of the sample. To maximize the empirical contribution of the samples, the PER caching mechanism is employed. By sorting training samples based on their TD-error magnitudes, high-value samples are effectively utilized.

$$p_i={\displaystyle \frac{1/\vartheta \left(i\right)}{{\displaystyle \sum _{j=1}^{N_{\mathrm{s}}}1/\vartheta \left(j\right)}}}$$

(34)

where $p_i$ is the probability that the ith sample is sampled, $i=1,2,\dots ,N_s$. $\vartheta \left(•\right)$ represents the rank order number of sample among all samples. $N_{\mathrm{s}}$ is the number of samples.

3.3. Training Process of the Proposed Modified TCN-PPO Algorithm

The proposed training flow based on the modified TCN-PPO method is shown in Figure 3. Firstly, initialize the parameters of the modified TCN-PPO agent network and start the environment initialization at the beginning of each round. Secondly, judge the current task time scale, and if it is the day-ahead stage, observe the environment state A based on the TCN and formulate the corresponding system day-ahead operation plan $a_t^{\mathrm{long}}$ based on Equation (24), which serves as the decision-making basis for the intra-day real-time scenario. After the execution of action $a_t^{\mathrm{long}}$ based on Equation (26), the reward $r_t^{\mathrm{long}}$ obtained by the agent is calculated, and the sample $\left\{{\widehat{s}}_t^{\mathrm{long}},a_t^{\mathrm{long}},r_t^{\mathrm{long}},{\widehat{s}}_{t+1}^{\mathrm{long}}\right\}$ is stored in the buffer D^long for training. Then, samples are drawn every N^long step based on the PER mechanism to update the agent network parameters. Similarly, in the case of the intraday real-time stage, the real-time scenario is adjusted based on the system’s day-ahead running schedule. Finally, at the end of each training round, the clipping rate $\epsilon$ is adjusted based on the adaptive clipping rate mechanism proposed in Equation (33). The above steps are repeated until the maximum training round is complete to complete the training of the proposed algorithm.

4. Case Studies

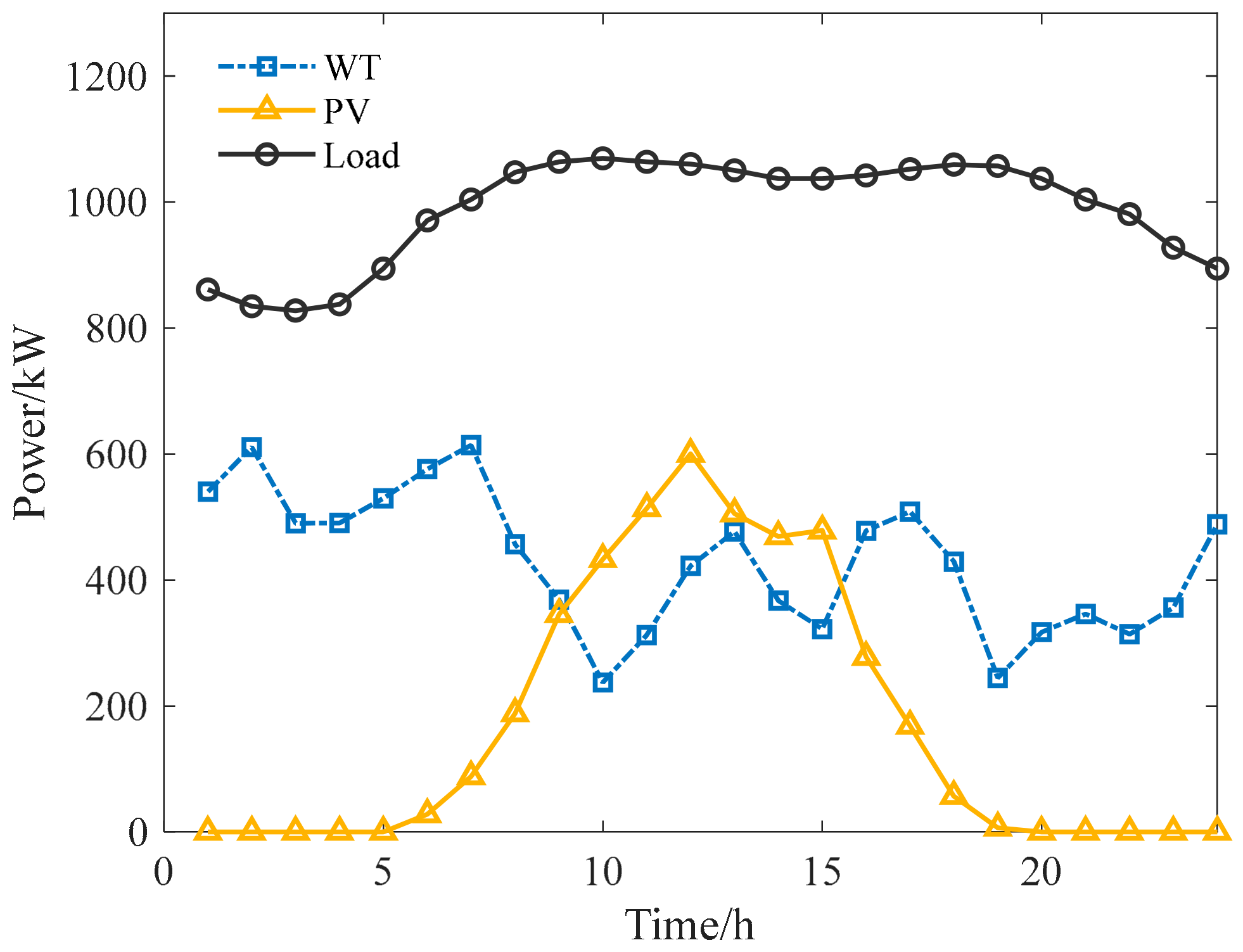
4.1. Case Study Setup

To validate the effectiveness of the proposed multi-time scale optimal scheduling strategy based on DRL for the electro-hydrogen coupling system, this paper conducts a case analysis using an industrial park’s electro-hydrogen system. Considering the operational characteristics of each component, the day-ahead and real-time scheduling intervals are set to 1 h and 15 min, respectively. The wind power unit has a rated capacity of 800 kW, while the photovoltaic system has a capacity of 600 kW. The system includes eight electrolyzers, each with a rated power of 360 kW. The energy storage system features a capacity of 800 kWh and a maximum charging/discharging power of 400 kW.

Table 1. Industrial time-of-use electricity prices.

	Time Interval	Price/(Yuan/kWh)
Off-peak period	0:00–8:00	0.31
Mid-peak period	12:00–17:00, 21:00–24:00	0.64
Peak period	8:00–12:00, 17:00–21:00	1.07

and

Table 2. Algorithm parameterization.

Parameters	Value
${\mu }^{\mathrm{ESS}}$/(yuan/kWh)	0.05
${\mu }^{\mathrm{EC}}$/(yuan/kWh)	0.5
${\mu }^{\mathrm{HFC}}$/(yuan/kWh)	0.04
${\mu }^{\mathrm{start}}$/(yuan/time)	234
${\lambda }_1^{\mathrm{pun}}$/(yuan/kWh)	0.5
${\lambda }_2^{\mathrm{pun}}$/(yuan/kWh)	0.5
${\lambda }_3^{\mathrm{pun}}$/(yuan/kWh)	1

detail the industrial time-of-use electricity prices and the parameter settings for the case studies, respectively [27]. Figure 4 illustrates the day-ahead wind and solar power outputs alongside the load forecast. The raw dataset underwent the following preprocessing pipeline: (1) Wind/PV generation data were processed with linear interpolation for missing value imputation followed by Z-score normalization; (2) electric load profiles were transformed into time-series features using a sliding window method (24 h window with 1 h stride); (3) electrolyzer operational state variables were encoded via one-hot representation for discrete control pattern recognition.

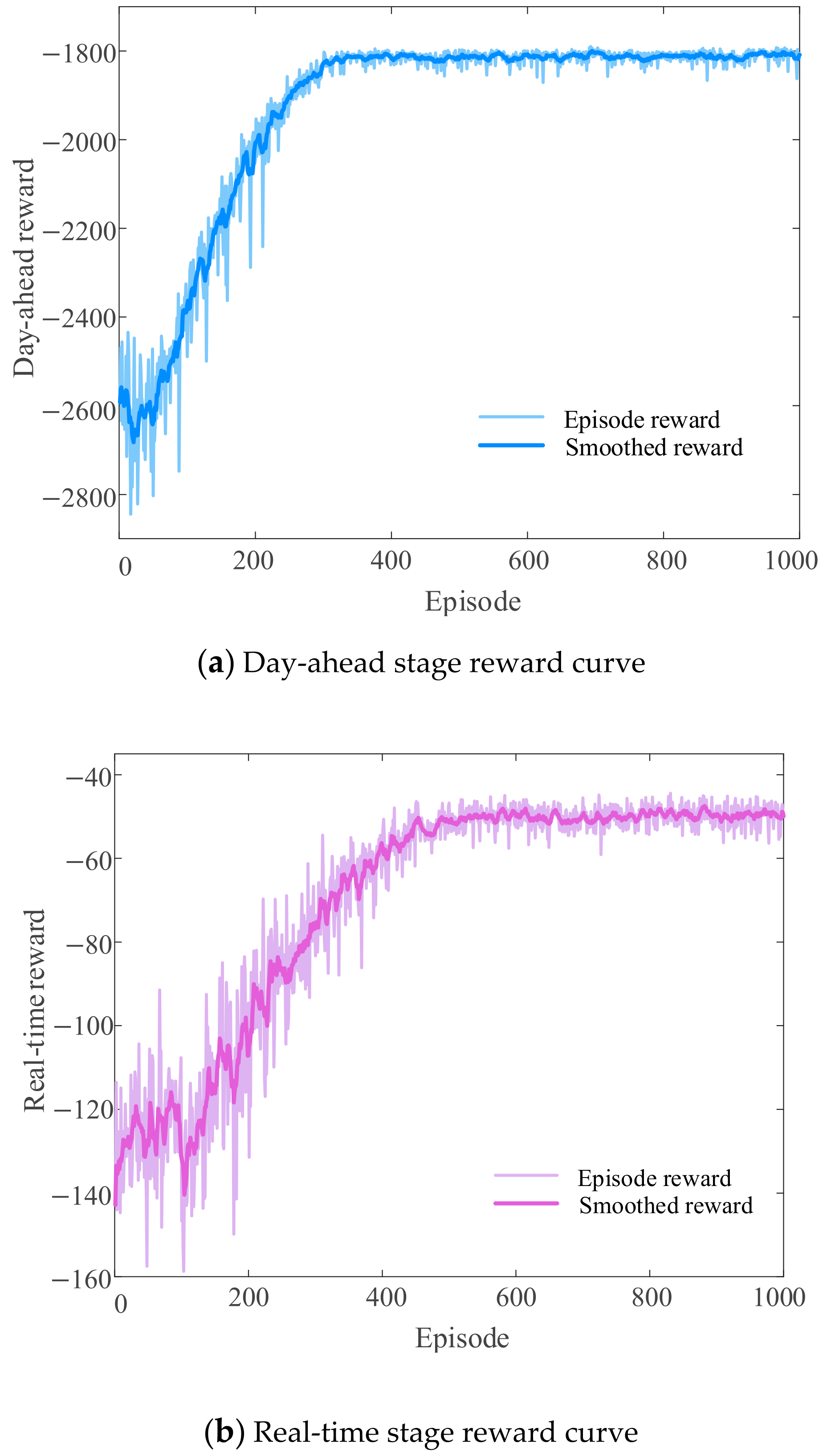
4.2. Analysis of the Training Process

With the modified TCN-PPO algorithm, the discount rate $\gamma$ is set to 0.98, the replay buffer capacity to 3000, and the mini-batch size to 120. The initial clipping rate ${\epsilon }_0$ is 0.25, while the information captures horizons ${\kappa }_1$ and ${\kappa }_2$ for long-time scale and short-time scale agents are 24 and 16, respectively. The update step lengths ($N^{\mathrm{long}}$ and $N^{\mathrm{short}}$) are both 16. Based on these settings, the training reward of the modified TCN-PPO algorithm is obtained, as shown in Figure 5. As shown in the figure, despite significant fluctuations in the agents’ reward during the initial stage, continuous training facilitates the attainment of stable, high rewards via an optimized system operation strategy, thereby ensuring the efficient operation of the electro-hydrogen coupling system. Specifically, the day-ahead reward exhibits relatively minor fluctuations, and the agent attains stable convergence after approximately 350 rounds, with an average reward of −1813.37. In contrast, the real-time reward demonstrates greater fluctuations and converges at a slower rate. During pre-training, the agents are required to explore the environment and refine their strategy using a higher clipping rate to adapt to real-time output and load variations. Ultimately, convergence is achieved after approximately 500 rounds, with the average reward stabilizing at −49.95, demonstrating that the agents effectively learn the optimal mapping between system states and scheduling strategies through iterative training.

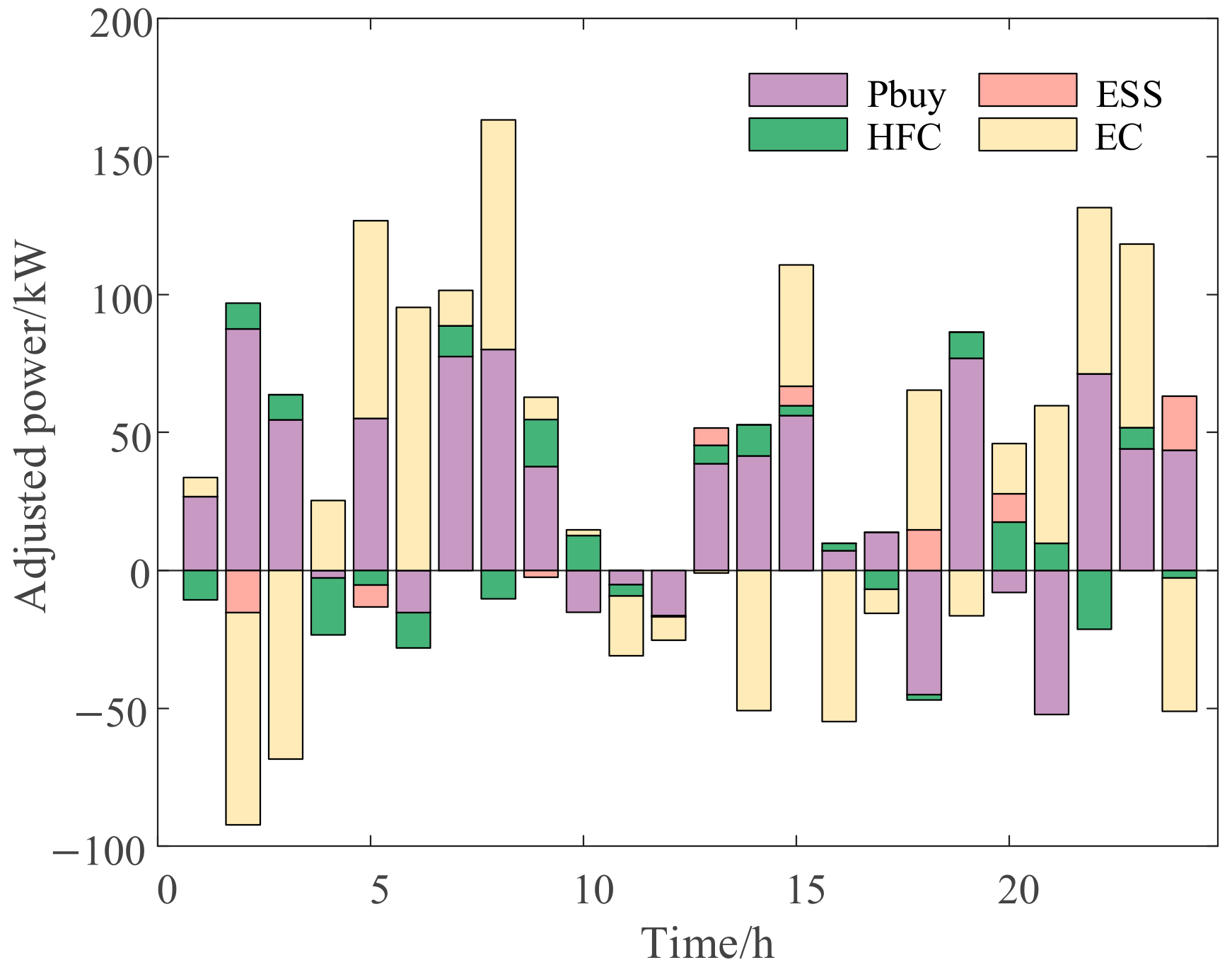
4.3. Analysis of the Testing Results

Based on the proposed modified TCN-PPO model, Figure 6 and Figure 7 illustrate the results of the day-ahead system power scheduling and the electrolyzer’s day-ahead production plan, respectively. As shown in the figures, the results indicate that the proposed method successfully develops an optimal operation strategy to ensure power balance during the day-ahead stage. Specifically, the agent charges the ESS from 00:00 to 08:00, taking advantage of lower electricity costs. From 08:00 to 12:00, the agent reduces the electrolyzer load to integrate wind power and enhances ESS output to alleviate high power purchase costs. In this period, the average purchased power is 1049.13 kW, representing a 41.74% reduction compared with the 00:00–08:00 interval. As shown in Figure 7, the electrolyzer’s average load from 08:00 to 12:00 is 1340.55 kW, a 28.53% reduction compared with the earlier interval. When PV output declines sharply in the evening, the agent employs ESS discharge to partially meet the load demand.

Furthermore, Figure 8 illustrates the real-time stage system power adjustments, with hourly data averaged across four intervals to enhance readability. As illustrated, the purchased power and electrolyzer power demonstrate substantial adjustments, whereas the adjustments for the ESS and fuel cell are relatively minor. Across different time intervals, power adjustments are significantly lower from 10:00 to 17:00, averaging merely 55.89 kW per hour, representing a 50.60% reduction compared with the 00:00–10:00 interval. Ultimately, the intraday short-time scale power purchase adjustment cost amounted to 486.14 yuan, whereas the system equipment operation adjustment cost totaled 629.80 yuan. In conclusion, the proposed method successfully optimizes the operation strategy of the electro-hydrogen coupling system, thereby improving economic efficiency and reducing carbon emissions.

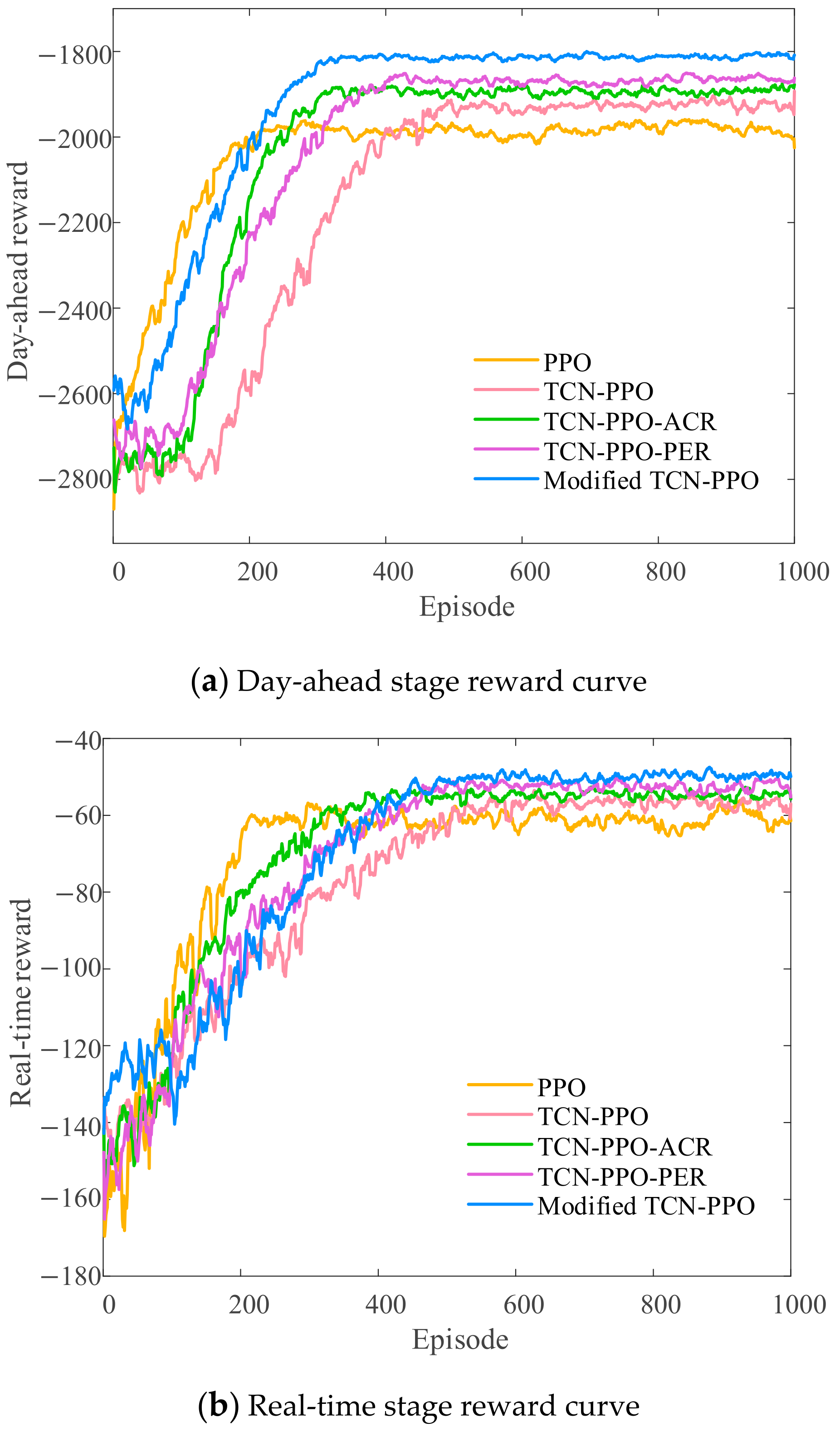
4.4. Comparison of Different Algorithms

To assess the efficacy of the proposed modified TCN-PPO algorithm, Figure 9 displays the cumulative reward curves of four DRL algorithms—DDPG, PPO, TCN-PPO, and the modified TCN-PPO—while

Table 3. A mean value of results for different DRL methods.

	DDPG	PPO	TCN-PPO	The Modified TCN-PPO
Power purchase cost/yuan	28,792.27	27,684.03	24,143.57	22,359.29
Operation cost/yuan	18,852.45	18,020.57	17,498.99	17,405.65
Start–stop cost/yuan	4500.33	4209.00	4147.67	3948.33

provides a summary of their simulation results. As shown, the DDPG algorithm yields the highest cumulative cost of ¥1.56 million, primarily attributed to its dependence on deterministic strategies and limited exploration capabilities, which hinder its ability to identify optimal solutions in complex environments. Consequently, the average daily power purchase cost for DDPG amounts to ¥28,792.27. In contrast, the PPO algorithm, utilizing a policy gradient method, demonstrates superior adaptability for electro-hydrogen coupling system scheduling, leading to a significant reduction in overall system cost. Furthermore, TCN-PPO enhances performance by effectively capturing temporal dynamics, achieving a cumulative cost of ¥1.37 million, which surpasses both DDPG and PPO. The proposed modified TCN-PPO attains the lowest cumulative cost of ¥1.31 million, corresponding to reductions of 16.03% and 12.67% compared with DDPG and PPO, respectively. This enhancement is attributed to improved state feature perception and adaptive reduction rate adjustments, which substantially enhance training quality and facilitate high-quality solutions in complex decision-making environments.

4.5. Analysis of Ablation Experiment

To rigorously validate the performance contributions of our algorithmic enhancements, we conduct comprehensive ablation studies comparing the following variants: PPO, TCN-PPO, TCN-PPO with adaptive clipping rate (TCN-PPO-ACR), TCN-PPO with prioritized experience replay (TCN-PPO-PER), and our proposed modified TCN-PPO. As demonstrated in Figure 10 (training reward curves) and

Table 4. Comparative training metrics of model variants.

	Day-Ahead Stage			Real-Time Stage
	Episodes to Convergence	Variance of Reward	Mean Converged Reward	Episodes to Convergence	Variance of Reward	Mean Converged Reward
PPO	200	24,162.28	−1983.62	200	614.18	−61.23
TCN-PPO	450	107,223.05	−1926.86	600	746.24	−57.09
TCN-PPO-ACR	300	85,146.11	−1893.84	350	724.66	−54.62
TCN-PPO-PER	400	83,788.75	−1867.43	500	852.21	−52.39
Modified TCN-PPO	350	57,540.32	−1813.37	500	797.06	−49.95

(quantitative metrics), PPO exhibited the fastest convergence (≈200 episodes) but yielded inferior rewards (−1983.62 and −61.23 for day-ahead and real-time phases, respectively). The integration of TCN substantially enhanced environmental state perception, increasing mean converged rewards by 6.15% in day-ahead scheduling at the cost of 27% slower convergence. The TCN-PPO-ACR variant achieved a 20.59% reduction in reward variance and a 1.71% reward improvement through dynamic clipping rate adaptation, particularly enhancing early-stage training efficiency and late-phase stability. TCN-PPO-PER demonstrated 3.08% and 8.23% reward gains in respective phases via prioritized sampling of high-learning-value experiences. Our final modified TCN-PPO synergistically integrates TCN’s multi-scale feature extraction (8.58% reward gain), ACR’s adaptive policy optimization (18.42% real-time improvement), and PER’s experience prioritization, achieving coordinated performance elevation beyond component-wise additive effects. These ablation results systematically quantify individual contribution ratios while confirming the framework’s holistic efficacy through multi-mechanism coordination.

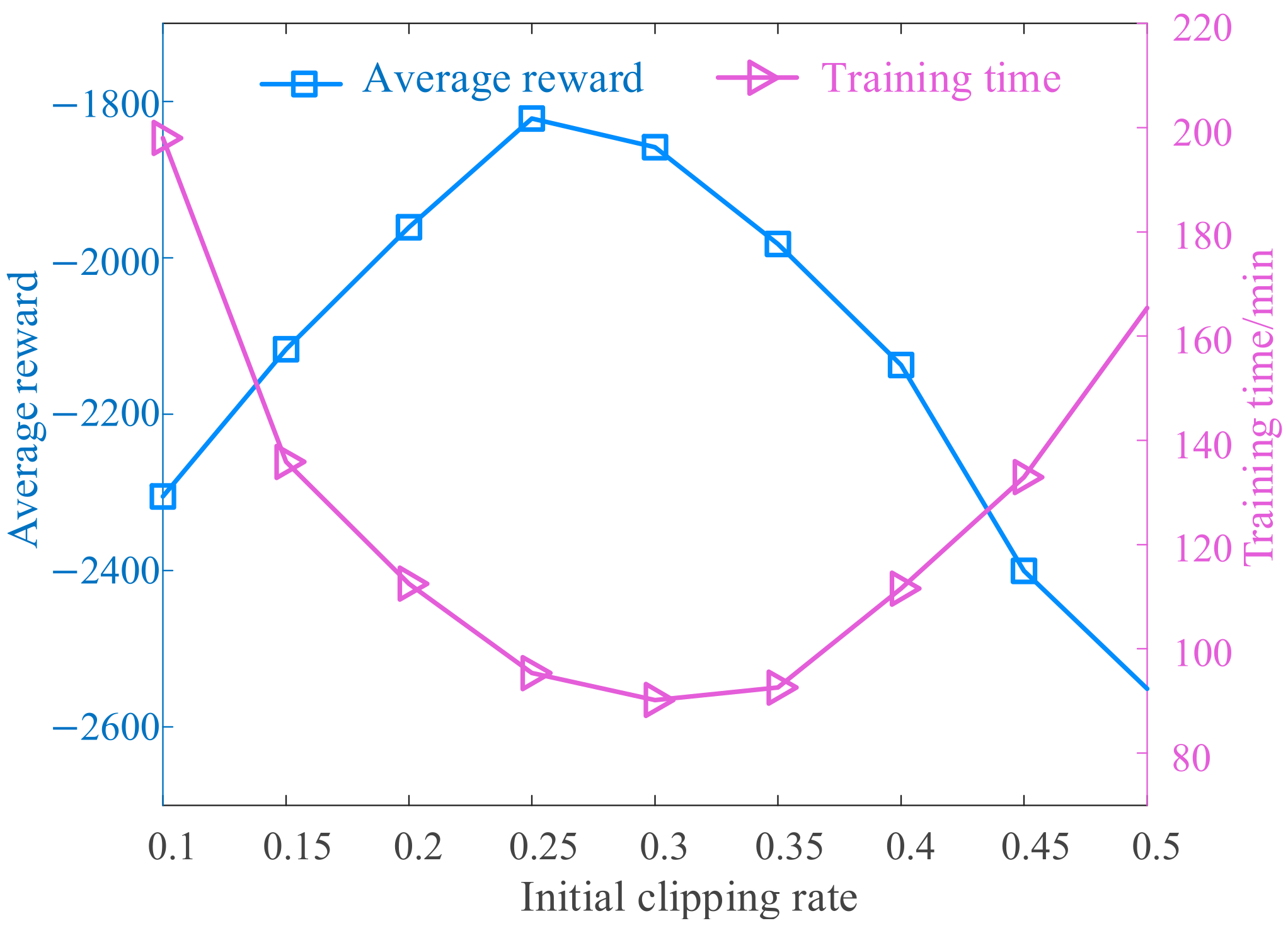
4.6. Analysis of Model Sensitivity

To assess the influence of the initial clipping rate on model performance, Figure 11 illustrates the average rewards achieved by agents with varying initial clipping rates over the training period. All results are calculated over 10 independent runs with different random seeds.

As shown in the figure, the average reward initially increases and subsequently declines with higher initial clipping rates, reaching a peak value of −1821.39 at a clipping rate of 0.25. Beyond this threshold, the reward reduces by approximately 7.02% for each incremental rise of 0.05 in the initial clipping rate. This reduction arises due to the higher clipping rate inducing excessive oscillations during training, which impedes the convergence toward a stable and effective strategy. Meanwhile, the training duration exhibits a U-shaped pattern, reducing initially and then increasing with higher clipping rates. The shortest training duration, 90.18 min, is achieved at a clipping rate of 0.3. However, at a clipping rate of 0.25, the training duration is 95.37 min, still relatively short and acceptable.

In conclusion, an initial clipping rate of 0.25 achieves an optimal balance between model performance and training efficiency.

5. Conclusions

In this paper, a multi-time scale optimal scheduling strategy for the electro-hydrogen coupling system based on the modified TCN-PPO algorithm is proposed. The DRL agents are utilized to develop day-ahead and real-time operation strategies for the coupling system, aiming to reduce the integrated system operation cost and mitigate real-time deviations. The experimental validation based on a regional electro-hydrogen coupling system yields the following conclusions:

(1)

The proposed optimal scheduling strategy for the electro-hydrogen coupling system employs a multi-time scale architecture that integrates the feature extraction capability of TCN and the decision optimization capability of DRL. By effectively formulating the production plan and real-time adjustment scheme in advance, the system’s real-time power adjustment cost is reduced to ¥629.80, significantly enhancing both economic efficiency and low-carbon operation.

(2)

Based on the TCN to capture multi-time scale environmental time-series characteristics, the DRL agents’ environmental perception and decision-making capabilities for the coupling system are enhanced. The cumulative cost of the proposed modified TCN-PPO is only ¥1.31 million during a 30-day test cycle, which is 12.67% lower compared with the PPO algorithm.

(3)

The proposed feature enhancement, adaptive clipping rate, and PER mechanisms enable the modified TCN-PPO algorithm to address the limitations of the PPO algorithm and achieve high-quality solutions for the multi-time scale optimal problem in the coupling system. Furthermore, model sensitivity experiments demonstrate that the model achieves an optimal balance between performance and stability when the initial clipping rate falls within the interval [0.25, 0.3].

Although the current DRL-based optimal scheduling strategy for the electro-hydrogen coupling system exhibits distinct advantages, the increasing complexity of electro-hydrogen loads and the diversification of energy management system components necessitate further exploration of the characteristics of demand-response loads, supercapacitors, and other equipment to optimize the coordinated operation of such systems.

While the current DRL-based optimization strategy for electricity-hydrogen coupled systems shows operational advantages, its neglect of second-level dynamic characteristics from fast-response devices like supercapacitors may limit millisecond-level power fluctuation mitigation capabilities in high renewable penetration scenarios. Future research should integrate demand-responsive loads and supercapacitor dynamics to enhance coordinated operational performance.

For practical implementation, future research should prioritize establishing a provincial hydrogen-electricity coupling network demonstration in Jiangsu Province, particularly focusing on dynamic subsidy mechanisms for valley-period hydrogen production. Scalability validation must address model generalization across heterogeneous multi-regional systems incorporating diverse electrolysis technologies (e.g., proton exchange membrane electrolyzers) while developing self-adaptive hyperparameter tuning mechanisms. Market integration requires extending the economic objective functions (Equations (1)–(4)) through carbon trading cost internalization and electricity market bidding revenue optimization. Critical engineering challenges include mitigating cloud-edge coordination latency and addressing equipment lifespan degradation from frequent start–stop cycles, to be resolved via hardware-in-the-loop testing with accelerated aging protocols.