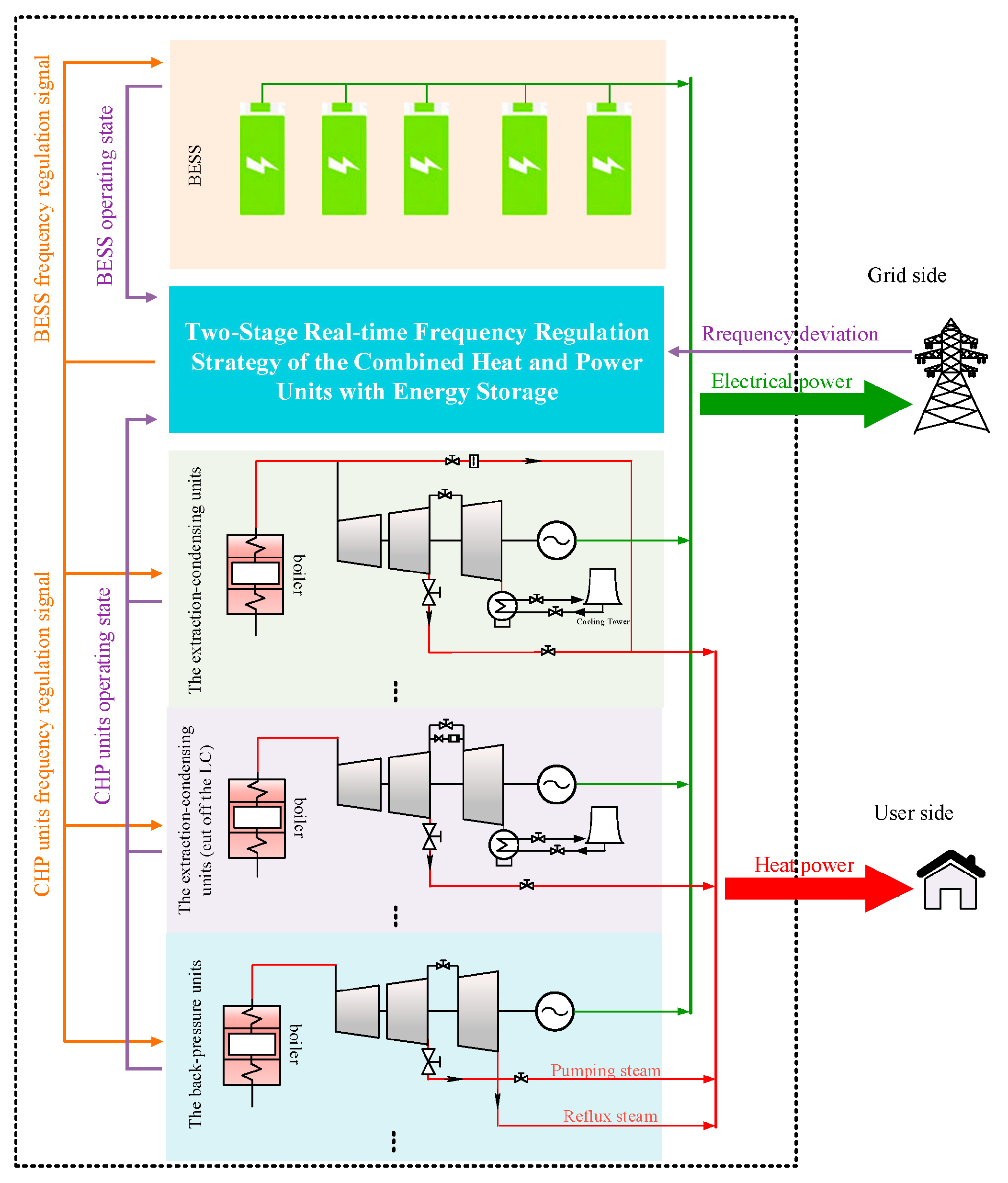
Two-Stage Real-Time Frequency Regulation Strategy of Combined Heat and Power Units with Energy Storage
Abstract
:1. Introduction
- (1)
- This study provides FR models for CHP plants in Northeast China. It proposes a two-stage real-time rolling FR strategy for CHP units with energy storage. In the first stage, the goal is to enhance the FR performance to increase the CHP plant’s benefits, while in the second stage, the strategy effectively reduces the FR operating cost.
- (2)
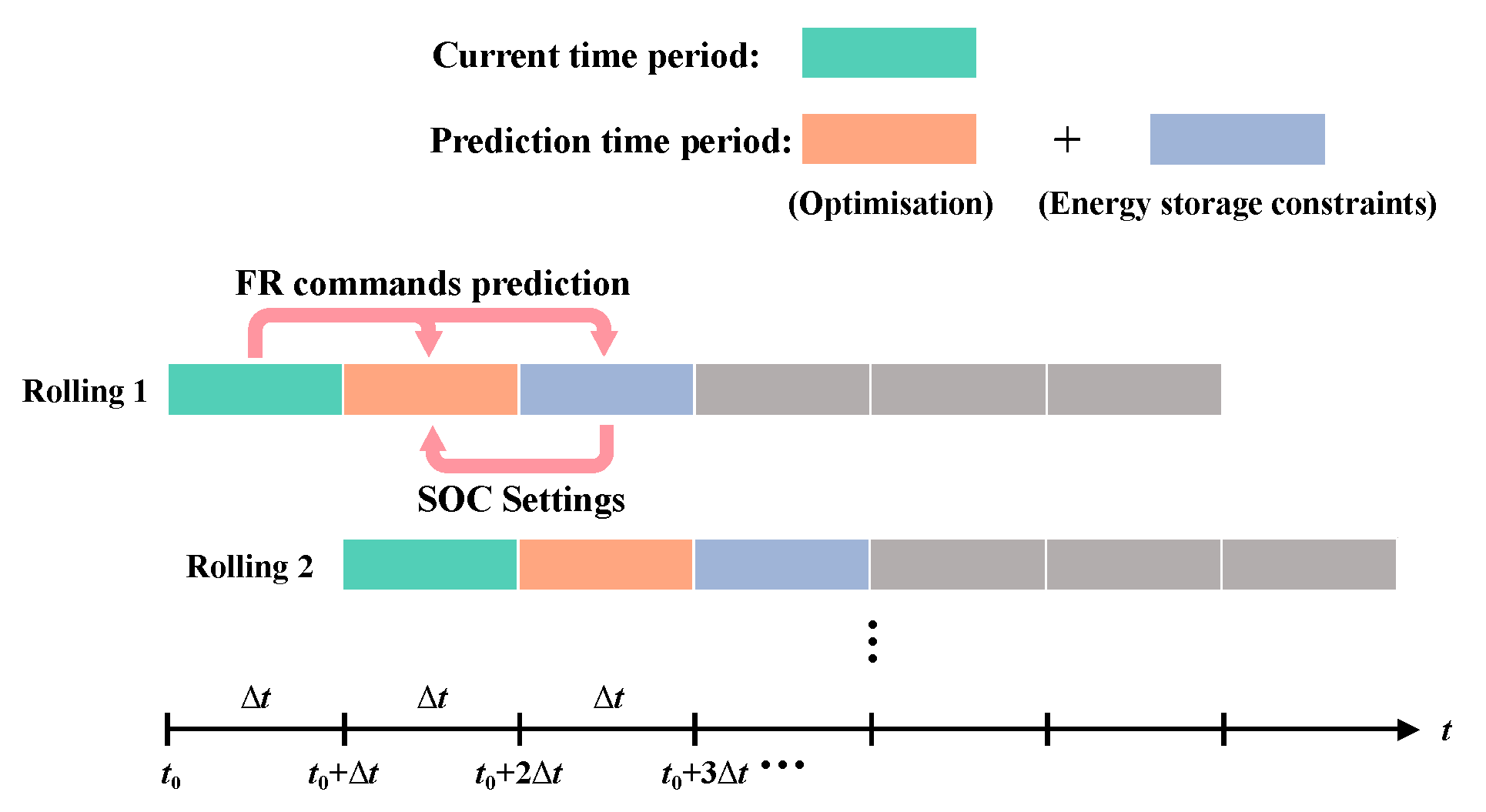
- Given the time-coupling characteristics of energy storage, an FR command prediction model is studied to identify the optimal SOC, meaning the energy storage can sustainably respond to FR commands with sufficient capacity.
- (3)
- By incorporating dynamic correction into the model predictive control (MPC) algorithm, the FR command prediction model effectively reduces the impact of prediction errors on the FR performance indicators, by updating the deviation between the actual and predicted FR commands in real time, and on the operating status of CHP units and energy storage.
2. Analysis of the FR Ancillary Service Policy in Northeast China
2.1. Compensation Rules for Thermal Power Plants Participating in FR Ancillary Service
2.1.1. Available Time Compensation
2.1.2. Regulation Electricity Quantity Compensation
2.2. Penalty Rules for Thermal Power Plants Participating in FR Ancillary Service
2.2.1. Scheduling Management and Availability Assessment
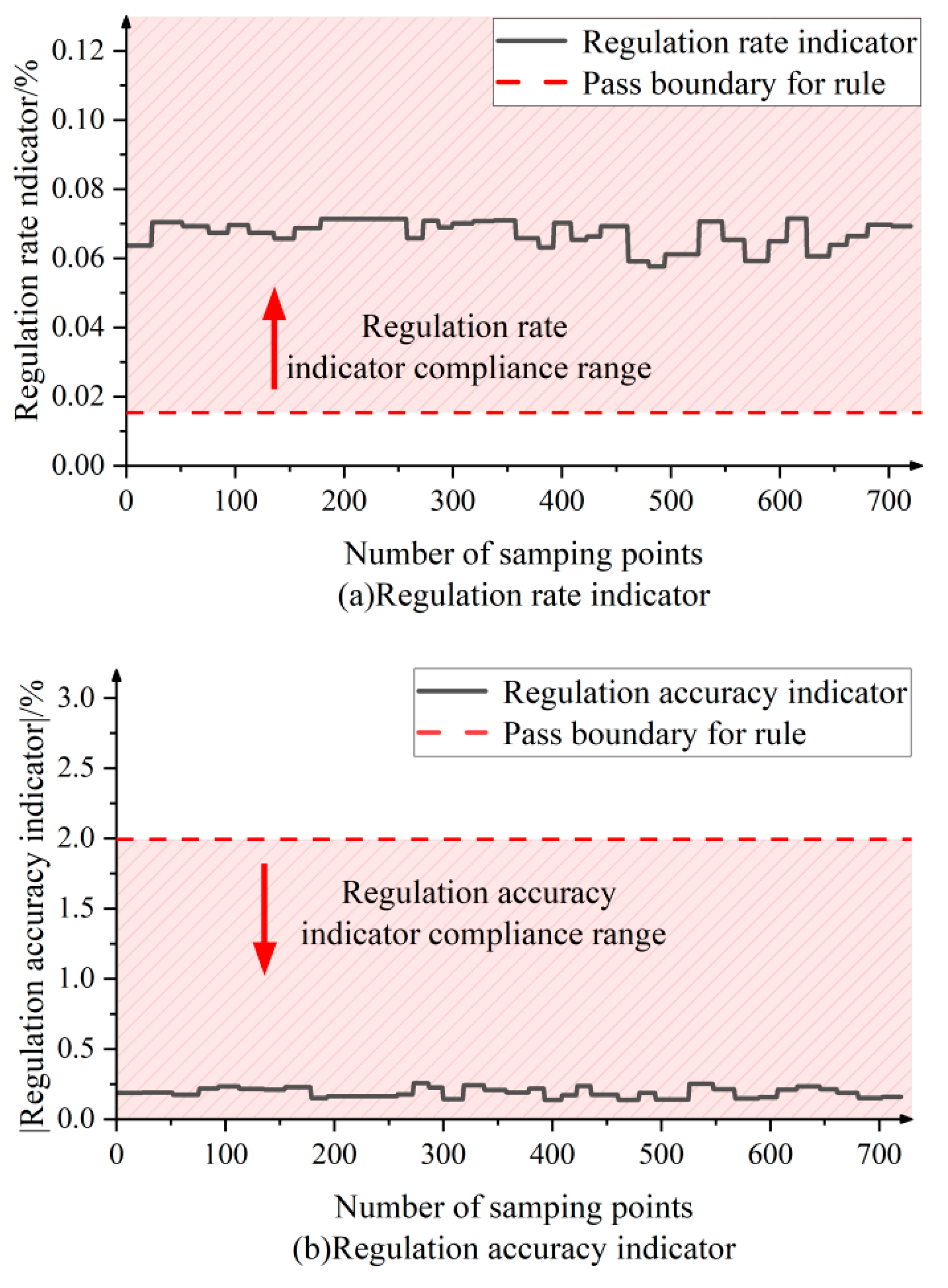
2.2.2. Regulation Rate Assessment
2.2.3. Regulation Accuracy Assessment
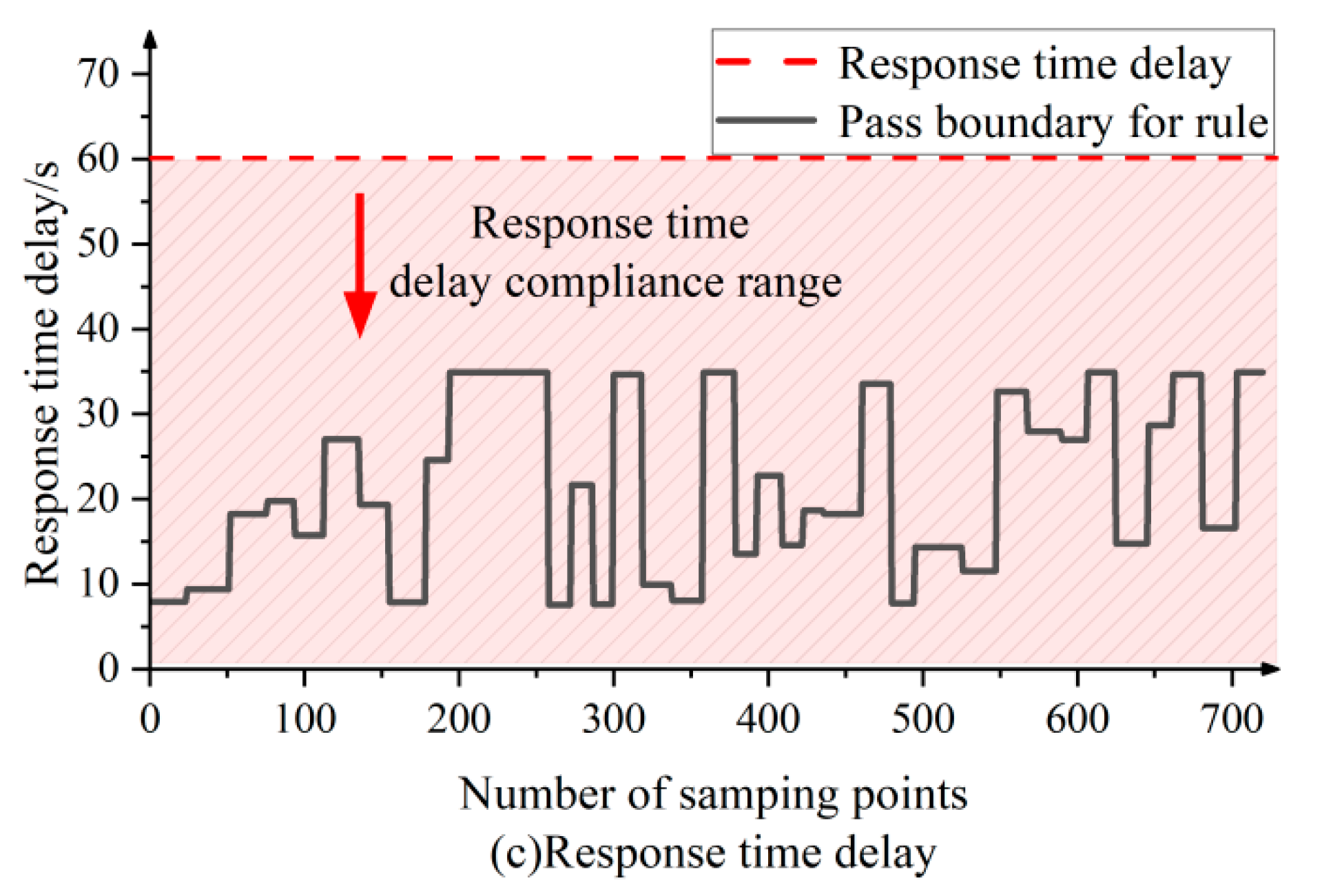
2.2.4. Compliance Rate Assessment of Response Time
3. Two-Stage Optimization Model for the CHP Plant
3.1. The First-Stage Optimization Model
3.1.1. Stage 1 Objective Function
- Compensation model of regulation electricity quantity;
- Penalty models about sub-indicators;
3.1.2. Stage 1 Constraints
- Constraints of the FR performance sub-indicators
- Power constraints for the CHP plant
3.2. The Second-Stage Optimization Model
3.2.1. Stage 2 Objective Function
- Coal consumption cost [22];
- Operating cost of the energy storage;
3.2.2. Stage 2 Constraints
- Power and heat load constraints;
- The feasible operation region constraints of CHP units;
- (1)
- The extraction condensing CHP unit (including the units cutting off the low-pressure cylinder);
- (2)
- The back-pressure CHP unit;
- The ramping rate constraints of CHP units;
- (3)
- The extraction condensing CHP unit;
- (4)
- The back-pressure CHP unit;
- SOC constraints of energy storage;
- Operating cost constraints of energy storage
3.3. Prediction Model of FR Commands
3.3.1. Historical Data Pre-Process
3.3.2. Single-Step Prediction Model for FR Commands
3.3.3. Multi-Step Prediction Model for FR Commands
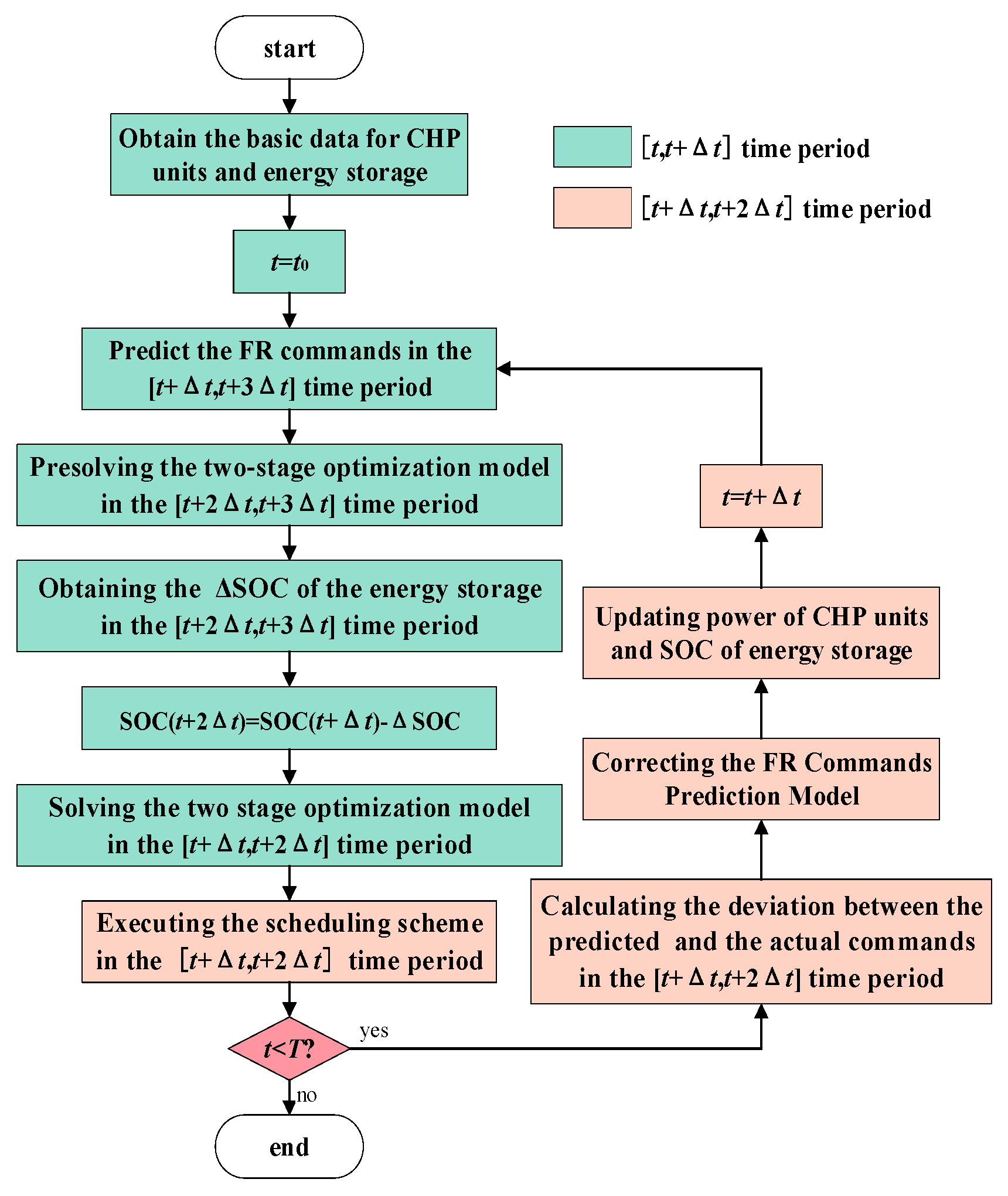
3.4. The Two-Stage Real-Time Rolling Optimization FR Strategy
4. Analysis of Case Studies
4.1. Basic Data
4.2. Comparison with Existing Strategies
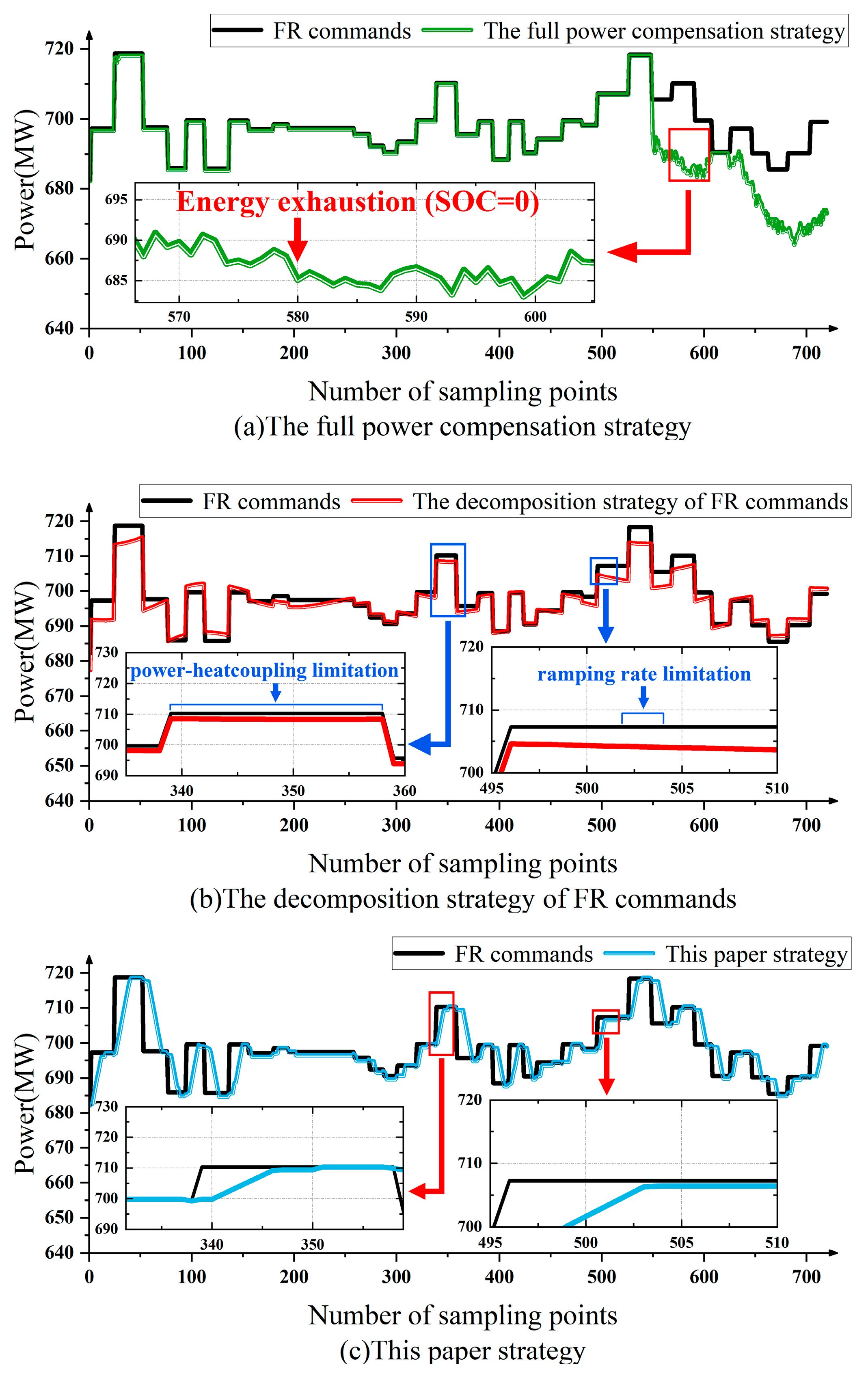
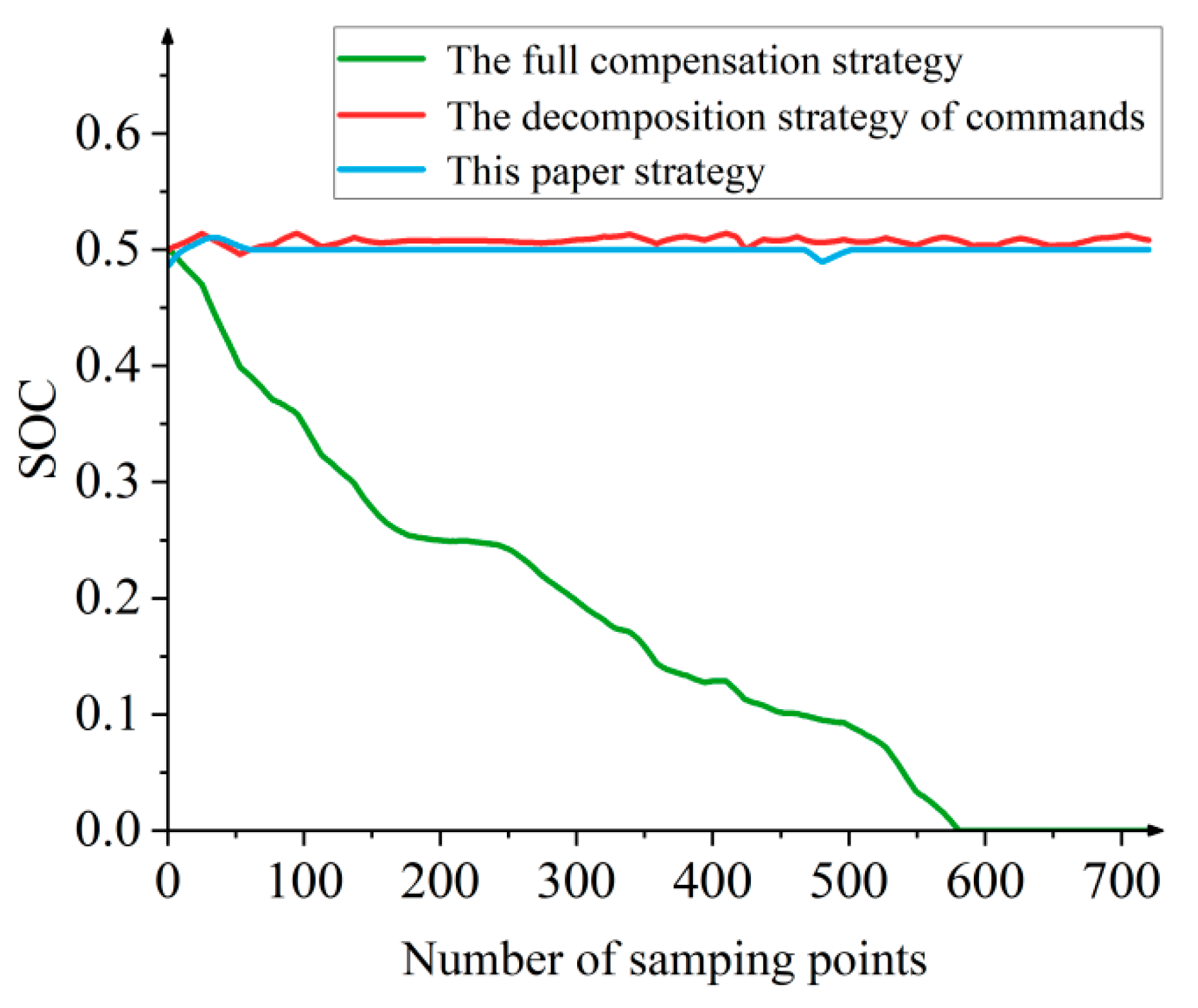
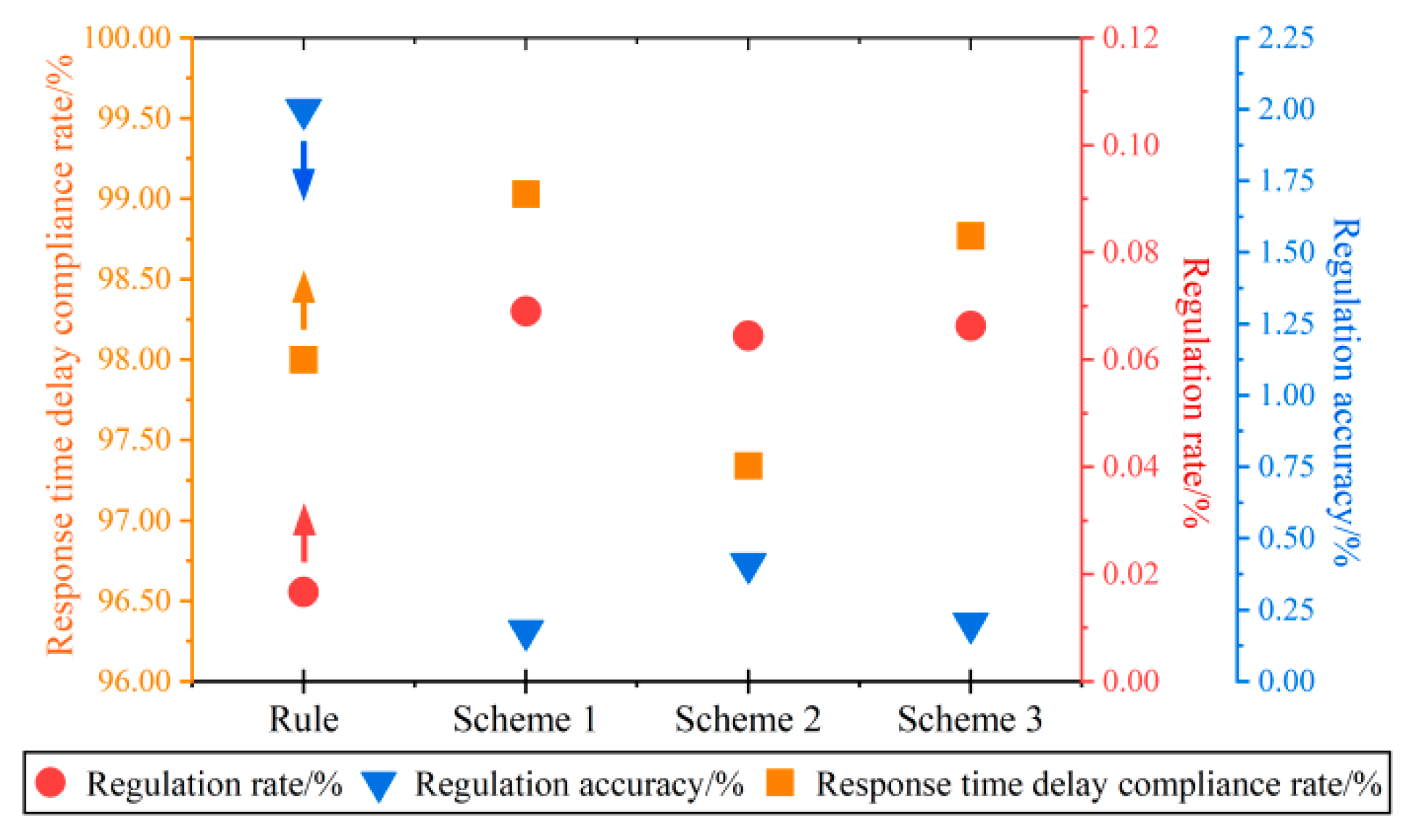
4.2.1. Comparison of Response Effects
4.2.2. Comparison of FR Operating Cost and Benefits
- Analysis of FR operating cost;
- Analysis of regulation electricity quantities’ compensation
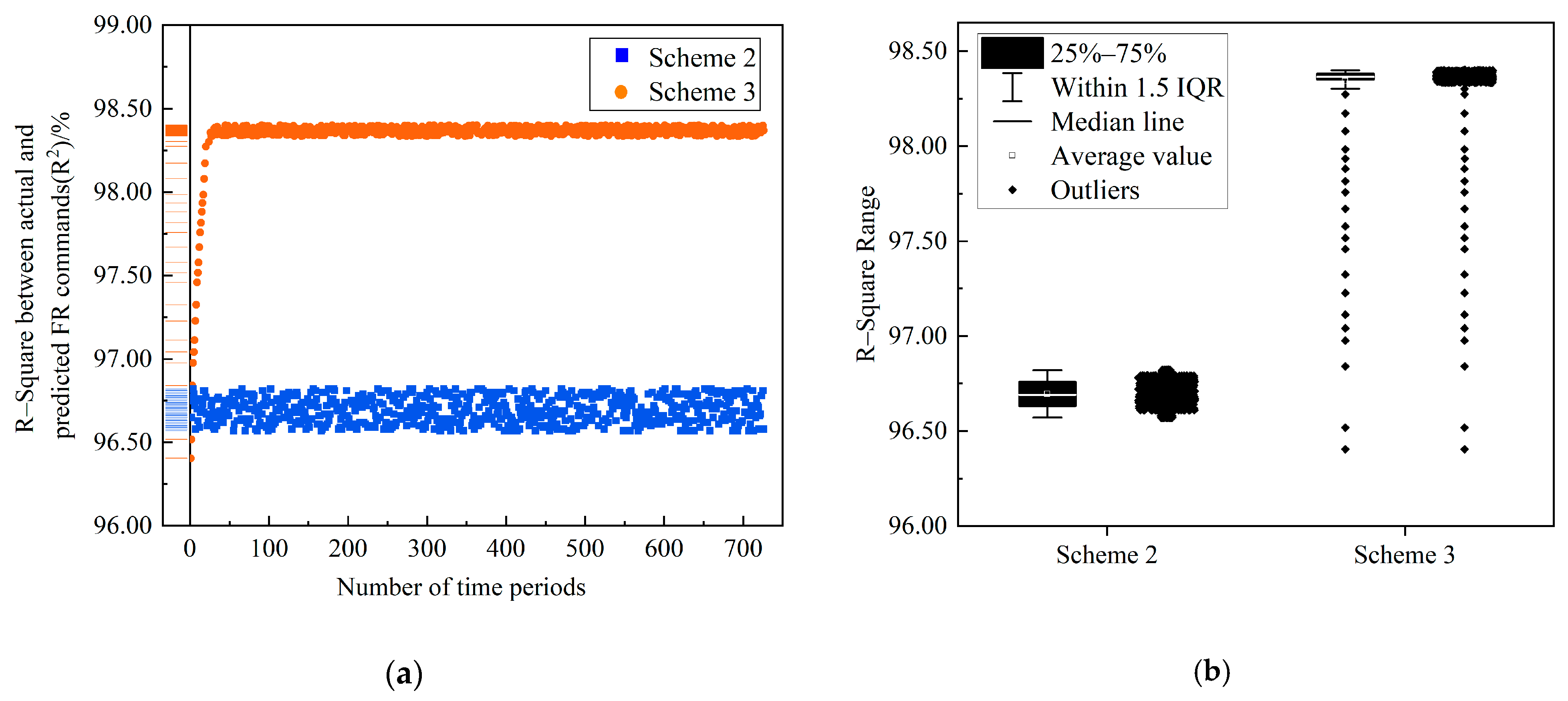
4.3. Analysis of the Impact of Rolling Optimization on FR Effects
5. Conclusions
- (1)
- The two-stage optimization model in this paper takes the overall FR benefits and operating cost of a CHP plant as optimization objectives, respectively. Through the energy complementarity between CHP units and energy storage, the optimal distribution of plant-level electrical and heat power is achieved while considering the improvement of FR performance sub-indicators. In terms of FR benefits, this paper’s strategy improves by 31.51% and 10.98% compared with the full power compensation strategy and FR command decomposition strategy, respectively. In terms of FR operating costs, there are reductions of 6.41% and 1.25%, respectively.
- (2)
- The two-stage real-time rolling FR strategy in this paper is based on the FR command prediction model and uses the rolling optimization algorithm, which includes a dynamic correction link. By introducing the deviation between the actual and predicted commands into the rolling process, the prediction accuracy can reach 98.34% after about 23 rolls, which is 1.65% higher than the traditional method. This reduction in FR command prediction errors effectively enhances the regulation accuracy and the response delay compliance of the FR process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Regulation electricity quantity compensation | |
| Penalties for different FR performance sub-indicators | |
| Compensation and FR performance sub-indicators’ assessment factor | |
| FR performance sub-indicators to the i-th FR command | |
| Standards of different FR performance sub-indicators’ assessment | |
| Steady-state power of the i-th FR proceeding | |
| FR dead-band | |
| Power change rate of energy storage | |
| Ramping rate of the d-th CHP unit for the i-th FR command | |
| Different moments when the plant responds to the i-th FR command | |
| Target power for the i-th FR command | |
| Electrical power output of the CHP plant | |
| Coal consumption cost of extraction condensing CHP units at time t | |
| Coal consumption cost of back-pressure CHP units at time t | |
| Operating cost of energy storage | |
| Maintenance cost of energy storage | |
| Allocation of investment cost of energy storage | |
| Discount rate | |
| Theoretical floating life of energy storage | |
| Coefficient of the quadratic term of the coal consumption function for extraction condensing CHP units | |
| Coefficient of the primary term of the coal consumption function for extraction condensing CHP units | |
| Coefficient of the constant term of the coal consumption function for extraction condensing CHP units | |
| Coefficient of the quadratic term of the coal consumption function for back-pressure CHP units | |
| Coefficient of the primary term of the coal consumption function for back-pressure CHP units | |
| Coefficient of the constant term of the coal consumption function for back-pressure CHP units | |
| Heat to electric power impact factor of the extraction condensing CHP unit | |
| Heat to electric power impact factor under the pure back-pressure working condition for the back-pressure unit | |
| Heat to electric power impact factor under the maximum extraction steam working condition for the back-pressure unit | |
| Power output of the p-th extraction condensing CHP unit at time t | |
| Heat output of the p-th extraction condensing CHP unit at time t | |
| Power output of energy storage at time t | |
| Power output of the j-th back-pressure CHP unit at time t | |
| Heat output of the j-th back-pressure CHP unit at time t | |
| State of charge of energy storage at time t | |
| Rate capacity of energy storage | |
| Charging power at time t of energy storage | |
| Discharging power at time t of energy storage | |
| Charging efficiency of energy storage | |
| Discharging efficiency of energy storage | |
| Equivalent number of cycles within the i-th FR instruction | |
| Maximum number of daily equivalent cycles |
Appendix A
Appendix A.1
| Prediction Model | MAE | R2/% |
|---|---|---|
| Auto-regressive integrated moving average (ARIMA) prediction model | 15.61 | 95.56 |
| Random forest prediction model | 6.92 | 97.22 |
| This paper’s prediction model | 1.08 | 98.71 |
Appendix A.2
Appendix A.3
References
- Shair, J.; Li, H.Z.; Hu, J.B.; Xie, X.R. Power system stability issues, classifications and research prospects in the context of high-penetration of renewables and power electronics. Renew. Sustain. Energy Rev. 2021, 145, 111111. [Google Scholar]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and classification of power system stability–revisited & extended. IEEE Trans. Power Syst. 2020, 36, 3271–3281. [Google Scholar]
- Ameli, H.; Qadrdan, M.; Strbac, G. Coordinated operation strategies for natural gas and power systems in presence of gas-related flexibilities. IET Energy Syst. Integr. 2019, 281, 3–13. [Google Scholar]
- Xu, X.; Wang, M.; Zhou, Y.; Wu, J. Unlock the flexibility of combined heat and power for frequency response by coordinative control with batteries. IEEE Trans. Ind. Inform. 2020, 17, 3209–3219. [Google Scholar]
- Ribó-Pérez, D.; Larrosa-López, L.; Pecondón-Tricas, D.; Alcázar-Ortega, M. A critical review of demand response products as resource for ancillary services: International experience and policy recommendations. Energies 2021, 14, 846. [Google Scholar] [CrossRef]
- Khoshjahan, M.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Dehghanian, P. Enhancing electricity market flexibility by deploying ancillary services for flexible ramping product procurement. Electr. Power Syst. Res. 2021, 191, 106878. [Google Scholar]
- German Network Rules Association. Available online: https://www.regelleistung.net/en-us/General-info/Germannetwork-rules-association (accessed on 18 March 2025).
- Xie, X.R.; Guo, Y.H.; Wang, B.; Dong, Y.P.; Mou, L.F.; Xue, F. Improving AGC performance of coal-fueled thermal generators using multi-MW scale BESS: A practical application. IEEE Trans. Smart Grid 2018, 9, 1769–1777. [Google Scholar]
- Zhao, Y.; Du, Y.; Li, H.; Guo, L.; Yang, Z.; Feng, Y. Frequency Regulation Power Allocation Method for Electric Vehicles Coordinated with Thermal Power Units in AGC. In Proceedings of the 2022 5th International Conference on Energy, Chongqing, China, 22–24 April 2022. [Google Scholar]
- Li, C.P.; Si, W.B.; Li, J.H.; Yan, G.G.; Jia, C. Two-layeroptimization of frequency modulated power of thermalgeneration and multi-storage system based onensemble empirical mode decomposition and multiobjective genetic algorithm. Trans. China Electrotech. Soc. 2024, 39, 2017–2032. [Google Scholar]
- Cui, D.; Jin, Y.C.; Wang, Y.B.; Yuan, Z.J.; Cai, G.W.; Liu, C.; Ge, W.C. Combined thermal power and battery low carbon scheduling method based on variational mode decomposition. Int. J. Electr. Power Energy Syst. 2023, 145, 108644. [Google Scholar]
- Zhang, P.; Xin, S.J.; Wang, Y.W.; Xu, Q.; Chen, C.; Chen, W.S.; Dong, H.Y. A Two-Layer Control Strategy for the Participation of Energy Storage Battery Systems in Grid Frequency Regulation. Energies 2024, 17, 664. [Google Scholar] [CrossRef]
- Ma, Q.; Wei, W.; Mei, S. A two-timescale operation strategy for battery storage in joint frequency and energy markets. IEEE Trans. Energy Mark. Policy Regul. 2023, 2, 200–213. [Google Scholar] [CrossRef]
- Diao, R.; Hu, Z.C.; Song, Y.H.; Mujeeb, A.; Liu, L.K. Cooperation mode and operation strategy for the union of thermal generating unit and battery storage to improve AGC performance. IEEE Trans. Power Syst. 2023, 38, 5290–5301. [Google Scholar] [CrossRef]
- Northeast Energy Regulatory Bureau of National Energy Administration of the People’s Republic of China. Implementation Rules for the Administration of Auxiliary Services for Grid-Connected Power Plants in Northeast China; Northeast Energy Regulatory Bureau of National Energy Administration of the People’s Republic of China: Shenyang, China, 2023.
- Yang, W.F.; Wen, Y.F.; Pandžić, H.; Zhang, W.Q. A multi-state control strategy for battery energy storage based on the state-of-charge and frequency disturbance conditions. Int. J. Electr. Power Energy Syst. 2020, 135, 107600. [Google Scholar] [CrossRef]
- Cui, H.; Yang, B.; Jiang, Y.; Tan, Z.X.; Cui, D.; Li, P. Strategy based on fuzzy control and self adaptive modification of SOC involved in secondary frequency regulation with battery energy storage. Power Syst. Prot. Control 2019, 47, 89–97. [Google Scholar]
- Peng, D.G.; Xu, Y.; Zhao, H.R. Research on intelligent predictive AGC of a thermal power unit based on control performance standards. Energies 2019, 12, 4073. [Google Scholar] [CrossRef]
- He, J.Q.; Shi, C.L.; Wei, T.Z.; Jia, D.Q. Stochastic model predictive control of hybrid energy storage for improving AGC performance of thermal generators. IEEE Trans. Smart Grid 2021, 13, 393–405. [Google Scholar] [CrossRef]
- Zhao, Y.T.; Wu, Z.; Gu, W.; Wang, J.X.; Wang, F.J.; Ma, Z.; Hu, M. Optimal Dispatch and Pricing of Industrial Parks Considering CHP Mode Switching and Demand Response. CSEE J. Power Energy Syst. 2023, 10, 2174–2185. [Google Scholar]
- Chen, H.D.; Meng, F.; Wang, Q.; Hou, F.; Wang, Y.; Zhang, Z.H. Influence of installed capacity of energy storage system and renewable energy power generation on power system performance. Energy Storage Sci. Technol. 2023, 12, 477–485. [Google Scholar]
- Ding, S.X.; Gu, W.; Lu, S.; Chen, X.G.; Yu, R.Z. Improving Operational Flexibility of Integrated Energy Systems Through Operating Conditions Optimization of CHP Units. CSEE J. Power Energy Syst. 2023, 9, 1854–1865. [Google Scholar]
- Shao, Y.J.; Ding, R.; Tian, Z.Z. An optimal configuration method for energy storage systems in distribution networks considering battery life. In Proceedings of the 2020 IEEE 3rd Student Conference on Electrical Machines and Systems, Jinan, China, 4–6 December 2020. [Google Scholar]
- Shao, Y.J. Optimal Operation and Configuration Research on Energy Storage Systems Considering the Battery Lifetime. Ph.D. Thesis, Shandong University, Jinan, China, 28 May 2022. [Google Scholar]
- Shaker, H.; Manfre, D.; Zareipour, H. Forecasting the aggregated output of a large fleet of small behind-the-meter solar photovoltaic sites. Renew. Energy 2020, 147, 1861–1869. [Google Scholar] [CrossRef]
- Mei, L. Research on Intelligent AGC Control Technology for Thermal Power Plant Based on KDD and Big Data. Ph.D. Thesis, Shanghai Electric Power University, Shanghai, China, 2018. [Google Scholar]
- Veeramsetty, V.; Reddy, K.R.; Santhosh, M.; Mohnot, A.; Singal, G. Short-term electric power load forecasting using random forest and gated recurrent unit. Electr. Eng. 2022, 104, 307–329. [Google Scholar]
- Zhang, Y.; Shen, Y.; Zhu, R.; Chen, Z.; Guo, T.; Lv, Q. Two-stage frequency regulation strategy of the combined heat and power plant with energy storage basing regulation indicators in northeast grid. Power Syst. Technol. 2024, 1–15. [Google Scholar] [CrossRef]
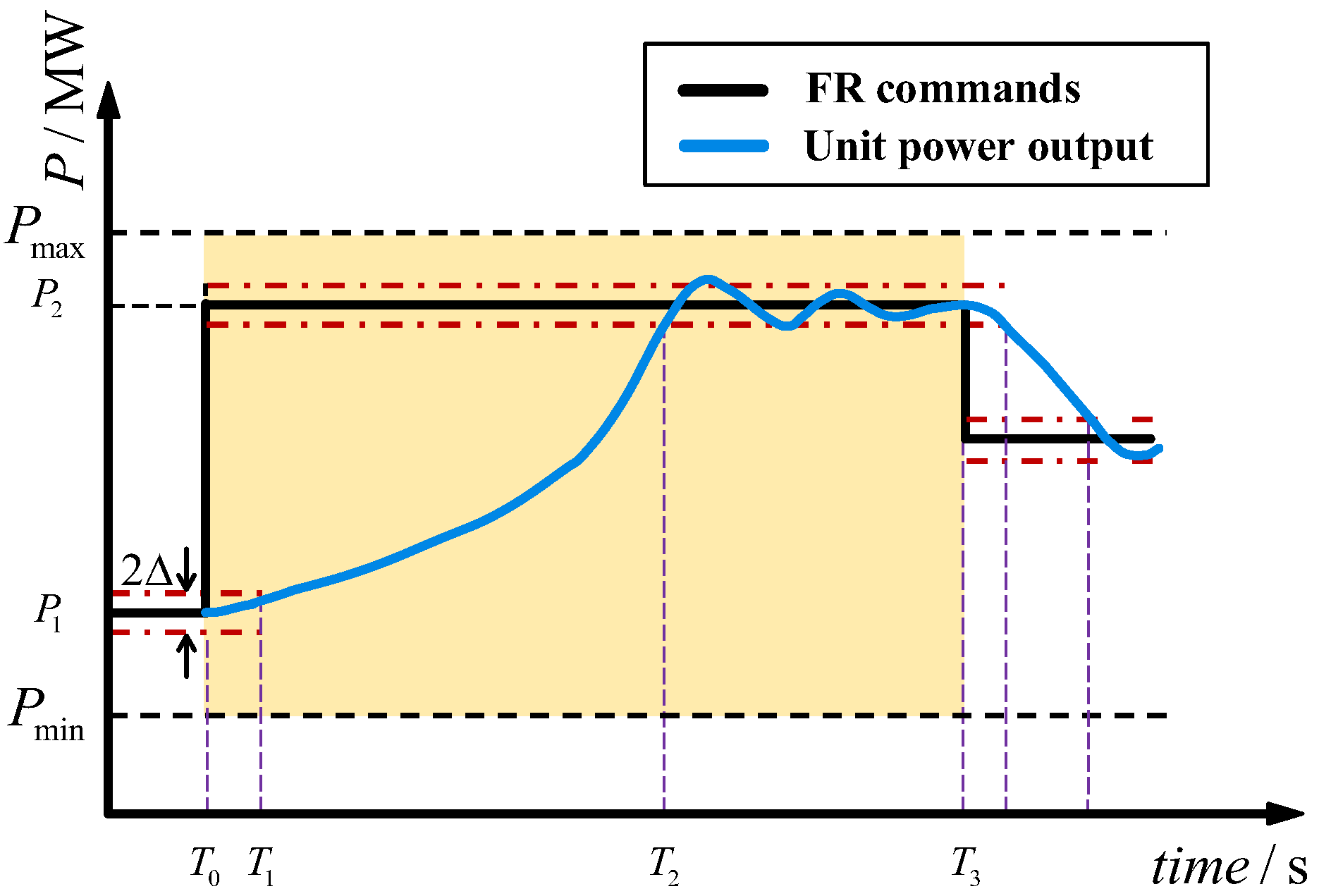


| The Standard, Penalty, and Compensation Factors | Values |
|---|---|
| Lower limit of regulation rate/s−1 | 0.017 |
| Upper limit of regulation accuracy/% | ±2 |
| Upper limit of response time delay/s | 60 |
| Lower limit of pass compliance rate boundary/% | 98 |
| Regulation electricity quantity compensation factor/$·MWh−1 | 16.59 |
| Penalty factor for regulation rate/$·point−1 | 1382.74 |
| Penalty factor for regulation accuracy/$·point−1 | 1382.74 |
| Penalty factor for compliance rate/$·point−1 | 138.27 |
| Input steps in the single-step prediction model | 8 |
| Strategies | Full Power | Decomposition | This Paper |
|---|---|---|---|
| Energy storage cost/$ | 1102.35 | 412.17 | 247.58 |
| CHP unit cost/$ | 13,071.92 | 13,074.69 | 13,073.31 |
| FR operating cost/$ | 14,174.27 | 13,486.86 | 13,320.89 |
| Electricity quantities’ compensation/$ | 53.94 | 70.54 | 81.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Shen, Y.; Zhu, R.; Chen, Z.; Guo, T.; Lv, Q. Two-Stage Real-Time Frequency Regulation Strategy of Combined Heat and Power Units with Energy Storage. Energies 2025, 18, 1953. https://doi.org/10.3390/en18081953
Zhang Y, Shen Y, Zhu R, Chen Z, Guo T, Lv Q. Two-Stage Real-Time Frequency Regulation Strategy of Combined Heat and Power Units with Energy Storage. Energies. 2025; 18(8):1953. https://doi.org/10.3390/en18081953
Chicago/Turabian StyleZhang, Yan, Yang Shen, Rui Zhu, Zhu Chen, Tao Guo, and Quan Lv. 2025. "Two-Stage Real-Time Frequency Regulation Strategy of Combined Heat and Power Units with Energy Storage" Energies 18, no. 8: 1953. https://doi.org/10.3390/en18081953
APA StyleZhang, Y., Shen, Y., Zhu, R., Chen, Z., Guo, T., & Lv, Q. (2025). Two-Stage Real-Time Frequency Regulation Strategy of Combined Heat and Power Units with Energy Storage. Energies, 18(8), 1953. https://doi.org/10.3390/en18081953








