The Strategic Selection of Concentrated Solar Thermal Power Technologies in Developing Countries Using a Fuzzy Decision Framework
Abstract
:1. Introduction
The Literature Review
2. The CSP Assessment Background
- Alternative 1: Gross capacity of 100 MW, parabolic trough (PT) with synthetic oil as the heat transfer fluid (HTF), no storage, and dry cooling;
- Alternative 2: Gross capacity of 170 MW, PT with synthetic oil as the HTF, molten salt for 3 h of TES, and dry cooling;
- Alternative 3: Gross capacity of 200 MW, PT with synthetic oil as the HTF, molten salt for 6 h of TES, and dry cooling;
- Alternative 4: Gross capacity of 110 MW, solar tower (ST), molten salt as the HTF and for 10 h of TES, and dry cooling;
- Alternative 5: Gross capacity of 200 MW, ST, molten salt as the HTF and for 12 h of TES, and dry cooling;
- Alternative 6: Gross capacity of 125 MW, linear Fresnel (LF) with direct steam generation (DSG), no storage, and dry cooling.
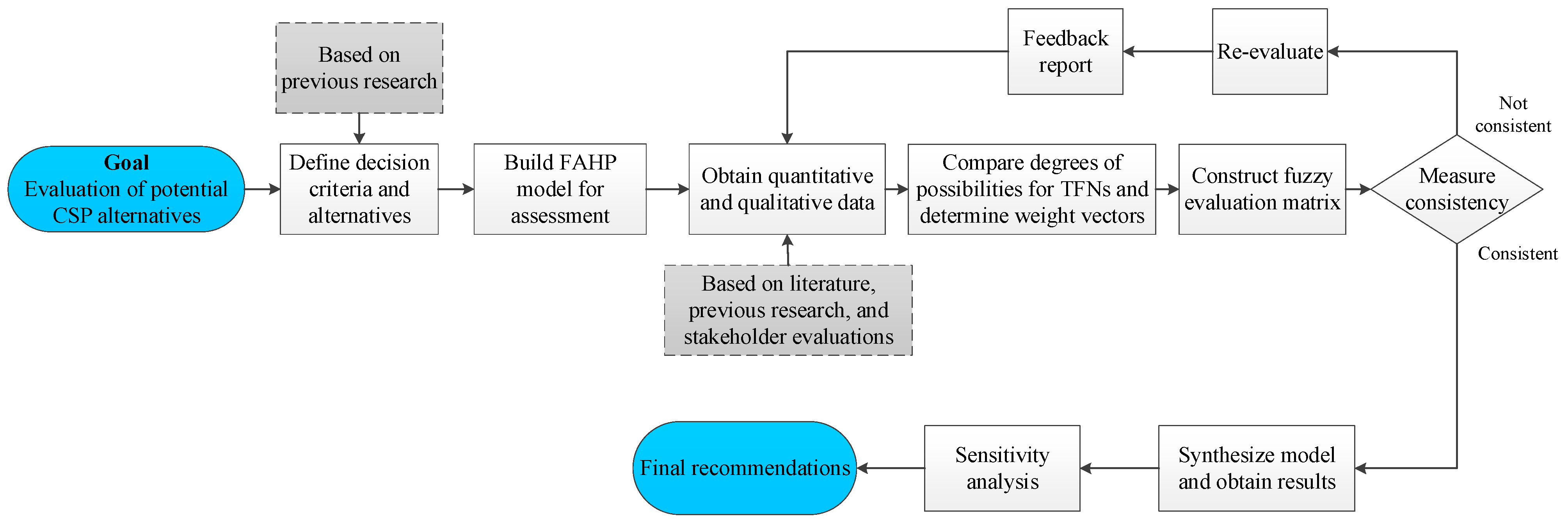
3. Methodology
3.1. Data Collection
3.2. Establishing Priority Weighting
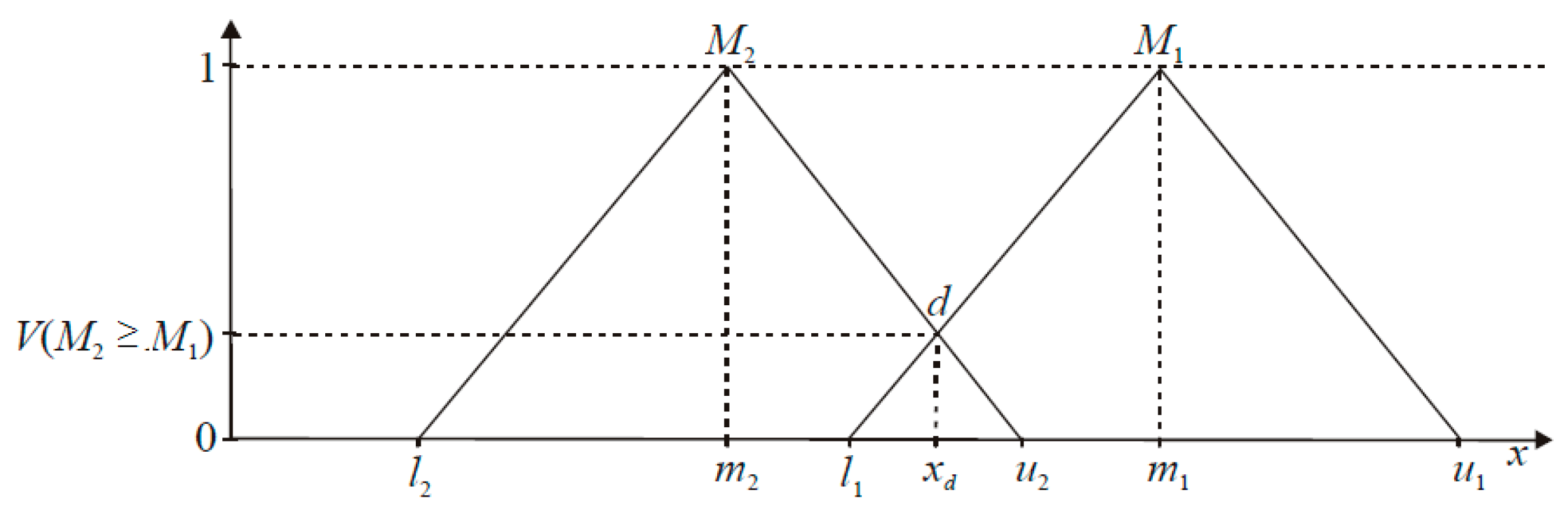
3.3. Comparing the Degrees of Possibility
3.4. Obtaining the Weight Vector
4. The Case Study
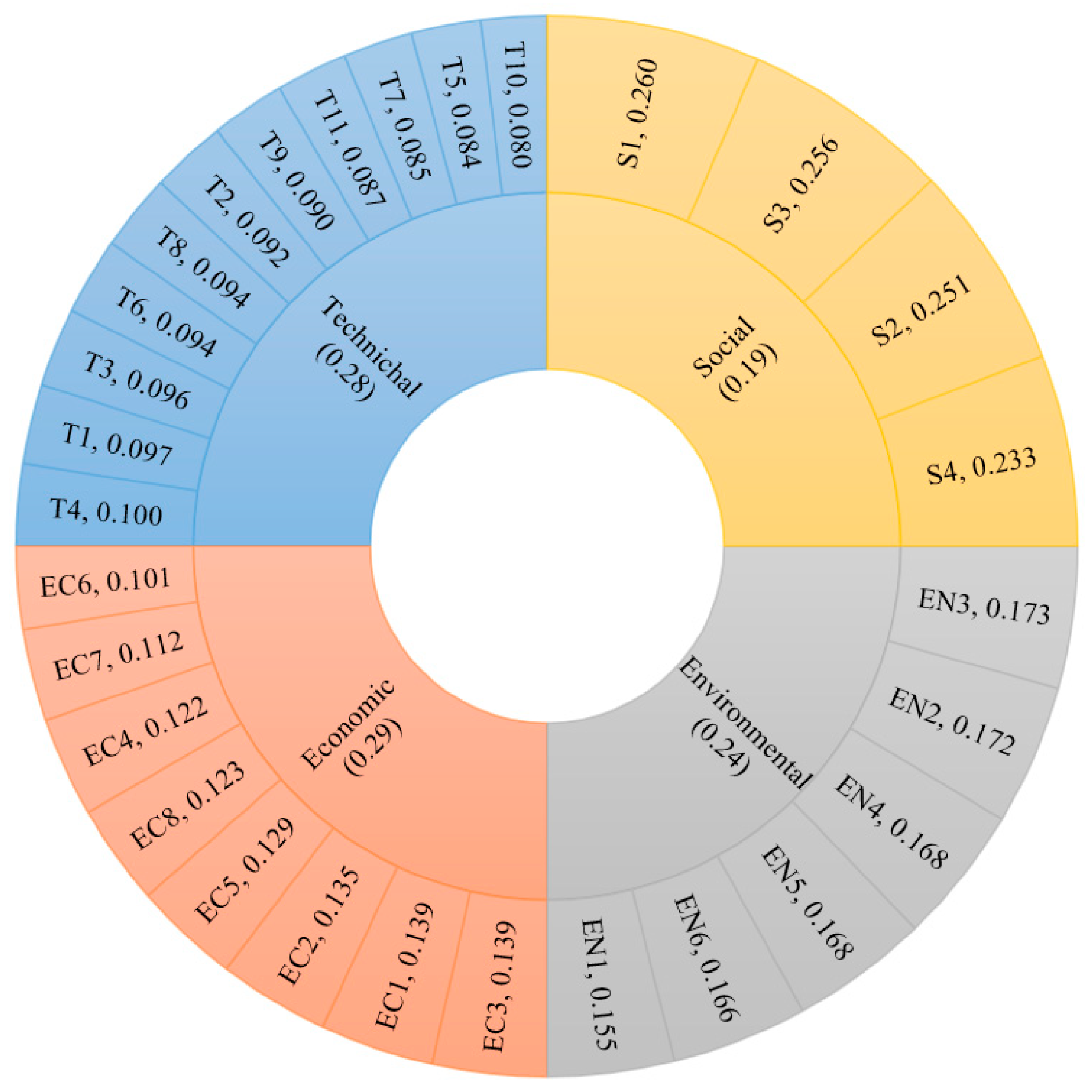
4.1. Criteria and Sub-Criteria Priority Weighting
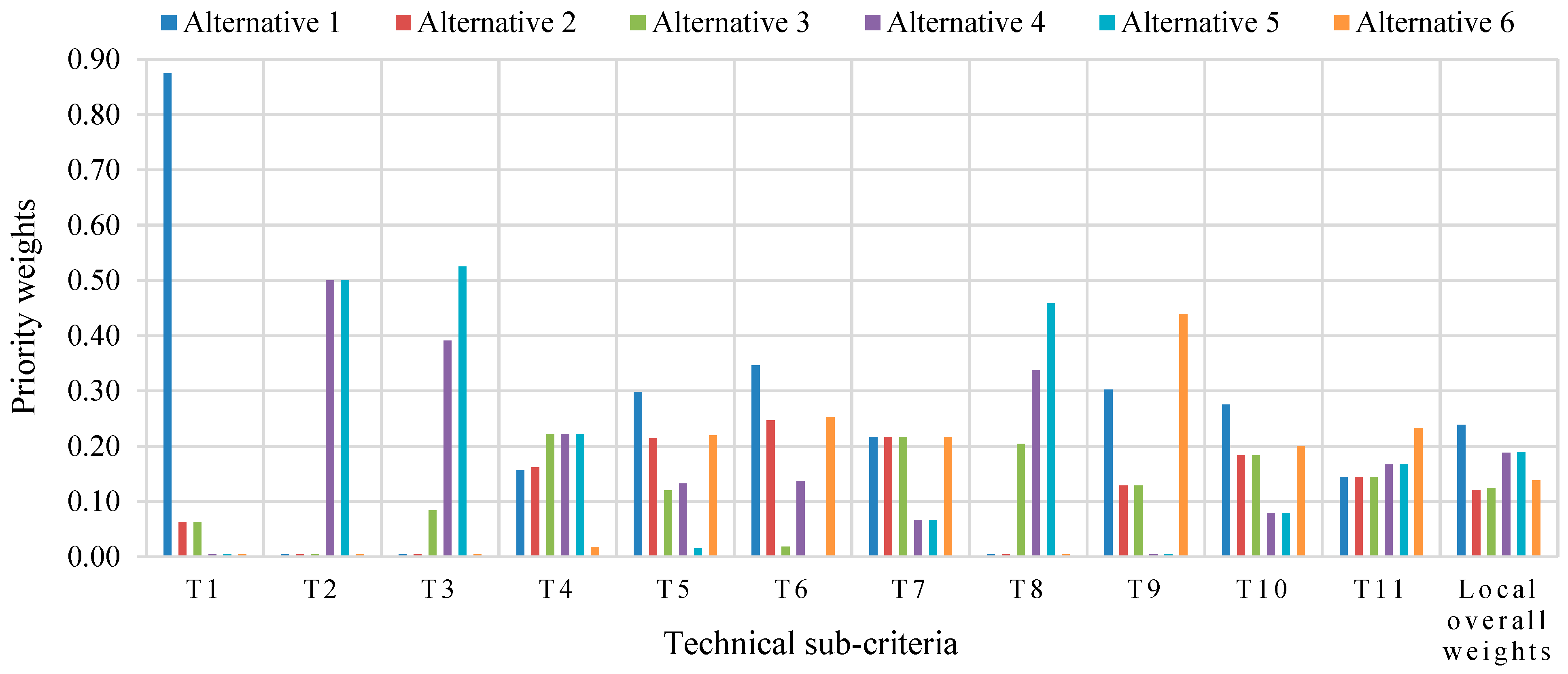
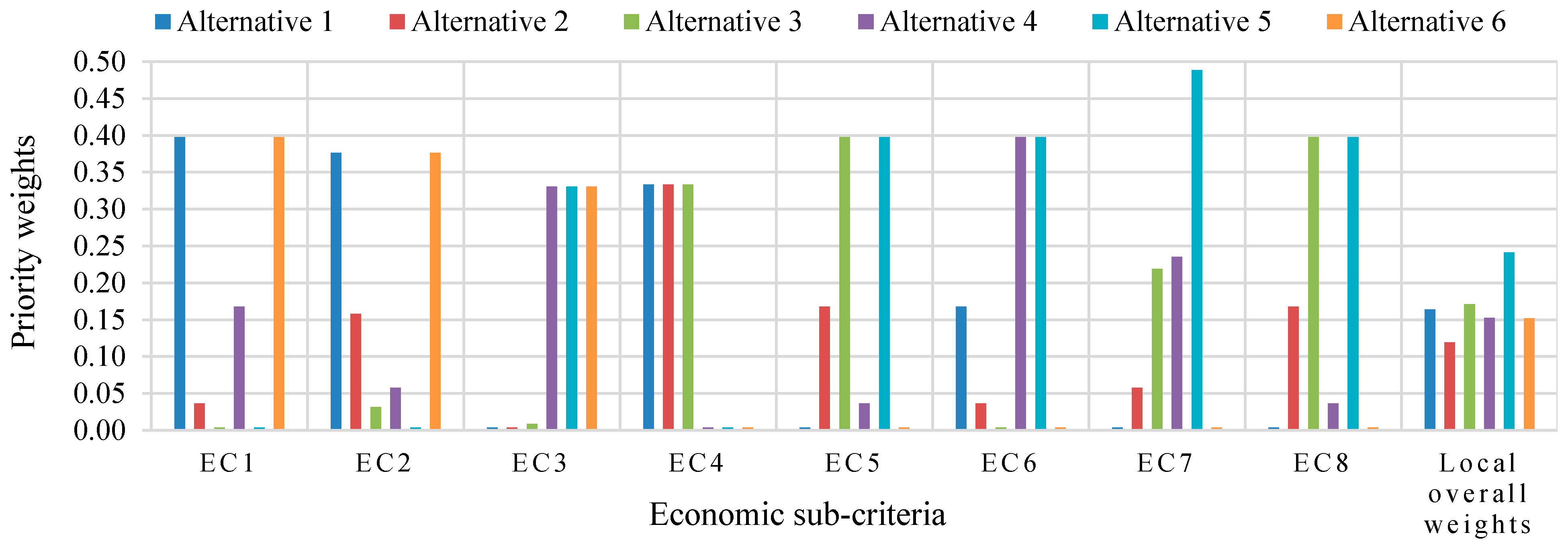
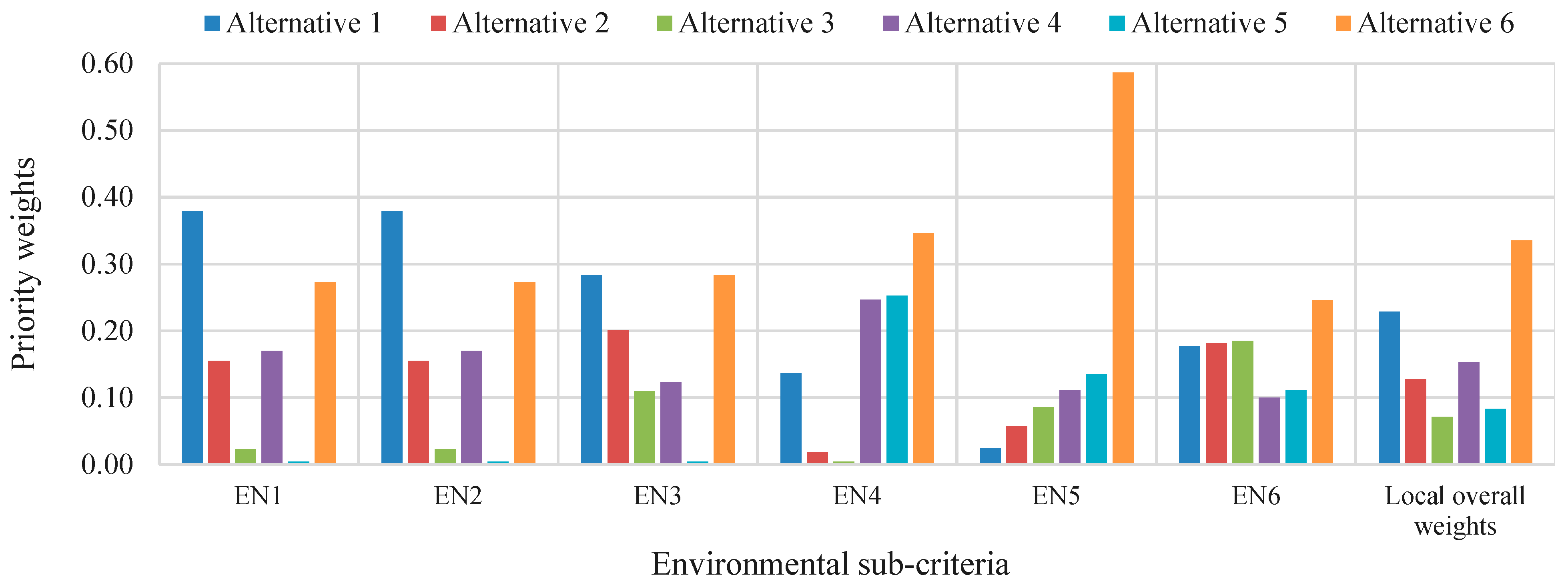
4.2. Results and Discussion
5. Conclusions and Implications
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviation | Meanning |
| ADP | Analytic Deliberative Process |
| AHP | Analytic Hierarchy Process |
| CRITIC | Criteria Importance through Intercriteria Correlation |
| CSP | Concentrated Solar Power |
| DNI | Direct Normal Irradiance |
| FAHP | Fuzzy Analytic Hierarchy Process |
| GHI | Global Horizontal Irradiance |
| IEA | International Energy Agency |
| LCA | Life Cycle Assessment |
| LCOE | Levelized Cost of Energy |
| LCOH | Levelized Cost of Heat |
| LF | Linear Fresnel |
| MCDM | Multi-Criteria Decision-Making |
| MENA | Middle East and North Africa |
| PD | Parabolic Dish |
| PROMETHEE | Preference Ranking Organization Method for Enrichment Evaluations |
| PT | Parabolic Trough |
| PV | Photovoltaic |
| QFD | Quality Function Deployment |
| R&D | Research and Development |
| RES | Renewable Energy Source |
| RNA | Rank Number of Alternatives |
| DSG | Direct Steam Generation |
| ST | Solar Tower |
| TES | Thermal Energy Storage |
| TFN | Triangular Fuzzy Number |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| VIKOR | Multi-Criteria Optimization and Compromise Solution |
References
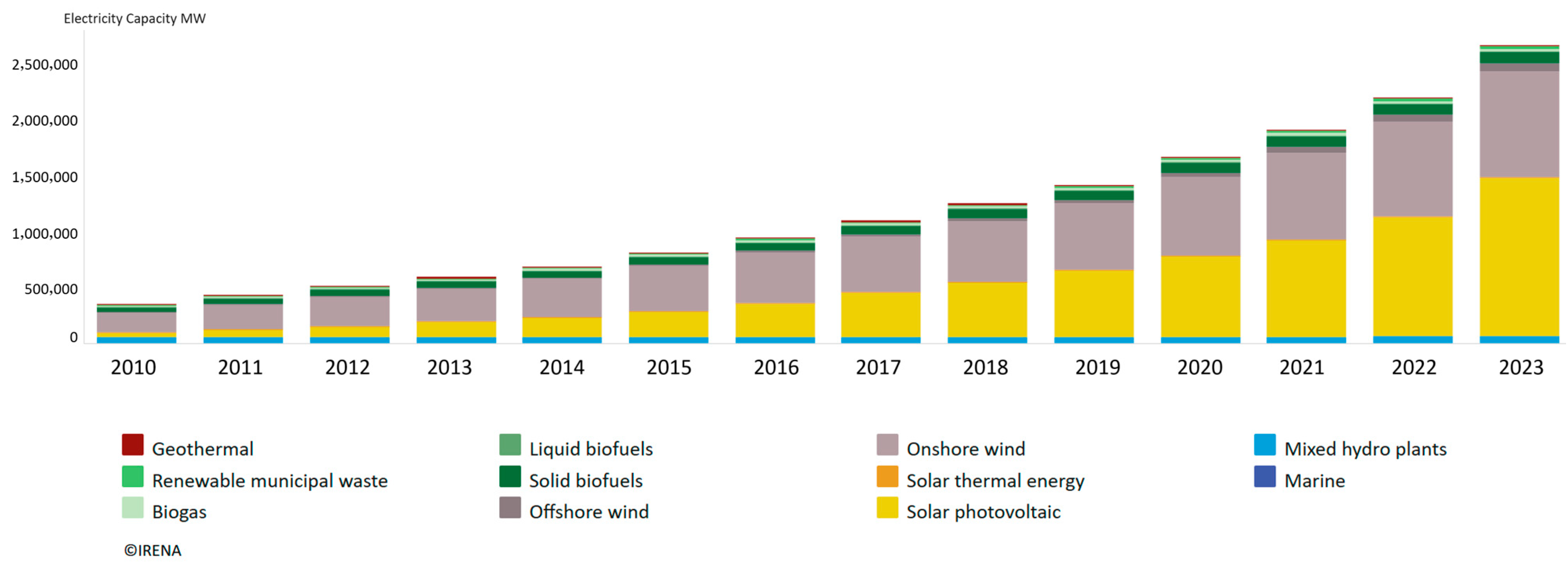
- IRENA Data & Statistics. International Renewable Energy Agency. 2024. Available online: https://public.tableau.com/app/profile/irena.resource/viz/IRENARETimeSeries/ExploreDashboard (accessed on 20 February 2025).
- Cédric, P.; Frankl, P.; Tam, C.; Abdelilah, Y.; Bahar, H.; Mueller, S.; Waldron, M. Technology Roadmap: Solar Thermal Electricity; International Energy Agency: Paris, France, 2014. [Google Scholar]
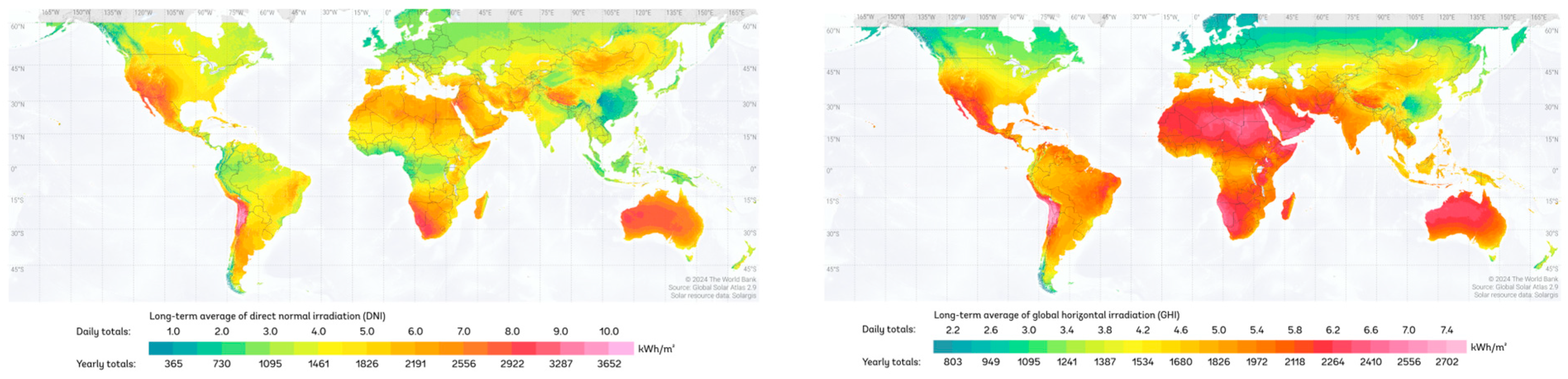
- SolarGIS. World Bank Group. 2025. Available online: https://solargis.com/resources/free-maps-and-gis-data (accessed on 13 February 2025).
- Bosetti, V.; Catenacci, M.; Fiorese, G.; Verdolini, E. The future prospect of PV and CSP solar technologies: An expert elicitation survey. Energy Policy 2012, 49, 308–317. [Google Scholar] [CrossRef]
- Bale, C.S.; Varga, L.; Foxon, T.J. Energy and complexity: New ways forward. Appl. Energy 2015, 138, 150–159. [Google Scholar] [CrossRef]
- Kulichenko, N.; Wirth, J. Concentrating Solar Power in Developing Countries: Regulatory and Financial Incentives for Scaling Up; World Bank Publications: Washington, DC, USA, 2012. [Google Scholar]
- Ahmad, S.; Tahar, R.M. Selection of renewable energy sources for sustainable development of electricity generation system using analytic hierarchy process: A case of Malaysia. Renew. Energy 2014, 63, 458–466. [Google Scholar] [CrossRef]
- Roni, M.M.; Hoque, I.U.; Ahmed, T. Comparative study of levelized cost of electricity (LCOE) for concentrating solar power (CSP) and photovoltaic (PV) plant in the southeastern region of Bangladesh. In Proceedings of the International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 7–9 February 2019. [Google Scholar]
- Khan, M.I.; Gutiérrez-Alvarez, R.; Asfand, F.; Bicer, Y.; Sgouridis, S.; Al-Ghamdi, S.G.; Kurniawan, T.A.; Abid, M.; Pesyridis, A.; Farooq, M. The economics of concentrating solar power (CSP): Assessing cost competitiveness and deployment potential. Renew. Sustain. Energy Rev. 2024, 200, 114551. [Google Scholar] [CrossRef]
- Alaqel, S.; Djajadiwinata, E.; Saeed, R.S.; Saleh, N.S.; Al-Ansary, H.; El-Leathy, A.; Danish, S.; Shafiq, T.; Golob, M.; Nguyen, C.; et al. Performance of the world’s first integrated gas turbine–solar particle heating and energy storage system. Appl. Therm. Eng. 2022, 215, 119049. [Google Scholar] [CrossRef]
- Kennedy, K.M.; Ruggles, T.H.; Rinaldi, K.; Dowling, J.A.; Duan, L.; Caldeira, K.; Lewis, S.A. The role of concentrated solar power with thermal energy storage in least-cost highly reliable electricity systems fully powered by variable renewable energy. Adv. Appl. Energy 2022, 6, 100091. [Google Scholar] [CrossRef]
- Rodat, S.; Thonig, R. Status of Concentrated Solar Power Plants Installed Worldwide: Past and Present Data. Clean Technol. 2024, 6, 365–378. [Google Scholar] [CrossRef]
- Orangzeb, S.; Qaisrani, M.A.; Shafiq, B.; Ahmed, N.; Sahar, M.S.U.; Ullah, S.; Farooq, M.U.; Jiabin, F. Potential Assessment and Economic Analysis of Concentrated Solar Power against Solar Photovoltaic Technology. Int. J. Energy Res. 2023, 1, 3611318. [Google Scholar] [CrossRef]
- Nixon, J.D.; Dey, P.K.; Davies, P.A. Which is the best solar thermal collection technology for electricity generation in north-west India? Evaluation of options using the analytical hierarchy process. Energy 2010, 35, 5230–5240. [Google Scholar] [CrossRef]
- Pratik, R.; Sasadhar, B. A comparative evaluation model for assessing solar energy capacity development of multiple geographical alternatives. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Kuala Lumpur, Malaysia, 7–10 December 2022. [Google Scholar]
- Ingenhoven, P.; Lee, L.; Saw, W.; Rafique, M.M.; Potter, D.; Nathan, G.J. Techno-economic assessment from a transient simulation of a concentrated solar thermal plant to deliver high-temperature industrial process heat. Renew. Sustain. Energy Rev. 2023, 185, 113626. [Google Scholar] [CrossRef]
- Aragonés-Beltrán, P.; Chaparro-González, F.; Pastor-Ferrando, J.-P.; Pla-Rubio, A. An AHP (Analytic Hierarchy Pro-cess)/ANP (Analytic Network Process)-based multi-criteria decision approach for the selection of solar-thermal power plant investment projects. Energy 2014, 66, 222–238. [Google Scholar] [CrossRef]
- Cavallaro, F. Multi-criteria decision aid to assess concentrated solar thermal technologies. Renew. Energy 2009, 34, 1678–1685. [Google Scholar] [CrossRef]
- Pitz-Paal, R.; Dersch, J.; Milow, B. European Concentrated Solar Thermal Road-Mapping (ECOSTAR); Coordinated action sustainable energy systems SES6-CT-2003-502578; European Commission: Cologne, Germany, 2005. [Google Scholar] [CrossRef]
- Peterseim, J.H.; White, S.; Tadros, A.; Hellwig, U. Concentrated solar power hybrid plants, which technologies are best suited for hybridisation? Renew. Energy 2013, 57, 520–532. [Google Scholar] [CrossRef]
- Nixon, J.D.; Dey, P.K.; Davies, P.A. Design of a novel solar thermal collector using a multi-criteria decision-making methodology. J. Clean. Prod. 2013, 59, 150–159. [Google Scholar] [CrossRef]
- Abouhawwash, M.; Jameel, M. Evaluation Factors of Solar Power Plants to Reduce Cost Under Neutrosophic Multi-Criteria Decision Making Model. Sustain. Mach. Intell. J. 2023, 2, 1–11. [Google Scholar] [CrossRef]
- Kassem, A.; Al-Haddad, K.; Komljenovic, D.; Schiffauerova, A. A value tree for identification of evaluation criteria for solar thermal power technologies in developing countries. Sustain. Energy Technol. Assess. 2016, 16, 18–32. [Google Scholar] [CrossRef]
- Bozbura, F.T.; Beskese, A.; Kahraman, C. Prioritization of human capital measurement indicators using fuzzy AHP. Expert Syst. Appl. 2007, 32, 1100–1112. [Google Scholar] [CrossRef]
- Chan, F.T.; Kumar, N. Global supplier development considering risk factors using fuzzy extended AHP-based approach. Omega 2007, 35, 417–431. [Google Scholar] [CrossRef]
- Demirel, T.; Demirel, N.Ç.; Kahraman, C. Fuzzy analytic hierarchy process and its application. In Fuzzy Multi-Criteria Decision Making: Theory and Applications with Recent Developments; Springer: Berlin/Heidelberg, Germany, 2008; pp. 53–83. [Google Scholar]
- Chang, D.-Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Zhu, K.-J.; Jing, Y.; Chang, D.-Y. A discussion on extent analysis method and applications of fuzzy AHP. Eur. J. Oper. Res. 1999, 116, 450–456. [Google Scholar] [CrossRef]
- Laarhoven, P.V.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Kassem, A.; Al-Haddad, K.; Komljenovic, D. Concentrated solar thermal power in Saudi Arabia: Definition and simulation of alternative scenarios. Renew. Sustain. Energy Rev. 2017, 80, 75–91. [Google Scholar] [CrossRef]
- Tang, Y.-C.; Beynon, M.J. Application and development of a fuzzy analytic hierarchy process within a capital investment study. J. Econ. Manag. 2005, 1, 207–230. [Google Scholar]
- Zheng, G.; Jing, H.H.Y.; Shi, G.; Zhang, X. Developing a fuzzy analytic hierarchical process model for building energy conservation assessment. Renew. Energy 2010, 35, 78–87. [Google Scholar] [CrossRef]
- Komljenovic, D.; Kecojevic, V. Multi-attribute selection method for materials handling equipment. Int. J. Ind. Syst. Eng. 2009, 4, 151–173. [Google Scholar] [CrossRef]
- Celik, M.; Er, I.D.; Ozok, A.F. Application of fuzzy extended AHP methodology on shipping registry selection: The case of Turkish maritime industry. Expert Syst. Appl. 2009, 36, 190–198. [Google Scholar] [CrossRef]
- Saaty, T.L. How to Make a Decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Saaty, T.; Vargas, L.G. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process; Springer Science & Business Media: Berlin, Germany, 2012; Volume 175. [Google Scholar]
- NREL. Concentrating Solar Power Projects. Available online: http://www.nrel.gov/csp/solarpaces/ (accessed on 1 March 2016).
- World Bank. Middle East and North Africa Region Assessment of the Local Manufacturing Potential for Concentrated Solar Power (CSP) Projects; The World Bank and ESMAP: Washington, DC, USA, 2011. [Google Scholar]
- Lemmer, V. Comparative Market Analysis and Economic Simulation for Morocco of the Parabolic Trough and Dish CSP Technologies. Master Thesis, University of Lisboa, Lisboa, Portugal, 2014. [Google Scholar]
- IRENA. Renewable Energy Technologies: Cost Analysis Series—Concentrated Solar Power; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2012. [Google Scholar]
- Forrester, J. The value of CSP with thermal energy storage in providing grid stability. Energy Procedia 2013, 49, 1632–1641. [Google Scholar] [CrossRef]
- Mills, D.A.; Wiser, R. An Evaluation of Solar Valuation Methods Used in Utility Planning and Procurement Processes; Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2012. [Google Scholar]
- Denholm, P.; Hummon, M. Simulating the Value of Concentrating Solar Power with Thermal Energy Storage in a Production Cost Model; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2012. [Google Scholar]
- IRENA. Concentrating Solar Power: Technology Brief; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2013. [Google Scholar]
- Lovegrove, K.; Watt, M.; Passey, R.; Pollock, G.; Wyder, J.; Dowse, J. Realising the Potential of Concentrating Solar Power in Australia: Summary for Stakeholders; Australian Solar Institute Pty, Limited: Newcastle, NSW, Australia, 2012. [Google Scholar]
- Burgherr, P.; Hirschberg, S.; Spada, M. Comparative assessment of accident risks in the energy sector. In Handbook of Risk Management in Energy Production and Trading; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Tyner, C.; Wasyluk, D. eSolar’s Modular, Scalable Molten Salt Power Tower Reference Plant Design. Energy Procedia 2014, 49, 1563–1572. [Google Scholar] [CrossRef]
- Peterseim, J.H.; White, S.; Tadros, A.; Hellwig, U. Concentrating solar power hybrid plants—Enabling cost effective synergies. Renew. Energy 2014, 67, 178–185. [Google Scholar] [CrossRef]
- Konstantin, P.; Kretschmann, J. Assessment of Technology Options for Development of Concentrating Solar Power in South Africa for the World Bank. Presentation Slideshow of Fichtner. In Proceedings of the ESMAP 2010, Johannesburg, South Africa, 9–10 December 2010. [Google Scholar]
- Cekirge, H.M.; Elhassan, A. A Comparison of Solar Power Systems (CSP): Solar Tower (ST) Systems versus Parabolic Trough (PT) Systems. Am. J. Energy Eng. 2015, 3, 29–36. [Google Scholar] [CrossRef]
- Zhu, G.; Wendelin, T.; Wagner, M.J.; Kutscher, C. History, current state, and future of linear Fresnel concentrating solar collectors. Sol. Energy 2014, 103, 639–652. [Google Scholar] [CrossRef]
- NREL. System Advisor Model Help; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2015. [Google Scholar]
- Padmanathan, P. Renewable Energy: A Compelling Value Proposition. In Proceedings of the Saudi Arabia Smart Grid Conference, Jeddah, Saudi Arabia, 6–8 December 2016. [Google Scholar]
- Agboola, O.P. The Potentials of Concentrating Solar Thermal Power (CSTP) in Meeting Saudi Future Energy Gap. In Proceedings of the World Congress on Engineering, London, UK, 5–7 July 2015; pp. 1111–1115. [Google Scholar]
- Ong, S.; Campbell, C.; Denholm, P.; Margolis, R.; Heath, G. Land-Use Requirements for Solar Power Plants in the United States; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2013. [Google Scholar]
- Fabrizi, F. CSP Technologies Environmental Impact; Energy Sector Management Assistance Program (ESMAP): Washington, DC, USA, 2012. [Google Scholar]
- Hernandez, R.R.; Easter, S.B.; Murphy-Mariscal, M.L.; Maestre, F.T.; Tavassoli, M.; Allen, E.B.; Barrows, C.W.; Belnap, J.; Ochoa-Hueso, R.; Ravi, S.; et al. Environmental impacts of utility-scale solar energy. Renew. Sustain. Energy Rev. 2014, 29, 766–779. [Google Scholar] [CrossRef]
- Burkhardt, J.J.; Heath, G.A.; Turchi, C.S. Life cycle assessment of a parabolic trough concentrating solar power plant and the impacts of key design alternatives. Environ. Sci. Technol. 2011, 45, 2457–2464. [Google Scholar] [CrossRef]
- Hang, Y.; Balkoski, K.; Meduri, P. Life Cycle Analysis of Linear Fresnel Solar Power Technology. In Proceedings of the ASME 2013 Power Conference, Boston, MA, USA, 29 July–1 August 2013; pp. 1–9. [Google Scholar]
- Lecho, Y.; de la Ru, C.; Sa, R. Life Cycle Environmental Impacts of Electricity Production by Solarthermal Power Plants in Spain. J. Sol. Energy Eng. 2008, 130, 021012. [Google Scholar] [CrossRef]
- Energy Analysis-Life Cycle Assessment Harmonization Results and Findings. Available online: https://www.nrel.gov/analysis/life-cycle-assessment.html (accessed on 9 February 2024).
- Burkhardt, J.J.; Heath, G.; Cohen, E. Life Cycle Greenhouse Gas Emissions of Trough and Tower Concentrating Solar Power Electricity Generation: Systematic Review and Harmonization. J. Ind. Ecol. 2012, 16, S93–S109. [Google Scholar] [CrossRef]
- Wagner, M.; Zhu, G. A direct-steam linear Fresnel performance model for NREL’s system advisor model. In Proceedings of the ASME 2012 6th International Conference on Energy Sustainability & 10th International Conference on Fuel Cell Science, Engineering and Technology, San Diego, CA, USA, 23–26 July 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012. [Google Scholar]
- Weinrebe, G.; Bohnke, M.; Trieb, F. Life cycle assessment of an 80 MW SEGS plant and a 30 MW Phoebus power tower. In Proceedings of the International Solar Engineering Conference “Solar Engineering 1998”, Albuquerque, NM, USA, 14–17 June 1998; pp. 417–424. [Google Scholar]
- CSP Prospects in Saudi Arabia 2014: A comparison of concentrated solar power and photovoltaics in the most promising solar market in the world. In Proceedings of the MENASOL, Dubau, United Arab Emirates, 6–7 May 2014.
- Lancereau, Q.; Rabut, Q.; Itskhokine, D.; Benmarraze, M. Wind Loads on Linear Fresnel Reflectors’ Technology: A Numerical Study. Energy Procedia 2015, 69, 116–125. [Google Scholar] [CrossRef]
- Wagner, M.J. Simulation and Predictive Performance Modeling of Utility-Scale Central Receiver System Power Plants. Master Thesis, University of Wisconsin, Madison, WI, USA, 12 December 2008. [Google Scholar]
- Perez, I.; Lopez, A.; Briceño, S.; Relancio, J. National Incentive Programs for CSP—Lessons Learned. Energy Procedia 2014, 49, 1869–1878. [Google Scholar] [CrossRef]

| Linguistic Scale | TFN Scale | TFN Reciprocal Scale |
|---|---|---|
| Just equal | (1,1,1) | (1,1,1) |
| Equally important | (1/2,1,3/2) | (2/3,1,2) |
| Weakly important | (1,3/2,2) | (1/2,2/3,1) |
| Strongly more important | (3/2,2,5/2) | (2/5,1/2,2/3) |
| Very strongly more important | (2,5/2,3) | (1/3,2/5,1/2) |
| Absolutely more important | (5/2,3,7/2) | (2/7,1/3,2/5) |
| Technical | Economic | Environmental | Social | |
|---|---|---|---|---|
| Technical | (1,1,1) | (1/2,2/3,1) (1/2,2/3,1) (1/3,2/5,1/2) | - (1/3,2/5,1/2) (1/2,2/3,1) | (2,5/2,3) (2/5,1/2,2/3) - |
| Economic | (1,3/2,2) (1,3/2,2) (2,5/2,3) | (1,1,1) | - (2/5,1/2,2/3) (3/2,2,5/2) | (5/2,3,7/2) (1/2,2/3,1) - |
| Environmental | - (2,5/2,3) (1,3/2,2) | - (3/2,2,5/2) (2/5,1/2,2/3) | (1,1,1) | - (1,3/2,2) - |
| Social | (1/3,2/5,1/2) (3/2,2,5/2) - | (2/7,1/3,2/5) (1,3/2,2) - | - (1/2,2/3,1) - | (1,1,1) |
| Technical | Economic | Environmental | Social | |
|---|---|---|---|---|
| Technical | (1,1,1) | (0.54,0.95,1.39) | (0.77,1.22,1.70) | (0.98,1.46,1.94) |
| Economic | (0.72,1.05,1.85) | (1,1,1) | (0.801.28,1.77) | (1.01,1.53,2.04) |
| Environmental | (0.59,0.82,1.30) | (0.56,0.78,1.25) | (1,1,1) | (0.75,1.21,1.70) |
| Social | (0.52,0.69,1.02) | (0.49,0.65,0.99) | (0.59,0.82,1.34) | (1,1,1) |
| Label | Sub-Criteria | Measurement Indicator | Type | Unit | Summarized Information |
|---|---|---|---|---|---|
| Technical | |||||
| T1 | Maturity | Total installed capacity | Continuous | MW | PT with synthetic oil (no storage): 2234 MW; PT with TES: 1180 MW; solar tower (ST): 640 MW; LF: 181 MW |
| T2 | Optical efficiency | Concentration level | Continuous | Suns | ST has a concentration level of up to 1000 suns, PT 70–80 suns, and LF 60 suns |
| T3 | Conversion efficiency | Capacity factor | Continuous | % | The capacity factors of alternatives 1 to 6 were 22.4%, 30%, 39.9%, 59.5%, 64.1%, and 27.1%, respectively |
| T4 | Reliability | Ability to support grid stability | Discrete | 1–5 Likert scale | PT (no TES): medium reliability (75% capacity credit); PT (TES): high (98%); ST (TES): high (98%); LF: medium (75%) |
| T5 | Deployment time | Required time for development and construction | Continuous | Months | Development: 18 months (all technologies); construction: 18–36 months, depending on plant capacity and configuration |
| T6 | Safety | Severe accidents throughout the energy chain | Continuous | Fatalities/GWh/y | CSP fatality rate: 0.035–0.202 fatalities/GWh (lowest among RESs); PVs: 0.245; wind: 1.89 fatalities/GWh |
| T7 | Scalability and modularity | Ability to scale and augment technology | Discrete | 1–5 Likert scale | PT and LF: high scalability (e.g., SEGS: 354 MW in 9 phases); ST: limited, but potential shown with modular designs like Sierra SunTower (5 MW) |
| T8 | Storage hours | Total time thermal energy can operate a plant at the rated capacity | Continuous | Hours | 8–12 h storage capacity with TES systems, ensuring flexibility and grid stability |
| T9 | Hybridization | Suitability for hybridization | Discrete | 1–5 Likert scale | Hybridization costs reduced by 28%; LF best for applications <450 °C, ST for >450 °C; common models: ISCC plants (e.g., Ain Beni Mathar) |
| T10 | Technology advancement potential | Potential for increased efficiency and cost reduction | Discrete | 1–5 Likert scale | PT: 15–30% cost reduction potential, limited improvement; ST: 15–25% cost reduction potential, significant improvement; LF: 15–35% cost reduction potential, very significant improvement. |
| T11 | Key components and availability of expertise | Availability of crucial hardware, software, and human resources expertise | Discrete | 1–5 Likert scale | MENA: lack of a skilled workforce for key CSP components (e.g., molten salt, absorber tubes); advanced industries required for local production |
| Economic | |||||
| EC1 | Capital cost | Initial plant cost | Continuous | MUSD | Cost ranges: LF (444–495 MUSD) < PT (941–1290 MUSD) < ST (1878–1948 MUSD): PT: lowest cost among TES systems |
| EC2 | Operation and maintenance (O&M) costs | Fixed and variable O&M costs | Continuous | USD/kWh | Annual O&M costs of alternatives 1 to 6 were estimated to be 4.1, 12.9, 17, 16, 27.3, and 4 MUSD, respectively |
| EC3 | Energy cost | Levelized cost of energy (LCOE) | Continuous | Cent/kWh | LCOE for alternatives 1 to 6, which were found to be 24.61, 26.29, 23.94, 14.99, 15.59, and 14.95 cent/kWh |
| EC4 | Market maturity | Technology providers | Discrete | Number of companies | PT: high (10+ providers); ST: medium (5+ providers); LF: medium (4+ providers) |
| EC5 | Economic feasibility | Net present value (NPV) | Continuous | MUSD | NPVs of alternatives 1 to 6 were 36.9, 96.2, 140.2, 70.3, 145.4, and 33.1 MUSD, respectively |
| EC6 | Fuel cost | Potential fuel consumption needed to operate a plant | Discrete | 1–5 Likert scale | Highest consumption: LF with DSG (250–350 °C); PT with synthetic oil (350–400 °C); ST with molten salt (up to 565 °C, no fossil fuel). A higher capacity requires more fuel; freeze protection fuel is minimal. |
| EC7 | Offsetting infrastructure cost | Capacity value | Continuous | USD/MWh | The annual capacity values for alternatives 1 to 6 were found to be 0.35, 6.04, 9.45, 7.76, 15.16, and 0.53 MUSD, respectively |
| EC8 | National economic benefit | Direct and indirect impact on the national economy | Continuous | National economic benefit index | The normalized values for the national economic benefit index of alternatives 1 to 6 were found to be 0.07, 0.18, 0.27, 0.14, 0.28, and 0.06, respectively. |
| Environmental | |||||
| EN1 | Required area | Land-use factor | Continuous | m2/MWh/y | PT: 15.8 m2/MWh/y; ST: 12.9 m²/MWh/y; LF: 16.2 m2/MWh/y; LF: more land required for larger capacities |
| EN2 | Emission reduction | Life cycle greenhouse gas (GHG) emissions | Continuous | g-CO2eq/kWh/y | Emissions: ST: 23 g-CO2/kWh; PT: 26 g-CO2/kWh; LF: 31 g-CO2/kWh; CSP emissions lower than PVs (43 g-CO2/kWh) |
| EN3 | Water consumption | Water consumption for cleaning | Continuous | L/MWh/y | Water usage: LF: 15 L/MWh; PT: 75 L/MWh; ST: 114 L/MWh; efficient robotic cleaning with flat LF mirrors |
| EN4 | Ecosystem disruption | Impact on surrounding environment | Discrete | 1–5 Likert scale | Minimal disruption; PT: risk of oil leaks; ST: greater impact on avian species due to high solar flux |
| EN5 | Life cycle assessment | Energy payback time (EPBT) | Continuous | Months | EPBT values: LF: 8.2 months; ST: 12.2 months; PT: 12.5 months; LF: best energy payback performance |
| EN6 | Impact of environmental conditions | Impact of soiling, humidity, temperature, and wind on energy production | Discrete | 1–5 Likert scale | Soiling impact: PT more than ST and LF; ST: sensitive to wind loads due to heliostats; molten salt systems: dependent on freeze protection |
| Social | |||||
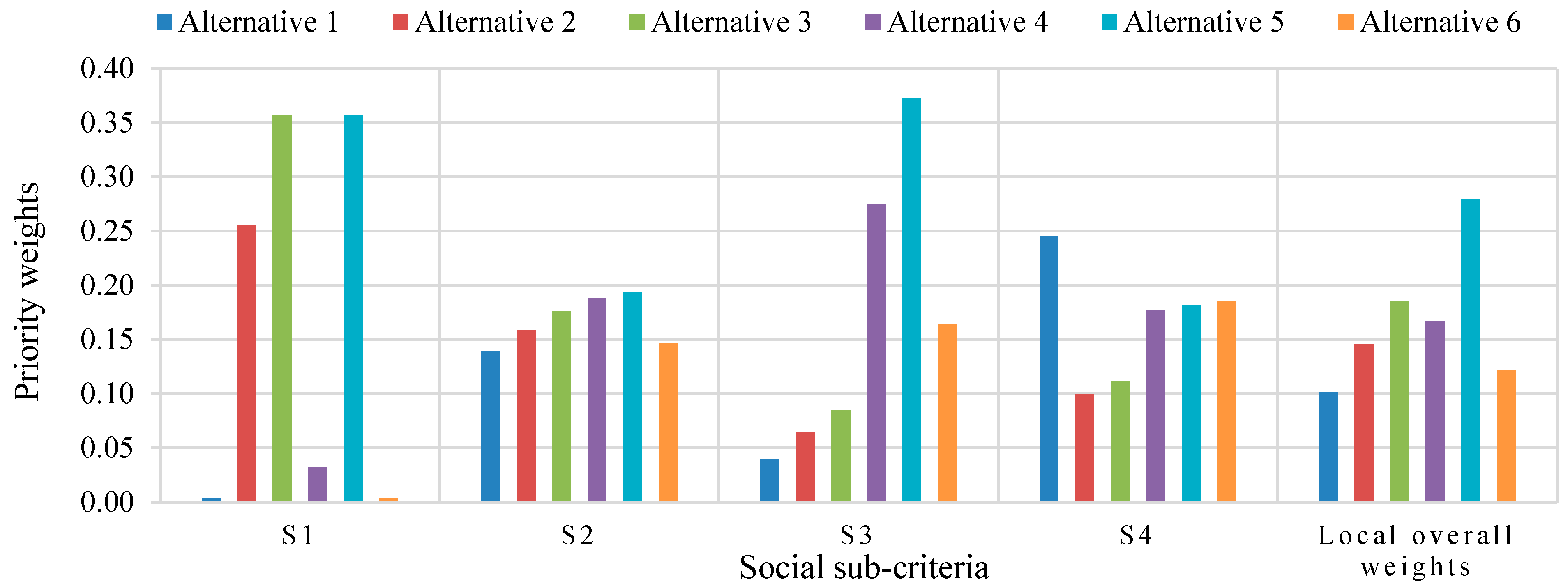
| S1 | Job creation | Employment opportunities | Continuous | One-year jobs/MW | Jobs created: LF: 1500 jobs; PT: 2454–2940 jobs; ST: 2900 jobs; larger plants: greater employment potential |
| S2 | Social and political acceptance | Acceptance rate | Discrete | 1–5 Likert scale | Community and politicians’ attitudes toward alternatives (subjective via questionnaire) |
| S3 | Local industrialization possibilities | Potential for manufacturing CSP plant components locally | Discrete | 1–5 Likert scale | Local industrialization: 45% initial costs, 90% O&M covered locally, 45% for local manufacturing; key components (e.g., mirrors, absorbers): international collaborations needed |
| S4 | Logistical feasibility | Potential for supporting mechanisms and regulations | Discrete | 1–5 Likert scale | Strong government incentives required; feed-in tariff (FiT) and R&D policies critical for CSP deployment (e.g., Spain, USA) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlKassem, A.; Al-Haddad, K.; Komljenovic, D.; Schiffauerova, A. The Strategic Selection of Concentrated Solar Thermal Power Technologies in Developing Countries Using a Fuzzy Decision Framework. Energies 2025, 18, 1957. https://doi.org/10.3390/en18081957
AlKassem A, Al-Haddad K, Komljenovic D, Schiffauerova A. The Strategic Selection of Concentrated Solar Thermal Power Technologies in Developing Countries Using a Fuzzy Decision Framework. Energies. 2025; 18(8):1957. https://doi.org/10.3390/en18081957
Chicago/Turabian StyleAlKassem, Abdulrahman, Kamal Al-Haddad, Dragan Komljenovic, and Andrea Schiffauerova. 2025. "The Strategic Selection of Concentrated Solar Thermal Power Technologies in Developing Countries Using a Fuzzy Decision Framework" Energies 18, no. 8: 1957. https://doi.org/10.3390/en18081957
APA StyleAlKassem, A., Al-Haddad, K., Komljenovic, D., & Schiffauerova, A. (2025). The Strategic Selection of Concentrated Solar Thermal Power Technologies in Developing Countries Using a Fuzzy Decision Framework. Energies, 18(8), 1957. https://doi.org/10.3390/en18081957










