Industrial Electricity Pricing and Renewable Energy: A Temporal Analysis of the Effect of Taxes
Abstract
:1. Introduction
2. Literature Review
3. Datasets and Methods
3.1. Datasets
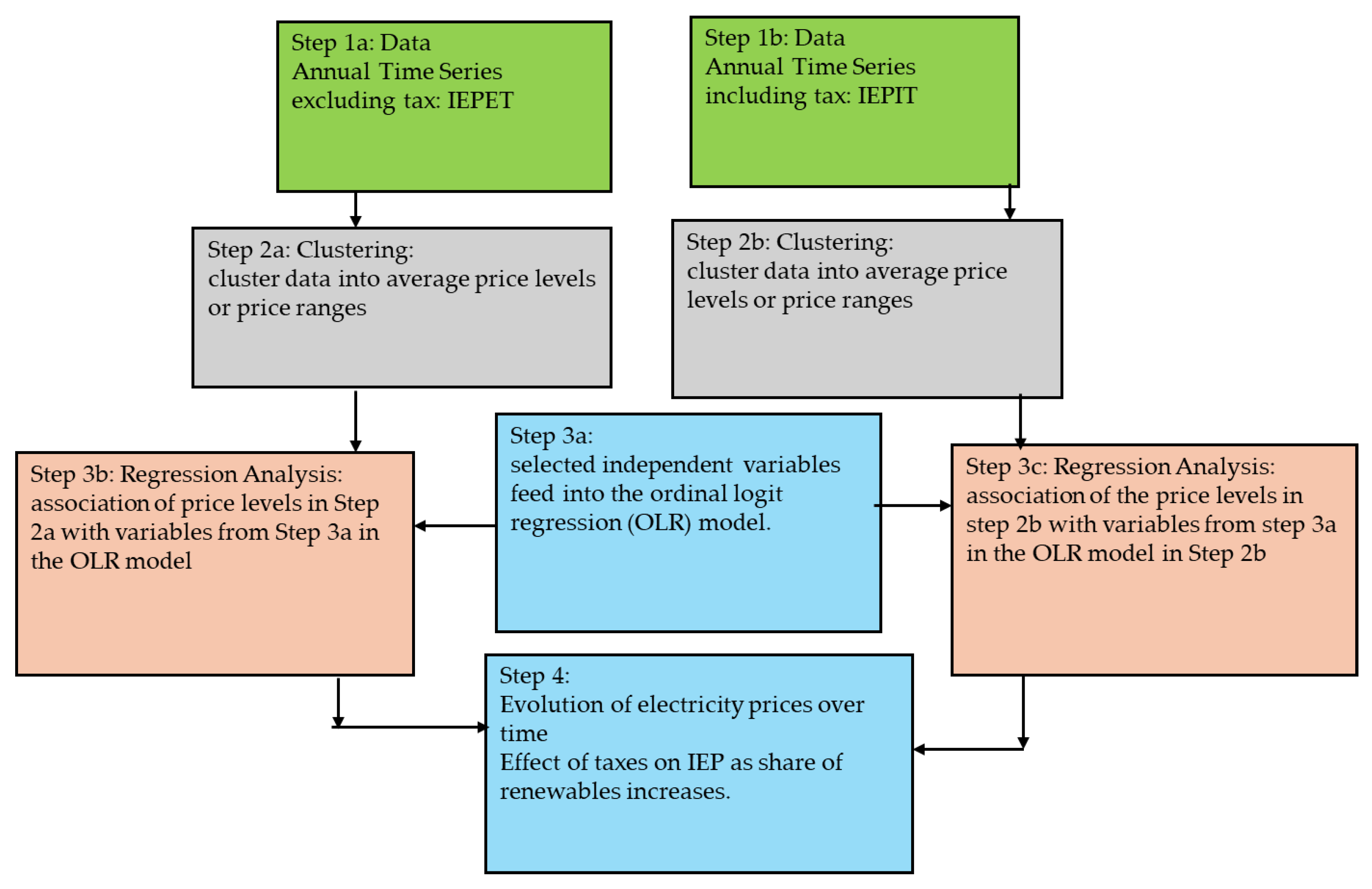
3.2. Method of Analysis
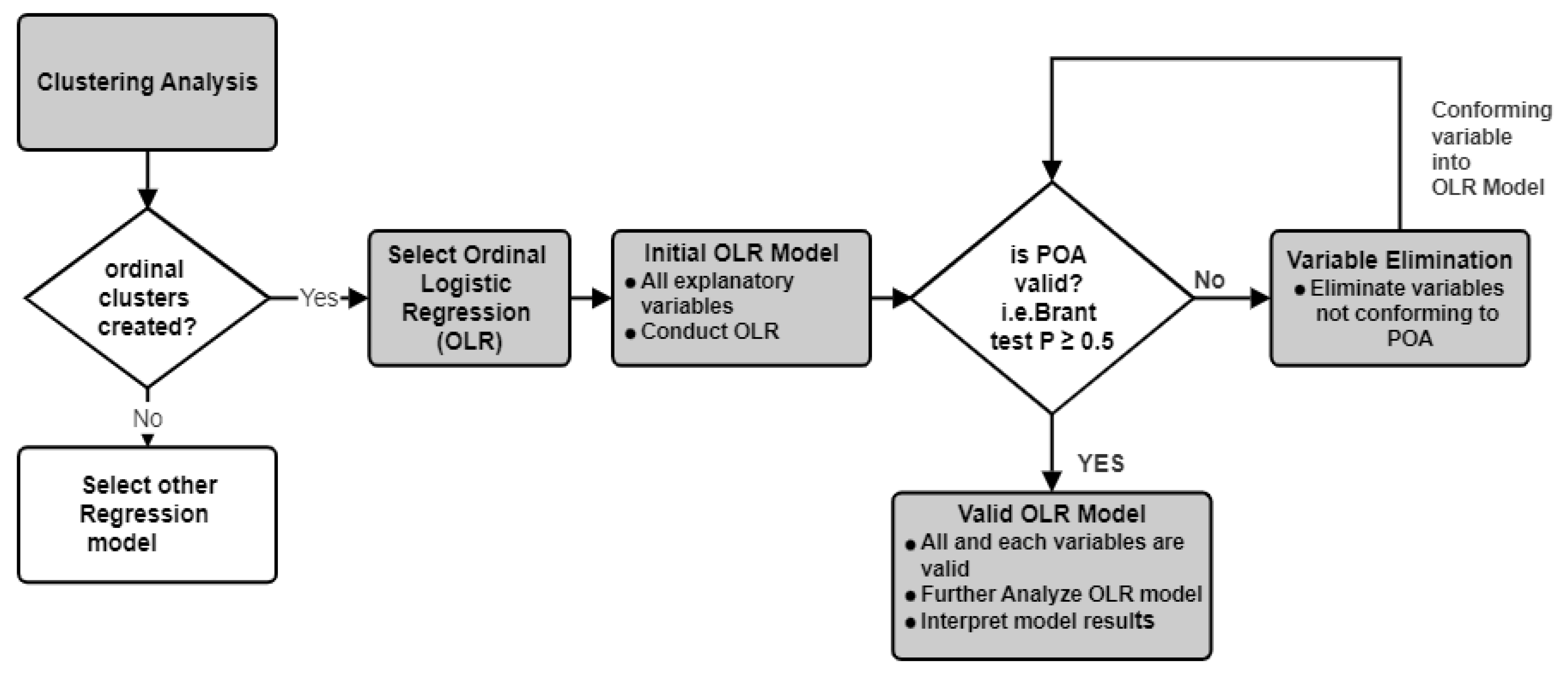
3.2.1. Determining the Pricing Cluster Levels
3.2.2. Ordinal Logistic Regression (OLR) Model
4. Results
4.1. Results of Cluster Analysis
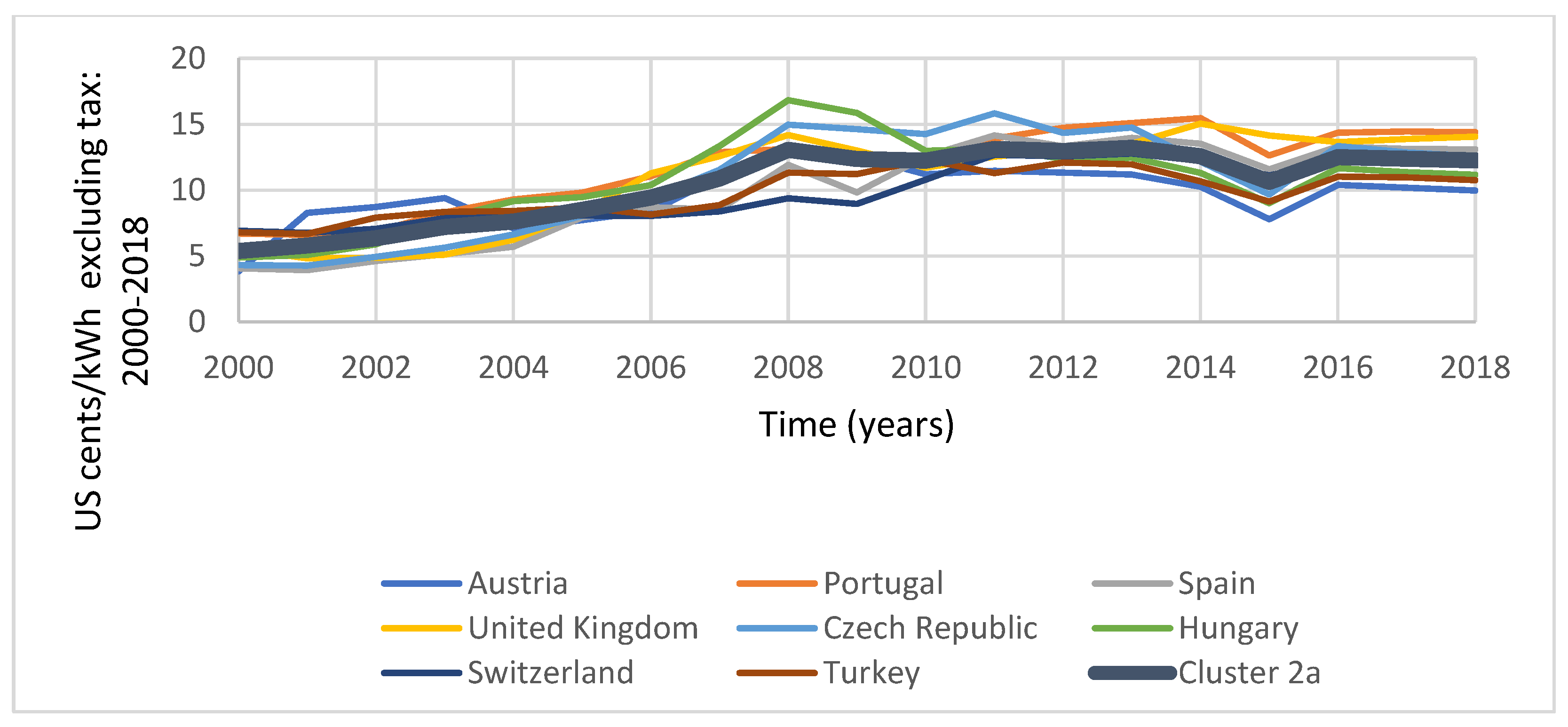
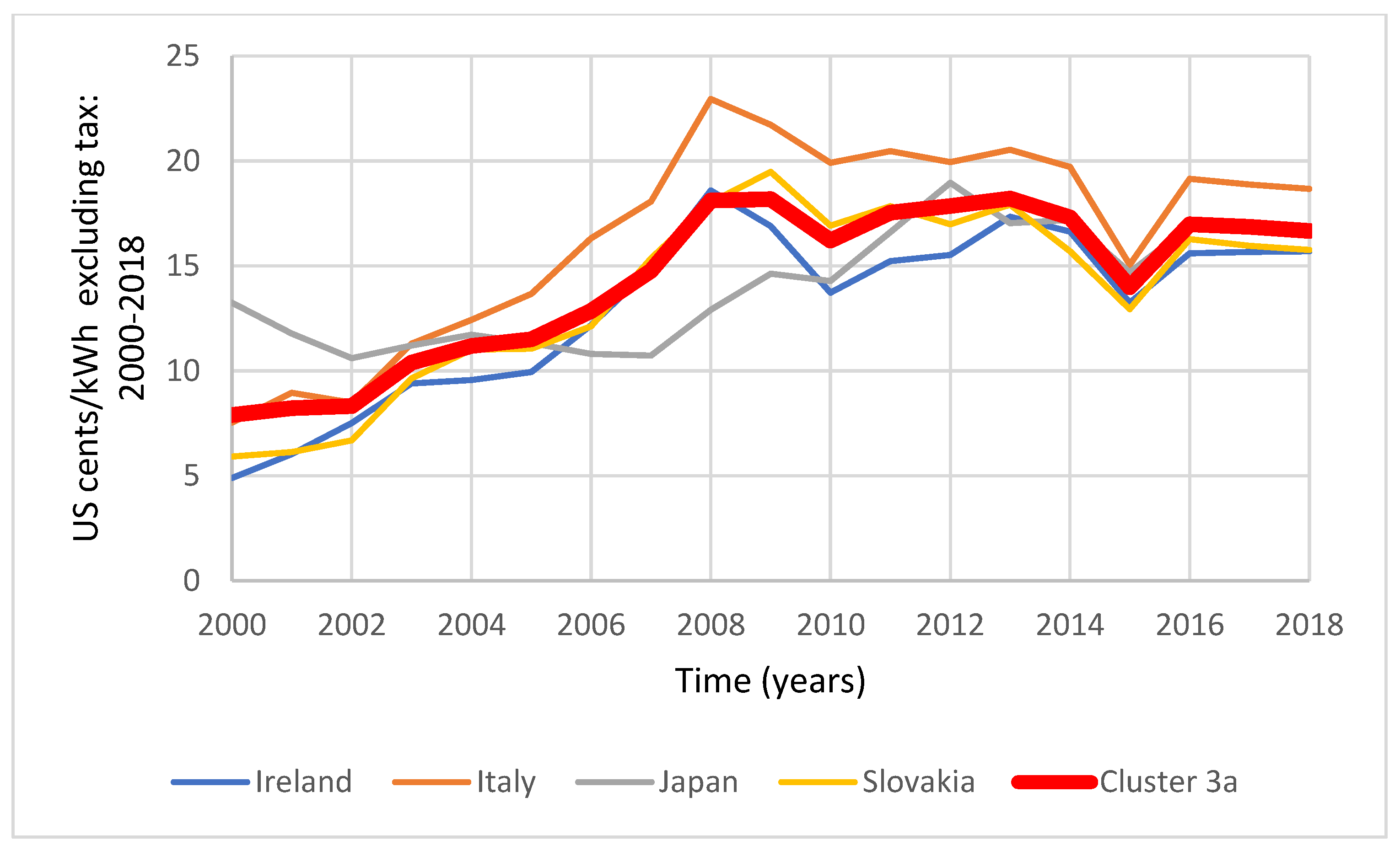
4.1.1. Industrial Electricity Pricing Excluding Tax
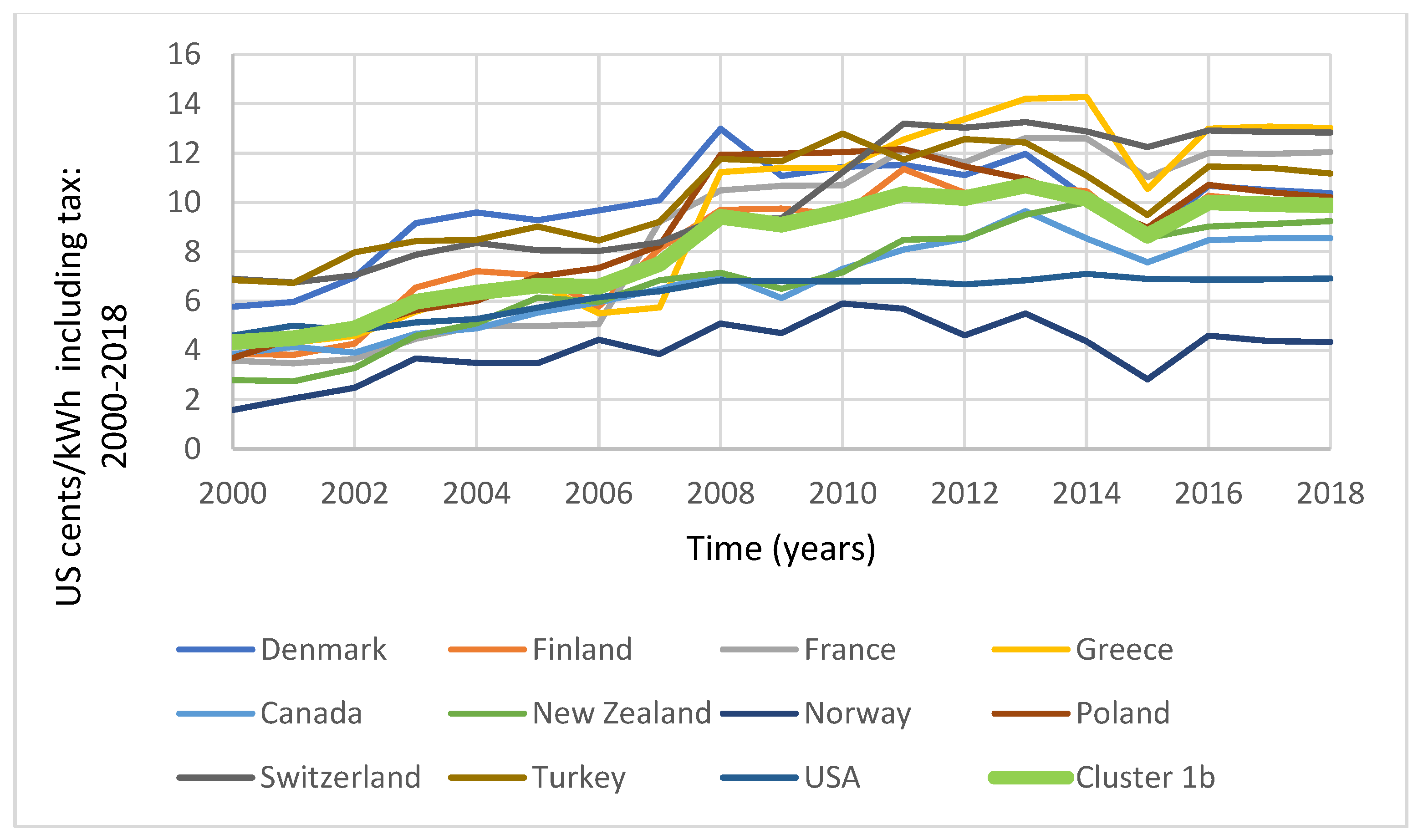
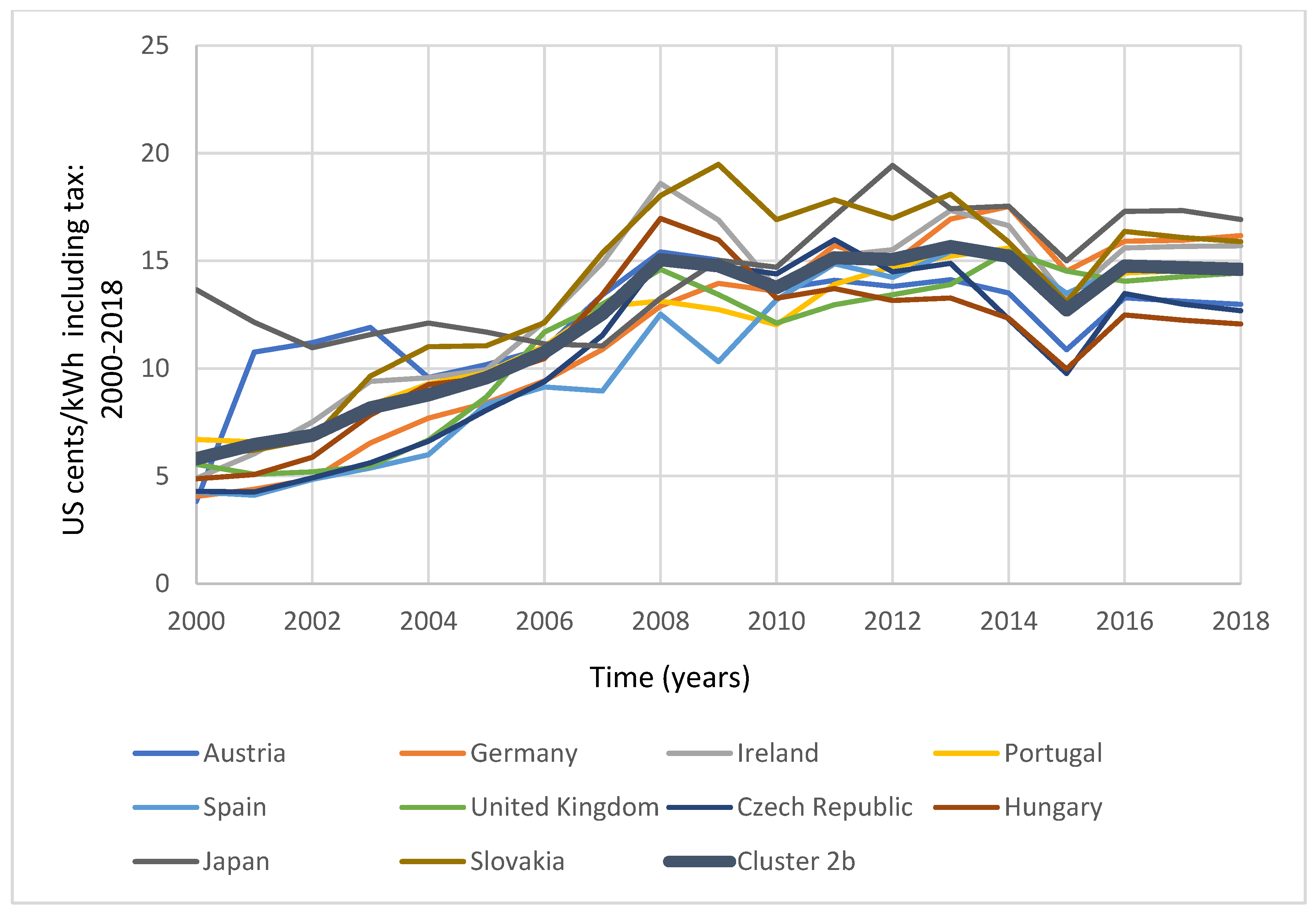
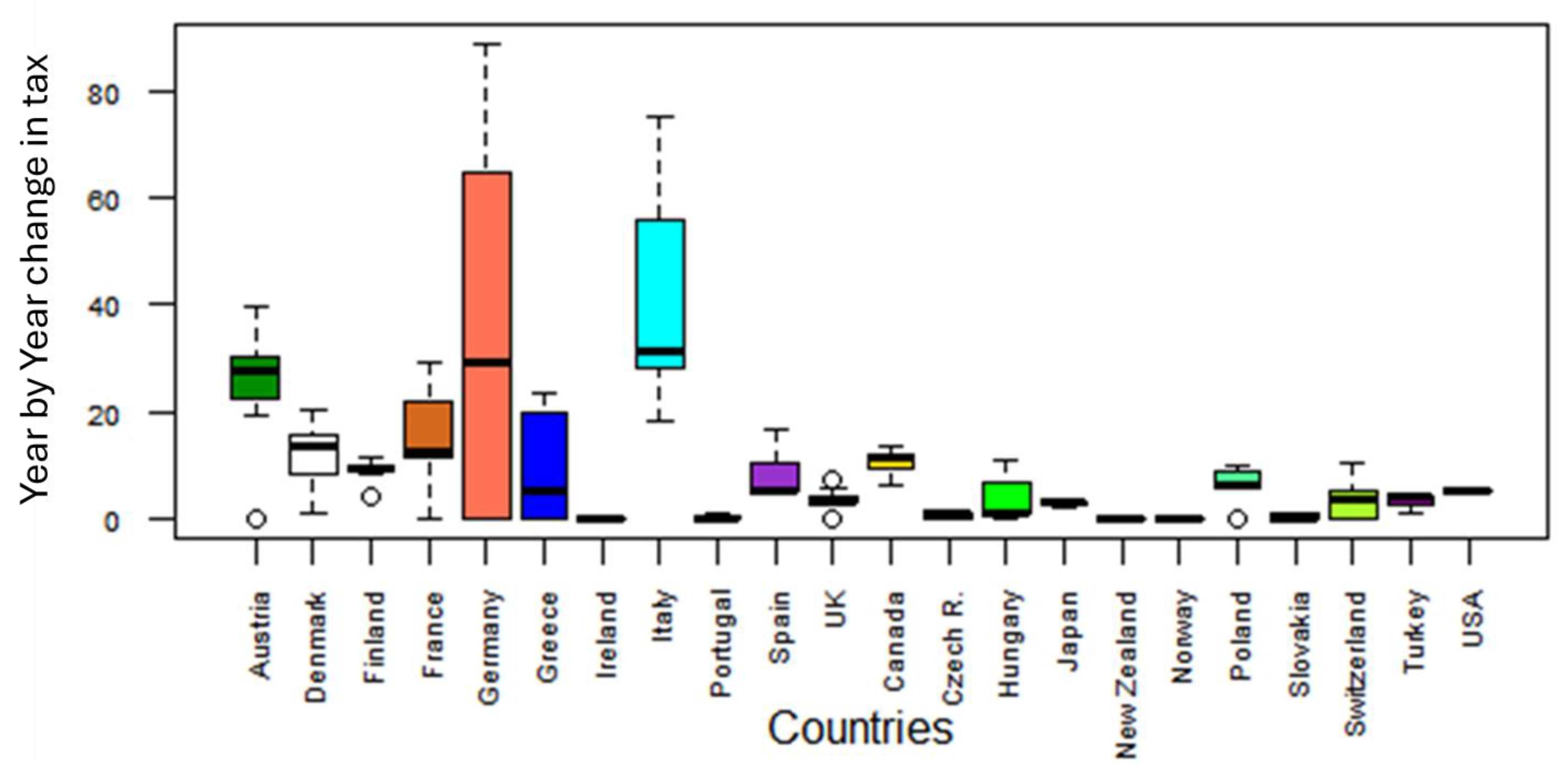
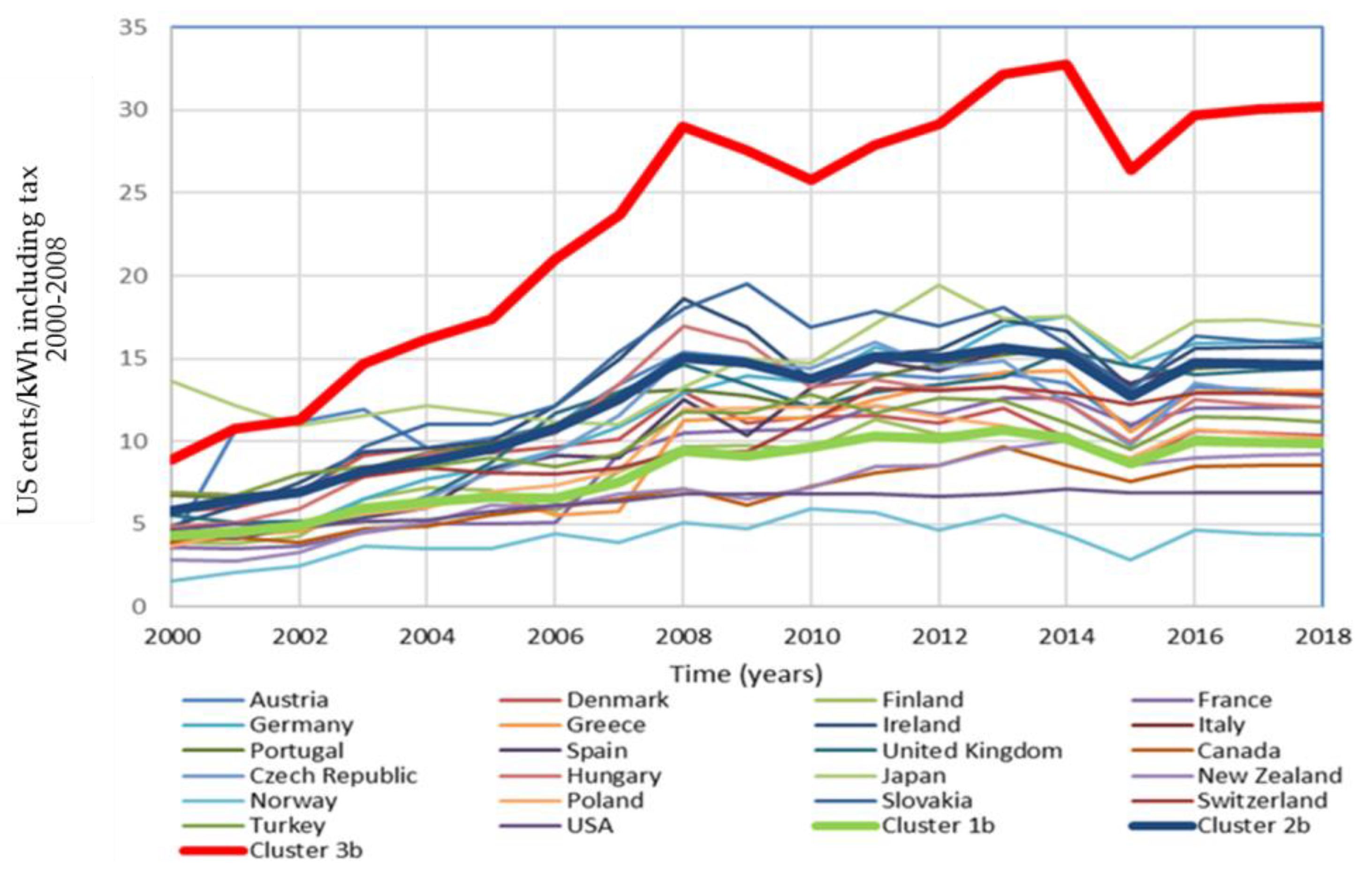
4.1.2. Industrial Electricity Pricing Including Tax
4.2. Results of Regression Analysis
4.2.1. Regression Results Excluding Tax
4.2.2. Regression Results Including Tax
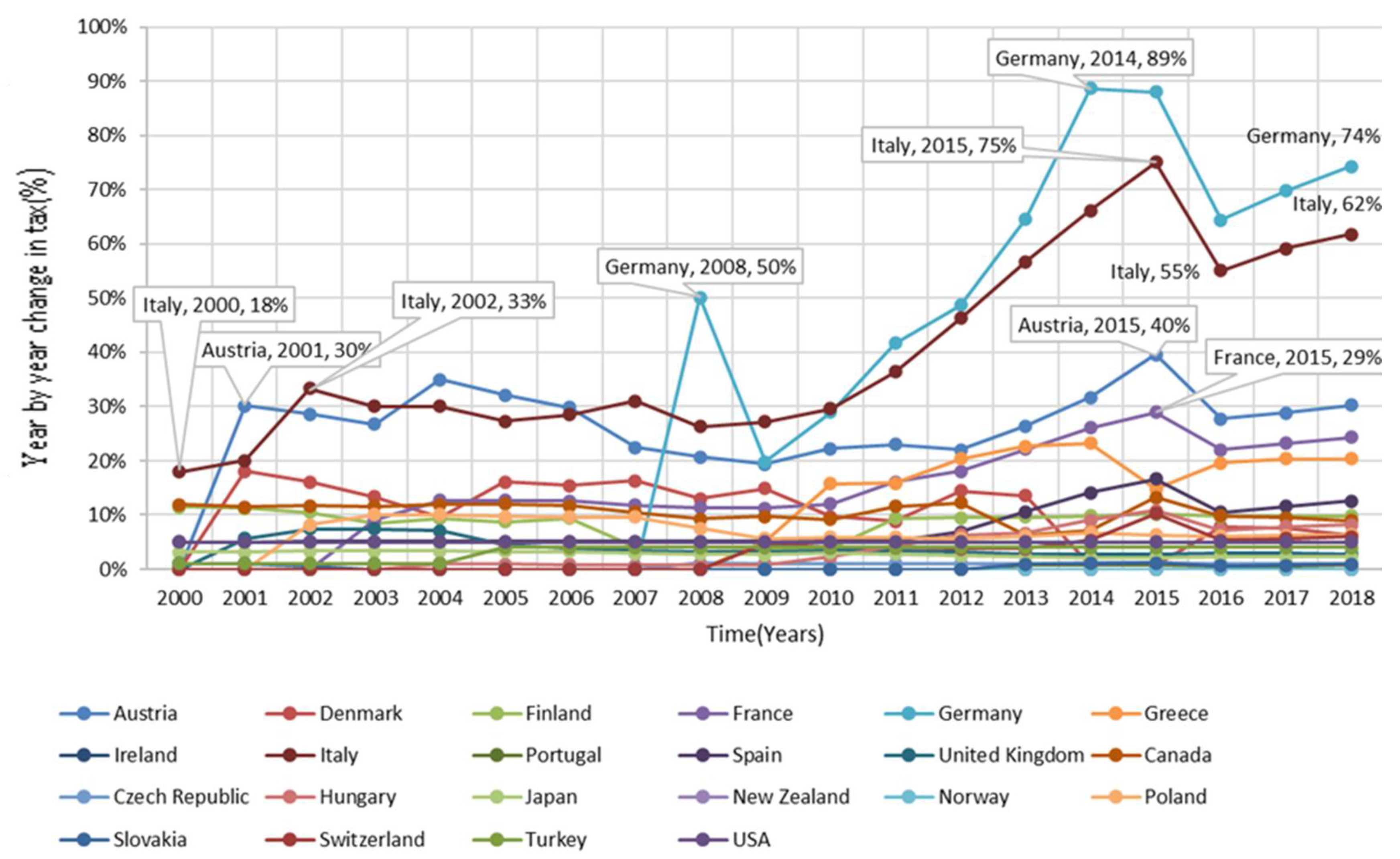
5. Discussion
5.1. Discussion on Cluster Analysis
5.1.1. Industrial Pricing Excluding Tax
5.1.2. Industrial Pricing Including Tax
5.2. Discussion on Regression Analysis
5.2.1. Regression Analysis Excluding Tax (Model 1c)
5.2.2. Regression Analysis Including Tax (Model 2b)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Reference Number. | Period of Study/Data | Country/Sector of Study | Methods | Findings |
|---|---|---|---|---|
| [22] | 1990 to 2021 | Russia/Power industry | Econometric analysis | Economic growth, financial development and CO2 emissions increase electricity use, while renewables lower this in the long run |
| [23] | 2000 to 2021 | 27 EU Countries and UK | Data gathering and nomenclature of territorial units for statistical geographical classification | Countries with high energy demand are leading the shift to renewable energy |
| [24] | 2010 to 2016 | Australia | Fixed effect regression analysis | Carbon tax has a significant impact on wholesale electricity prices and creates energy substitution effects |
| [25] | 2007 to 2016 | EU 28 Countries plus Norway | Panel vector autoregressive estimation approach | High electricity taxes result in high electricity prices and further promote responsible production and consumption |
| [26] | 1990 to 2010 | Poland | Multivariate quantile on quantile regression with Granger causality | Effective carbon taxes and an increase in renewables are crucial policies for reducing emissions |
| [27] | 1981 to 2016 | India/Industrial electricity | Two-threshold non-linear auto regressive distributed lag model | Effect on reaching net-zero emissions when industrial electricity prices are lowered |
| [28] | 2023 | Korea/Baland Industrial Complex | Systems model analysis | The critical role of regional electricity tariffs and carbon pricing in energy system feasibility |
| [31] | 2024 to 2050 | China/Zhejiang region | Computable general equilibrium model | Carbon taxes are less effective than carbon emissions control, and stricter carbon pricing leads to a reduction in carbon intensity, but slows GDP |
| [29] | 2003 to 2019 | China/285 Chinese cities | Difference-in Difference-methodology | Cities subscribing to critical peak industrial electricity pricing had a reduction in greenhouse gas emissions |
| [30] | 2006 to 2016 | China/Chinese Industrial listed Enterprises | Ramseys optimal pricing and slacks-based measure Directional distance function | Electricity price cross-subsidies, affect the green factor’s total productivity by improving resource allocation |
| Abbreviation | Full Meaning |
|---|---|
| IEP | Industrial electricity pricing |
| REG | Share of renewables generated |
| IEPET | Industrial electricity pricing excluding tax |
| IEPIT | Industrial electricity pricing including tax |
| TEG | Total electricity generated per year |
| TWH | Terawatt hour |
| GDPpc | Gross domestic product per capita |
| EIE | Greenhouse gas emissions by energy industries as a percentage of total emissions |
| ED | Energy dependency |
| OLR | Ordinal logistic regression |
| POA | Proportional odds assumption |
| Data Type | Number of Observations | Minimum Value | Maximum Value | Mean | Standard Deviation |
|---|---|---|---|---|---|
| IEPET (US cents) | 418 | 1.580139 | 22.94675 | 9.700091 | 4.063308 |
| IEPIT (US cents) | 418 | 1.580139 | 32.76514 | 10.64532 | 5.050645 |
| REG | 418 | 0.000000 | 0.51 | 0.051 | 0.077 |
| GDPpc | 418 | 7774.482 | 4,262,321 | 386,160.4 | 966,938.0 |
| EIE | 418 | 6.06 | 48.81 | 27.95 | 11.04 |
| ED | 418 | −843.481879 | 93.981260 | 11.192270 | 149.064917 |


References
- Xu, D.; Abbas, S.; Rafique, K.; Ali, N. The race to net-zero emissions: Can green technological innovation and environmental regulation be the potential pathway to net-zero emissions? Technol. Soc. 2023, 75, 102364. [Google Scholar] [CrossRef]
- Xenos, D.P.; Noor, I.M.; Matloubi, M.; Cicciotti, M.; Haugen, T.; Thornhill, N.F. Demand-side management and optimal operation of industrial electricity consumers: An example of an energy-intensive chemical plant. Appl. Energy 2016, 182, 418–433. [Google Scholar] [CrossRef]
- Fischer, D.; Surmann, A.; Lindberg, K.B. Impact of emerging technologies on the electricity load profile of residential areas. Energy Build. 2020, 208, 109614. [Google Scholar] [CrossRef]
- Irandoust, M. Innovations and renewables in the Nordic countries: A panel causality approach. Technol. Soc. 2018, 54, 87–92. [Google Scholar] [CrossRef]
- Aziz, S.; Jahan, S.M. Determinants of international development investments in renewable energy in developing countries. Energy Sustain. Dev. 2023, 74, 215–230. [Google Scholar] [CrossRef]
- Wang, K.; Yu, M.; Niu, D.; Liang, Y.; Peng, S.; Xu, X. Short-term electricity price forecasting based on similarity day screening, two-layer decomposition technique and Bi-LSTM neural network. Appl. Soft Comput. 2023, 136, 110018. [Google Scholar] [CrossRef]
- Macedo, D.P.; Marques, A.C.; Damette, O. The impact of the integration of renewable energy sources in the electricity price formation: Is the Merit-Order Effect occurring in Portugal? Util. Policy 2020, 66, 101080. [Google Scholar] [CrossRef]
- Dehghan, H.; Amin-Naseri, M.R. A simulation-based optimization model to determine optimal electricity prices under various scenarios considering stakeholders’ objectives. Energy 2022, 238, 121853. [Google Scholar] [CrossRef]
- Cieplinski, A.; D’alessandro, S.; Marghella, F. Assessing the renewable energy policy paradox: A scenario analysis for the Italian electricity market. Renew. Sustain. Energy Rev. 2021, 142, 110838. [Google Scholar] [CrossRef]
- Kolb, S.; Dillig, M.; Plankenbühler, T.; Karl, J. The impact of renewables on electricity prices in Germany-An update for the years 2014–2018. Renew. Sustain. Energy Rev. 2020, 134, 110307. [Google Scholar] [CrossRef]
- Lebepe, P.; Mathaba, T.N.D. Impact assessment of electricity shortage on enterprises: A systematic literature review. Energy Sustain. Dev. 2024, 81, 101468. [Google Scholar] [CrossRef]
- Koster, G.; Van Sark, W.; Ricker, B. Solar potential for social benefit: Maps to sustainably address energy poverty utilizing open spatial data in data poor settings. Energy Sustain. Dev. 2024, 80, 101453. [Google Scholar] [CrossRef]
- Li, K.; Yuan, W. The nexus between industrial growth and electricity consumption in China–New evidence from a quantile-on-quantile approach. Energy 2021, 231, 120991. [Google Scholar] [CrossRef]
- Ai, H.; Xiong, S.; Li, K.; Jia, P. Electricity price and industrial green productivity: Does the “low-electricity price trap” exist? Energy 2020, 207, 118239. [Google Scholar] [CrossRef]
- González, J.S.; Alonso, C.Á. Industrial electricity prices in Spain: A discussion in the context of the European internal energy market. Energy Policy 2021, 1148, 111930. [Google Scholar] [CrossRef]
- Yang, Y.; Faruqui, A. Reducing electricity prices and establishing electricity markets in China: Dos and don’ts. Electr. J. 2019, 32, 106633. [Google Scholar] [CrossRef]
- International-Energy-Agency. Electricity Market Report—December 2020-Report Extract 2020 Global Overview: Price. 2020. Available online: https://www.iea.org/reports/electricity-market-report-december-2020/2020-global-overview-prices (accessed on 30 December 2024).
- Trebbien, J.; Rydin Gorjão, L.; Praktiknjo, A.; Schäfer, B.; Witthaut, D. Understanding electricity prices beyond the merit order principle using explainable AI. Energy AI 2023, 13, 100250. [Google Scholar] [CrossRef]
- Adom, P.K.; Insaidoo, M.; Minlah, M.K.; Abdallah, A.-M. Does renewable energy concentration increase the variance/uncertainty in electricity prices in Africa? Renew. Energy 2017, 107, 81–100. [Google Scholar] [CrossRef]
- Del-Río, B.; Fernández-Sainz, A.; De Alegria, I.M. Industrial electricity prices in the European Union following restructuring: A comparative panel-data analysis. Util. Policy 2019, 60, 100956. [Google Scholar] [CrossRef]
- Moreno, B.; García-Álvarez, M.T.; Ramos, C.; Fernández-Vázquez, E.A. General Maximum Entropy Econometric approach to model industrial electricity prices in Spain: A challenge for the competitiveness. Appl. Energy 2014, 135, 815–824. [Google Scholar] [CrossRef]
- Kilinc-Ata, N.; Proskuryakova, L.N. Empirical analysis of the Russian power industry’s transition to sustainability. Util. Policy 2023, 82, 101586. [Google Scholar] [CrossRef]
- Hassan, Q.; Nassar, A.K.; Al-Jiboory, A.K.; Viktor, P.; Telba, A.A.; Awwad, E.M.; Amjad, A.; Fakhruldeen, H.F.; Algburi, S.; Mashkoor, S.C.; et al. Mapping Europe renewable energy landscape: Insights into solar, wind, hydro, and green hydrogen production. Technol. Soc. 2024, 77, 102535. [Google Scholar] [CrossRef]
- Gonçalves, R.; Menezes, F. The carbon tax and the crisis in Australia’s National Electricity Market. Energy Econ. 2024, 133, 107522. [Google Scholar] [CrossRef]
- Karimu, A.; Bali Swain, R. Implication of electricity taxes and levies on sustainable development goals in the European Union. Energy Policy 2023, 177, 113553. [Google Scholar] [CrossRef]
- Musibau, H.; Gold, K.L.; Abdulrasheed, Z.; Muili, H.A. Poland’s net-zero pathways: Moderating role of carbon tax and renewable energy on electricity generation through a novel multivariate quantile-on-quantile regression approach. J. Environ. Manage. 2025, 380, 124848. [Google Scholar] [CrossRef]
- Tran, N.D.; Sahu, N.C. Asymmetric price response of industrial electricity demand in India. Util. Policy 2023, 82, 101552. [Google Scholar] [CrossRef]
- Kang, M.; Park, S.; Cho, K. An Empirical Study of the Economic Net-Zero Energy Mix in Industrial Complexes. Energies 2024, 17, 5404. [Google Scholar] [CrossRef]
- Wang, K.; Zhong, C.; Yu, R. The greenhouse gas reduction effect of critical peak pricing for industrial electricity: Evidence from 285 Chinese cities, 2003–2019. Energy Policy 2024, 190, 114147. [Google Scholar] [CrossRef]
- Xie, L.; Huang, Z. Electricity price cross-subsidies and enterprises’ green total factor productivity: Empirical evidence from Chinese industrial listed enterprises. J. Asian Econ. 2025, 96, 101848. [Google Scholar] [CrossRef]
- Shi, B.; Jiang, Q.; Shi, M.; Managi, S. Exploring the Effects of Carbon Pricing and Carbon Quota Control on the Energy Transition Towards Carbon Neutrality: A Computable General Equilibrium Analysis of the Zhejiang Region of China. Energies 2025, 18, 1029. [Google Scholar] [CrossRef]
- Oyewole, G.J.; Thopil, G.A. Data clustering: Application and trends. Artif. Intell. Rev. 2023, 56, 6439–6475. [Google Scholar] [CrossRef] [PubMed]
- Heistrene, L.; Machlev, R.; Perl, M.; Belikov, J.; Baimel, D.; Levy, K.; Mannor, S.; Levron, Y. Explainability-based Trust Algorithm for electricity price forecasting models. Energy AI 2023, 14, 100259. [Google Scholar] [CrossRef]
- Iwabuchi, K.; Kato, K.; Watari, D.; Taniguchi, I.; Catthoor, F.; Shirazi, E.; Onoye, T. Flexible electricity price forecasting by switching mother wavelets based on wavelet transform and Long Short-Term Memory. Energy AI 2022, 10, 100192. [Google Scholar] [CrossRef]
- Rhodes, J.D.; Cole, W.J.; Upshaw, C.R.; Edgar, T.F.; Webber, M.E. Clustering analysis of residential electricity demand profiles. Appl. Energy 2014, 135, 461–471. [Google Scholar] [CrossRef]
- Motlagh, O.; Berry, A.; O’neil, L. Clustering of residential electricity customers using load time series. Appl. Energy 2019, 237, 11–24. [Google Scholar] [CrossRef]
- Liu, C.; Wang, X.; Huang, Y.; Liu, Y.; Li, R.; Li, Y.; Liu, J. A Moving Shape-based Robust Fuzzy K-modes Clustering Algorithm for Electricity Profiles. Electr. Power Syst. Res. 2020, 187, 106425. [Google Scholar] [CrossRef]
- Müller, I.M. Feature selection for energy system modeling: Identification of relevant time series information. Energy AI 2021, 4, 100057. [Google Scholar] [CrossRef]
- Ruiz, L.; Pegalajar, M.; Arcucci, R.; Molina-Solana, M.A. Time-Series Clustering Methodology for Knowledge Extraction in Energy Consumption Data. Expert Syst. Appl. 2020, 160, 113731. [Google Scholar] [CrossRef]
- Salehi, M.; Rezaei, M.M. An improved probabilistic load flow in distribution networks based on clustering and Point estimate methods. Energy AI 2023, 14, 100272. [Google Scholar] [CrossRef]
- Gov.UK. International Industrial Energy Prices. 2024. Available online: https://www.gov.uk/government/statistical-data-sets/international-industrial-energy-prices (accessed on 19 October 2024).
- Department-For-Business-Energy & Industrial-Strategy. International Comparisons—Data Sources and Methodologies. 2014. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/647135/International_price_methodology_-_updated_Sept_2017.pdf (accessed on 19 October 2024).
- OECD-Data. Exchange Rates. 2020. Available online: https://data.oecd.org/conversion/exchange-rates.htm (accessed on 19 October 2024).
- International-Energy-Agency. World Energy Balances: Overview. 2020. Available online: https://www.iea.org/reports/world-energy-balances-overview (accessed on 27 April 2024).
- THE-WORLD-BANK-DATABANK. World Development Indicators. 2020. Available online: https://databank.worldbank.org/source/world-development-indicators (accessed on 27 April 2024).
- Oosthuizen, A.M.; Inglesi-Lotz, R.; Thopil, G.A. The relationship between renewable energy and retail electricity prices: Panel evidence from OECD countries. Energy 2022, 238, 121790. [Google Scholar] [CrossRef]
- OECD-Data. Air and GHG Emissions, OECD Air and Climate Statistics. 2021. Available online: https://www.oecd-ilibrary.org/environment/air-and-ghg-emissions/indicator/english_93d10cf7-en (accessed on 15 August 2024).
- European-Commission. Climate Action: EU Emissions Trading System (EU ETS). Available online: https://climate.ec.europa.eu/eu-action/eu-emissions-trading-system-eu-ets_en (accessed on 10 August 2024).
- THE-WORLD-BANK. Energy Imports, Net (% of Energy Use). 2018. Available online: https://data.worldbank.org/indicator/EG.IMP.CONS.ZS (accessed on 25 July 2024).
- Moreno, B.; López, A.J.; García-Álvarez, M.T. The electricity prices in the European Union. The role of renewable energies and regulatory electric market reforms. Energy 2012, 48, 307–313. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. Determining the Best Number of Clusters in a Data Set. 2015. Available online: https://bioconductor.statistik.tu-dortmund.de/cran/web/packages/NbClust/NbClust.pdf (accessed on 9 April 2024).
- Venables, W.; Ripley, B. Modern Applied Statistics; Fourth, S., Ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Hlavac, M. Stargazer: Well-Formatted Regression and Summary Statistics Tables Package, Version 5.2.1; 2018. Available online: https://cran.R-project.org/package=stargazer (accessed on 27 April 2024).
- Xu, R.; Wunsch, D.C. Clustering algorithms in biomedical research: A review. IEEE Rev. Biomed. Eng. 2010, 3, 120–154. [Google Scholar] [CrossRef] [PubMed]
- Pereira, M.M.; Frazzon, E.M. A data-driven approach to adaptive synchronization of demand and supply in omni-channel retail supply chains. Int. J. Inf. Manag. 2021, 57, 102165. [Google Scholar] [CrossRef]
- Carreon, A.; Barwey, S.; Raman, V. A generative adversarial network (GAN) approach to creating synthetic flame images from experimental data. Energy AI 2023, 13, 100238. [Google Scholar] [CrossRef]
- Liao, T.W. Clustering of time series data—A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Al-Wakeel, A.; Wu, J. K-means based cluster analysis of residential smart meter measurements. Energy Procedia 2016, 88, 754–760. [Google Scholar] [CrossRef]
- Rajabi, A.; Eskandari, M.; Ghadi, M.J.; Li, L.; Zhang, J.; Siano, P. A comparative study of clustering techniques for electrical load pattern segmentation. Renew. Sustain. Energy Rev. 2020, 120, 109628. [Google Scholar] [CrossRef]
- Zhou, Y. Advances of machine learning in multi-energy district communities—Mechanisms, applications and perspectives. Energy AI 2022, 10, 100187. [Google Scholar] [CrossRef]
- Nguyen, H.-T.; Domingo, P.; Vervisch, L.; Nguyen, P.-D. Machine learning for integrating combustion chemistry in numerical simulations. Energy AI 2021, 5, 100082. [Google Scholar] [CrossRef]
- Sekula, M.N. OptCluster: An R Package for Determining the Optimal Clustering Algorithm and Optimal Number of Clusters. Master’s Thesis, University of Louisville, Louisville, KY, USA, 2015. [Google Scholar]
- Sanguineti, F.; Maran, T. Navigating the clouds: Cultural influences on technology acceptance in the workplace. Technol. Soc. 2024, 77, 102553. [Google Scholar] [CrossRef]
- Liu, X.; Koirala, H. Ordinal regression analysis: Using generalized ordinal logistic regression models to estimate educational data. J. Mod. Appl. Stat. Methods 2012, 11, 21. [Google Scholar] [CrossRef]
- Brant, R. Assessing proportionality in the proportional odds model for ordinal logistic regression. Biometrics 1990, 46, 1171–1178. [Google Scholar] [CrossRef] [PubMed]
- Bilder, C.R.; Loughin, T.M. Analysis of Categorical Data with R; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- UCLA:-STATISTICAL-CONSULTING-GROUP. How Do I Interpret the Coefficients in an Ordinal Logistic Regression in R? 2021. Available online: https://stats.idre.ucla.edu/r/faq/ologit-coefficients/ (accessed on 22 January 2024).
- Mauracher, C.; Procidano, I.; Valentini, M. How Product Attributes and Consumer Characteristics Influence the WTP, Resulting in a Higher Price Premium for Organic Wine. Sustainability 2019, 11, 1428. [Google Scholar] [CrossRef]
- Kasza, J.; Wolfe, R. Interpretation of commonly used statistical regression models: Interpretation of regression models. Respirology 2014, 19, 14–21. [Google Scholar] [CrossRef]
- Fullerton, A.S.; Xu, J. The proportional odds with partial proportionality constraints model for ordinal response variables. Soc. Sci. Res. 2012, 41, 182–198. [Google Scholar] [CrossRef]
- Schlegel, B.; Steenbergen, M. Brant: Test for Parallel Regression Assumption. R Package Version 0.2-0. 2020. Available online: https://benjaminschlegel.ch/r/brant/ (accessed on 17 February 2025).
- Ghiani, E.; Galici, M.; Mureddu, M.; Pilo, F. Impact on Electricity Consumption and Market Pricing of Energy and Ancillary Services during Pandemic of COVID-19 in Italy. Energies 2020, 13, 3357. [Google Scholar] [CrossRef]
- Gore, K.; Rigot-Müller, P.; Coughlan, J. Cost-benefit assessment of shore side electricity: An Irish perspective. J. Environ. Manag. 2023, 326, 116755. [Google Scholar] [CrossRef]
- Finnish-Energy-Industries. Energy Taxation in Europe, Japan and The United States. 2010. Available online: https://www.elektormagazine.com/news/Energy-Taxation-in-Europe--Japan-and-The-United-States (accessed on 9 April 2024).
- Peña, J.I.; Rodríguez, R. Are EU’s Climate and Energy Package 20-20-20 targets achievable and compatible? Evidence from the impact of renewables on electricity prices. Energy 2019, 183, 477–486. [Google Scholar] [CrossRef]
- IEEE-Spectrum. Germany’s Energiewende, 20 Years-Later. 2020. Available online: https://spectrum.ieee.org/energy/renewables/germanys-energiewende-20-years-later? (accessed on 9 April 2024).
- Halbrügge, S.; Schott, P.; Weibelzahl, M.; Buhl, H.U.; Fridgen, G.; Schöpf, M. How did the German and other European electricity systems react to the COVID-19 pandemic? Appl. Energy 2021, 285, 116370. [Google Scholar] [CrossRef]
- Min, H. Examining the Impact of Energy Price Volatility on Commodity Prices from Energy Supply Chain Perspectives. Energies 2022, 15, 7957. [Google Scholar] [CrossRef]
- Aguirre, G.; Lazo, J.; Watts, D. Regulatory response to COVID-19 in the Ibero-American electricity sector: Policy implications and critical analysis of support measures. Energy Policy 2023, 183, 113852. [Google Scholar] [CrossRef]
- Khudaykulova, M.; Yuanqiong, H.; Khudaykulov, A. Economic Consequences and Implications of the Ukraine-Russia War. Int. J. Manag. Sci. Bus. Adm. 2022, 8, 44–52. [Google Scholar] [CrossRef]
- Zhai, Z.; Zhang, L.; Hou, X.; Yang, Q.; Huang, Z. Price elasticity of electricity demand in China—A new instrument variable based on marketization policy. Energy Sustain. Dev. 2023, 76, 101275. [Google Scholar] [CrossRef]

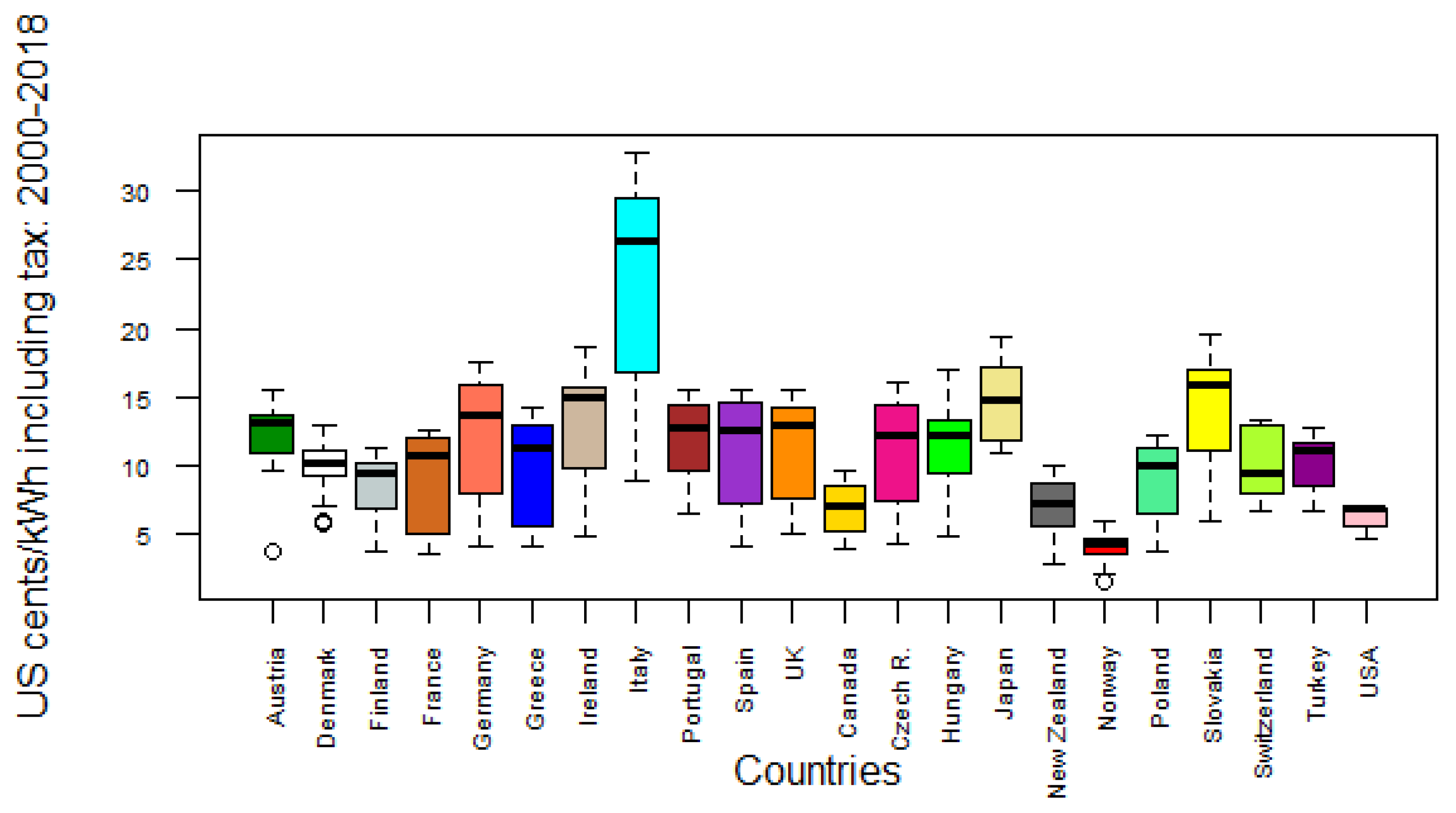
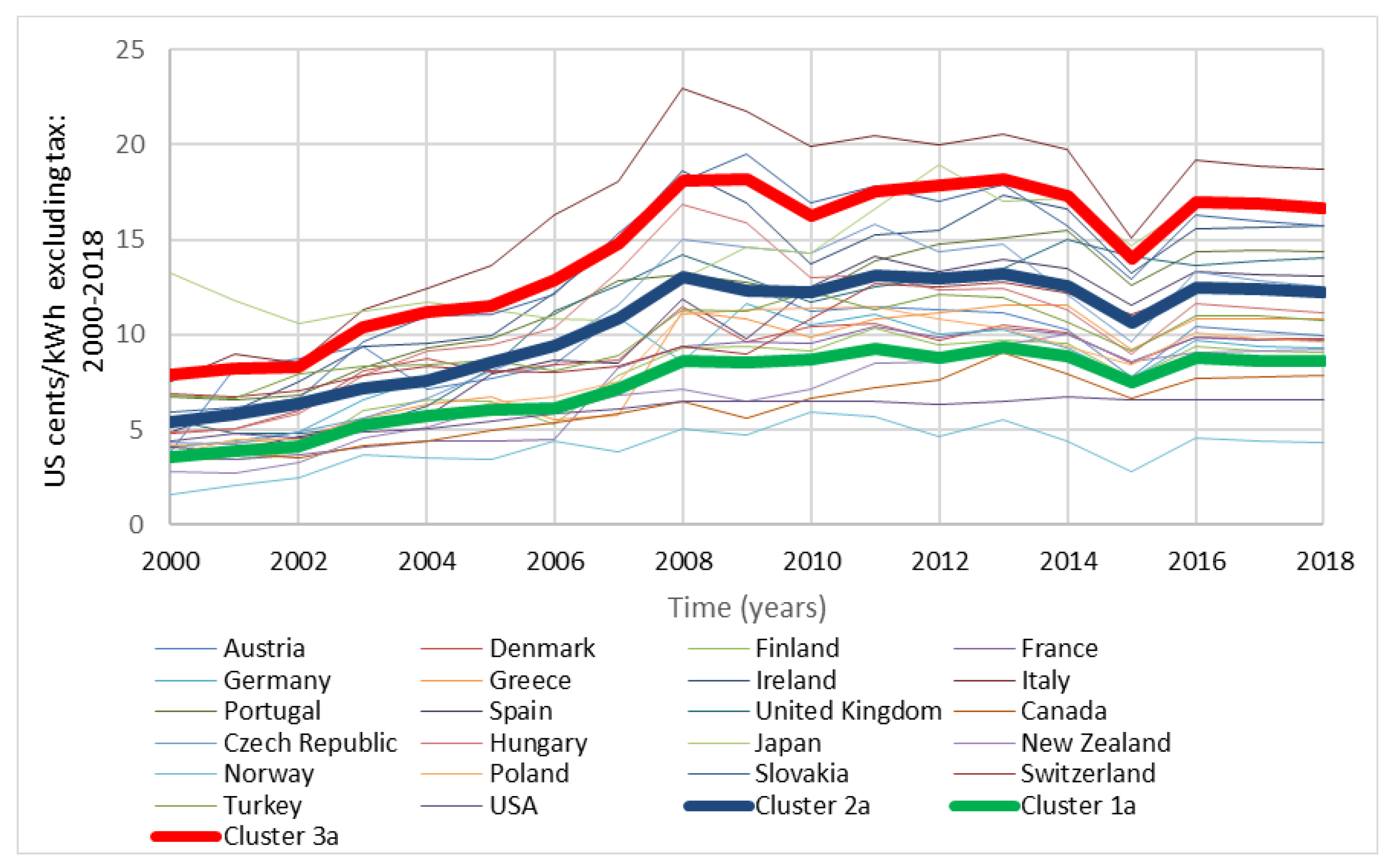
| Cluster 1a (Low-Range) Price Range (Cents/kWh): 3.954–8.622 | Cluster 2a (Median-Range) Price Range (Cents/kWh): 5.373–12.253 | Cluster 3a (High-Range) Price Range (Cents/kWh): 7.898–16.666 |
|---|---|---|
| Denmark | Austria | Ireland |
| Finland | Portugal | Italy |
| France | Spain | Japan |
| Greece | UK | Slovakia |
| Germany | Czech Republic | |
| Canada | Hungary | |
| New Zealand | Switzerland | |
| Norway | Turkey | |
| Poland | ||
| USA |
| Cluster 1b (Low-Range) Price Range (Cents/kWh): 4.331–9.877 | Cluster 2b (Median-Range) Price Range (Cents/kWh): 5.808–14.606 | Cluster 3b (High-Range) Price Range (Cents/kWh): 8.893–30.200 |
|---|---|---|
| Denmark | Austria | |
| Finland | Germany | Italy |
| France | Ireland | |
| Greece | Portugal | |
| Canada | Spain | |
| New Zealand | UK | |
| Norway | Czech Republic | |
| Poland | Hungary | |
| Switzerland | Japan | |
| Turkey | Slovakia | |
| USA |
| Independent Variables | Model 1a Logit Coefficient | Model 1a Brant Test | Model 1b Logit Coefficient | Model 1b Brant Test | Model 1c Logit Coefficient | Model 1c Brant Test |
|---|---|---|---|---|---|---|
| REG | 1.2369 | 0.82 | −0.1406 | 0.98 | 0.3434 | 0.7 |
| GDPpc | 0.0061 | 0.11 | 0.0005 | 0.11 | 0.0007 | 0.2 |
| EIE | −0.0577 | 0.02 | - | - | - | - |
| ED | 0.0286 | 0.06 | 0.0326 | 0.02 | - | - |
| Model (All variables) * | n/a | 0.03 | n/a | 0.06 | n/a | 0.4 |
| Independent Variable | Logit Coefficient (Log Odds) | Odds Ratio | Std Error | t-Value | p-Value | 95% Confidence Interval for Logit Coefficient (2.5%, 97.5%) |
|---|---|---|---|---|---|---|
| REG | 0.3434 | 1.410 *** | 0.0059 | 394.44 | 0 | (0.3318, 0.35502) |
| GDPpc | 0.0007 | 1.001 *** | 0.0001 | 5.21 | 0 | (0.0004, 0.0009) |
| Independent Variables | Model 2a Logit Coefficient | Model 2a Brant Test | Model 2b Logit Coefficient | Model 2b Brant Test |
|---|---|---|---|---|
| REG | 4.8069 | 0.27 | 4.03 | 0.37 |
| GDPpc | 0.0003 | 0.06 | 0.0005 | 0.07 |
| EIE | −0.0087 | 0.54 | −0.0081 | 0.93 |
| ED | 0.0327 | 0 | - | |
| Model (All variables) * | n/a | 0 | n/a | 0.25 |
| Independent Variable | Logit Coefficient (Log −Odds) | Odds Ratio | Std Error | t-Value | p-Value | 95% Confidence Interval for Logit Coefficient (2.5%, 97.5%) |
|---|---|---|---|---|---|---|
| REG | 4.03 | 56.26 *** | 0.0061 | 652.10 | 0.00 | (4.0179, 4.0421) |
| GDPpc | 0.0005 | 1.001 *** | 0.0001 | 4.8471 | 0.00 | (0.0003, 0.0007) |
| EIE | −0.0081 | 0.992 | 0.009 | −0.9071 | 0.36 | (−0.0258, 0.0094) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oyewole, G.J.; Thopil, G.A. Industrial Electricity Pricing and Renewable Energy: A Temporal Analysis of the Effect of Taxes. Energies 2025, 18, 2026. https://doi.org/10.3390/en18082026
Oyewole GJ, Thopil GA. Industrial Electricity Pricing and Renewable Energy: A Temporal Analysis of the Effect of Taxes. Energies. 2025; 18(8):2026. https://doi.org/10.3390/en18082026
Chicago/Turabian StyleOyewole, Gbeminiyi John, and George Alex Thopil. 2025. "Industrial Electricity Pricing and Renewable Energy: A Temporal Analysis of the Effect of Taxes" Energies 18, no. 8: 2026. https://doi.org/10.3390/en18082026
APA StyleOyewole, G. J., & Thopil, G. A. (2025). Industrial Electricity Pricing and Renewable Energy: A Temporal Analysis of the Effect of Taxes. Energies, 18(8), 2026. https://doi.org/10.3390/en18082026






