Comprehensive Investigation of Efficiency Improvement in Voltage Source Inverter Using Hybrid Carrier-Based Modulation

Abstract

Voltage Source Inverters (VSIs) are essential in variable-speed drive applications, where Pulse-Width Modulation (PWM) signals are typically generated using a fixed-carrier (FC) signal. Increasing the FC frequency helps smoothen the inverter’s output current, improving motor performance. However, this comes at the expense of increased switching losses, reduced efficiency, and potential thermal management challenges. The Hybrid Carrier-based PWM (HCPWM) technique presents an alternative by dynamically alternating between two sawtooth carrier signals with different frequencies. This method aims to achieve higher efficiency without compromising system performance. However, selecting optimal carrier pairs to maximize efficiency across various speed and load conditions while maintaining total harmonic distortion within acceptable limits remains a challenge. This study provides a comprehensive experimental evaluation of the HCPWM approach, benchmarking it against conventional FCPWM. The results demonstrate that HCPWM enhances energy efficiency under all tested conditions, making it a viable and cost-effective solution for VSI-driven motor applications without introducing additional system cost or complexity.

1. Introduction

Voltage Source Inverters (VSIs) are widely used in applications such as Variable-Speed Drives (VSDs) for motor control, renewable energy systems to integrate solar and wind power into the grid, and uninterruptible power supplies for backup power [1,2,3,4]. As in other power electronic circuits, modern control of VSIs relies on Pulse-Width Modulation (PWM) strategies. A well-designed PWM strategy not only offers controllable output voltage but also allows users to increase the quality of output waveforms. Although VSI inverters have matured inverter topology that provide successive control over motor parameters such as speed, torque, and direction, investigations of new PWM strategies that provide higher efficiency and power quality have still been attracting significant interest. Several PWM techniques have been introduced so far, aiming to decrease the total harmonic distortion (THD) of the VSI output and increase inverter efficiency. The available PWM techniques can be mainly categorized as Hysteresis PWM (HPWM), Sinusoidal PWM (SPWM), Harmonic Injection-based PWM (HIPWM), Space Vector PWM (SVPWM), and Discontinuous PWM (DPWM) [5,6,7,8]. THD is the main parameter to define the quality of the inverter’s output. Increasing the switching frequency obviously increases the output quality, which is desirable for motor operation [9]. However, the higher switching frequency means higher switching losses. Therefore, the determination of the optimum carrier frequency is a trade-off between waveform quality, efficiency, and other performance parameters. IEC-61000-3-2 is an international standard that regulates the limitation of harmonic components caused by equipment that uses less than 16 A to maintain power quality of the power grid [10]. According to IEEE 519-2014, which is another important standard, the THD of the current output must be less than 5% until the 49th harmonic [11]. For the VSI-based motor drive system, maintaining a THD level that satisfies the IEEE regulation is always a research concern.

As mentioned above, various PWM optimization methods have been proposed to enhance power quality and efficiency in power converters. Among them, HPWM naturally operates as a closed-loop control system that maintains the error between the reference and measured variable within a predefined hysteresis band. Unfortunately, the switching frequency of this method is continuously varying, which makes effective filter design difficult. Except HPWM, other PWM techniques are based on a comparison between reference signal and carrier signal. Adjustable Discontinuous PWM (ADPWM) is proposed in [12], which adjusts the non-switching period from 0° to 120° of the fundamental cycle effectively, reducing current THD in the low-speed region and improving efficiency at high speeds. Its dynamic adjustable capability ensures a gradual increase in the non-switching period based on the modulation index (MI), resulting in optimized performance and THD depending on operating conditions. However, the method does not achieve high efficiency in the low-speed region, which limits its effectiveness for variable-speed applications. Sawtooth carrier-based PWM (SCPWM) technique has been introduced in [13] by modifying the classical sawtooth carrier signal for the reduction in common mode voltage (CMV) in the peak-to-peak amplitude. This method is easily adaptable to symmetrical multiphase VSI with an odd phase number. However, the SCPWM scheme deteriorates the output current. The Multicarrier Generalized Discontinuous PWM (MC-GDPWM) method for a two-level VSI is introduced in [14] to reduce DC-link capacitor current while maintaining low switching losses by selectively comparing single- and double-carrier signals according to the modulation signal. According to the experimental results, the method reduces voltage ripples and improves efficiency but increases the distortion in phase currents which is not preferrable for AC motors.

Hybrid Carrier-based Modulation techniques (HCPWM) have started to attract more attention in VSI systems to enhance efficiency and reduce current THD. The capability of such PWM techniques allows one to modify the reference modulation signals, manipulate carrier waveforms of different shapes, multiplex switching frequencies, or optimize switching patterns to improve output performance. HCPWM techniques may provide better performance if they are properly optimized, making them suitable for variable-speed applications. The HCPWM method proposed in [15] is designed for two parallel interleaved two-level VSIs. It effectively combines space-vector principles with a carrier-based approach, optimizing switching sequences to reduce harmonic distortion and improve efficiency. However, the increased switching frequency results in higher switching losses, which may limit its practicality in high-power applications despite its improved current ripple performance. Another HCPWM method is suggested in [16] to improve the performance of VSIs, which modifies the modulation signal and uses the HC signal. This method improves THD and power loss, but the drawback of this method is limited compatibility with the proposed carrier signal and PWM reference signal. Another HCPWM method was proposed in [17] with an enhanced carrier-based PWM strategy to address challenges in three-level neutral-point-clamped (NPC) inverters over a wide frequency range. By integrating three improved PWM techniques, the method mitigated narrow pulse issues at low modulation indices, ensured synchronized modulation at various carrier ratios, and achieved square-wave modulation at high frequencies, thereby improving voltage accuracy and reducing harmonic distortion. However, the complexity of implementing multiple PWM strategies and the increased computational burden could pose challenges in real-time control applications. The HCPWM described in [18] differed from the previously mentioned HCPWM methods structurally. Instead of using particular FC signals in a separate comparison with reference signal, it combined them into a single-carrier waveform, thereby preventing additional switching losses. The proposed HCPWM improved efficiency while maintaining lower THD. The performance method was analyzed in a narrow speed range and switching frequency, which was not adequate to demonstrate its effectiveness on efficiency and THD. Furthermore, the method needed to be accompanied by a closed-loop speed control, which is the key feature of VSDs. This paper aims to bridge the gap by conducting a comprehensive investigation into the efficiency improvement provided by HCPWM at various speeds under load conditions.

2. VSI Inverter Basics and Control Principles

The analysis of the proposed method was carried out by using a three-phase VSI inverter connected to a Squirrel-Cage Induction Motor (SCIM) as shown in Figure 1. The VSI inverter was composed of six IGBT switches named T_AH, T_AL, T_BH, T_BL, T_CH, and T_CL. The IGBT switches on each arm should be operated complementarily to prevent short circuits on the DC side. The output of the inverter was connected to the three-phase winding of the motor.

2.1. SPWM Basics

SPWM is the most common modulation method used in VSI inverters to control the output speed and power of a motor drive system. Modulation signals ($M_a,M_b,M_c$) are calculated by (1), and each signal is 120 deg phase-shifted from each other as in (2). As shown in Figure 2, an FC signal is compared with three-phase reference modulation signals, resulting in logic pulses called modulation indexes [19]. These modulation indexes are applied to the upper-side IGBT switches (T_AH, T_BH, T_CH) while their complements are applied to the lower-side ones (T_AL, T_BL, T_CL). The output voltage is usually pulsative, but sinusoidal waveform can be produced for the output current, which is more important for smooth torque production in an AC motor. The mathematical expression for the SPWM is described by

$$M=Vsin(\omega t+\theta )$$

(1)

$$\left[M_a{M}_b{M}_c{]=[M}_{\theta =0°}{M}_{\theta =120°}{M}_{\theta =-120°}\right]$$

(2)

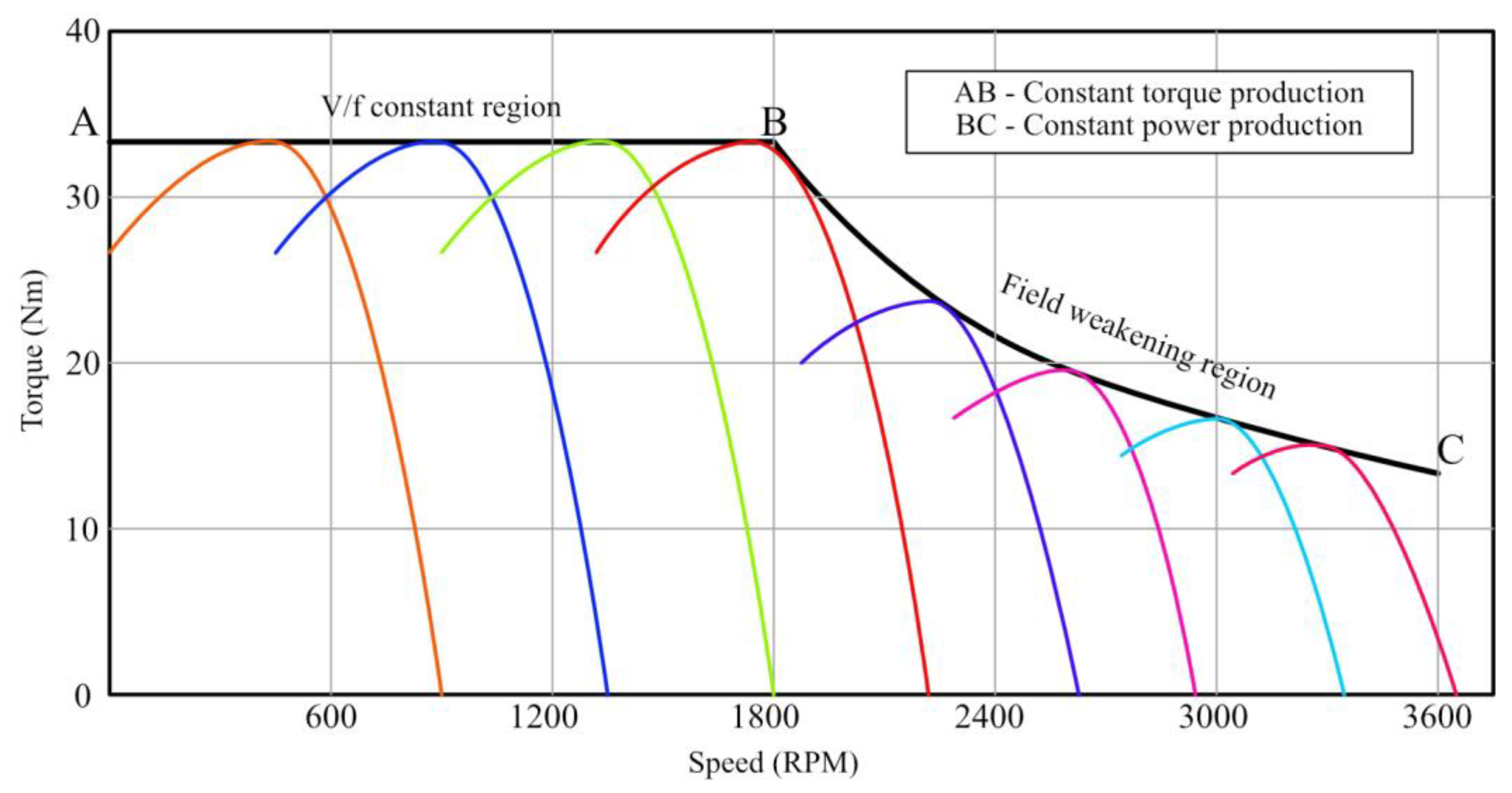
2.2. Voltage by Frequency Control

A control method is usually necessary for operating AC motors effectively. Figure 3 displays the typical control characteristic of an AC motor. The motor torque is kept at maximum value from zero to the rated speed. Therefore, the zero-to-rated-speed region is usually called the constant torque region. This can be practically achieved by Voltage by frequency (V/f) control, which is extensively used for general VSD applications. It maintains the ratio between the applied voltage and frequency to produce the rated torque until the rated speed [20,21,22,23,24].

The V/f ratio is defined by using the rated voltage and rated frequency. The applied voltage can be increased until the rated voltage. Subsequently, a further increase can only be obtained by increasing the frequency, resulting in a decrease in motor torque as in Figure 3. This region is called field weakening or constant power region. The output voltage and the limitation are analytically expressed by

$$V_{out}=\left\{(V_n-V_{min}/f_n)+V_{min}\right\}\times f_{ref}$$

(3)

$$V_{out}=\left\{\begin{array}{c}{V}_n, V_{out}\ge V_n\\ V_{out}, V_{min}<V_{out }<V_n \\ V_{min}, V_{out}\le V_{min}\end{array}\right.$$

(4)

where V_out is the applied voltage, V_n and f_n are the rated motor voltage and frequency, respectively, V_min is the minimum applied voltage, and f_ref is the frequency of the modulation signal.

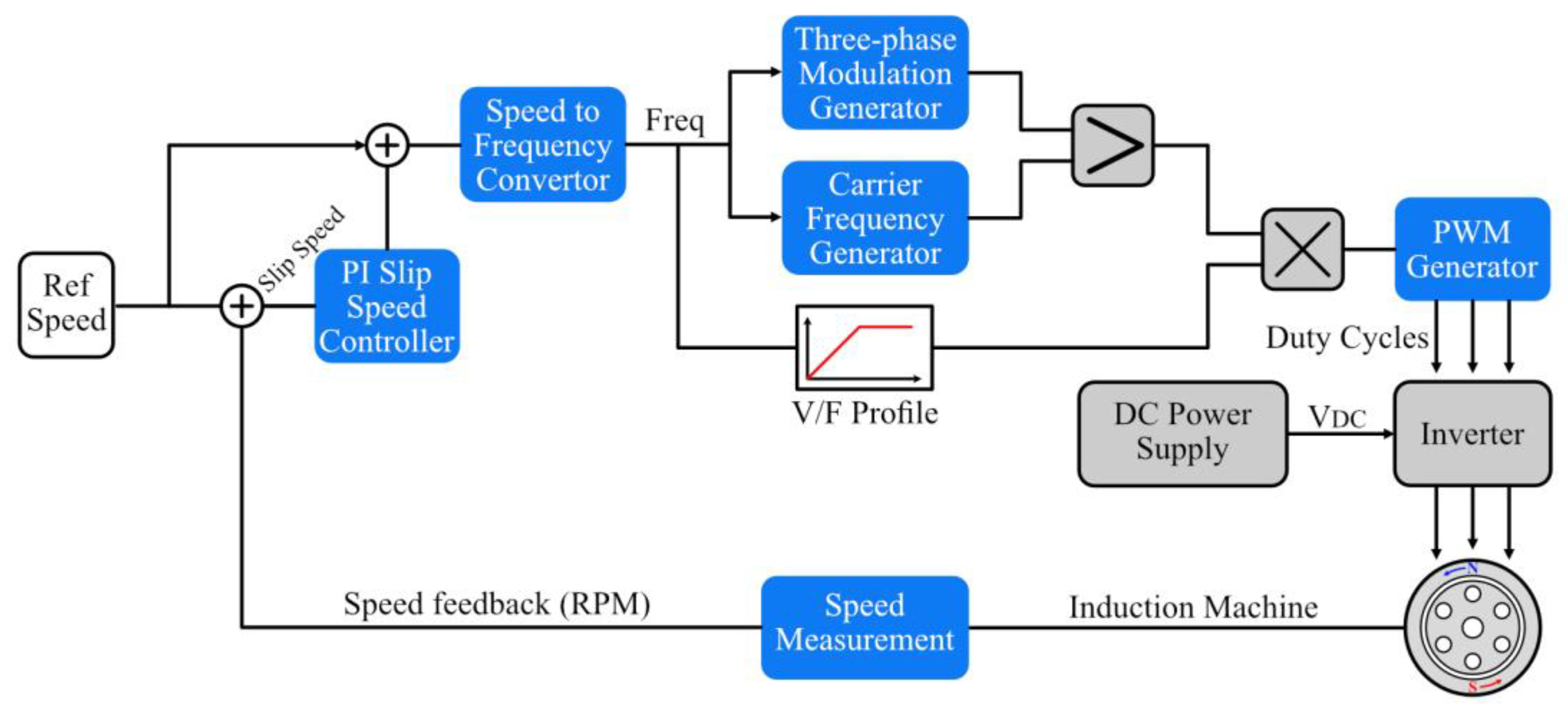
2.3. Closed-Loop Speed Control

In some VSD applications, the motor speed needs to be kept constant when the load is applied, changed, or removed. A closed-loop control is necessary to keep the speed at the desired level. Figure 4 illustrates the overall control structure of the induction motor, which includes closed-speed control together with V/f control.

In motor operation, the induction motor operates at slightly less than the synchronous speed, resulting in a speed difference known as slip speed. To make a proper speed control, this slip speed needs to be compensated [22,23]. For this purpose, the feedback speed is measured by an incremental encoder, and the slip speed is calculated by subtracting the measured speed from the desired speed. The error value is fed into the PI controller, and the resultant value from the PI controller is added to the desired speed to compensate for the slip effect. The saturation limit is applied to the PI controller to prevent the stall condition where the speed difference between the rotating speed and feedback speed is within the allowable region. The mathematical representation of PI control is described in (5):

$$\mathrm{u}\left(\mathrm{t}\right)=K_p\mathrm{e}\left(\mathrm{t}\right)+K_i{{\displaystyle \int }}_{min}^{max}e\left(t\right)dt$$

(5)

where e(t) is the slip speed, and K_p and K_i are the proportional and integral gain of the controller.

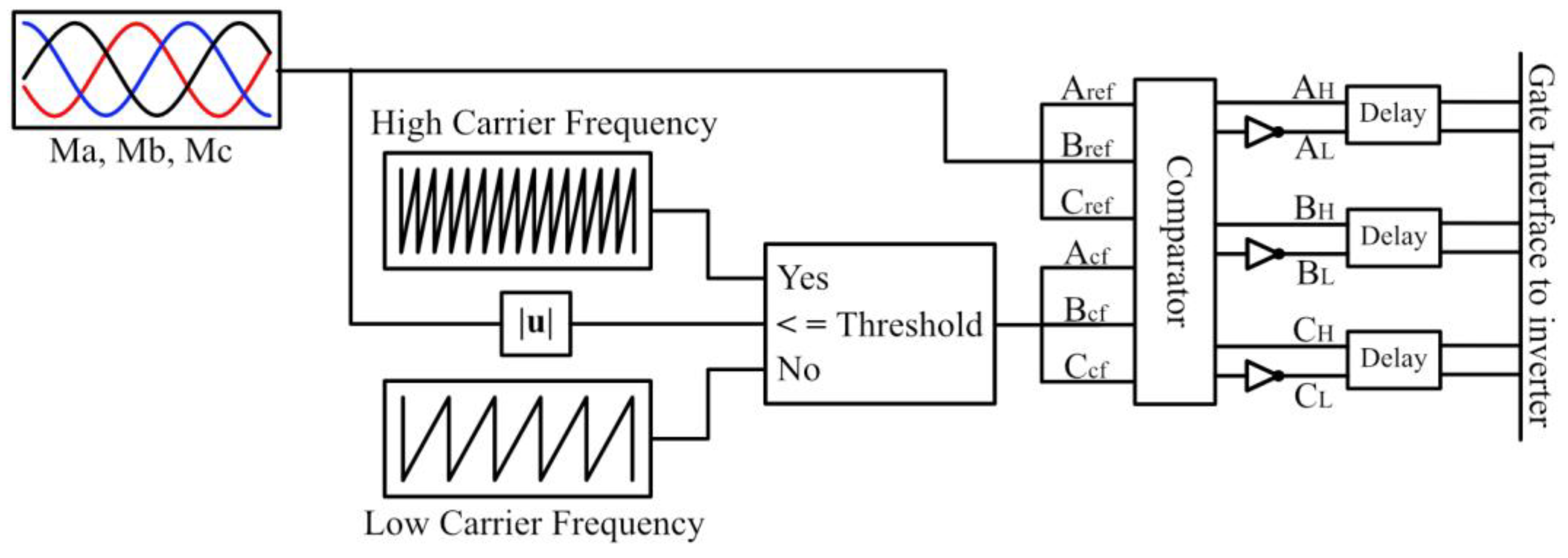
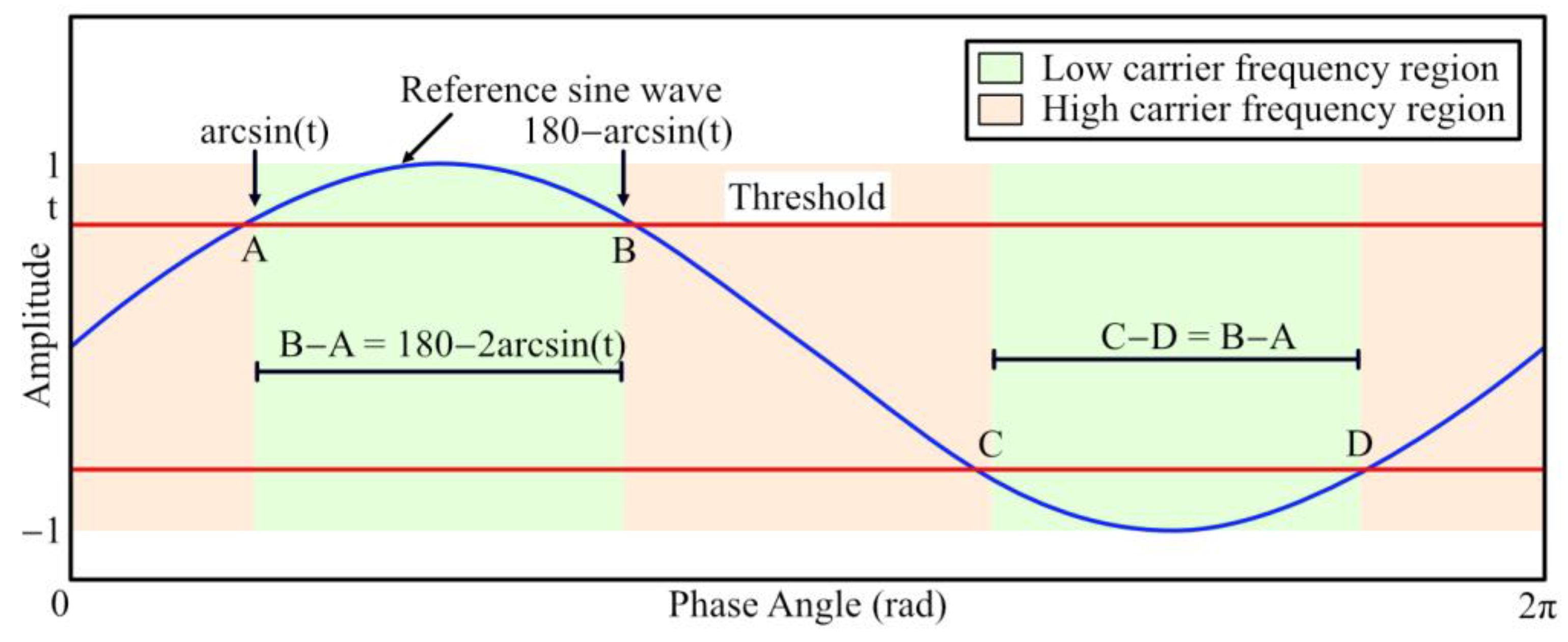
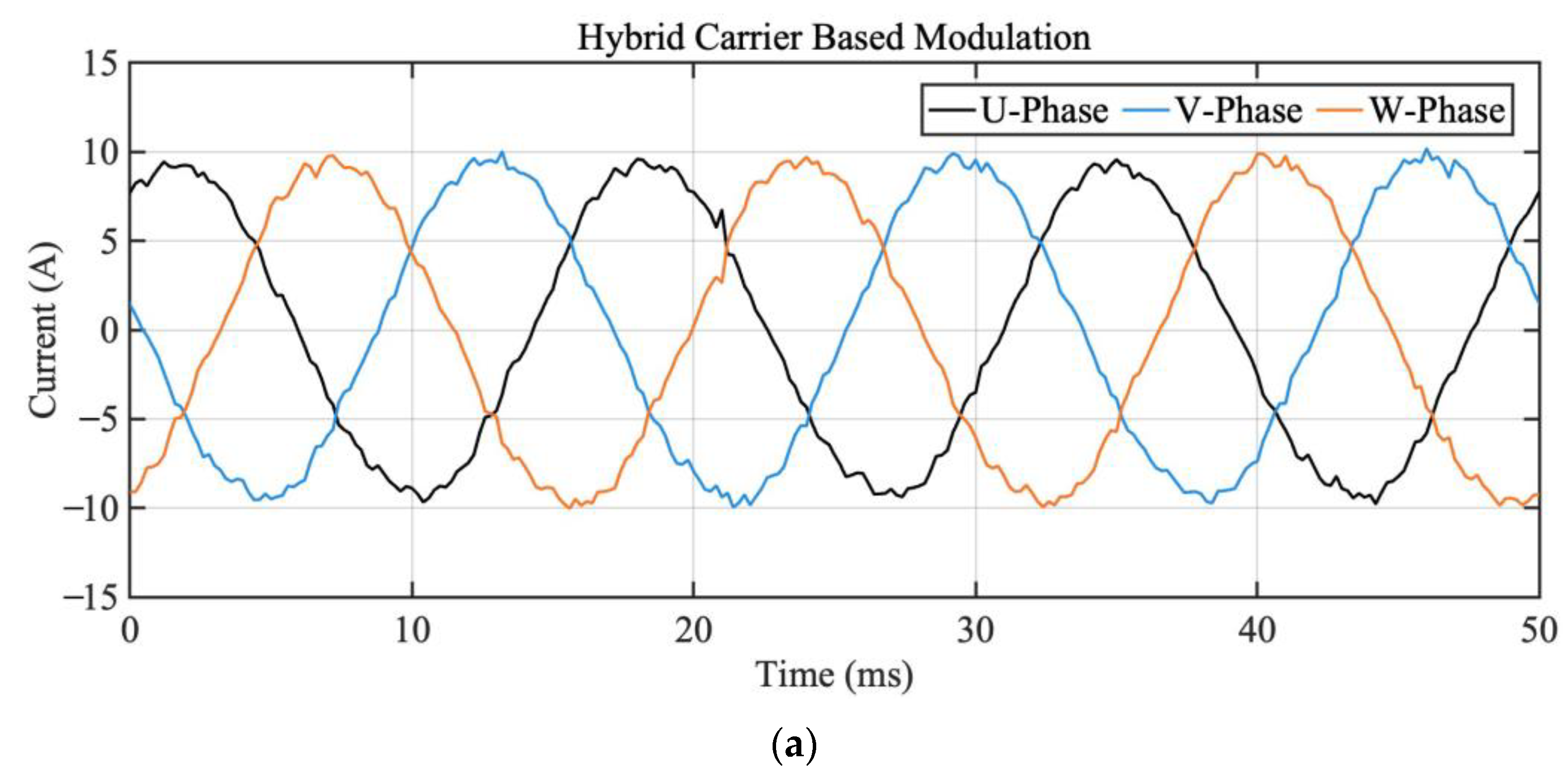
3. HCPWM Basics

The HCPWM method modifies the resultant carrier signal by combining two different FCs. In this section, the design and implementation of HCPWM is discussed.

3.1. Design of HC

HC is formed by using a pair of low and high frequency FCs. A threshold criterion that controls a switch decides which FC is active at each moment. The advantage of this method is that the obtained HC waveform does not lose periodicity, as seen in Figure 5. The modulation signal is compared with the threshold value before deciding which FC will be used in PWM generation. The low-frequency FC is applied when the modulation signal is lower than the threshold, and the high-frequency FC is applied in the opposite situation, as described in (6).

$$\mathrm{HC}=\left\{\begin{array}{c}{\mathrm{FC}}_{\mathrm{L}},\left|Vsin(\omega t+\theta )\right|>\mathrm{T}\\ {\mathrm{FC}}_{\mathrm{H}},\left|Vsin(\omega t+\theta )\right|\le \mathrm{T}\end{array}\right.$$

(6)

where

• HC = hybrid carrier signal;
• FC_H = high-frequency saw-tooth wave;
• FC_L = low-frequency saw-tooth wave;
• T = threshold value.

Figure 5. Gate signal generated by Hybrid Carrier-based Modulation with reference sine wave.

Figure 5. Gate signal generated by Hybrid Carrier-based Modulation with reference sine wave.

Three carrier frequencies are required for a three-phase system and 120 deg phase shift between each phase.

$$\left[\begin{array}{ccc}{A}_{cf}& B_{cf}& C_{cf}\end{array}\right]=\begin{array}{ccc}[H{C}_{\theta =0}& H{C}_{\theta =120}& H{C}_{\theta =-120}]\end{array}$$

(7)

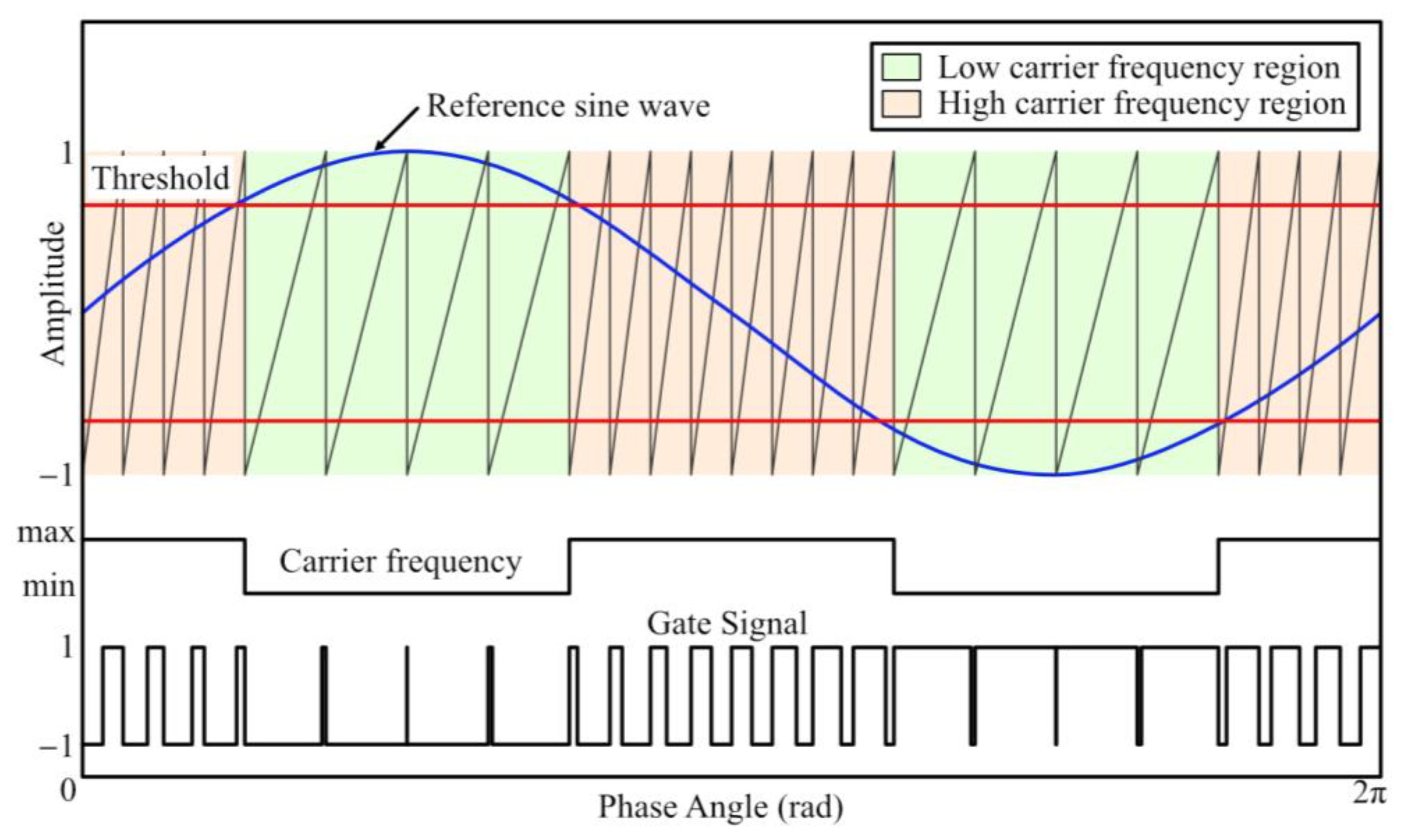
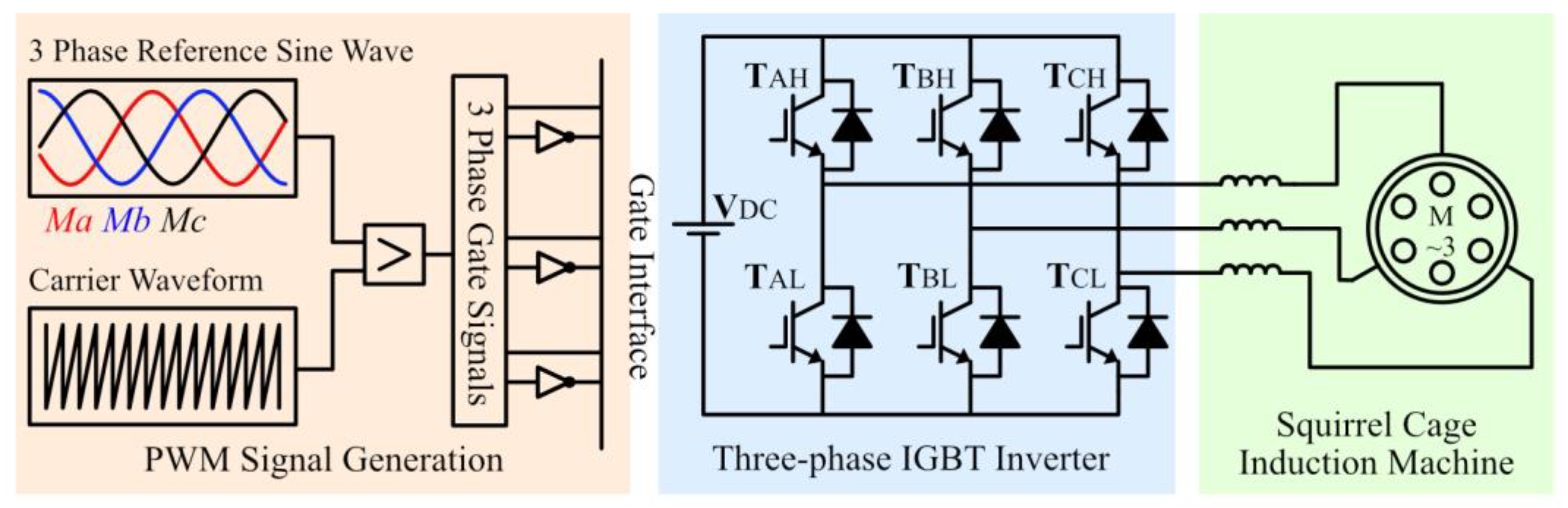
3.2. HCPWM Implementation

The development procedure of the HCPWM was carried out using visual programming in the MATLAB r2024a Simulink environment. This process was broadly divided into two main stages: hybrid carrier signal generation and three-phase gate signal generation using the hybrid carrier signal. In Figure 6, the absolute value of the three-phase reference modulation signals ($M_a,M_b,M_c$) is passed through the compare block, which evaluates the input signals and determines the high-frequency components and low-frequency components for each period based on a predefined threshold value. This results in the formation of three hybrid carrier signals ($A_{cf},B_{cf},C_{cf}$), which are essential for modulating the inverter’s switching states. The generated carrier signals are further processed in the gate signal generation part, to produce the upper-side gate signals ($A_H,B_H,C_H$) and lower-side gate signals ($A_L,B_L,C_L$). To ensure reliable operation and prevent shoot-through faults, dead time between upper-side and lower-side signals were considered before feeding the signals to the transistor gates. This dead-time implementation effectively introduced a small delay between the switching events of complementary switches. Additionally, the entire system was designed to operate in hybrid modulation conditions while maintaining precise and stable output waveforms.

4. Inverter’s Switching Loss and Efficiency

4.1. Switching Loss

The efficiency of the motor drive system depends on the total power loss of the inverter. Power losses can be divided into conduction loss and switching loss [25,26,27,28]. Conduction in IGBT switches and freewheeling diode losses causes conduction losses in inverters. Switching losses include the activation and deactivation of the inverter switches and diodes. The activation loss of the fast recovery diode is comparatively small and was considered negligible in this study. The reduction in switching losses with HCPWM is calculated as shown in Figure 7.

$${\mathrm{FC}}_{\mathrm{L}}\%+{\mathrm{FC}}_{\mathrm{H}}\%=100\%$$

(8)

$${\mathrm{FC}}_{\mathrm{L}}\%={\displaystyle \frac{2\times [180-2\times {sin}^{-1}\mathrm{T}]}{360}}\times 100\%$$

(9)

$${\mathrm{FC}}_{\mathrm{H}}\%=100-{\mathrm{FC}}_{\mathrm{L}}\%$$

(10)

The Switching Loss Reduction rate (SLR%) can be calculated by

$$\mathrm{SLR}\%=({\displaystyle \frac{{\mathrm{F}}_{\mathrm{L}}}{{\mathrm{F}}_{\mathrm{H}}}}\times {\mathrm{FC}}_{\mathrm{L}}\%+{\mathrm{FC}}_{\mathrm{H}}\%)$$

(11)

where SLR is the total switching loss reduction, F_L is the frequency of the low carrier signal, and F_H is the frequency of the high carrier signal. As an example, an FC of 4 kHz is used for the classical method and a 2–4 kHz pair is used to calculate the switching losses of HCPWM while assuming a threshold value of 0.7071.

$$\begin{array}{cc}{\mathrm{CF}}_{\mathrm{L}}\%& ={\displaystyle \frac{2\times \left[180-2\times {\sin }^{-1}0.7071\right]}{360}}\times 100\%\hfill \\ & \text{=50\%}\end{array}$$

$$\begin{array}{cc}\hfill \mathrm{New}\mathrm{switching}\mathrm{loss}& =\left({\displaystyle \frac{2\times {10}^3}{4\times {10}^3}}\times 50\%\right)+50\%\hfill \\ & \text{= 75\%}\hfill \end{array}$$

$$\text{SLR\% = 100 − 75 = 25\%}$$

From the above calculation, the HCPWM method can save 25% switching loss compared to the classical FCPWM method value according to the FC_H, FC_L, and threshold value.

4.2. Power and Energy Efficiency

The efficiency measurement of a motor depends on the operating conditions, particularly whether the motor runs at a fixed or variable speed. For fixed-speed operation, a three-phase power measurement is sufficient to determine efficiency, as the input and output power can be directly compared. In a three-phase motor, power and efficiency are calculated as

$$P\left(\mathrm{t}\right)=v_a\left(t\right)i_a\left(t\right)+v_b\left(t\right)i_b\left(t\right)+v_c\left(t\right)i_c\left(t\right)$$

(12)

$${\eta }_{P }={\displaystyle \frac{P_{out}}{P_{in}-P_{loss}}}\times 100\%$$

(13)

• $v_a\left(t\right),v_b\left(t\right),v_c\left(t\right)$ = instantaneous phase voltages;
• $i_a\left(t\right),i_b\left(t\right),i_c\left(t\right)$ = instantaneous phase currents;
• ${\eta }_{P }$ = power efficiency.

However, in variable-speed drive systems such as EV applications, power consumption fluctuates, making an accurate efficiency evaluation impossible. Therefore, an energy measurement, which accounts for power fluctuations over time, becomes necessary to obtain the true efficiency of the entire operational cycle, ensuring a more reliable performance evaluation [29,30]. The energy and efficiency calculations are determined by

$$W={{\displaystyle \int }}_{t1}^{t2}p\left(t\right)dt$$

(14)

$${\eta }_{w }={\displaystyle \frac{W_{out}}{W_{in }-W_{loss}}}\times 100\%$$

(15)

where W is the total energy consumed, p(t) is the instantaneous power at time t, t₁ and t₂ are the start and end times of measurement, respectively, and ${\eta }_{W }$ is the energy efficiency.

5. Results

To verify the performance of the HCPWM method, various experimental tests were performed, and the results are discussed in this section.

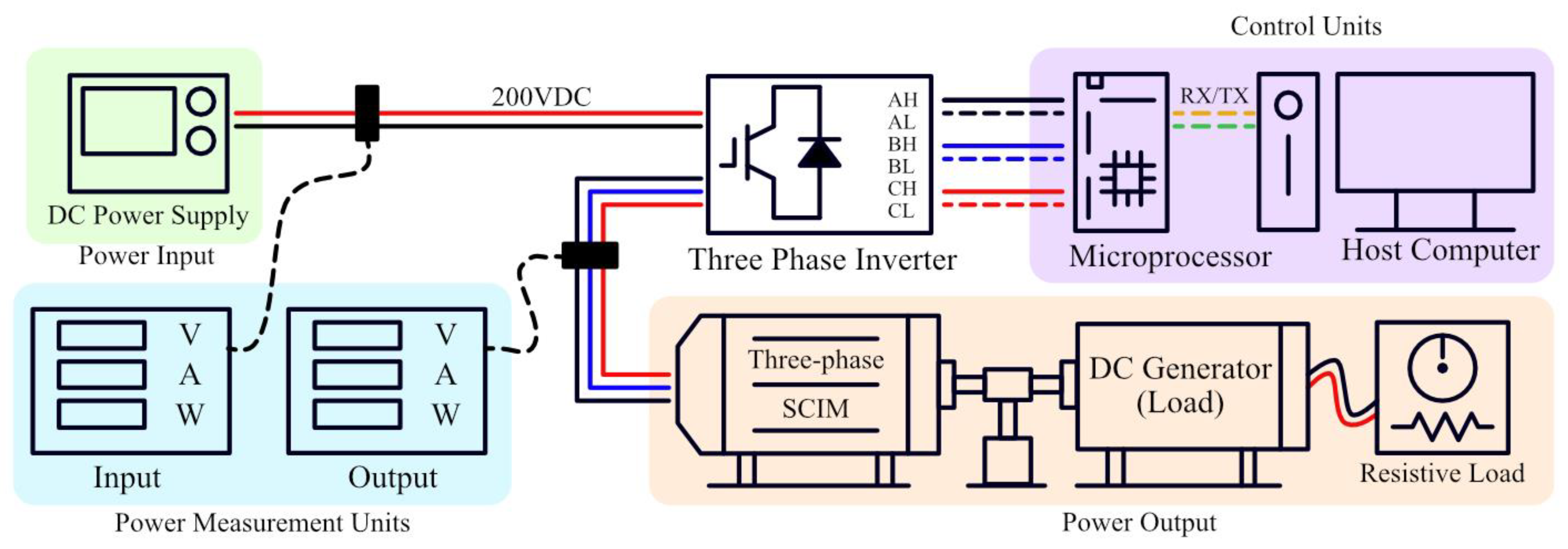
5.1. Experimental Configuration and Conditions

For the experiment purpose, the HCPWM technique was compared with the FCPWM method to validate its performance and efficiency. The simple representation of the overall system is illustrated in Figure 8. A 1.5 kW, three-phase Squirrel-Cage Induction Motor (SCIM) was driven by an MWINV-9R122C 9.1 kVA IGBT inverter. MATLAB Simulink’s environment was used to prepare the program and deploy it to the motor control development board named LAUNCHXL-F28379D for implementation. Another Simulink file was prepared to monitor signals and send commands to the microprocessor for switching between the control methods, which were the classical FCPWM method and the HCPWM method. Thus, testing conditions such as V/f control and other critical parameters remained the same for a fair comparison. A DC machine together with a variable-resistive load was used to mechanically load the SCIM during the tests. A voltage of 200 V DC was applied to the VSI inverter throughout the experiment. The overall experiment setup is displayed in Figure 9. Two HIOKI PW3336 power meters were connected to the input and output side of the inverter to measure electrical parameters such as power and THD during experiment. Current and voltage waveforms could also be observed from the host program designed in Simulink.

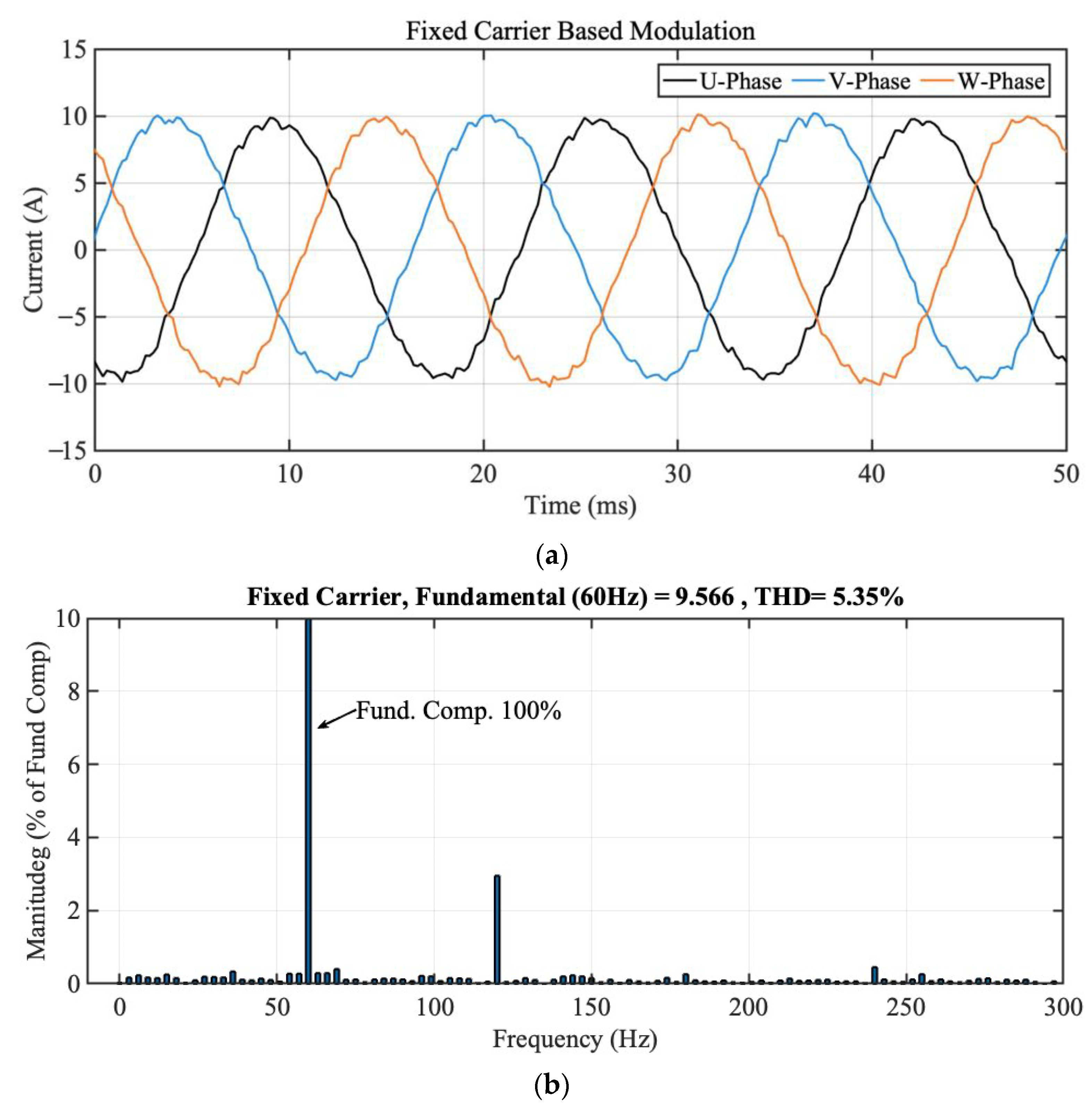
5.2. THD and Efficiency at Steady-State Operation

Measurements for THD and efficiency of the inverter were conducted while the SCIM operated at a constant speed and was mechanically loaded with 1 kW of power. The switching frequency of the FC method was kept at 4 kHz, while the HC method employed a 2–4 kHz pattern. Figure 10 and Figure 11 show the current waveforms and current THDs at 1800 rpm for the FCPWM and HCPWM methods, respectively. As seen in the figures, there was no significant change in THD values when the switching frequency varied from 4 kHz to 2–4 kHz.

To investigate the optimal switching pattern that maximized efficiency while keeping THD within standard limits, experiments were conducted at various speeds and switching frequencies. The overall measurements covered a speed range from 900 rpm to 1800 rpm, with the switching frequency varying between 2 kHz and 12 kHz. The THD analysis, presented in Figure 12, indicated that increasing the switching frequency improved THD performance, particularly at higher speeds. At 900 rpm, THD levels remained relatively low, mostly under 3%, regardless of the switching frequency. This suggests that increasing the switching frequency at that speed may not be beneficial, as the current already exhibits low harmonic distortion. However, as the speed increased to 1500 rpm and especially to 1800 rpm, the impact of the switching frequency became more significant. At 1800 rpm, the THD for 2–4 kHz exceeded 5%, which violated the harmonic limits recommended by IEEE 519-2014. To comply with the standard, increasing the switching frequency to 6 kHz or higher was necessary. Figure 13 illustrates the efficiency comparison between the FCPWM and HCPWM methods, considering the same motor speed and switching frequency range used in the THD analysis. The results show that HCPWM (represented by dashed bars) consistently outperformed FCPWM (represented by solid bars) across all speeds and switching frequencies. At 900 RPM, the hybrid carrier with a hybrid pattern of 2–4 kHz achieved the highest efficiency. As the speed increased to 1200–1500 RPM, the 2–4 kHz pattern remained the most efficient, and the efficiency gap between HCPWM and FCPWM widened. At 1800 RPM, HCPWM with a hybrid pattern of 6–12 kHz achieved peak efficiency. Overall, HCPWM demonstrated superior performance across all speeds, with the 2–4 kHz range being optimal at low speeds and the 6–12 kHz range being optimal at high speeds. These findings confirmed that hybrid switching significantly enhanced inverter efficiency, making HCPWM the preferred choice for variable-speed applications.

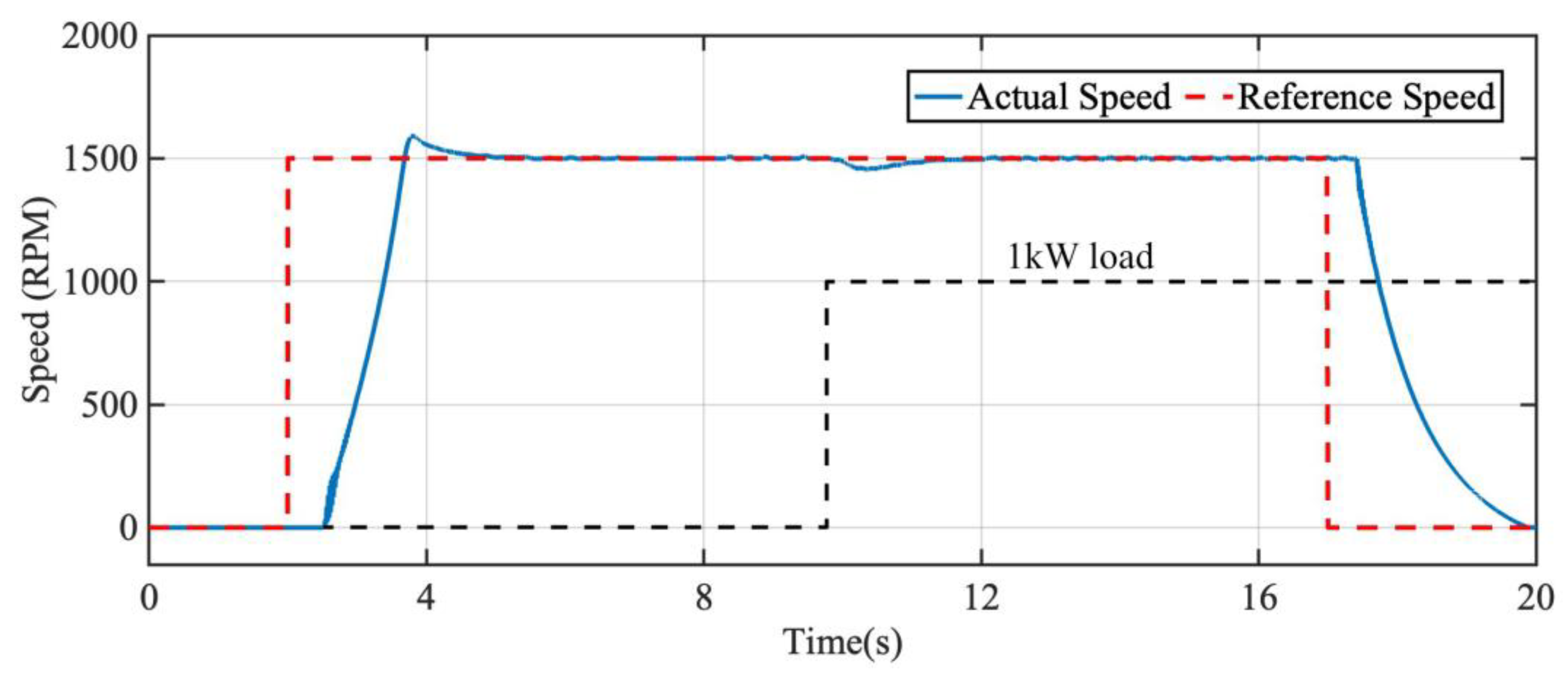
5.3. Efficiency Comparison in Dynamic Operation

Variation in speed and load is common in VSD applications such as CNC machines and EVs. To evaluate performance under dynamic operation, the HC method was combined with a PI controller for speed control and V/f control to maximize torque production. In that experiment, the SCIM started under no-load conditions, reached the speed defined by the reference input, and then a 1 kW load was applied to the motor midway through the test. Figure 14 displays the variations in reference speed, motor speed, and load torque at 1500 rpm. The overall operation lasted 20 s, after which the motor stopped. The PI controller functioned properly, maintaining the speed at the reference level despite the sudden application of the load torque.

As described in Section 4.2, efficiency calculation using power measurements may be inaccurate. Therefore, energy measurement was used for dynamic operations. The energy supplied to the inverter (input energy) and the energy delivered by the inverter (output energy) were measured with power analyzers during the experiment, while the reference speed was set to 900, 1200, 1500, and 1800 rpm, following the profile shown in Figure 14. As seen in the figure, the motor speed accurately followed the reference speed. Limited overshoot during acceleration and undershoot during load change indicated that the PI controller functioned properly. The SCIM was continuously loaded with a constant power of 1 kW throughout the experiment to observe the effect of speed variation on inverter efficiency. The switching frequencies for FCPWM and HCPWM were set to 6 kHz and 3–6 kHz, respectively.

Table 1. Energy efficiency and current THD comparison of VSI inverter with FC and HC methods.

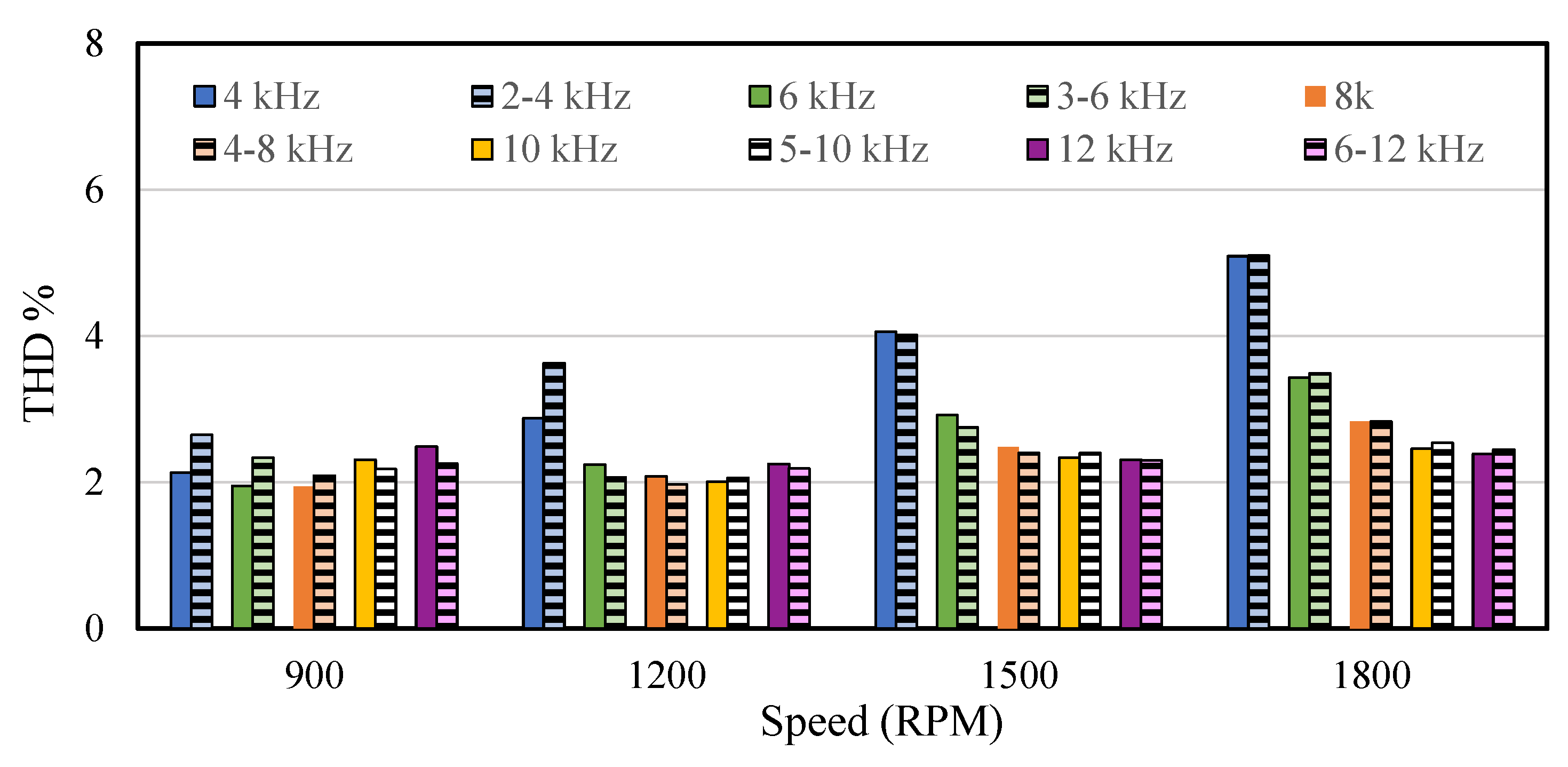
Parameter		Carrier Type/Frequency
		Fixed Carrier 6 kHz	Hybrid Carrier 3–6 kHz
900 RPM	Input energy (Wh)	4.127	3.896
	Output energy (Wh)	3.932	3.721
	Efficiency (%)	95.28	95.51
1200 RPM	Input energy (Wh)	3.915	3.848
	Output energy (Wh)	3.765	3.712
	Efficiency (%)	96.17	96.47
1500 RPM	Input energy (Wh)	3.788	3.761
	Output energy (Wh)	3.656	3.645
	Efficiency (%)	96.52	96.92
1800 RPM	Input energy (Wh)	3.646	3.627
	Output energy (Wh)	3.529	3.523
	Efficiency (%)	96.79	97.13

Efficiency of FC (orange color), Efficiency of HC (green color).

presents the input and output energy measurements of the inverter for both the FCPWM and HCPWM methods. As shown in the table, HCPWM provided better efficiency than FCPWM across the entire speed range.

6. Conclusions

This study investigated the performance of the HCPWM method in VSD applications, aiming to minimize inverter switching losses while maintaining THD within standard limits. Unlike traditional FCPWM, which requires higher switching frequencies for smoother output currents, HCPWM alternates between two carrier signals of different frequencies. This enhances inverter efficiency without adding complexity or cost, making it a strong alternative for practical implementation. Experimental results confirmed that, with optimal carrier frequency pairs, HCPWM effectively reduced switching losses while keeping THD lower than FCPWM. As a result, the motor experienced reduced harmonic distortion, improving motor efficiency and overall system performance. Additionally, by lowering switching frequency, HCPWM limited the temperature rise due to switching losses, contributing to improved system reliability. This is particularly beneficial for industrial VSD applications where thermal management and power efficiency are critical. The dynamic behavior of HCPWM was also evaluated under V/f control, showing sufficient performance for various VSD applications. However, further research is needed to integrate HCPWM with advanced control strategies, such as FOC, and validate its long-term reliability under diverse conditions. These findings highlight HCPWM as a promising and efficient modulation technique for improving energy efficiency and power quality in inverter-driven motor systems.