An Investigation into the Saliency Ratio of Fractional-Slot Concentrated-Winding Generators for Offshore Wind Power
Abstract
:1. Introduction
2. Investigation into Saliency Ratios of 3 MW Machines
2.1. Model Setup and Inductance Calculations
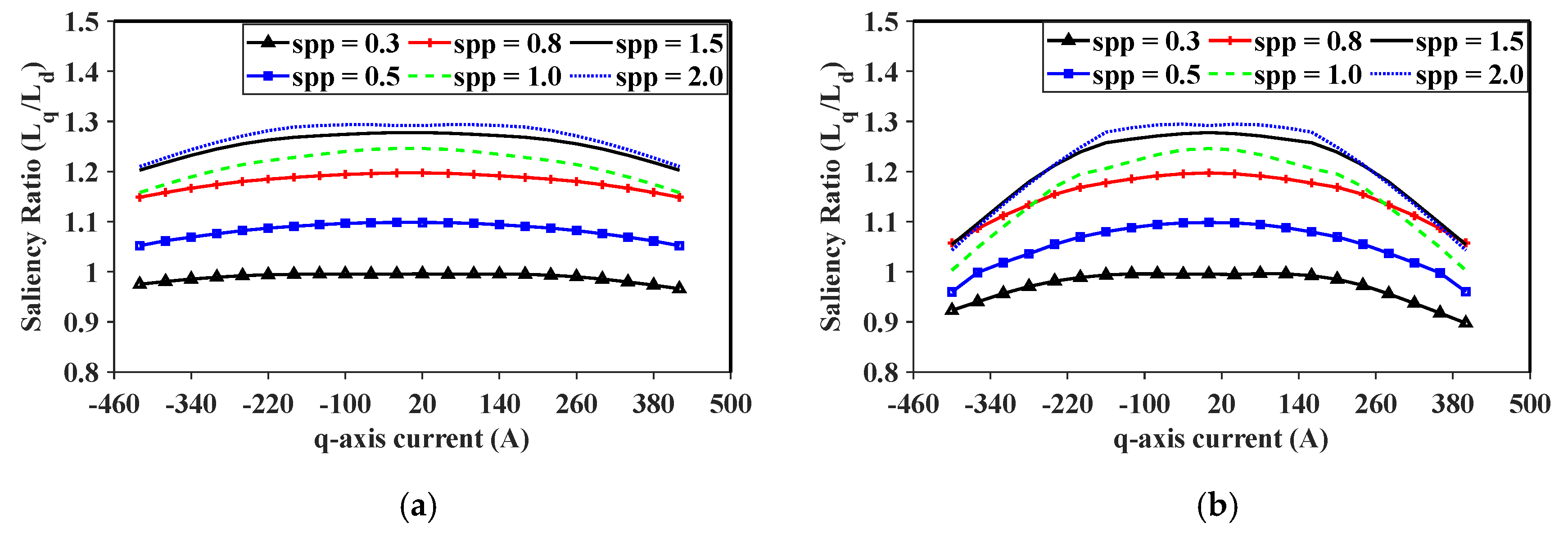
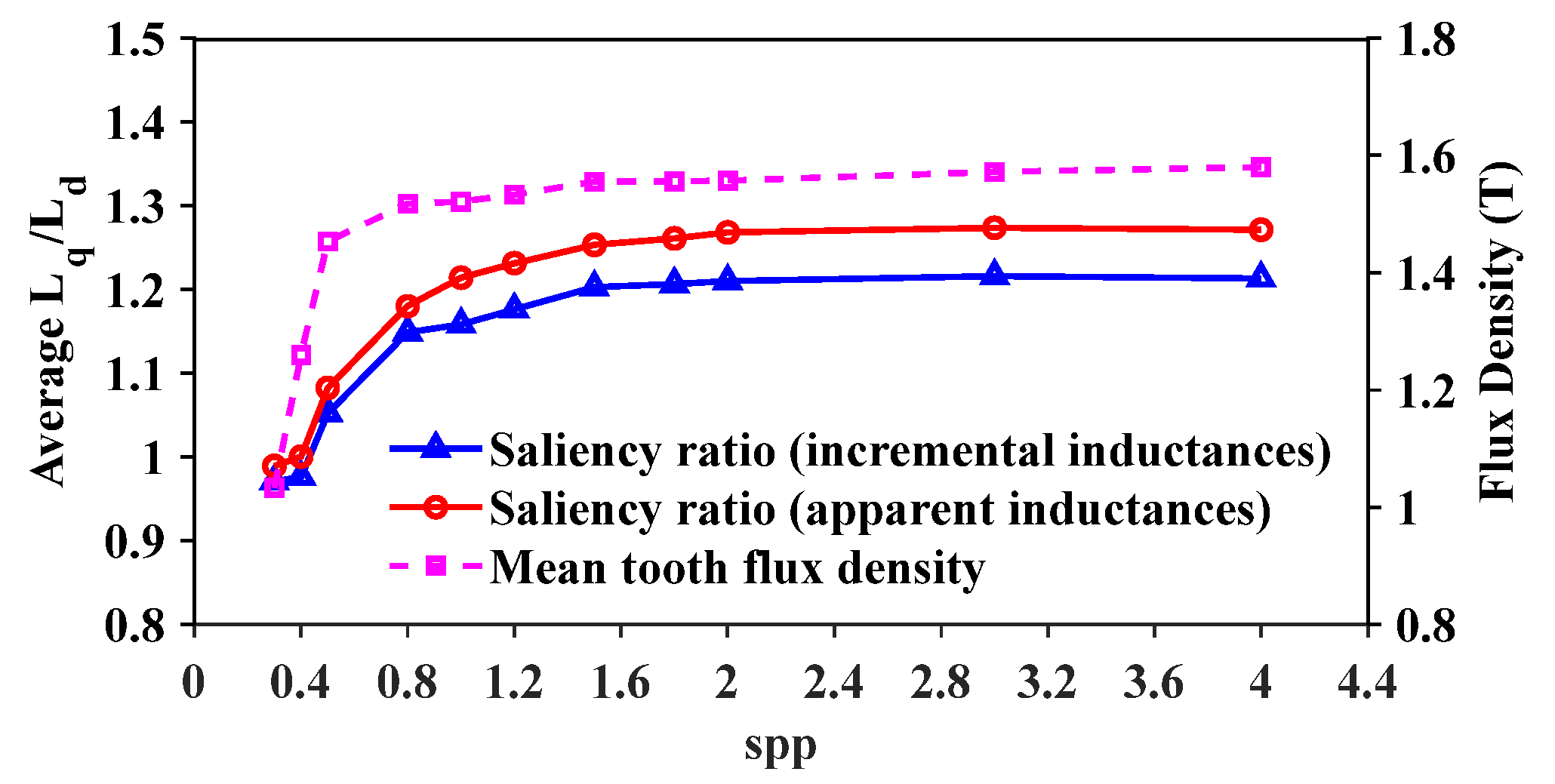
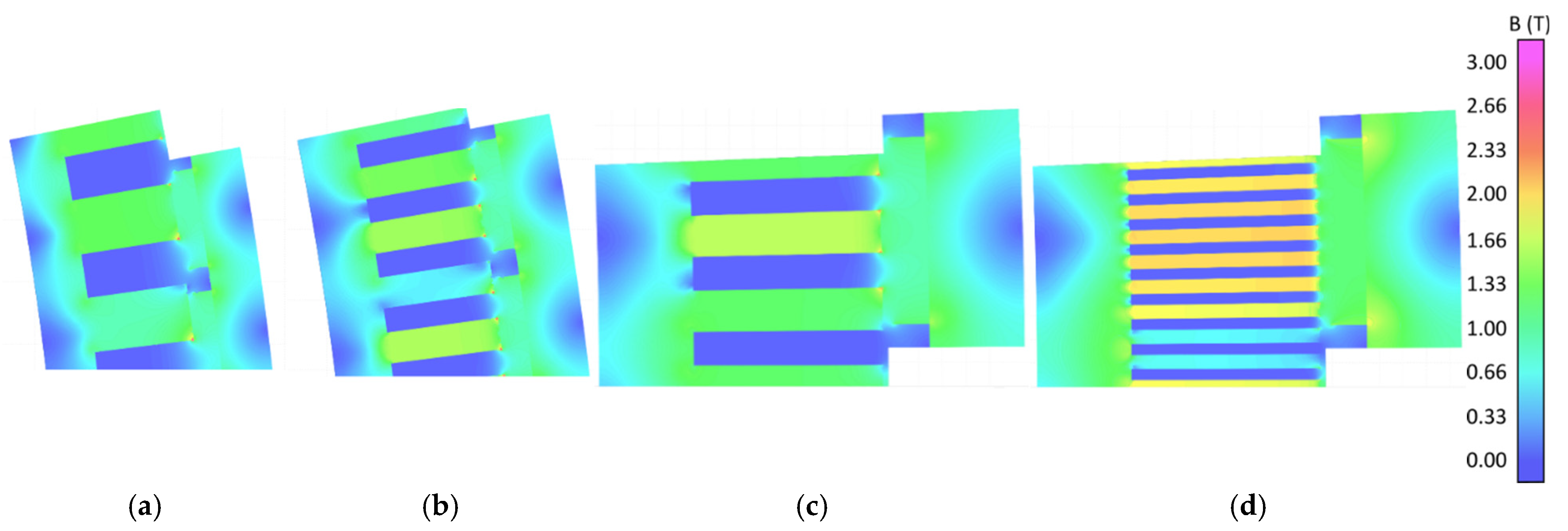
2.2. Saliency of Different Slots per Pole per Phase (Spp) Ratios
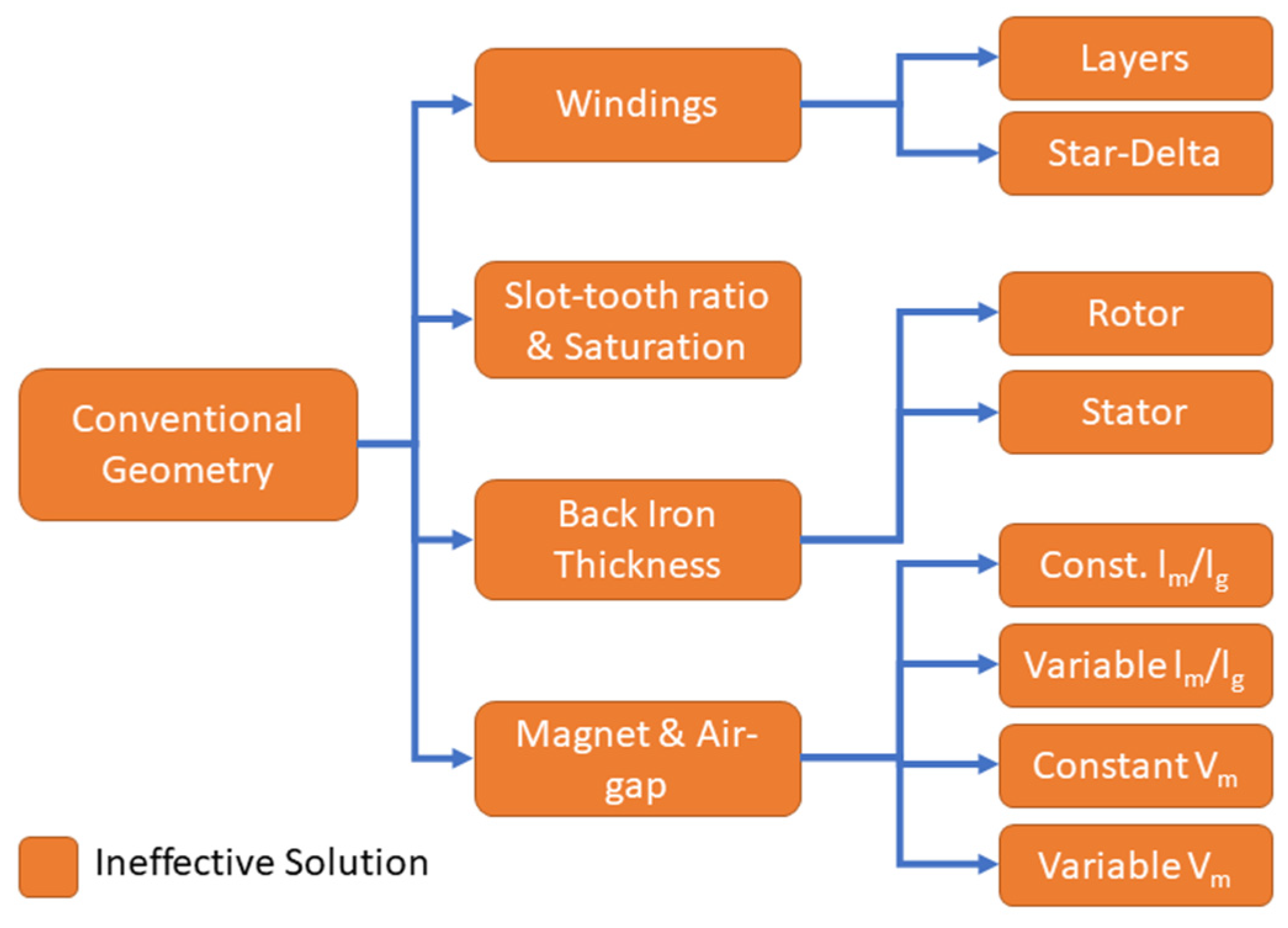
3. Conventional Geometry Modification
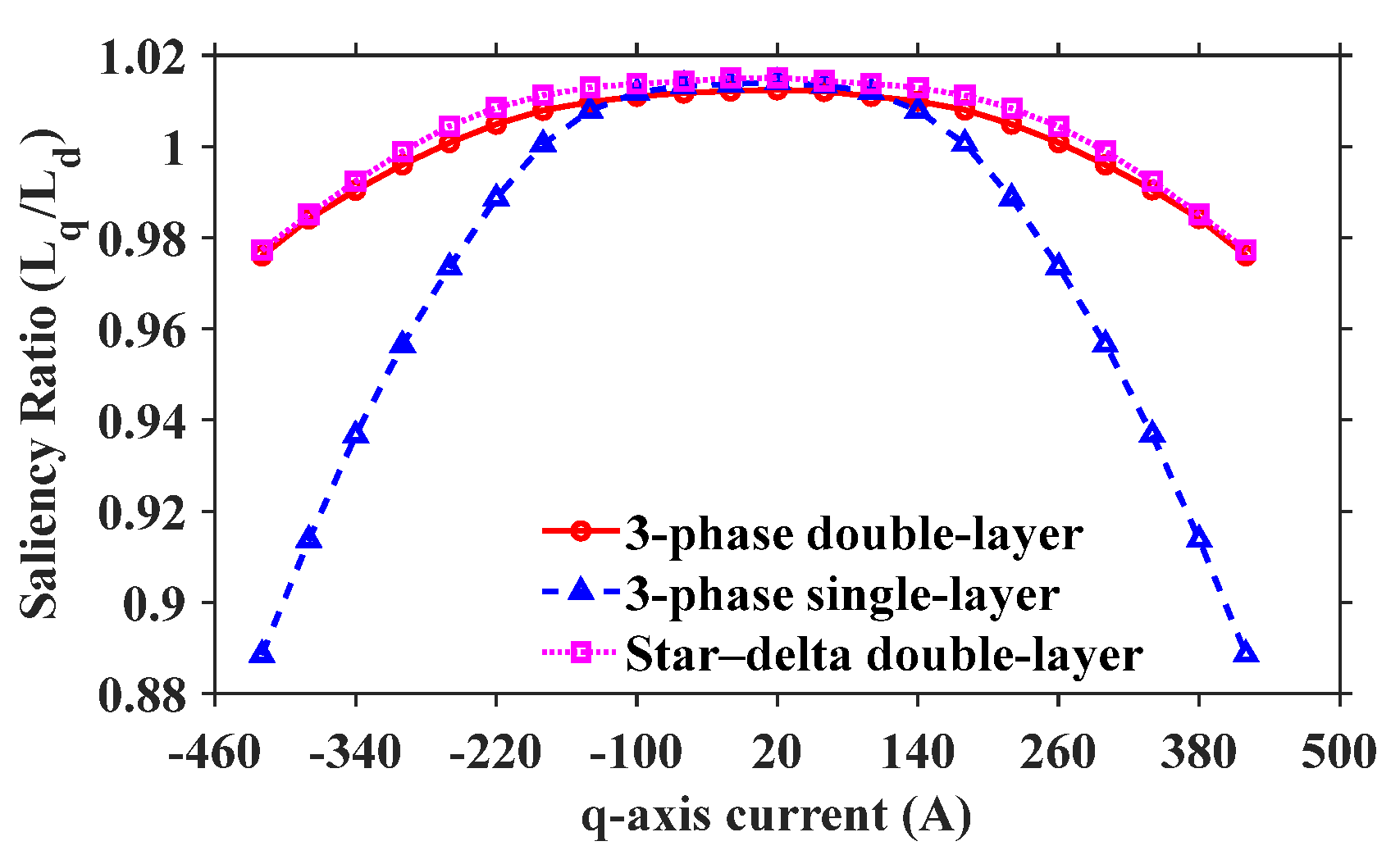
3.1. Winding Layout
3.2. Slot–Tooth Ratio
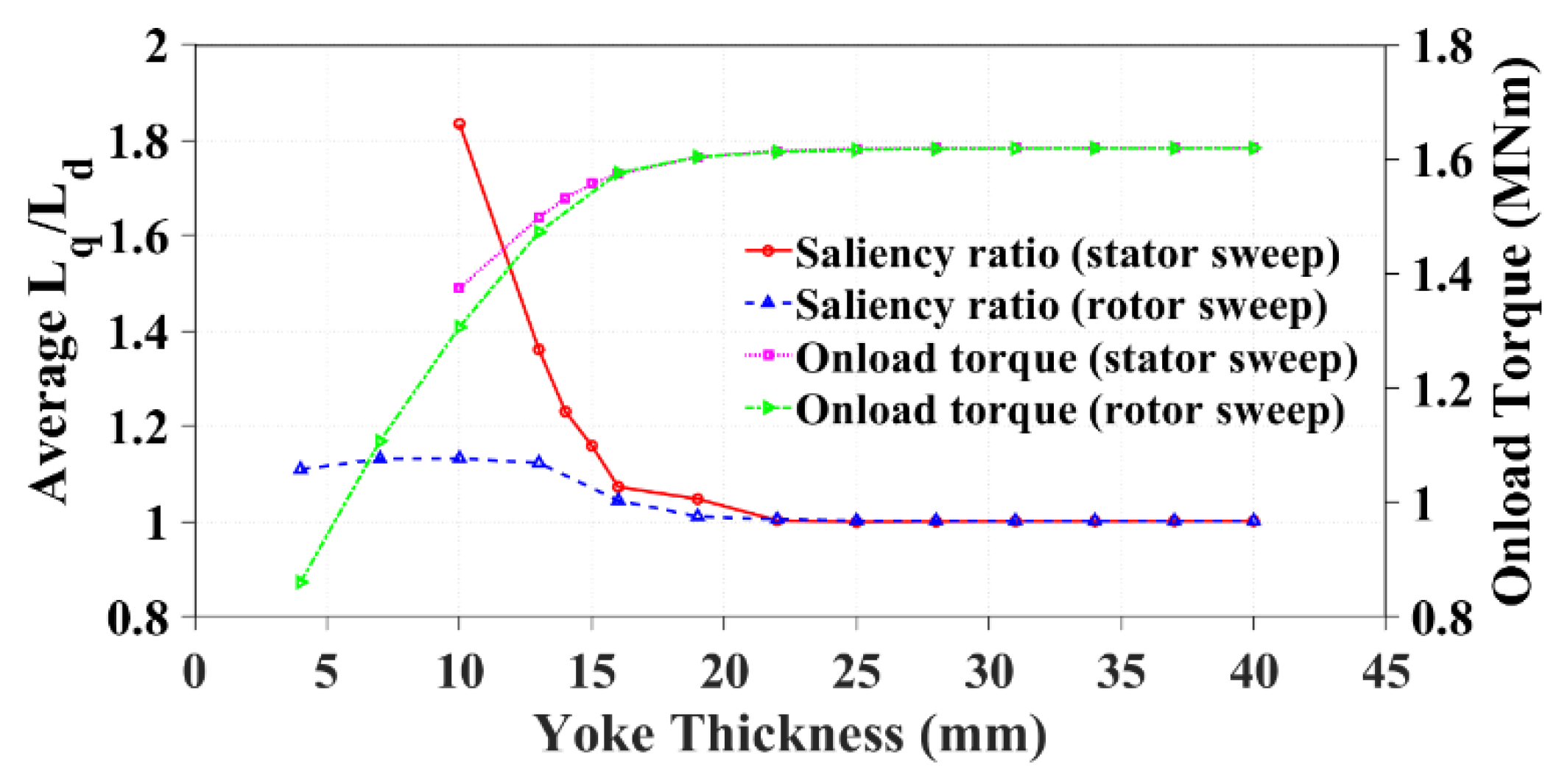
3.3. Back-Iron Thickness
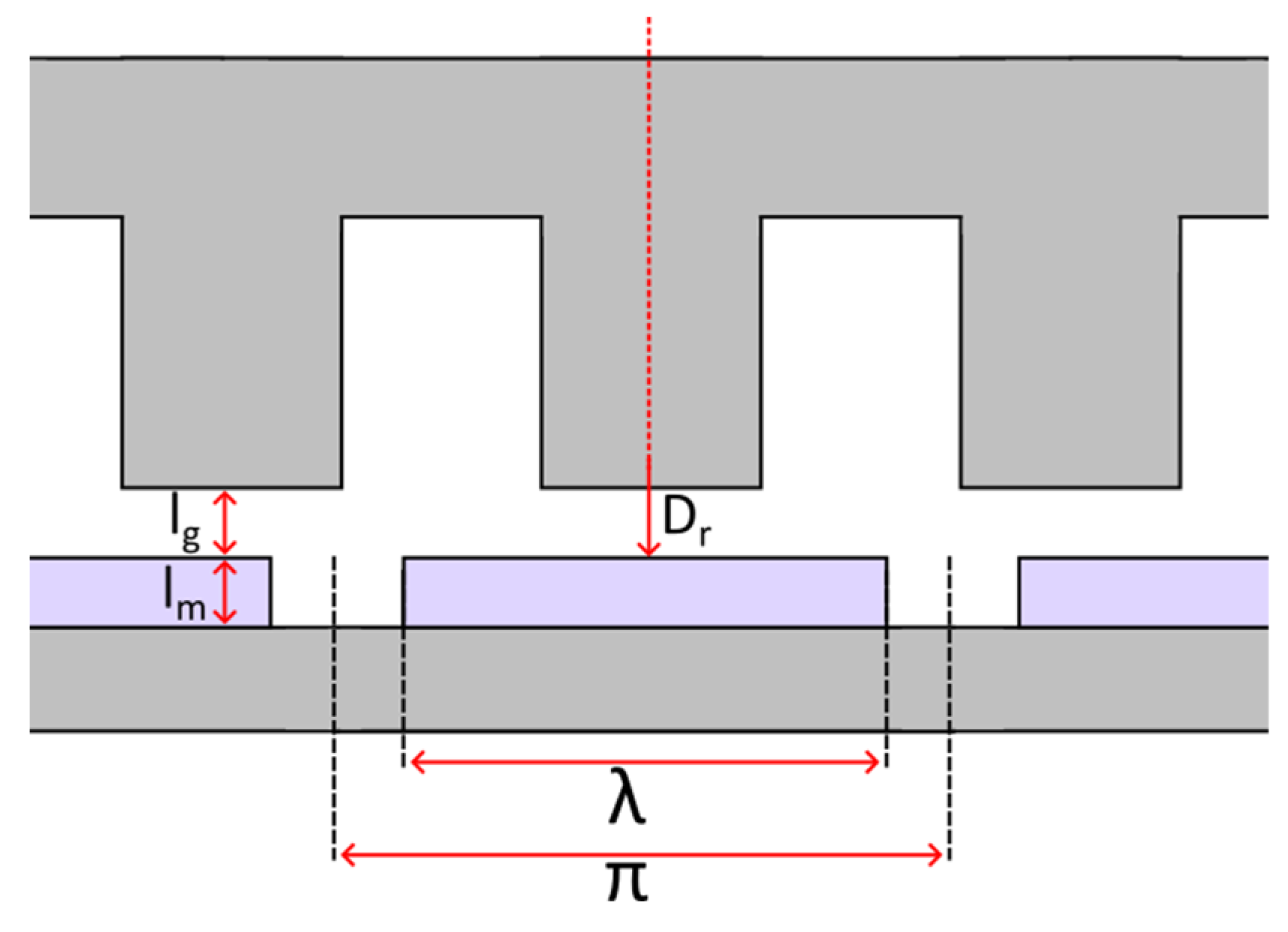
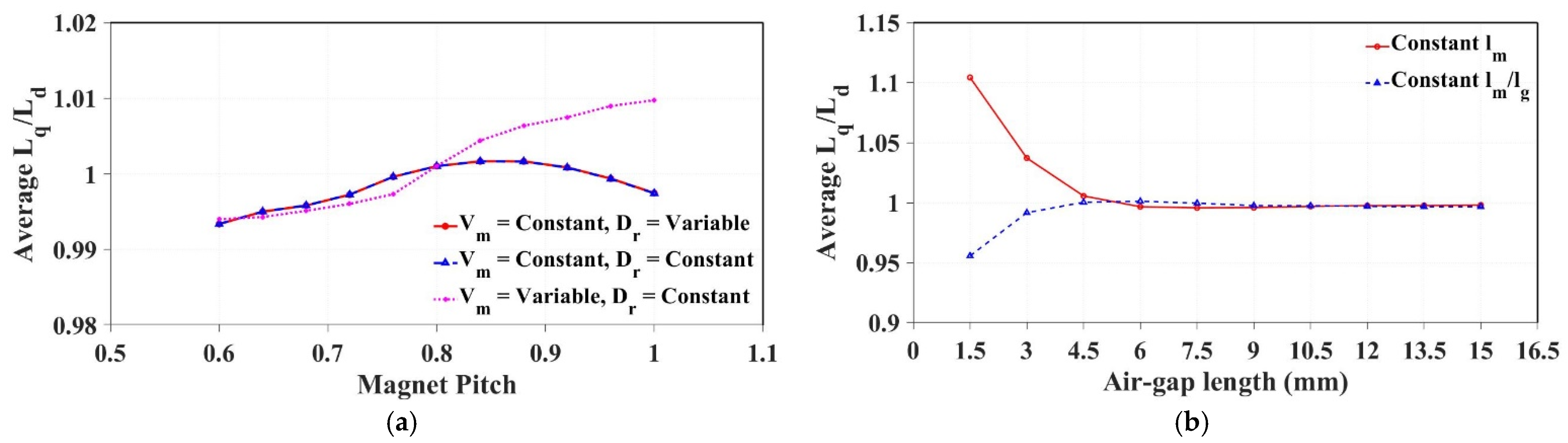
3.4. Magnet and Air-Gap Dimensions
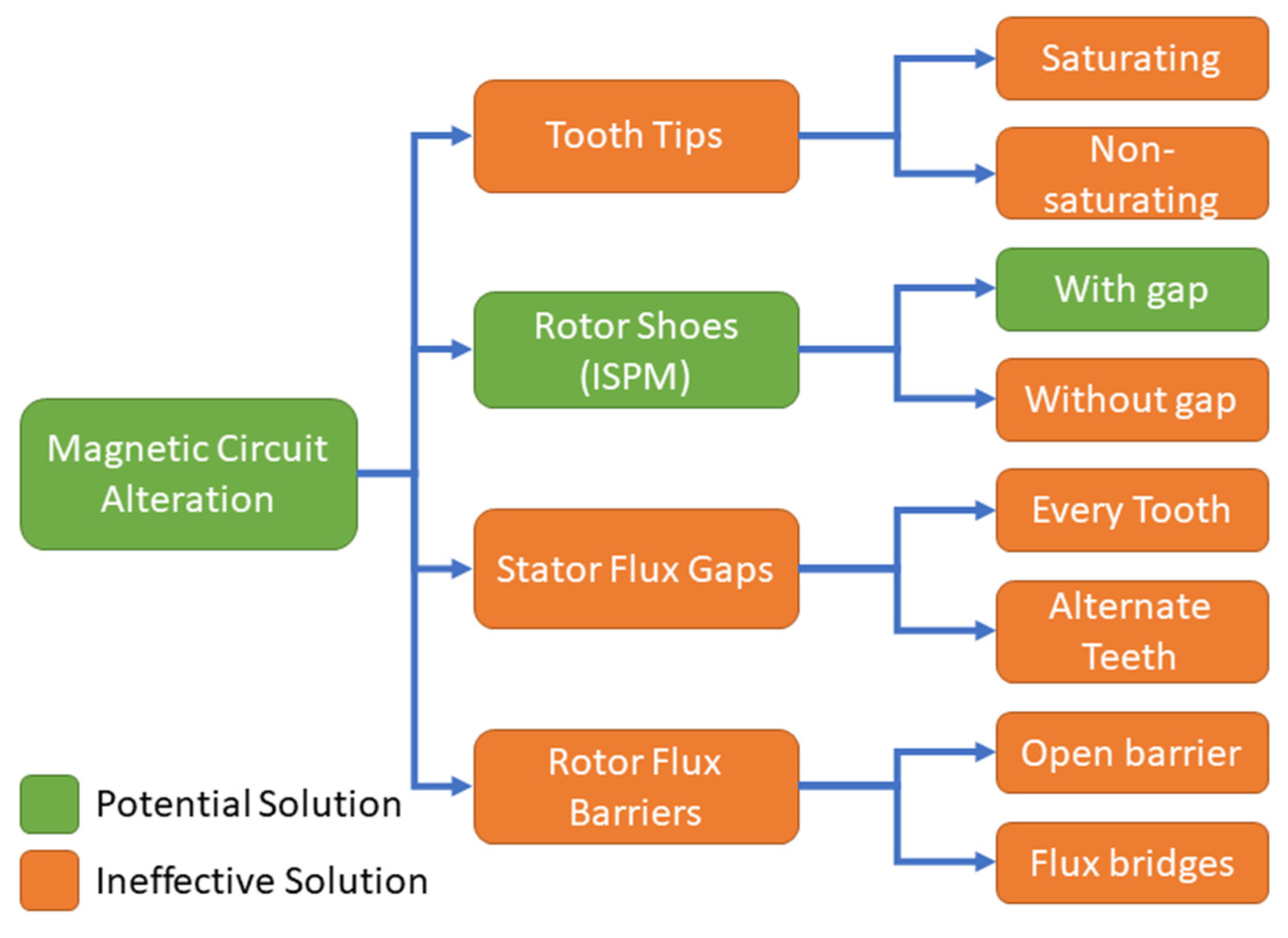
4. Magnetic Circuit Alteration
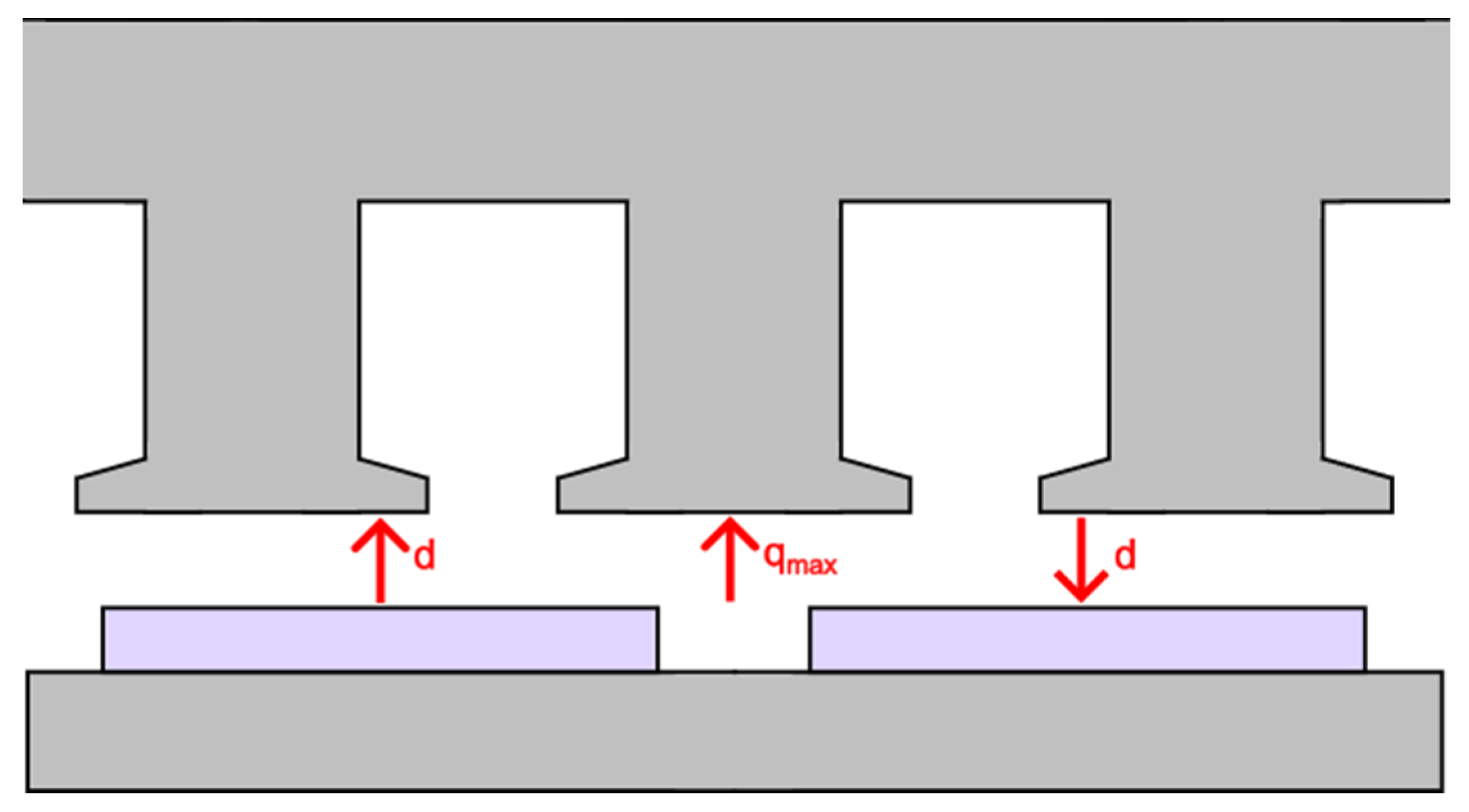
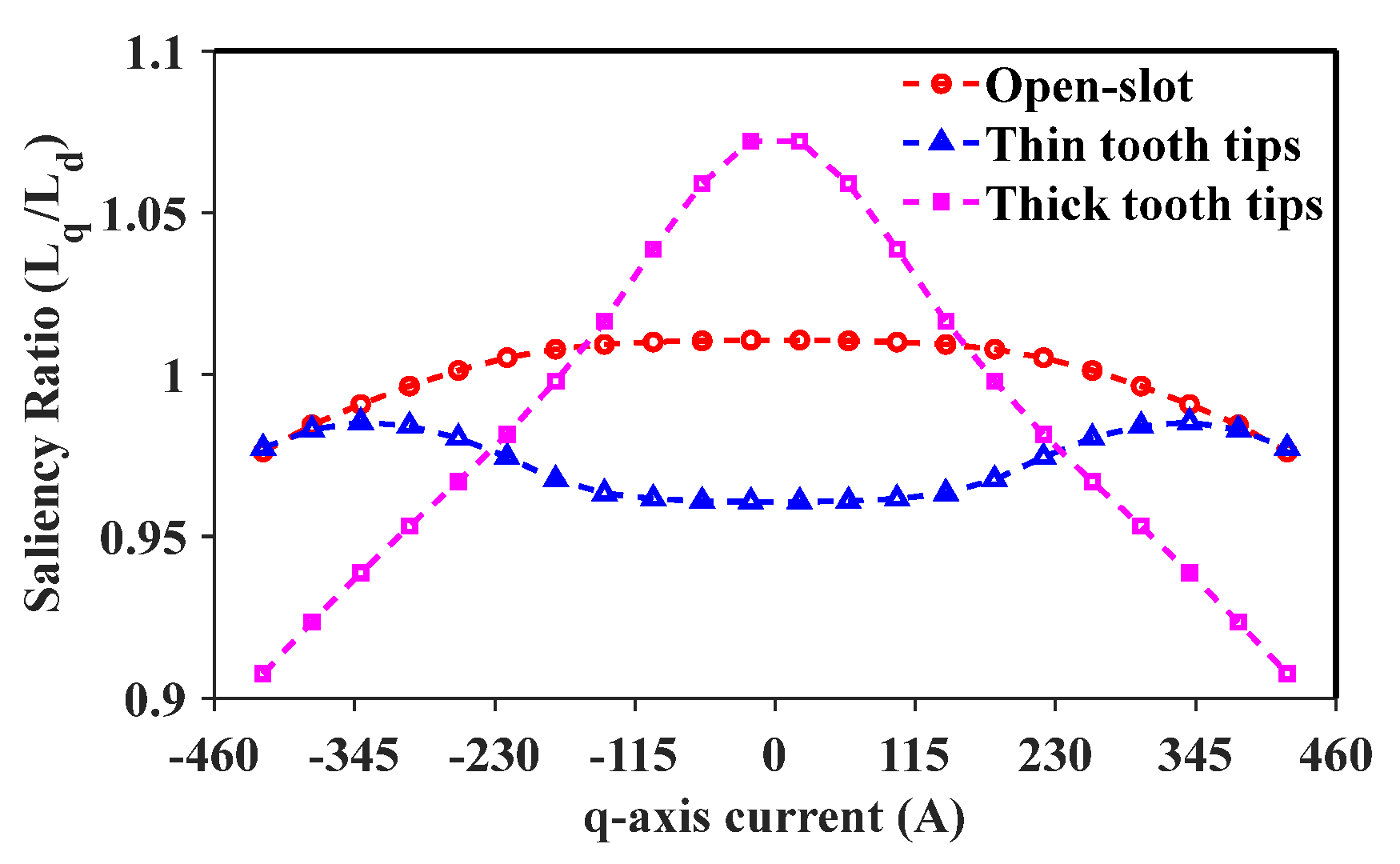
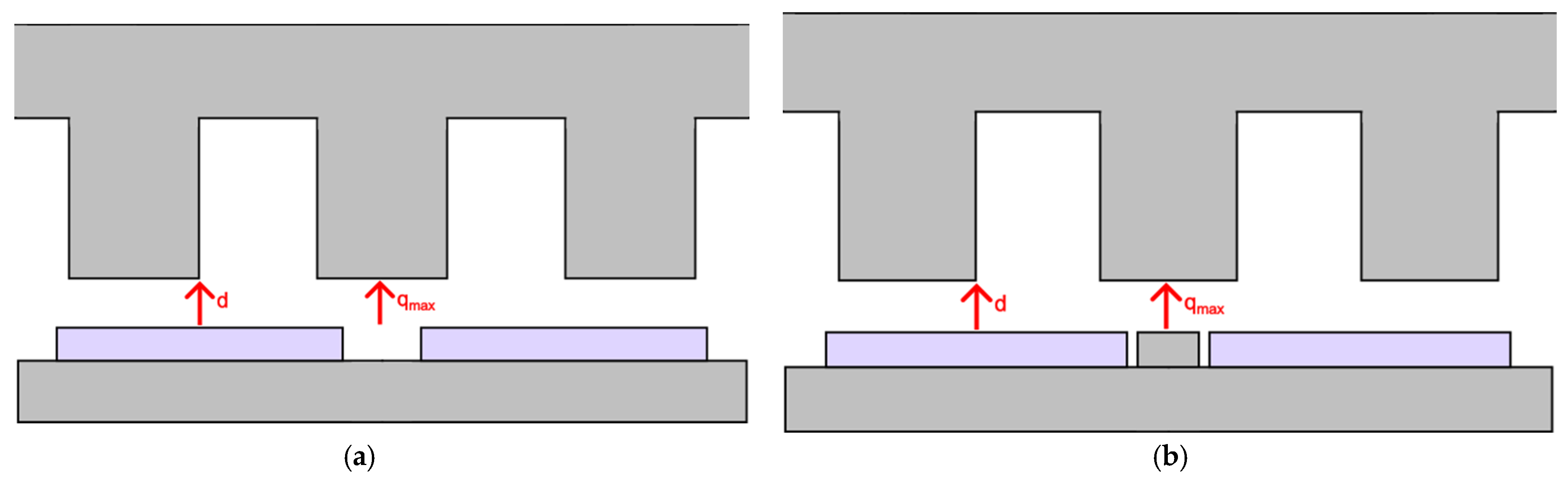
4.1. Addition of Tooth Tips
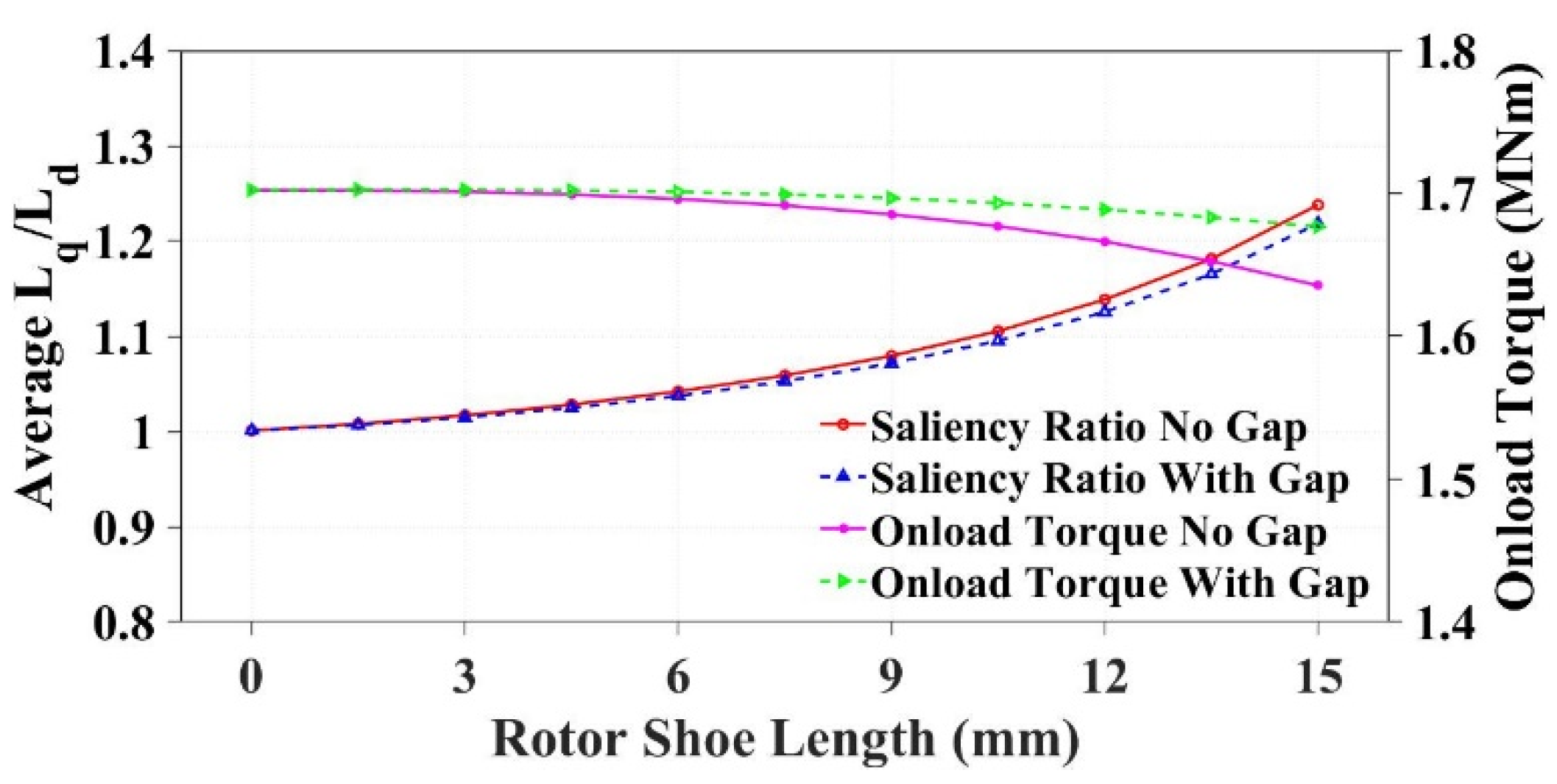
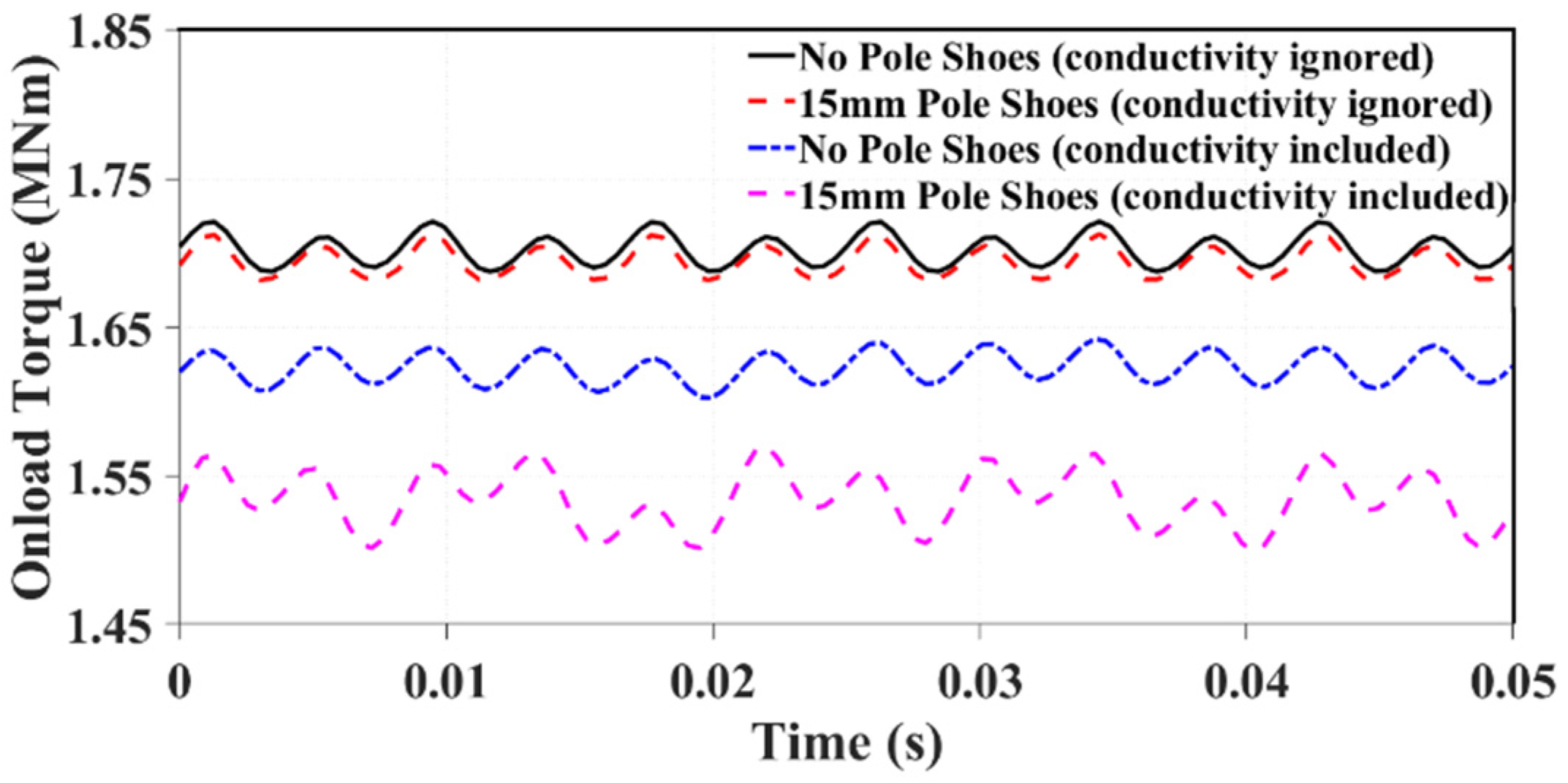
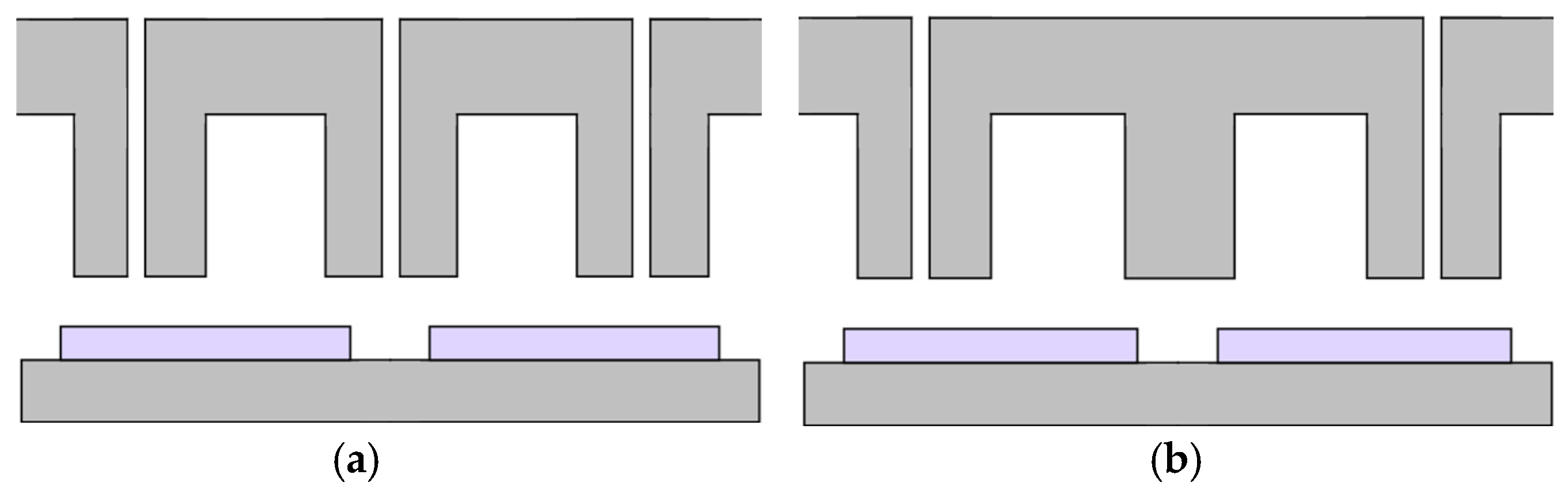
4.2. Addition of Rotor Shoes
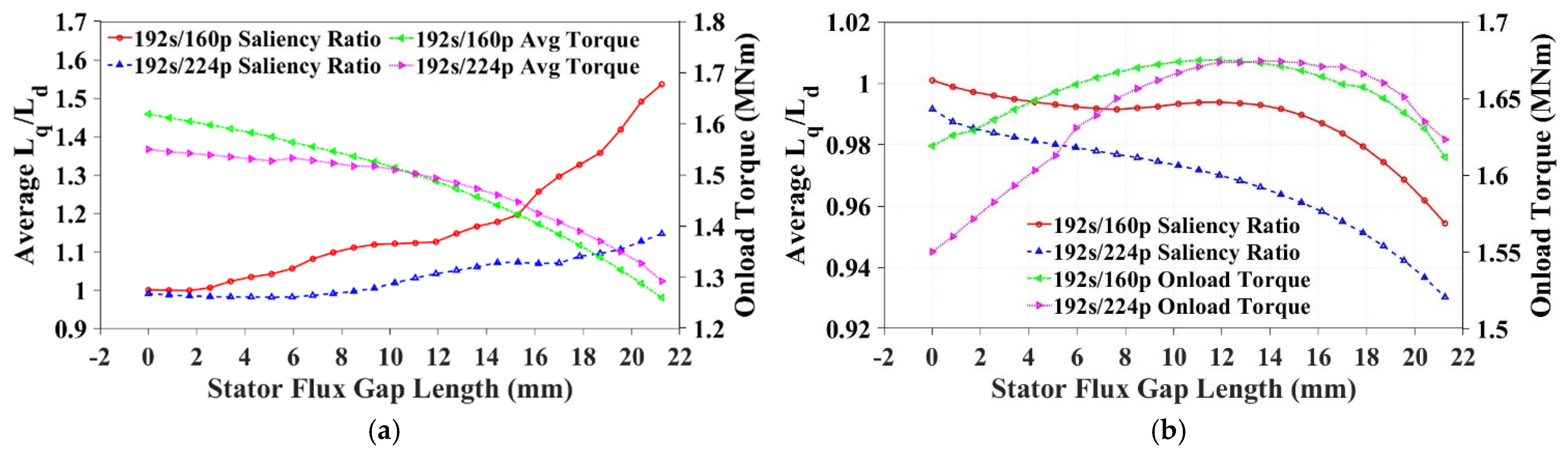
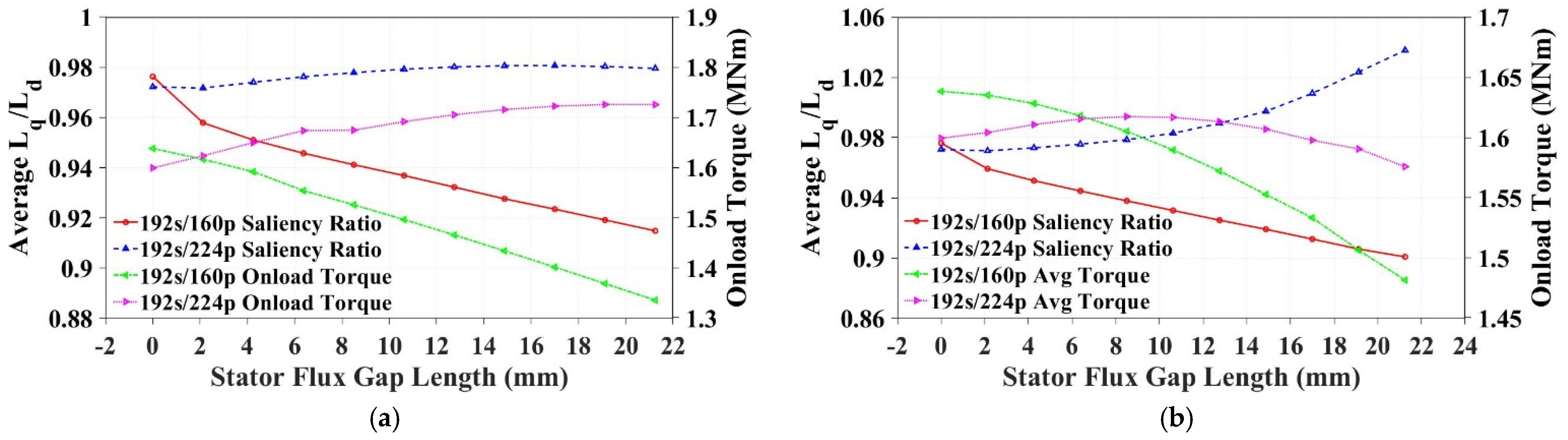
4.3. Stator Flux Gaps
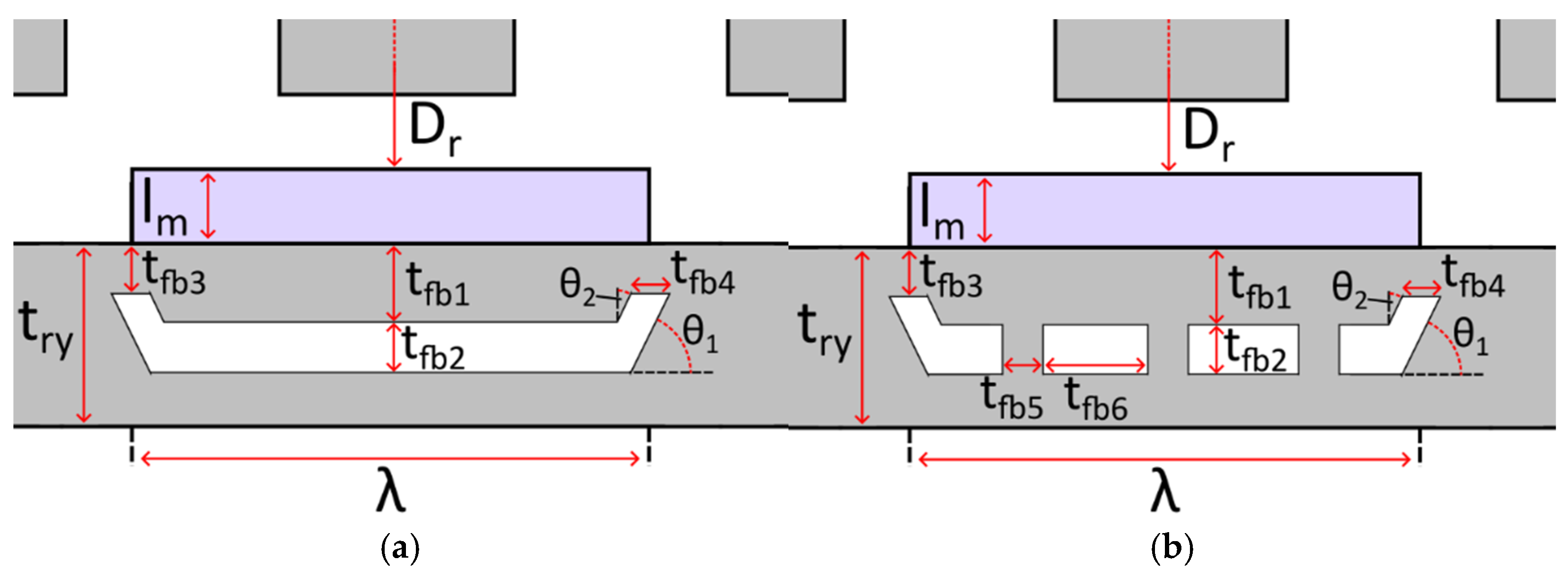
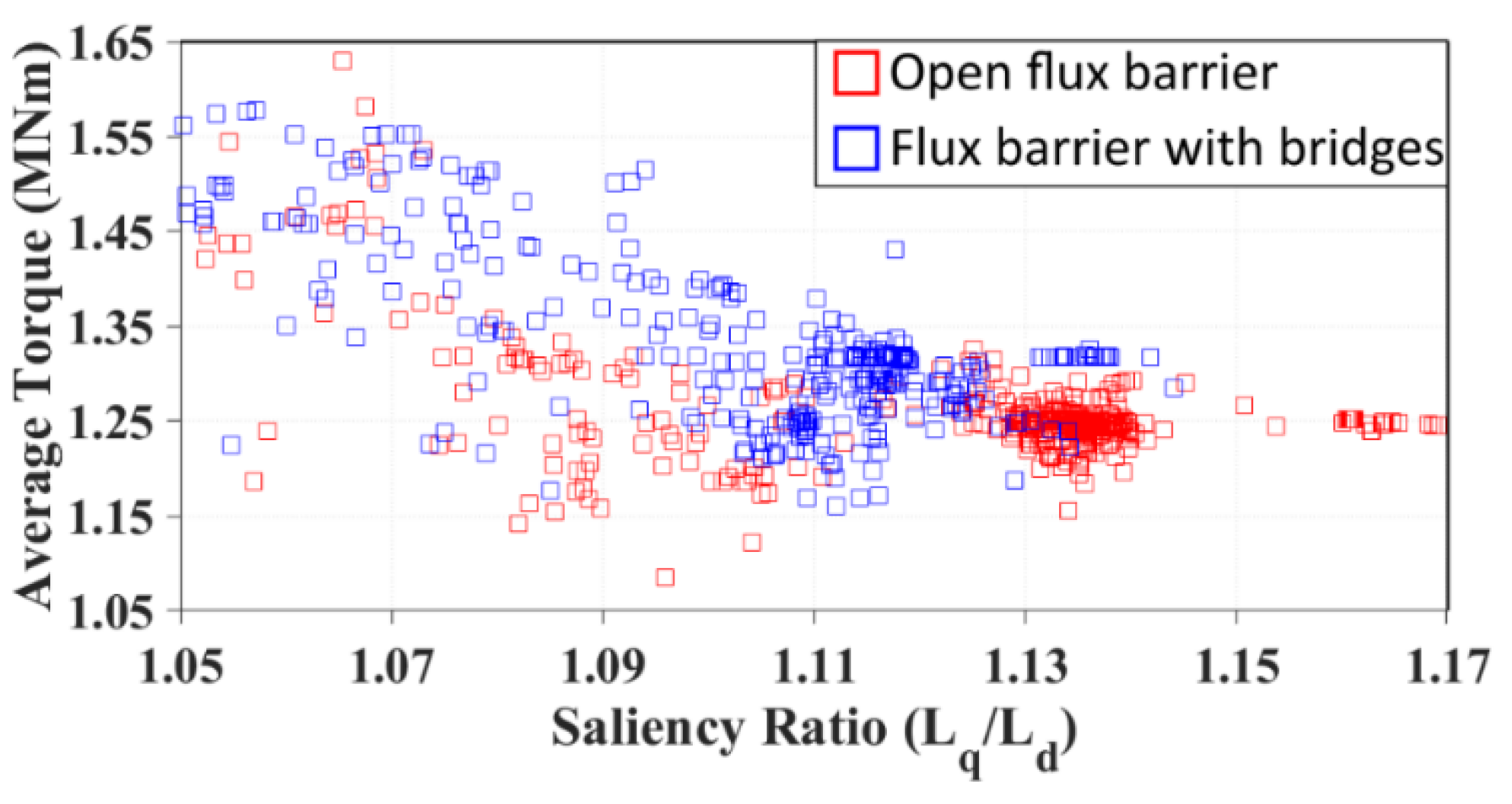
4.4. Rotor Flux Barriers
5. Design of 3 MW FSCW Machine with High Saliency Ratio
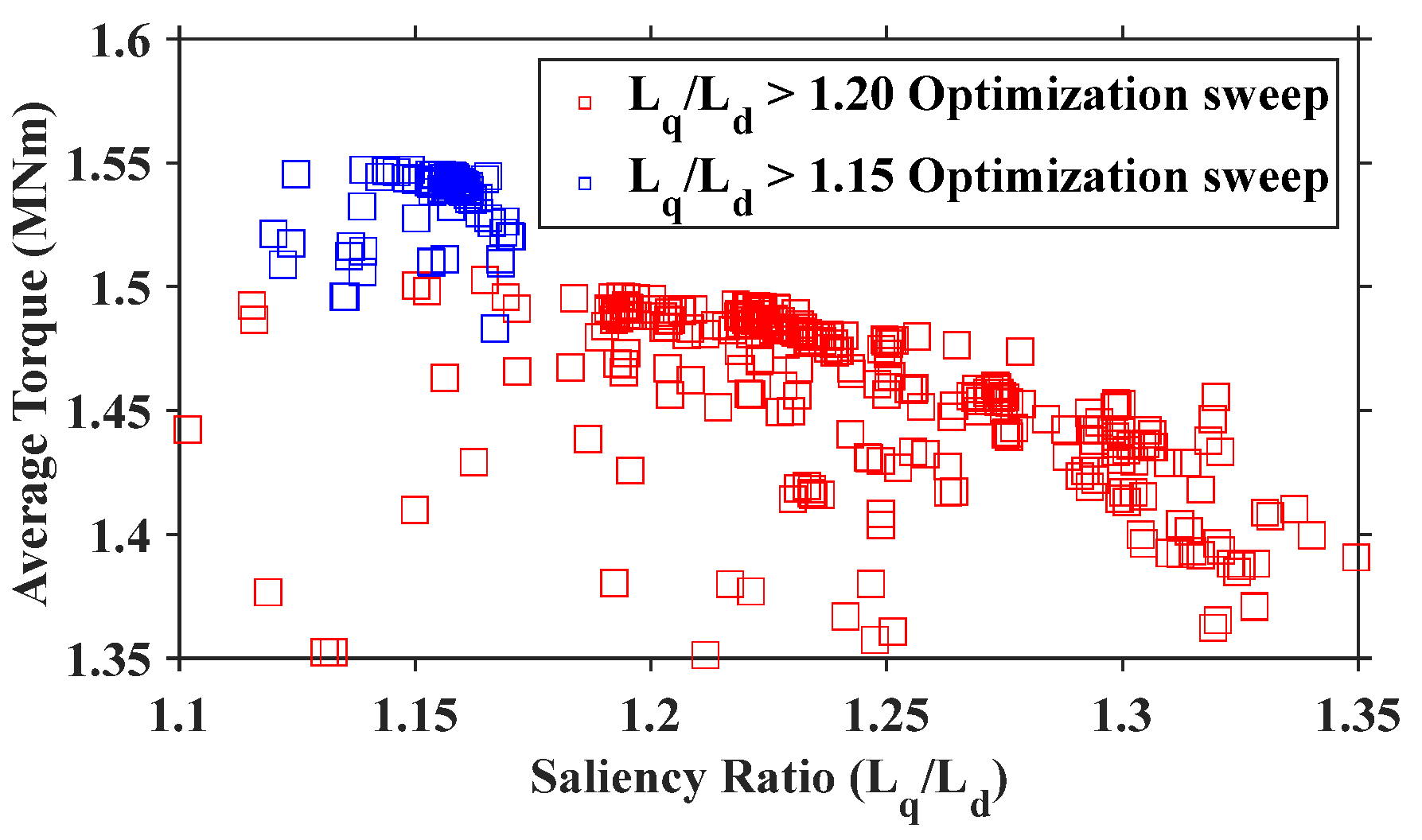
5.1. Optimization Process
5.2. Machine Comparison
6. Conclusions
- (1)
- The composition of the magnetic circuit was unaltered, i.e., conventional geometry was maintained.
- (2)
- The magnetic circuit was altered through the addition or removal of rotor/stator steel.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| d- and q-axis self-inductances | |
| d- and q-axis mutual inductances | |
| d- and q-axis currents | |
| d- and q-axis flux linkages | |
| PM flux linkages | |
| spp | Slots per pole per phase |
| lm | Magnet thickness |
| lg | Air-gap length |
| Vm | Magnet volume |
| β | Slot–tooth ratio |
| Dr | Rotor outer diameter |
| λ | Magnet arc |
| σ | Conductivity |
References
- Wu, R.; Slemon, G.R. A permanent magnet motor drive without a shaft sensor. IEEE Trans. Ind. Appl. 1991, 27, 1005–1011. [Google Scholar] [CrossRef]
- Chen, Z.; Tomita, M.; Doki, S.; Okuma, S. An extended electromotive force model for sensorless control of interior permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2003, 50, 288–295. [Google Scholar] [CrossRef]
- Yang, S.-C.; Suzuki, T.; Lorenz, R.D.; Jahns, T.M. Surface-permanent-magnet synchronous machine design for saliency-tracking self-sensing position estimation at zero and low speeds. IEEE Trans. Ind. Appl. 2011, 47, 2103–2116. [Google Scholar] [CrossRef]
- Jang, J.-H.; Sul, S.-K.; Ha, J.-I.; Ide, K.; Sawamura, M. Sensorless drive of surface-mounted permanent-magnet motor by high-frequency signal injection based on magnetic saliency. IEEE Trans. Ind. Appl. 2003, 39, 1031–1039. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Wang, S.; Guo, Y.; Xu, W. Nonlinear magnetic model of surface mounted PM machines incorporating saturation saliency. IEEE Trans. Magn. 2009, 45, 4684–4687. [Google Scholar] [CrossRef]
- Tangudu, J.K.; Jahns, T.M.; El-Refaie, A. Unsaturated and saturated saliency trends in fractional-slot concentrated-winding interior permanent magnet machines. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010. [Google Scholar]
- Pouramin, A.; Dutta, R.; Rahman, M.F.; Xiao, D. Inductances of a fractional-slot concentrated-winding interior PM synchronous machine considering effects of saturation and cross magnetization. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Leidhold, R. Position sensorless control of PM synchronous motors based on zero-sequence carrier injection. IEEE Trans. Ind. Electron. 2011, 58, 5371–5379. [Google Scholar] [CrossRef]
- Yang, S.-C.; Lorenz, R.D. Surface permanent-magnet machine self-sensing at zero and low speeds using improved observer for position, velocity, and disturbance torque estimation. IEEE Trans. Ind. Appl. 2012, 48, 151–160. [Google Scholar] [CrossRef]
- Hoang Duy, T.; Phung Anh, T. Surface-mounted permanent magnet synchronous motor design ready for sensorless control at zero and low speed. In Proceedings of the 2022 11th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 21–24 November 2022. [Google Scholar]
- Bianchi, N.; Bolognani, S.; Jang, J.-H.; Sul, S.-K. Advantages of inset PM machines for zero-speed sensorless position detection. IEEE Trans. Ind. Appl. 2008, 44, 1190–1198. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Faggion, A.; Fornasiero, E. Analysis and experimental tests of the sensorless capability of a fractional-slot inset PM motor. IEEE Trans. Ind. Appl. 2015, 51, 224–231. [Google Scholar] [CrossRef]
- Zhang, Z.; Xia, C.; Wang, H.; Shi, T. Analytical field calculation and analysis of surface inset permanent magnet machines with high saliency ratio. IEEE Trans. Magn. 2016, 52, 8108612. [Google Scholar] [CrossRef]
- Krizan, J.A.; Sudhoff, S.D. A design model for salient permanent-magnet machines with investigation of saliency and wide-speed-range performance. IEEE Trans. Energy Convers. 2013, 28, 95–105. [Google Scholar] [CrossRef]
- Rudden, I.; Li, G.-J.; Zhu, Z.-Q.; Duke, A.; Clark, R. Analysis of MW-level offshore wind turbine generators with dual star–delta fractional-slot windings. Energies 2024, 17, 2958. [Google Scholar] [CrossRef]
- Rudden, I.; Wang, P.; Li, H.; Li, G.J.; Zhu, Z.Q.; Duke, A.; Clark, R. DQ analysis of fractional-slot machines with star-delta concentrated winding. IEEE Access 2024, 12, 84680–84690. [Google Scholar] [CrossRef]
- Li, G.J.; Zhu, Z.Q.; Chu, W.Q.; Foster, M.P.; Stone, D.A. Influence of flux gaps on electromagnetic performance of novel modular PM machines. IEEE Trans. Energy Convers. 2014, 29, 716–726. [Google Scholar] [CrossRef]
- Yao, Y.; Lu, Q. Comparative study of E-Core and C-Core modular PM linear machines with different slot/pole combinations. IEEE Trans. Magn. 2017, 53, 8110307. [Google Scholar] [CrossRef]
- Kang, J.; Sun, L.; Guedes Soares, C. Fault tree analysis of floating offshore wind turbines. Renew. Energy 2019, 133, 1455–1467. [Google Scholar] [CrossRef]
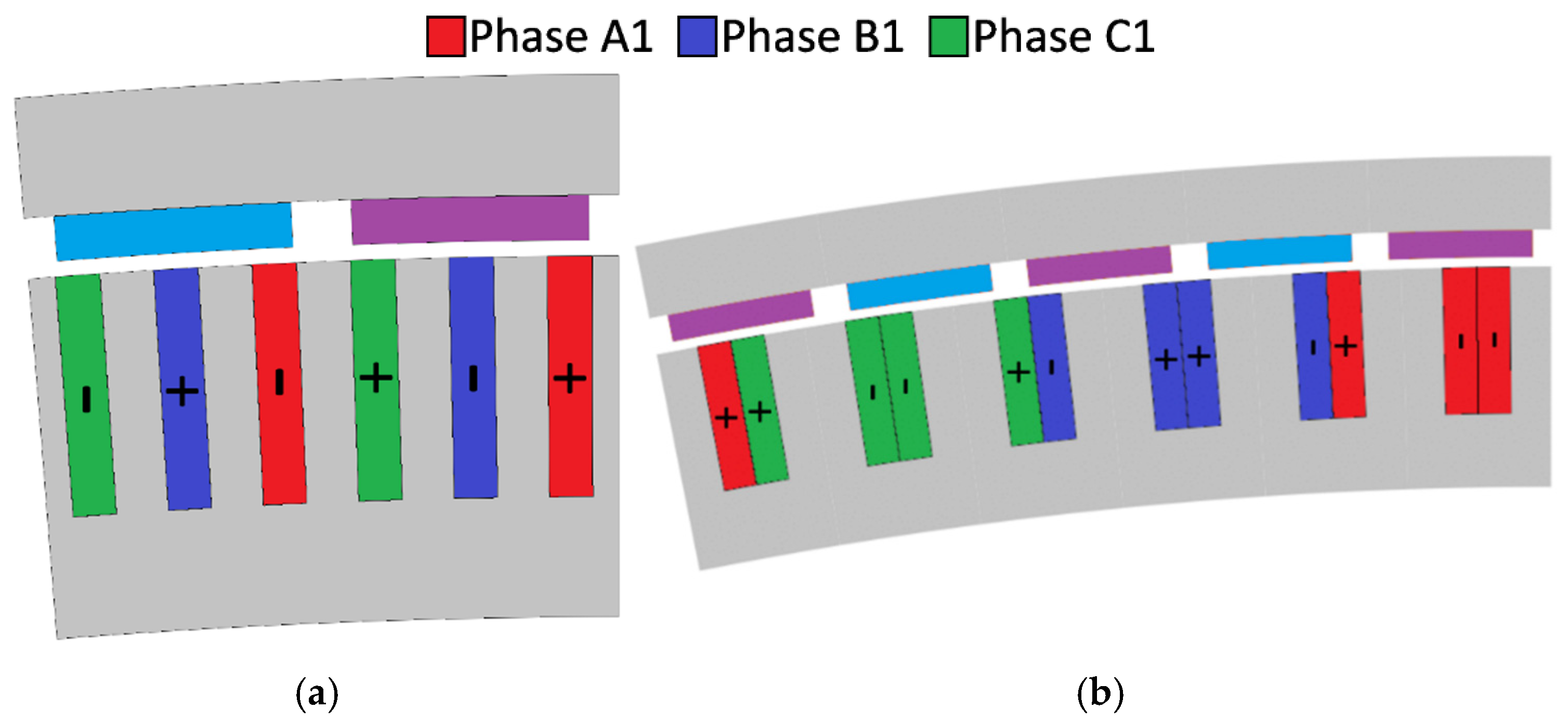
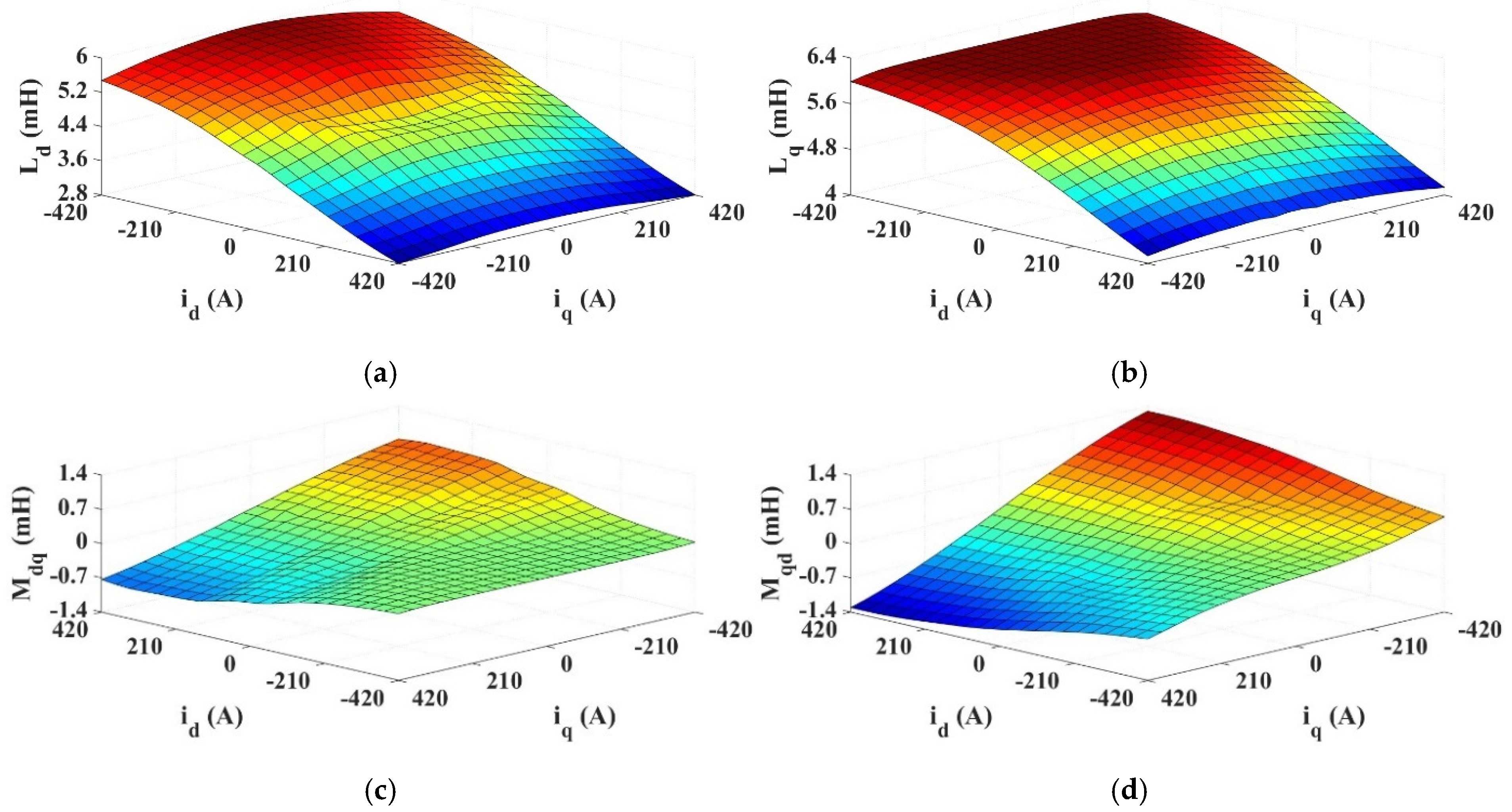
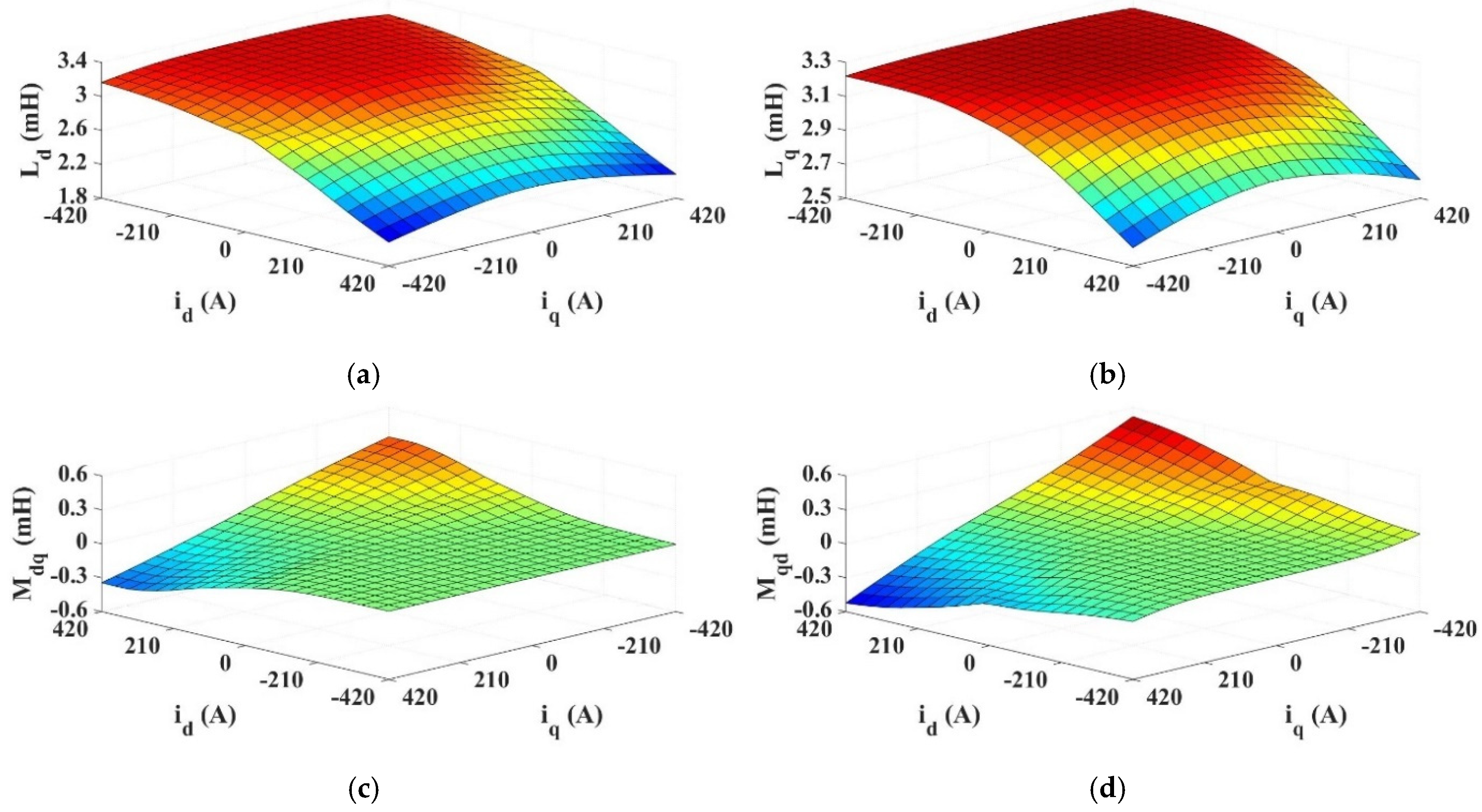
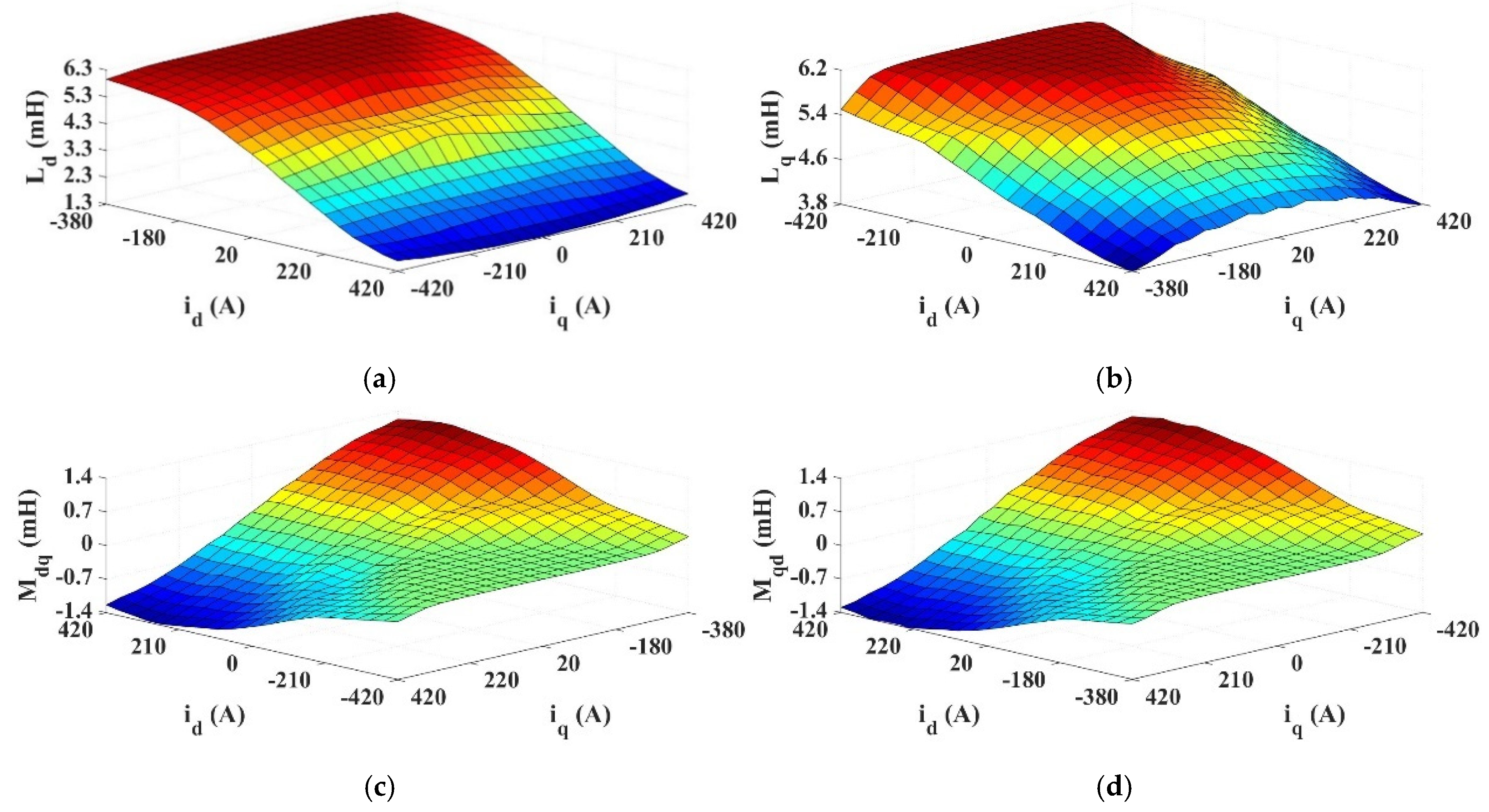
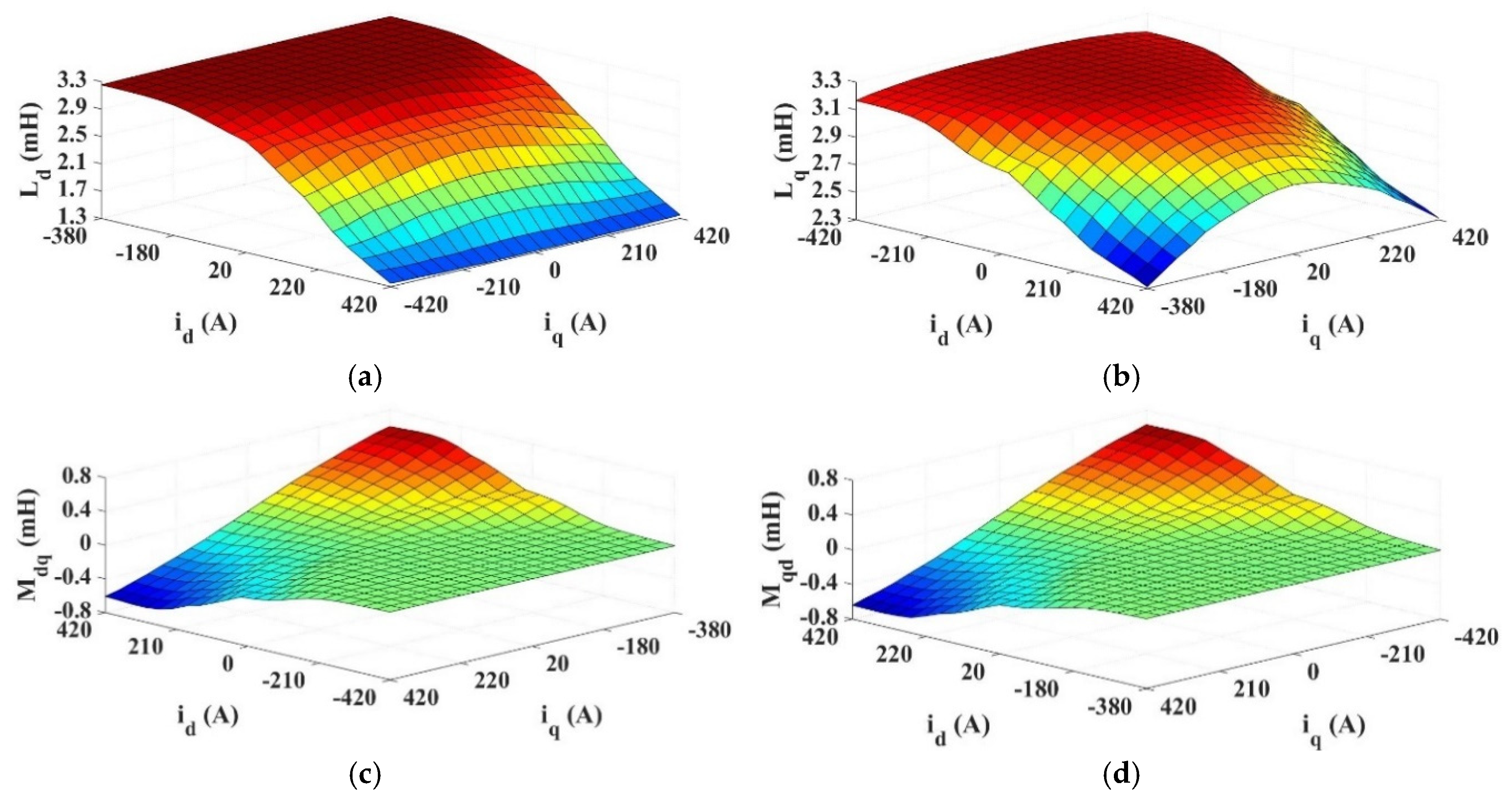
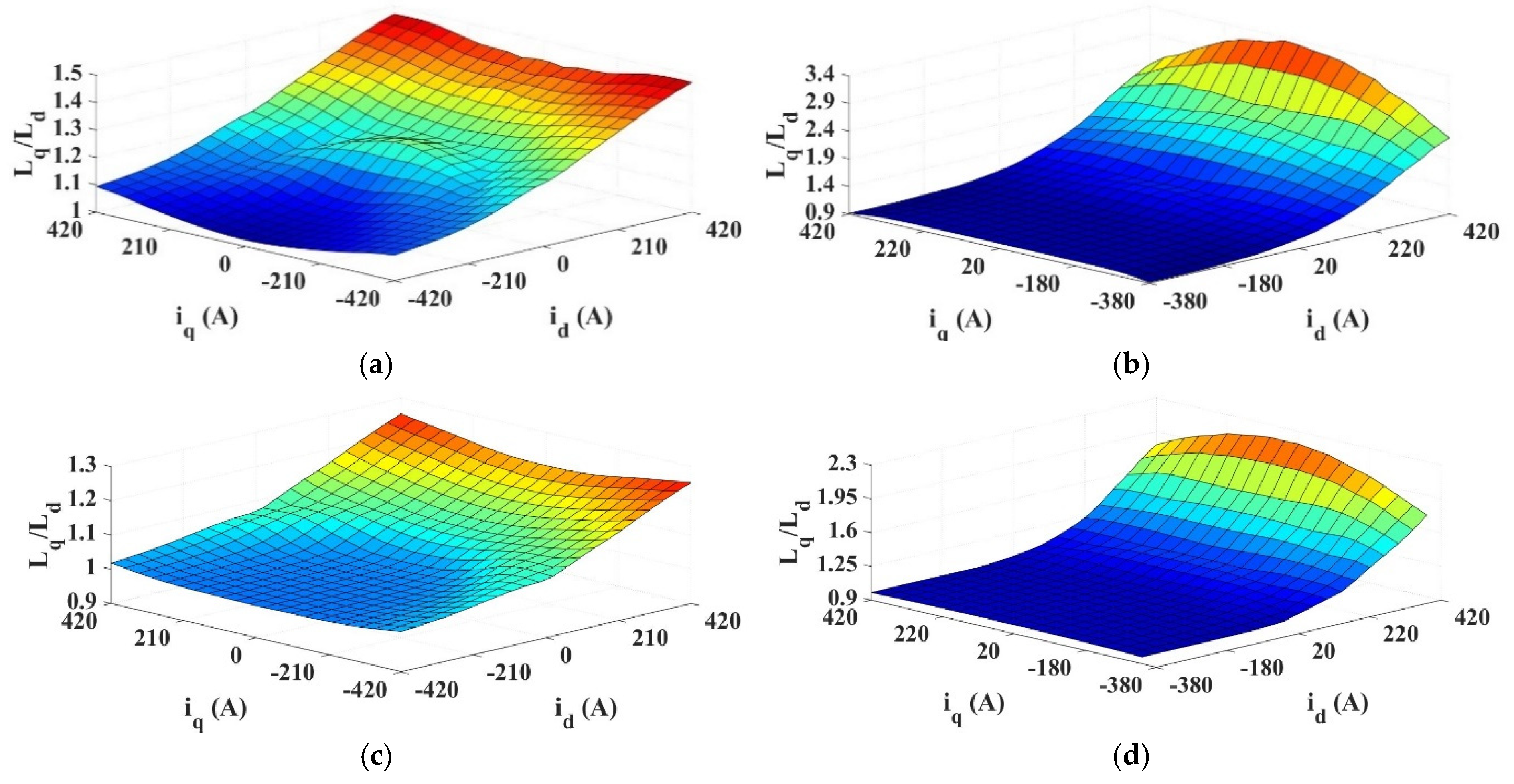
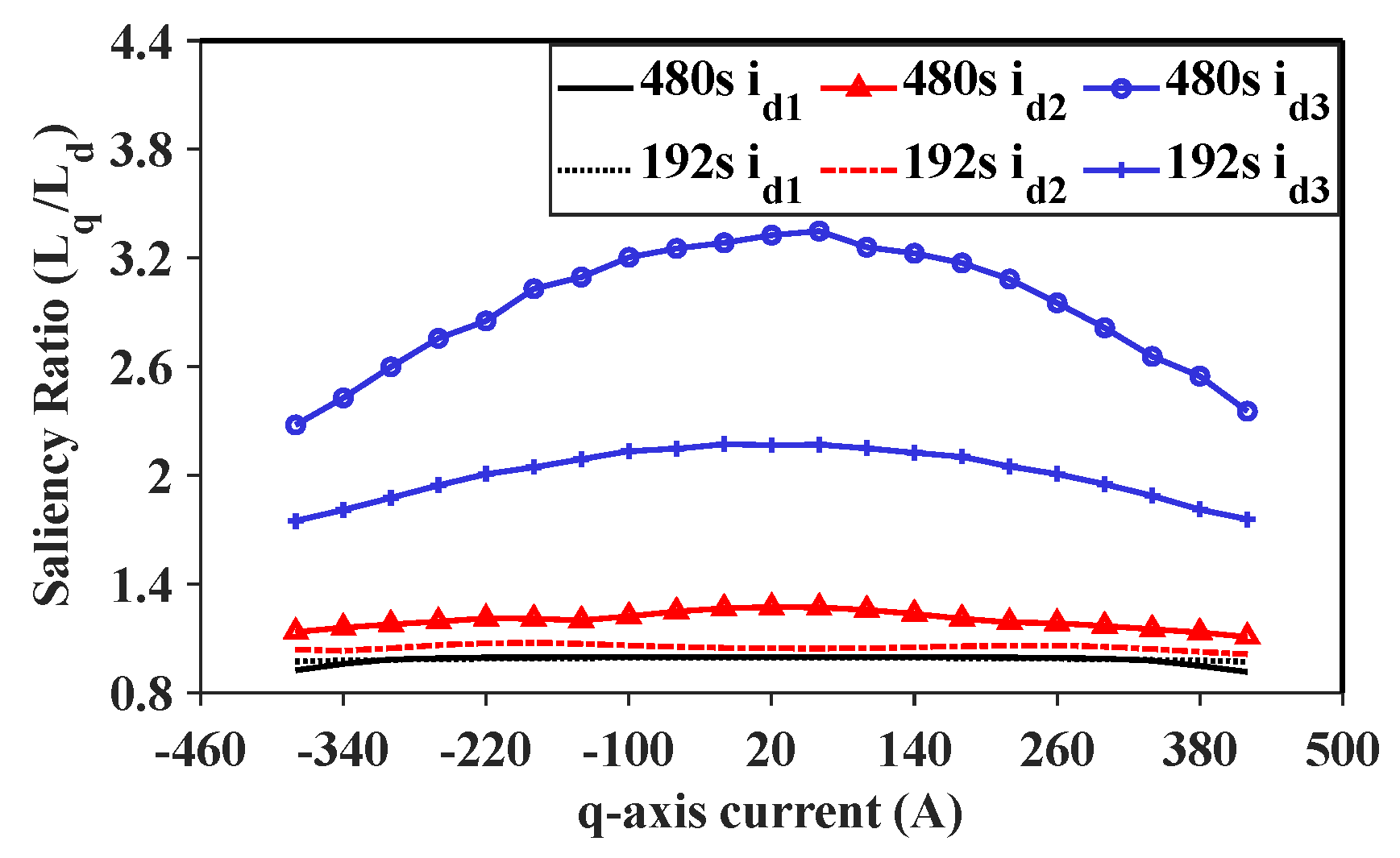
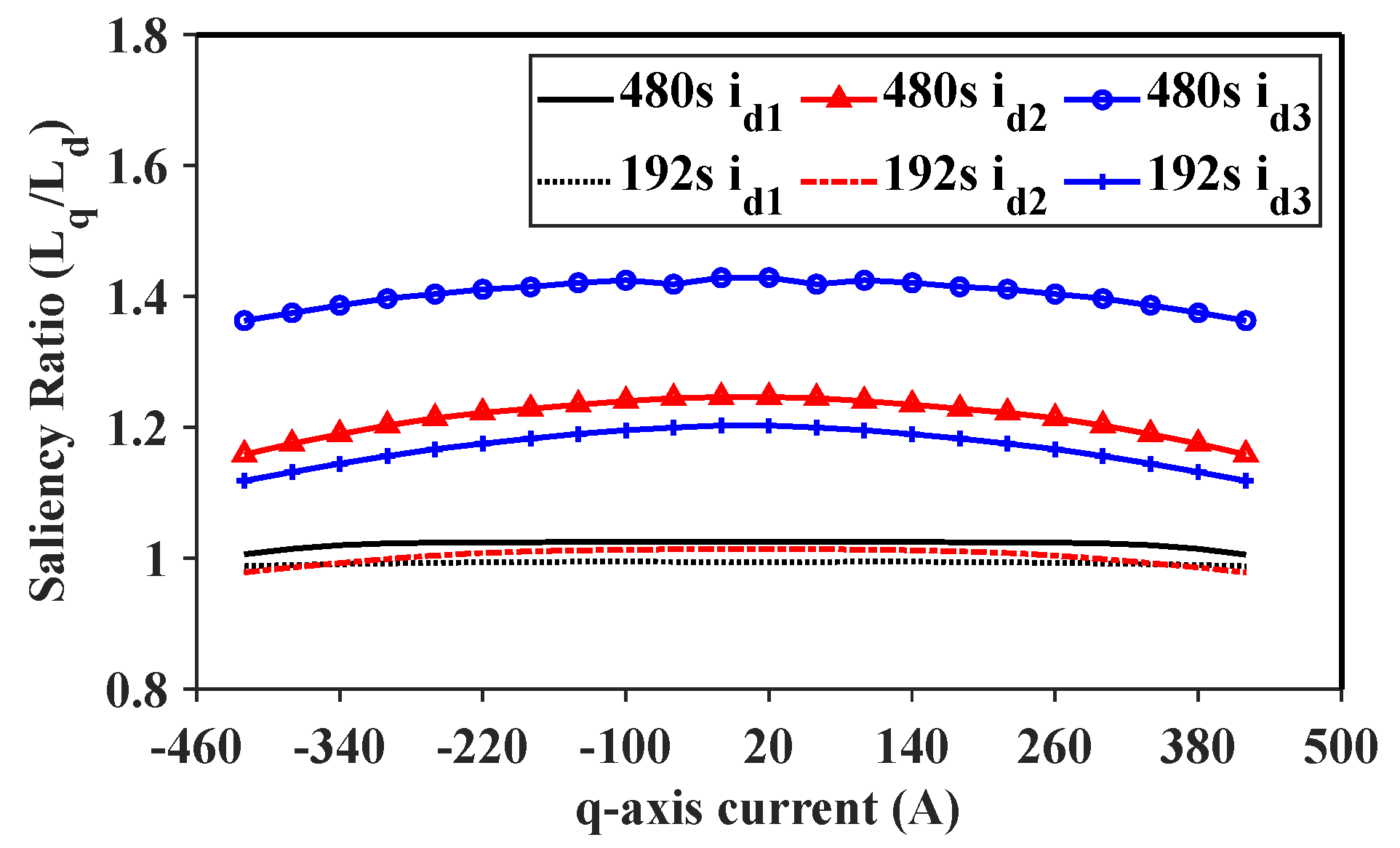




| Slot number | 480 | Winding layers | 1 |
| Pole number | 160 | Slot width to tooth width ratio (β) | 5/11 |
| Rotor inner radius (m) | 2.5 | Rated speed (RPM) | 15 |
| Air-gap length (mm) | 5 | Number of turns per coil | 12 |
| Magnet length (mm) | 15 | Number of parallel strings | 20 |
| Slot height (mm) | 80 | Rated current (Arms) | 160 |
| Yoke height (mm) | 40 | Magnet–span ratio | 0.8 |
| Stack length (m) | 1.2 | Magnet remanence (T) | 1.237 |
| Slot Number | Slots per Pole per Phase (spp) | Conductors per Slot | Coil Pitch |
|---|---|---|---|
| 144 | 0.3 | 40 | 1 |
| 192 | 0.4 | 30 | 1 |
| 240 | 0.5 | 24 | 2 |
| 384 | 0.8 | 15 | 2 |
| 480 | 1.0 | 12 | 3 |
| 576 | 1.2 | 10 | 4 |
| 720 | 1.5 | 8 | 4 |
| 864 | 1.8 | 6.66 | 5 |
| 960 | 2.0 | 6 | 6 |
| 1440 | 3.0 | 4 | 9 |
| 1920 | 4.0 | 3 | 12 |
| σ | Average Torque (MNm) | Torque Ripple (kNm) | Torque Ripple (%) | |
|---|---|---|---|---|
| No Pole Shoes | No | 1.7023 | 3.3698 | 0.0198 |
| No Pole Shoes | Yes | 1.623 | 3.987 | 0.0246 |
| 15 mm Pole Shoes | No | 1.6942 (−0.48%) | 3.0880 (−8.36%) | 0.0182 |
| 15 mm Pole Shoes | Yes | 1.535 (−5.42%) | 7.003 (+75.65%) | 0.0456 |
| Optimization Study 1 | Optimization Study 2 | |
|---|---|---|
| Objective Functions | Maximize average torque | Maximize average torque |
| Saliency ratio ≥ 1.2 | Saliency ratio ≥ 1.2 | |
| Constraints | Machine outer radius ≤ 2555 mm | Machine outer radius ≤ 2555 mm |
| Magnet area ≤ 1181.63 mm2 | Magnet area ≤ 1181.63 mm2 | |
| Model Parameters | 105 < phase angle (°) < 120 | 105 < phase angle (°) < 120 |
| 4900 < Dr (mm) < 5100 | 4900 < Dr (mm) < 5100 | |
| 10 < lm (mm) < 20 | 10 < lm (mm) < 20 | |
| 0.6 < λ < 0.9 | 0.6 < λ < 0.9 | |
| 20 < try (mm) < 60 | 20 < try (mm) < 60 | |
| 2 < tfb1 (mm) < 20 | 2 < tfb1 (mm) < 20 | |
| 2 < tfb2 (mm) < 10 | 2 < tfb2 (mm) < 10 | |
| 2 < tfb3 (mm) < 15 | 2 < tfb3 (mm) < 15 | |
| 2 < tfb4 (mm) < 15 | 2 < tfb4 (mm) < 15 | |
| 10 < θ1 (°) < 45 | 5 < tfb5 (mm) < 20 | |
| 0.05 < θ2 (°) < 0.5 | 5 < tfb6 (mm) < 20 | |
| 10 < θ1 (°) < 45 | ||
| 0.05 < θ2 (°) < 0.5 |
| Optimization Study 1 | Optimization Study 2 | |
|---|---|---|
| Objective Functions | Maximize average torque | Maximize average torque |
| Saliency ratio ≥ 1.2 | Saliency ratio ≥ 1.15 | |
| Constraints | Machine outer radius ≤ 2555 mm | Machine outer radius ≤ 2555 mm |
| Magnet area ≤ 1181.63 mm2 | Magnet area ≤ 1181.63 mm2 | |
| Model Parameters | 105 < phase angle (°) < 120 | 100 < phase angle (°) < 110 |
| 10 < magnet height (mm) < 20 | 14 < magnet height (mm) < 16 | |
| 0.6 < magnet pitch < 0.9 | 0.75 < magnet pitch < 0.85 | |
| 0 < shoe height (mm) < 20 | 8 < shoe height (mm) < 12 | |
| 0.1 < shoe pitch < 0.4 | 0.13 < shoe pitch < 0.17 | |
| 2440 < rotor inner radius (mm) < 2540 | 2490 < rotor inner radius (mm) < 2510 | |
| 20 < rotor yoke thickness (mm) < 60 | 35 < rotor yoke thickness (mm) < 45 |
| Conventional | |||
|---|---|---|---|
| Air-gap radius (mm) | 2500 | 2496.5 | 2511.7 |
| Rotor yoke thickness (mm) | 40 | 39.2 | 23.9 |
| Magnet height (mm) | 15 | 15.1 | 18.5 |
| Magnet pitch | 0.8 | 0.794 | 0.644 |
| Rotor shoe height (mm) | n/a | 10.1 | 15.9 |
| Rotor shoe pitch | n/a | 0.156 | 0.105 |
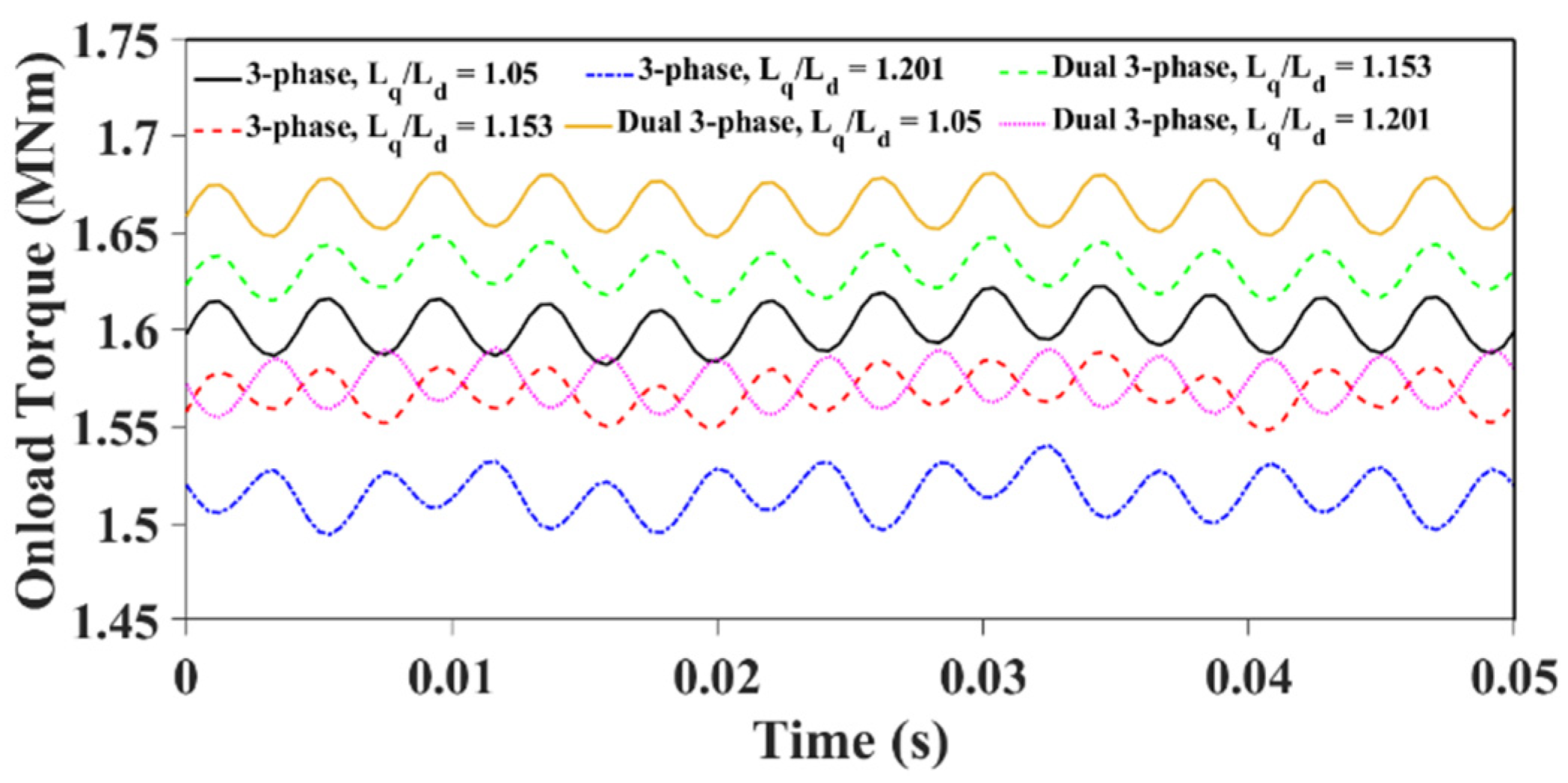
| Average Torque (MNm) | Torque Ripple (KNm) | Torque Ripple (%) | Mech Power (MW) | |
|---|---|---|---|---|
| Conventional three-phase | 1.60 | 40.4 | 2.52 | 2.51 |
| Salient (1.15) three-phase | 1.57 | 40.2 | 2.57 | 2.47 |
| Salient (1.2) three-phase | 1.52 | 45.8 | 3.02 | 2.39 |
| Conventional dual three-phase | 1.66 | 33.2 | 1.99 | 2.61 |
| Salient (1.15) dual three-phase | 1.63 | 33.8 | 2.08 | 2.56 |
| Salient (1.2) dual three-phase | 1.57 | 35.9 | 2.28 | 2.47 |
| Stator Loss (kW) | Rotor Loss (kW) | PM Loss (kW) | Efficiency (%) | Stator Power (MW) | |
|---|---|---|---|---|---|
| Conventional three-phase | 17.6 | 57.1 | 43.2 | 93.48 | 2.35 |
| Salient (1.15) three-phase | 18.1 | 92.6 | 43.6 | 91.85 | 2.26 |
| Salient (1.2) three-phase | 15.8 | 74.8 | 26.7 | 93.13 | 2.22 |
| Conventional dual three-phase | 17.8 | 43.5 | 44.3 | 94.19 | 2.46 |
| Salient (1.15) dual three-phase | 17.4 | 77.1 | 42.3 | 92.85 | 2.38 |
| Salient (1.2) dual three-phase | 16.3 | 69.7 | 27.5 | 93.53 | 2.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudden, I.; Li, G.-J.; Zhu, Z.-Q.; Duke, A.; Clark, R. An Investigation into the Saliency Ratio of Fractional-Slot Concentrated-Winding Generators for Offshore Wind Power. Energies 2025, 18, 2057. https://doi.org/10.3390/en18082057
Rudden I, Li G-J, Zhu Z-Q, Duke A, Clark R. An Investigation into the Saliency Ratio of Fractional-Slot Concentrated-Winding Generators for Offshore Wind Power. Energies. 2025; 18(8):2057. https://doi.org/10.3390/en18082057
Chicago/Turabian StyleRudden, Isaac, Guang-Jin Li, Zi-Qiang Zhu, Alexander Duke, and Richard Clark. 2025. "An Investigation into the Saliency Ratio of Fractional-Slot Concentrated-Winding Generators for Offshore Wind Power" Energies 18, no. 8: 2057. https://doi.org/10.3390/en18082057
APA StyleRudden, I., Li, G.-J., Zhu, Z.-Q., Duke, A., & Clark, R. (2025). An Investigation into the Saliency Ratio of Fractional-Slot Concentrated-Winding Generators for Offshore Wind Power. Energies, 18(8), 2057. https://doi.org/10.3390/en18082057








