Optimal and Sustainable Operation of Energy Communities Organized in Interconnected Microgrids
Abstract
:1. Introduction
- -
- The proposed algorithm ensures a reduction in the energy community’s daily operational costs by enabling efficient power sharing between the interconnected microgrids, regulating local generators’ output, and utilizing PEVs for power management, thereby minimizing the need for additional energy storage systems. This integrated approach better aligns with the needs of energy communities organized in interconnected microgrids, as it effectively deals with the complexities of distributed energy resources and diverse load profiles, ensuring efficient energy management across multiple interacting microgrids.
- -
- Achieving net-zero energy exchange between the energy community and the main grid is crucial for enhancing energy independence and improving overall system resilience. By balancing local generation and consumption, this approach optimizes resource utilization within the energy community while decreasing reliance on external power sources.
- -
- Reducing power losses in the distribution lines connecting the microgrids is crucial for improving the overall efficiency of energy distribution within interconnected systems. By minimizing these losses, more of the locally generated electricity is effectively utilized, which enhances system reliability and reduces operational costs. This optimization of power flow also contributes to a more sustainable energy network by ensuring that less energy is wasted in energy distribution, making the entire system more efficient and resilient.
- -
- Reducing greenhouse gas (GHG) emissions from local generators by setting appropriate constraints is essential for promoting environmental sustainability and aligning with global climate goals. By optimizing generator operations and limiting GHG emissions, this approach minimizes the carbon footprint of energy production while ensuring the seamless use of reliable, locally sourced power.
- -
- The proposed method is designed to be adaptable and scalable, making it applicable across different regions with varying characteristics, including areas with limited solar potential or high energy consumption. The optimization framework does not depend solely on high renewable energy generation but rather focuses on the coordinated management of all locally available resources—RESs, local generators, and PEVs—to achieve economic and environmental benefits.
- -
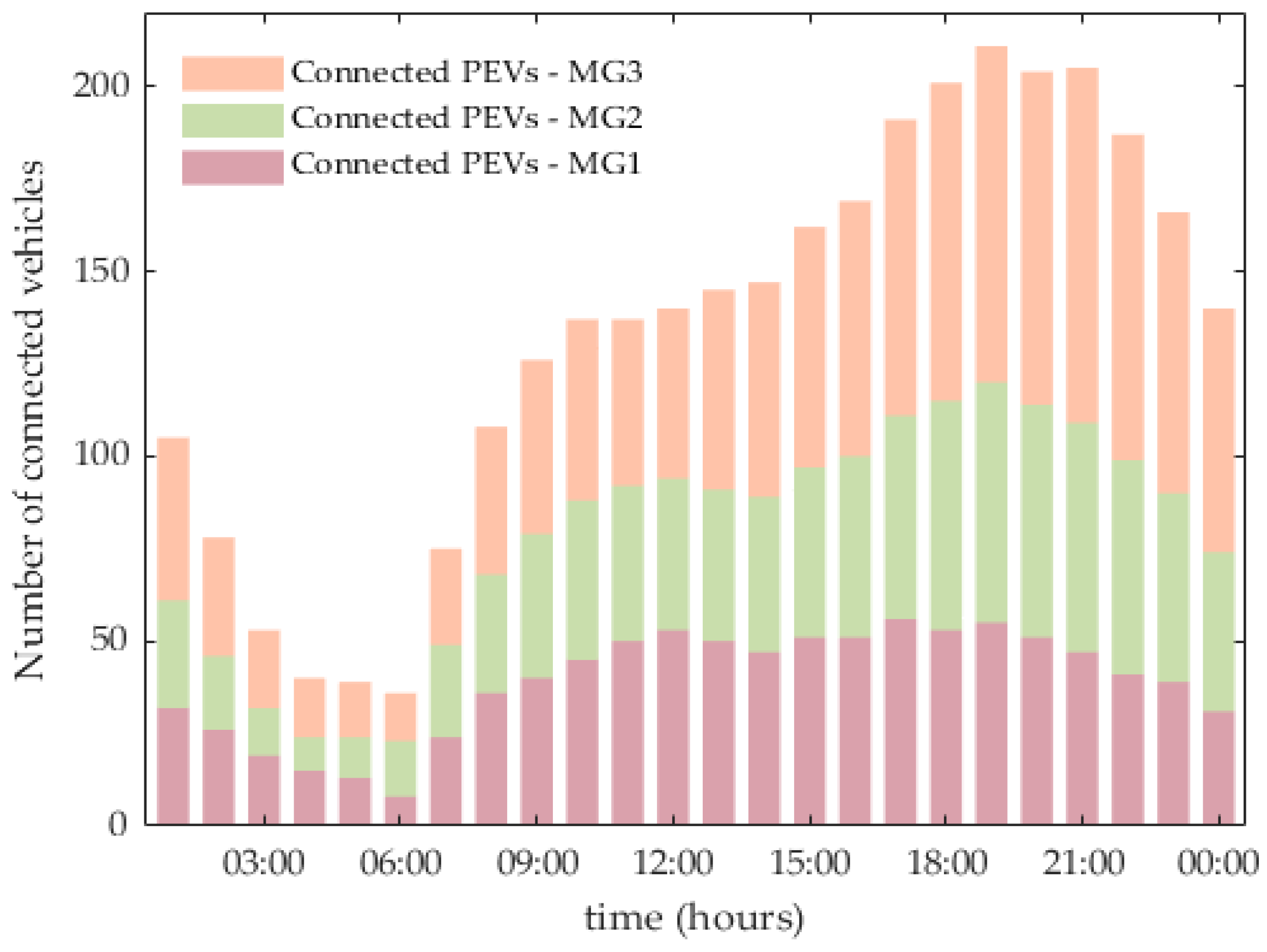
- The microgrids examined in our framework take advantage of a large number of PEVs, which provide a dynamic, dispersed, and flexible storage solution. PEVs can adjust their active power in real time, based on price signals and local demand fluctuations, enabling them to act as distributed energy storage units that respond to internal MG needs, optimizing both energy storage and overall microgrid operation. Compared to traditional storage systems, using PEVs provides economic benefits, as it minimizes additional infrastructure costs.
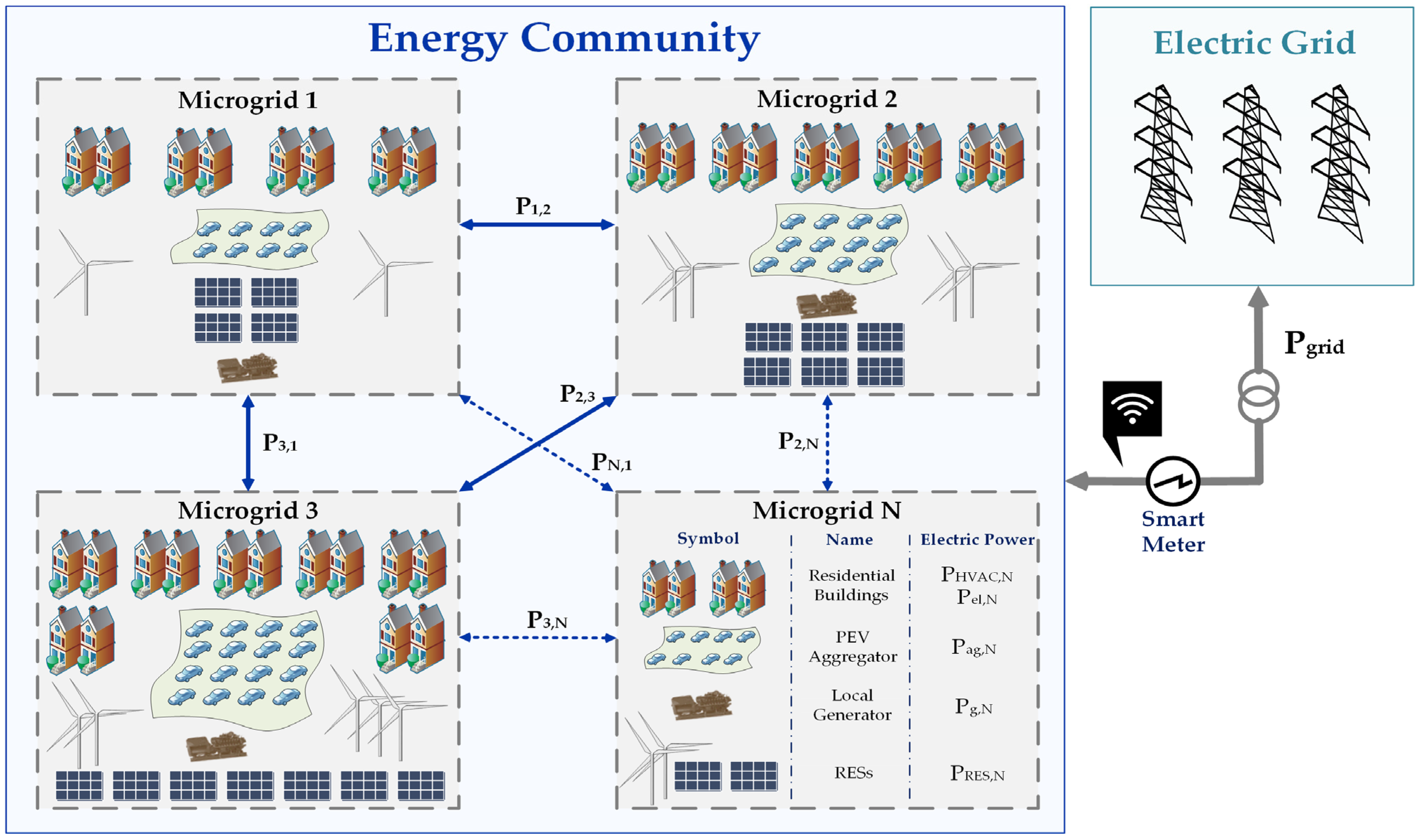
2. Proposed System Overall Description
3. Energy Community Component Modeling
3.1. Building Thermal and Electrical Load Modeling
3.2. PEV Aggregator Modeling
3.3. Auxiliary Generator Modeling
3.4. Microgrid- and Energy Community-Level Load Modeling
4. Optimization of Energy Community Operation
4.1. First Optimization Level
- –
- Minimum and maximum power of PEV aggregator constraint:
- –
- Minimum and maximum stored energy of PEV aggregator constraint:
4.2. Second Optimization Level
- –
- Energy community power balance constraint:
- –
- Minimum and maximum power exchanged with main grid constraint:
- –
- Net-zero energy constraint:
- Minimum and maximum power of generators constraint:
- GHG emissions constraint:
- Minimum and maximum transmission line power constraints:
- –
- Microgrid power balance constraint:where is the electricity price; is the power that EC exchanges with the main grid; are the minimum and maximum power that EC can exchange with the main grid; is the power that the mgth microgrid exchanges with the main grid; is the power produced by the RESs of the mgth microgrid; are the upper and lower power bounds of the gth generator; is the total emission upper limit of generators; the index denotes the number of a distribution line connecting the microgrids of the energy community; is the current of the kth distribution line; the index denotes the number of microgrids to which the mg microgrid is interconnected; is the power exchanged between microgrids mg and j; is the power flowing in the kth distribution line; is the resistance of the line; denotes if there is a connection point between the mgth microgrid and the main grid; and / are the lines’ lower/upper power bounds.
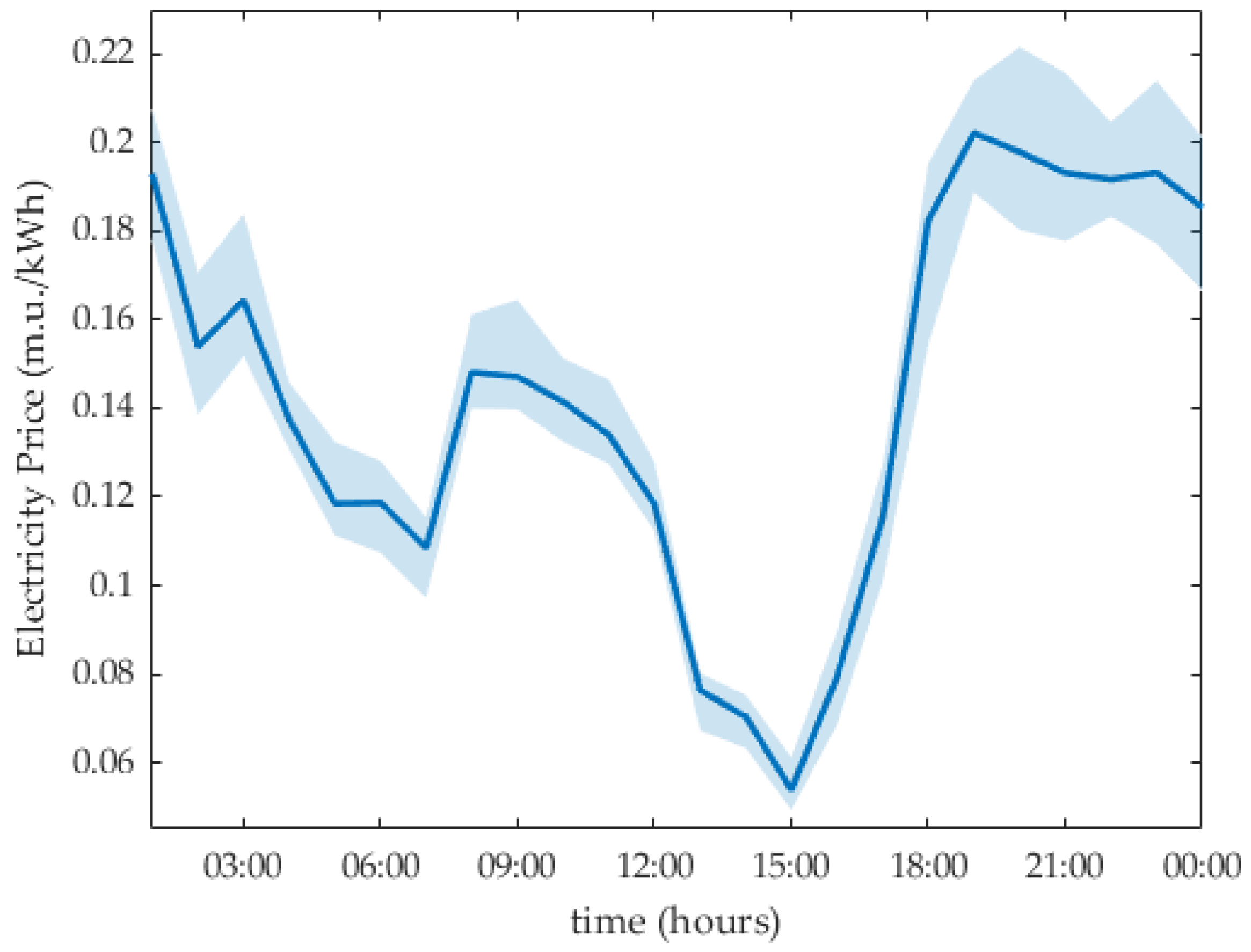
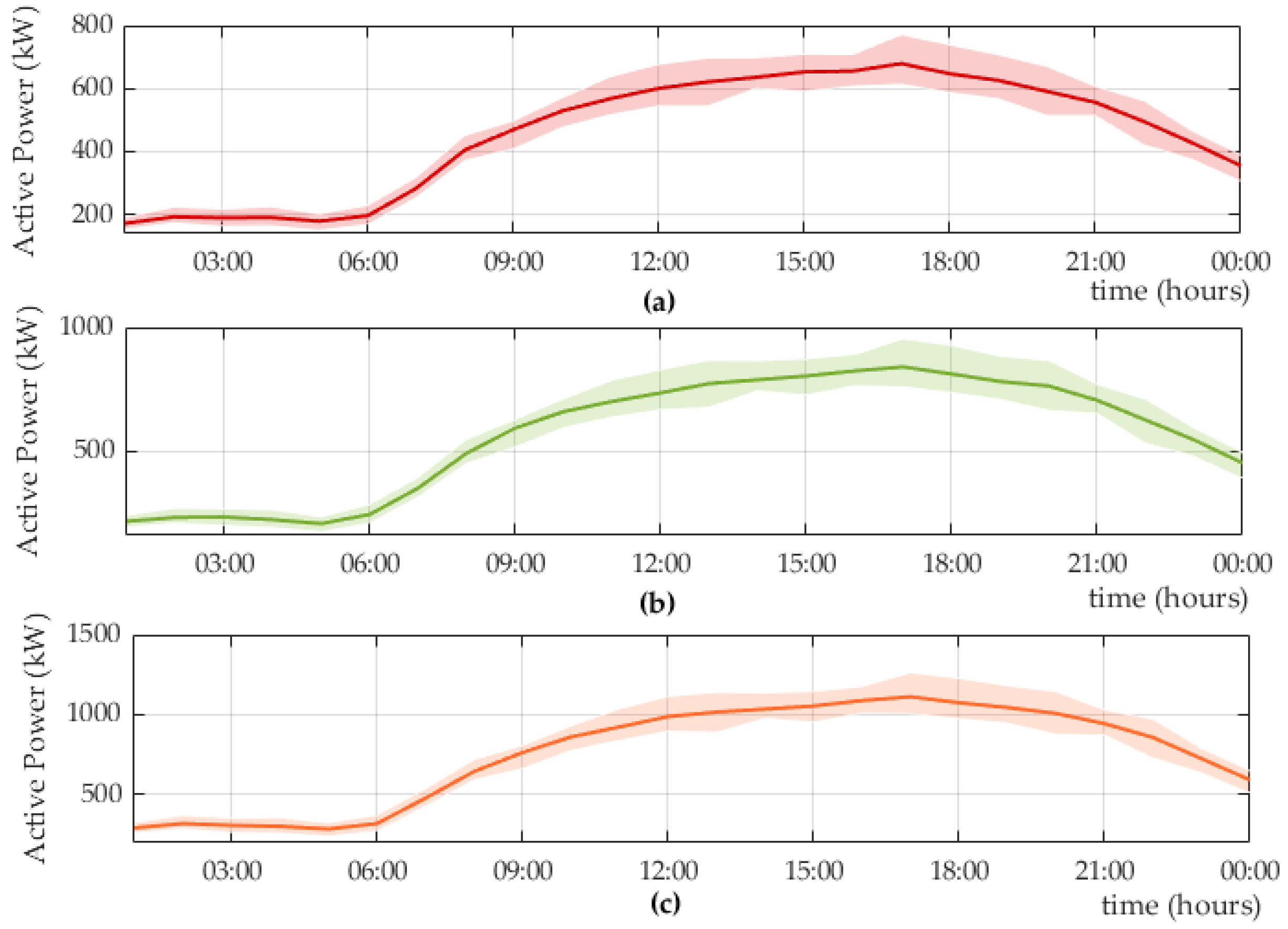
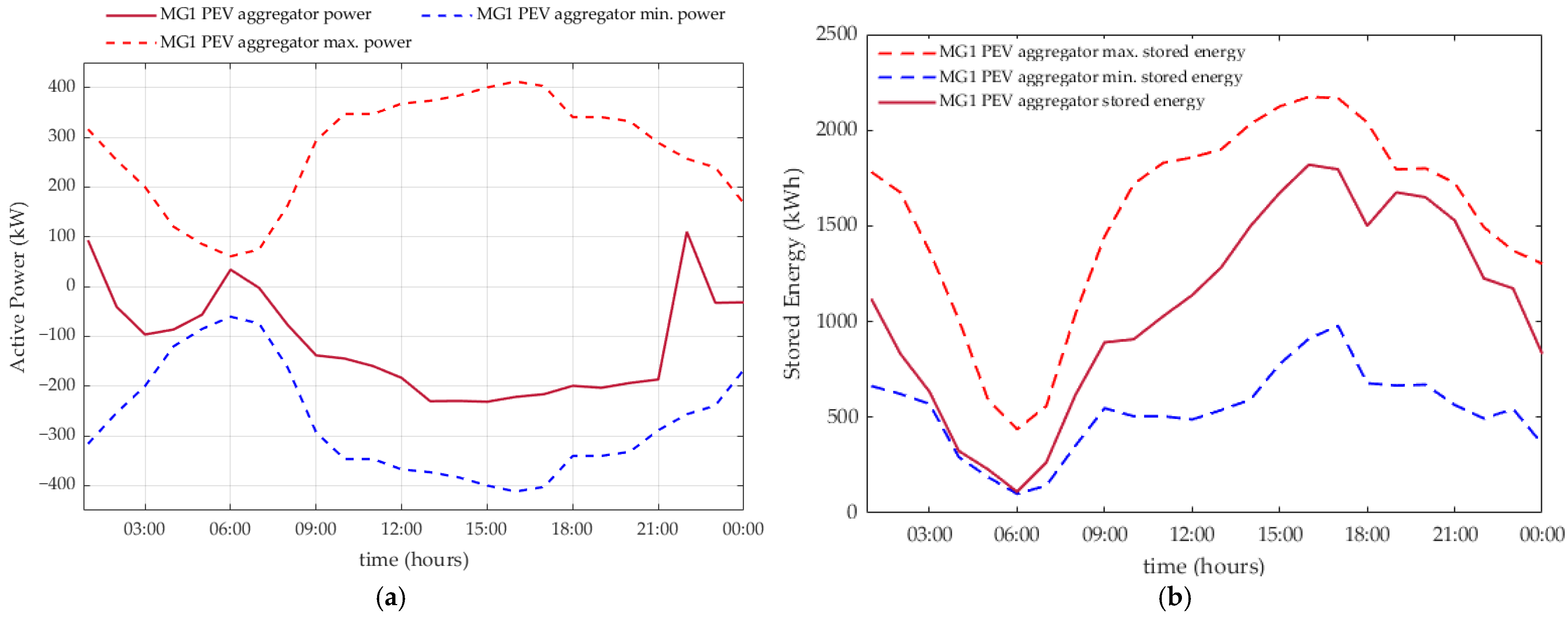
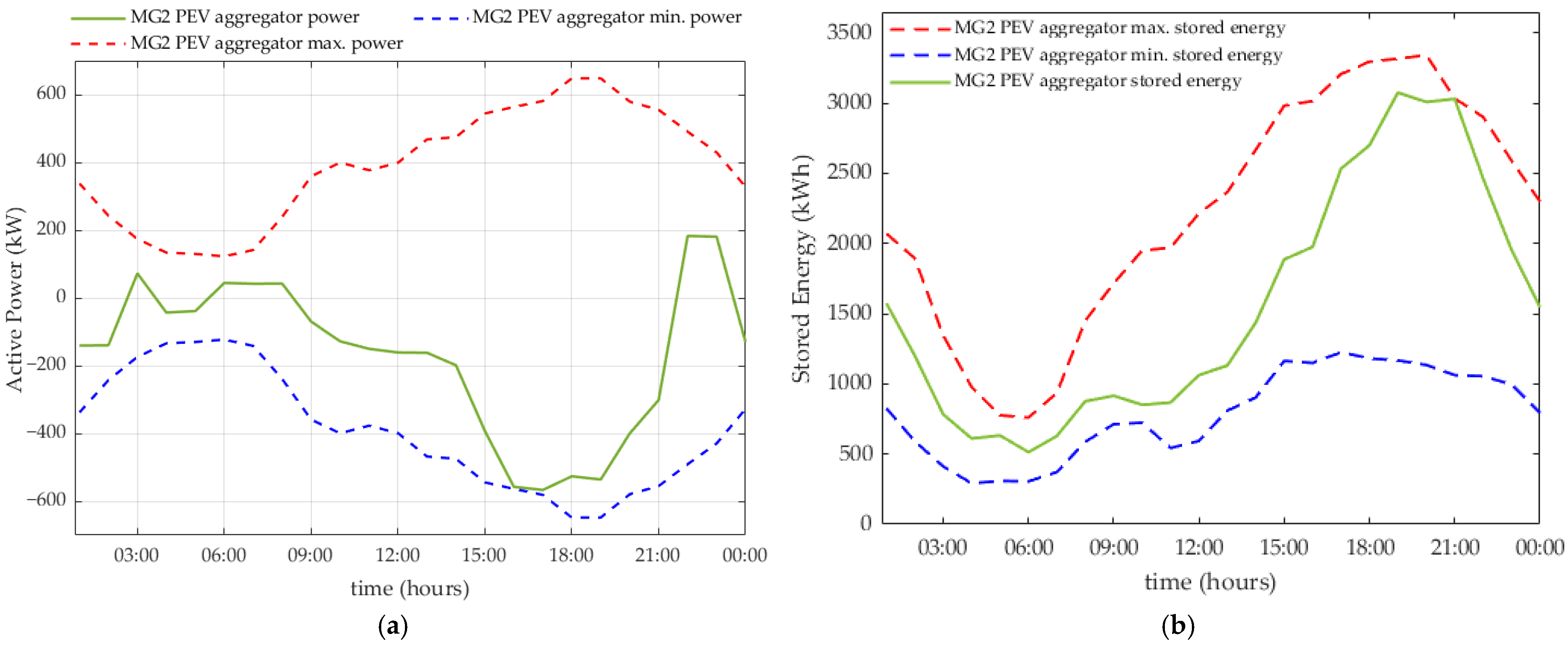
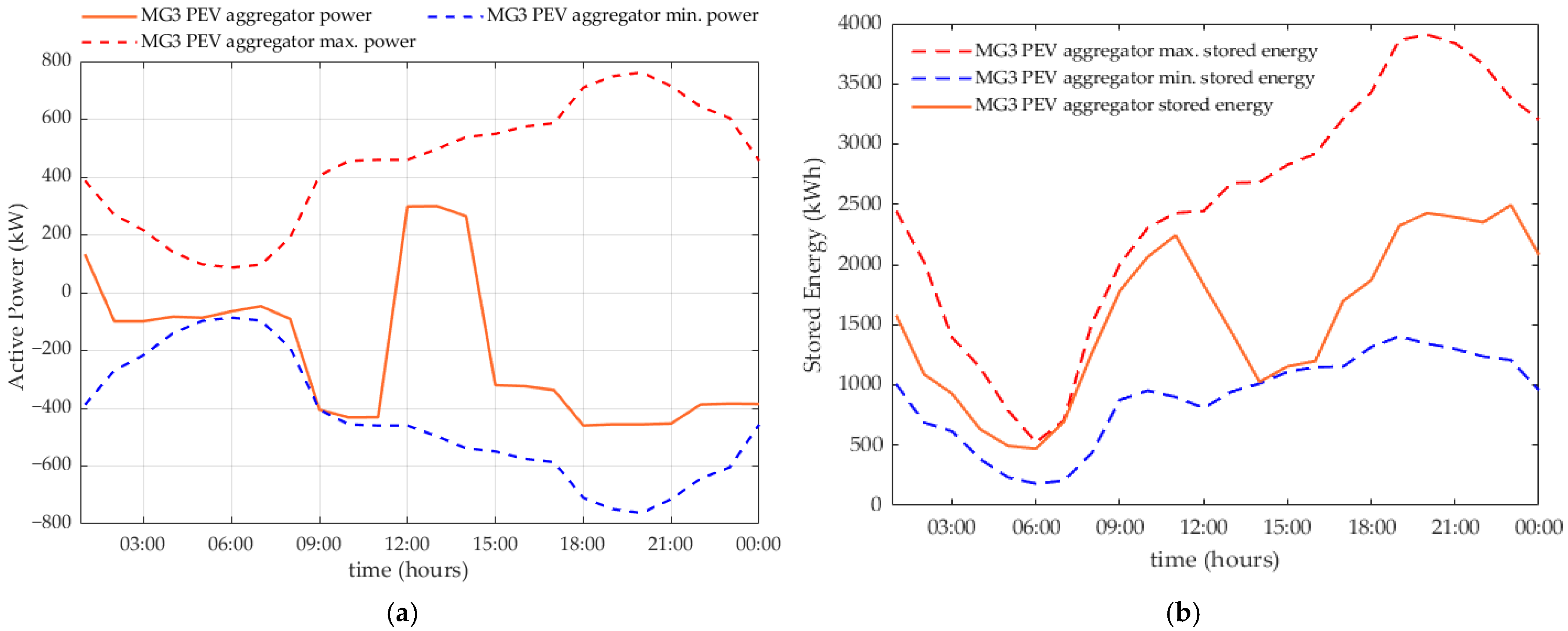
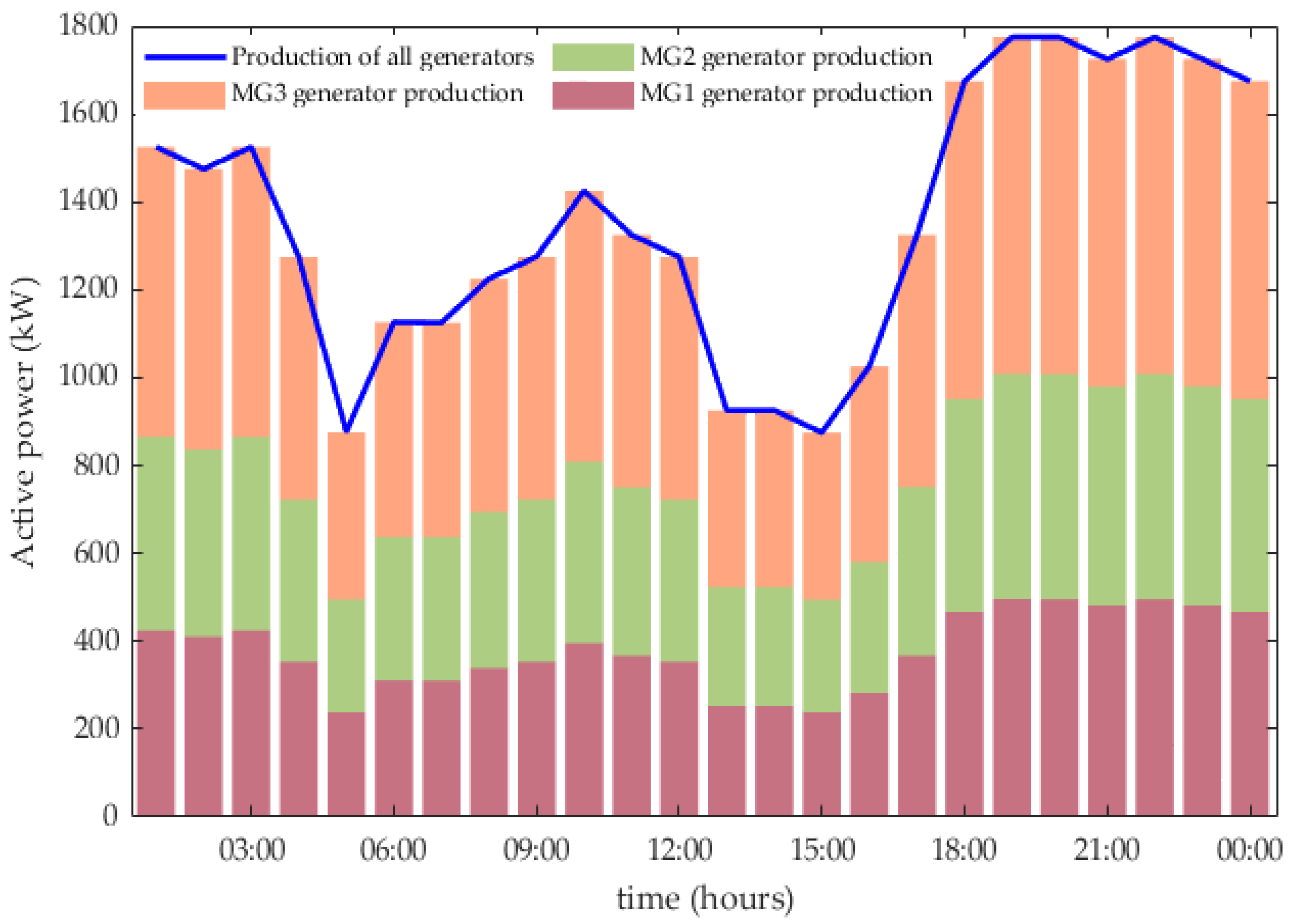
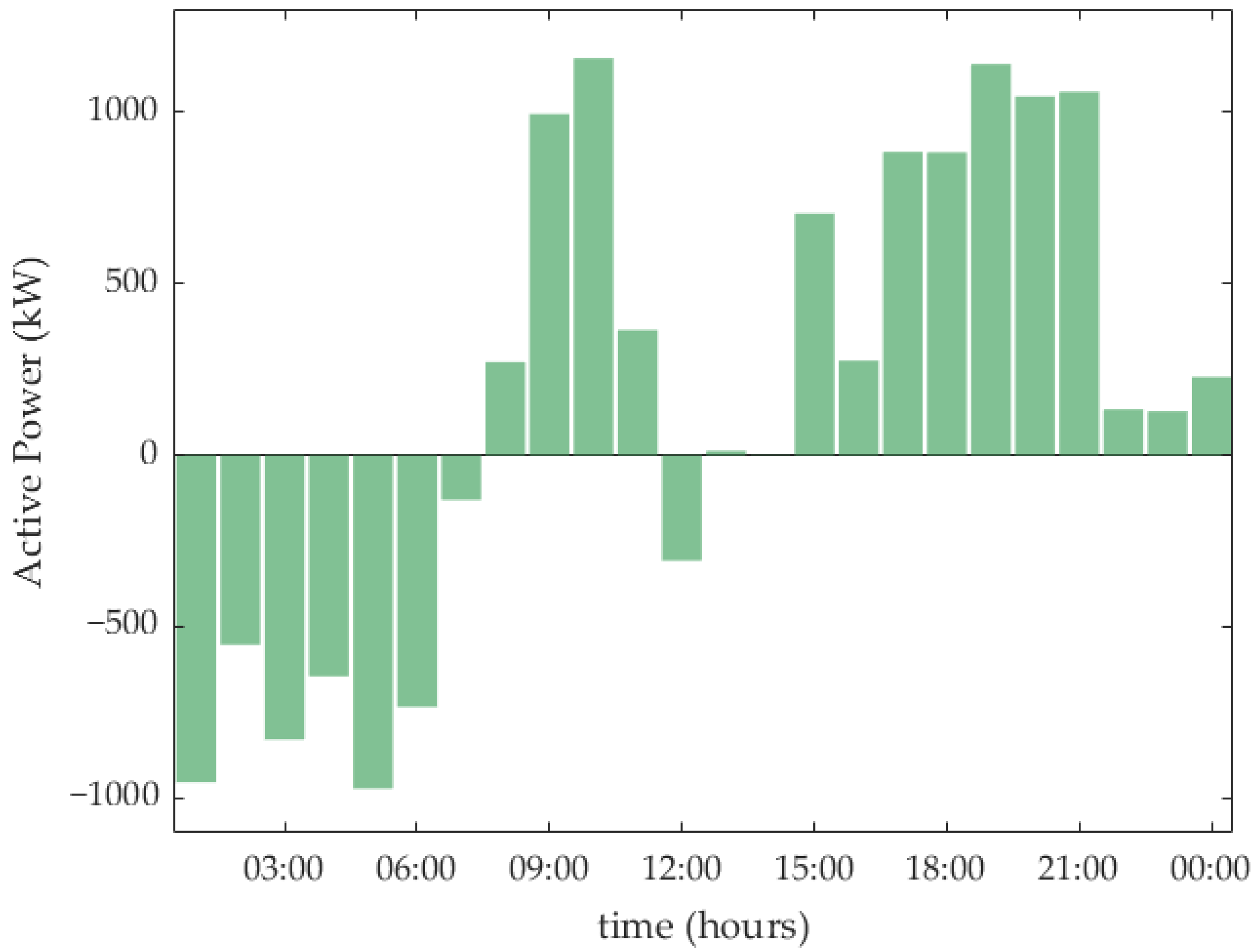
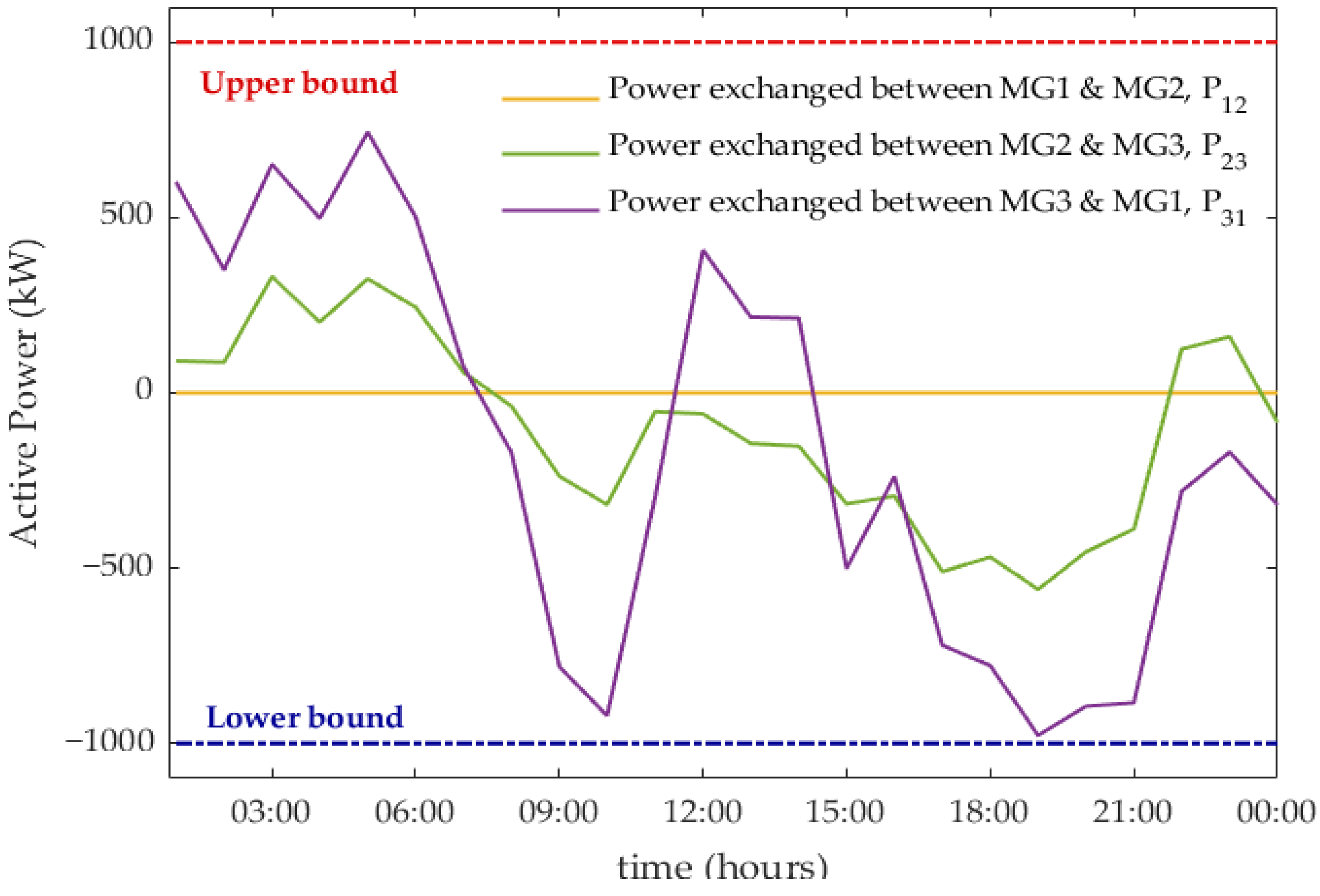
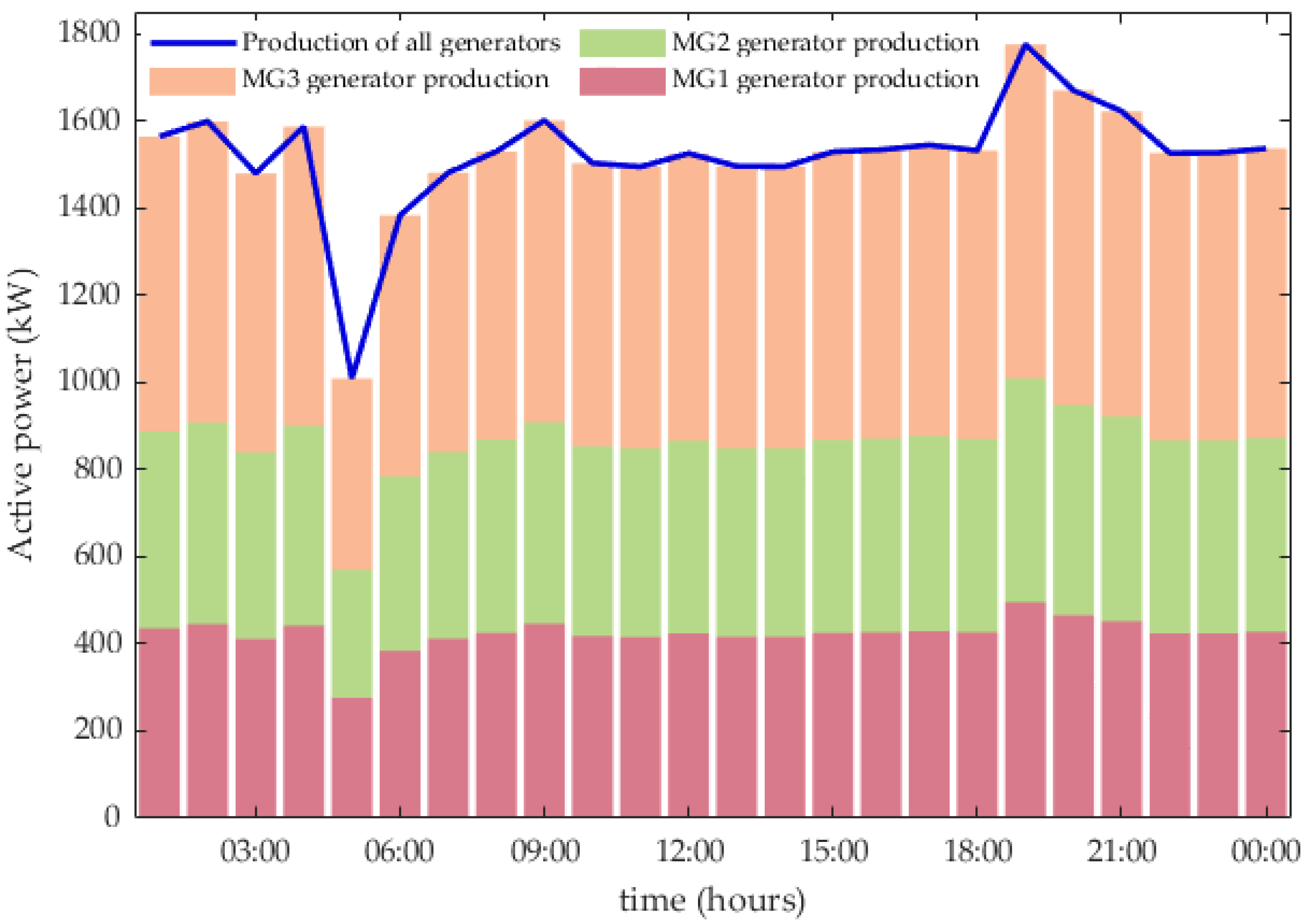
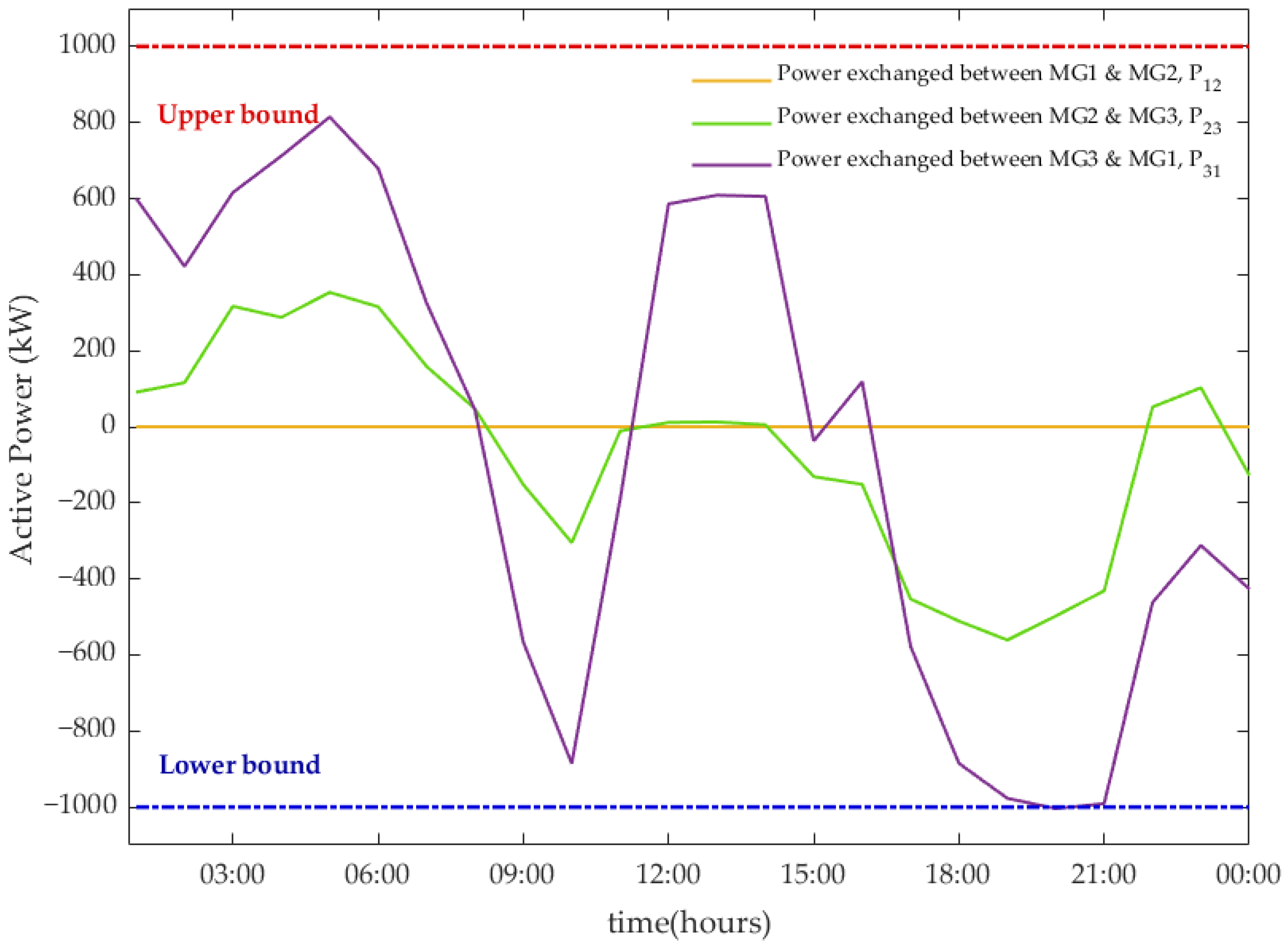
5. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dorahaki, S.; Rashidinejad, M.; Ardestani, S.F.F.; Abdollahi, A.; Salehizadeh, M.R. An integrated model for citizen energy communities and renewable energy communities based on clean energy package: A two-stage risk-based approach. Energy 2023, 277, 127727. [Google Scholar] [CrossRef]
- Cosic, A.; Stadler, M.; Mansoor, M.; Zellinger, M. Mixed-integer linear programming based optimization strategies for renewable energy communities. Energy 2021, 237, 121559. [Google Scholar] [CrossRef]
- Weckesser, T.; Dominković, D.F.; Blomgren, E.M.V.; Schledorn, A.; Madsen, H. Renewable Energy Communities: Optimal sizing and distribution grid impact of photovoltaics and battery storage. Appl. Energy 2021, 301, 117408. [Google Scholar] [CrossRef]
- Gomes, L.; Vale, Z. Costless renewable energy distribution model based on cooperative game theory for energy communities considering its members’ active contributions. Sustain. Cities Soc. 2024, 101, 105060. [Google Scholar] [CrossRef]
- Sudhoff, R.; Schreck, S.; Thiem, S.; Niessen, S. Operating Renewable Energy Communities to Reduce Power Peaks in the Distribution Grid: An Analysis on Grid-Friendliness, Different Shares of Participants, and Economic Benefits. Energies 2022, 15, 5468. [Google Scholar] [CrossRef]
- Gjorgievski, V.Z.; Cundeva, S.; Georghiou, G.E. Social arrangements, technical designs and impacts of energy communities: A review. Renew. Energy 2021, 169, 1138–1156. [Google Scholar] [CrossRef]
- Maślak, G.; Orłowski, P. Microgrid Operation Optimization Using Hybrid System Modeling and Switched Model Predictive Control. Energies 2022, 15, 833. [Google Scholar] [CrossRef]
- Nazemi, S.D.; Mahani, K.; Ghofrani, A.; Amini, M.; Kose, B.E.; Jafari, M.A. Techno-Economic Analysis and Optimization of a Microgrid Considering Demand-Side Management. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, Q.; Xue, M.; Geng, G. Energy Management of Microgrid in Grid-Connected and Stand-Alone Modes. In Proceedings of the IEEE Transactions on Power Systems, New York, NY, USA, 7 March 2013; IEEE: New York, NY, USA, 2013; Volume 28, pp. 3380–3389. [Google Scholar] [CrossRef]
- Hussain, A.; Kim, H.-M. A Rule-Based Modular Energy Management System for AC/DC Hybrid Microgrids. Sustainability 2025, 17, 867. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Kim, J.; Begovic, M.M. Robust Optimization Based Optimal DG Placement in Microgrids. In Proceedings of the IEEE Transactions on Smart Grid, New York, NY, USA, 8 September 2014; IEEE: New York, NY, USA, 2014; Volume 5, pp. 2173–2182. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, J. The Energy Management and Optimized Operation of Electric Vehicles Based on Microgrid. In Proceedings of the IEEE Transactions on Power Delivery, New York, NY, USA, 13 May 2014; IEEE: New York, NY, USA, 2014; Volume 29, pp. 1427–1435. [Google Scholar] [CrossRef]
- Kampezidou, S.; Vasios, O.; Meliopoulos, S. Multi-Microgrid Architecture: Optimal Operation and Control. In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Acosta, M.N.; Gonzalez-Longatt, F.; Topić, D.; Andrade, M.A. Optimal Microgrid–Interactive Reactive Power Management for Day–Ahead Operation. Energies 2021, 14, 1275. [Google Scholar] [CrossRef]
- Shuai, Z.; Sun, Y.; Shen, Z.J.; Tian, W.; Tu, C.; Li, Y.; Yin, X. Microgrid stability: Classification and a review. Renew. Sustain. Energy Rev. 2016, 58, 167–179. [Google Scholar] [CrossRef]
- Zhang, L.; Ruan, Z.; Li, S.; Wu, S. Cooperative operation optimization for rural multi-microgrid and county-integrated energy operators considering typical energy scenarios. J. Renew. Sustain. Energy 2024, 16, 044703. [Google Scholar] [CrossRef]
- Ye, T.; Huang, Y.; Yang, W.; Cai, G.; Yang, Y.; Pan, F. Safe multi-agent deep reinforcement learning for decentralized low-carbon operation in active distribution networks and multi-microgrids. Appl. Energy 2025, 387, 125609. [Google Scholar] [CrossRef]
- Moungos, K.A.; Kyriakou, D.G.; Kanellos, F.D. Towards the integration of interconnected microgrids to deregulated electricity markets. Electr. Power Syst. Res. 2025, 239, 111264. [Google Scholar] [CrossRef]
- Merabet, A.; Al-Durra, A.; El-Fouly, T.; El-Saadany, E.F. Optimization and energy management for cluster of interconnected microgrids with intermittent non-polluting and diesel generators in off-grid communities. Electr. Power Syst. Res. 2025, 241, 111319. [Google Scholar] [CrossRef]
- Han, D.; Lee, J.H. Two-stage stochastic programming formulation for optimal design and operation of multi-microgrid system using data-based modeling of renewable energy sources. Appl. Energy 2021, 291, 116830. [Google Scholar] [CrossRef]
- Kyriakou, D.G.; Kanellos, F.D.; Tsekouras, G.J.; Moungos, K.A. Effective and Local Constraint-Aware Load Shifting for Microgrid-Based Energy Communities. Energies 2025, 18, 343. [Google Scholar] [CrossRef]
- Barone, G.; Brusco, G.; Menniti, D.; Pinnarelli, A.; Sorrentino, N.; Vizza, P.; Burgio, A.; ABayod-Rújula, Á. A Renewable Energy Community of DC Nanogrids for Providing Balancing Services. Energies 2021, 14, 7261. [Google Scholar] [CrossRef]
- Wu, P.; Huang, W.; Tai, N.; Liang, S. A novel design of architecture and control for multiple microgrids with hybrid AC/DC connection. Appl. Energy 2018, 210, 1002–1016. [Google Scholar] [CrossRef]
- Hou, H.; Wang, Z.; Chen, Y.; Wang, Q.; Zhao, B.; Zhang, Q.; Xie, C. Multi-stage hybrid energy management strategy for reducing energy abandonment and load losses among multiple microgrids. Int. J. Electr. Power Energy Syst. 2023, 148, 108773. [Google Scholar] [CrossRef]
- Zou, H.; Mao, S.; Wang, Y.; Zhang, F.; Chen, X.; Cheng, L. A Survey of Energy Management in Interconnected Multi-Microgrids. IEEE Access 2019, 7, 72158–72169. [Google Scholar] [CrossRef]
- Santos, A.; McGuckin, N.; Nakamoto, H.Y.; Gray, D.; Liss, S. Summary of Travel Trends: 2009 National Household Travel Survey; US Department of Transportation; Federal Highway Admin: Washington, DC, USA, 2011. Available online: http://nhts.ornl.gov/2009/pub/stt.pdf (accessed on 1 April 2025).
- Kyriakou, D.G.; Kanellos, F.D. Energy and power management system for microgrids of large—Scale building prosumers. IET Energy Syst. Integr. 2023, 5, 228–244. [Google Scholar] [CrossRef]
- Kyriakou, D.G.; Kanellos, F.D. Optimal Operation of Microgrids Comprising Large Building Prosumers and Plug-In Electric Vehicles Integrated into Active Distribution Networks. Energies 2022, 15, 6182. [Google Scholar] [CrossRef]
- Kanellos, F.D. Optimal power management with GHG emissions limitation in all-electric ship power systems comprising energy storage systems. IEEE Trans. Power Syst. 2014, 29, 330–339. [Google Scholar] [CrossRef]








| PEV Type | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Battery capacity (kWh) | 77 | 45 | 26.8 | 66.5 |
| (kWh) | 69.3/7.7 | 40/4.5 | 24.12/2.7 | 60/6.65 |
| (kW) | 11/−11 | 7.2/−7.2 | 6.6/−6.6 | 11/−11 |
| GEN1 | GEN2 | GEN3 | |
|---|---|---|---|
| Technical minimum (kW) | 125 | 150 | 200 |
| Technical maximum (kW) | 500 | 600 | 800 |
| Consumed fuel cost (m.u./h) |
| Transmission line capacity limits (kW), | −1000/1000 |
| Power limits exchanged with the main grid (kW), | −1000/3000 |
| Operation Scenario | SC1 | SC2 | SC3 |
|---|---|---|---|
| Optimization of EC operation | ✓ | ✓ | ✓ |
| Net-zero energy exchange | - | ✓ | ✓ |
| GHG emissions limitation | - | - | ✓ |
| Daily operational costs (m.u.) | 3952 | 4052 | 4155 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koumaniotis, E.K.; Kyriakou, D.G.; Kanellos, F.D. Optimal and Sustainable Operation of Energy Communities Organized in Interconnected Microgrids. Energies 2025, 18, 2087. https://doi.org/10.3390/en18082087
Koumaniotis EK, Kyriakou DG, Kanellos FD. Optimal and Sustainable Operation of Energy Communities Organized in Interconnected Microgrids. Energies. 2025; 18(8):2087. https://doi.org/10.3390/en18082087
Chicago/Turabian StyleKoumaniotis, Epameinondas K., Dimitra G. Kyriakou, and Fotios D. Kanellos. 2025. "Optimal and Sustainable Operation of Energy Communities Organized in Interconnected Microgrids" Energies 18, no. 8: 2087. https://doi.org/10.3390/en18082087
APA StyleKoumaniotis, E. K., Kyriakou, D. G., & Kanellos, F. D. (2025). Optimal and Sustainable Operation of Energy Communities Organized in Interconnected Microgrids. Energies, 18(8), 2087. https://doi.org/10.3390/en18082087






