Spatio-Temporal Adaptive Voltage Coordination Control Strategy for Distribution Networks with High Photovoltaic Penetration
Abstract
1. Introduction
- A dynamic zonal control strategy based on the voltage quality risk prognostication coefficient (VQRPC) for functional zones is proposed. The voltage control strategy is utilized flexibly in order to ensure good voltage quality while alleviating the heavy data sampling workload brought by real-time control to the DN.
- A functional area-based DESS available capacity management mechanism is proposed to improve the homogenization of the SOC while coordinating the DESS output in functional areas.
- A novel vine model threshold band (VMTB) strategy is proposed to improve the frequent voltage fluctuations caused by the strong stochasticity of PV output.
- A deviation optimization management (DOM) strategy based on SOC management is proposed to increase the available capacity of the DESS while avoiding deep charging/deep discharging of the DESS.
2. Mathematical Formulation
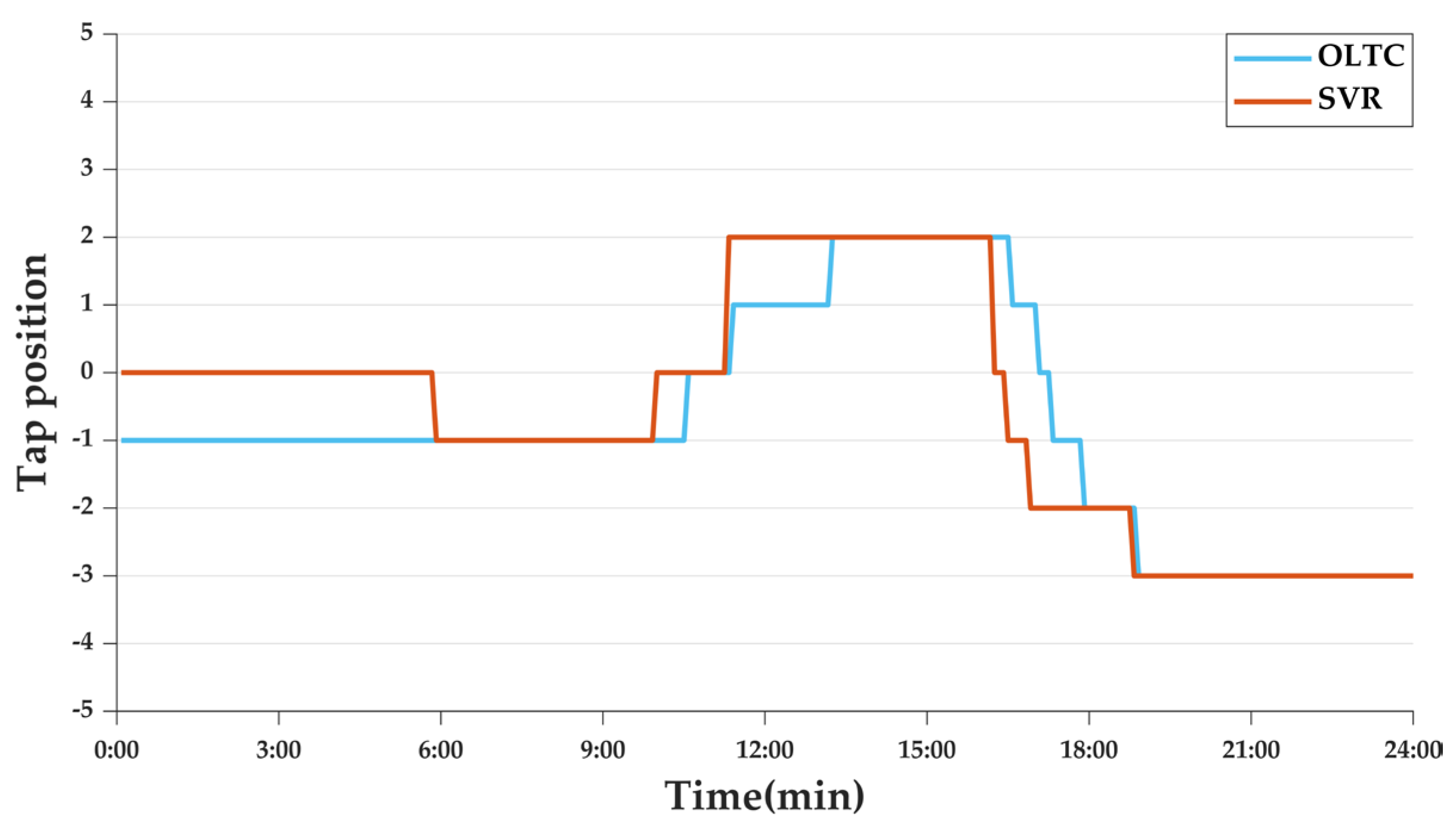
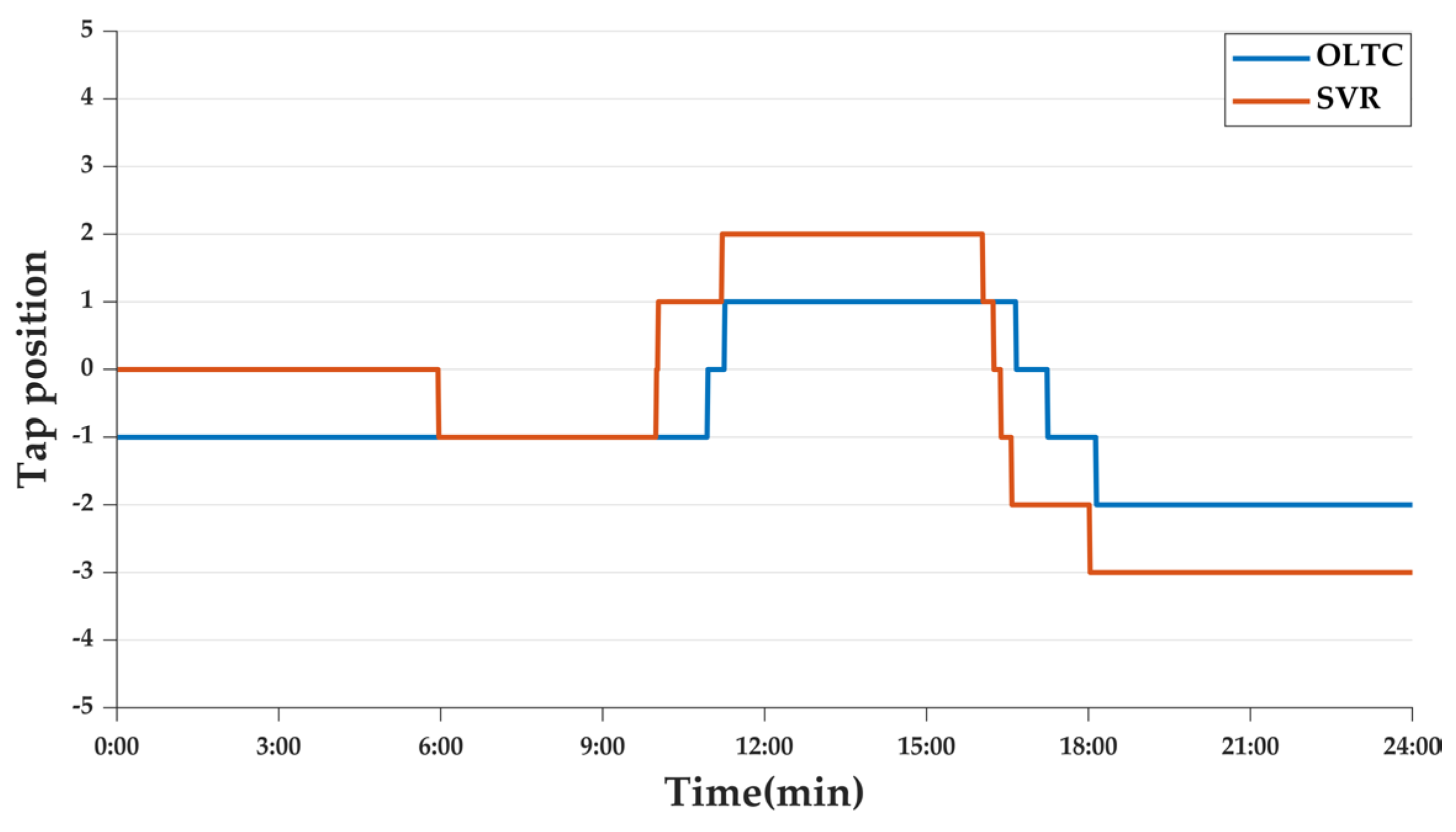
2.1. OLTC
2.2. SVR
2.3. DESS
2.4. EVs
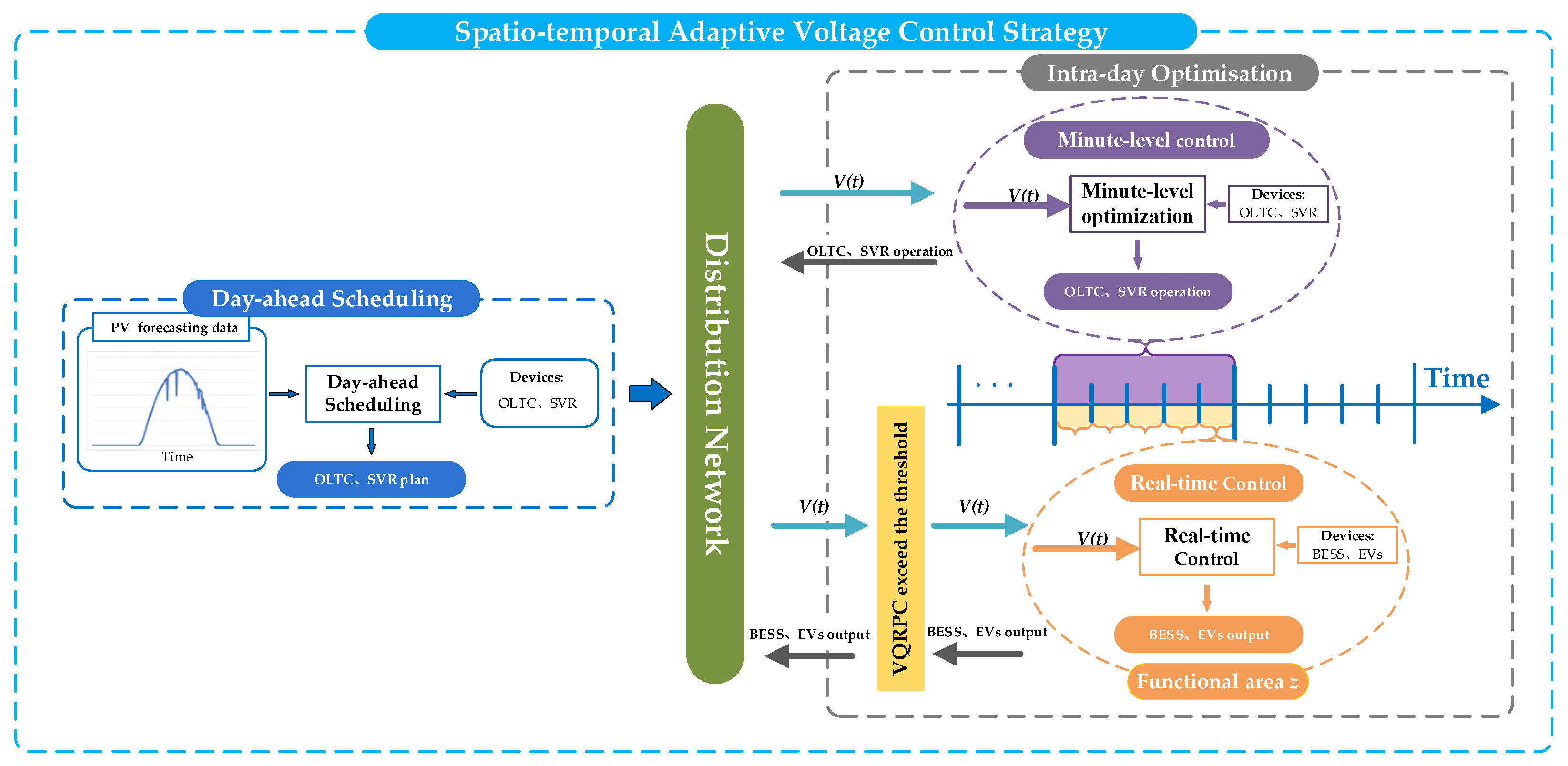
3. Spatio-Temporal Adaptive Voltage Coordination Control Strategy for Distribution Networks with High Photovoltaic Penetration
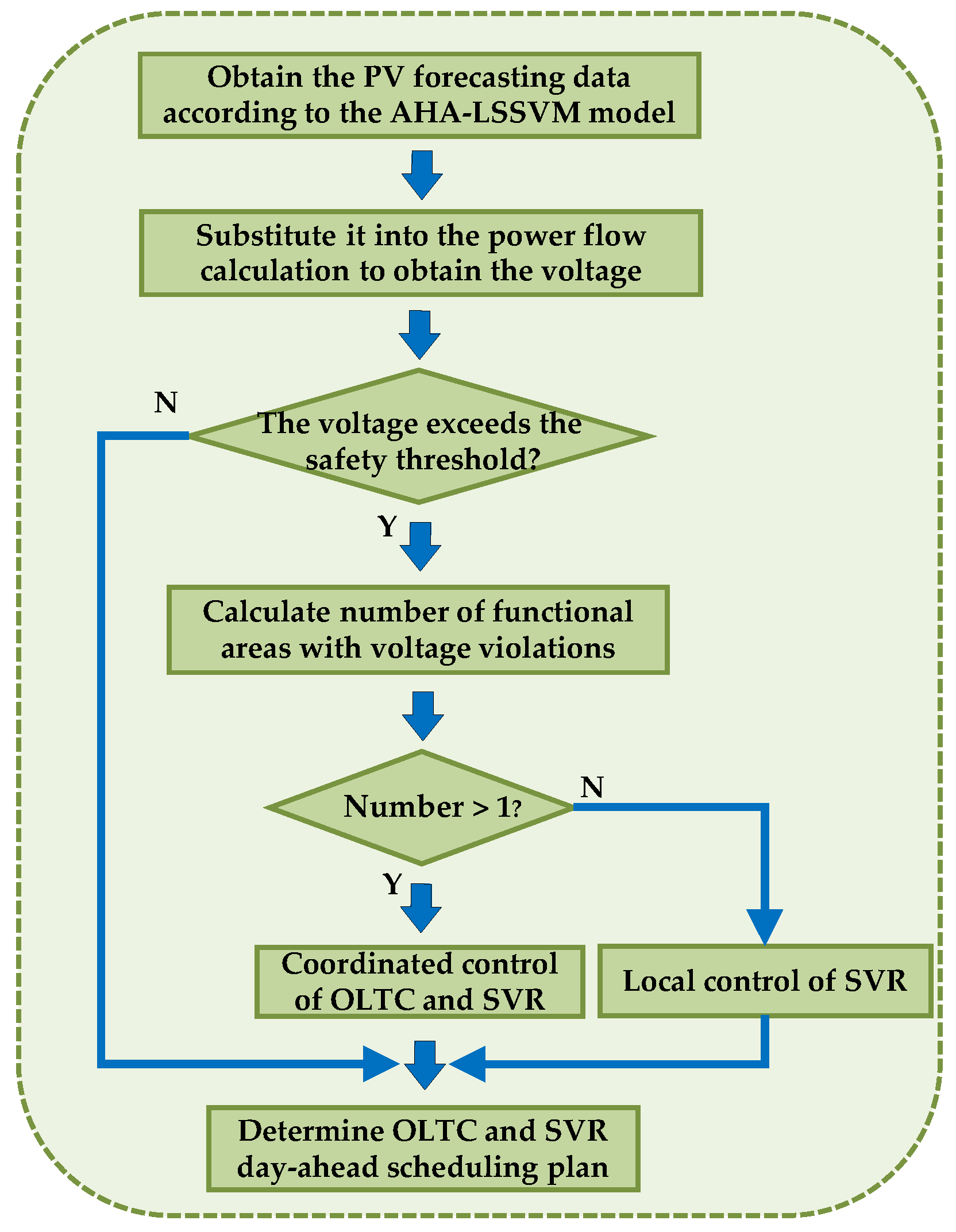
3.1. Day-Ahead Scheduling
3.2. Intra-Day Optimization
3.2.1. VQRPC
- VARPC
- 2.
- VFRPC
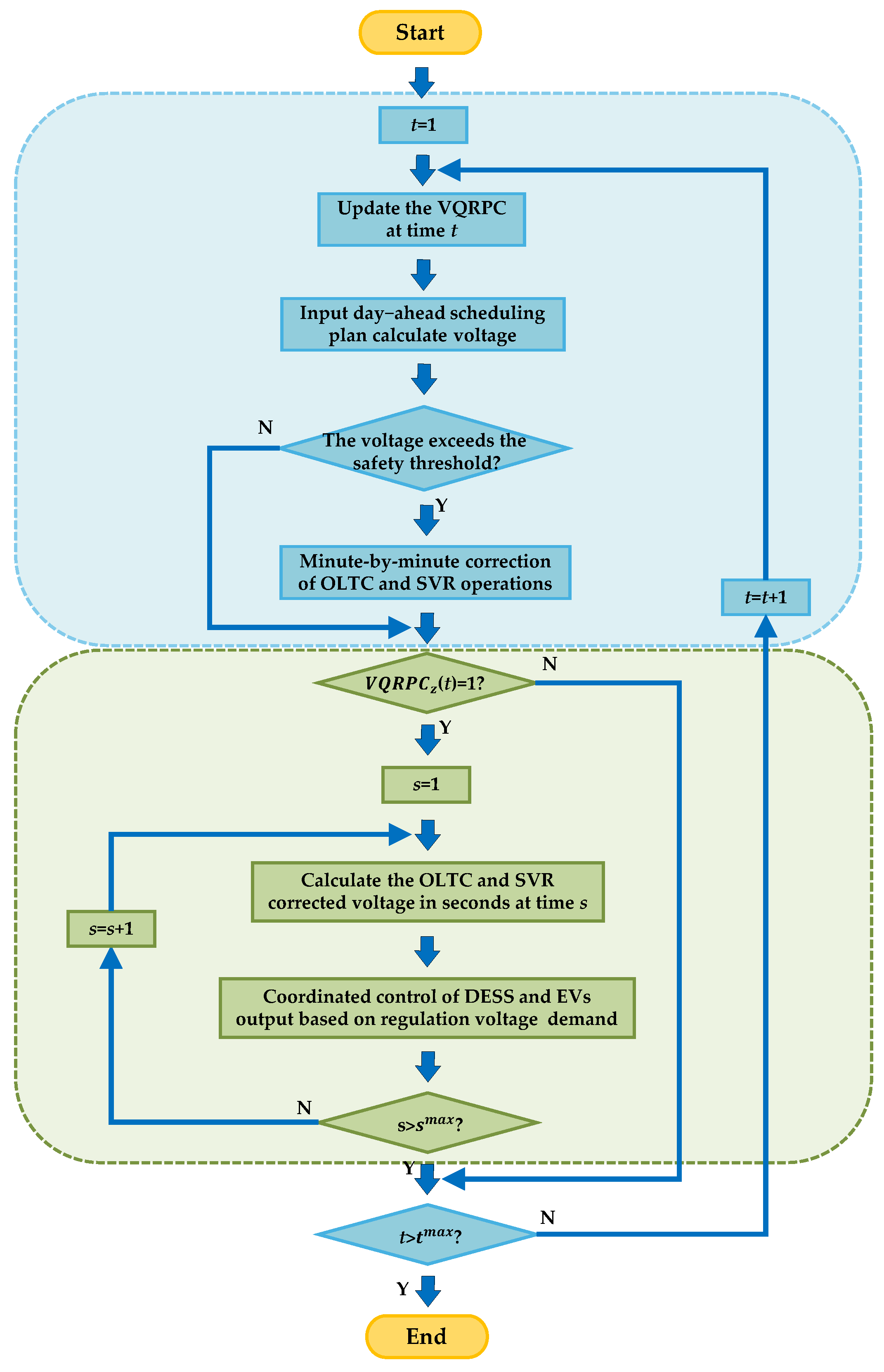
3.2.2. Minute-Level Optimization
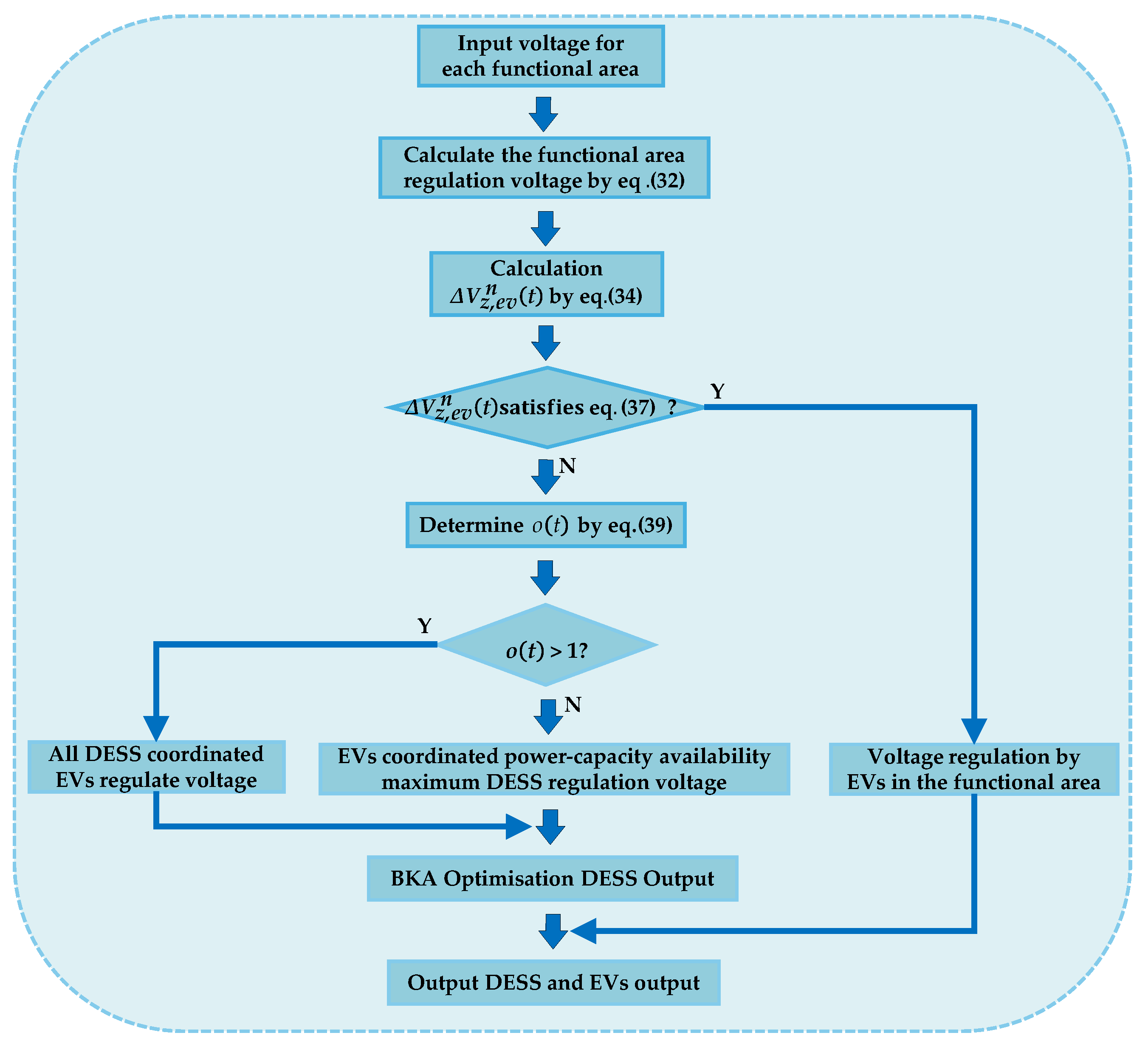
3.2.3. Real-Time Adaptive Control
- Voltage regulation mode
- DESS Available Capacity Management Mechanism
- 2.
- VFS-DOM mode
- VFS mode
- VMTB
- DOM mode
- VMTB adjustment
- 3.
- Comprehensive optimization mode
4. Case Study
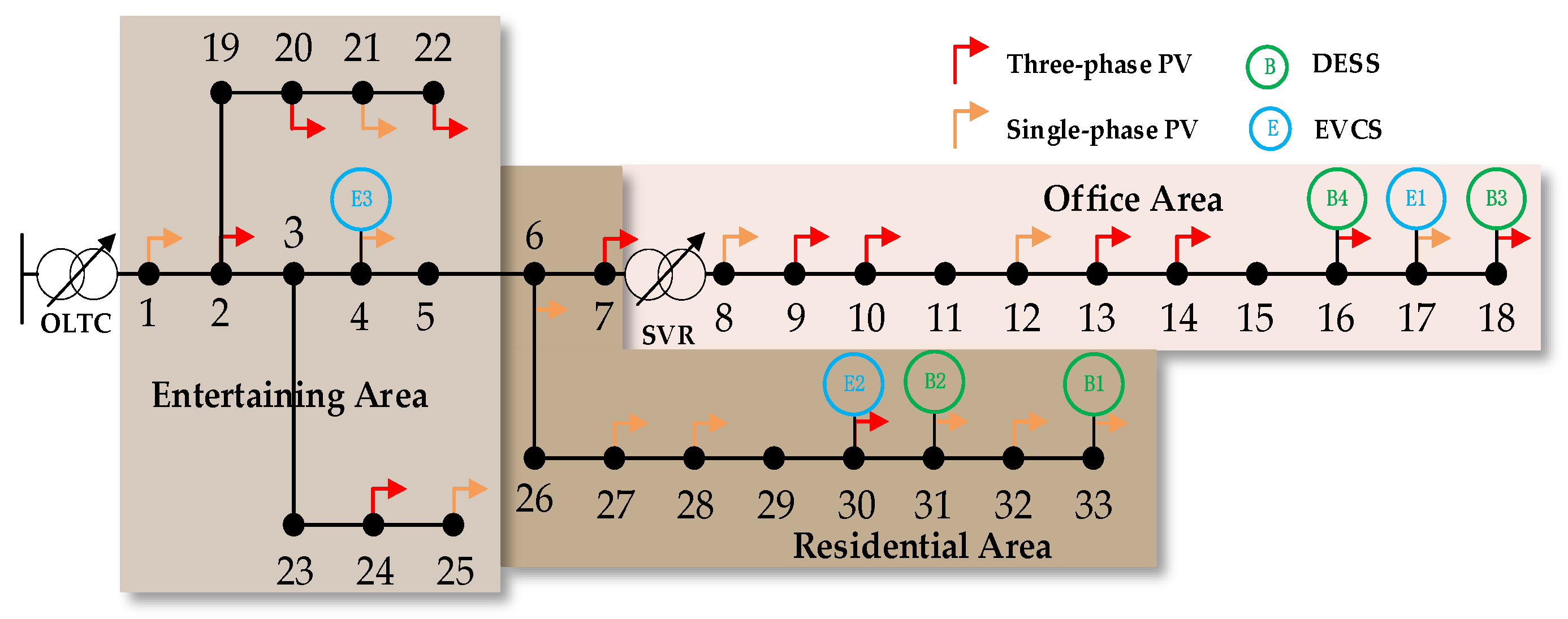
4.1. Simulation Conditions
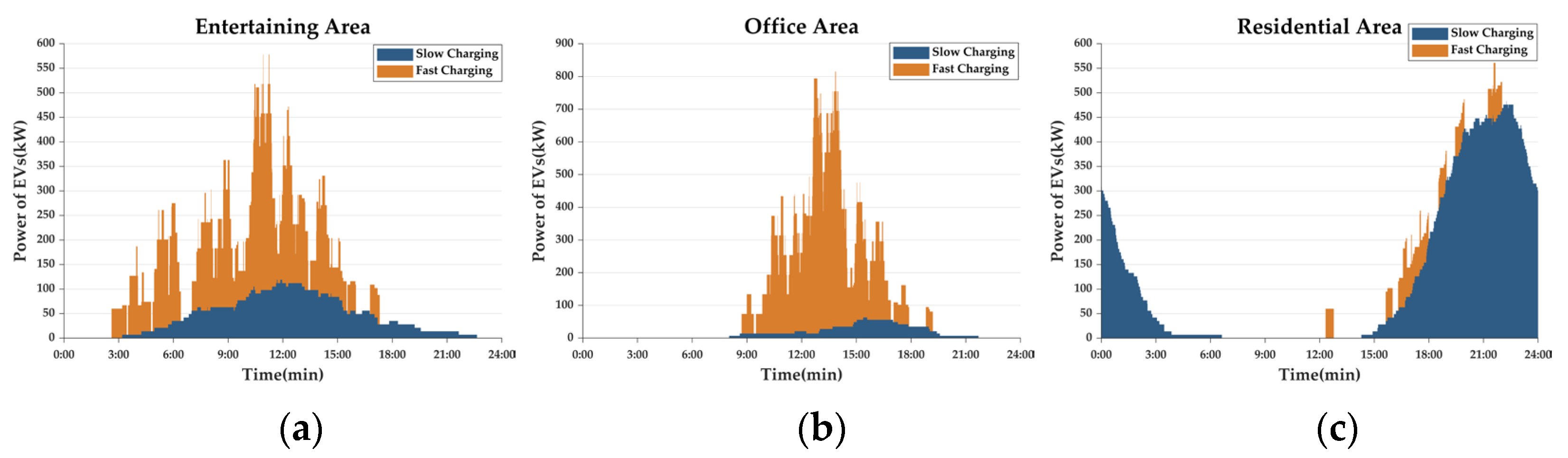
- It is assumed that a total of 100 EVs are charging at the EV station in the functional area throughout the day and that the number of idle EVs is equal to the number of charging EVs in real time.
- Referring to the 2022 China electric vehicle user charging behavior white paper [48], the fast- and slow-charging ratios for office, residential and entertainment areas are set at 9:1, 1:9 and 7:3, respectively.
- The charging start time follows a normal distribution differentiated by the functional area, with office areas concentrated in the late afternoon , residential areas peaking in the evening , and entertainment areas showing a tendency to charge all day during the day .
4.2. Case Study and Discussion
- Day-ahead scheduling stage (5 min)
- Intra-day optimization stage
- Minute timescale (1 min)
- Real-time (10 s)
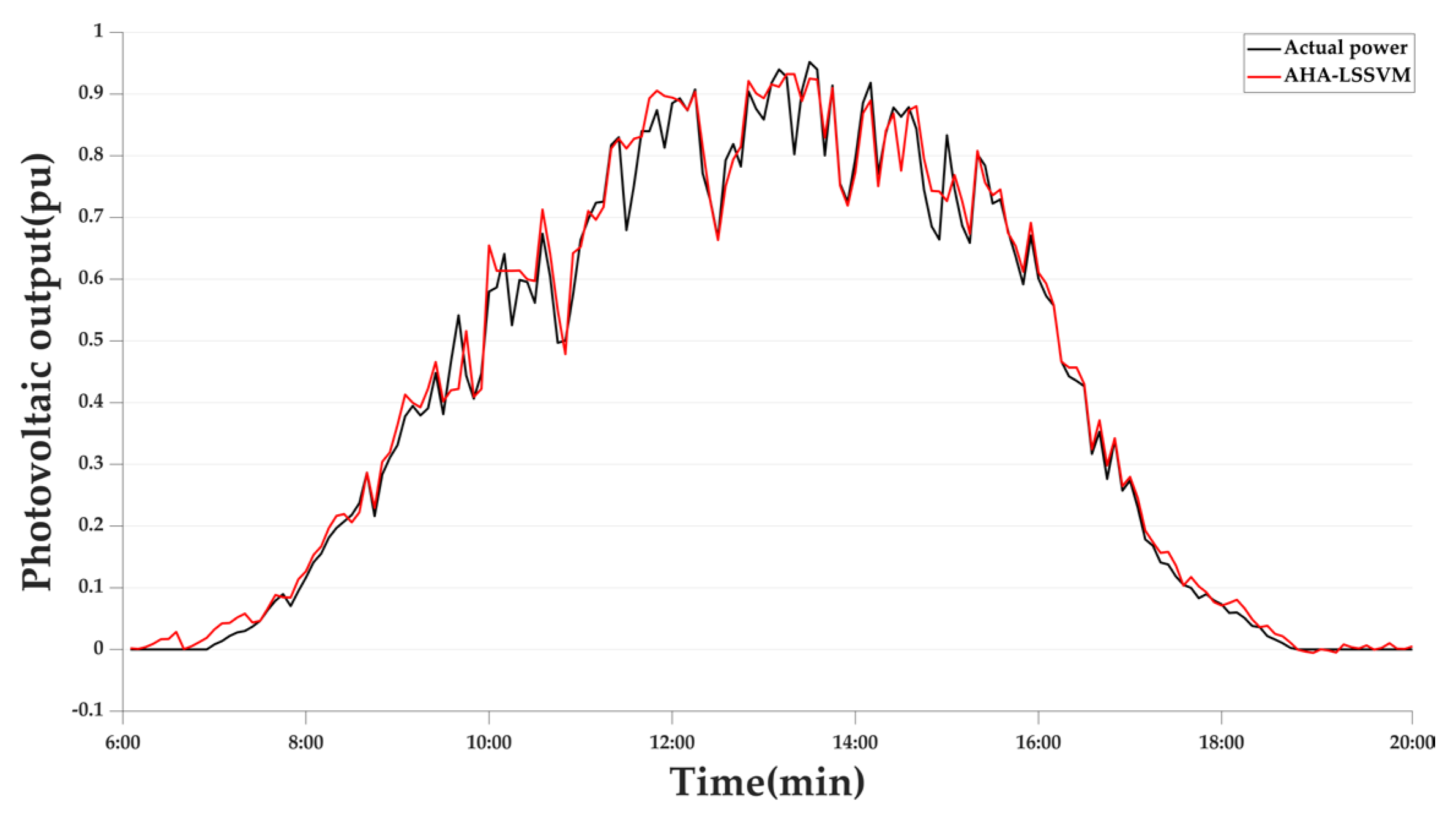
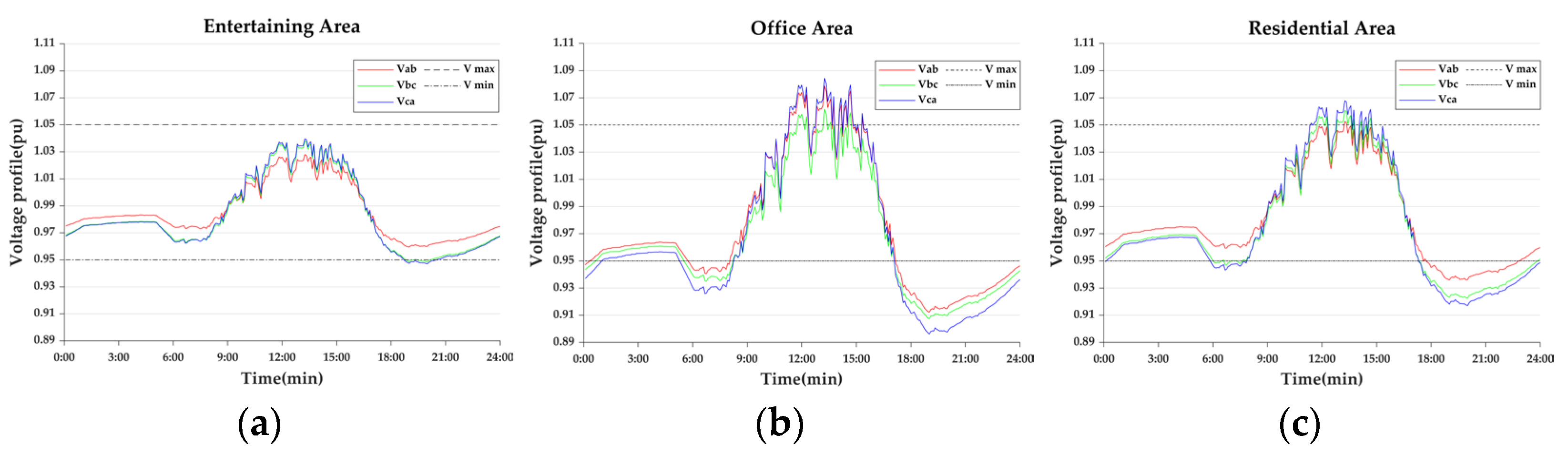
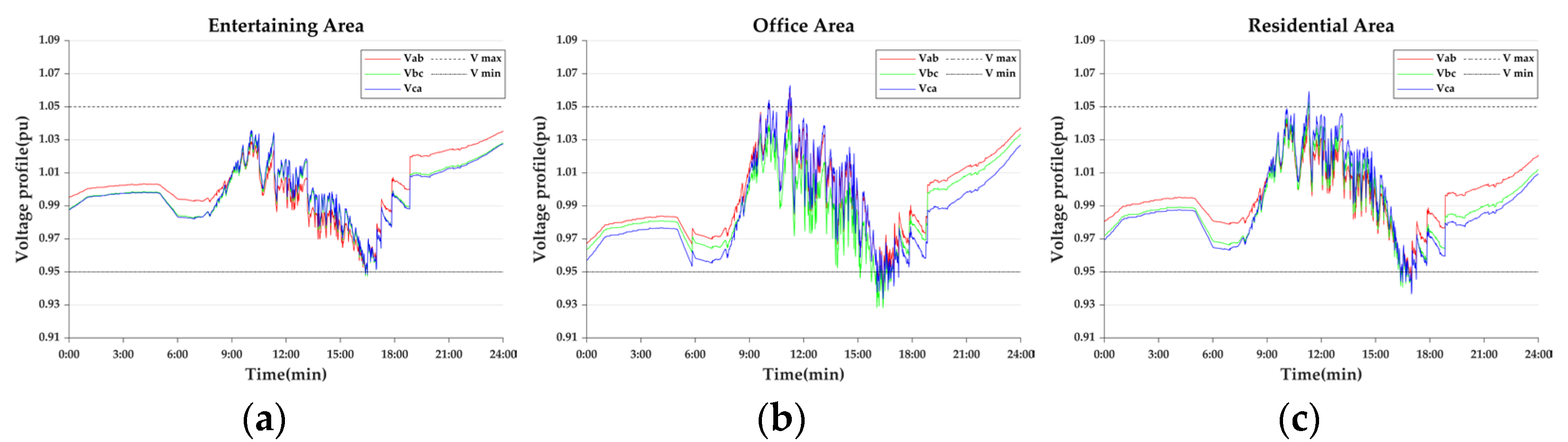
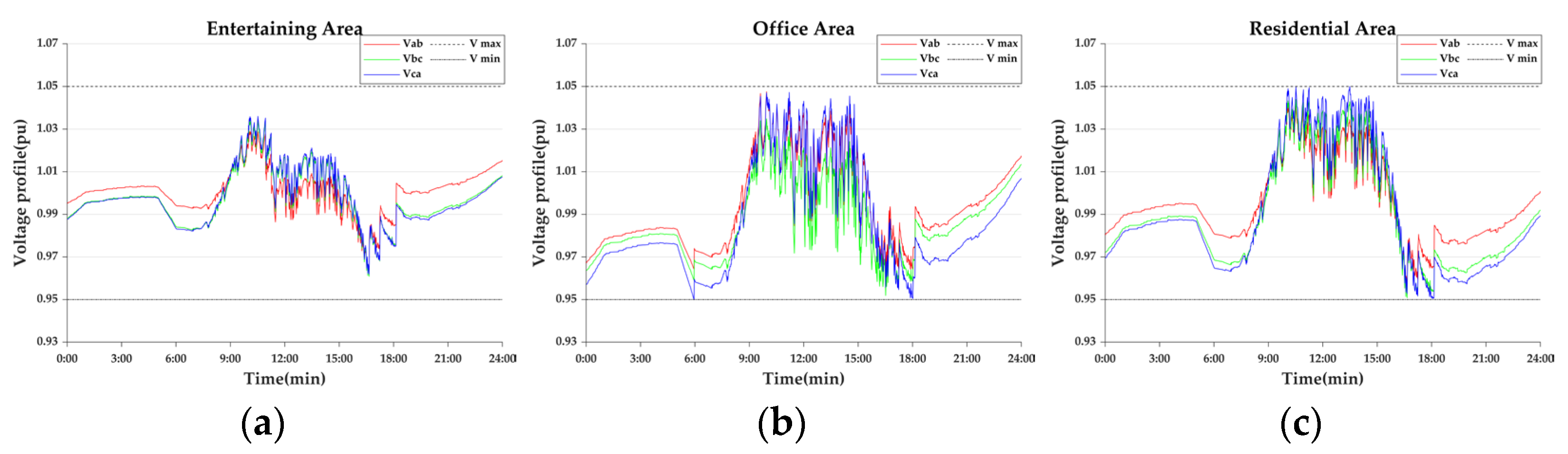
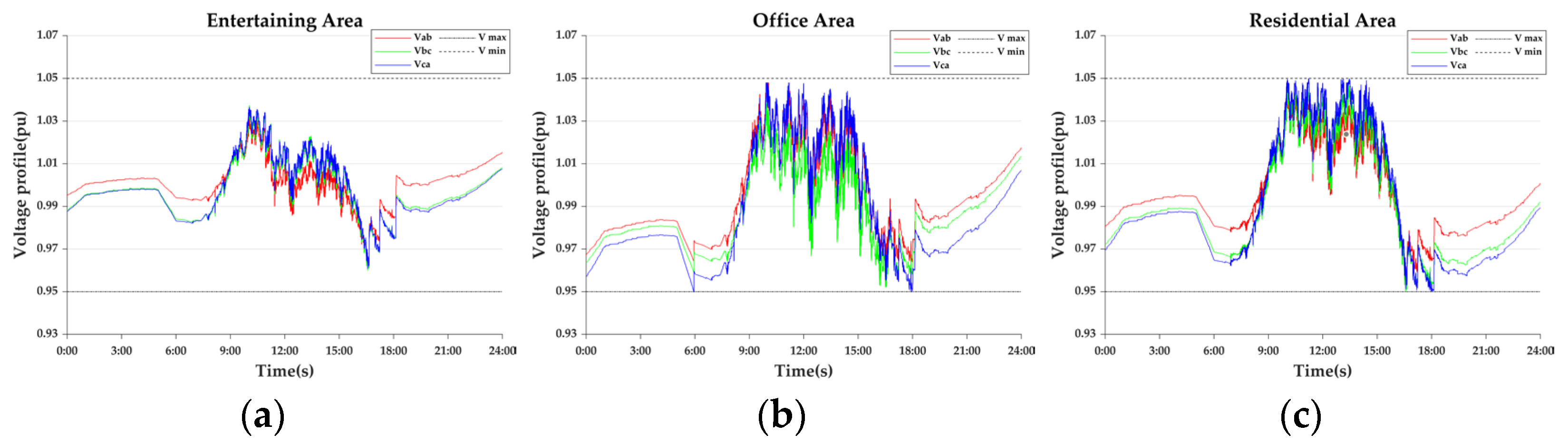
- Case 1-1: The Original Day-ahead Voltage
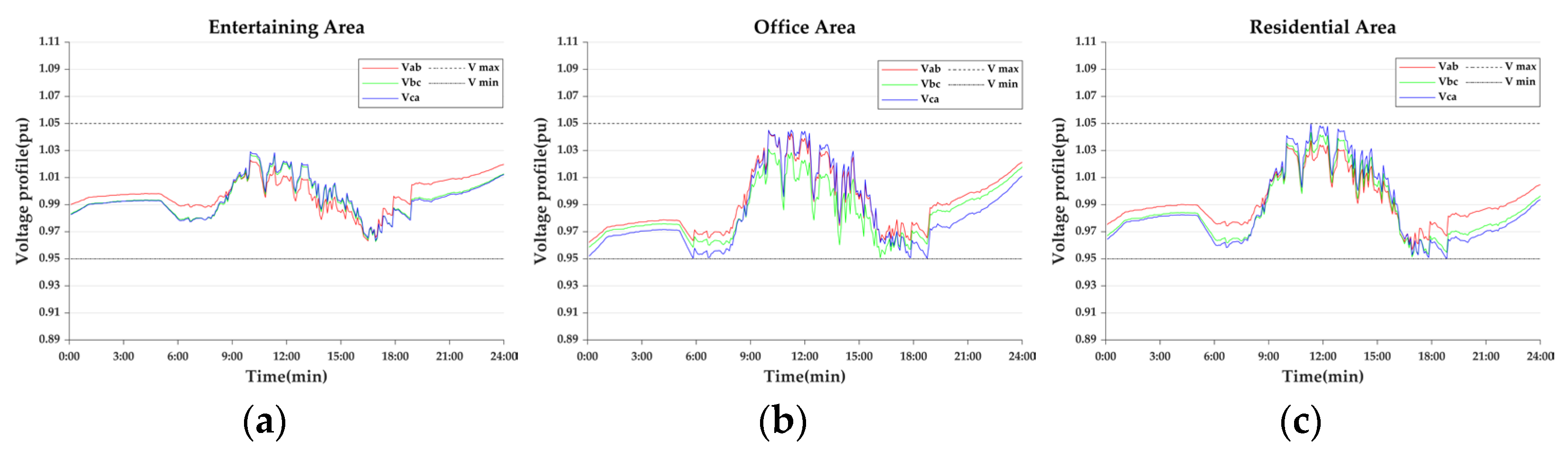
- Case 1-2: Day-ahead Scheduling
- Case 2-1: Intra-day-day-ahead optimisation
- Case 2-2: Intra-day minute-by-minute optimisation
- Case 2-3: Only minute-by-minute optimisation
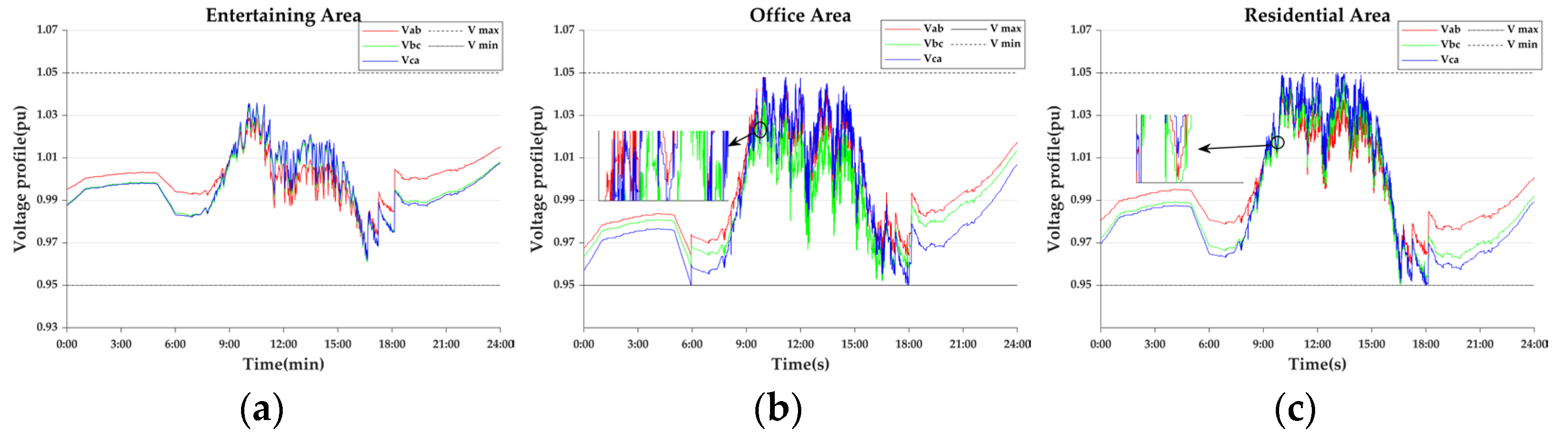
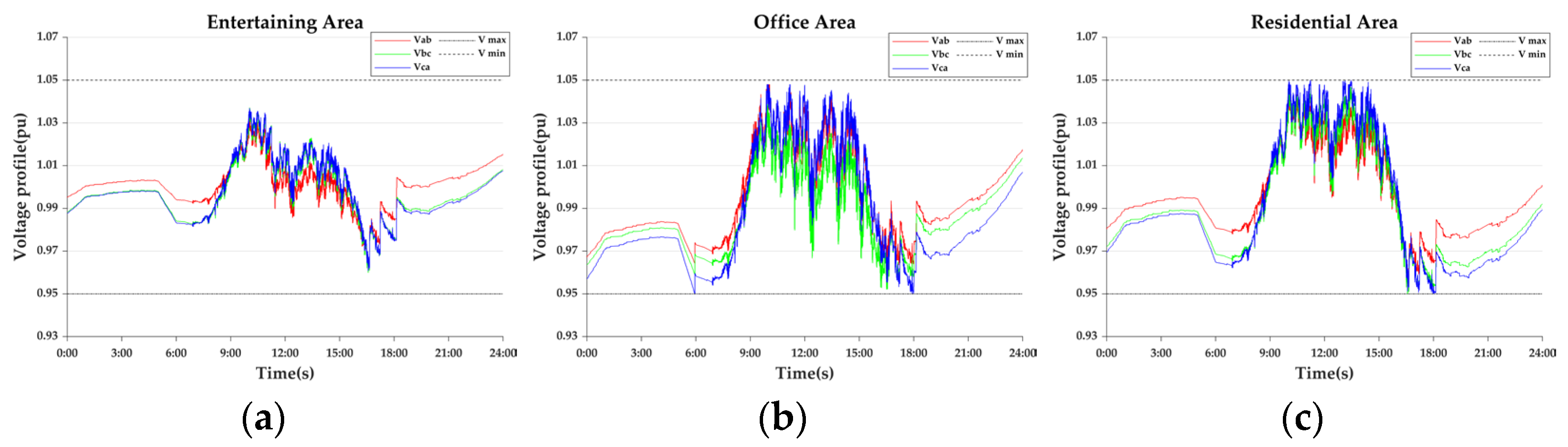
- Case 2-4: Real-time control
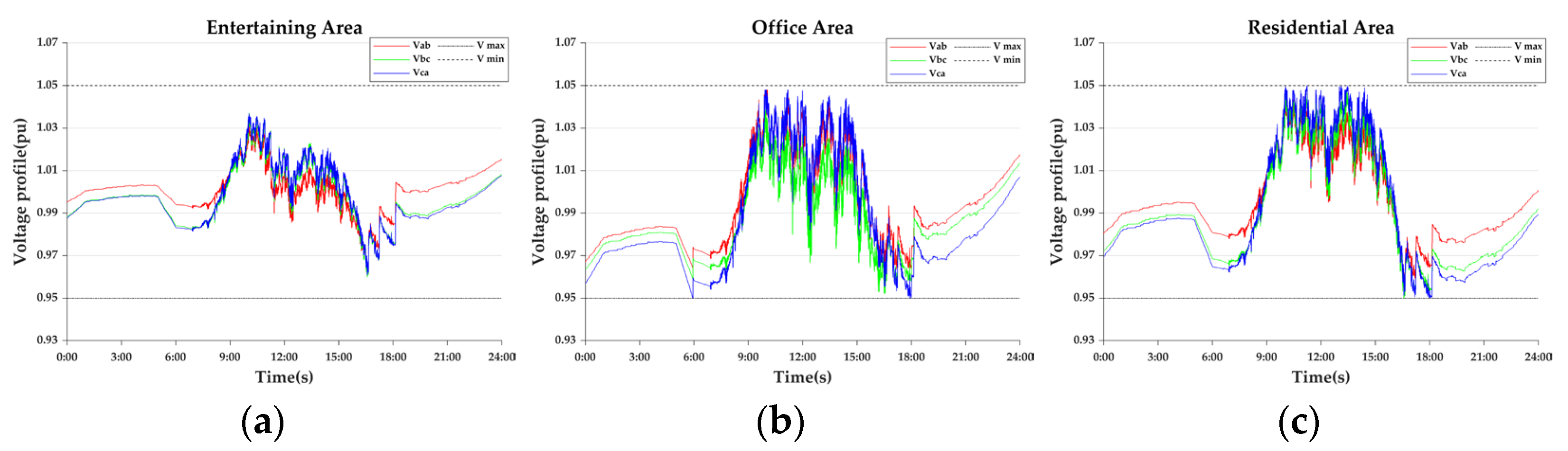
- Case 2-5: Adaptive real-time control
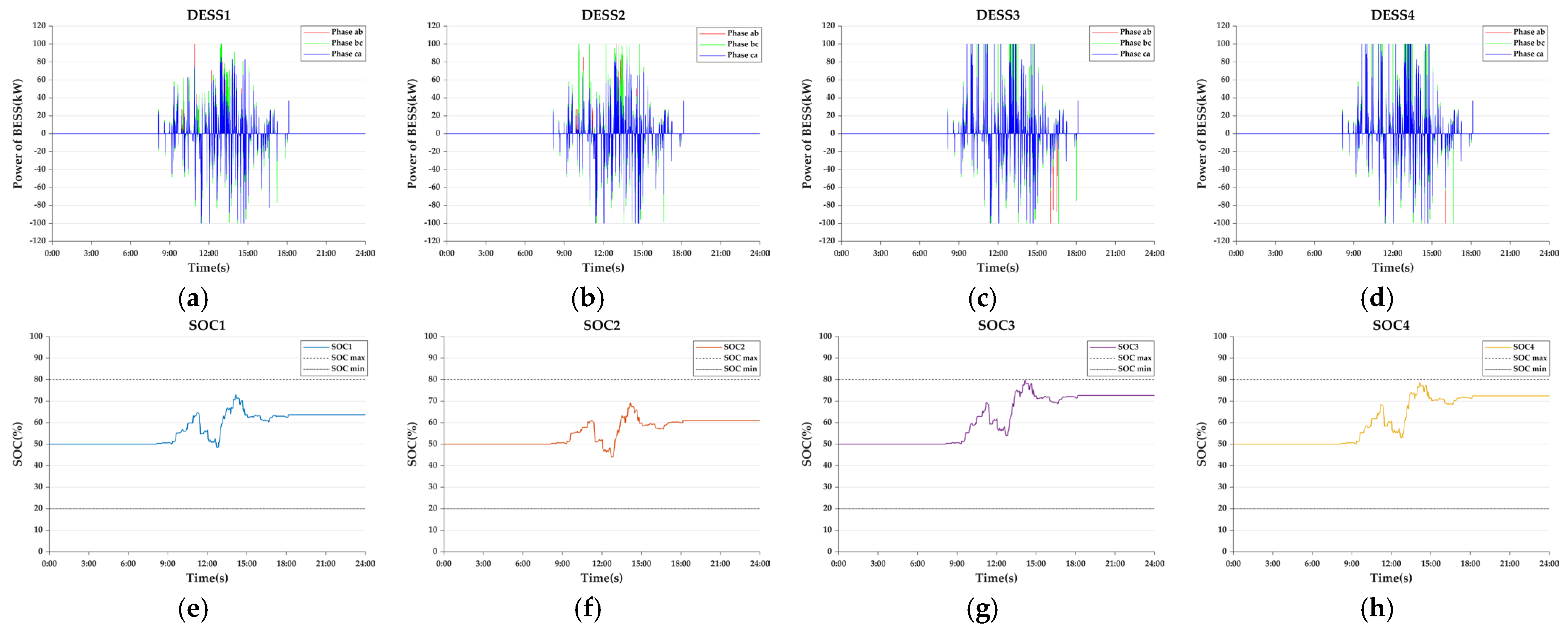
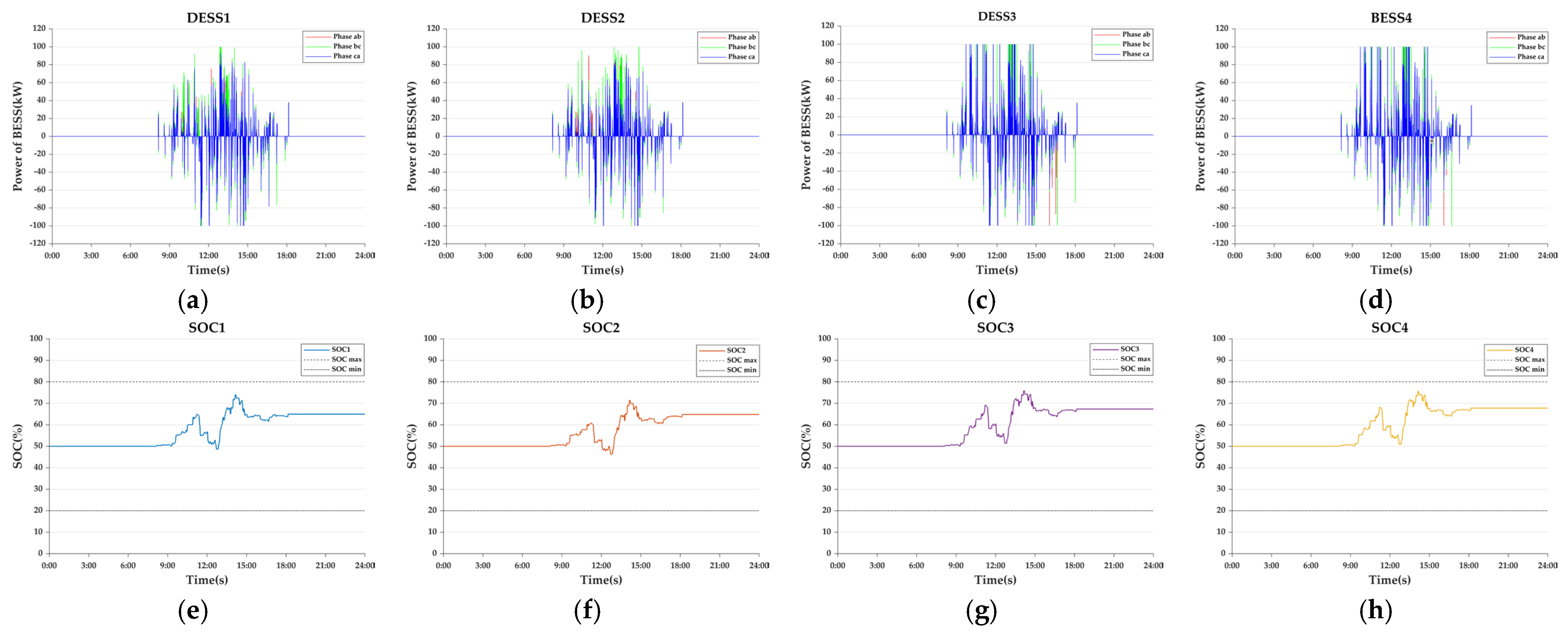
- Case 2-6: DOM
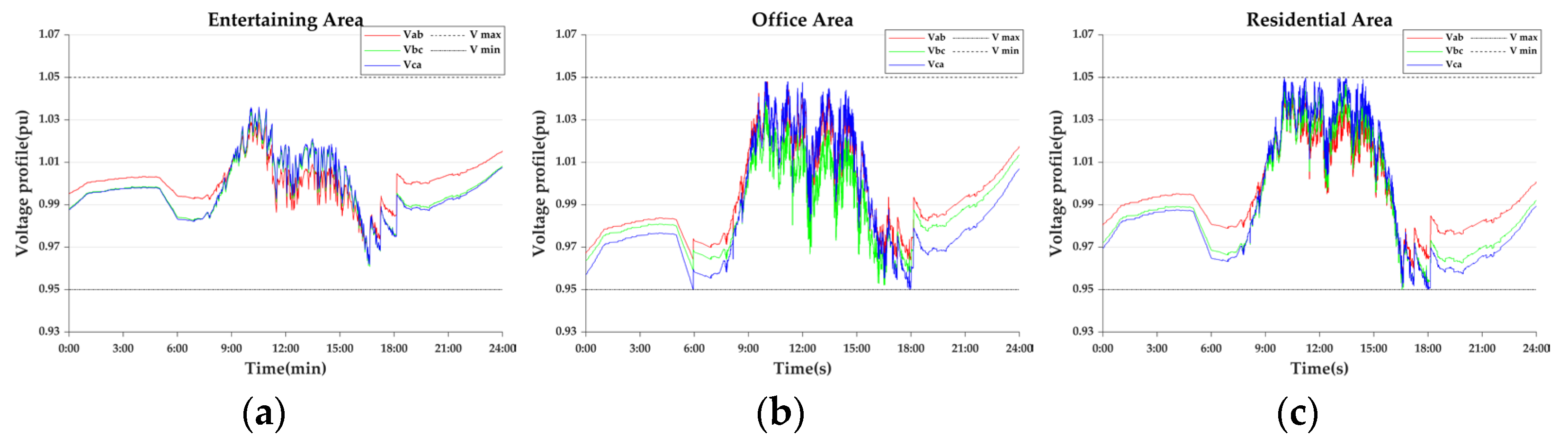
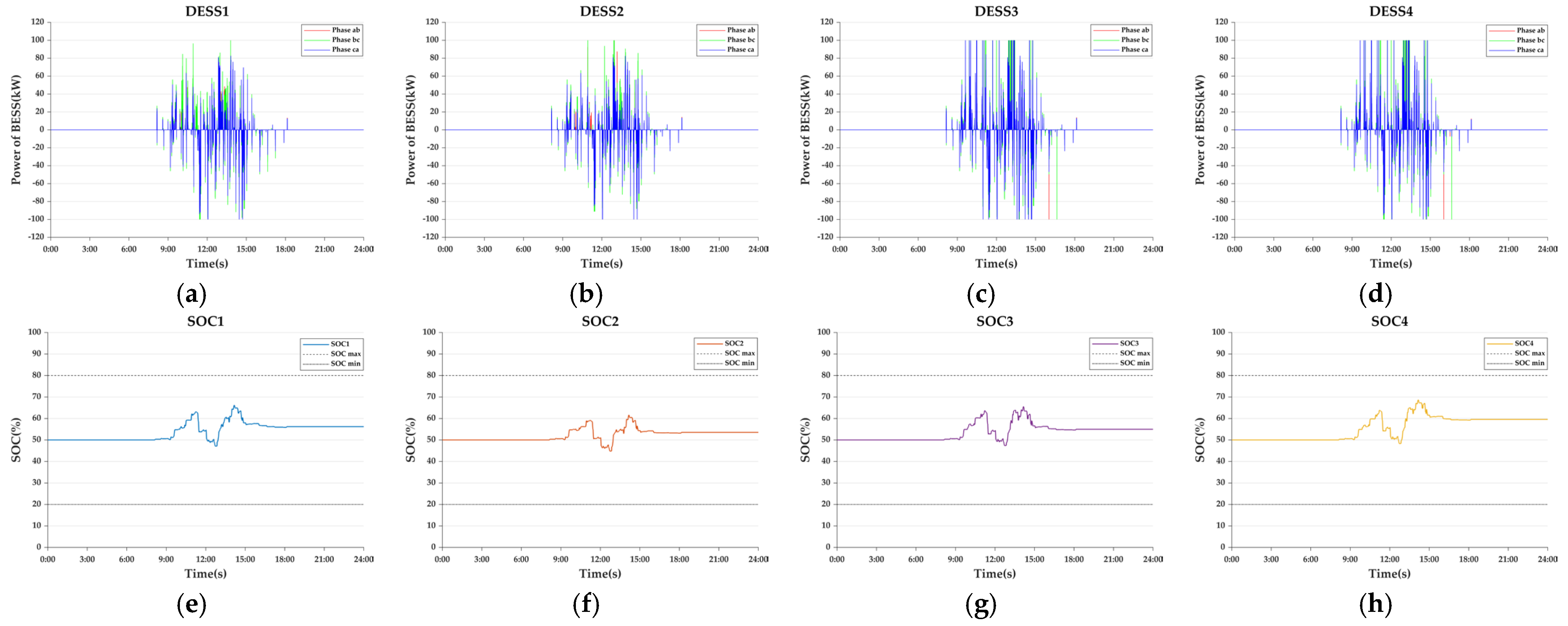
- Case 2-7: EV, DESS Coordination Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
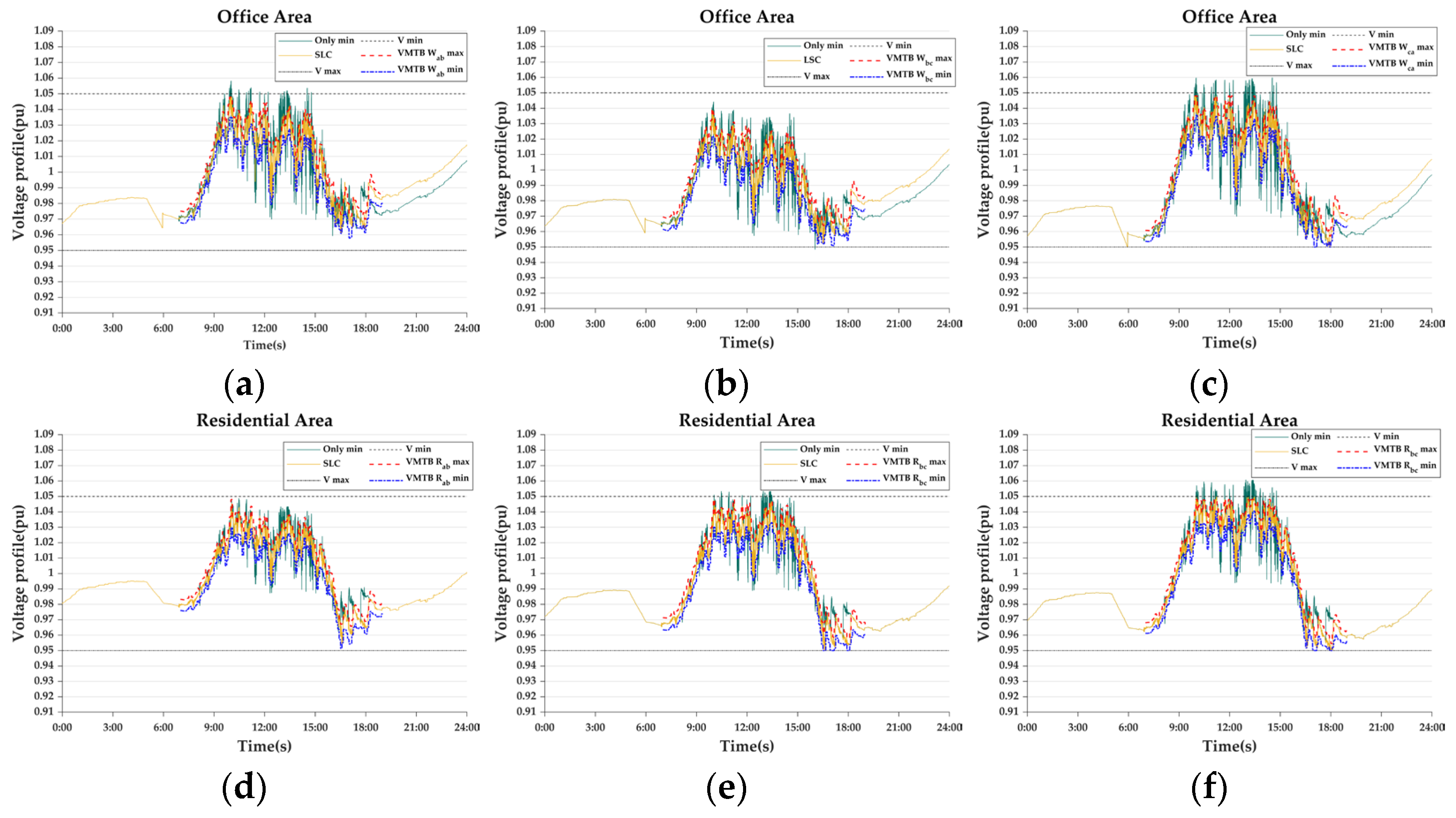
Appendix C
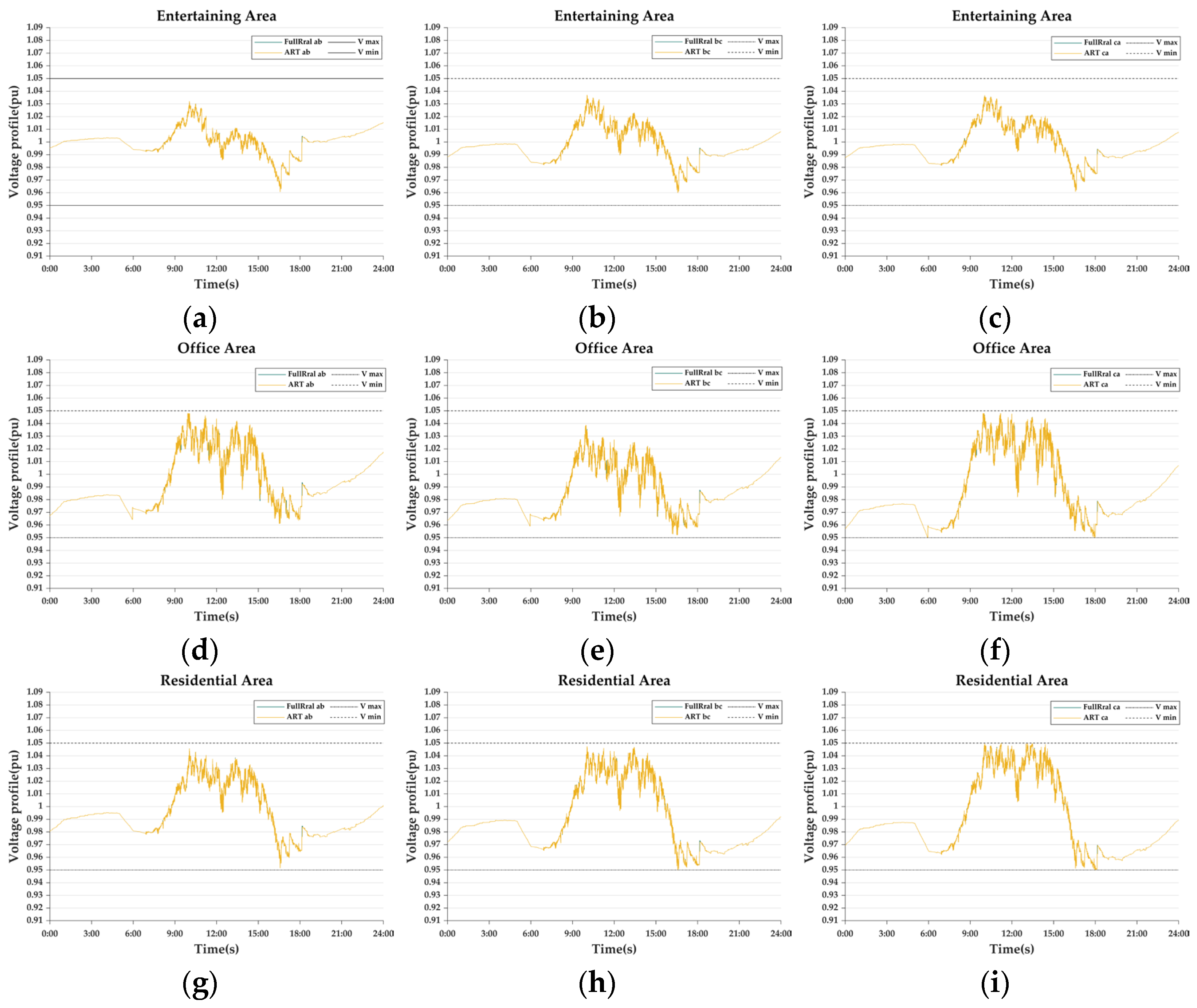
References
- Wang, X.; Wang, G.; Chen, T.; Zeng, Z.; Heng, C.K. Low-Carbon City and Its Future Research Trends: A Bibliometric Analysis and Systematic Review. Sustain. Cities Soc. 2023, 90, 104381. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, Y.; Chen, T.; Lucchi, E. Optimized Community-Level Distributed Photovoltaic Generation (DPVG): Aesthetic, Technical, Economic, and Environmental Assessment of Building Integrated Photovoltaic (BIPV) Systems. J. Build. Eng. 2025, 103, 112085. [Google Scholar] [CrossRef]
- Ufa, R.A.; Malkova, Y.Y.; Rudnik, V.E.; Andreev, M.V.; Borisov, V.A. A Review on Distributed Generation Impacts on Electric Power System. Int. J. Hydrog. Energy 2022, 47, 20347–20361. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, F.; Min, H.; Tian, H.; Hu, W.; Liu, J. Review on Optimal Planning of New Power Systems with Distributed Generations and Electric Vehicles. Energy Rep. 2023, 9, 501–509. [Google Scholar] [CrossRef]
- Kharrazi, A.; Sreeram, V.; Mishra, Y. Assessment Techniques of the Impact of Grid-Tied Rooftop Photovoltaic Generation on the Power Quality of Low Voltage Distribution Network—A Review. Renew. Sustain. Energy Rev. 2020, 120, 109643. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, Y.; Yuan, Y. The Short-Term Forecasting of Distributed Photovoltaic Power Considering the Sensitivity of Meteorological Data. J. Clean. Prod. 2025, 486, 144599. [Google Scholar] [CrossRef]
- Kang, W.; Guan, Y.; Wang, H.; Vasquez, J.C.; Agundis-Tinajero, G.D.; Guerrero, J.M. Distributed Control of Virtual Energy Storage Systems for Voltage Regulation in Low Voltage Distribution Networks Subjects to Varying Time Delays. Appl. Energy 2024, 376, 124295. [Google Scholar] [CrossRef]
- Emrani-Rahaghi, P.; Hashemi-Dezaki, H.; Ketabi, A. Efficient Voltage Control of Low Voltage Distribution Networks Using Integrated Optimized Energy Management of Networked Residential Multi-Energy Microgrids. Appl. Energy 2023, 349, 121391. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Wu, S.; Liu, N.; Liu, X.; Hu, Y.; Fu, Y. Explainable Time-Varying Directional Representations for Photovoltaic Power Generation Forecasting. J. Clean. Prod. 2024, 468, 143056. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, X.; Sun, Y.; Liu, X.; Dong, Z.Y. Multistep Photovoltaic Power Forecasting Based on Multi-Timescale Fluctuation Aggregation Attention Mechanism and Contrastive Learning. Int. J. Electr. Power Energy Syst. 2025, 164, 110389. [Google Scholar] [CrossRef]
- Mahmoud, K.; Lehtonen, M. Three-Level Control Strategy for Minimizing Voltage Deviation and Flicker in PV-Rich Distribution Systems. Int. J. Electr. Power Energy Syst. 2020, 120, 105997. [Google Scholar] [CrossRef]
- Ferdowsi, F.; Mehraeen, S.; Upton, G.B. Assessing Distribution Network Sensitivity to Voltage Rise and Flicker under High Penetration of Behind-the-Meter Solar. Renew. Energy 2020, 152, 1227–1240. [Google Scholar] [CrossRef]
- Yu, P.; Zhang, H.; Hu, Z.; Song, Y. Voltage Control of Distribution Grid with District Cooling Systems Based on Scenario-Classified Reinforcement Learning. Appl. Energy 2025, 377, 124415. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, P.; Ji, H.; Zhao, J.; Xi, W.; Wu, J.; Wang, C. Combined Central-Local Voltage Control of Inverter-Based DG in Active Distribution Networks1. Appl. Energy 2024, 372, 123813. [Google Scholar] [CrossRef]
- Song, G.; Wu, Q.; Jiao, W.; Lu, L. Distributed Coordinated Control for Voltage Regulation in Active Distribution Networks Based on Robust Model Predictive Control. Int. J. Electr. Power Energy Syst. 2025, 166, 110529. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Y.; Zhao, J.; Qiu, G.; Yin, H.; Li, Z. Physical-Assisted Multi-Agent Graph Reinforcement Learning Enabled Fast Voltage Regulation for PV-Rich Active Distribution Network. Appl. Energy 2023, 351, 121743. [Google Scholar] [CrossRef]
- Zhang, Z.; da Silva, F.F.; Guo, Y.; Bak, C.L.; Chen, Z. Double-Layer Stochastic Model Predictive Voltage Control in Active Distribution Networks with High Penetration of Renewables. Appl. Energy 2021, 302, 117530. [Google Scholar] [CrossRef]
- Ahmad, A.B.; Ooi, C.A.; Ali, O.; Charin, C.; Maharum, S.M.M.; Swadi, M.; Salem, M. Renewable Integration and Energy Storage Management and Conversion in Grid Systems: A Comprehensive Review. Energy Rep. 2025, 13, 2583–2602. [Google Scholar] [CrossRef]
- Li, S.; Liu, B.; Li, X. A Robust and Optimal Voltage Control Strategy for Low-Voltage Grids Utilizing Group Coordination of Photovoltaic and Energy Storage Systems via Consensus Algorithm. Int. J. Hydrog. Energy 2024, 78, 1332–1343. [Google Scholar] [CrossRef]
- Abdalla, A.N.; Nazir, M.S.; Tao, H.; Cao, S.; Ji, R.; Jiang, M.; Yao, L. Integration of Energy Storage System and Renewable Energy Sources Based on Artificial Intelligence: An Overview. J. Energy Storage 2021, 40, 102811. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Junaid Alvi, M.; Kim, H.-J. Towards a Smarter Battery Management System for Electric Vehicle Applications: A Critical Review of Lithium-Ion Battery State of Charge Estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- González, I.; Calderón, A.J.; Folgado, F.J. IoT Real Time System for Monitoring Lithium-Ion Battery Long-Term Operation in Microgrids. J. Energy Storage 2022, 51, 104596. [Google Scholar] [CrossRef]
- Tao, Z.; Zhao, Z.; Wang, C.; Huang, L.; Jie, H.; Li, H.; Hao, Q.; Zhou, Y.; See, K.Y. State of Charge Estimation of Lithium Batteries: Review for Equivalent Circuit Model Methods. Measurement 2024, 236, 115148. [Google Scholar] [CrossRef]
- Wang, H.; Ye, Y.; Wang, Q.; Tang, Y.; Strbac, G. An Efficient LP-Based Approach for Spatial-Temporal Coordination of Electric Vehicles in Electricity-Transportation Nexus. IEEE Trans. Power Syst. 2023, 38, 2914–2925. [Google Scholar] [CrossRef]
- Fan, P.; Yang, J.; Ke, S.; Wen, Y.; Liu, X.; Ding, L.; Ullah, T. A Multilayer Voltage Intelligent Control Strategy for Distribution Networks with V2G and Power Energy Production-Consumption Units. Int. J. Electr. Power Energy Syst. 2024, 159, 110055. [Google Scholar] [CrossRef]
- Qian, J.; Jiang, Y.; Liu, X.; Wang, Q.; Wang, T.; Shi, Y.; Chen, W. Federated Reinforcement Learning for Electric Vehicles Charging Control on Distribution Networks. IEEE Inter. Things J. 2024, 11, 5511–5525. [Google Scholar] [CrossRef]
- Çelik, D.; Khan, M.A.; Khosravi, N.; Waseem, M.; Ahmed, H. A Review of Energy Storage Systems for Facilitating Large-Scale EV Charger Integration in Electric Power Grid. J. Energy Storage 2025, 112, 115496. [Google Scholar] [CrossRef]
- Yu, H.; Niu, S.; Shang, Y.; Shao, Z.; Jia, Y.; Jian, L. Electric Vehicles Integration and Vehicle-to-Grid Operation in Active Distribution Grids: A Comprehensive Review on Power Architectures, Grid Connection Standards and Typical Applications. Renew. Sustain. Energy Rev. 2022, 168, 112812. [Google Scholar] [CrossRef]
- Qi, T.; Ye, C.; Zhao, Y.; Li, L.; Ding, Y. Deep Reinforcement Learning Based Charging Scheduling for Household Electric Vehicles in Active Distribution Network. J. Mod. Power Syst. Clean Energy 2023, 11, 1890–1901. [Google Scholar] [CrossRef]
- Liu, D.; Zeng, P.; Cui, S.; Song, C. Deep Reinforcement Learning for Charging Scheduling of Electric Vehicles Considering Distribution Network Voltage Stability. Sensors 2023, 23, 1618. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhang, R.; Wang, Y.; Shi, P.; Wang, X.; Chen, B.; Fan, C.; Chen, G. A Deep Reinforcement Learning Based Charging and Discharging Scheduling Strategy for Electric Vehicles. Energy Rep. 2024, 12, 4854–4863. [Google Scholar] [CrossRef]
- Hu, D.; Ye, Z.; Gao, Y.; Ye, Z.; Peng, Y.; Yu, N. Multi-Agent Deep Reinforcement Learning for Voltage Control With Coordinated Active and Reactive Power Optimization. IEEE Trans. Smart Grid 2022, 13, 4873–4886. [Google Scholar] [CrossRef]
- Hu, R.; Wang, W.; Wu, X.; Chen, Z.; Jing, L.; Ma, W.; Zeng, G. Coordinated Active and Reactive Power Control for Distribution Networks with High Penetrations of Photovoltaic Systems. Sol. Energy 2022, 231, 809–827. [Google Scholar] [CrossRef]
- Emarati, M.; Barani, M.; Farahmand, H.; Aghaei, J.; del Granado, P.C. A Two-Level over-Voltage Control Strategy in Distribution Networks with High PV Penetration. Int. J. Electr. Power Energy Syst. 2021, 130, 106763. [Google Scholar] [CrossRef]
- Khan, H.A.; Zuhaib, M.; Rihan, M. Voltage Fluctuation Mitigation with Coordinated OLTC and Energy Storage Control in High PV Penetrating Distribution Network. Electr. Power Syst. Res. 2022, 208, 107924. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, Q.; Gao, H.; Huang, S.; Zhou, B.; Li, C. Double-Time-Scale Coordinated Voltage Control in Active Distribution Networks Based on MPC. IEEE Trans. Sustain. Energy 2020, 11, 294–303. [Google Scholar] [CrossRef]
- Song, G.; Wu, Q.; Tan, J.; Jiao, W.; Chen, J. Stochastic MPC Based Double-Time-Scale Voltage Regulation for Unbalanced Distribution Networks with Distributed Generators. Int. J. Electr. Power Energy Syst. 2024, 155, 109687. [Google Scholar] [CrossRef]
- Yan, Q.; Chen, X.; Xing, L.; Guo, X.; Zhu, C. Multi-Timescale Voltage Regulation for Distribution Network with High Photovoltaic Penetration via Coordinated Control of Multiple Devices. Energies 2024, 17, 3830. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H. Black-Winged Kite Algorithm: A Nature-Inspired Meta-Heuristic for Solving Benchmark Functions and Engineering Problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Li, G.; Cui, G.; Zhao, Y.; Sun, R.; Yuan, H.; Li, L. Mid-Infrared C2H6 Telemetry Sensor Using 3.34 Μm ICL Based on Optimized Light Receiving System and BKA-DELM Model. Opt. Lasers Eng. 2025, 186, 108799. [Google Scholar] [CrossRef]
- Zhang, S.; Fu, Z.; An, D.; Yi, H. Network Security Situation Assessment Based on BKA and Cross Dual-Channel. J. Supercomput. 2025, 81, 461. [Google Scholar] [CrossRef]
- Octaviano, M.E.F.; de Araujo, L.R.; Penido, D.R.R. Allocation of BESS and State of Charge Management in Unbalanced Distribution Networks Considering the State of Health. Electr. Power Syst. Res. 2025, 242, 111467. [Google Scholar] [CrossRef]
- Vaičys, J.; Gudžius, S.; Jonaitis, A.; Račkienė, R.; Blinov, A.; Peftitsis, D. A Case Study of Optimising Energy Storage Dispatch: Convex Optimisation Approach with Degradation Considerations. J. Energy Storage 2024, 97, 112941. [Google Scholar] [CrossRef]
- Luo, L.; He, P.; Zhou, S.; Lou, G.; Fang, B.; Wang, P. Optimal Scheduling Strategy of EVs Considering the Limitation of Battery State Switching Times. Energy Rep. 2022, 8, 918–927. [Google Scholar] [CrossRef]
- Wang, W.; Tang, A.; Wei, F.; Yang, H.; Xinran, L.; Peng, J. Electric Vehicle Charging Load Forecasting Considering Weather Impact. Appl. Energy 2025, 383, 125337. [Google Scholar] [CrossRef]
- Afshar, M.; Mohammadi, M.R.; Abedini, M. A Novel Spatial–Temporal Model for Charging Plug Hybrid Electrical Vehicles Based on Traffic-Flow Analysis and Monte Carlo Method. ISA Trans. 2021, 114, 263–276. [Google Scholar] [CrossRef]
- Habib, S.; Ahmad, F.; Gulzar, M.M.; Ahmed, E.M.; Bilal, M. Electric Vehicle Charging Infrastructure Planning Model with Energy Management Strategies Considering EV Parking Behavior. Energy 2025, 316, 134421. [Google Scholar] [CrossRef]
- White Paper on Charging Behavior of Electric Vehicle Users in China 2022. Available online: https://www.nea.gov.cn/2023-03/20/c_1310703965.htm (accessed on 20 February 2025).






| Parameter | Value |
|---|---|
| Voltage grade (kV) | 35 |
| Total load (MW) | 14.8 |
| Total PV power (MW) | 15.6 |
| Rated voltage (pu) | 1.0 |
| Limit of node voltage (pu) | [0.95, 1.05] |
| Day-ahead scheduling sample interval (min) | 5 |
| Minute-level optimization sample interval (min) | 1 |
| Real-time optimization control sample interval (s) | 10 |
| Device | Location | Parameter | Value |
|---|---|---|---|
| DESS1 DESS2 DESS3 DESS4 | Bus 33 Bus 31 Bus 18 Bus 16 | Capacity (kWh) | 150 |
| Power limit (kW) | [−100, 100] | ||
| Charging/discharging efficiency (%) | 100 | ||
| SOC limit (%) | [20, 80] | ||
| Initial SOC (%) | 50 | ||
| EVCS1 EVCS2 EVCS3 | Bus 17 Bus 30 Bus 4 | Fast charging power (kW) | 60 |
| Slow charging power (kW) | 7 | ||
| Charging/discharging efficiency (%) | 90 | ||
| OLTC | HV Bus–MV Bus | Tap range | [−5, 5] |
| Per tap (%) | 2 | ||
| SVR | Bus 7–Bus 8 | Tap range | [−5, 5] |
| Per tap (%) | 1 |
| Parameter | Value |
|---|---|
| sampling points | 5 |
| PV output start time (h) | 6:55 |
| PV output end time (h) | 18:40 |
| Penalty value | 1000 |
| Upper limit of deviation (%) | 0.3 |
| Lower limit of deviation (%) | −0.3 |
| PV output peak time (h) | 12:00 |
| Expected before (%) | 0.6 |
| Expected after (%) | 0.4 |
| Weight | 0.55 |
| Weight | 0.45 |
| Constant | 0.1 |
| 3 |
| OLTC | SVR | DESS | EV | |||
|---|---|---|---|---|---|---|
| Case 1: Day-ahead scheduling | Case 1-1 | |||||
| Case 1-2 | ✓ | ✓ | ||||
| Case 2: Intra-day optimization | Case 2-1 | ✓ | ✓ | |||
| Case 2-2 | ✓ | ✓ | ||||
| Case 2-3 | ✓ | ✓ | ||||
| Case 2-4 | ✓ | ✓ | VRFS | |||
| Case 2-5 | ✓ | ✓ | VRFS | |||
| Case 2-6 | ✓ | ✓ | VRFS | DOM | ||
| Case 2-7 | ✓ | ✓ | VRFS | DOM | ✓ | |
| Entertaining Area | Office Area | Residential Area | |
|---|---|---|---|
| 0 | 1.83 | 2.46 | |
| 5.34 | 19.22 | 14.11 |
| DESS1 | DESS2 | DESS3 | DESS4 | |
|---|---|---|---|---|
| 72.89 | 69.26 | 79.83 | 78.82 | |
| 48.47 | 43.68 | 50.00 | 50.00 |
| Entertaining Area | Office Area | Residential Area | |
|---|---|---|---|
| Case 2-3 | 5.34 | 19.22 | 14.11 |
| Case 2-4 | 3.78 | 11.43 | 8.51 |
| Case 2-5 | 3.85 | 11.81 | 8.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zhang, X.; Yan, Q.; Li, Y. Spatio-Temporal Adaptive Voltage Coordination Control Strategy for Distribution Networks with High Photovoltaic Penetration. Energies 2025, 18, 2093. https://doi.org/10.3390/en18082093
Chen X, Zhang X, Yan Q, Li Y. Spatio-Temporal Adaptive Voltage Coordination Control Strategy for Distribution Networks with High Photovoltaic Penetration. Energies. 2025; 18(8):2093. https://doi.org/10.3390/en18082093
Chicago/Turabian StyleChen, Xunxun, Xiaohong Zhang, Qingyuan Yan, and Yanxue Li. 2025. "Spatio-Temporal Adaptive Voltage Coordination Control Strategy for Distribution Networks with High Photovoltaic Penetration" Energies 18, no. 8: 2093. https://doi.org/10.3390/en18082093
APA StyleChen, X., Zhang, X., Yan, Q., & Li, Y. (2025). Spatio-Temporal Adaptive Voltage Coordination Control Strategy for Distribution Networks with High Photovoltaic Penetration. Energies, 18(8), 2093. https://doi.org/10.3390/en18082093






