Comparative Study of White Shark Optimization and Combined Meta-Heuristic Algorithm for Enhanced MPPT in Photovoltaic Systems
Abstract
1. Introduction
- Investigating the structural framework of the WSO and benchmarking its performance against the proposed hybrid MHA techniques;
- Implementing both the WSO and the proposed hybrid model in an MPPT system and analyzing their effectiveness in terms of tracking speed, accuracy, and adaptability.
2. White Shark Optimizer
2.1. Movement Speed Toward Prey
2.2. Movement Toward Optimal Prey
2.3. Movement Toward the Best White Shark
3. Proposed Hybrid Meta-Heuristic Algorithm for MPPT
3.1. Particle Swarm Optimization
3.2. Differential Evolution Algorithm
3.3. Grey Wolf Optimizer
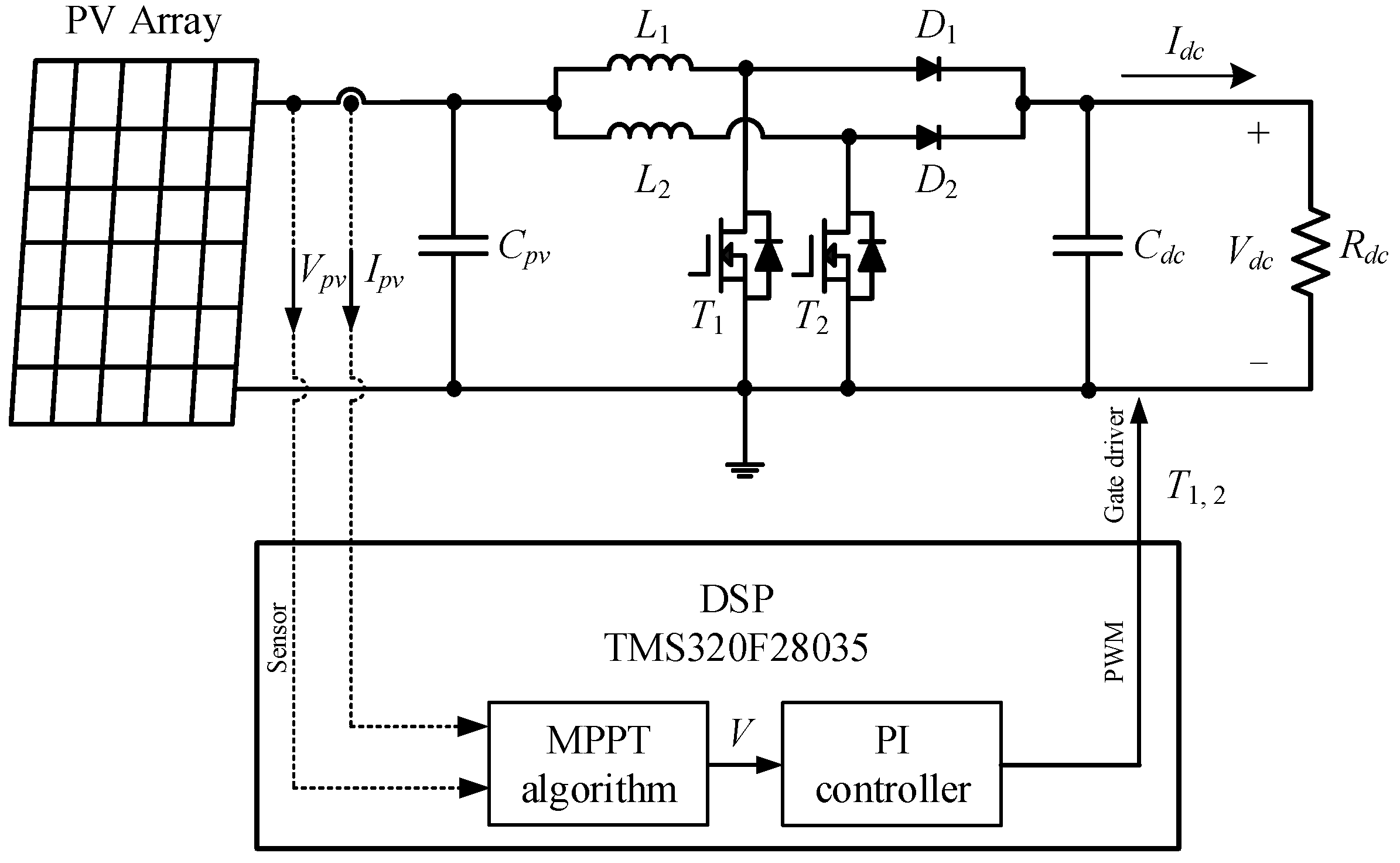
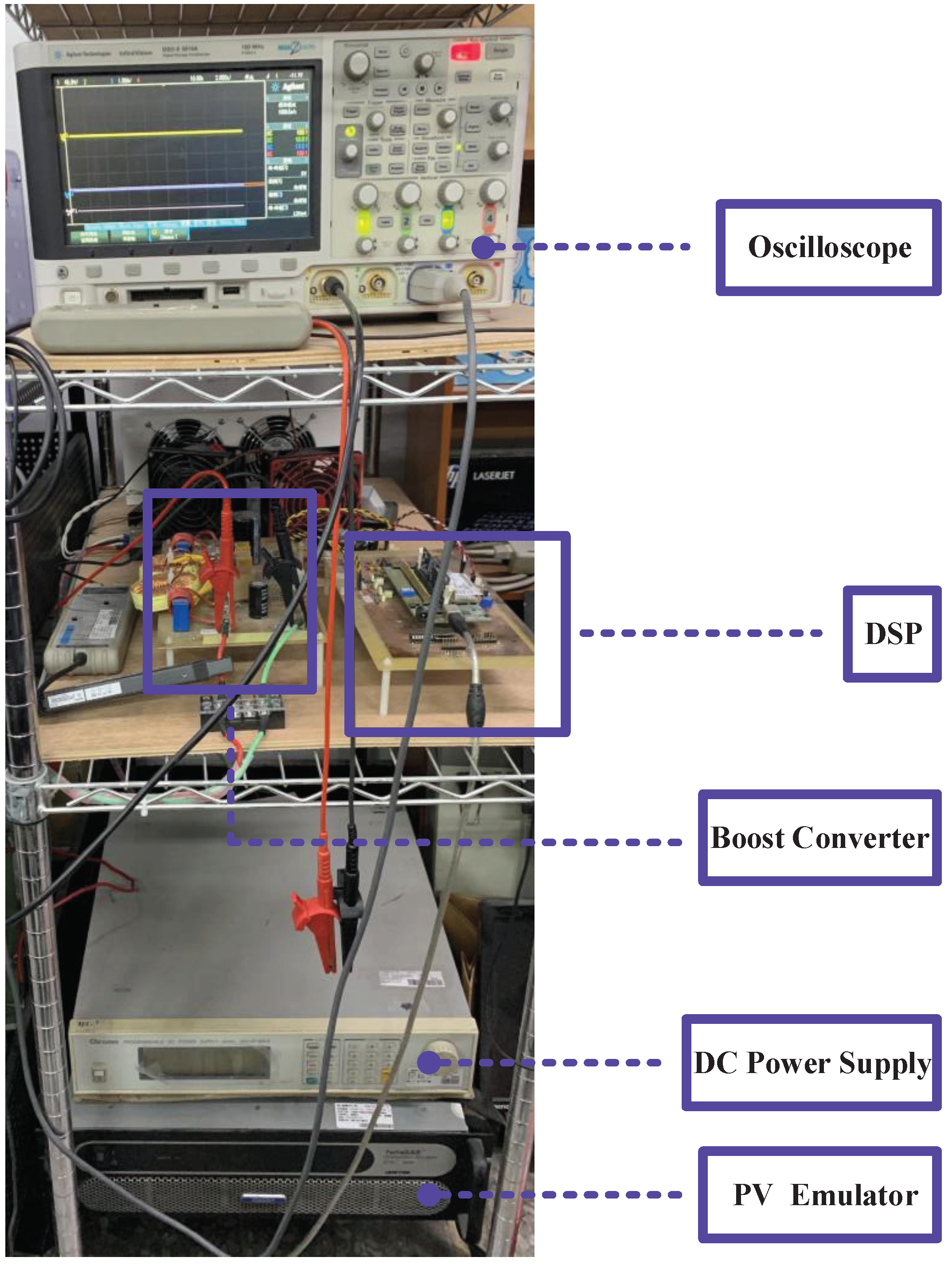
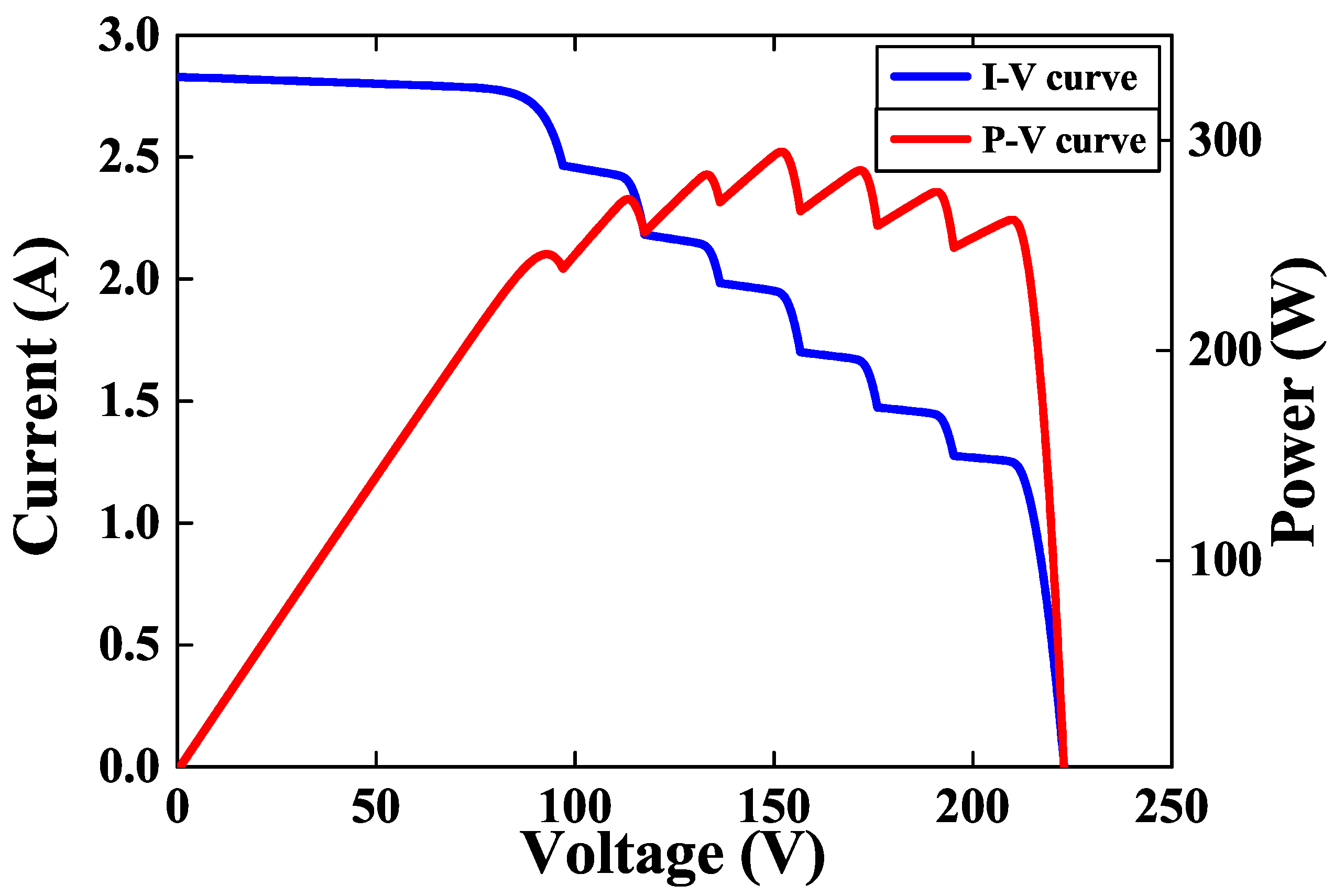
4. Experiment and Results
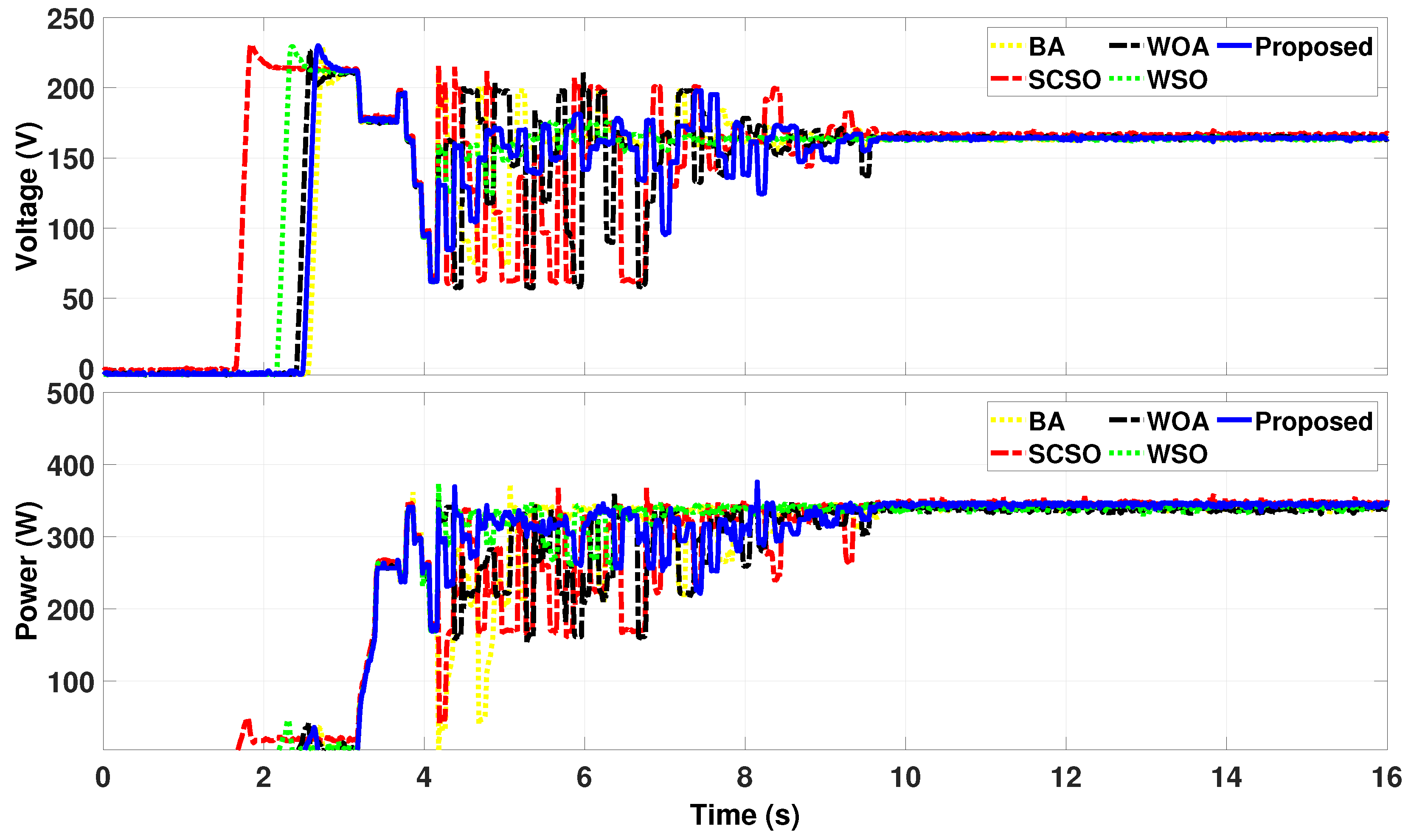
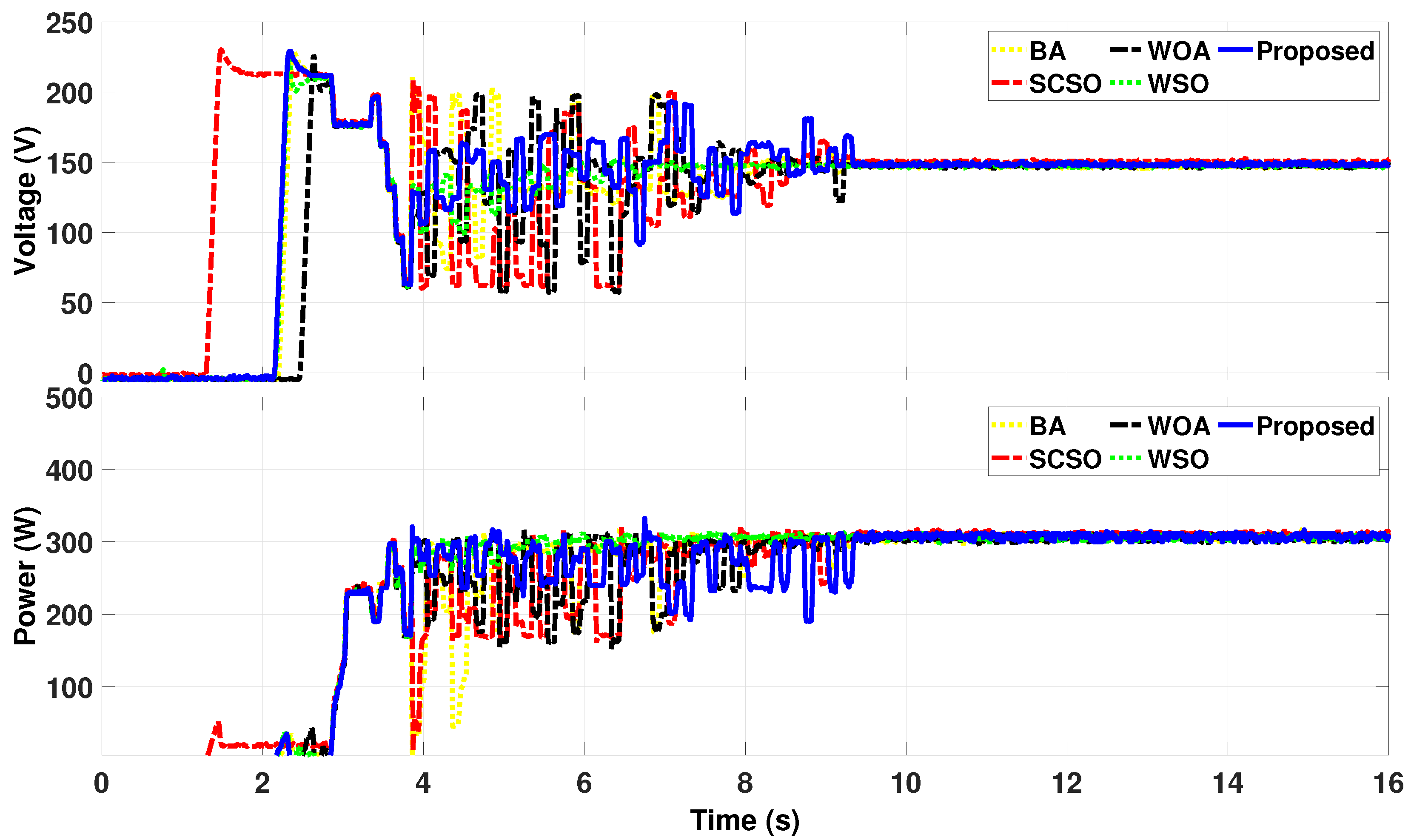
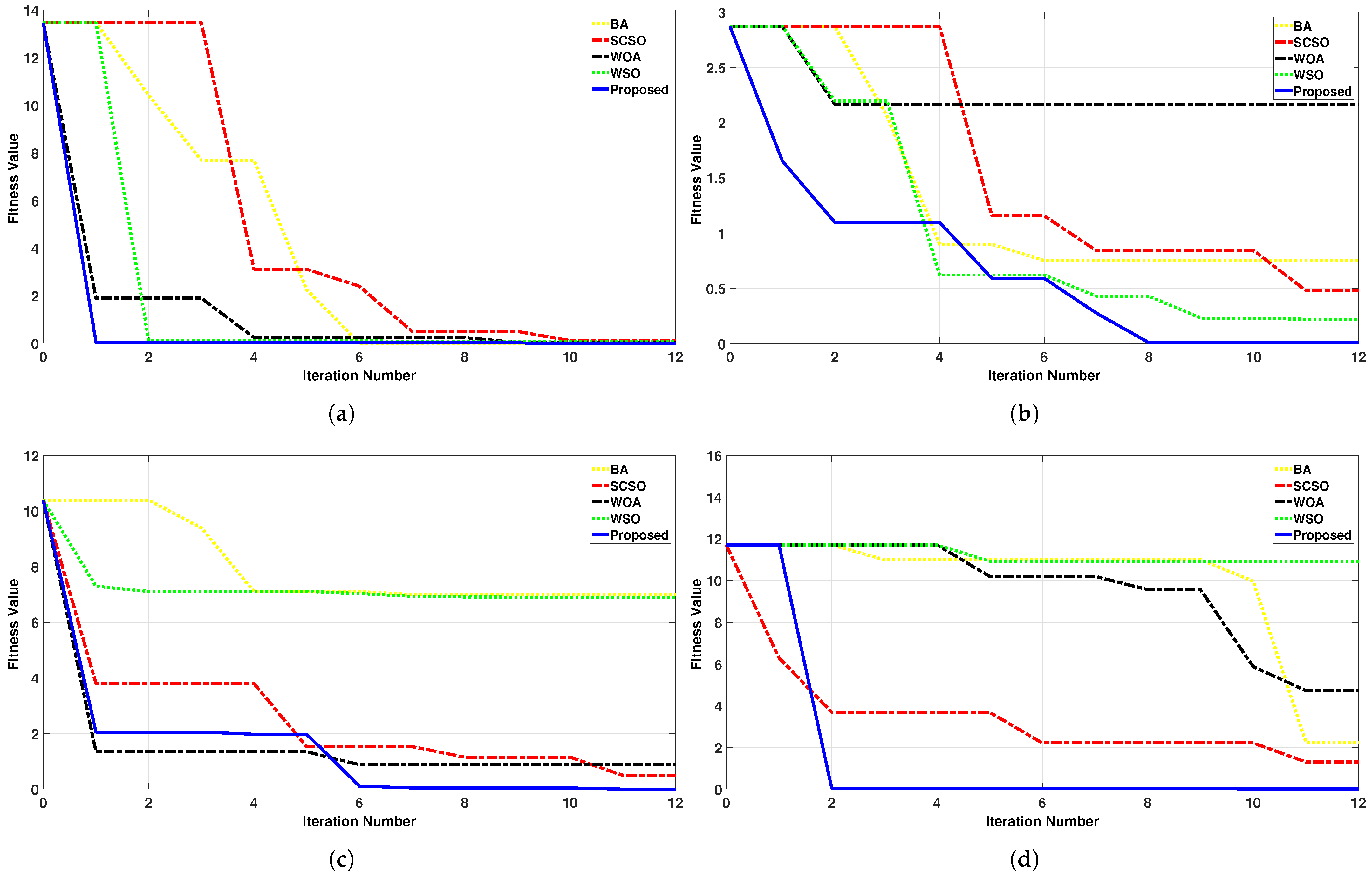
4.1. Static Case Results
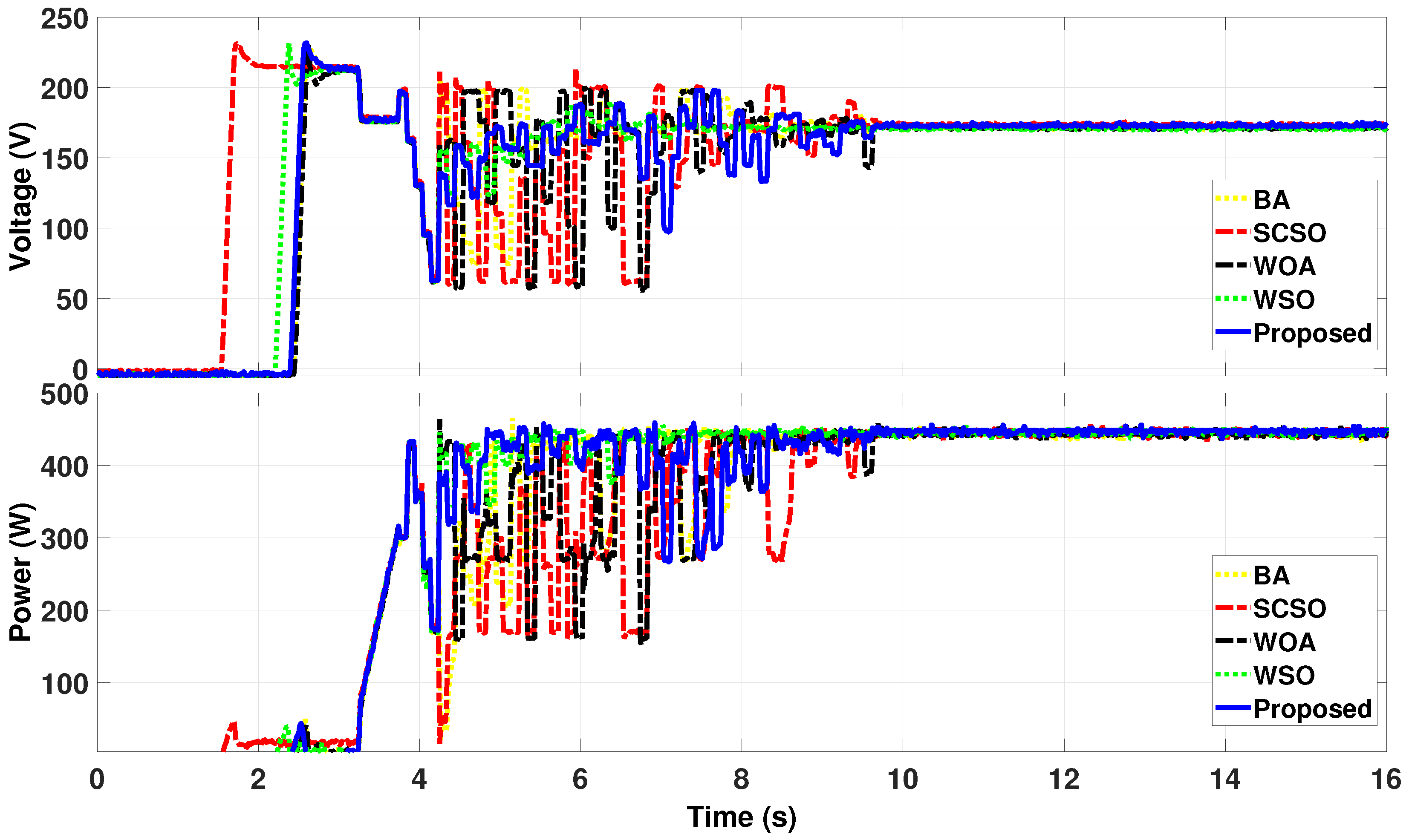
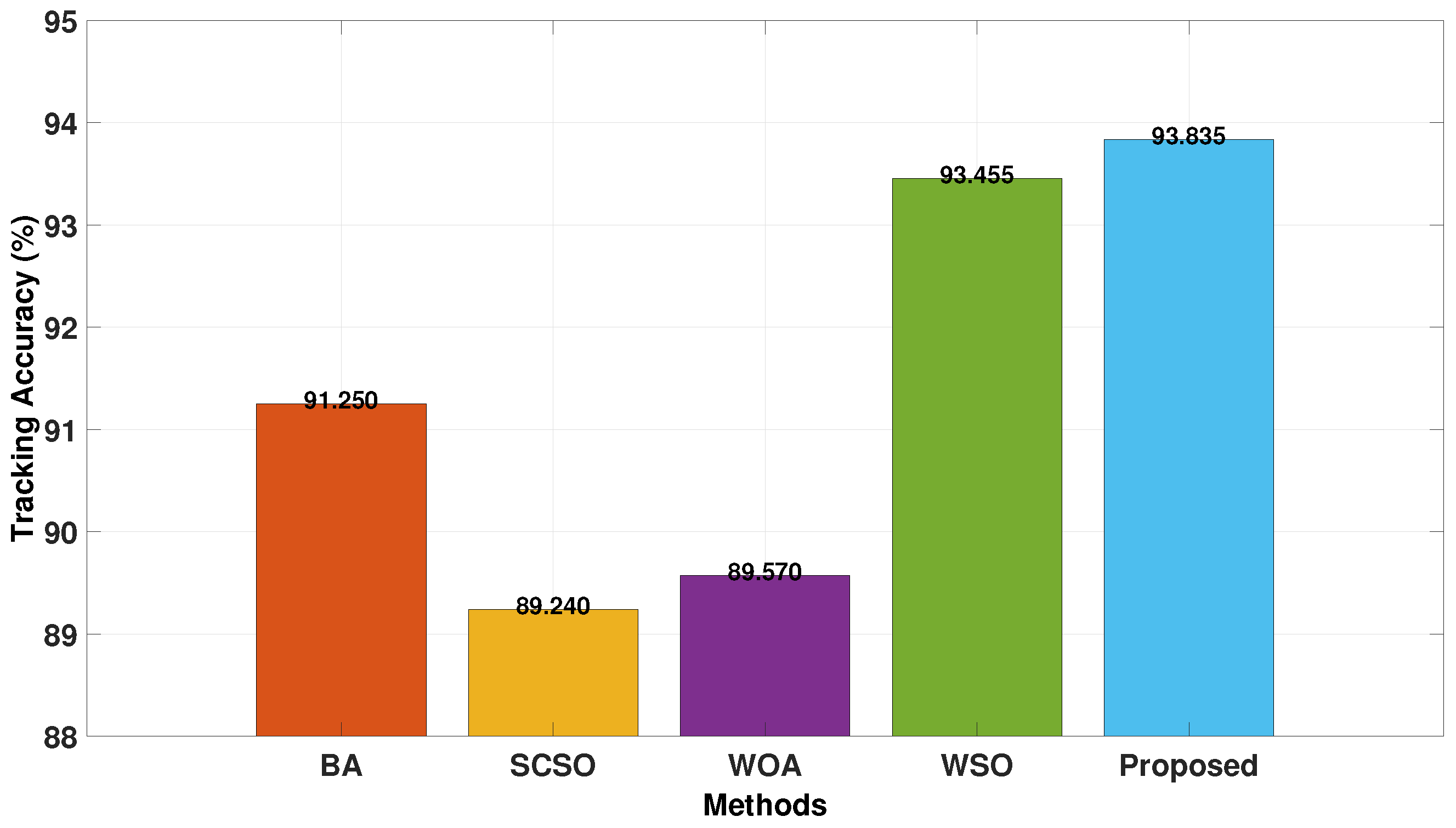
4.2. Dynamic Case Results
4.2.1. Dynamic Case 1
4.2.2. Dynamic Case 2
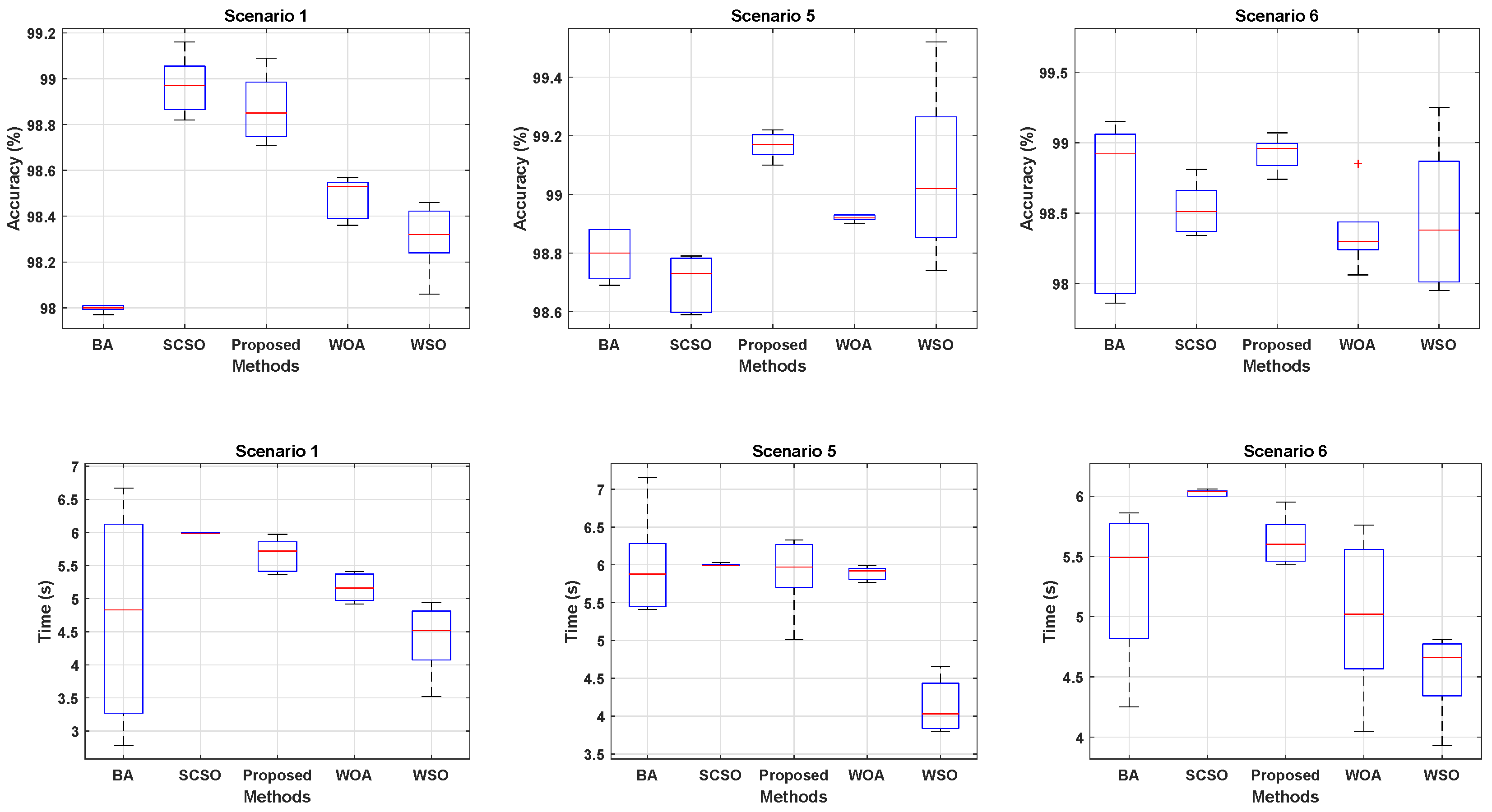
4.3. Discussions
- WSO exhibits a faster convergence than the hybrid model due to its inherently connected phases, inspired by natural biological processes. In contrast, the hybrid approach requires additional coordination time, as it combines distinct algorithms with differing optimization mechanisms.
- The hybrid method effectively explores the search space through PSO, the DEA, and the GWO, ensuring comprehensive optimization. While this enhances tracking efficiency, findings indicate that efficiency is more critical than speed in dynamic conditions. Notably, the proposed method achieves the highest dynamic tracking efficiency, which measures the ability of an MPPT approach to adapt to time-varying P-V curves. A higher dynamic tracking efficiency reflects superior MPPT performance.These insights underscore the trade-off between speed and efficiency, suggesting that while WSO provides rapid convergence, the hybrid approach offers enhanced adaptability and precision in dynamic environments.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclature
Abbreviations
| MHA | metaheuristic algorithm |
| MPPT | maximum power point tracking |
| PSO | particle swarm optimization |
| DEA | differential evolution algorithm |
| GWO | grey wolf optimizer |
| WSO | white shark optimizer |
| PV | photovoltaic |
| PSC | partial shading condition |
| GA | genetic algorithm |
| HHO | horse herd optimization |
| ChOA | chimp optimization algorithm |
| HRA | horse racing algorithm |
| DBO | dung beetle optimization |
| P&O | perturb and observe |
| InC | incremental conductance |
| GMPP | global maximum power point |
| GSS | golden section search |
| ABC | artificial bee colony |
| BA | bat algorithm |
| CS | cuckoo search |
| HBA | honey badger algorithm |
| ACO | ant colony optimization |
| ST-PSO | self-tuning particle swarm optimization |
| CSO | cat swarm optimization |
| WCO | water cycle optimization |
| FA | firefly algorithm |
| SO | snake optimizer |
| USC | uniform shading condition |
| MF | mayfly algorithm |
| GEO | golden eagle optimization |
| FLC | fuzzy logic controller |
| FPSO | fuzzy particle swarm optimization |
| DSP | digital signal processor |
| GPIO | general-purpose input/output |
| A/D | analog-to-digital |
| ePWM | enhanced pulse width modulation |
| SPI | serial peripheral interface |
| SCSO | sand cat swarm optimization |
| WOA | whale optimization algorithm |
Nomenclature
| MPPT System | |
| sampling interval | |
| efficiency of dynamic tracking | |
| PV current | |
| the previously identified GMPP | |
| the threshold for the GMPP | |
| load | |
| voltage of DC power supply | |
| PV voltage | |
| Parameters of All Algorithms | |
| minimum boundary | |
| T | maximum number of iteration |
| t | current number of iteration |
| maximum boundary | |
| the most optimal global position | |
| present position | |
| the personal best position | |
| Parameters of BA | |
| A | loudness |
| r | pulse rate |
| Parameters of DEA | |
| crossover rate | |
| F | scaling factor |
| Parameters of GWO | |
| A | coefficient vector |
| a | convergence constant |
| C | coefficient vector |
| D | the distance between an individual wolf and the next possible position |
| the position where the individual wolf is commanded by | |
| the position where the individual wolf is commanded by | |
| the position where the individual wolf is commanded by | |
| the fittest solution | |
| the second best solutions | |
| the third best solutions | |
| Parameters of PSO | |
| acceleration coefficient | |
| acceleration coefficient | |
| velocity of particle | |
| w | inertia weight |
| Parameter of SCSO | |
| sensitivity range | |
| Parameters of WSO | |
| revised location of the white shark | |
| constriction factor | |
| acceleration coefficient | |
| binary vector | |
| binary vector | |
| random vector | |
| random vector | |
| the distance between the shark and its prey | |
| f | wave motion frequency |
| maximum oscillation frequency | |
| minimum oscillation frequency | |
| movement force | |
| maximum velocity adjustment | |
| minimum velocity adjustment | |
| shark’s sensory intensity | |
| velocity vector | |
| logical vector |
References
- Naoussi, S.R.D.; Saatong, K.T.; Molu, R.J.J.; Mbasso, W.F.; Bajaj, M.; Louzazni, M.; Berhanu, M.; Kamel, S. Enhancing MPPT performance for partially shaded photovoltaic arrays through backstepping control with Genetic Algorithm-optimized gains. Sci. Rep. 2024, 14, 3334. [Google Scholar] [CrossRef] [PubMed]
- Refaat, A.; Ali, Q.A.; Elsakka, M.M.; Elhenawy, Y.; Majozi, T.; Korovkin, N.V.; Elfar, M.H. Extraction of maximum power from PV system based on horse herd optimization MPPT technique under various weather conditions. Renew. Energy 2024, 220, 119718. [Google Scholar] [CrossRef]
- Ashraf, H.M.; Elahi, M.; Kim, C.H. A novel technique using stretching, repulsion, and chimp optimization algorithm to find global maximum power point considering complex partial shading conditions. Int. J. Circuit Theory Appl. 2024, 52, 1322–1341. [Google Scholar] [CrossRef]
- Ngo, S.; Chiu, C.S.; Ngo, T.D. A Novel Horse Racing Algorithm Based MPPT Control for Standalone PV Power Systems. Energies 2022, 15, 7498. [Google Scholar] [CrossRef]
- Mai, C.; Zhang, L.; Chao, X.; Hu, X.; Wei, X.; Li, J. A novel MPPT technology based on dung beetle optimization algorithm for PV systems under complex partial shade conditions. Sci. Rep. 2024, 14, 6471. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Lian, K.L.; Jhang, J.H.; Tian, I.S. A Maximum Power Point Tracking Method Based on Perturb-and-Observe Combined With Particle Swarm Optimization. IEEE J. Photovoltaics 2014, 4, 626–633. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A New MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System Under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2016, 7, 181–188. [Google Scholar] [CrossRef]
- Nugraha, D.A.; Lian, K.L.; Suwarno. A Novel MPPT Method Based on Cuckoo Search Algorithm and Golden Section Search Algorithm for Partially Shaded PV System. Can. J. Electr. Comput. Eng. 2019, 42, 173–182. [Google Scholar] [CrossRef]
- Sathasivam, K.; Garip, I.; Saeed, S.H.; Yais, Y.; Alanssari, A.I.; Hussein, A.A.; Hammoode, J.A.; Lafta, A.M. A Novel MPPT Method Based on PSO and ABC Algorithms for Solar Cell. Electr. Power Components Syst. 2024, 52, 653–664. [Google Scholar] [CrossRef]
- Liao, C.Y.; Subroto, R.K.; Millah, I.S.; Lian, K.L.; Huang, W.T. An Improved Bat Algorithm for More Efficient and Faster Maximum Power Point Tracking for a Photovoltaic System Under Partial Shading Conditions. IEEE Access 2020, 8, 96378–96390. [Google Scholar] [CrossRef]
- Chao, K.H.; Rizal, M.N. A Hybrid MPPT Controller Based on the Genetic Algorithm and Ant Colony Optimization for Photovoltaic Systems under Partially Shaded Conditions. Energies 2021, 14, 2902. [Google Scholar] [CrossRef]
- Chtita, S.; Motahhir, S.; El Hammoumi, A.; Chouder, A.; Benyoucef, A.S.; El Ghzizal, A.; Derouich, A.; Abouhawwash, M.; Askar, S. A novel hybrid GWO–PSO-based maximum power point tracking for photovoltaic systems operating under partial shading conditions. Sci. Rep. 2022, 12, 10637. [Google Scholar] [CrossRef]
- Refaat, A.; Elbaz, A.; Khalifa, A.E.; Mohamed Elsakka, M.; Kalas, A.; Hegazy Elfar, M. Performance evaluation of a novel self-tuning particle swarm optimization algorithm-based maximum power point tracker for porton exchange membrane fuel cells under different operating conditions. Energy Convers. Manag. 2024, 301, 118014. [Google Scholar] [CrossRef]
- Gundogdu, H.; Demirci, A.; Tercan, S.M.; Cali, U. A Novel Improved Grey Wolf Algorithm Based Global Maximum Power Point Tracker Method Considering Partial Shading. IEEE Access 2024, 12, 6148–6159. [Google Scholar] [CrossRef]
- Chao, K.H.; Nguyen, T.B.N. Global Maximum Power Point Tracking of a Photovoltaic Module Array Based on Modified Cat Swarm Optimization. Appl. Sci. 2024, 14, 2853. [Google Scholar] [CrossRef]
- Jabbar, R.I.; Mekhilef, S.; Mubin, M.; Alshammari, O.; Kazaili, A. A Fast MPPT Method Based on Improved Water Cycle Optimization Algorithm for Photovoltaic Systems Under Partial Shading Conditions and Load Variations. IEEE Open J. Ind. Electron. Soc. 2024, 5, 1324–1338. [Google Scholar] [CrossRef]
- Teshome, D.F.; Lee, C.H.; Lin, Y.W.; Lian, K.L. A Modified Firefly Algorithm for Photovoltaic Maximum Power Point Tracking Control Under Partial Shading. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 661–671. [Google Scholar] [CrossRef]
- Mohammed, K.K.; Mekhilef, S. Improved Snake Optimizer Algorithm-Based GMPPT With a Fast Response to the Load Variations Under Different Weather Conditions for PV Systems. IEEE Trans. Ind. Electron. 2024, 71, 7147–7157. [Google Scholar] [CrossRef]
- Mo, S.; Ye, Q.; Jiang, K.; Mo, X.; Shen, G. An improved MPPT method for photovoltaic systems based on mayfly optimization algorithm. Energy Rep. 2022, 8, 141–150. [Google Scholar] [CrossRef]
- Millah, I.S.; Chang, P.C.; Teshome, D.F.; Subroto, R.K.; Lian, K.L.; Lin, J.F. An Enhanced Grey Wolf Optimization Algorithm for Photovoltaic Maximum Power Point Tracking Control Under Partial Shading Conditions. IEEE Open J. Ind. Electron. Soc. 2022, 3, 392–408. [Google Scholar] [CrossRef]
- Qasim, M.A.; Alwan, N.T.; PraveenKumar, S.; Velkin, V.I.; Agyekum, E.B. A New Maximum Power Point Tracking Technique for Thermoelectric Generator Modules. Inventions 2021, 6, 88. [Google Scholar] [CrossRef]
- Pandey, A.K.; Singh, V.; Jain, S. Maximum Power Point Tracking Algorithm Based on Fuzzy Logic Control Using P-V and I-V Characteristics for PV Array. IEEE Trans. Ind. Appl. 2023, 59, 4572–4583. [Google Scholar] [CrossRef]
- Letting, L.; Munda, J.; Hamam, Y. Optimization of a fuzzy logic controller for PV grid inverter control using S-function based PSO. Sol. Energy 2012, 86, 1689–1700. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Sagar Bhaskar, M.; Blaabjerg, F.; Sharma, A. Fuzzy SVPWM-based inverter control realisation of grid integrated photovoltaic-wind system with fuzzy particle swarm optimisation maximum power point tracking algorithm for a grid-connected PV/wind power generation system: Hardware implementation. IET Electr. Power Appl. 2018, 12, 962–971. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.; Awadallah, M.A. White Shark Optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl.-Based Syst. 2022, 243, 108457. [Google Scholar] [CrossRef]
- Hu, K.; Cao, S.; Li, W.; Zhu, F. An Improved Particle Swarm Optimization Algorithm Suitable for Photovoltaic Power Tracking Under Partial Shading Conditions. IEEE Access 2019, 7, 143217–143232. [Google Scholar] [CrossRef]
- Tey, K.S.; Mekhilef, S.; Yang, H.T.; Chuang, M.K. A differential evolution based MPPT method for photovoltaic modules under partial shading conditions. Int. J. Photoenergy 2014, 2014, 945906. [Google Scholar] [CrossRef]
- Alwan, N.T.; Majeed, M.H.; Shcheklein, S.E.; Ali, O.M.; PraveenKumar, S. Experimental Study of a Tilt Single Slope Solar Still Integrated with Aluminum Condensate Plate. Inventions 2021, 6, 77. [Google Scholar] [CrossRef]
- PraveenKumar, S.; Kumar, A. Thermodynamic, environmental and economic analysis of solar photovoltaic panels using aluminium reflectors and latent heat storage units: An experimental investigation using passive cooling approach. J. Energy Storage 2025, 112, 115487. [Google Scholar] [CrossRef]
- da Rocha, M.V.; Sampaio, L.P.; da Silva, S.A.O. Comparative analysis of MPPT algorithms based on Bat algorithm for PV systems under partial shading condition. Sustain. Energy Technol. Assess. 2020, 40, 100761. [Google Scholar] [CrossRef]
- Li, L.; Zhao, W.; Wang, H.; Xu, Z.; Ding, Y. Sand cat swarm optimization based maximum power point tracking technique for photovoltaic system under partial shading conditions. Int. J. Electr. Power Energy Syst. 2024, 161, 110203. [Google Scholar] [CrossRef]
- Kumar, C.; Rao, R.S. A novel global MPP tracking of photovoltaic system based on whale optimization algorithm. Int. J. Renew. Energy Dev. 2016, 5, 225–232. [Google Scholar] [CrossRef]
- Kadhim, N.A.; Obed, A.A.; Abid, A.J.; Kotb, H.; Emara, A. Optimal PV Reconfiguration Under Partial Shading Based on White Shark Optimization. IEEE Access 2024, 12, 27385–27398. [Google Scholar] [CrossRef]
- Gui, Q.; Wang, L.; Ding, C.; Xu, W.; Li, X.; Yu, F.; Wang, H. Multi-Peak Photovoltaic Maximum Power Point Tracking Method Based on Honey Badger Algorithm Under Localized Shading Conditions. Energies 2025, 18, 1258. [Google Scholar] [CrossRef]
- Bouselham, L.; Hajji, M.; Hajji, B.; Bouali, H. A New MPPT-based ANN for Photovoltaic System under Partial Shading Conditions. Energy Procedia 2017, 111, 924–933. [Google Scholar] [CrossRef]


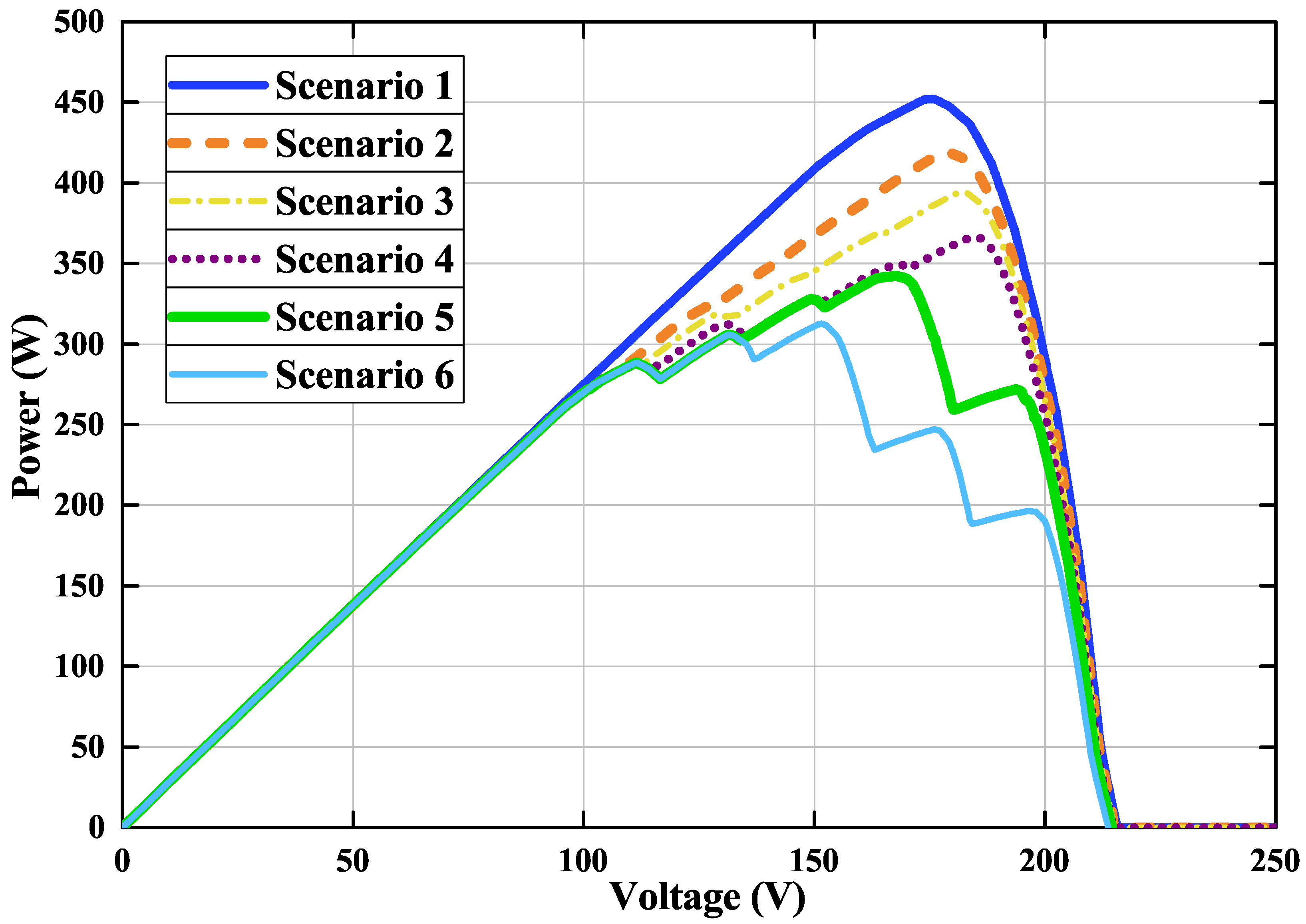

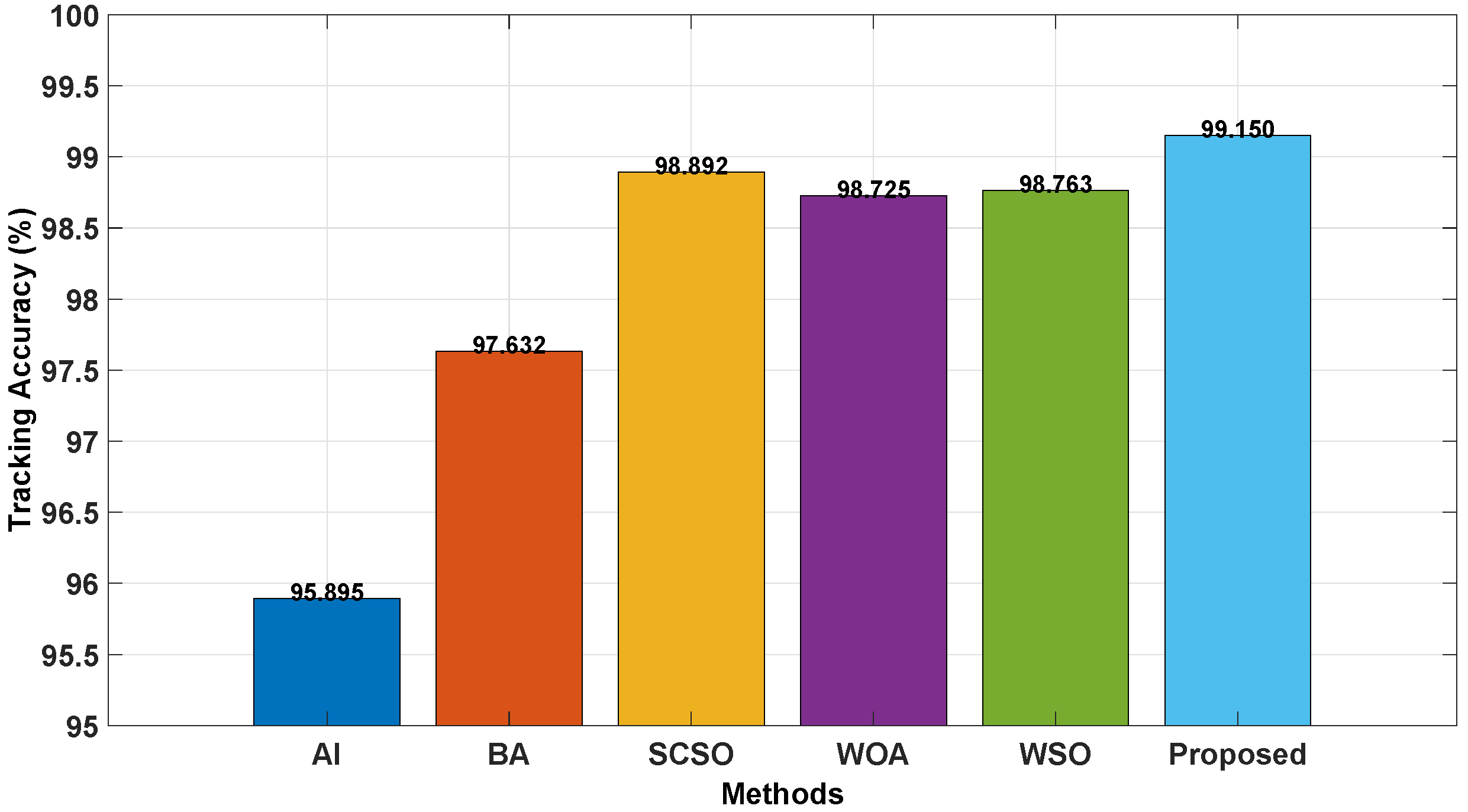


| PV Module | Scenario | Temperature (°C) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1–7 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 25 |
| 8 | 1000 | 940 | 910 | 800 | 850 | 750 | 25 |
| 9 | 1000 | 900 | 850 | 800 | 800 | 850 | 25 |
| 10 | 1000 | 880 | 820 | 760 | 750 | 350 | 25 |
| 11 | 1000 | 860 | 790 | 720 | 500 | 500 | 25 |
| Algorithm | Parameters | |
|---|---|---|
| Hybrid | PSO | w = 0.3; = 1.5; = 1.5 |
| DEA | F = 0.5; = 0.9 | |
| GWO | a = 2 | |
| BA | = 2; = 0; A = 0.9; r = 0.1 | |
| SCSO | = 2 | |
| WOA | a = 2; b = 1; | |
| WSO | = 1.5; = 0.5; = 6.25; = 100; = 0.0005 |
| Algorithm | Scenario | Average | |||
|---|---|---|---|---|---|
| No. 1 | No. 5 | No. 6 | |||
| BA [31] | Accuracy STD CI | 98.00% 0.016 (97.986, 98.014) | 98.78% 0.068 (98.720, 98.840) | 98.58% 0.558 (98.091, 99.069) | 98.45% |
| SCSO [32] | Accuracy STD CI | 98.97% 0.118 (98.867, 99.073) | 98.70% 0.086 (98.625, 98.775) | 98.53% 0.171 (98.380, 98.680) | 98.73% |
| Proposed | Accuracy STD CI | 98.87% 0.136 (98.703, 99.041) | 99.17% 0.042 (99.116, 99.220) | 98.92% 0.109 (98.824, 99.016) | 98.99% |
| WOA [33] | Accuracy STD CI | 98.48% 0.086 (98.405, 98.555) | 98.92% 0.008 (98.913, 98.927) | 98.36% 0.260 (98.132, 98.588) | 98.59% |
| WSO [34] | Accuracy STD CI | 98.31% 0.139 (98.188, 98.432) | 99.07% 0.267 (98.836, 99.304) | 98.47% 0.479 (98.050, 98.890) | 98.62% |
| BA [31] | Time (s) STD CI | 4.73 1.463 (3.448, 6.012) | 5.98 0.632 (5.426, 6.534) | 5.27 0.588 (4.755, 5.785) | 5.33 |
| SCSO [32] | Time (s) STD CI | 5.99 0.007 (5.984, 5.996) | 6.00 0.015 (5.987, 6.013) | 6.03 0.025 (6.008, 6.052) | 6.01 |
| Proposed | Time (s) STD CI | 5.66 0.233 (5.456, 5.864) | 5.90 0.471 (5.487, 6.313) | 5.63 0.186 (5.467, 5.793) | 5.73 |
| WOA [33] | Time (s) STD CI | 5.17 0.196 (4.998, 5.342) | 5.89 0.082 (5.818, 5.962) | 5.01 0.599 (4.485, 5.535) | 5.36 |
| WSO [34] | Time (s) STD CI | 4.40 0.498 (3.963, 4.837) | 4.14 0.326 (3.854, 4.426) | 4.53 0.321 (4.249, 4.811) | 4.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Farisi, F.K.; Fan, Z.-K.; Lian, K.-L. Comparative Study of White Shark Optimization and Combined Meta-Heuristic Algorithm for Enhanced MPPT in Photovoltaic Systems. Energies 2025, 18, 2110. https://doi.org/10.3390/en18082110
Al Farisi FK, Fan Z-K, Lian K-L. Comparative Study of White Shark Optimization and Combined Meta-Heuristic Algorithm for Enhanced MPPT in Photovoltaic Systems. Energies. 2025; 18(8):2110. https://doi.org/10.3390/en18082110
Chicago/Turabian StyleAl Farisi, Fajar Kurnia, Zhi-Kai Fan, and Kuo-Lung Lian. 2025. "Comparative Study of White Shark Optimization and Combined Meta-Heuristic Algorithm for Enhanced MPPT in Photovoltaic Systems" Energies 18, no. 8: 2110. https://doi.org/10.3390/en18082110
APA StyleAl Farisi, F. K., Fan, Z.-K., & Lian, K.-L. (2025). Comparative Study of White Shark Optimization and Combined Meta-Heuristic Algorithm for Enhanced MPPT in Photovoltaic Systems. Energies, 18(8), 2110. https://doi.org/10.3390/en18082110







