Adaptive Gain-Based Double-Loop Full-Order Terminal Sliding Mode Control of a Surface-Mounted PMSM System

Abstract

This article proposes a new adaptive gain, full-order terminal sliding mode control algorithm for the speed regulation of a surface-mounted permanent magnet synchronous motor (SPMSM) control system. To deal with the mismatched uncertainties in the double-loop nonlinear system of the SPMSMs, a virtual control technique is constructed with the full-order terminal sliding mode control to ensure that the tracking error trajectory can converge to equilibrium in finite time. Owing to the integral control law, the output signals of the controllers are smoothed, with the chattering phenomenon attenuated and the gain-margin overestimation avoided. Comprehensive simulation and experimental results have been carried out to demonstrate the superiority of the proposed method in improving tracking accuracy, rapidness, and robustness to the matched and mismatched uncertainties.

1. Introduction

The surface-mounted permanent magnet synchronous motor (SPMSM), renowned for its high power factor and fast dynamic response, is widely used in industrial applications [1,2]. The inherent nonlinear characteristics of the PMSM, coupled with external disturbances such as load torque variations and parameter deviations, render the design of its controller a challenging endeavor. This complexity has motivated the development of diverse control methodologies for PMSM systems, encompassing techniques such as proportional-integral (PI) control, adaptive control, model predictive control, and sliding mode control (SMC) [3,4,5,6,7].

Generally, the mathematical model of the SPMSM belongs to a category of second-order nonlinear systems characterized by both matched and mismatched uncertainties [8,9]. In the field orientation control (FOC) of SPMSMs, the matched uncertainties composed of the parameter variations in the current loops can be compensated by the voltage control law, whereas the mismatched uncertainties containing both parameter variations and load torque fluctuations in the speed loop cannot be handled straightforwardly [10,11]. In existing works, the controllers are generally based on the reduced-order model of the SPMSM without considering the influence of mismatched uncertainties [12,13]. In [12], a model predictive current control based on a sliding mode speed controller is proposed for the PMSM system by designing the speed and current controllers separately. In reference [13], a novel reaching law based on sliding mode control (SMC) is introduced for the speed regulation of PMSMs. However, the current controller is implemented as a PI controller, which fails to account for the second-order characteristics inherent in the PMSM dynamics. Consequently, there is a need for advanced control strategies for the SPMSMs that can effectively counteract the effects of mismatched uncertainties and enhance disturbance rejection capabilities.

Thanks to the strong robustness to external disturbances and low sensitivity to modeling errors and system parameter perturbations, the SMC has attracted significant attention in many applications, especially in the PMSM control system [14,15,16]. Some SMC-based methods have been proposed to deal with mismatched uncertainties [17,18,19,20,21]. In [17], a quasi-sliding mode controller utilizing the saturation function is designed for the PMSM system with mismatched uncertainties. However, the boundary-layer-based SMC would decrease the control accuracy. The integral sliding mode control (ISMC) ensures that system states asymptotically converge to zero [18], while the mismatched disturbances are constrained under the assumptions of being slowly varying or constant [19]. In [20], a disturbance observer-based sliding mode control (DOBSMC) is developed to suppress persistent uncertainties in the system, provided they can be accurately estimated. However, this approach also inherits the restrictive assumptions, like those in ISMC [21]. Both ISMC and DOBSMC commonly rely on the premise that disturbances are either slowly varying or constant, which fundamentally limits the robustness and efficacy of these control methodologies.

The inherent chattering imperfection caused by the high-frequency switching function becomes an extreme restriction in applying SMC [22,23]. In the d- and q-axis current controllers, the output voltages are designed to be smooth, necessarily because the α- and β-axis voltages transformed from the output voltages, regarded as the input signals of the space vector pulse width modulation (SVPWM), must be continuous without chattering. Therefore, a chattering-free algorithm is needed in the control law design for the current controllers. In the speed controller, the output currents must be continuous for two reasons:

• The d- and q-axis currents cannot track their high-frequency switching references generated by traditional SMC methods.
• The d- and q-axis voltages contain the derivatives of the d- and q-axis currents, and the derivatives of high-frequency switching currents would lead to singularity [24,25].

Unless the chattering problem can be solved, the traditional SMC should not be directly applied to PMSM control systems. Meanwhile, there is still no SMC-based method that can take into account the smoothness of the output signals in both the speed and the current controllers for PMSM control systems with mismatched uncertainties, although many chattering-free SMC-based methods have already been proposed [26,27,28].

After thoroughly reviewing and analyzing the existing literature, this paper proposes a full-order terminal sliding mode (FOTSM) control algorithm-based virtual control technique for dealing with the matched and mismatched uncertainties in the SPMSM control system. The chattering is attenuated, and the smooth output signals of speed and current controllers can be acquired employing integral control law [29]. The accuracy, rapidness, and anti-disturbance of controllers can be improved, and the high-performance control of the SPMSM control system can be realized. The innovation and challenges can be outlined as follows:

• Disturbance-rejection performance for both the matched and mismatched uncertainties in SPMSM systems is simultaneously improved when designing the speed and current controllers.
• The distinctive integral-type control law guarantees continuous control input, which is indicative of rapid and precise system response. This control strategy introduces a distinctive approach to resolving the chattering phenomenon observed in both virtual and real control signals, thereby mitigating the ripple effect in speed and current dynamics.
• The adaptive switching gain is designed to prevent the overcontrol deficiency caused by the algebraic loop issue and to save energy in the dynamic procedure of the SPMSM control system.

This paper is structured as follows: Section 2 presents the mathematical model of the SPMSM under matched and mismatched disturbances. Section 3 designs the control frameworks based on FOTSM. Section 4 demonstrates simulation and experimental results. Finally, Section 5 provides the concluding remarks.

2. The Model of SPMSM with Uncertainties

The mathematical model of SPMSM is expressed by

$$\left\{\begin{array}{l}\dot{\omega }=(1.5P_n{\psi }_f{i}_q-T_L)/J\\ {\dot{i}}_q=(-R{i}_q+u_{sq}-P_n\omega (L{i}_d+{\psi }_f))/L\\ {\dot{i}}_d=(-R{i}_d+u_{sd}+P_n\omega L{i}_q)/L\end{array}\right.$$

(1)

where u_sd,q are the stator voltages of d- and q- axis, and i_d,q are the stator currents of the d- and q-axis. The d-axis and q-axis inductances of SPMSM are equal to L. R is the stator resistance, ψ_f the flux linkage, P_n the number of pole pairs, ω the rotor mechanical angular velocity, J the moment of inertia, and T_L the load torque.

It defines speed tracking error and current tracking errors as e_ω = ω_ref − ω, e_iq = i_qref − i_q, e_id = i_dref − i_d; then, according to (1), the error dynamics can be expressed by

$$\left\{\begin{array}{l}{\dot{e}}_{\omega }={\dot{\omega }}_{ref}-G{i}_q+T_L/J\\ {\dot{i}}_q=-P_n\omega i_d-P{i}_q-Q{P}_n{\psi }_f\omega +Q{u}_{sq}\\ {\dot{e}}_{i_d}=-P_n\omega i_q+P{i}_d-Q{u}_{sd}\end{array}\right.$$

(2)

where G = 3P_nψ_f/(2J), P = R/L,Q = 1/L. The virtual control signal is defined by $\tilde{u}$ = Gi_qref.

Considering the influence of aging and temperature, the parameters of the SPMSMs may be changed by

$$R=R_0+\Delta R,L=L_0+\Delta L,J=J_0+\Delta J$$

(3)

where ${\left[·\right]}_0$ and $∆\left[·\right]$ are the nominal and the changed values.

In order to analyze the mismatched and matched uncertainties, some definitions are expressed as

$$\begin{array}{c}\delta ={\displaystyle \frac{1}{(J_0+\Delta J)}}-{\displaystyle \frac{1}{J_0}}=-{\displaystyle \frac{\Delta J}{J_0(J_0+\Delta J)}},\hspace{1em}\Delta Q={\displaystyle \frac{1}{L_0+\Delta L}}-{\displaystyle \frac{1}{L_0}}=-{\displaystyle \frac{\Delta L}{L_0(L_0+\Delta L)}},\\ \Delta P={\displaystyle \frac{R_0+\Delta R}{L_0+\Delta L}}-{\displaystyle \frac{R_0}{L_0}}={\displaystyle \frac{L_0\Delta R-R_0\Delta L}{L_0(L_0+\Delta J)}}\end{array}$$

(4)

and the boundaries of the uncertainties are assumed by

$$\begin{array}{c}\left|\delta \right|\le M_{\delta }<1, \left|T_L/J\right|\le M_{T_L/J}, \left|\Delta P\right|\le M_{R/L}, \left|{\dot{T}}_L/J\right|\le M_{d{T}_L/J},\\ \left|\Delta Q\right|\le M_{1/L}, \left|u_{sd,q}\right|\le \sqrt{2}{u}_e, \left|i_{d,q}\right|\le \sqrt{2}{i}_e\end{array}$$

(5)

where M_δ, M_TL/J, M_R/L, M_dTL/J, and M_1/L are positive constants, u_e is the rated voltage, and i_e the rated current.

Therefore, the error dynamics can be rewritten as follows:

$$\left\{\begin{array}{l}{\dot{e}}_{\omega }={\dot{\omega }}_{ref}-\tilde{u}+d_{\omega }+G{e}_{iq}\\ {\dot{i}}_q=-P_n\omega i_d-P_0{i}_q+(Q_0+\Delta Q)u_{sq}-Q_0{P}_n{\psi }_f\omega +d_{iq}\\ {\dot{e}}_{i_d}=-P_n\omega i_q+P_0{i}_d-(Q_0+\Delta Q)u_{sd}+d_{id}\end{array}\right.$$

(6)

where the uncertainties are expressed by

$$d_{\omega }=T_L/J-\delta \tilde{u}, d_{iq}=\Delta P{i}_q-\Delta Q{P}_n{\psi }_f\omega , d_{id}=\Delta P{i}_d$$

(7)

The matched uncertainties and their derivatives are assumed bounded, which should satisfy the following conditions:

$$\left|d_{id}\right|\le M_{dd}, \left|d_{iq}\right|\le M_{dq}, \left|{\dot{d}}_{id}\right|\le M_{ddd}, \left|{\dot{d}}_{iq}\right|\le M_{ddq}$$

(8)

where

$$\begin{array}{l}{M}_{dd}=M_{R/L}\left|i_d\right|, M_{dq}=M_{R/L}\left|i_q\right|+M_{1/L}{P}_n{\psi }_f\omega \\ M_{ddd}=M_{R/L}(P_0\left|i_d\right|+(Q_0+M_{1/L})\sqrt{2}{u}_e+M_{dd})\\ M_{ddq}=M_{R/L}(P_0\left|i_q\right|+(Q_0+M_{1/L})\sqrt{2}{u}_e+M_{dq})+M_{1/L}{P}_n{\psi }_f(1.5P_n{\psi }_f\left|i_q\right|/J+M_{T_L/J})\end{array}$$

(9)

To achieve decoupling between the d- and q-axis currents and voltages, a feedforward compensation term is developed for the d- and q-axis voltages as follows:

$$u_s=T-H+u$$

(10)

where u_s = [u_sq, u_sd]^T, u = [u_q, u_d]^T, i = [i_q, i_d]^T, T = [0, P_nω/Q; −P_nω/Q, 0], and H = [P_n ψ_f ω, 0]^T.

Therefore, (6) can be reformed into

$${\dot{e}}_{\omega }={\dot{\omega }}_{ref}-\tilde{u}+d_{\omega }+G{e}_{iq}$$

(11a)

$${\dot{i}}_q=-P_0{i}_q+Q_0{u}_q+\Delta Q{u}_q+d_{iq}$$

(11b)

$${\dot{e}}_{id}=P_0{i}_d-Q_0{u}_d+\Delta Q{u}_d+d_{id}$$

(11c)

The block diagram of the FOC system for the SPMSM is presented in Figure 1.

The speed error dynamics and the q-axis current dynamics collectively constitute a second-order, single-input, single-output (SISO) nonlinear system characterized by parameter mismatches and uncertainties.

Lemma 1. 

(Finite-time convergence [30]) Consider the system $\dot{x}$ = f(x), f(x) = 0, x ∈ Rⁿ, if there exists a positive definite continuous function V(x): U→R, real number $c$ and $\alpha$ satisfy c > 0, 0 < α < 1, and a neighborhood U₀ ⸦ U of the origin such that $\dot{V}$ (x) + cV^α(x) ≤ 0, x ⸦ U₀, then V(x) can converge to zero in a finite time t_r, t_r ≤ V^1−α(x(0))/(c(1 − α)).

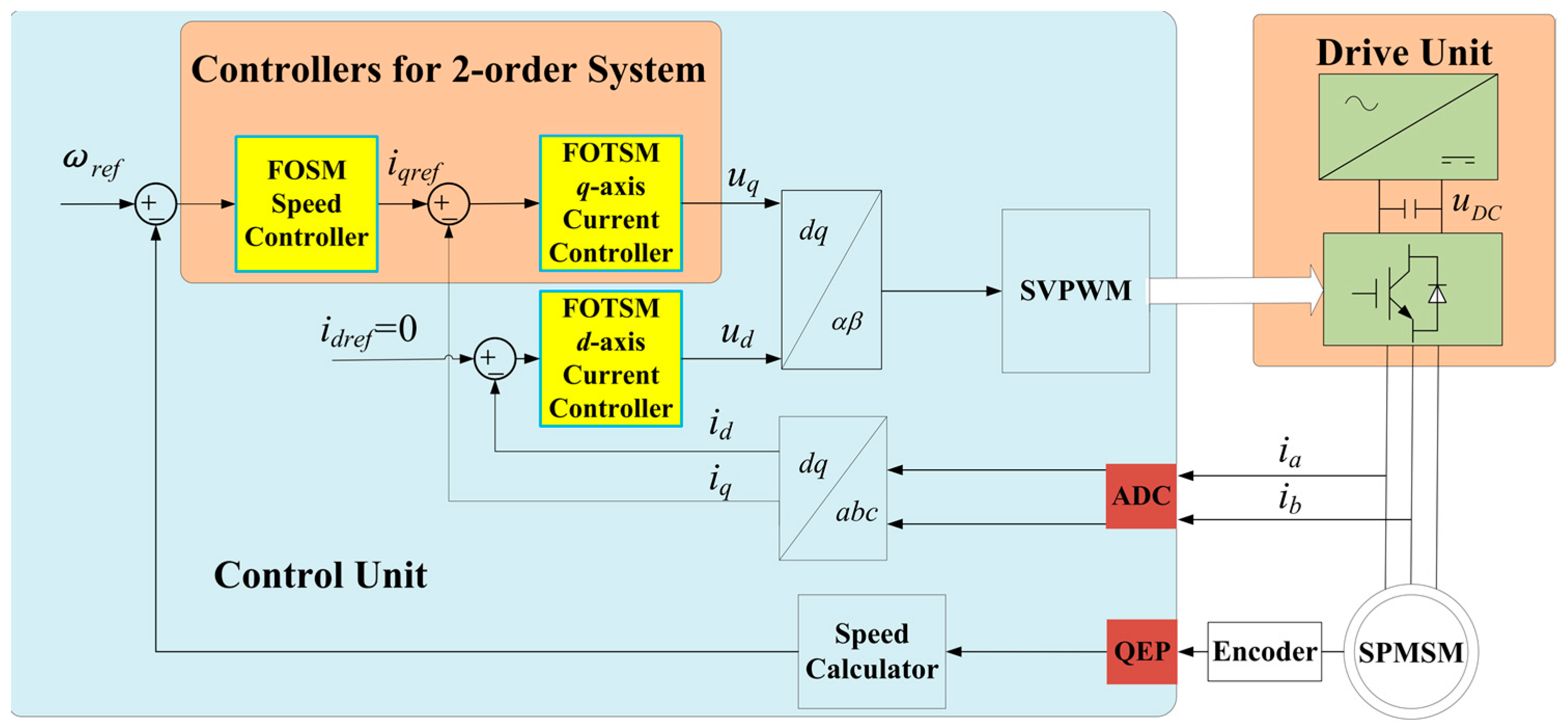
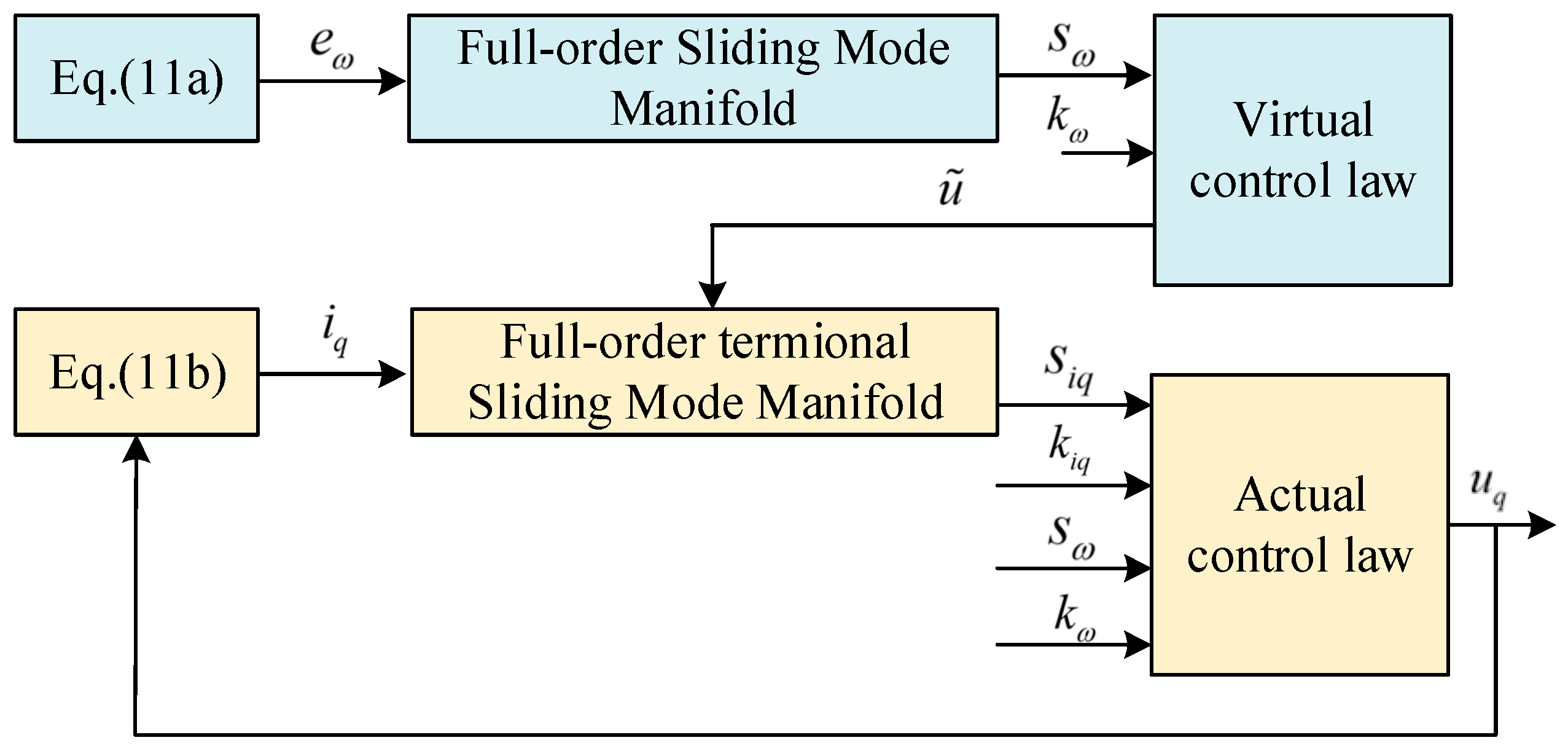
3. Controller Design Based on the FOTSM

This paper aims to design a full-order sliding mode-based controller such that the speed can track its reference accurately and rapidly even in the presence of mismatched uncertainties. The full-order sliding mode controller design for the SPMSM can be divided into two steps:

• The speed controller is designed to make the speed track its reference, i.e., d_ω can be forced to approach zero rapidly by the VCL ũ. The virtual control technique is synthesized into the design of the speed controller, and the VCL ũ is utilized to cope with the mismatched uncertainties d_ω;
• In the current loops, the control strategy of i_ref = 0 is adopted to realize the decoupled control for the FOC system based on the SPMSM. The d- and q-axis current controllers are designed to make the d- and q-axis currents i_d,q track their references accurately and rapidly. The current errors e_id,iq can be forced to converge to zero in finite time by the actual control laws u_d,q, which are used to compensate the matched uncertainties d_id,iq.

For the speed-loop error dynamics (11a), a full-order sliding manifold s_ω is designed as

$$s_{\omega }={\dot{e}}_{\omega }+C_1{e}_{\omega }$$

(12)

where C₁ is a positive constant.

Remark 1. 

The sliding manifold is designed utilizing the full-order sliding mode (FOSM) approach [29], thus, the error systems behave as desirable full-order dynamics rather than reduced-order dynamics during the sliding-mode motion. The control law can be designed as the integral type, which avoids the introduction of the high-frequency switching signal. Due to eliminating the high-frequency switching signal in the VCL, i_qref is a smooth signal, which means the chattering in i_qref can be eliminated. Benefitting from the above characteristics, the q-axis current can be forced to track its reference quickly and accurately, and, meanwhile, the singularity problem caused by the derivative of the q-axis reference current can be avoided.

Proposition 1. 

Considering the speed-loop error dynamics (11a), a full-order sliding manifold (12) is defined, and the FOSM speed controller incorporating integral virtual control with adaptive gain is designed, ensuring that the speed error dynamics approach zero provided that the q-axis current error converges to zero. The corresponding equations are detailed as follows:

$$\tilde{u}={\tilde{u}}_{eq}+{\tilde{u}}_n$$

(13a)

$${\tilde{u}}_{eq}={\dot{\omega }}_{ref}+C_1{e}_{\omega }$$

(13b)

$${\tilde{u}}_n={\displaystyle {\int }_0^t{k}_{\omega }\mathrm{sgn}(s_{\omega })d\tau }$$

(13c)

$$k_{\omega }={\displaystyle \frac{M_{\delta }{M}_{d\omega eq}+M_{d{T}_L/J}+{\eta }_{\omega }}{1-M_{\delta }}}$$

(13d)

where M_dωeq is the upper bound of ũ and η_ω is a positive constant.

Proof. 

Substituting (11), (13a), and (13b) into (12), the full-order sliding manifold is

$$\begin{array}{c}{s}_{\omega }={\dot{\omega }}_{ref}-\tilde{u}+d_{\omega }+G{e}_{iq}+C_1{e}_{\omega }\\ =-{\tilde{u}}_n-\delta {\tilde{u}}_n+G{e}_{iq}+T_L/J\end{array}$$

(14)

Selecting the Lyapunov function V_ω = 0.5$s_{\omega }^2$ and computing its time derivative yields

$$\begin{array}{ll}{\dot{V}}_{\omega }& =s_{\omega }{\dot{s}}_{\omega }\\ & =-s_{\omega }{\dot{\tilde{u}}}_n-s_{\omega }\delta \dot{\tilde{u}}+s_{\omega }{\dot{T}}_L/J+s_{\omega }G{\dot{e}}_{iq}\\ & =-s_{\omega }{\dot{\tilde{u}}}_n-s_{\omega }\delta {\dot{\tilde{u}}}_n-s_{\omega }\delta {\dot{\tilde{u}}}_{eq}+s_{\omega }{\dot{T}}_L/J+s_{\omega }G{\dot{e}}_{iq}\end{array}$$

(15)

Combining with the boundaries (5) and the integral switching law (13c) will yield

$${\dot{V}}_{\omega }\le -k_{\omega }(1-M_{\delta })\left|s_{\omega }\right|+M_{\delta }\left|s_{\omega }\right|{\dot{\tilde{u}}}_{eq}+\left|s_{\omega }\right|M_{d{T}_L/J}+s_{\omega }G{\dot{e}}_{iq}$$

(16)

The derivative of ${\dot{\tilde{u}}}_{eq}$ (13b) can be expressed as

$${\dot{\tilde{u}}}_{eq}={\ddot{\omega }}_{ref}+C_1{\dot{e}}_{\omega }$$

(17)

The upper bound of ${\dot{\tilde{u}}}_{eq}$ can be estimated as

$$\left|{\dot{\tilde{u}}}_{eq}\right|\le M_{d\omega eq}$$

(18)

where M_dωeq can be expressed by

$$M_{d\omega eq}=\left|{\ddot{\omega }}_{ref}\right|+C_1(\left|{\dot{\omega }}_{ref}\right|+G(1+M_{\delta })\sqrt{2}{i}_e+M_{T_L/J})$$

(19)

Then, it will yield

$${\dot{V}}_{\omega }\le -\left|s_{\omega }\right|(k_{\omega }(1-M_{\delta })-M_{\delta }{M}_{d\omega eq}-M_{dd})+G{s}_{\omega }{\dot{e}}_{iq}$$

(20)

Considering the adaptive gain (13d), it can yield

$${\dot{V}}_{\omega }\le -{\eta }_{\omega }\sqrt{2}{V}_{\omega }^{1/2}+G{s}_{\omega }{\dot{e}}_{iq}$$

(21)

According to Lemma 1, it is obvious that if the q-axis current tracking error e_iq and its derivative ${\dot{e}}_{iq}$ can converge to zero in finite time by the later Theorem 1, it will yield

$${\dot{V}}_{\omega }\le -\sqrt{2}{\eta }_{\omega }{V}_{\omega }^{1/2}<0, \mathrm{for} V_{\omega }\ne 0.$$

(22)

As seen from (22), the speed error dynamics (11a) can reach the sliding manifold s_ω = 0 in a finite time t_rω ≤ |s_ω0|/η_ω. Afterwards, e_ω and its derivative ${\dot{e}}_{\omega }$ can be forced to asymptotically approach to zero along the manifold s_ω(t) = 0, where the mismatched uncertainties can be handled by the VCL $\tilde{u}$. Hence, the proof is completed. □

Considering the q-axis current dynamics in (11b), a full order terminal sliding manifold s_iq can be constructed by

$$s_{iq}={\dot{e}}_{iq}+C_2{e}_{iq}^{p/q}$$

(23)

where C₂ is a positive constant, and p and q are odd, which should satisfy 0 < p/q < 1.

Theorem 1. 

For the q-axis current dynamics in (11b), a full order terminal sliding manifold in (23) is first chosen. Then, an FOTSM-based q-axis current controller with both the integral actual and virtual control laws in Proposition 1 can be designed, where the q-axis current dynamics can be regulated to reach the ideal sliding motion s_iq(t) = 0 from the initial condition s_iq(t) ≠ 0 in finite time t_rq, t_rq ≤ |s_rq(0)|/η_iq, and afterwards, e_iq and its derivative ${\dot{e}}_{iq}$ can converge to zero in finite time t_sq from any initial condition s_iq(t) ≠ 0, t_sq ≤ t_rq +q |e_iq (t_rq)|/(C₂(q − p)). Related equations can be found by

$$u_q=u_{qn}+u_{qeq}$$

(24a)

$$u_{qeq}=Q_0^{-1}(P_0{i}_q+C_2{e}^{p/q}+G^{-1}({\ddot{\omega }}_{ref}+C_1{\dot{\omega }}_{ref}))-Q_0^{-1}{G}^{-1}(C_{1}G{i}_q-k_{\omega }\mathrm{sgn}{s}_{\omega })$$

(24b)

$$u_n={\displaystyle {\int }_0^t{k}_{iq}\mathrm{sgn}(s_{iq})}d\tau$$

(24c)

$$k_{iq}={\displaystyle \frac{M_{1/L}{M}_{dqeq}+M_{ddq}+G^{-1}{C}_1{M}_{d{T}_L/J}+{\eta }_{iq}}{Q_0-M_{1/L}}}$$

(24d)

where M_dωeq is the upper bound of the derivative of u_qeq, as illustrated by

$$M_{dqeq}=(P_0+C_2)(P_0\left|i_q\right|+(Q_0+M_{1/L})\sqrt{2}{u}_e+M_{dq})$$

(25)

and η_iq is a positive constant.

Proof. 

Substituting (11b) and (24a) into (23), the full order terminal sliding manifold is reformed into

$$\begin{array}{ll}{s}_{iq}& ={\dot{i}}_{qref}+P_0{i}_q-Q_0{u}_q-\Delta Q{u}_q-d_{iq}+C_2{e}_{iq}^{p/q}\\ & =-Q_0{u}_{qn}-\Delta Q{u}_q-d_{iq}+C_1{G}^{-1}d\omega \end{array}$$

(26)

Selecting the Lyapunov function V_iq = 0.5$s_{iq}^2$ and computing its time derivative yields

$${\dot{V}}_{iq}=s_{iq}{\dot{s}}_{iq}=-s_{iq}(Q_0{\dot{u}}_{qu}+\Delta Q{\dot{u}}_q+{\dot{d}}_{iq}-C_1{G}^{-1}{\dot{d}}_{\omega })$$

(27)

which can then be rewritten as

$${\dot{V}}_{iq}=s_{iq}{\dot{s}}_{iq}=-s_{iq}(Q_0{\dot{u}}_{qn}+\Delta Q{\dot{u}}_q+{\dot{d}}_{iq})+s_{iq}{C}_1{G}^{-1}({\dot{T}}_L/J-\delta \dot{\tilde{u}})$$

(28)

Substituting (24a) into (28) will yield

$$\begin{array}{ll}{\dot{V}}_{iq}& =-s_{iq}(Q_0{\dot{u}}_{qn}+\Delta Q{\dot{u}}_{qn}+\Delta Q{\dot{u}}_{qeq}+{\dot{d}}_{iq})+s_{iq}{C}_1{G}^{-1}({\dot{T}}_L/J-\delta \dot{\tilde{u}})\\ & \le s_{iq}(-k_{iq}{Q}_0+k_{iq}|\Delta Q|+|\Delta Q\left|\right|{\dot{u}}_{qeq}\left|\right|{\dot{d}}_{iq}|)+s_{iq}{C}_1{G}^{-1}(|{\dot{T}}_L/J|+|\delta \left|\right|\dot{\tilde{u}}|)\end{array}$$

(29)

According to (13) and (19), the upper bound of ũ is estimated by

$$\left|\dot{\tilde{u}}\right|\le \left|{\dot{\tilde{u}}}_{eq}\right|+\left|{\dot{\tilde{u}}}_n\right|\le M_{d\omega eq}+\sqrt{2}{k}_{\omega }$$

(30)

Combined with variable switching gain (24d), it will yield

$${\dot{V}}_{iq}\le -\sqrt{2}{\eta }_{iq}{V}^{1/2}<0, \mathrm{for} V_{iq}\ne 0.$$

(31)

The q-axis current dynamics (11b) can reach the sliding manifold s_iq(t) = 0 from any initial condition s_iq(t) ≠ 0 in finite time t_rq ≤ |s_iq(0)|/η_iq. The total time t_sq from s_iq(t) ≠ 0 to ${\dot{e}}_{iq}=0$ and e_iq = 0 satisfies

$$t_{sq}\le t_{rq}+q|e_{iq}(t_{rq}){|}^{1-p/q}/(C_2(q-p))$$

(32)

The speed-loop error e_ω can be guaranteed to converge to zero when e_iq and ${\dot{e}}_{iq}$ converge to zero. Hence, the proof is completed. □

Remark 2. 

The simple diagram of the FOTSM controller for the second-order SISO system, as proposed in the paper, is shown in Figure 2. Under the action of the integral actual control law, the output signal can be smoothed without the high-frequency switching signal. Hence, the FOTSM can guarantee that the control system has finite-time convergence and a strong disturbance rejection capability to uncertainties.

Considering the d-axis current error dynamics in (11c), it can be assumed to be a first-order system, which means only the matched uncertainties exist. Therefore, a full-order terminal sliding manifold can be constructed by

$$s_{id}={\dot{e}}_{id}+C_3{e}_{id}^{p/q}$$

(33)

where C₃ is a positive constant, and p and q are odd, which should meet 0 < p/q < 1.

Theorem 2. 

For the d-axis current error dynamics (11c), a full-order terminal sliding manifold (33) is selected, and an FOTSM-based d-axis current controller with the integral actual control law and the variable gain is designed, in which the d-axis current error dynamics can reach the ideal sliding motion s_i (t) = 0 from the initial condition s_id (t) ≠ 0 in finite time t_rd, t_rd ≤ |s_id (0)|/η_id, then e_id and its derivative ${\dot{e}}_{id }$ can be forced to converge to zero in finite time t_sd, t_sd ≤ t_rd +q |e_id (t_rd)|/(C₃(q − p)). Related equations can be found by

$$u_d=u_{dn}+u_{deq}$$

(34a)

$$u_{deq}=P_0{i}_d/Q_0$$

(34b)

$$u_{dn}={\displaystyle {\int }_0^t{k}_{id}\mathrm{sgn}(s_{id})}d\tau$$

(34c)

$$k_{id}={\displaystyle \frac{M_{1/L}{M}_{dded}+M_{ddd}+{\eta }_{id}}{Q_0-M_{1/L}}}$$

(34d)

where M_dqeq is the upper bound of u_qeq, as illustrated by

$$M_{dqeq}=(P_0+C_2)(P_0|i_q|+(Q_0+M_{1/L})\sqrt{2}{u}_e+M_{dq})$$

(35)

and η_iq is a positive constant.

Proof. 

Substituting (34a) and (34b) into (33), the full order terminal sliding manifold is reformed into

$$\begin{array}{ll}{s}_{id}& =P_0{i}_d-Q_0{u}_d-\Delta Q{u}_d-d_{id}+C_3{e}_{id}^{p/q}\\ & =-Q_0{u}_{dn}-Q{u}_d-d_{id}\end{array}$$

(36)

Selecting the Lyapunov function $V_{id}=0.5s_{id}^2$ and computing its time derivative yields

$${\dot{V}}_{id}=s_{id}{\dot{s}}_{id}=-s_{id}(Q_0{\dot{u}}_{dn}+\Delta Q{\dot{u}}_d+{\dot{d}}_{id})$$

(37)

Substituting (34a) into (37) will yield

$$\begin{array}{ll}{\dot{V}}_{id}& =-s_{id}(Q_0{\dot{u}}_{dn}+\Delta Q{\dot{u}}_{dn}+\Delta Q{\dot{u}}_{deq}+{\dot{d}}_{id})\\ & \le s_{id}(-k_{id}{Q}_0+k_{id}|\Delta Q|+|\Delta Q\left|\right|{\dot{u}}_{deq}|+|{\dot{d}}_{id}|)\end{array}$$

(38)

Combined with (34d) will yield

$${\dot{V}}_{id}\le -\sqrt{2}{\eta }_{id}{V}_{id}^{1/2}<0, \mathrm{for} :V_{id}\ne 0$$

(39)

Similar to Theorem 1, the d-axis current error dynamics in (11c) can reach s_id = 0 from any initial condition s_id ≠ 0 in a finite time t_rd, t_rd ≤ |s_id (0)|/η_id. Then, e_id and $\dot{e}$_id can converge to zero in finite time. The total time from s_id ≠ 0 to e_id = 0 and $\dot{e}$_id = 0 satisfies

$$t_{sd}\le t_{rd}+q|e_{id}(t_{rd}){|}^{1-p/q}/(C_3(q-p))$$

(40)

Hence, the proof is completed. □

Remark 3. 

Using the virtual law ũ and actual laws u_d,q, the matched and mismatched uncertainties in the FOC system based on the SPMSM can be thoroughly compensated, which can improve the rapidity, accuracy, and disturbance rejection capability of the SPMSM system.

4. Experiments

To validate the effectiveness of the proposed method, a comprehensive experiment was conducted on an SPMSM experimental platform (Wuhan Heli Changrong Electromechanical Co., Ltd., Wuhan, China) utilizing the TMS320F28335 controller (Texas Instruments, Dallas, TX, USA), driven by an inserted PMSM (IPMSM), as depicted in Figure 3. The SPMSM parameters are provided in

Table 1. Main parameters of the SPMSM.

Symbol	Name	Value and Unit
P	Rated power	3 kW
nN	Rated speed	2000 rpm
Pn	Polar logarithm	3
R	Stator resistance	0.8 Ω
L	Stator inductance	5 mH
J	Moment of inertia	0.00378 kg·m2
ψf	Rotor flux linkage	0.35 Wb
T	Rated torque	14 N m
ue	Rated voltage	380 V
ie	Rated current	5.2 A

, while the speed and current controller parameters for the three methods are detailed in

Table 2. Controller design parameters in experiment.

Method Controller Name		Gain Value
PI	Speed PI	kp = 50, ki = 20
	Current PI	kp = 110, ki = 50
linear sliding mode (LSM)	Speed LSM	s = 10eω, k = 1100
	Current PI	kp = 50, ki = 30
FOTSM	Speed FOSM	$s_{\omega }={\dot{e}}_{\omega }+500e_{\omega },{\eta }_{\omega }=15$
	q-axis current FOTSM	$s_{iq}={\dot{e}}_{iq}+500e_{iq}^{3/5},{\eta }_{iq}=15$
	d-axis current FOTSM	$s_{id}={\dot{e}}_{id}+500e_{id}^{3/5},{\eta }_{id}=15$

. Considering uncertainties arising from aging and temperature variations, the values of R, L, and J in the control algorithm are adjusted to 150% of their nominal values.

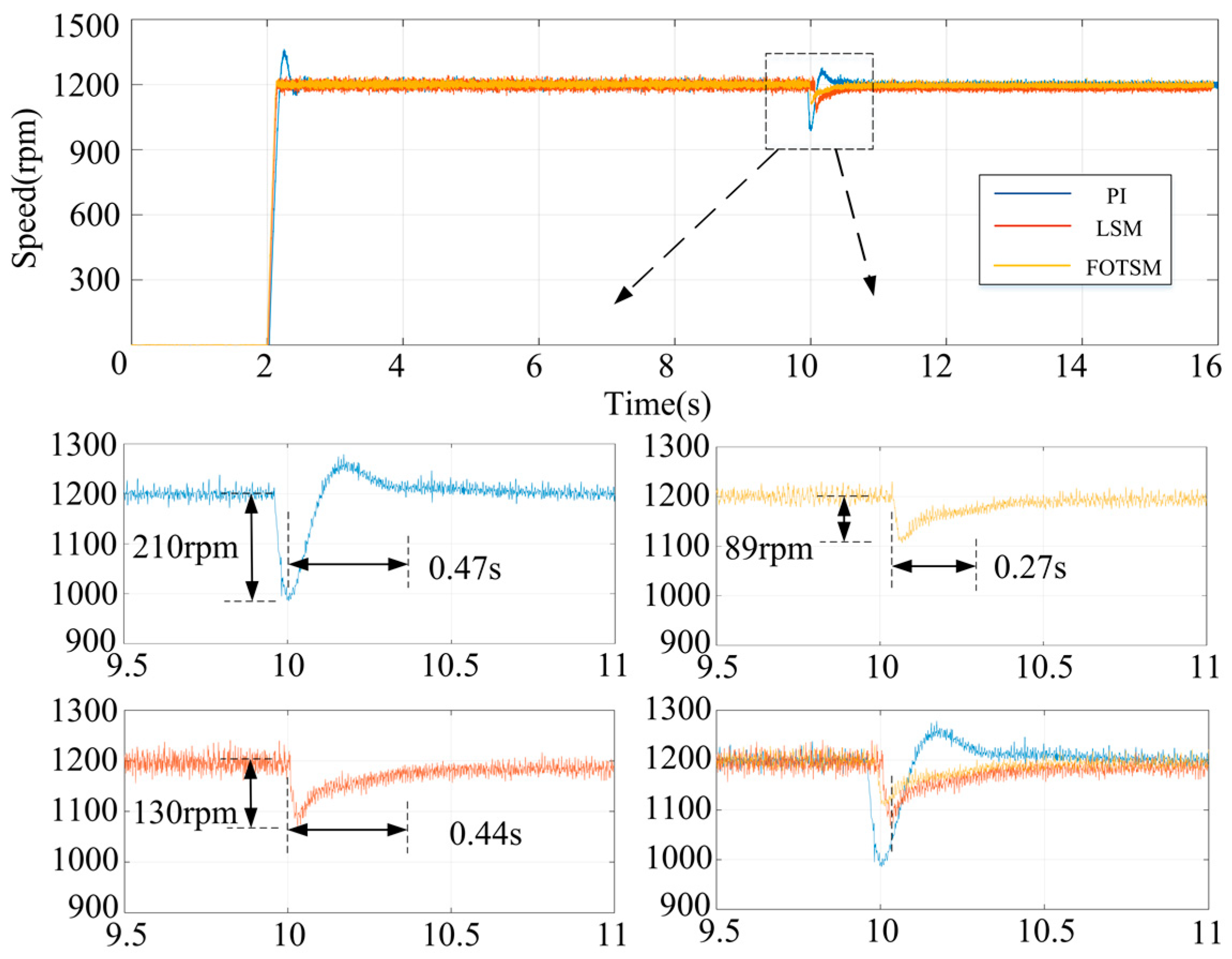
4.1. Response to Small Load Addition

A comprehensive comparative analysis is conducted to evaluate the start-up and load addition performance under the three control methods (PI, LSM, and FOTSM). The reference speed is prescribed at 500 rpm, with a load torque of 5 N m introduced at 10 s. As illustrated in Figure 4, the speed and current responses of the three methods are presented for detailed comparison. Observing Figure 4a, the PI method exhibits a significant overshoot of 25.6%, whereas the other two methods demonstrate minimal overshoot. The settling times of the speed response during the initialization phase are recorded as 0.439 s, 0.236 s, and 0.205 s for PI, LSM, and FOTSM, respectively. Upon the application of the load torque at 10 s, the speed degradation under the three methods is measured as 93 rpm, 65 rpm, and 50 rpm, respectively. Furthermore, the recovery period of the speed response under each method is observed to be 0.41 s, 0.38 s, and 0.08 s, respectively. These results indicate that the proposed FOTSM method achieves superior dynamic characteristics in terms of response rapidity and resilience against disturbances compared to the other two methods.

From Figure 4b, it is evident that the q-axis current regulated by FOTSM attains steady state more promptly than the other two approaches. Specifically, the FOTSM exhibits a lower current ripple magnitude compared to LSM, which underscores its enhanced ability to attenuate chattering and produce a smoother output signal, facilitated by the integral control law.

4.2. Response to Large Load Addition

To further investigate the disturbance rejection capability of the proposed approach, an augmented load torque of 10 N m is applied at 10 s. A comparative analysis of the speed and q-axis current responses under the three control methods is presented in Figure 5. As shown in Figure 5a, the speed decrements under the three methods are 115 rpm, 99 rpm, and 53 rpm, respectively. The corresponding response recovery times for the speed are 0.42 s, 0.4 s, and 0.096 s, respectively, which highlights that the FOTSM exhibits superior disturbance rejection capability with faster convergence compared to the other methods. Furthermore, as depicted in Figure 5b, the q-axis current response by FOTSM demonstrates faster dynamic characteristics during both the start-up and load addition processes, outperforming both PI and LSM in terms of response speed. Additionally, the q-axis current ripple by FOTSM is significantly smaller than that by LSM, which further validates the effectiveness of the proposed method in suppressing chattering and achieving smoother current regulation.

4.3. Speed-Reverse Response

The comparison of speed performance under the three methods is shown in Figure 6 under the speed-reverse condition where the reference speed is from 0 rpm to 500 rpm at 2 s, and back to −500 rpm at 10 s. From Figure 6a, it is noted that only the PI has an overshoot of the speed while the other two methods exhibit minimal overshoot during the transient of the speed-reverse operation. The recovery time under the three methods is 0.31 s, 0.35 s, and 0.13 s, respectively, which illustrates that FOTSM has better dynamic performance in rapidity. It can be concluded that the q-axis current ripple and chattering under FOTSM are much smaller than those under LSM.

4.4. High-Speed Response

The speed performances of the SPMSM under the three methods are evaluated under high-speed conditions. The reference speed is set to 1200 rpm, and a load of 5 N m is applied at 10 s. The results clearly demonstrate that only the PI method exhibits an overshoot, while the other two methods do not. Furthermore, the proposed method achieves the reference speed more rapidly than both PI and LSM during the start-up process, as illustrated in Figure 7. The speed drops under the three methods are 210 rpm, 130 rpm and 89 rpm, respectively, when adding the load. The recovery time of the speed response under the three methods is 0.47 s, 0.44 s, and 0.27 s, respectively, which further illustrates that the FOTSM has the best performance in terms of anti-disturbance and rapidity.

Moreover, to make the comparative results more comprehensive in this paper, the improved sliding mode reaching law (SMRL)-based SMC in [26] and predictive function control (PFC) in [31] is shown in

Table 3. Performance comparison of controllers.

Items	Control Scheme	PI	PFC	SMRL	FOTSM
Start up-low speed	Settling time (s)	0.44	0.24	-	0.205
	Overshoot (%)	25	5.7	-	0
Add load-low speed	Speed drop (rpm)	93	36	-	50
	Recovery time (s)	0.41	0.193	-	0.096
Start up-high speed	Settling time (s)	0.23	-	0.045	0.133
	Overshoot (%)	9.2	-	0	0
Add load-high speed	Speed drop (rpm)	445	-	390	92
	Recovery time (s)	0.7	-	0.4	0.31

. The reference speeds for both SMRL and PFC are 1600 rpm and 500 rpm. The set values of the load in [26,31] are 5 N m and 2.5 N m. As depicted in Table 3, the proposed method has a slight advantage in rapidness and disturbance rejection capability.

5. Conclusions

This research presents an innovative adaptive-gain FOTSM control strategy tailored for double-loop SPMSM systems subjected to mismatched uncertainties. Our contribution lies in the development of a unique FOTSM-based VCL, which enables high-performance control of the SPMSM system. Distinguishing itself from existing control methods, the proposed approach is derived from the full-order nonlinear mathematical model of the SPMSM, ensuring that both matched and mismatched uncertainties in the system are comprehensively addressed. This enhances the disturbance rejection capability of the SPMSM system significantly. By leveraging the virtual control methodology based on FOTSM, the speed and current tracking errors are driven to converge to zero. The proposed method reveals three significant advantages.

• The matched and mismatched uncertainties in SPMSM systems are incorporated into the control algorithm design, and the virtual control signal is specially engineered to effectively counteract these uncertainties, ensuring robust control performance under diverse operating conditions.
• The innovatively designed integral-type law addresses the chattering prompted by high-frequency switching terms, thus deriving smooth current-reference and voltage signals, which are essential for precise system control.
• The adaptive law for the switching gain is proven highly effective in suppressing the over-control caused by the algebraic loop issue, thus leading to energy savings in the convergence procedure of the SPMSM control system.

Although the control performance of the proposed method is excellent, the definition of the disturbance boundary is too conservative, and an adaptive method can be used to improve it in the future.