Piezoelectric Particulate Composite for Energy Harvesting from Mechanical Vibration
Abstract
:1. Introduction
2. Materials and Methods
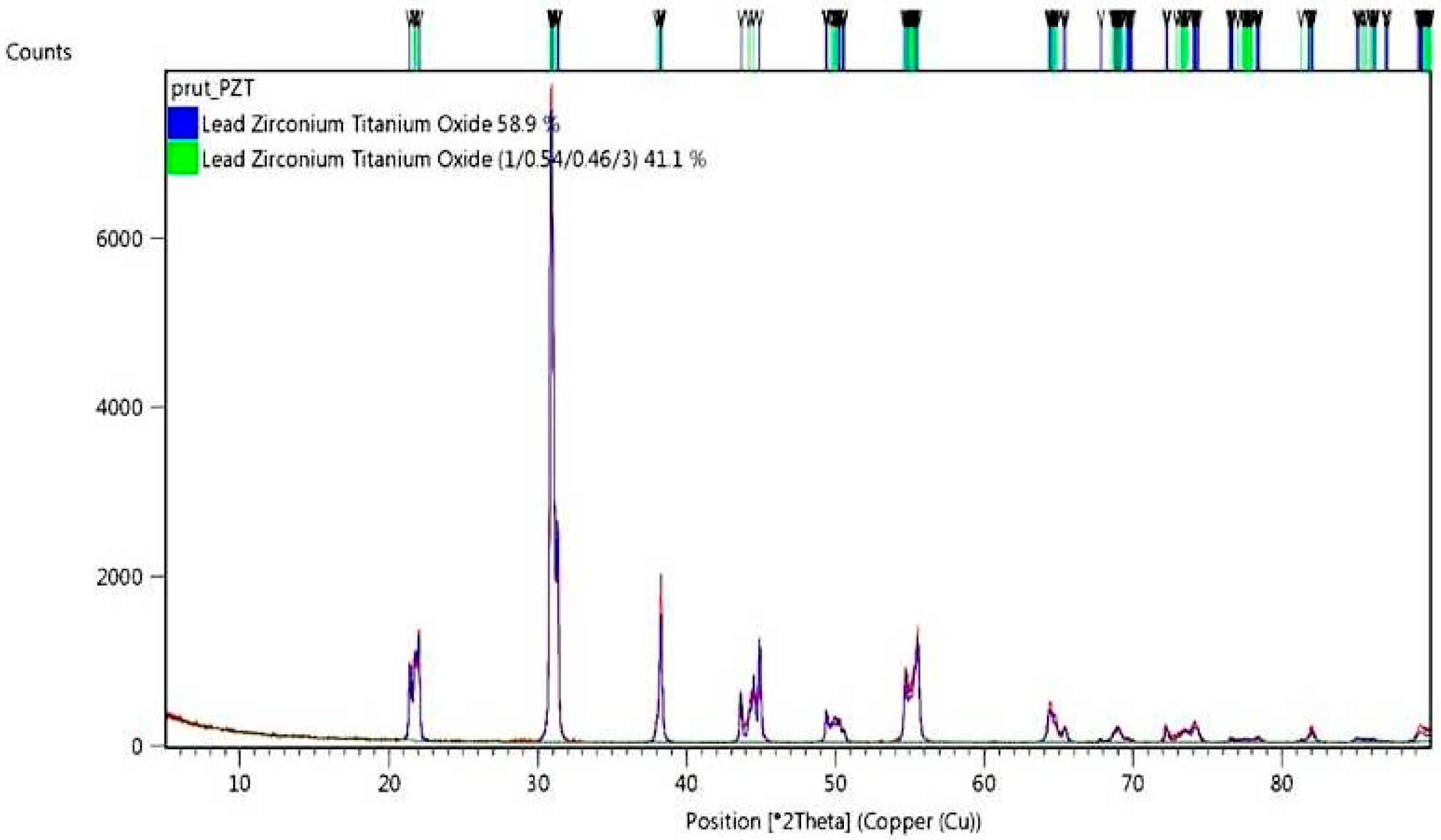
2.1. Manufacturing of Piezoelectric Material
- Mixing the PZT grains and Duracryl Plus powder in a rotational dissolver, manufactured by Pendraulik-Teja, for 30 min. The volume fraction of PZT grains in the mixture was 50% and 40%. Liquid monomer was added during the mixing process.
- Creating the prismatic beam in a special prototype metal mold. The general dimensions of the formed beam were permanent: length 110 mm, width 28 mm. The value of thickness depended on the volume fraction of the PZT powder.
- Polishing the composite beam surfaces by the Rotopol-22 Struers device.
- Covering the composite beam surface with two copper electrodes.
- Poling the composite beam in a special prototype polarization stand, given in Figure 4.
2.2. Methods Used in Laboratory Research
2.3. Methods Used in Numerical Research
3. Results
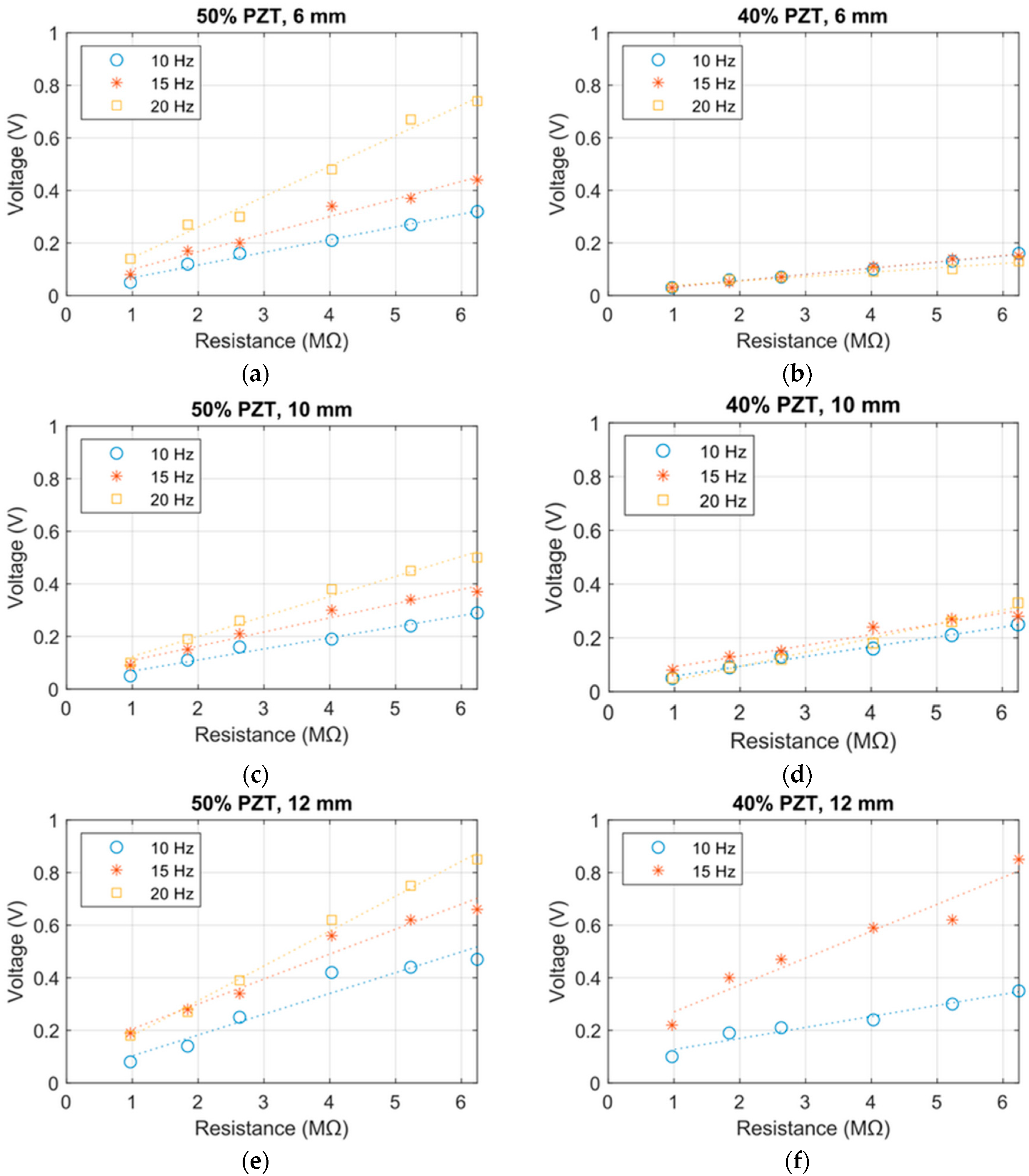
3.1. Results of the Laboratory Research
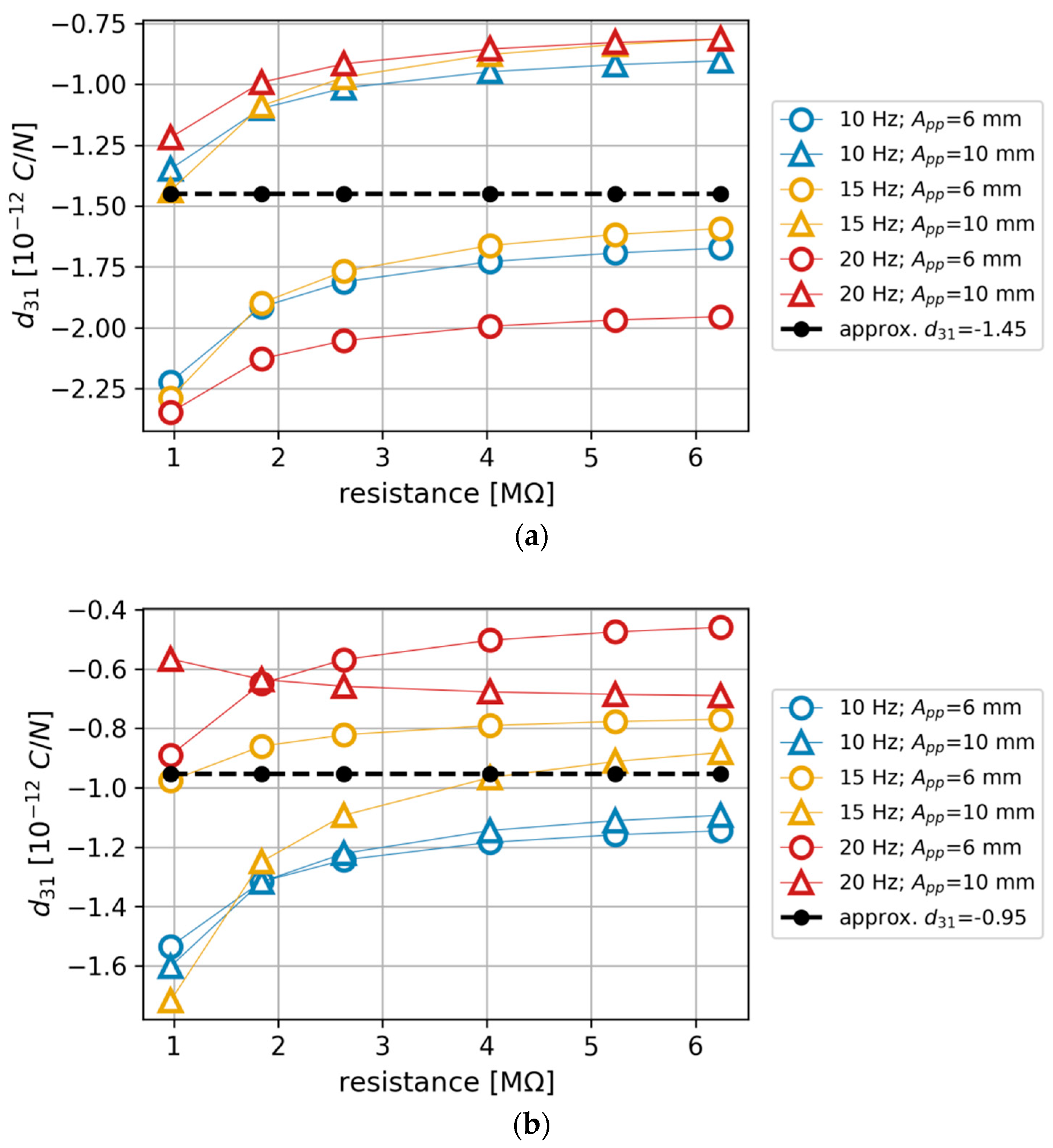
3.2. Results of the Numerical Research
- εm—dielectric constant of polymer (εm = 3)
- εi—dielectric constant of PZT (εi = 1700)
- vi—volume fraction of PZT
- —effective Young modulus for the composite
- —thickness of the piezoelectric layer
- —total thickness of the composite
- —piezoelectric coefficient of the piezoelectric layer
- —Young modulus of the piezoelectric layer ()
- Beam containing an initial 50 vol. % PZT: d31 = −1.43 pC/N
- Beam containing an initial 40 vol. % PZT: d31 =−0.945 pC/N
4. Discussion
5. Conclusions
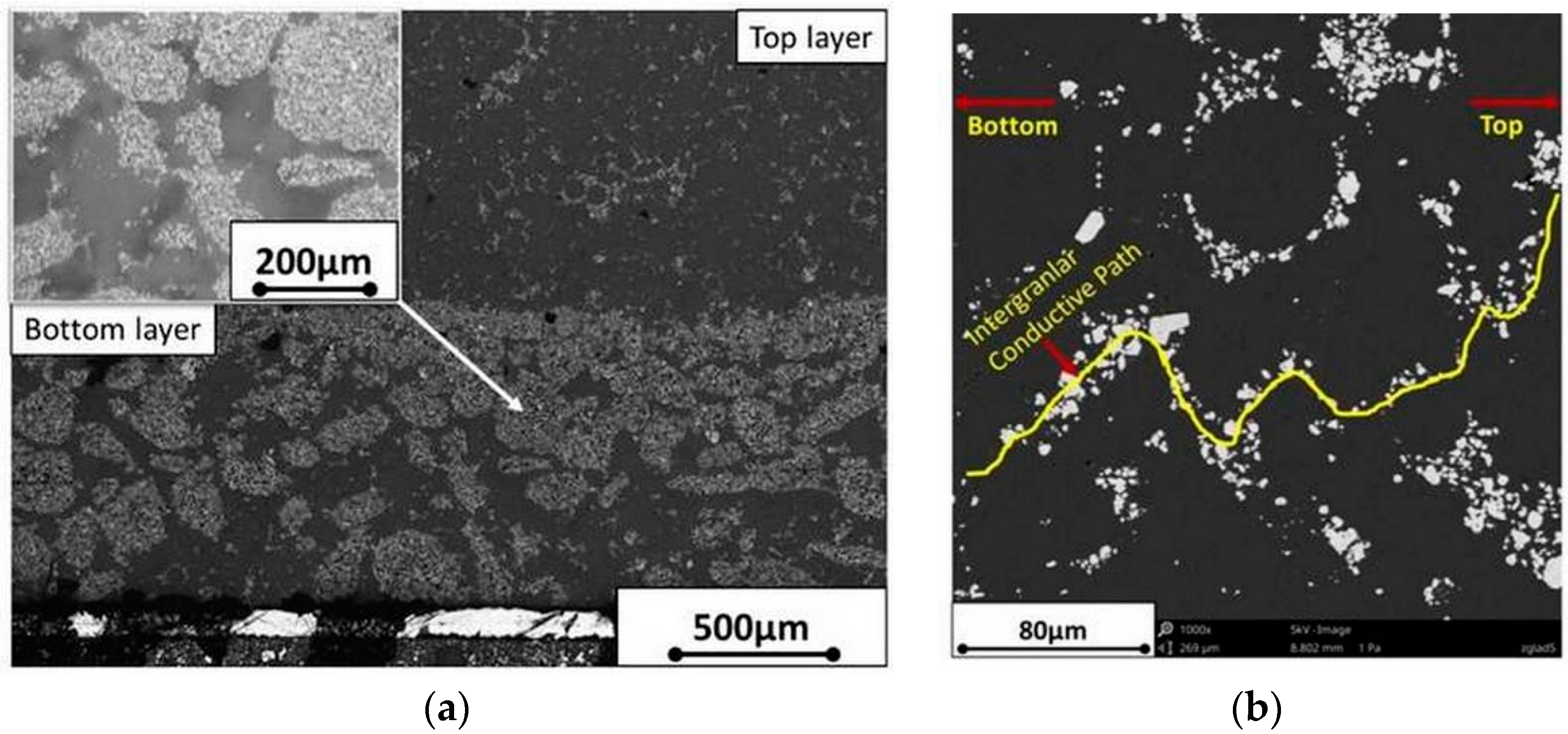
- A piezoelectric particulate composite, which contains two layers, harvests electric energy from mechanical vibration in a bending mode. The first layer should contain large particles of ceramic piezoelectric phase in the resin. Electric energy is generated as a result of the tension or compression in this layer. The second layers should contain a resin with well-dispersed low concentration of fine piezoelectric particles. Electric energy is transferred from the first layer to the electrode on the second layer through conductive paths within the second layer
- A sedimentation process can be used for manufacturing of the particulate composite, which contains the above-mentioned two layers. Because of bi-modal powder size distribution and agglomeration effect, larger PZT particles and agglomerates quickly sink to the bottom of the liquid resin (bottom layer). Due to the viscosity and rate of cross-linking of the resin, very fine particles remain in the upper layer of the produced composite, creating randomly distributed conductive paths (top layer)
- A change in bottom layer thickness in the investigated composite results in change of the neutral axis position. Thickness of the whole manufactured composite should be selected so as to locate the neutral axis between the top and bottom layers.
Author Contributions
Funding
Conflicts of Interest
References
- Fitzgerald, P.C.; Malekjafarian, A.; Bhowmik, B.; Prendergast, L.J.; Cahill, P.; Kim, C.W.; Hazra, B.; Pakrashi, V.; OBrien, E.J. Scour damage detection and structural health monitoring of a laboratory-scaled bridge using a vibration energy harvesting device. Sensors 2019, 19, 2572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khazaee, M.; Rezaniakolaie, A.; Moosavian, A.; Rosendahl, L. A novel method for autonomous remote condition monitoring of rotating machines using piezoelectric energy harvesting approach. Sens. Actuators A Phys. 2019, 295, 37–50. [Google Scholar] [CrossRef]
- Karan, S.K.; Maiti, S.; Lee, J.H.; Mishra, Y.K.; Khatua, B.B.; Kim, J.K. Recent Advances in Self-Powered Tribo-/Piezoelectric Energy Harvesters: All-In-One Package for Future Smart Technologies. Adv. Funct. Mater. 2020, 2004446. [Google Scholar] [CrossRef]
- Cahill, P.; Hazra, B.; Karoumi, R.; Mathewson, A.; Pakrashi, V. Vibration energy harvesting based monitoring of an operational bridge undergoing forced vibration and train passage. Mech. Syst. Signal Process. 2018, 106, 265–283. [Google Scholar] [CrossRef] [Green Version]
- Khazaee, M.; Rezaniakolaie, A.; Rosendahl, L. A broadband macro-fiber-composite piezoelectric energy harvester for higher energy conversion from practical wideband vibrations. Nano Energy 2020, 76, 104978. [Google Scholar] [CrossRef]
- Alsaadi, A.; Shi, Y.; Pan, L.; Tao, J.; Jia, Y. Vibration energy harvesting of multifunctional carbon fibre composite laminate structures. Compos. Sci. Technol. 2019, 178, 1–10. [Google Scholar] [CrossRef]
- Li, S.; Crovetto, A.; Peng, Z.; Zhang, A.; Hansen, O.; Wang, M.; Wang, F. Bi-resonant structure with piezoelectric PVDF films for energy harvesting from random vibration sources at low frequency. Sens. Actuators A Phys. 2016, 247, 547–554. [Google Scholar] [CrossRef] [Green Version]
- Dai, Q.; Ng, K. Investigation of electromechanical properties of piezoelectric structural fiber composites with micromechanics analysis and finite element modeling. Mech. Mater. 2012, 53, 29–46. [Google Scholar] [CrossRef]
- Zhao, S.; Erturk, A. Electroelastic modeling and experimental validations of piezoelectric energy harvesting from broadband random vibrations of cantilevered bimorphs. Smart Mater. Struct. 2012, 22, 015002. [Google Scholar] [CrossRef]
- Paknejad, A.; Rahimi, G.; Farrokhabadi, A.; Khatibi, M.M. Analytical solution of piezoelectric energy harvester patch for various thin multilayer composite beams. Compos. Struct. 2016, 154, 694–706. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, L.; Scarpa, F.; Leng, J.; Liu, Y. A novel composite multi-layer piezoelectric energy harvester. Compos. Struct. 2018, 201, 121–130. [Google Scholar] [CrossRef]
- Andrews, C.; Lin, Y.; Tang, H.; Sodano, H.A. Influence of aspect ratio on effective electromechanical coupling of nanocomposites with lead zirconate titanate nanowire inclusion. J. Intell. Mater. Syst. Struct. 2011, 22, 1879–1886. [Google Scholar] [CrossRef]
- Li, R.; Zhou, J.; Liu, H.; Pei, J. Effect of polymer matrix on the structure and electric properties of piezoelectric lead zirconatetitanate/polymer composites. Materials 2017, 10, 945. [Google Scholar] [CrossRef] [Green Version]
- Khaliq, J.; Deutz, D.B.; Frescas, J.A.C.; Vollenberg, P.; Hoeks, T.; van der Zwaag, S.; Groen, P. Effect of the piezoelectric ceramic filler dielectric constant on the piezoelectric properties of PZT-epoxy composites. Ceram. Int. 2017, 43, 2774–2779. [Google Scholar] [CrossRef]
- Van den Ende, D.A.; Bory, B.F.; Groen, W.A.; Van der Zwaag, S. Improving the d33 and g33 properties of 0-3 piezoelectric composites by dielectrophoresis. J. Appl. Phys. 2010, 107, 024107. [Google Scholar] [CrossRef]
- James, N.K.; Van Den Ende, D.; Lafont, U.; van der Zwaag, S.; Groen, W.A. Piezoelectric and mechanical properties of structured PZT-epoxy composites. J. Mater. Res. 2013, 28, 635–641. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Le, M.Q.; Zahhaf, O.; Capsal, J.F.; Cottinet, P.J.; Petit, L. Enhancing dielectric and piezoelectric properties of micro-ZnO/PDMS composite-based dielectrophoresis. Mater. Des. 2020, 108783. [Google Scholar] [CrossRef]
- Khanbareh, H.; van der Zwaag, S.; Groen, W.A. In-situ poling and structurization of piezoelectric particulate composites. J. Intell. Mater. Syst. Struct. 2017, 28, 2467–2472. [Google Scholar] [CrossRef] [Green Version]
- Van Loock, F.; Deutz, D.B.; van der Zwaag, S.; Groen, W.A. Exploring the piezoelectric performance of PZT particulate-epoxy composites loaded in shear. Smart Mater. Struct. 2016, 25, 085039. [Google Scholar] [CrossRef]
- CROW’s Polymer Physics. Available online: http://polymerdatabase.com (accessed on 10 August 2020).
- Kumar, S.; Sagar, S.; Gupta, M. Studies of Dielectric Constant of Some Polymer/Ceramic Composite Materials: A Conformational Study. Int. J. Res. Sci. Innov. 2015, 10, 37–39. [Google Scholar]
- Gowdhaman, P.; Antonyraj, K.; Annamalai, V. An effective approach on physical and dielectric properties of PZT-PVDF composites. Int. J. Adv. Sci. Res. 2015, 8, 322–328. [Google Scholar]
- Jain, A.; KJ, P.; Sharma, A.K.; Jain, A.; PN, R. Dielectric and piezoelectric properties of PVDF/PZT composites: A review. Polym. Eng. Sci. 2015, 55, 1589–1616. [Google Scholar] [CrossRef]
- Kushch, V.I.; Springhetti, S.; Shmegera, S.V. Effective permittivity of composite elastomer with account of electric conductivity of phases and imperfect interface. Int. J. Eng. Sci. 2018, 123, 51–61. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Deraemaeker, A.; Nasser, H.; Benjeddou, A.; Preumont, A. Mixing rules for the piezoelectric properties of macro fiber composites. J. Intell. Mater. Syst. Struct. 2019, 20, 1475–1482. [Google Scholar] [CrossRef] [Green Version]
- Grzybek, D.; Kata, D.; Sapiński, B.; Sikora, W. Impact of PZT layer properties in a cantilever beam on energy harvesting performance. In Proceedings of the 20th International Carpathian Control Conference (ICCC), Krakow-Wieliczka, Poland, 26–29 May 2019. [Google Scholar]




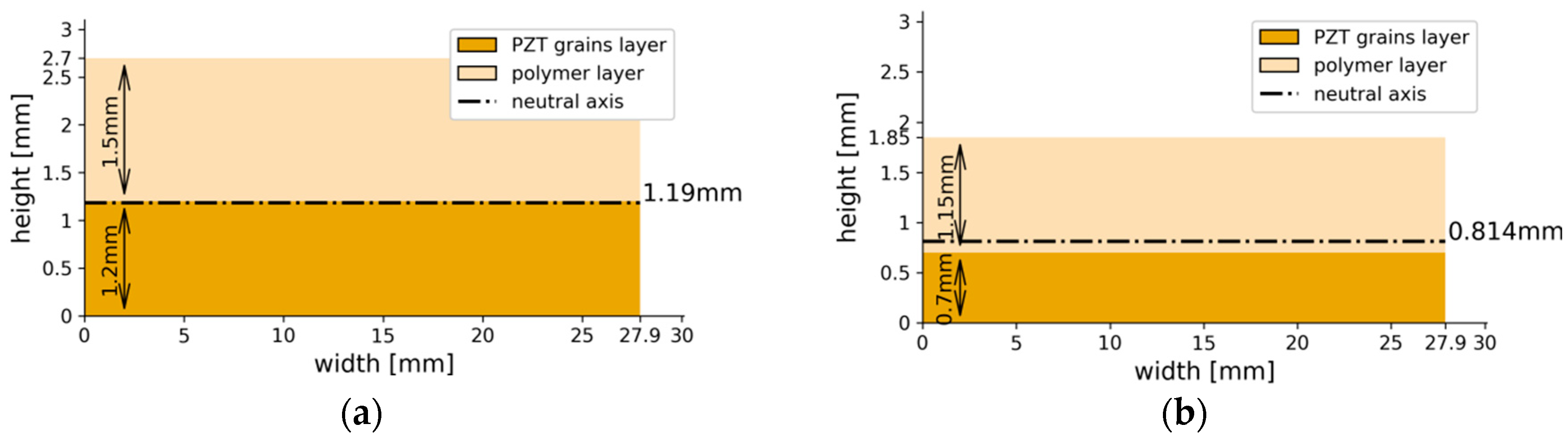

| Parameter | PZT Grains Layer | Polymer Layer |
|---|---|---|
| Young modulus, | 2.81 | 1.72 |
| Poisson ratio, | 0.3 | 0.36 |
| Dielectric constant, | 28.5 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzybek, D.; Kata, D.; Sikora, W.; Sapiński, B.; Micek, P.; Pamuła, H.; Huebner, J.; Rutkowski, P. Piezoelectric Particulate Composite for Energy Harvesting from Mechanical Vibration. Materials 2020, 13, 4925. https://doi.org/10.3390/ma13214925
Grzybek D, Kata D, Sikora W, Sapiński B, Micek P, Pamuła H, Huebner J, Rutkowski P. Piezoelectric Particulate Composite for Energy Harvesting from Mechanical Vibration. Materials. 2020; 13(21):4925. https://doi.org/10.3390/ma13214925
Chicago/Turabian StyleGrzybek, Dariusz, Dariusz Kata, Wojciech Sikora, Bogdan Sapiński, Piotr Micek, Hanna Pamuła, Jan Huebner, and Paweł Rutkowski. 2020. "Piezoelectric Particulate Composite for Energy Harvesting from Mechanical Vibration" Materials 13, no. 21: 4925. https://doi.org/10.3390/ma13214925





