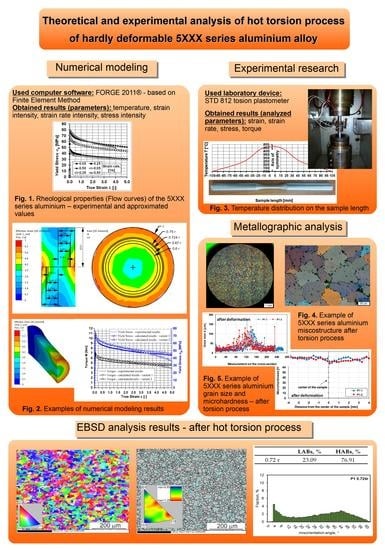
Theoretical and Experimental Analysis of the Hot Torsion Process of the Hardly Deformable 5XXX Series Aluminium Alloy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Process Parameters
2.2. Methods
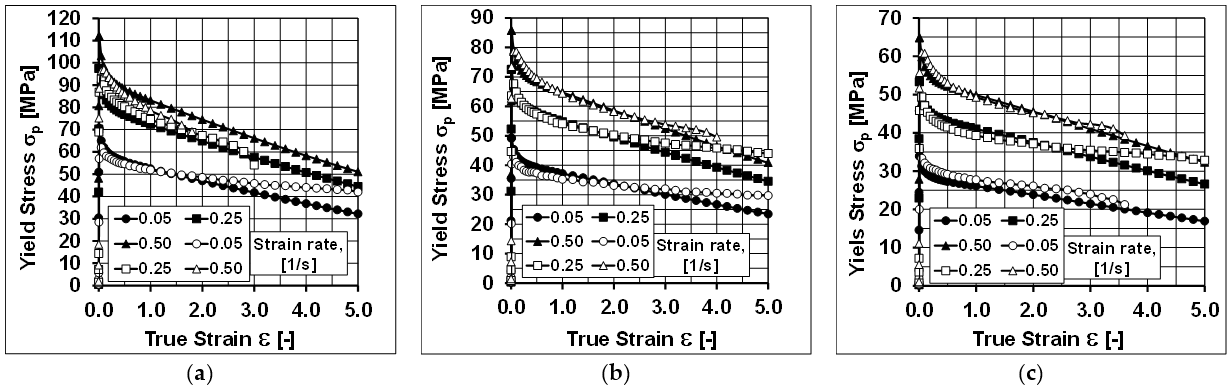
2.2.1. Numerical Research: Mathematical Model Using FORGE 2011® Software
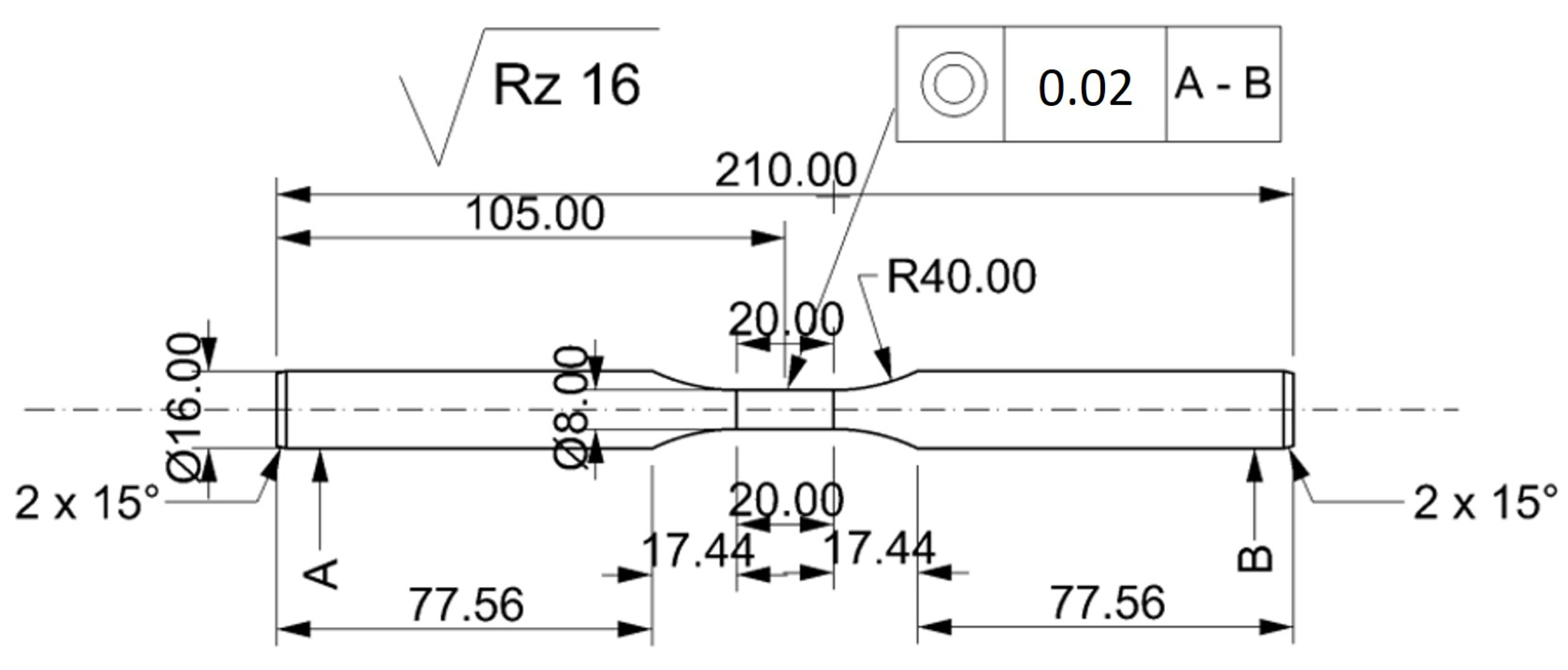
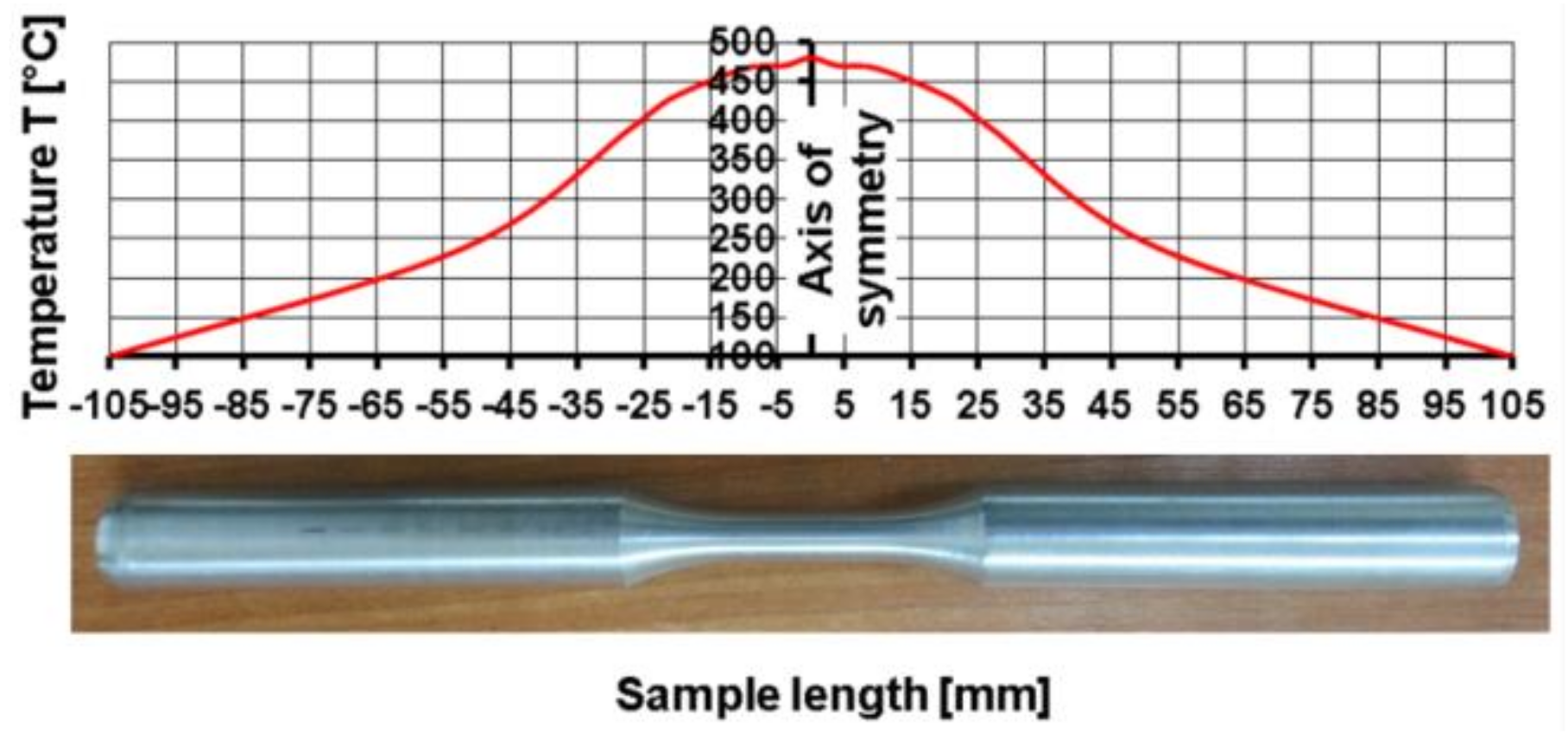
2.2.2. Experimental Research
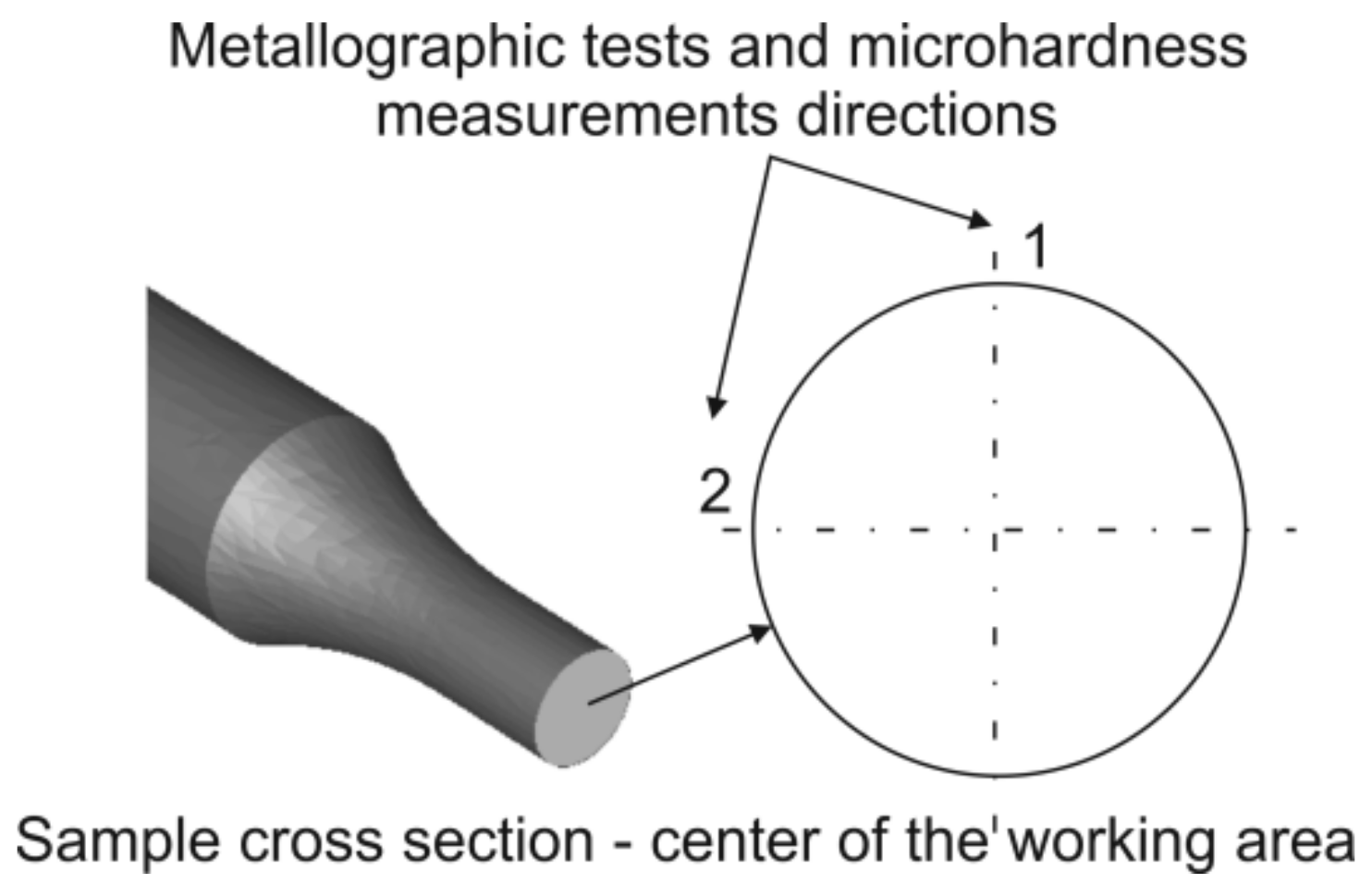
2.2.3. Metallographic Analysis and Microhardness Measurements
3. Results
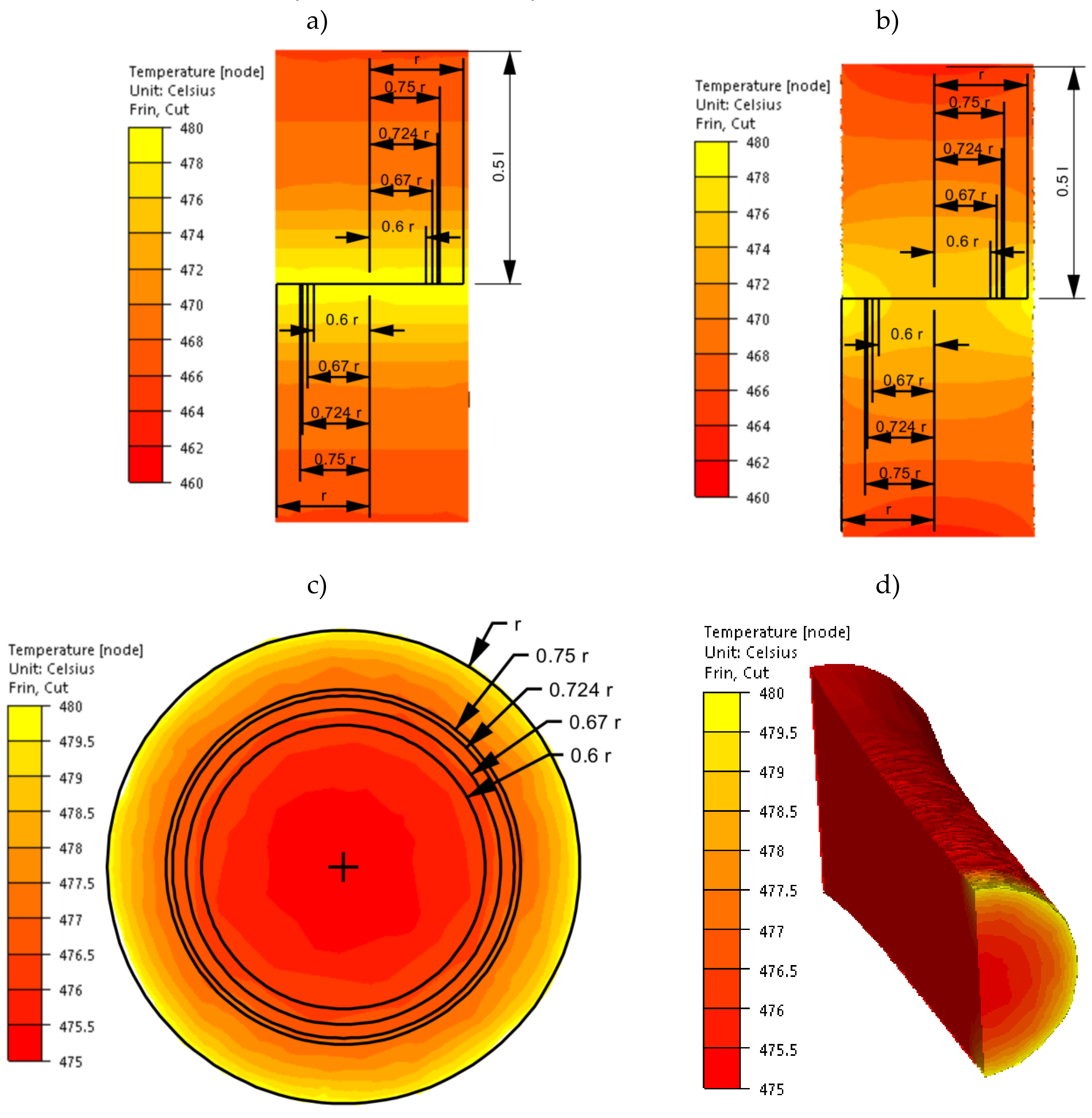
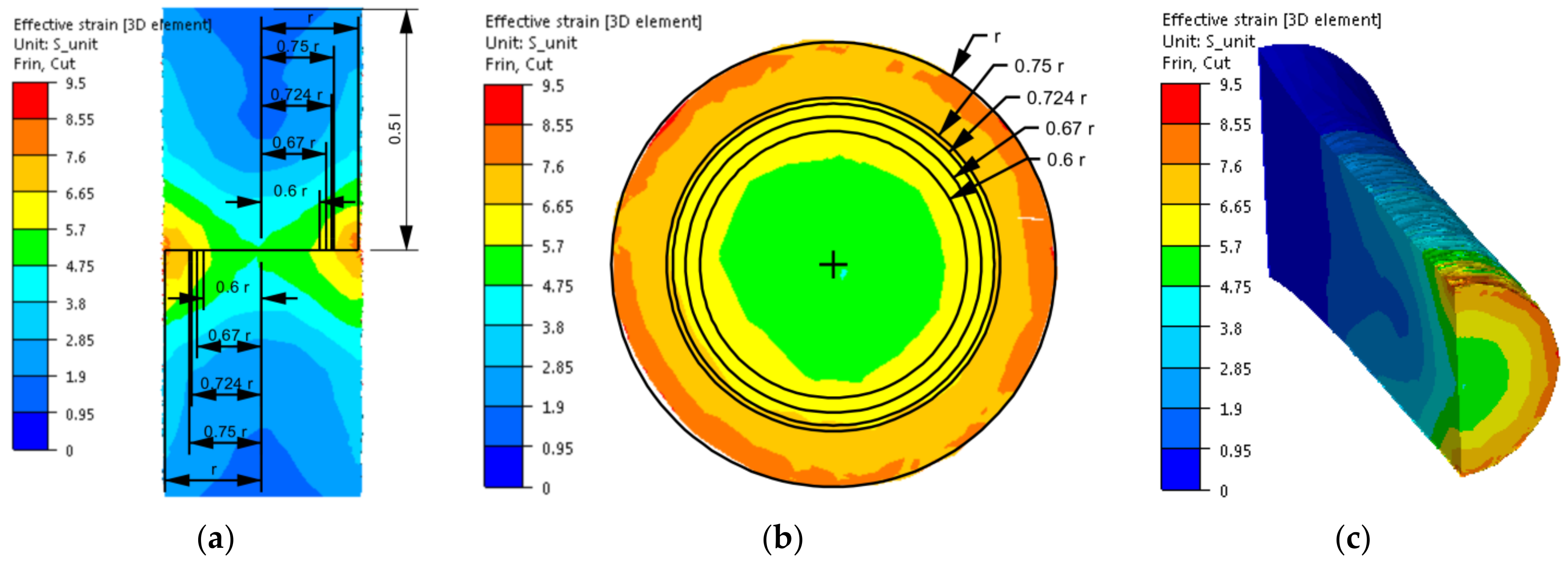
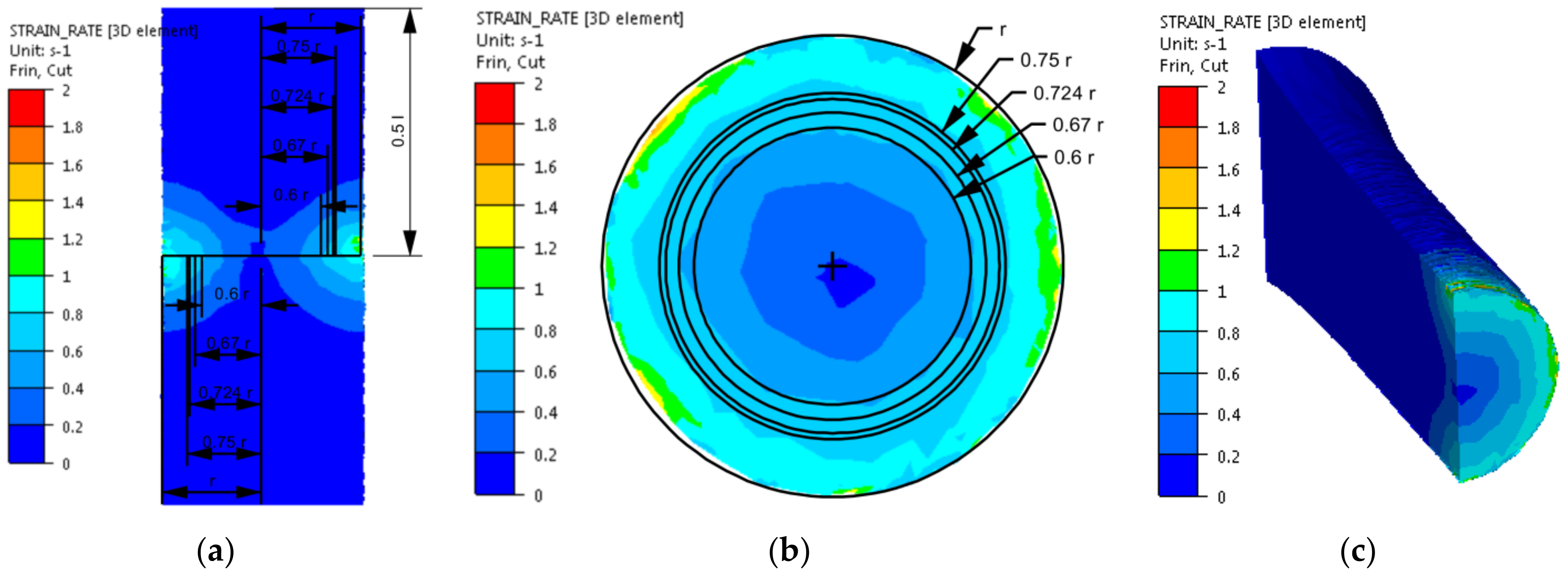
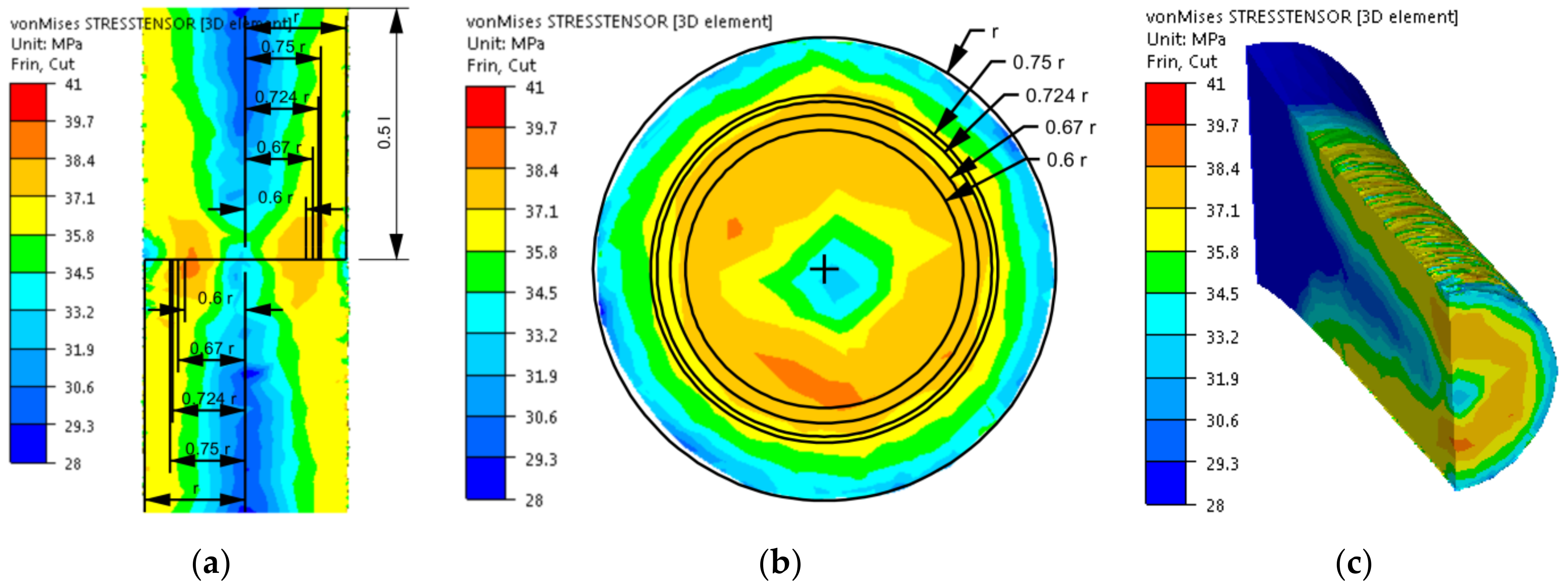
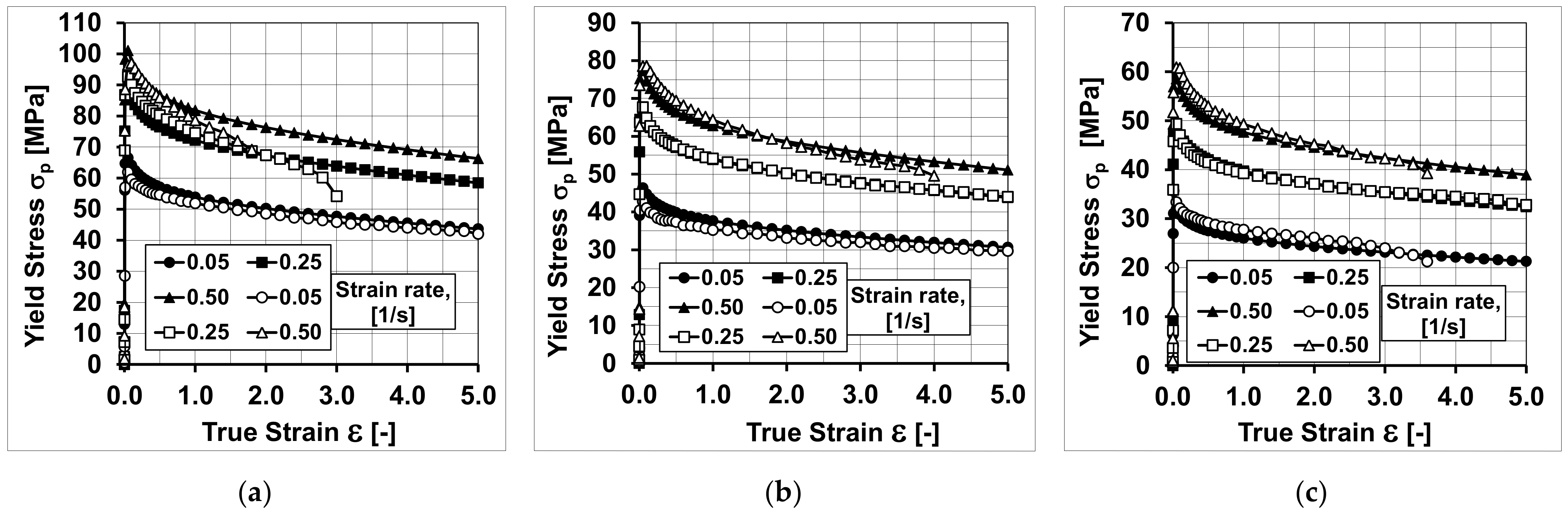
3.1. Analysis of the Numerical Research Results: Problem with the Mathematical Model’s Accuracy
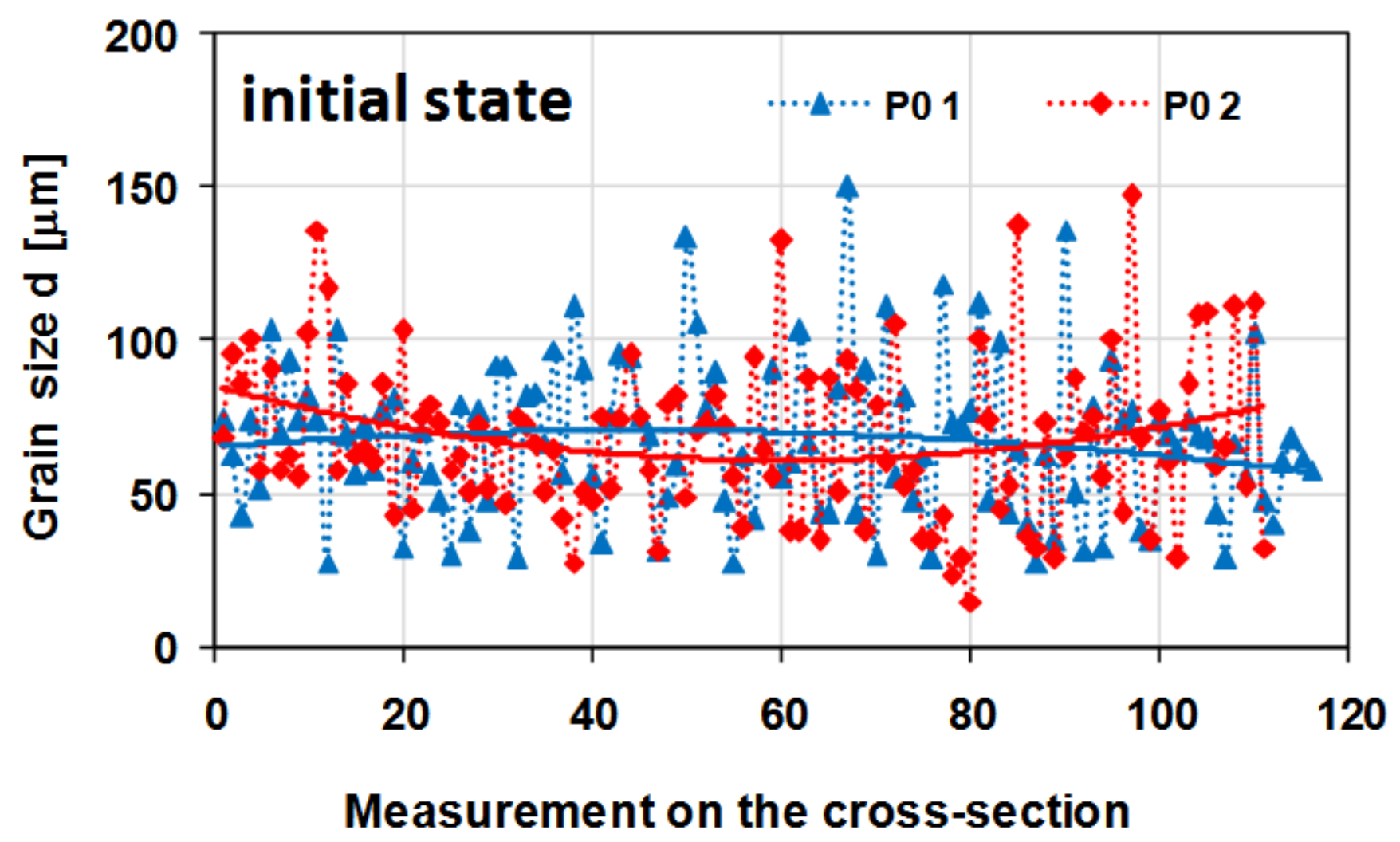
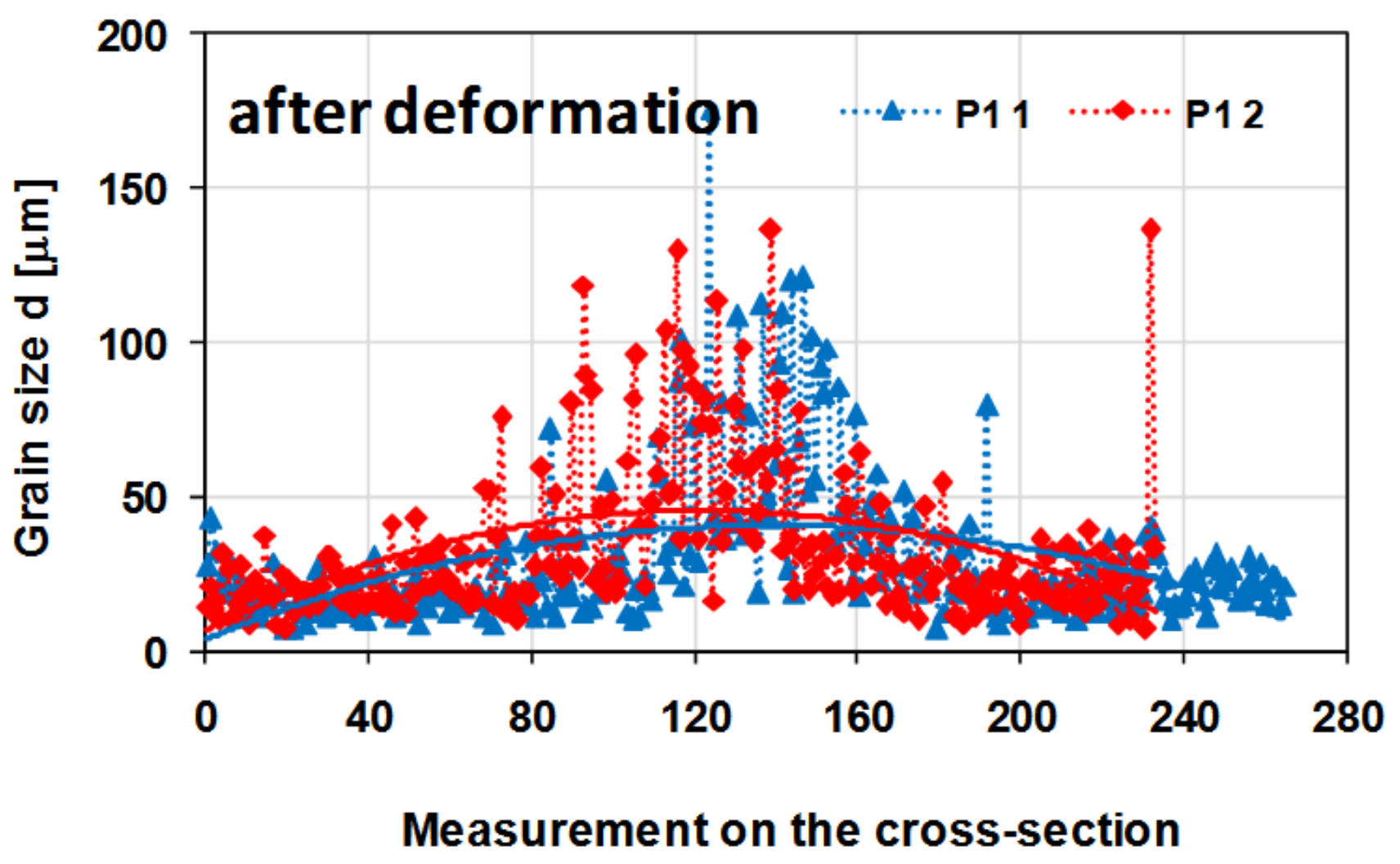
3.2. Analysis of the Experimental Research Results
4. Directions of Future Studies
5. Discussion and Conclusions
- The condition for the correct determination of the strain parameters’ distribution and the stress intensity in the torsion test is the high accuracy of the mathematical model describing the rheological properties of the tested material and the correct determination of the initial and boundary conditions, consistent with the experimental tests;
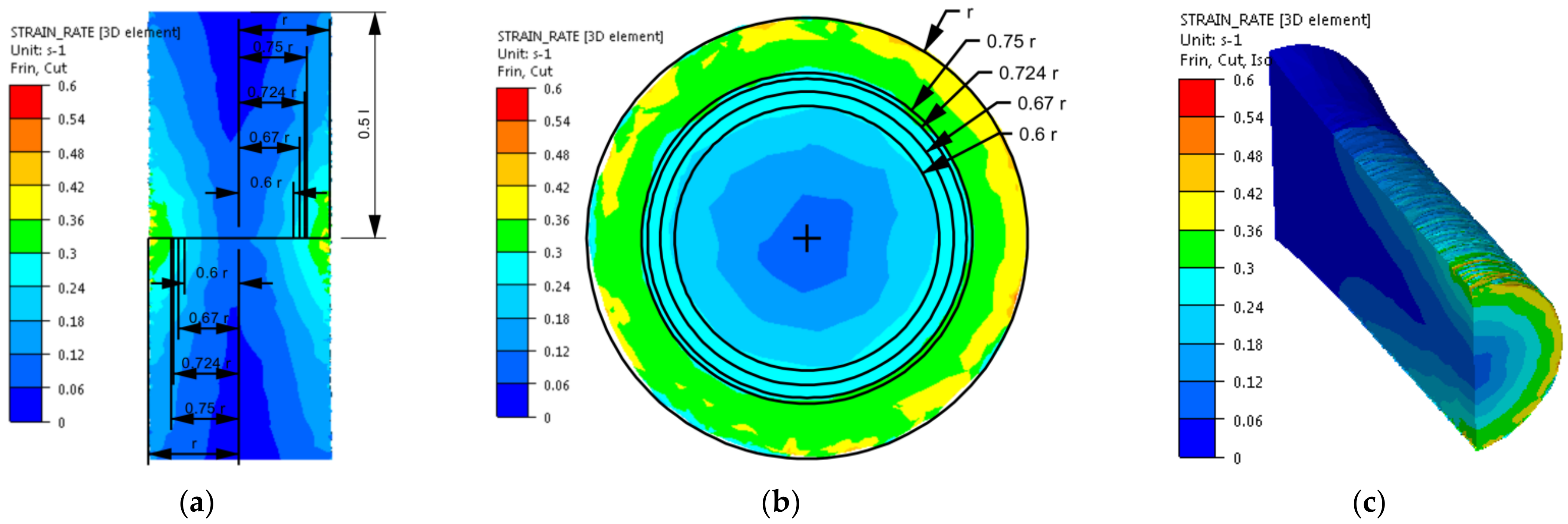
- As representative radii, defining the area in which the values of strain and stress parameters correspond to the average values on the cross-section of the torsion samples and, at the same time, to the values obtained in experimental tests, radii equal to 0.67 r and 0.724 r can be taken;
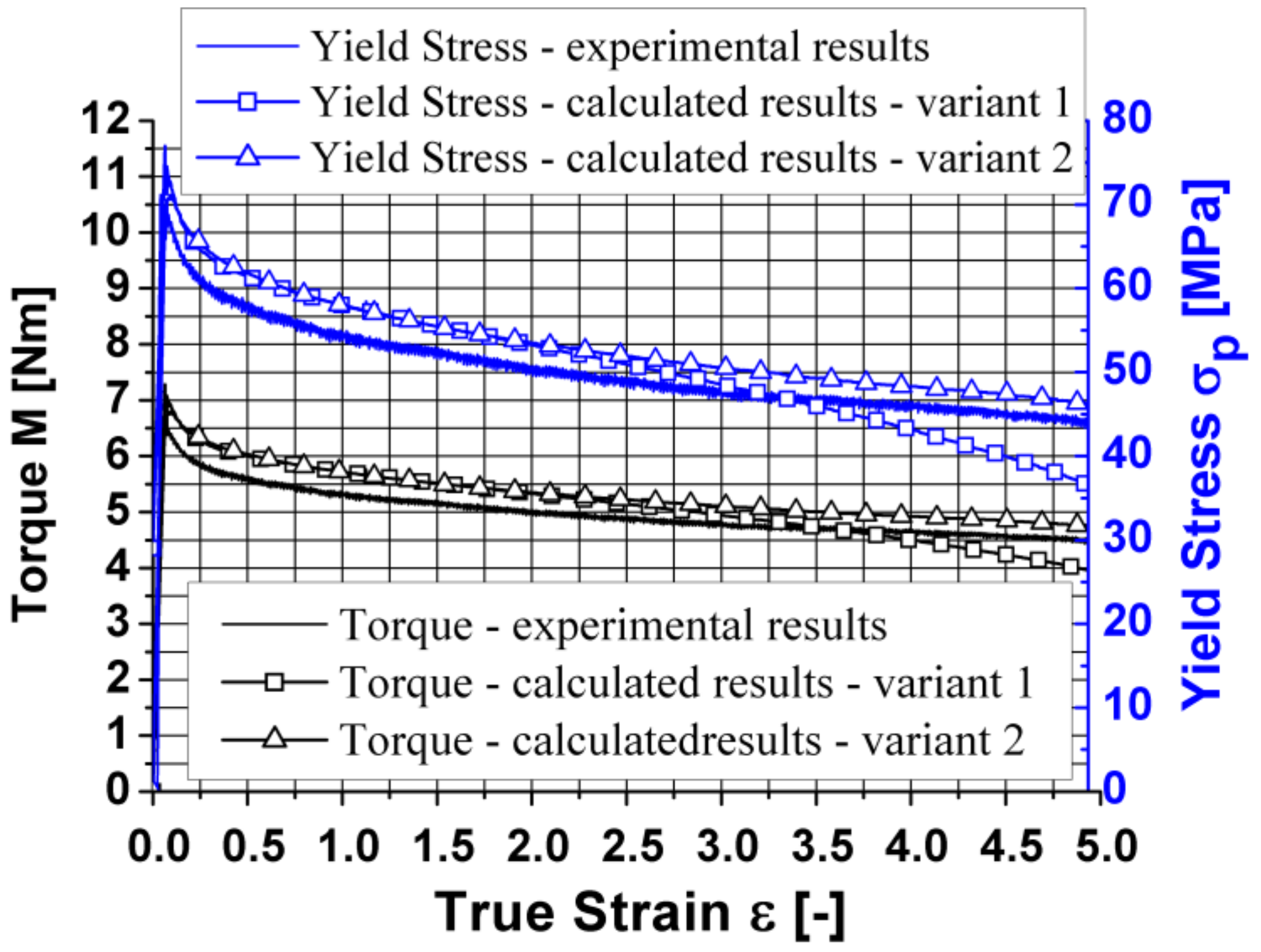
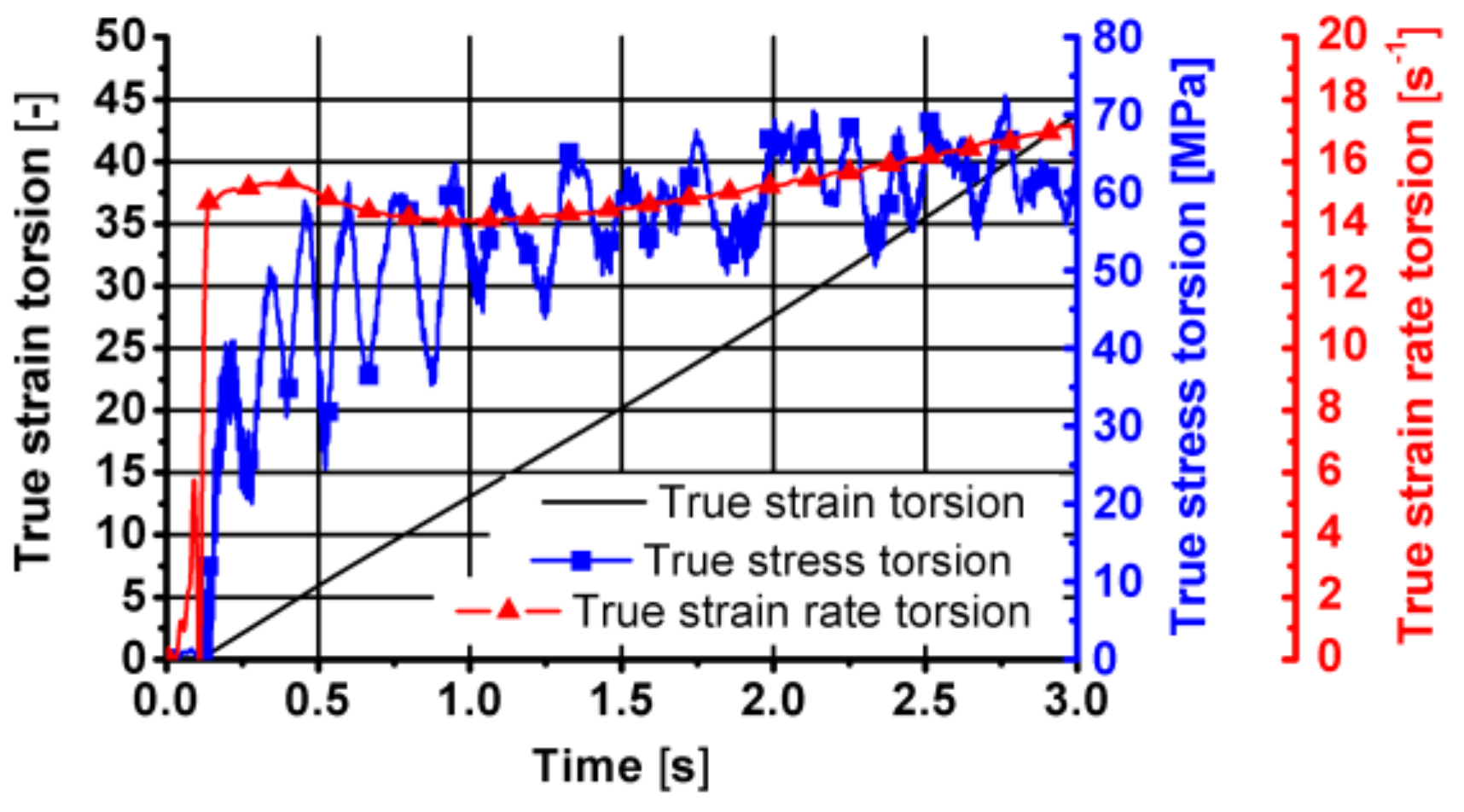
- Using the coefficients of the rheological properties model presented in Table 2, a high agreement was obtained between the recorded and the calculated values of the torsion moment and the yield stress;
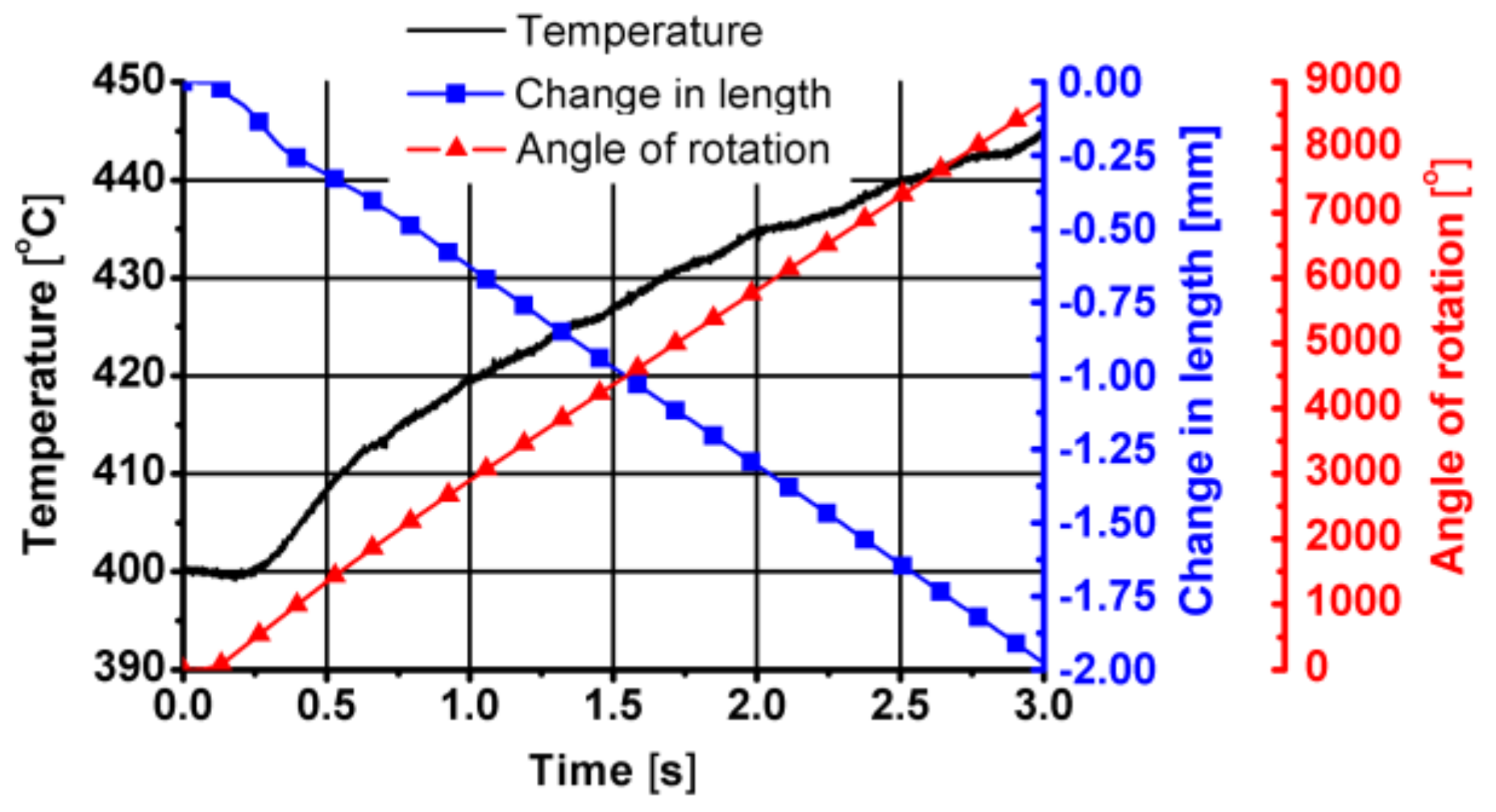
- The heating and temperature control system installed in the STD 812 torsion plastometer ensures an even temperature distribution along the length and cross-section of the measurement base of the torsion samples;
- As a result of deformation in the hot torsion process, a significant fragmentation of the microstructure of the tested alloy was obtained. It was proved that the grain size distribution on the sample cross-section was inhomogeneous and typical for a torsion test. The diversity of the microstructure on the cross-section after the hot torsion results from the inhomogeneity of the strain parameters such as strain intensity, strain rate intensity and stress inhomogeneity. The largest grains occurred in the sample axis, where the strain intensity value was the smallest, and the smallest in the surface area, where the strain intensity value reached its maximum value;
- No significant differences were found in the level of the microhardness of the material after homogenisation and after the hot torsion process. However, it has been shown that the distribution of microhardness on the sample cross-section after the hot torsion was more inhomogeneous, which is caused by a greater differentiation of the grain size on the cross-section. The lack of diversity in the level of microhardness is related to the fact that under the conditions of hot deformation of aluminium alloys, the strengthening effect caused by plastic deformation was eliminated by softening as a consequence of the structural renewal processes;
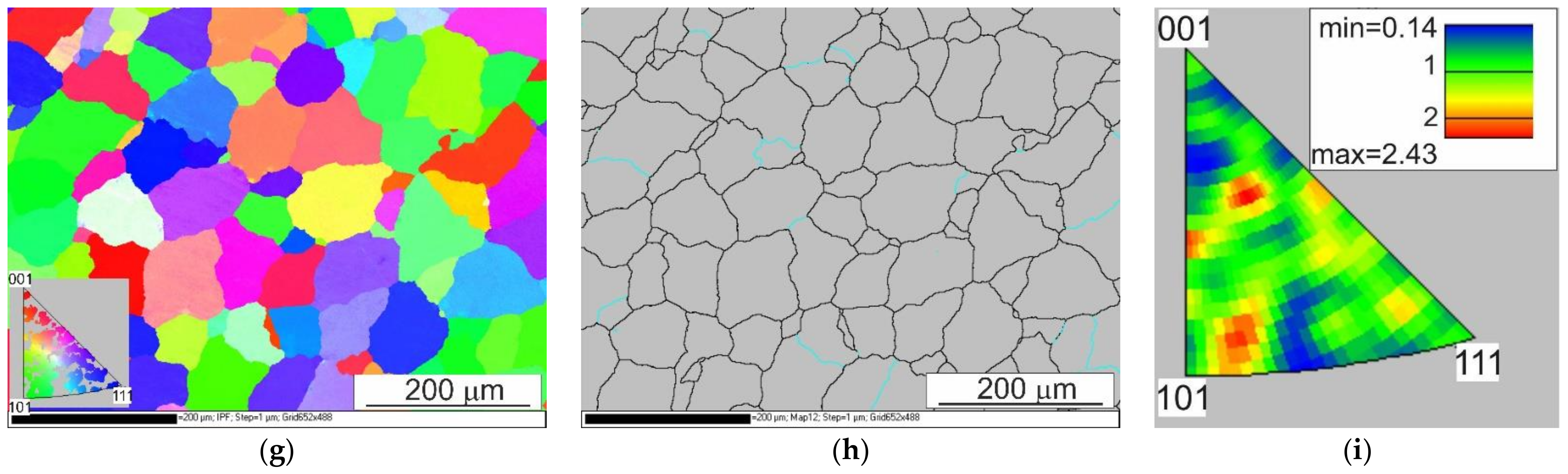
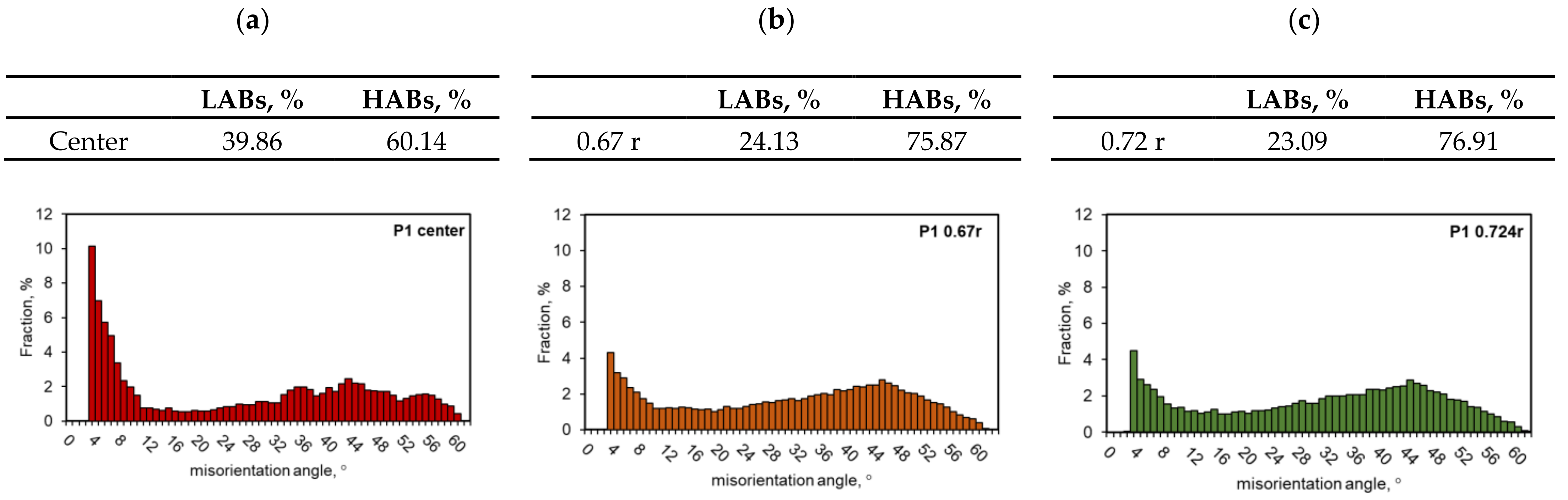
- The results of the EBSD analysis after the hot torsion present that the sample axis was dominated by the directions around the <001> pole. At a distance of 2.68 mm from the centre of the sample (0.67 r), the distribution of the texture intensity was focused around the <111> pole, while at a distance of 2.9 mm from the centre (0.724 r), the intensity distributions were centred around the <112> and <111> poles. In addition, it was proved that the fraction of large disorientation angles increased along with the distance from the sample axis, and the share of large disorientation angles above 15° was comparable for the distance from the sample axis of 2.68 mm (0.67 r) and 2.9 mm (0.724 r) and amounted to about 75% in the axis of the sample, large angles of disorientation constituted 60% of the studied population;
- The obtained results of metallographic analyses confirm the necessity to define a representative area for the assessment of the microstructure of the material after the torsion process as well as indicate the need to analyse the microstructure of the torsion samples in a strictly defined zone, for which local values of the strain intensity, strain rate intensity and stress intensity should be determined.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dyja, H.; Gałkin, A.; Knapiński, M. Reologia Metali Odkształcanych Plastycznie (Rheology of Plastically Deformed Metals); Czestochowa University of Technology: Częstochowa, Poland, 2010; ISBN 9788371934711. [Google Scholar]
- Grosman, F.; Hadasik, E. Technologiczna Plastyczność Metali, Badania Plastometryczne (The Technological Plasticity of Metals, Plastometric Testing); Silesian University of Technology: Gliwice, Poland, 2005; pp. 11–12. ISBN 837335204X. [Google Scholar]
- Hadasik, E.; Schindler, I. Plasticity of Metallic Materials—Deformation Behavior, Structure Development, Testing, Modeling; Silesian University of Technology: Gliwice, Poland, 2004; pp. 39–64, 143–167. ISBN 8373351973. [Google Scholar]
- Lenard, J.G. Modelling Hot Deformations of Steel. An Approach to Understanding and Behavior; Springer-Verlag: Berlin/Heidelberg, Germany, 1989; pp. 19–34. ISBN 9783642525179. [Google Scholar] [CrossRef]
- Scheider, I.; Brocks, W.; Cornec, A. Procedure for the determination of true stress-strain curves from tensile tests with rectangular cross-section specimens. J. Eng. Mater. Technol. 2004, 126, 70–76. [Google Scholar] [CrossRef]
- Sińczak, J. Podstawy Procesów Przeróbki Plastycznej (Fundamentals of Plastic Forming Processes); Akapit Scientific Publisher: Krakow, Poland, 2010; pp. 473–524. ISBN 9788360958728. [Google Scholar]
- Dróżdż, T.; Dyja, H.; Mrożek, J. Pomiar i sterowanie plastometrem skrętnym przy zastosowaniu techniki komputerowej (Measurement and control of a torsion plastometer using computer technology). Metrol. Syst. Pomiar. 1993, 16, 335–342. [Google Scholar]
- Moreira Jorge, A.; Balancin, O. Prediction of steel flow stresses under hot working conditions. Mater. Res. 2005, 8, 309–315. [Google Scholar] [CrossRef]
- López, B.; Urcola, J.J. Hot deformation characteristics of Inconel 625. Mater. Sci. Technol. 1996, 12, 673–678. [Google Scholar] [CrossRef]
- Biswas, S.; Beausir, B.; Toth, L.S.; Suwas, S. Evolution of texture and microstructure during hot torsion of a magnesium alloy. Acta Mater. 2013, 61, 5263–5277. [Google Scholar] [CrossRef]
- Eddahbi, M.; Borrego, A.; Mongea, M.A.; González-Doncel, G. Microstructure gradient after hot torsion deformation of powder metallurgical 6061 Al alloy. Mater. Sci. Eng. A 2012, 555, 154–164. [Google Scholar] [CrossRef] [Green Version]
- Ducki, K.; Mendala, J.; Wojtynek, L. The characteristic of deformability of Fe-Ni superalloy during high-temperature deformation. In Proceedings of the 27th International Conference on Metallurgy and Materials—METAL 2018, Brno, Czech Republic, 23–55 May 2018; pp. 348–353. [Google Scholar]
- Patil, R.D.; Gore, P.N. Review the effect of specimen geometry on torsion test results. Int. J. Innov. Res. Sci. Eng. Technol. 2013, 2, 7567–7574. [Google Scholar]
- Laber, K.; Kawałek, A.; Sawicki, S.; Dyja, H.; Borowski, J.; Leśniak, D.; Jurczak, H. Investigations of plasticity of hard-deformed aluminium alloys of 5XXX series using torsion plastometer. Arch. Metall. Mater. 2016, 61, 1853–1860. [Google Scholar] [CrossRef] [Green Version]
- Siciliano, F.; Allen, B.; Ferguson, D. Hot torsion tests—A reliable rolling simulation method for C-Mn steels. Mater. Sci. Forum 2017, 879, 1783–1787. [Google Scholar] [CrossRef]
- Pernis, R.; Bidulská, J.; Kvačkaj, T.; Pokorný, I. Application of the torsion test in calculating the extrusion force. Arch. Metall. Mater. 2011, 56, 81–85. [Google Scholar] [CrossRef]
- De Souza Nunes, L.G.; Pereira Machado, M.L. Simulation of the accumulative roll-bonding process through warm torsion test. J. Mater. Res. Technol. 2018, 7, 326–330. [Google Scholar] [CrossRef]
- Mikloweit, A.; Bambach, M.; Pietryga, M.; Hirt, G. Development of a testing procedure to determine the bond strength in joining-by-forming processes. Adv. Mater. Res. 2014, 966–967, 481–488. [Google Scholar] [CrossRef]
- Wang, S.; Dunlap, A.; Möhring, K.; Lohmar, J.; Schwedt, A.; Aretz, A.; Walther, F.; Hirt, G. Torsion plastometer trials to investigate the effect of non-proportional loading paths in caliber rolling on damage and performance of metal parts. Prod. Eng. 2020, 14, 17–32. [Google Scholar] [CrossRef] [Green Version]
- Rule, J.R.; Lippold, J.C. Physical simulation of friction stir welding and processing of nickel-base alloys using hot torsion, Metall. Mater. Trans. A 2013, 44, 3649–3663. [Google Scholar] [CrossRef]
- Laber, K.; Kułakowska, A.; Dyja, H. Physical modelling of the process of rolling AlZn5.5MgCu aluminium alloy bars on the RSP14/40 three-high reeling mill. In Proceedings of the 27th International Conference on Metallurgy and Materials—METAL Brno, Czech Republic, 23–25 May 2018; pp. 1599–1604, ISBN 9788087294840. [Google Scholar]
- Horsinka, J.; Drozd, K.; Kliber, J.; Ostroushko, D.; Černý, M.; Mamuzic, I. Strain and strain rate in torsion test. In Proceedings of the 20th International Conference on Metallurgy and Materials—METAL, Brno, Czech Republic, 18–20 May 2011; pp. 383–389, ISBN 9788087294246. [Google Scholar]
- Cepeda-Jiménez, C.; Hidalgo, P.; Carsí, M.; Ruano, O.; Carreño, F. Microstructural characterization by electron backscatter diffraction of a hot worked Al–Cu–Mg alloy. Mater. Sci. Eng. A 2011, 528, 3161–3168. [Google Scholar] [CrossRef] [Green Version]
- Van Geertruyden, W.H.; Misiolek, W.Z.; Wang, P.T. Grain structure evolution in a 6061 aluminum alloy during hot torsion. Mater. Sci. Eng. A 2006, 419, 105–114. [Google Scholar] [CrossRef]
- Gołębski, R.; Szarek, A. Diagnosis of the operational gear wheel Wear. Teh. Vjesn. Tech. Gaz. 2019, 26, 658–661. [Google Scholar] [CrossRef]
- Blum, W.; Zhu, Q.; Merkel, R.; McQueen, H.J. Geometric dynamic recrystallization in hot torsion of A1-5Mg-0.6Mn (AA5083). Mater. Sci. Eng. A 1996, 205, 23–30. [Google Scholar] [CrossRef]
- Shkatov, V.; Mazur, I. Modeling the dynamic recrystallization and flow curves using the kinetics of static recrystallization. Materials 2019, 12, 3024. [Google Scholar] [CrossRef] [Green Version]
- Lv, J.; Zheng, J.H.; Yardley, V.A.; Shi, Z.; Lin, J. A review of microstructural evolution and modeling of aluminium alloys under hot forming conditions. Metals 2020, 10, 1516. [Google Scholar] [CrossRef]
- Poletti, M.C.; Simonet-Fotso, T.; Halici, D.; Canelo-Yubero, D.; Montheillet, F.; Piot, D.; Kovács, Z.; Schell, N.; Tolnai, D. Continuous dynamic recrystallization during hot torsion of an aluminum alloy. J. Phys. Conf. Ser. 2019, 1270. [Google Scholar] [CrossRef]
- Xia, X.; McQueen, H.J. Deformation behaviour and microstructure of a 20% Al2O3 reinforced 6061 Al composite. Appl. Compos. Mater. 1997, 4, 333–347. [Google Scholar] [CrossRef]
- Maizza, G.; Pero, R.; Richetta, M.; Montanari, R. Continuous dynamic recrystallization (CDRX) model for aluminum alloys. J. Mater. Sci. 2017, 53, 4563–4573. [Google Scholar] [CrossRef]
- Kawasaki, M.; Lee, H.-J.; Ahn, B.; Zhilyaev, A.P.; Langdon, T.G. Evolution of hardness in ultrafine-grained metals processed by high-pressure torsion. J. Mater. Res. Technol. 2014, 3, 311–318. [Google Scholar] [CrossRef] [Green Version]
- Pereira, P.H.R.; Huang, Y.; Langdon, T.G. Examining the microhardness evolution and thermal stability of an Al–Mg–Sc alloy processed by high-pressure torsion at a high temperature. J. Mater. Res. Technol. 2017, 6, 348–354. [Google Scholar] [CrossRef]
- Ahmadkhaniha, D.; Huang, Y.; Jaskari, M.; Järvenpää, A.; Sohi, M.H.; Zanella, C.; Karjalainen, L.P.; Langdon, T.G. Effect of high-pressure torsion on microstructure, mechanical properties and corrosion resistance of cast pure Mg. J. Mater. Sci. 2018, 53, 16585–16597. [Google Scholar] [CrossRef] [Green Version]
- Laber, K.; Kawałek, A.; Sawicki, S.; Dyja, H.; Borowski, J.; Leśniak, D.; Jurczak, H. Application of torsion test for determination of rheological properties of 5019 Aluminium Alloy. Key Eng. Mater. 2016, 682, 356–361. [Google Scholar] [CrossRef]
- Forge2011®. Reference Guide, Sophia-Antipolis, Version 3.3 EN; Transvalor: Sophia Antipolis, France, 2011. [Google Scholar]
- Chenot, J.L.; Fourment, L.; Coupez, T.; Ducloux, R.; Wey, E. Forge3®: A general tool for practical optimisation of forging sequence of complex 3-D parts in industry. In Proceedings of the International Conference on Forging and Related Technology (ICFT’98), Birmingham, UK, 27–28 April 1998; Professional Engineering Publishing: Suffort, UK, 1998; pp. 113–122. [Google Scholar]
- Gavrus, A.; EMassoni, E.; Chenot, J.L. An inverse analysis using a finite element model for identification of rheological parameters. J. Mater. Process. Technol. 1996, 60, 447–454. [Google Scholar] [CrossRef]
- Hoff, N.J. Approximate analysis of structures in the presence of moderately large steps deformation. Q. Appl. Mech. 1954, 2, 49. [Google Scholar] [CrossRef] [Green Version]
- Norton, F.H. Creep of Steel at High Temperature; McGraw Hill: New York, NY, USA, 1929. [Google Scholar]
- Koczurkiewicz, B. Podstawy technologii Wytwarzania Blach Grubych ze Stali Niskowęglowych z Mikrododatkami Przeznaczonych na Rury Przewodowe (Basics of the Technology for the Production of Low-Carbon Steel Plates with Micro-Additives for Line Pipes); Czestochowa University of Technology: Czestochowa, Poland, 2016; ISBN 9788363989361. ISSN 2391-632X. [Google Scholar]
- Mróz, S. Teoretyczno-Technologiczne Podstawy Walcowania Prętów Bimetalowych w Wykrojach (Theoretical and Technological Basics of the Bimetallic Bars Rolling Process in Grooves); Czestochowa University of Technology: Czestochowa, Poland, 2015; ISBN 9788363989231. [Google Scholar]
- Suliga, M. Analiza Wielostopniowego Ciągnienia Drutów Stalowych z Dużymi Prędkościami w Ciągadłach Konwencjonalnych i Hydrodynamicznych (Analysis of the Multi-Stage Dawing Process of Steel Wires at High Speeds in Conventional and Hydrodynamic Dies); Czestochowa University of Technology: Czestochowa, Poland, 2013; ISBN 9788363989046. [Google Scholar]
- Hensel, A.; Spittel, T. Strength and the Need for Labor; Bildsomer Formgeburgs, Verfahren, VEB Deutscher Verlag für Grundstoffindustrie: Leipzig, Germany, 1979. [Google Scholar]
- Laber, K.; Dyja, H.; Kawałek, A. Numerical modelling of the torsion testing on the STD 812 torsion plastometer. In Proceedings of the 26th International Conference on Metallurgy and Materials—METAL 2017, Brno, Czech Republic, 24–26 May 2017; pp. 465–471, ISBN 9788087294796. [Google Scholar]
- Laber, K. The influence of the mathematical model accuracy of the rheological properties of a 5xxx series aluminium alloy on the strain parameters and stress intensity in hot torsion testing. J. Chem. Technol. Metall. 2021, 56, 417–423. [Google Scholar]
- Jiang, F.; Zhang, H.; Su, J.; Sun, Y. Constitutive characteristics and microstructure evolution of 7150 aluminium alloy during isothermal and non-isothermal multistage hot compression. Mater. Sci. Eng. A 2015, 636, 459–469. [Google Scholar] [CrossRef]
- McQueen, H.J. Development of dynamic recrystallization theory. Mater. Sci. Eng. A 2004, 387–389, 203–208. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization phenomena in metallic materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- McQueen, H.J.; Blum, W. Dynamic recovery: Sufficient mechanism in the hot deformation of Al (<99.99). Mater. Sci. Eng. A 2000, 290, 95–107. [Google Scholar]











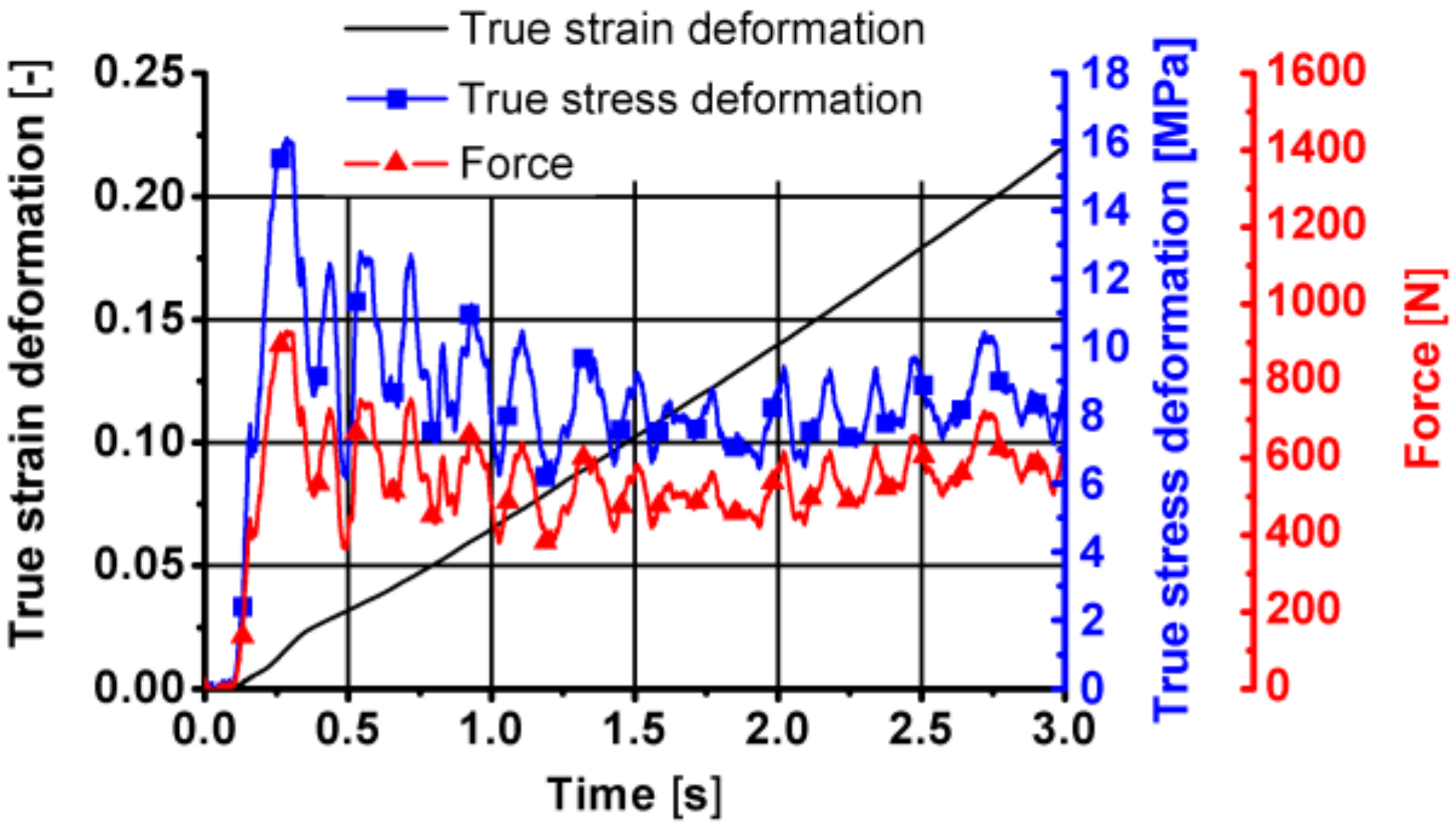

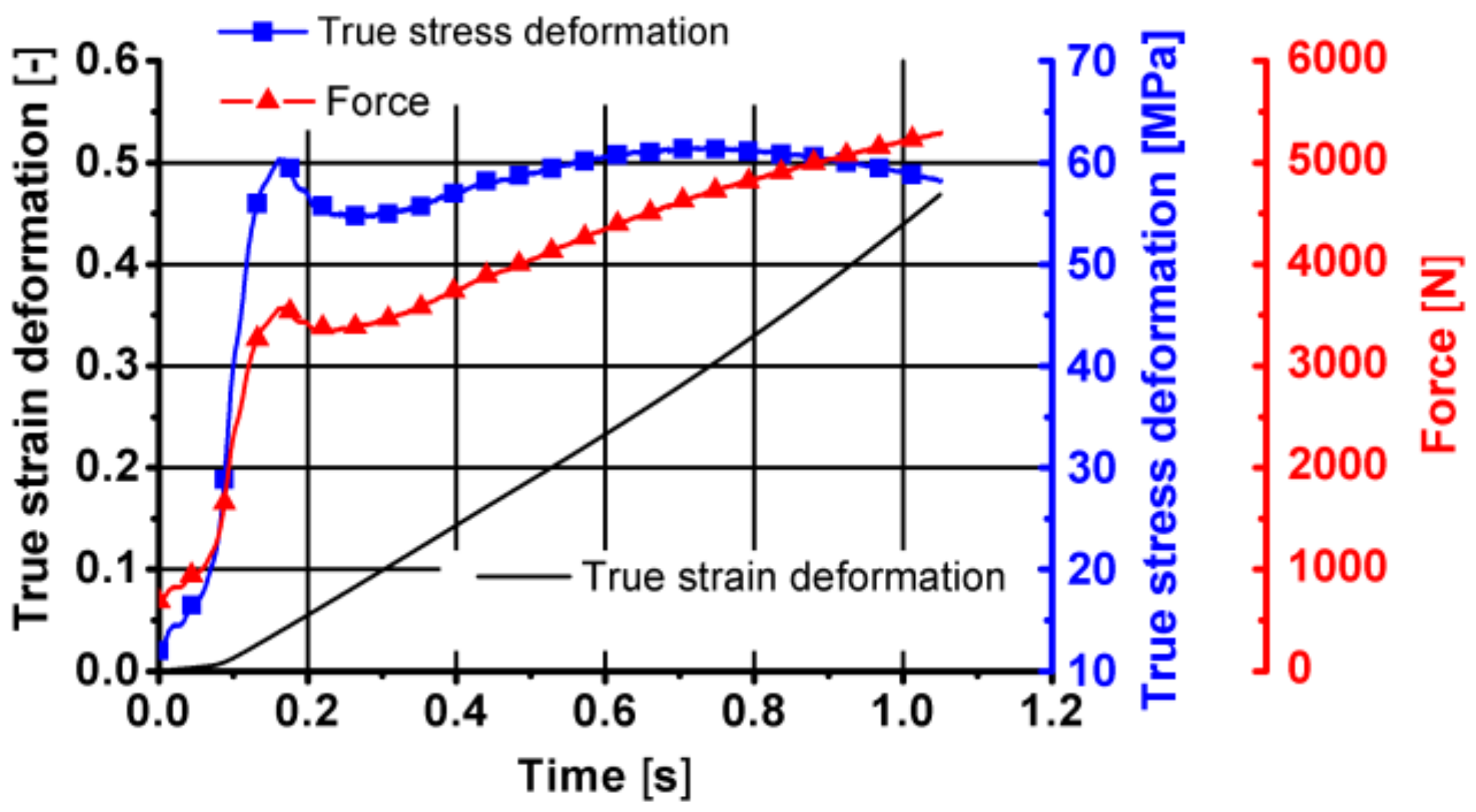
| A | m1 | m2 | m3 | m4 | m5 | m7 | m8 | m9 |
|---|---|---|---|---|---|---|---|---|
| 0.271553 | −0.00957753 | −0.0823773 | −0.246413 | −0.000573716 | 0.000622463 | −0.164103 | 0.00101501 | 1.65143 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laber, K.B.; Leszczyńska-Madej, B. Theoretical and Experimental Analysis of the Hot Torsion Process of the Hardly Deformable 5XXX Series Aluminium Alloy. Materials 2021, 14, 3508. https://doi.org/10.3390/ma14133508
Laber KB, Leszczyńska-Madej B. Theoretical and Experimental Analysis of the Hot Torsion Process of the Hardly Deformable 5XXX Series Aluminium Alloy. Materials. 2021; 14(13):3508. https://doi.org/10.3390/ma14133508
Chicago/Turabian StyleLaber, Konrad Błażej, and Beata Leszczyńska-Madej. 2021. "Theoretical and Experimental Analysis of the Hot Torsion Process of the Hardly Deformable 5XXX Series Aluminium Alloy" Materials 14, no. 13: 3508. https://doi.org/10.3390/ma14133508
APA StyleLaber, K. B., & Leszczyńska-Madej, B. (2021). Theoretical and Experimental Analysis of the Hot Torsion Process of the Hardly Deformable 5XXX Series Aluminium Alloy. Materials, 14(13), 3508. https://doi.org/10.3390/ma14133508