Prediction of Surface Roughness of Abrasive Belt Grinding of Superalloy Material Based on RLSOM-RBF
Abstract
:1. Introduction
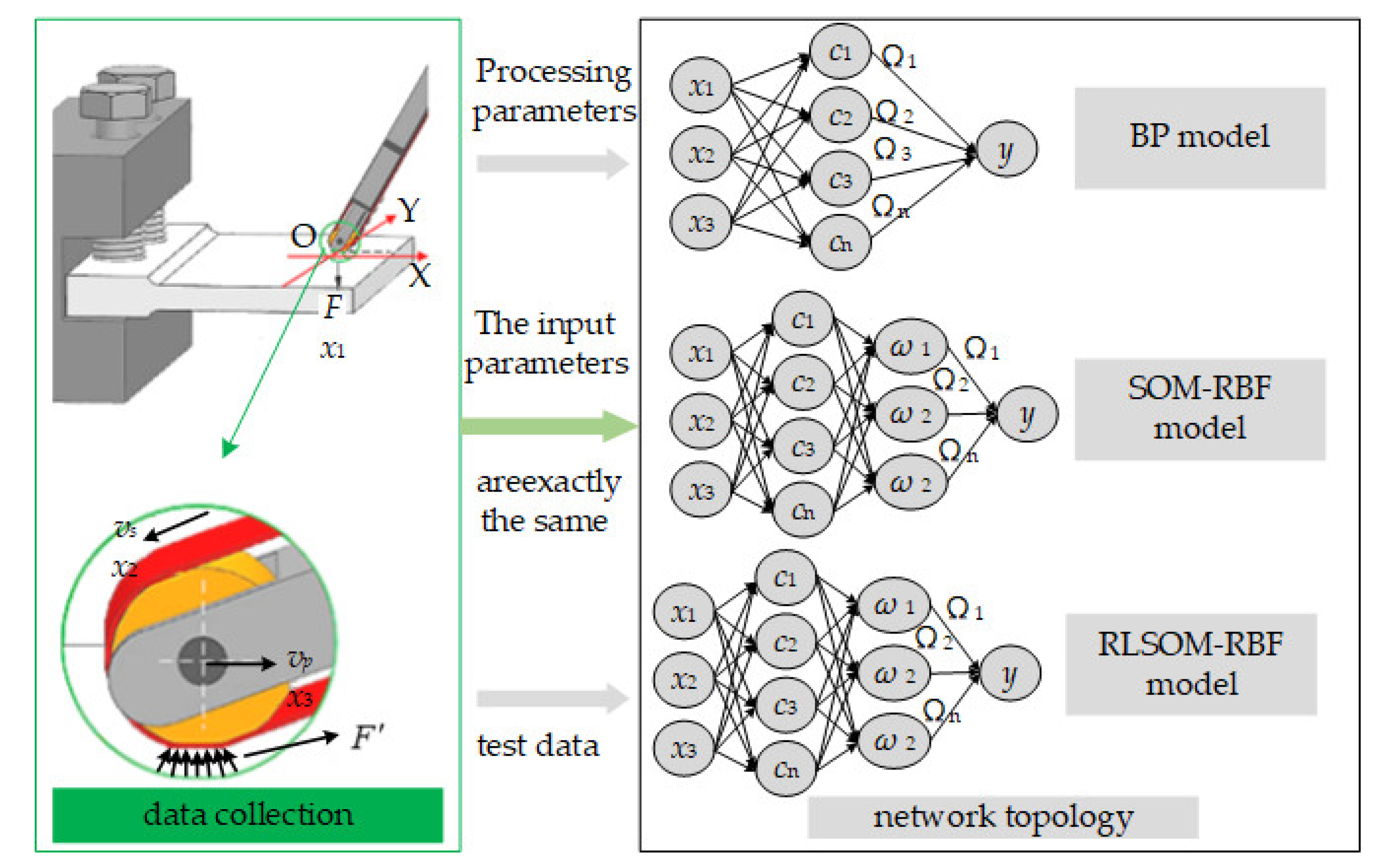
2. Prediction Model of Surface Roughness of Abrasive Belt Grinding of Superalloy Material
2.1. Abrasive Belt Grinding System
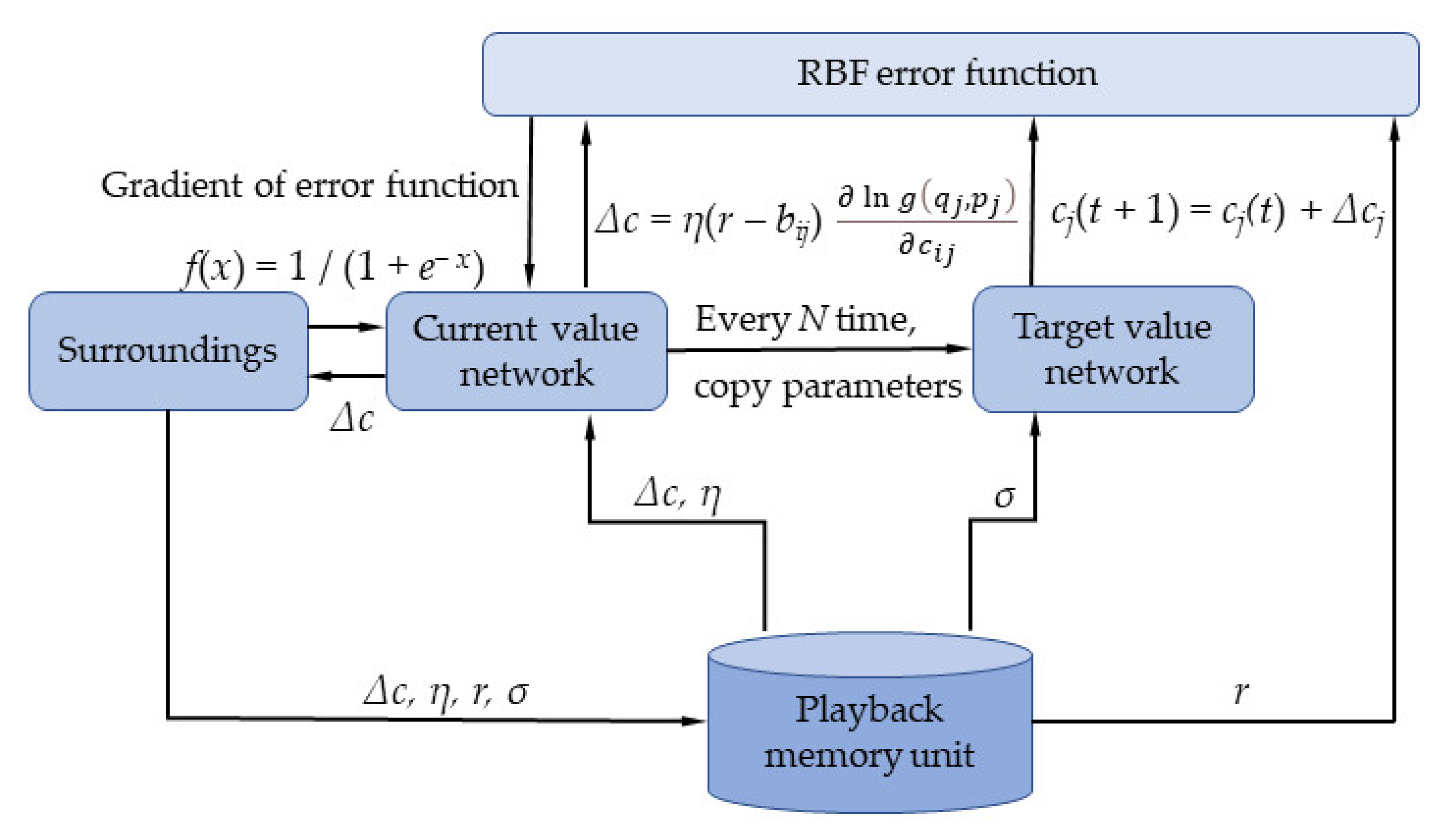
2.2. Radial Basis Function Center Training Method for Strengthening Self-Organizing Mapping
2.3. Establishment of Prediction Model of Superalloy Surface Roughness Based on Radial Basis Function Neural Network
2.3.1. Input and Output Neurons
2.3.2. Selection of Hidden Layer Parameters
3. Abrasive Belt Grinding Experiment and Experimental Results
4. Discussion and Analysis
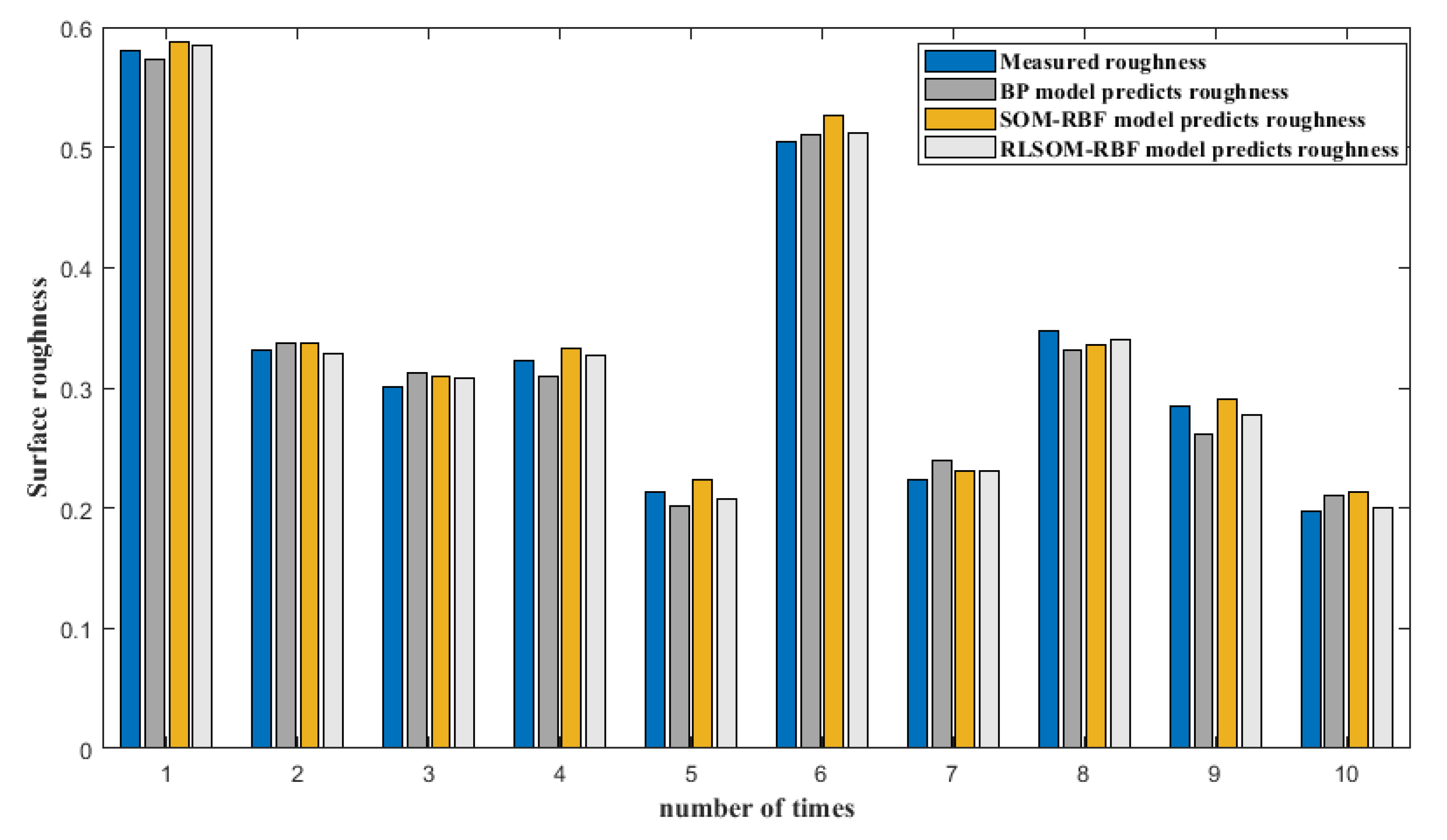
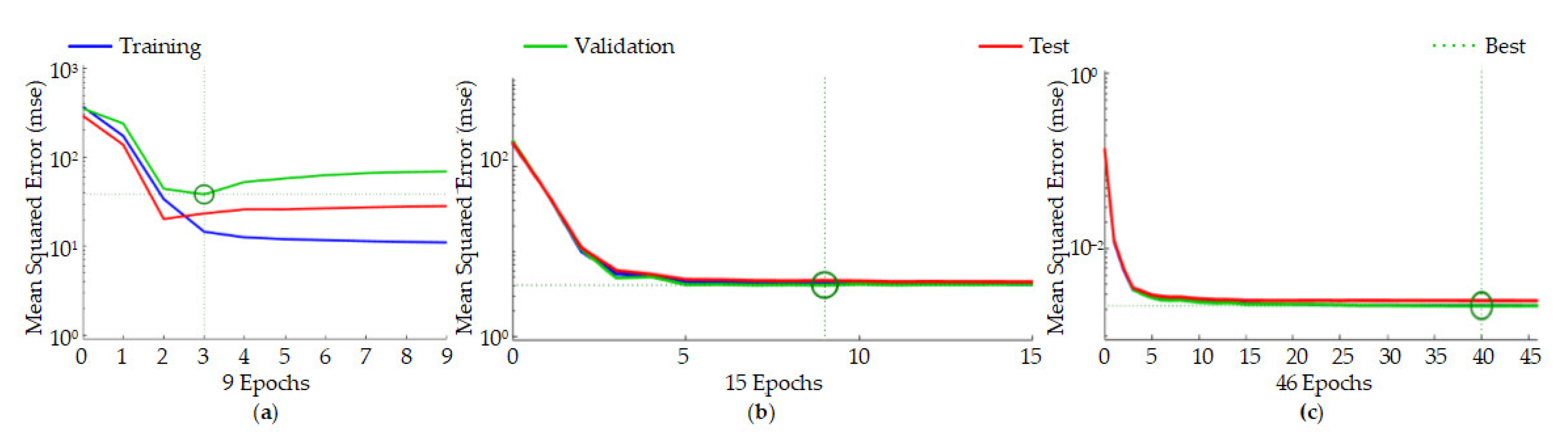
4.1. Simulation Results
4.2. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Serial Number | Abrasive Belt Speed/(m/s) | Feed Rate/(m/s) | Grinding Pressure/(N) | Measuring Point 1 | Measuring Point 2 | Measuring Point 3 | Measuring Point 4 | Measuring Point 5 | Measuring Point 6 | Measuring Point 7 | Measuring Point 8 | Measuring Point 9 | Average | Measured Surface Roughness/(μm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 0.02 | 10 | 0.581 | 0.574 | 0.583 | 0.571 | 0.571 | 0.580 | 0.571 | 0.569 | 0.576 | 0.575 | 0.581 |
| 2 | 10 | 0.02 | 10 | 0.584 | 0.581 | 0.584 | 0.573 | 0.584 | 0.572 | 0.583 | 0.587 | 0.589 | 0.582 | |
| 3 | 10 | 0.02 | 10 | 0.574 | 0.577 | 0.578 | 0.587 | 0.583 | 0.579 | 0.584 | 0.583 | 0.601 | 0.583 | |
| 4 | 10 | 0.02 | 10 | 0.583 | 0.590 | 0.580 | 0.582 | 0.572 | 0.583 | 0.579 | 0.592 | 0.588 | 0.583 | |
| 5 | 10 | 0.02 | 10 | 0.590 | 0.581 | 0.585 | 0.587 | 0.578 | 0.583 | 0.590 | 0.581 | 0.582 | 0.584 | |
| 6 | 10 | 0.04 | 20 | 0.349 | 0.339 | 0.346 | 0.343 | 0.344 | 0.322 | 0.335 | 0.329 | 0.326 | 0.337 | 0.326 |
| 7 | 10 | 0.04 | 20 | 0.346 | 0.319 | 0.324 | 0.319 | 0.339 | 0.346 | 0.343 | 0.344 | 0.322 | 0.334 | |
| 8 | 10 | 0.04 | 20 | 0.343 | 0.326 | 0.326 | 0.349 | 0.346 | 0.343 | 0.344 | 0.322 | 0.335 | 0.337 | |
| 9 | 10 | 0.04 | 20 | 0.344 | 0.319 | 0.319 | 0.329 | 0.322 | 0.322 | 0.322 | 0.324 | 0.324 | 0.325 | |
| 10 | 10 | 0.04 | 20 | 0.322 | 0.324 | 0.324 | 0.322 | 0.335 | 0.329 | 0.326 | 0.194 | 0.196 | 0.297 | |
| 11 | 10 | 0.06 | 30 | 0.309 | 0.302 | 0.302 | 0.304 | 0.294 | 0.292 | 0.305 | 0.309 | 0.306 | 0.303 | 0.293 |
| 12 | 10 | 0.06 | 30 | 0.296 | 0.304 | 0.194 | 0.304 | 0.304 | 0.304 | 0.304 | 0.302 | 0.194 | 0.278 | |
| 13 | 10 | 0.06 | 30 | 0.291 | 0.302 | 0.302 | 0.306 | 0.295 | 0.194 | 0.300 | 0.301 | 0.302 | 0.288 | |
| 14 | 10 | 0.06 | 30 | 0.304 | 0.304 | 0.294 | 0.302 | 0.296 | 0.302 | 0.286 | 0.294 | 0.295 | 0.297 | |
| 15 | 10 | 0.06 | 30 | 0.304 | 0.302 | 0.296 | 0.294 | 0.305 | 0.304 | 0.308 | 0.296 | 0.299 | 0.301 | |
| 16 | 18 | 0.02 | 20 | 0.322 | 0.324 | 0.324 | 0.322 | 0.335 | 0.329 | 0.326 | 0.194 | 0.196 | 0.297 | 0.300 |
| 17 | 18 | 0.02 | 20 | 0.335 | 0.324 | 0.324 | 0.324 | 0.324 | 0.322 | 0.194 | 0.322 | 0.326 | 0.311 | |
| 18 | 18 | 0.02 | 20 | 0.329 | 0.322 | 0.322 | 0.324 | 0.324 | 0.322 | 0.335 | 0.329 | 0.326 | 0.326 | |
| 19 | 18 | 0.02 | 20 | 0.326 | 0.194 | 0.194 | 0.324 | 0.324 | 0.324 | 0.324 | 0.322 | 0.194 | 0.281 | |
| 20 | 18 | 0.02 | 20 | 0.319 | 0.302 | 0.302 | 0.326 | 0.194 | 0.194 | 0.324 | 0.319 | 0.302 | 0.287 | |
| 21 | 18 | 0.04 | 30 | 0.216 | 0.245 | 0.269 | 0.234 | 0.229 | 0.217 | 0.216 | 0.209 | 0.218 | 0.228 | 0.214 |
| 22 | 18 | 0.04 | 30 | 0.209 | 0.226 | 0.227 | 0.269 | 0.234 | 0.229 | 0.217 | 0.224 | 0.227 | 0.229 | |
| 23 | 18 | 0.04 | 30 | 0.218 | 0.227 | 0.216 | 0.234 | 0.229 | 0.217 | 0.264 | 0.216 | 0.234 | 0.228 | |
| 24 | 18 | 0.04 | 30 | 0.198 | 0.194 | 0.201 | 0.178 | 0.198 | 0.186 | 0.188 | 0.206 | 0.247 | 0.200 | |
| 25 | 18 | 0.04 | 30 | 0.184 | 0.188 | 0.186 | 0.186 | 0.184 | 0.184 | 0.183 | 0.182 | 0.188 | 0.185 | |
| 26 | 18 | 0.06 | 10 | 0.504 | 0.501 | 0.500 | 0.498 | 0.502 | 0.501 | 0.501 | 0.511 | 0.519 | 0.504 | 0.274 |
| 27 | 18 | 0.06 | 10 | 0.510 | 0.524 | 0.521 | 0.517 | 0.528 | 0.523 | 0.528 | 0.521 | 0.506 | 0.520 | |
| 28 | 18 | 0.06 | 10 | 0.498 | 0.503 | 0.509 | 0.519 | 0.506 | 0.524 | 0.518 | 0.521 | 0.521 | 0.513 | |
| 29 | 18 | 0.06 | 10 | 0.499 | 0.498 | 0.479 | 0.496 | 0.497 | 0.499 | 0.489 | 0.487 | 0.478 | 0.491 | |
| 30 | 18 | 0.06 | 10 | 0.500 | 0.486 | 0.498 | 0.499 | 0.487 | 0.495 | 0.490 | 0.509 | 0.498 | 0.326 | |
| 19 | 26 | 0.02 | 30 | 0.216 | 0.245 | 0.269 | 0.234 | 0.229 | 0.217 | 0.216 | 0.209 | 0.218 | 0.228 | 0.224 |
| 32 | 26 | 0.02 | 30 | 0.209 | 0.226 | 0.227 | 0.269 | 0.234 | 0.229 | 0.217 | 0.224 | 0.227 | 0.229 | |
| 33 | 26 | 0.02 | 30 | 0.218 | 0.227 | 0.216 | 0.234 | 0.229 | 0.217 | 0.264 | 0.216 | 0.234 | 0.228 | |
| 34 | 26 | 0.02 | 30 | 0.198 | 0.194 | 0.201 | 0.208 | 0.198 | 0.196 | 0.208 | 0.206 | 0.247 | 0.206 | |
| 35 | 26 | 0.02 | 30 | 0.226 | 0.226 | 0.227 | 0.269 | 0.234 | 0.229 | 0.217 | 0.216 | 0.227 | 0.230 | |
| 36 | 26 | 0.04 | 10 | 0.369 | 0.379 | 0.351 | 0.351 | 0.390 | 0.396 | 0.394 | 0.390 | 0.322 | 0.371 | 0.347 |
| 37 | 26 | 0.04 | 10 | 0.351 | 0.351 | 0.349 | 0.346 | 0.343 | 0.344 | 0.322 | 0.335 | 0.329 | 0.341 | |
| 38 | 26 | 0.04 | 10 | 0.349 | 0.349 | 0.346 | 0.343 | 0.344 | 0.322 | 0.335 | 0.329 | 0.326 | 0.338 | |
| 39 | 26 | 0.04 | 10 | 0.346 | 0.319 | 0.344 | 0.351 | 0.349 | 0.346 | 0.343 | 0.344 | 0.321 | 0.340 | |
| 40 | 26 | 0.04 | 10 | 0.343 | 0.346 | 0.346 | 0.349 | 0.346 | 0.343 | 0.344 | 0.352 | 0.335 | 0.345 | |
| 41 | 26 | 0.06 | 20 | 0.324 | 0.324 | 0.324 | 0.322 | 0.194 | 0.302 | 0.286 | 0.264 | 0.245 | 0.287 | 0.268 |
| 42 | 26 | 0.06 | 20 | 0.324 | 0.302 | 0.286 | 0.264 | 0.245 | 0.234 | 0.238 | 0.226 | 0.227 | 0.261 | |
| 43 | 26 | 0.06 | 20 | 0.322 | 0.264 | 0.245 | 0.234 | 0.238 | 0.226 | 0.227 | 0.226 | 0.301 | 0.254 | |
| 44 | 26 | 0.06 | 20 | 0.194 | 0.302 | 0.286 | 0.324 | 0.302 | 0.286 | 0.264 | 0.245 | 0.226 | 0.270 | |
| 45 | 26 | 0.06 | 20 | 0.199 | 0.192 | 0.322 | 0.324 | 0.324 | 0.192 | 0.195 | 0.322 | 0.326 | 0.266 | |
| 46 | 32 | 0.08 | 40 | 0.204 | 0.194 | 0.199 | 0.197 | 0.199 | 0.197 | 0.196 | 0.198 | 0.196 | 0.198 | 0.198 |
| 47 | 32 | 0.08 | 40 | 0.208 | 0.209 | 0.198 | 0.196 | 0.194 | 0.199 | 0.197 | 0.204 | 0.195 | 0.200 | |
| 48 | 32 | 0.08 | 40 | 0.192 | 0.204 | 0.195 | 0.194 | 0.198 | 0.196 | 0.197 | 0.206 | 0.191 | 0.197 | |
| 49 | 32 | 0.08 | 40 | 0.194 | 0.192 | 0.196 | 0.199 | 0.192 | 0.196 | 0.204 | 0.205 | 0.196 | 0.197 | |
| 50 | 32 | 0.08 | 40 | 0.192 | 0.195 | 0.194 | 0.198 | 0.196 | 0.197 | 0.209 | 0.194 | 0.191 | 0.196 |
References
- Hu, Z.; Liu, L.; Jin, T.; Sun, X. Development of the Ni-Base Single Crystal Superalloys. Aeroengine 2005, 3, 1–7. [Google Scholar]
- Li, Y.; Zou, B.; Shi, Z.; Huang, C.; Li, L.; Liu, H.; Zhu, H.; Yao, P.; Liu, J. Wear patterns and mechanisms of sialon ceramic end-milling tool during high speed machining of nickel-based super alloy. Ceram. Int. 2021, 47, 5690–5698. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Q.; Wang, M.H.; Zheng, Y.H.; Kong, X.J. A predictive model of milling surface roughness. Int. J. Adv. Manuf. Tech. 2020, 108, 2755–2762. [Google Scholar] [CrossRef]
- Liu, Y.; Song, S.Y.; Xiao, G.J.; He, Y.; Huang, Y.; Liu, S.; Jiahua, S.L. The method and experiment research on down-stroke abrasive belt grinding under micro feeding for noise reduction surface. J. Bionic Eng. 2021, 18, 958–973. [Google Scholar] [CrossRef]
- Xiao, G.J.; Huang, Y. Micro-stiffener surface characteristics with belt polishing processing for titanium alloys. Int. J. Adv. Manuf. Technol. 2019, 100, 349–359. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, G.; Zhao, H.; Zou, L.; Zhao, L.; Liu, Y.; Dai, W. Residual stress of belt polishing for the micro-stiffener surface on the titanium alloys. Procedia CIRP 2018, 71, 11–15. [Google Scholar] [CrossRef]
- Li, C.; Li, X.L.; Huang, S.Q.; Li, L.Q.; Zhang, F.H. Ultra-precision grinding of Gd3Ga5O12 crystals with graphene oxide coolant: Material deformation mechanism and performance evaluation. J. Manuf. Process. 2021, 61, 417–427. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Li, C.; Piao, Y.; Hou, N.; Hu, K.N. Characterization of surface and subsurface defects induced by abrasive machining of optical crystals using grazing incidence X-ray diffraction and molecular dynamics. J. Adv. Res. 2021. [Google Scholar] [CrossRef]
- Huang, Y.; He, S.; Xiao, G.J.; Li, W.; Jiahua, S.L.; Wang, W.X. Effects research on theoretical-modelling based suppression of the contact flutter in blisk belt grinding. J. Manuf. Process. 2020, 54, 309–317. [Google Scholar] [CrossRef]
- Fan, W.G.; Wang, W.X.; Wang, J.D.; Zhang, X.L.; Qian, C.; Ma, T.F. Microscopic contact pressure and material removal modeling in rail grinding using abrasive belt. Proc. Inst. Mech. Eng. Part B-J. Eng. 2021, 235, 3–12. [Google Scholar] [CrossRef]
- Xiao, G.J.; Song, K.K.; Liu, S.; Wu, Y.; Wang, W.X. Comprehensive investigation into the effects of relative grinding direction on abrasive belt grinding process. J. Manuf. Process. 2021, 62, 753–761. [Google Scholar] [CrossRef]
- Xiao, G.J.; He, Y.; Huang, Y.; He, S.; Wang, W.X.; Wu, Y. Bionic microstructure on titanium alloy blade with belt grinding and its drag reduction performance. Proc. Inst. Mech. Eng. Part B-J. Eng. 2020. [Google Scholar] [CrossRef]
- Hu, W.Y.; Liao, W.H.; Liu, T.T.; Xiao, X.Z.; Gu, M.F.; Li, S.B. Prediction model of surface roughness of fused deposition modeling parts. J. Central South Univ. (Sci. Tech.) 2020, 51, 2460–2470. [Google Scholar]
- Klocke, F.; Gierlings, S.; Brockmann, M.; Veselovac, D. Force-based temperature modeling for surface integrity prediction in broaching nickel-based alloys. Procedia Cirp. 2014, 13, 314–319. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Zhang, X.K.; Wu, Z.Q.; Ma, J.Y.; Liao, X.P.; Hu, S.S. Prediction of surface roughness for compacted graphite cast iron based on support vector machine. Surf. Tech. 2020, 49, 339–346. [Google Scholar] [CrossRef]
- Wu, Y.H.; Wang, H.; Sun, J.; Wang, H.; Li, S.H. Modeling and prediction of surface quality of silicon nitride ceramic grinding. Surf. Tech. 2020, 49, 281–289. [Google Scholar] [CrossRef]
- Yi, G.Q.; Gong, Y.D.; Li, Y.Q.; Song, J.L. Study on the grinding surface and subsurface quality of novel point grinding wheels. J. Northeast. Univ (Nat. Sci.) 2019, 40, 835–840. [Google Scholar] [CrossRef]
- Ma, L.J.; Gong, Y.D.; Chen, X.H. Study on surface roughness model and surface forming mechanism of ceramics in quick point grinding. Int. J. Mach. Tools Manuf. 2014, 77, 82–92. [Google Scholar] [CrossRef]
- Liu, W.N.; Cai, Z.J.; Li, Y.F.; Ren, C.Z. Numerical simulation and experiments of abrasive flow polishing for nozzle micro-holes. Chin. J. Mech. Eng. 2017, 28, 13–19. [Google Scholar] [CrossRef]
- Lin, X.; Li, H. Enhanced pareto particle swarm approach for multi-objective optimization of surface grinding process. In Proceedings of the 2008 Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 20–22 December 2008. [Google Scholar]
- Guo, W.C.; Wu, C.J.; Ding, Z.S.; Zhou, Q.Z. Prediction of surface roughness based on a hybrid feature selection method and long short-term memory network in grinding. Int. J. Adv. Manuf. Technol. 2021, 112, 2853–2871. [Google Scholar] [CrossRef]
- Gu, Q.W.; Deng, Z.H.; Lv, L.S.; Liu, T.; Teng, H.Z.; Wang, D.F.; Yuan, J.L. Prediction research for surface topography of internal grinding based on mechanism and data model. Int. J. Adv. Manuf. Technol. 2021, 113, 821–836. [Google Scholar] [CrossRef]
- Liu, G.L.; Yu, J.B. Machining roughness prediction based on knowledge-based deep belief network. Chin. J. Mech. Eng. 2019, 55, 94–106. [Google Scholar]
- Amamou, R.; Fredj, N.B.; Fnaiech, F. Improved method for grinding force prediction based on neural network. Int. J. Adv. Manuf. Tech. 2008, 39, 656–668. [Google Scholar] [CrossRef]
- Prabhu, S.; Uma, M.; Vinayagam, B.K. Surface roughness prediction using Taguchi-fuzzy logic-neural network analysis for CNT nanofluids based grinding process. Neural Comput. Appl. 2015, 26, 41–55. [Google Scholar] [CrossRef]
- Sedighi, M.; Afshari, D. Creep feed grinding optimization by an integrated GA-NN system. J. Intell. Manuf. 2010, 21, 657–663. [Google Scholar] [CrossRef]
- Pandiyan, V.; Caesarendra, W.; Tjahjowidodo, T.; Tan, H.H. In-process tool condition monitoring in compliant abrasive belt grinding process using support vector machine and genetic algorithm. J. Manuf. Process. 2018, 31, 199–213. [Google Scholar] [CrossRef]




| X/Y/Z Axis Positioning Accuracy | X/Y/Z Axis Repeat Positioning Accuracy | A-Axis Positioning Accuracy | Surface Roughness Ra |
|---|---|---|---|
| 0.015 mm | 0.01 mm | 0.01° | 0.1 μm~0.8 μm |
| Chemical Composition (%) | ||||||
| Ni | Cr | Al | Mo | Ti | C | Nb |
| 52.30 | 18.90 | 0.52 | 3.08 | 1.06 | 0.04 | 5.30 |
| Mn | Si | Cu | Ta | Co | P | Fe |
| <0.20 | <0.20 | <0.20 | <0.20 | <0.20 | <0.20 | remaining |
| Mechanical Properties | ||||||
| Elastic modulus E/GPa | Thermal conductivity λ/W.m | Elongation δ/% | Hardness HB (Room temperature) | Impact value aK/(J.cm−2) | Shrinkage rate ψ/% | Melting point /°C |
| 205 | 14.65 | 15 | 346–450 | 573 | 41 | 1260–1320 |
| Abrasive Belt Speed (m/s) | Feed Rate (m/s) | Grinding Pressure (N) |
|---|---|---|
| 0 | 0 | 0 |
| 5 | 0.01 | 5 |
| 10 | 0.02 | 10 |
| 18 | 0.04 | 20 |
| 26 | 0.06 | 30 |
| 32 | 0.08 | 40 |
| 40 | 0.10 | 50 |
| Serial Number | Abrasive Belt Speed (m/s) | Feed Rate (m/s) | Grinding Pressure (N) | Measured Surface Roughness (μm) |
|---|---|---|---|---|
| 1 | 10 | 0.02 | 10 | 0.581 |
| 2 | 10 | 0.04 | 20 | 0.332 |
| 3 | 10 | 0.06 | 30 | 0.301 |
| 4 | 18 | 0.02 | 20 | 0.322 |
| 5 | 18 | 0.04 | 30 | 0.214 |
| 6 | 18 | 0.06 | 10 | 0.505 |
| 7 | 26 | 0.02 | 30 | 0.224 |
| 8 | 26 | 0.04 | 10 | 0.347 |
| 9 | 26 | 0.06 | 20 | 0.284 |
| 10 | 32 | 0.08 | 40 | 0.198 |
| Expected Output | BP | SOM-RBF | RLSOM-RBF | |||
|---|---|---|---|---|---|---|
| Predictive Value (μm) | Relative Error | Predictive Value (μm) | Relative Error | Predictive Value (μm) | Relative Error | |
| 0.581 | 0.473 | −1.3% | 0.587 | 1% | 0.584 | 0.52% |
| 0.332 | 0.337 | 1.5% | 0.337 | 1.5% | 0.329 | −0.90% |
| 0.301 | 0.312 | 3.7% | 0.310 | 2.9% | 0.308 | 2.3% |
| 0.322 | 0.310 | 3.7% | 0.333 | 3.4% | 0.327 | −1.5% |
| 0.214 | 0.202 | −5.6% | 0.224 | 4.6% | 0.208 | −2.8% |
| 0.505 | 0.511 | 1.2% | 0.526 | 5.1% | 0.512 | 1.4% |
| 0.224 | 0.239 | 6.7% | 0.231 | 3.1% | 0.231 | 3.1% |
| 0.347 | 0.332 | −4.3% | 0.355 | 2.3% | 0.340 | 2% |
| 0.284 | 0.261 | −8.1% | 0.290 | 2.1% | 0.278 | −2.8% |
| 0.198 | 0.210 | 6.1% | 0.213 | 7.5% | 0.198 | 0 |
| Mean relative error | 3.55% | 3.35% | 1.732% | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Song, S.; Zhang, Y.; Li, W.; Xiao, G. Prediction of Surface Roughness of Abrasive Belt Grinding of Superalloy Material Based on RLSOM-RBF. Materials 2021, 14, 5701. https://doi.org/10.3390/ma14195701
Liu Y, Song S, Zhang Y, Li W, Xiao G. Prediction of Surface Roughness of Abrasive Belt Grinding of Superalloy Material Based on RLSOM-RBF. Materials. 2021; 14(19):5701. https://doi.org/10.3390/ma14195701
Chicago/Turabian StyleLiu, Ying, Shayu Song, Youdong Zhang, Wei Li, and Guijian Xiao. 2021. "Prediction of Surface Roughness of Abrasive Belt Grinding of Superalloy Material Based on RLSOM-RBF" Materials 14, no. 19: 5701. https://doi.org/10.3390/ma14195701
APA StyleLiu, Y., Song, S., Zhang, Y., Li, W., & Xiao, G. (2021). Prediction of Surface Roughness of Abrasive Belt Grinding of Superalloy Material Based on RLSOM-RBF. Materials, 14(19), 5701. https://doi.org/10.3390/ma14195701







