A Review of Finite Element Analysis and Artificial Neural Networks as Failure Pressure Prediction Tools for Corroded Pipelines
Abstract
:1. Introduction
2. Conventional Residual Strength Assessment Methods
| Method | Fundamental Equation | Governing Assumption | Material Restriction | Defect Idealization |
|---|---|---|---|---|
| ASME B31G | NG-18 | Flow stress-dependent mechanism causes the pipe failure. Therefore, it can be described by the tensile properties of the pipe. | Low toughness | Parabolic or rectangular |
| Modified B31G | NG-18 | Low toughness | Mixed shape | |
| SHELL 92 | NG-18 | - | Rectangular | |
| RSTRENG | NG-18 | Effective area | ||
| DNV RP-F101 | NG-18 | Plastic collapse (plastic flow) controls pipe failure where the ultimate tensile strength is the flow stress. | Moderate toughness | Rectangular |
| Corroded Pipe Strength (CPS) | Extensive numerical studies (validated against test data) | Moderate toughness | Step shape | |
| PCORRC criteria | Moderate to high toughness | Elliptical |
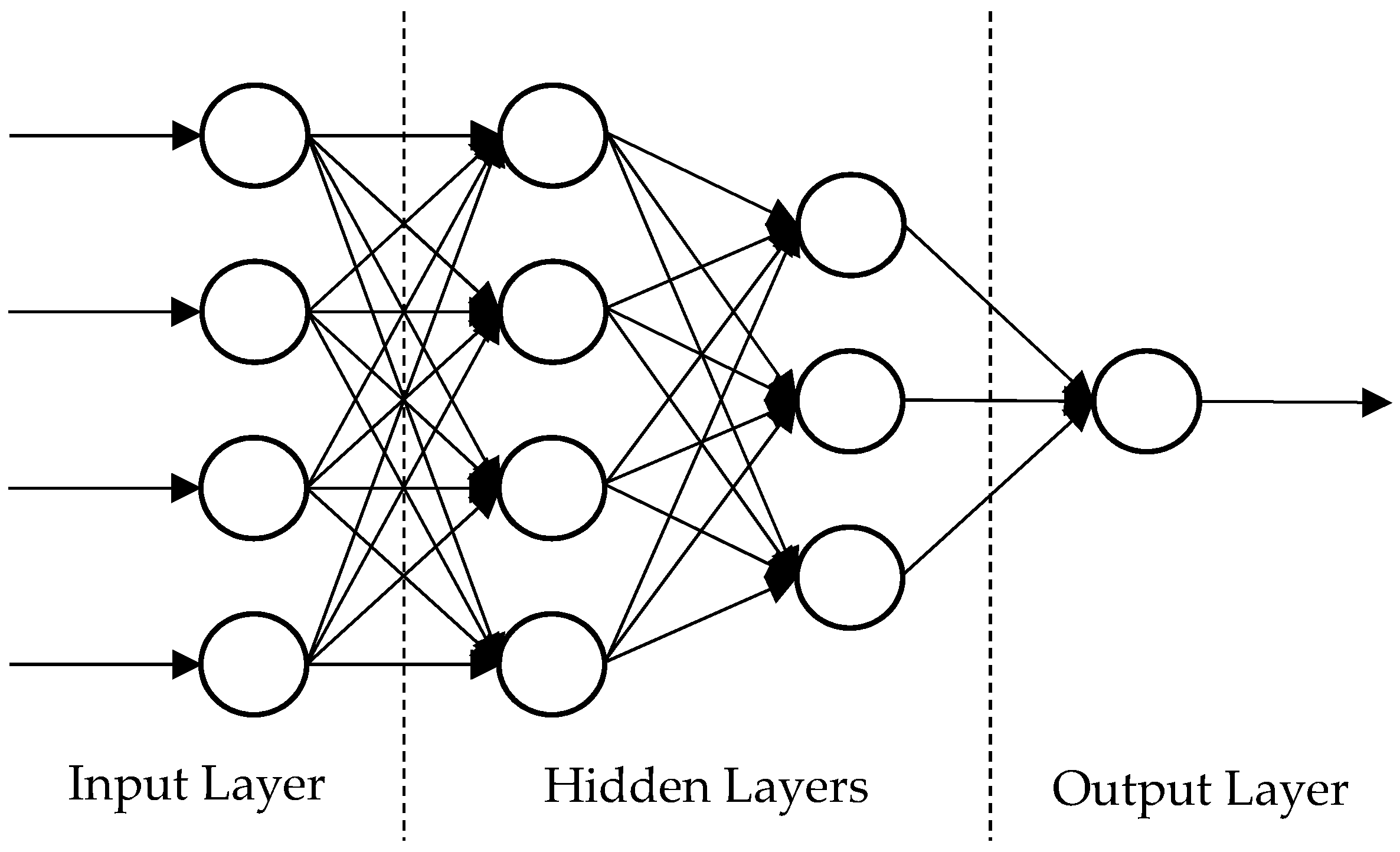
3. Artificial Neural Network as a Corroded Pipeline Failure Pressure Prediction Tool
4. Finite Element Method (FEM) as a Corrosion Defect Assessment Method
5. Integration of Finite Element Method and Artificial Neural Network as Residual Strength Prediction Tool
| Author | Field | Summary | Methodology |
|---|---|---|---|
| Javadi and Tan (2003) [77] | Computer Science | ANN is incorporated in FEM to substitute conventional constitutive material model. | ANN as part of the FEA framework. |
| Hashash et al., (2004) [78] | Civil Engineering | Models constituting ANN are incorporated in the FEM to address issues related to its numerical implementation. | |
| Gulikers (2018) [76] | Aerospace | Data generated through a series of FEA of a chosen substructure were used to train the ANN. The trained ANN was then integrated into the FEM as user material subroutine. | |
| Low and Chao (1992) [79] | Electrical Engineering | ANN models for solving problems related to inverse electromagnetic fields are developed using FEM to generate training data. | The ANN is developed based on training data generated using FEA. |
| Gudur and Dixit (2008) [80] | Mechanical Engineering | ANN to produce optimum parameters for process modeling is developed using FEM to generate training data. | |
| Umbrello et al., (2008) [81] | MechanicalEngineering | An ANN was developed to predict residual stresses and optimal conditions during steel processing using data generated using FEM for training and validation of the model. | |
| Shahani et al., (2008) [82] | Mechanical Engineering | An ANN model is developed to substitute time-consuming simulation process using data generated from FEM to train the model. | |
| Tohidi and Sharifi (2016) [83] | Civil Engineering | An empirical model is developed to predict the residual ultimate strength based on the ANN model. | An empirical solution is derived based on the ANN model trained using data generated from FEA. |
| Vijaya Kumar et al., (2021) [1] | Mechanical Engineering | An empirical model is developed to predict the failure pressure of an API 5L X80 pipe based on an ANN model. | |
| Lo et al., (2021) [27] | Mechanical Engineering | An empirical model is developed to predict the residual strength of an API 5L X65 pipe based on an ANN model. |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.V.; Karuppanan, S.; Ovinis, M. Failure Pressure Prediction of High Toughness Pipeline with a Single Corrosion Defect Subjected to Combined Loadings Using Artificial Neural Network (ANN). Metals 2021, 11, 373. [Google Scholar] [CrossRef]
- Arumugam, T.; Karuppanan, S.; Ovinis, M. Finite element analyses of corroded pipeline with single defect subjected to internal pressure and axial compressive stress. Mar. Struct. 2020, 72, 102746. [Google Scholar] [CrossRef]
- Belachew, C.T.; Ismail, M.C.; Karuppanan, S. Burst Strength Analysis of Corroded Pipelines by Finite Element Method. J. Appl. Sci. 2011, 11, 1845–1850. [Google Scholar] [CrossRef]
- Vanaei, H.; Eslami, A.; Egbewande, A. A review on pipeline corrosion, in-line inspection (ILI), and corrosion growth rate models. Int. J. Press. Vessel. Pip. 2017, 149, 43–54. [Google Scholar] [CrossRef]
- Zhang, B.; Ma, X. A review—Pitting corrosion initiation investigated by TEM. J. Mater. Sci. Technol. 2019, 35, 1455–1465. [Google Scholar] [CrossRef]
- Cosham, A.; Hopkins, P.; Macdonald, K. Best practice for the assessment of defects in pipelines—Corrosion. Eng. Fail. Anal. 2007, 14, 1245–1265. [Google Scholar] [CrossRef]
- Boukhari, Y.; Boucherit, M.N.; Zaabat, M.; Amzert, S.; Brahimi, K. Artificial Intelligence to Predict Inhibition Performance of Pitting Corrosion. J. Fundam. Appl. Sci. 2017, 9, 309–322. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.-X.; Xu, X.-L.; Yu, Z.-W. Pitting-corrosion on internal wall of tee-pipe joined with main-pipe for seawater tank-washing system of a tanker. Eng. Fail. Anal. 2019, 104, 439–447. [Google Scholar] [CrossRef]
- DNV. Recommended Practice DNV-RP-F101; DNV: Oslo, Norway, 2017. [Google Scholar]
- Xu, W.-Z.; Li, C.B.; Choung, J.; Lee, J.-M. Corroded pipeline failure analysis using artificial neural network scheme. Adv. Eng. Softw. 2017, 112, 255–266. [Google Scholar] [CrossRef]
- Chauhan, V.; Brister, J. A Review of Methods for Assessing the Remaining Strength of Corroded Pipelines; PRCI: Chantilly, VA, USA, 2009. [Google Scholar]
- Gao, J.; Yang, P.; Li, X.; Zhou, J.; Liu, J. Analytical prediction of failure pressure for pipeline with long corrosion defect. Ocean Eng. 2019, 191, 106497. [Google Scholar] [CrossRef]
- Amaya-Gómez, R.; Sanchez-Silva, M.; Bastidas-Arteaga, E.; Schoefs, F.; Muñoz, F. Reliability assessments of corroded pipelines based on internal pressure—A review. Eng. Fail. Anal. 2019, 98, 190–214. [Google Scholar] [CrossRef]
- Chiodo, M.S.; Ruggieri, C. Failure assessments of corroded pipelines with axial defects using stress-based criteria: Numerical studies and verification analyses. Int. J. Press. Vessel. Pip. 2009, 86, 164–176. [Google Scholar] [CrossRef]
- Lee, G.H.; Pouraria, H.; Seo, J.K.; Paik, J.K. Burst strength behaviour of an aging subsea gas pipeline elbow in different external and internal corrosion-damaged positions. Int. J. Nav. Arch. Ocean Eng. 2015, 7, 435–451. [Google Scholar] [CrossRef] [Green Version]
- Arumugam, T.; Karuppanan, S.; Ovinis, M. Residual strength analysis of pipeline with circumferential groove corrosion subjected to internal pressure. Mater. Today Proc. 2019, 29, 88–93. [Google Scholar] [CrossRef]
- Mavaddat, N.; Ahderom, S.; Tiporlini, V.; Alameh, K. Simulation of biomedical signals and images using Monte Carlo methods for training of deep learning networks. In Deep Learning Techniques for Biomedical and Health Informatics; Elsevier Inc.: Amsterdam, The Netherlands, 2020; pp. 213–236. [Google Scholar] [CrossRef]
- Buc, D.; Masarova, G. Application of Monte Carlo Simulation in the field of Mechanical Engineering. J. Interdiciplinary Res. 2003, 3, 74–91. [Google Scholar]
- Amar, J. The Monte Carlo method in science and engineering. Comput. Sci. Eng. 2006, 8, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Denning, R. Applied R&M Manual for Defence Systems. In GR-77 Issue 2012; MoD, Abbey Wood: Bristol, UK, 2012; pp. 1–8. [Google Scholar]
- Wang, Y.-L.; Li, C.-M.; Chang, R.-R.; Huang, H.-R. State evaluation of a corroded pipeline. J. Mar. Eng. Technol. 2016, 15, 88–96. [Google Scholar] [CrossRef]
- El-Abbasy, M.S.; Senouci, A.; Zayed, T.; Mirahadi, F.; Parvizsedghy, L. Artificial neural network models for predicting condition of offshore oil and gas pipelines. Autom. Constr. 2014, 45, 50–65. [Google Scholar] [CrossRef]
- Tchórzewska-cieślak, B.; Pietrucha-urbanik, K. Analysis of the gas network failure and failure prediction using the Monte Carlo simulation method Analiza awaryjności sieci gazowych oraz prognozowanie awarii z zastosowaniem symulacyjnej metody Monte Carlo. Eksploat. Niezawodn. 2016, 18, 254–259. [Google Scholar] [CrossRef]
- Chaves, I.A.; Ppgmne-ufpr, F.U.; Machado, R.D. Estimation of Failure Probability in Corroded Oil Pipelines through Monte Carlo Simulation Method Applying the Bootstrap Technique. Int. J. Appl. Sci. Technol. 2014, 4, 141–152. [Google Scholar]
- Theodoridis, S. Monte Carlo Methods; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Li, F.; Wang, W.; Xu, J.; Yi, J.; Wang, Q. Comparative study on vulnerability assessment for urban buried gas pipeline network based on SVM and ANN methods. Process. Saf. Environ. Prot. 2018, 122, 23–32. [Google Scholar] [CrossRef]
- Lo, M.; Karuppanan, S.; Ovinis, M. Failure Pressure Prediction of a Corroded Pipeline with Longitudinally Interacting Corrosion Defects Subjected to Combined Loadings Using FEM and ANN. J. Mar. Sci. Eng. 2021, 9, 281. [Google Scholar] [CrossRef]
- Xu, W.Z.; Li, C.B.; Choung, J.; Lee, J.M. Residual strength calculation & residual life prediction of general corrosion pipeline. Eng. Fail. Anal. 2019, 1, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Gurney, K. An Introduction to Neural Networks; Routledge: London, UK, 1997. [Google Scholar]
- De Masi, G.; Gentile, M.; Vichi, R.; Bruschi, R.; Gabetta, G. Machine learning approach to corrosion assessment in subsea pipelines. In Proceedings of the Oceans 2015—Genova, Genova, Italy, 18–21 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zimek, A.; Schubert, E. Outlier Detection. In Encyclopedia of Database Systems; Springer: New York, NY, USA, 2017; pp. 1–5. [Google Scholar]
- Stevo, B. Modeling Mechanisms of Cognition-Emotion Interaction in Artificial Neural Networks, since 1981. Procedia Comput. Sci. 2014, 41, 255–263. [Google Scholar]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Song, H.; Zhang, Y.; Yin, X.; Wang, L.; Wang, W.; Xia, F. How to improve the prediction accuracy of the ANN model to underground water content effectively. In Proceedings of the 2011 International Symposium on Water Resource and Environmental Protection, Xi’an, China, 20–22 May 2011; Volume 1, pp. 350–353. [Google Scholar] [CrossRef]
- Panchal, F.S.; Panchal, M. Review on Methods of Selecting Number of Hidden Nodes in Artificial Neural Network. Int. J. Comput. Sci. Mob. Comput. 2014, 3, 455–464. [Google Scholar]
- Shobha, G.; Rangaswamy, S. Machine Learning, 1st ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 38. [Google Scholar]
- Talabis, M.R.M.; McPherson, R.; Miyamoto, I.; Martin, J. Chapter 1—Analytics Defined. In Finding Security Insights, Patterns and Anomalies in Big Data; Syngress: Burlington, MA, USA, 2015; pp. 1–12. [Google Scholar]
- Zhu, X.; Goldberg, A.B. Introduction to Semi-Supervised Learning; Morgan & Claypool Publishers: San Rafael, CA, USA, 2009. [Google Scholar]
- Zhu, X. Semi-Supervised Learning Literature Survey Contents; University of Wisconsin: Madison, WI, USA, 2007. [Google Scholar]
- Hagan, M.; Menhaj, M. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Wen, K.; He, L.; Liu, J.; Gong, J. An optimization of artificial neural network modeling methodology for the reliability assessment of corroding natural gas pipelines. J. Loss Prev. Process. Ind. 2019, 60, 1–8. [Google Scholar] [CrossRef]
- Shuai, Y.; Shuai, J.; Liu, C. Research on the reliability methods of corroded pipeline. Pet. Sci. Bull. 2017, 2, 288–297. [Google Scholar]
- Shemyakin, A.; Prost, L.R. The Recycler Electron Cooler; Office of Scientific and Technical Information ({OSTI}): Oak Ridge, TN, USA, 2013. [CrossRef] [Green Version]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [Green Version]
- Kuang, P.; Wang, H. 3D Bounding Box Generative Adversarial Nets. In Proceedings of the International Conference on Advances in Computer Technology, Information Science and Communications—CTISC, Xiamen, China, 15–17 March 2019; pp. 117–121. [Google Scholar] [CrossRef]
- Maass, W.; Natschläger, T.; Markram, H. Real-Time Computing Without Stable States: A New Framework for Neural Computation Based on Perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef]
- Hayes, B. First Links in the Markov Chain. Am. Sci. 2013, 101, 92. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Broomhead, D.; Jones, R.; McWhirter, J.; Shepherd, T. Systolic array for nonlinear multidimensional interpolation using radial basis functions. Electron. Lett. 1990, 26, 7–9. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Zangenehmadar, Z.; Moselhi, O. Assessment of Remaining Useful Life of Pipelines Using Different Artificial Neural Networks Models . J. Perform. Constr. Facil. 2017, 30, 04016032. [Google Scholar] [CrossRef]
- Shirzad, A.; Tabesh, M.; Farmani, R. A Comparison between Performance of Support Vector Regression and Artificial Neural Network in Prediction of Pipe Burst Rate in Water Distribution Networks. KSCE J. Civ. Eng. 2014, 18, 941–948. [Google Scholar] [CrossRef]
- Chin, K.T.; Arumugam, T.; Karuppanan, S.; Ovinis, M. Failure pressure prediction of pipeline with single corrosion defect using artificial neural network. Pipeline Sci. Technol. 2020, 4, 10–17. [Google Scholar] [CrossRef]
- Soares, E.; Bruère, V.M.; Afonso, S.M.B.; Willmersdorf, R.B.; Lyra, P.R.M.; Bouchonneau, N. Structural integrity analysis of pipelines with interacting corrosion defects by multiphysics modeling. Eng. Fail. Anal. 2018, 97, 91–102. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. Manual for Determining the Remaining Strength of Corroded Pipelines: Supplement to ASME B31 Code for Pressure Piping; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Szabó, B.; Babuška, I. Introduction to Finite Element Analysis; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 1–15. [Google Scholar]
- Kim, N.-H. Nonlinear Finite Element Analysis Procedure. In Introduction to Nonlinear Finite Element Analysis; Springer: New York, NY, USA, 2015; pp. 81–140. [Google Scholar] [CrossRef]
- Cronin, D.S. Finite Element Analysis of Complex Corrosion Defects. In Proceedings of the ASME Pressure Vessels and Piping Conference, Vancouver, BC, Canada, 5–9 August 2002; pp. 55–61. [Google Scholar] [CrossRef]
- Sadowski, A.J.; Rotter, J.M. Solid or shell finite elements to model thick cylindrical tubes and shells under global bending. Int. J. Mech. Sci. 2013, 74, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Filho, J.E.A.; Machado, R.; Bertin, R.J.; Valentini, M. On the failure pressure of pipelines containing wall reduction and isolated pit corrosion defects. Comput. Struct. 2014, 132, 22–33. [Google Scholar] [CrossRef]
- CSA. Z662-07: Limit State Equation for Burst of Large Leaks and Rupture for Corrosion Defect; Canadian Standards Association: Mississauga, ON, Canada, 2007. [Google Scholar]
- De Andrade, E.Q.; Benjamin, A.C.; Machado, P.R.S.; Pereira, L.C.; Jacob, B.; Carneiro, E.G.; Guerreiro, J.N.C.; Silva, R.C.C.; Noronha, D.B. Finite Element Modeling of the Failure Behavior of Pipelines Containing Interacting Corrosion Defects. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Hamburg, Germany, 4–9 June 2006; Volume 2006. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, Y.P.; Moon, M.; Bang, W.H.; Oh, K.H.; Kim, W.S. The Prediction of Failure Pressure of Gas Pipeline with Multi Corroded Region. Mater. Sci. Forum 2005, 475–479, 3323–3326. [Google Scholar] [CrossRef]
- Netto, T.A.; Ferraz, U.; Estefen, S. The effect of corrosion defects on the burst pressure of pipelines. J. Constr. Steel Res. 2005, 61, 1185–1204. [Google Scholar] [CrossRef]
- Wang, W.; Yi, J.; Liu, T. Prediction of residual life for oil and gas pipe with local corroded defects. Procedia Eng. 2011, 26, 2415–2421. [Google Scholar] [CrossRef] [Green Version]
- Mokhtari, M.; Melchers, R.E. A new approach to assess the remaining strength of corroded steel pipes. Eng. Fail. Anal. 2018, 93, 144–156. [Google Scholar] [CrossRef]
- Alberta Energy Regulator. Report 2013-B: Pipeline Performance in Alberta, 1990–2012; Alberta Energy Regulator: Calgary, AB, Canada, 2013.
- Cosham, A.; Palmer, A.; Hopkins, P. The Assessment of Corrosion in Pipeline-Guidance in The Pipeline Defect Assessment Manual (PDAM). In Proceedings of the Pipeline Pigging and Integrity Management Conference, Amsterdam, The Netherlands, 17–18 May 2004. [Google Scholar]
- Su, C.-L.; Li, X.; Zhou, J. Failure pressure analysis of corroded moderate-to-high strength pipelines. China Ocean Eng. 2016, 30, 69–82. [Google Scholar] [CrossRef]
- Zhu, X.-K. A New Material Failure Criterion for Numerical Simulation of Burst Pressure of Corrosion Defects in Pipelines. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference, Boston, Massachusetts, USA, 19–23 July 2015. [Google Scholar] [CrossRef]
- Zhu, X.-K. Assessment Methods and Technical Challenges of Remaining Strength for Corrosion Defects in Pipelines. In Proceedings of the ASME 2018 Pressure Vessels and Piping Conference, Prague, Czech Republic, 15–20 July 2018. [Google Scholar] [CrossRef]
- Choi, J.; Goo, B.; Kim, J.; Kim, Y.; Kim, W. Development of limit load solutions for corroded gas pipelines. Int. J. Press. Vessel. Pip. 2003, 80, 121–128. [Google Scholar] [CrossRef]
- Besel, M.; Zimmermann, S.; Kalwa, C.; Koppe, T.; Liessem, A. Corrosion Assessment Method Validation for High-Grade Line Pipe. In Proceedings of the 2010 8th International Pipeline Conference, Calgary, AB, Canada, 27 September–1 October 2010; pp. 385–394. [Google Scholar] [CrossRef]
- Terán, G.; Capula-Colindres, S.; Velázquez, J.C.; Fernández-Cueto, M.J.; Angeles-Herrera, D.; Herrera-Hernández, H. Failure Pressure Estimations for Pipes with Combined Corrosion Defects on the External Surface: A Comparative Study. Int. J. Electrochem. Sci. 2017, 11, 10152–10176. [Google Scholar] [CrossRef]
- Belachew, C.T.; Ismail, M.C.; Karuppanan, S. Evaluation of Available Codes for Capacity Assessment of Corroded Pipelines; NACE Asis Pacific: Kuala Lumpur, Malaysia, 2009. [Google Scholar]
- Gulikers, T. An Integrated Machine Learning and Finite Element Analysis Framework, Applied to Composite Substructures including Damage; Delft University of Technology: Delft, The Netherlands, 2018. [Google Scholar]
- Javadi, A.A.; Tan, T.P. Neural network for constitutive modelling in finite element analysis. Comput. Assist. Mech. 2003, 10, 523–530. [Google Scholar]
- Hashash, Y.M.A.; Jung, S.; Ghaboussi, J. Numerical implementation of a neural network based material model in finite element analysis. Int. J. Numer. Methods Eng. 2004, 59, 989–1005. [Google Scholar] [CrossRef]
- Low, T.S.; Chao, M.B. The Use of Finite Elements and Neural Network for teh Solution of Inverse Electromagnetic Problems. IEEE Trans. Magn. 1992, 28, 2811–2813. [Google Scholar] [CrossRef]
- Gudur, P.; Dixit, U. A neural network-assisted finite element analysis of cold flat rolling. Eng. Appl. Artif. Intell. 2008, 21, 43–52. [Google Scholar] [CrossRef]
- Umbrello, D.; Ambrogio, G.; Filice, L.; Shivpuri, R. A hybrid finite element method–artificial neural network approach for predicting residual stresses and the optimal cutting conditions during hard turning of AISI 52100 bearing steel. Mater. Des. 2008, 29, 873–883. [Google Scholar] [CrossRef]
- Shahani, A.; Setayeshi, S.; Nodamaie, S.; Asadi, M.; Rezaie, S. Prediction of influence parameters on the hot rolling process using finite element method and neural network. J. Mater. Process. Technol. 2009, 209, 1920–1935. [Google Scholar] [CrossRef]
- Tohidi, S.; Sharifi, Y. Load-carrying capacity of locally corroded steel plate girder ends using artificial neural network. Thin-Walled Struct. 2016, 100, 48–61. [Google Scholar] [CrossRef]
- Silva, R.; Guerreiro, J.; Loula, A. A study of pipe interacting corrosion defects using the FEM and neural networks. Adv. Eng. Softw. 2007, 38, 868–875. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Zhang, J.; Liu, X.; Li, X.; Zhou, J. Failure assessment of X80 pipeline with interacting corrosion defects. Eng. Fail. Anal. 2015, 47, 67–76. [Google Scholar] [CrossRef]

| Method | Flow Stress, σf | Folias Factor, M |
|---|---|---|
| ASME B31G | ||
| Modified B31G | ||
| RSTRENG | ||
| SHELL 92 | ||
| DNV RP-F101 |
| Learning Paradigms | Algorithms | Remarks |
|---|---|---|
| Supervised learning |
|
|
| Unsupervised learning |
|
|
| Semisupervised learning |
|
|
| Reinforcement learning |
|
|
| Architecture | Function |
|---|---|
| Feedforward neural network (FFNN) | Theoretically models the relationship between the input and output based on the training dataset [30]. |
| Radial basis function (RBF) | Similar to an FFNN but uses radial basis activation function [31]. |
| Recurrent neural networks (RNNs) | Uses data with no timeline and is a suitable option for advancing or completing information [32]. |
| Long/short-term memory (LSTM) | Contains memory cell that overcomes the exploding gradient problem and learns complex sequences in the form of music or art [33]. |
| Gated recurrent units (GRU) | Similar to LSTM but is faster and easier to run [34]. |
| Autoencoders (AEs) | Used to encode data by compressing them [35]. |
| Variational autoencoders (VAEs) | Relies on Bayesian mathematics pertaining to probabilistic inference to rule out improbable relations among inputs and outputs [36]. |
| Denoising autoencoders (DAEs) | Used for noisy data where the model can be trained to learn details rather than the broader features of a data [37]. |
| Sparse autoencoders (SAEs) | Used to extract details and small features from a given dataset [38]. |
| Deep belief networks (DBNs) | Used to represent data as a probabilistic model, classify data, and generate new data [39]. |
| Convolutional neural networks (CNNs) | Used for image or audio processing [40]. |
| Deconvolutional networks (DNs) | Reversed convolutional networks, also called inverse graphics networks [41]. |
| Deep convolutional inverse graphics networks (DCIGNs) | Used to model complex transformations on images [42]. |
| Generative adversarial networks (GANs) | Two networks working together with one generating content and the other judging the contents [43]. |
| Liquid state machines (LSMs) | Used to create a spiking-like pattern where there is a change in the output only when a certain threshold is reached [44,45]. |
| Echo state networks (ESNs) | Similar to FFNN but utilizes random connections within the nodes [46]. |
| Deep residual networks (DRNs) | Used in learning patterns that are up to 150 layers deep [47]. |
| Capsule network (CapsNet) | Used in transferring information about an input using Hebbian learning, the values of which correct predictions of output in the next layer [48]. |
| Kohonen networks (KNs) | Used to classify data without supervision by utilizing competitive learning [49]. |
| Attention networks (ANs) | Used to visualize insight into which input features correspond with what output features [50]. |
| Activation Function | Equation | Range | |
|---|---|---|---|
| Linear | Linear function | f(x) = x | −infinity to infinity |
| Nonlinear | Sigmoid or logistic function | 0 to 1 | |
| Tanh or hyperbolic Tangent function | f(x) = tanh(x) | −1 to 1 | |
| Rectified linear unit (ReLU) | f(x) = max(0, x) | 0 to infinity |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vijaya Kumar, S.D.; Lo Yin Kai, M.; Arumugam, T.; Karuppanan, S. A Review of Finite Element Analysis and Artificial Neural Networks as Failure Pressure Prediction Tools for Corroded Pipelines. Materials 2021, 14, 6135. https://doi.org/10.3390/ma14206135
Vijaya Kumar SD, Lo Yin Kai M, Arumugam T, Karuppanan S. A Review of Finite Element Analysis and Artificial Neural Networks as Failure Pressure Prediction Tools for Corroded Pipelines. Materials. 2021; 14(20):6135. https://doi.org/10.3390/ma14206135
Chicago/Turabian StyleVijaya Kumar, Suria Devi, Michael Lo Yin Kai, Thibankumar Arumugam, and Saravanan Karuppanan. 2021. "A Review of Finite Element Analysis and Artificial Neural Networks as Failure Pressure Prediction Tools for Corroded Pipelines" Materials 14, no. 20: 6135. https://doi.org/10.3390/ma14206135
APA StyleVijaya Kumar, S. D., Lo Yin Kai, M., Arumugam, T., & Karuppanan, S. (2021). A Review of Finite Element Analysis and Artificial Neural Networks as Failure Pressure Prediction Tools for Corroded Pipelines. Materials, 14(20), 6135. https://doi.org/10.3390/ma14206135






