Effect of Nanoparticles Surface Bonding and Aspect Ratio on Mechanical Properties of Highly Cross-Linked Epoxy Nanocomposites: Mesoscopic Simulations
Abstract
:1. Introduction
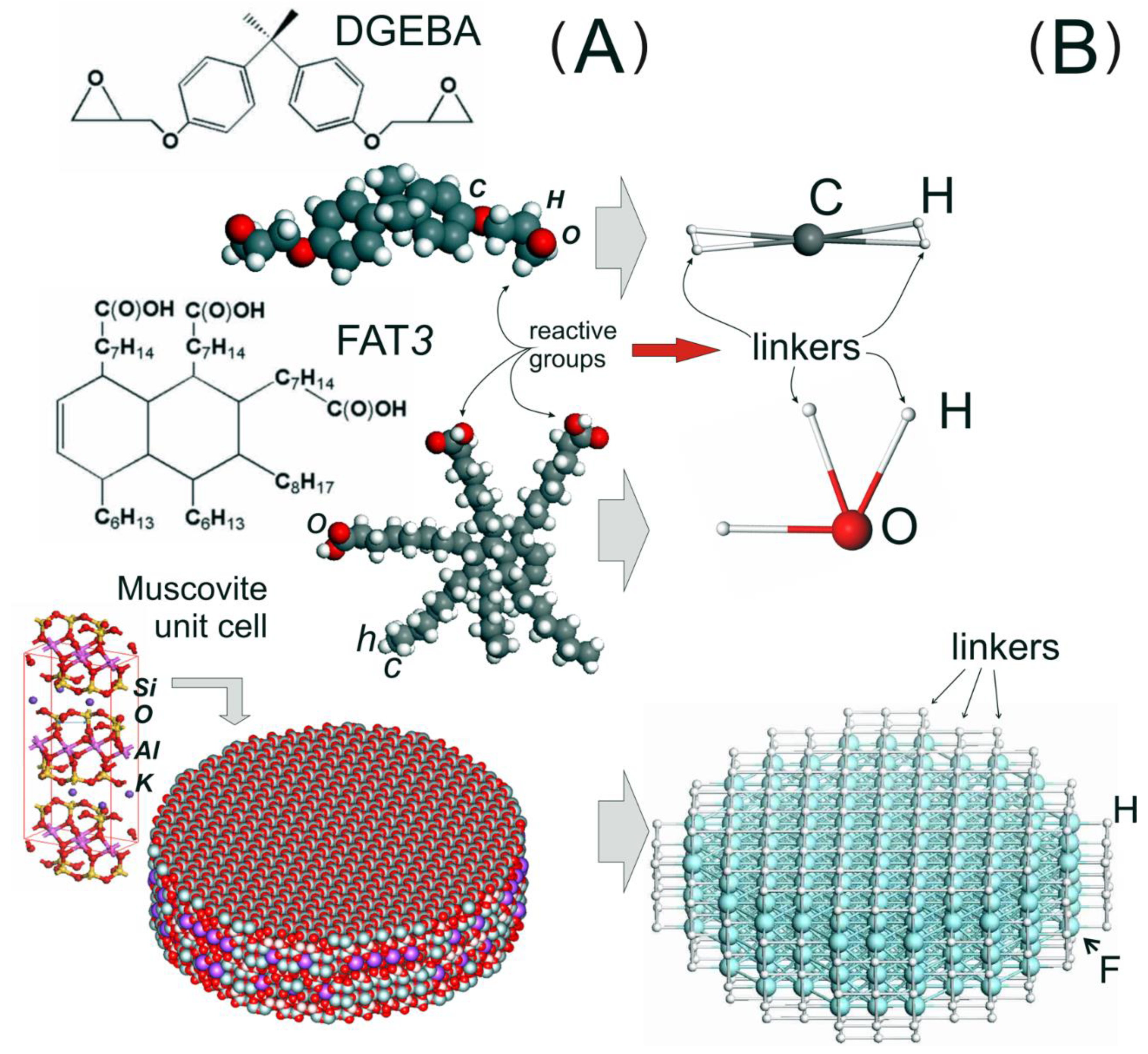
2. Model and Parameterization
3. Methodology of Simulations
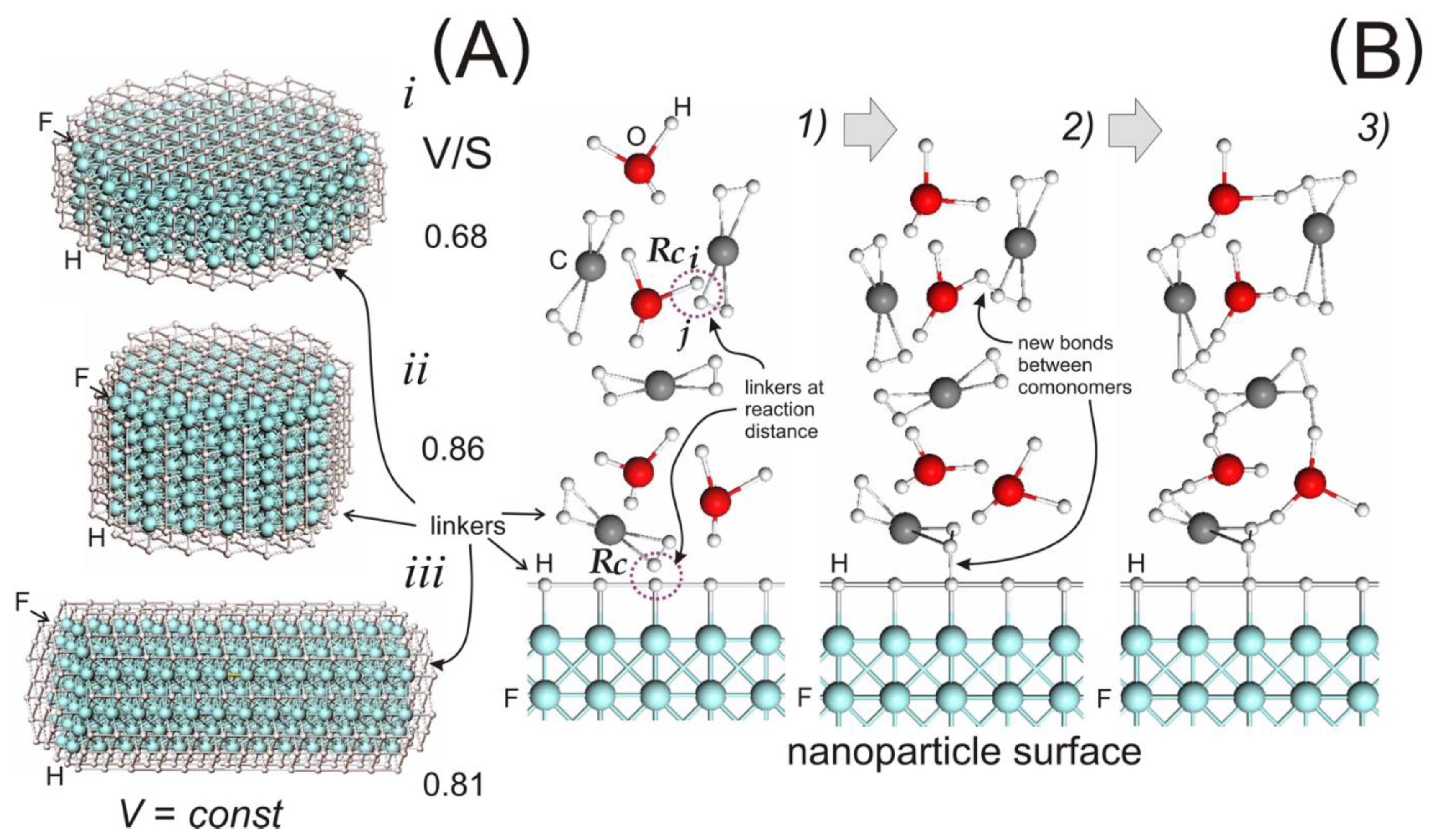
3.1. Systems Preparation
3.2. Stress–Strain Response Calculation
3.3. Topological Analysis
4. Results and Discussion
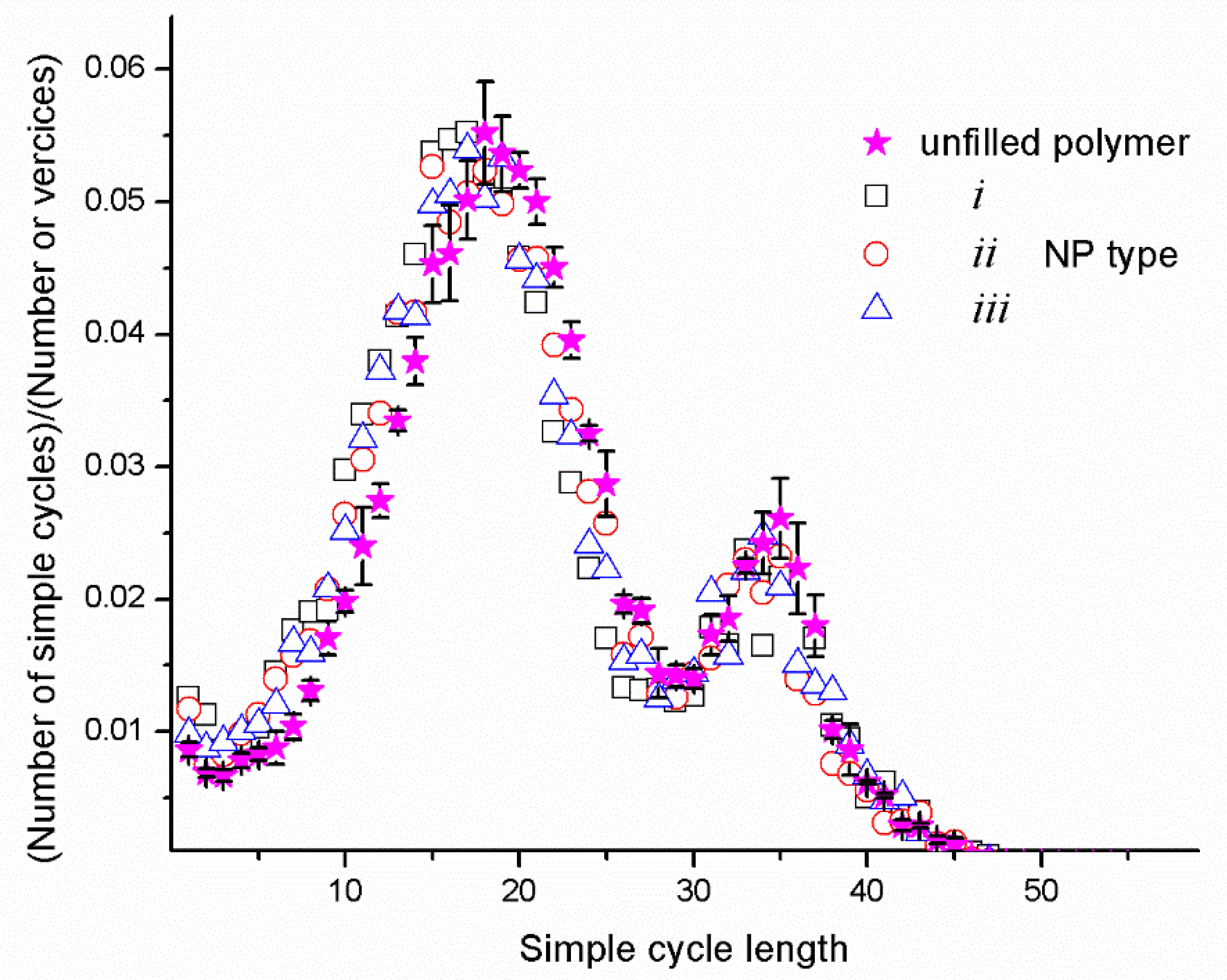
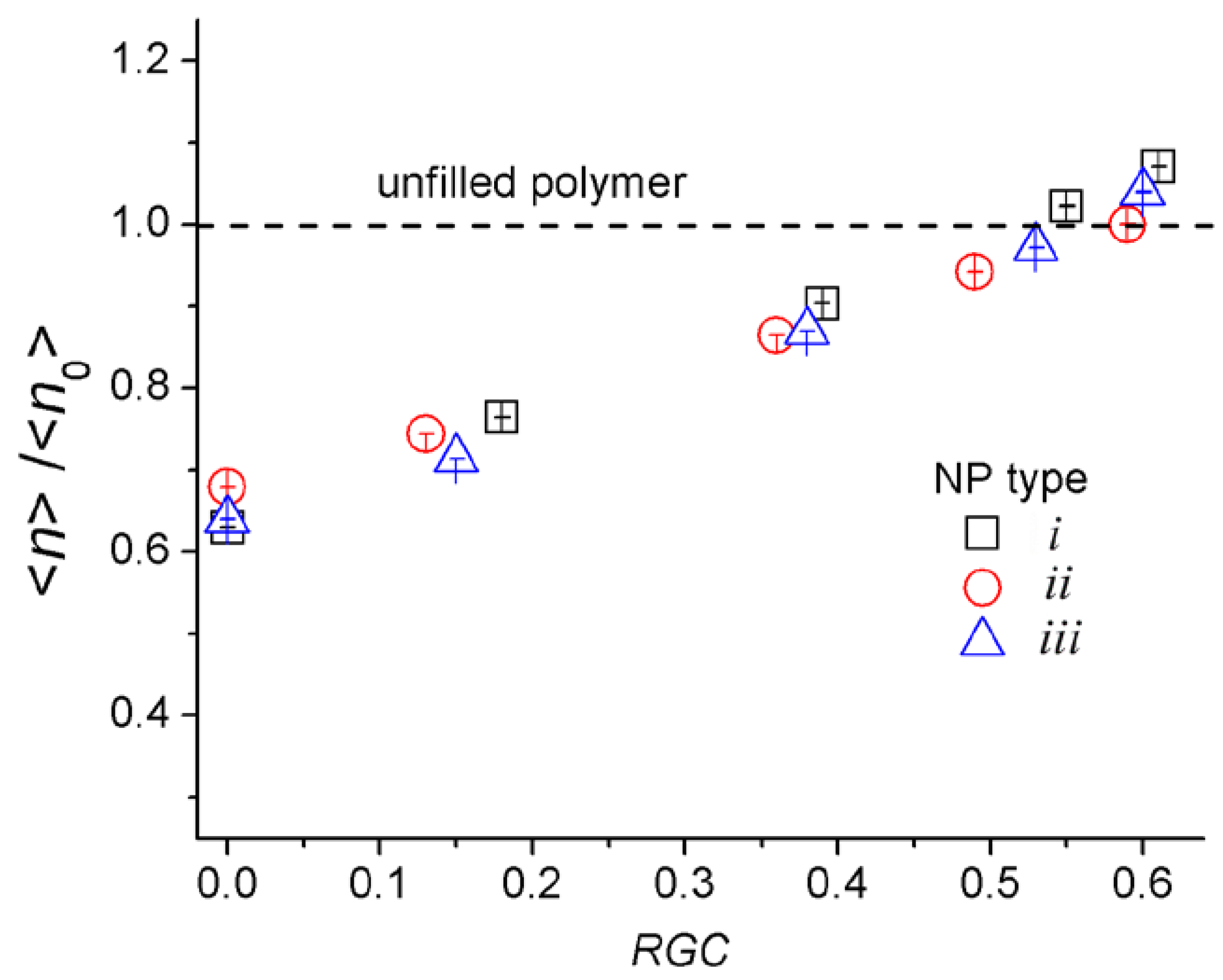
4.1. Simple Cycles and Load-Bearing Chains
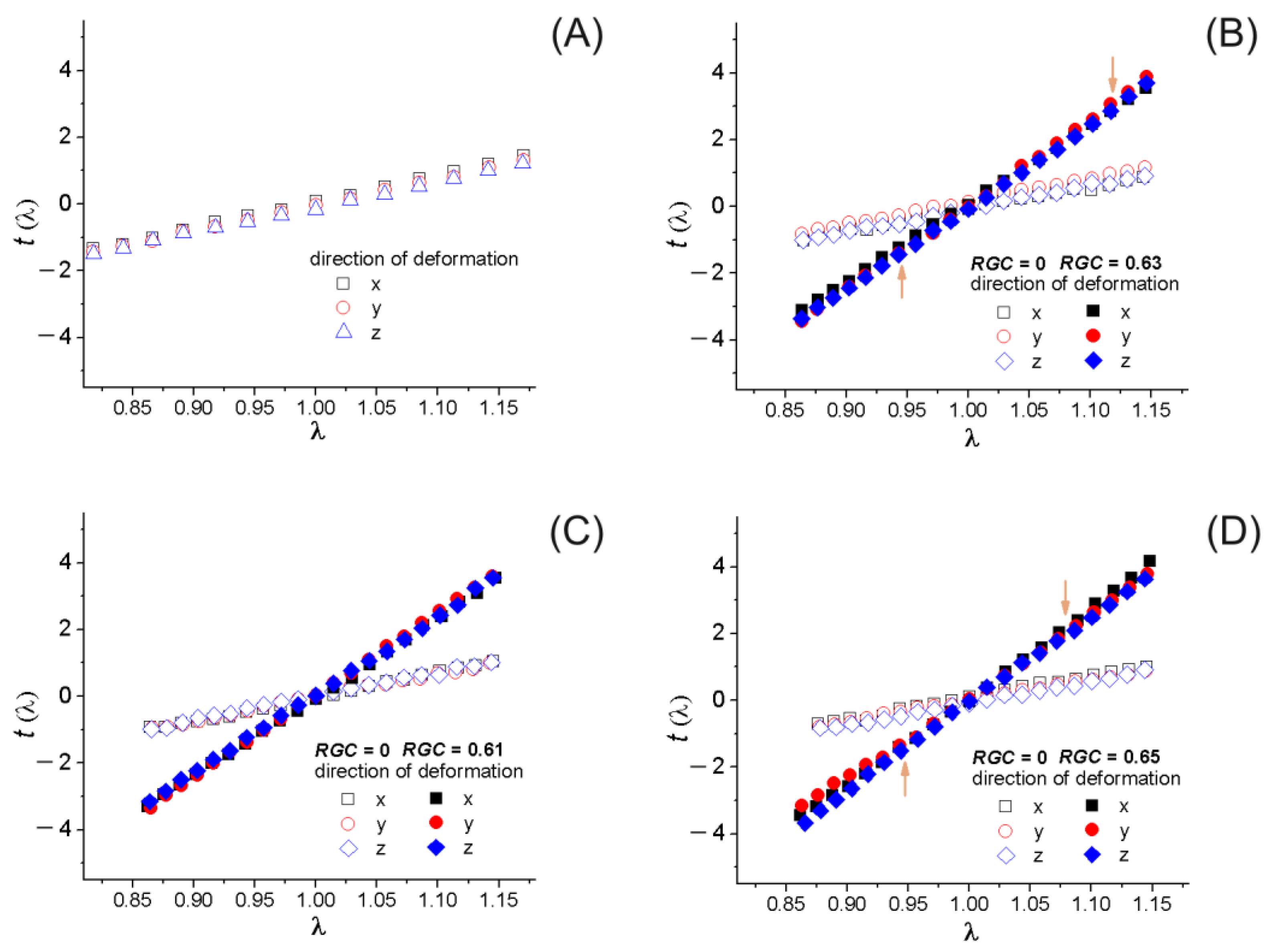
4.2. Mechanical Response
4.3. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akelah, A. Polymers in Food Processing Industries. In Functionalized Polymeric Materials in Agriculture and the Food Industry; Springer US: Boston, MA, USA, 2013; pp. 195–248. ISBN 9781461470601. [Google Scholar]
- Pop, O.L.; Pop, C.R.; Dufrechou, M.; Vodnar, D.C.; Socaci, S.A.; Dulf, F.V.; Minervini, F.; Suharoschi, R. Edible Films and Coatings Functionalization by Probiotic Incorporation: A Review. Polymers 2019, 12, 12. [Google Scholar] [CrossRef] [Green Version]
- Pandey, M.; Choudhury, H.; Abdul-Aziz, A.; Bhattamisra, S.K.; Gorain, B.; Carine, T.; Wee Toong, T.; Yi, N.J.; Win Yi, L. Promising Drug Delivery Approaches to Treat Microbial Infections in the Vagina: A Recent Update. Polymers 2020, 13, 26. [Google Scholar] [CrossRef]
- Beltrán Sanahuja, A.; Valdés García, A. New Trends in the Use of Volatile Compounds in Food Packaging. Polymers 2021, 13, 1053. [Google Scholar] [CrossRef]
- Schadler, L.S.; Brinson, L.C.; Sawyer, W.G. Polymer Nanocomposites: A Small Part of the Story. JOM 2007, 59, 53–60. [Google Scholar] [CrossRef]
- Vollath, D. Nanoparticles—Nanocomposites—Nanomaterials: An Introduction for Beginners; Wiley-VCH: Weinheim, Germany, 2013; ISBN 9783527334605. [Google Scholar]
- Bhattacharya, M. Polymer Nanocomposites-A Comparison between Carbon Nanotubes, Graphene, and Clay as Nanofillers. Materials 2016, 9, 262. [Google Scholar] [CrossRef]
- Ahn, C.; Kim, S.-M.; Jung, J.-W.; Park, J.; Kim, T.; Lee, S.E.; Jang, D.; Hong, J.-W.; Han, S.M.; Jeon, S. Multifunctional Polymer Nanocomposites Reinforced by 3D Continuous Ceramic Nanofillers. ACS Nano 2018, 12, 9126–9133. [Google Scholar] [CrossRef]
- Bee, S.-L.; Abdullah, M.A.A.; Bee, S.-T.; Sin, L.T.; Rahmat, A.R. Polymer Nanocomposites Based on Silylated-Montmorillonite: A Review. Prog. Polym. Sci. 2018, 85, 57–82. [Google Scholar] [CrossRef]
- Dantas de Oliveira, A.; Augusto Gonçalves Beatrice, C. Polymer Nanocomposites with Different Types of Nanofiller. In Nanocomposites—Recent Evolutions; IntechOpen: London, UK, 2019; ISBN 9781789850116. [Google Scholar]
- Rudnik, E. Compostable Polymer Materials; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780080994420. [Google Scholar]
- Zhang, K.; Wang, L.; Wang, F.; Wang, G.; Li, Z. Preparation and Characterization of Modified-Clay-Reinforced and Toughened Epoxy-Resin Nanocomposites. J. Appl. Polym. Sci. 2004, 91, 2649–2652. [Google Scholar] [CrossRef]
- Ha, S.R.; Ryu, S.H.; Park, S.J.; Rhee, K.Y. Effect of Clay Surface Modification and Concentration on the Tensile Performance of Clay/epoxy Nanocomposites. Mater. Sci. Eng. A Struct. Mater. 2007, 448, 264–268. [Google Scholar] [CrossRef]
- Ray, S.S. Recent Trends and Future Outlooks in the Field of Clay-Containing Polymer Nanocomposites. Macromol. Chem. Phys. 2014, 215, 1162–1179. [Google Scholar] [CrossRef]
- Ianchis, R.; Rosca, I.D.; Ghiurea, M.; Spataru, C.I.; Nicolae, C.A.; Gabor, R.; Raditoiu, V.; Preda, S.; Fierascu, R.C.; Donescu, D. Synthesis and Properties of New Epoxy-Organolayered Silicate Nanocomposites. Appl. Clay Sci. 2015, 103, 28–33. [Google Scholar] [CrossRef]
- Osman, M.A.; Rupp, J.E.P.; Suter, U.W. Effect of non-ionic surfactants on the exfoliation and properties of polyethylene-layered silicate nanocomposites. Polymer 2005, 46, 8202–8209. [Google Scholar] [CrossRef]
- Mittal, V. Mechanical and gas permeation properties of compatibilized polypropylene–layered silicate nanocomposites. J. Appl. Polym. Sci. 2008, 107, 0021–8995. [Google Scholar] [CrossRef]
- Zanjanijam, A.R.; Hajian, M.; Koohmareh, G.A. Fabrication of Single Wall Carbon Nanotubes-Based Poly(vinyl butyral) Nanocomposites with Enhanced Mechanical and Thermal Properties. J. Macromol. Sci. Part A 2014, 51, 369–377. [Google Scholar] [CrossRef]
- Shabani, A.; Babaei, A.; Zanjanijam, A.R. Does Nanoclay Addition Always Lead to Amelioration? Dual Effects of the Nanoclay on the PA-6/EVOH/SEBS Ternary Blends. Polym. Adv. Technol. 2019, 30, 983–997. [Google Scholar] [CrossRef]
- Huskić, M.; Žigon, M.; Ivanković, M. Comparison of the Properties of Clay Polymer Nanocomposites Prepared by Montmorillonite Modified by Silane and by Quaternary Ammonium Salts. Appl. Clay Sci. 2013, 85, 109–115. [Google Scholar] [CrossRef]
- Zabihi, O.; Ahmadi, M.; Nikafshar, S.; Preyeswary, K.C.; Naebe, M. A Technical Review on Epoxy-clay Nanocomposites: Structure, Properties, and Their Applications in Fiber Reinforced Composites. Compos. B. Eng. 2018, 135, 1–24. [Google Scholar] [CrossRef]
- Yang, L.; Phua, S.L.; Teo, J.K.H.; Toh, C.L.; Lau, S.K.; Ma, J.; Lu, X. A Biomimetic Approach to Enhancing Interfacial Interactions: Polydo-pamine-coated Clay as Reinforcement for Epoxy resin. ACS Appl. Mater. Interfaces 2011, 3, 3026–3032. [Google Scholar] [CrossRef]
- Xidas, P.I.; Triantafyllidis, K.S. Effect of the Type of Alkylammonium Ion Clay Modifier on the Structure and Thermal/mechanical Properties of Glassy and Rubbery Epoxy–clay Nanocomposites. Eur. Polym. J. 2010, 46, 404–417. [Google Scholar] [CrossRef]
- Triantafillidis, C.S.; LeBaron, P.C.; Pinnavaia, T.J. Thermoset Epoxy–clay Nanocomposites: The Dual Role of α,ω-Diamines as Clay Surface Modifiers and Polymer Curing Agents. J. Solid State Chem. 2002, 167, 354–362. [Google Scholar] [CrossRef]
- Zaman, I.; Nor, F.M.; Manshoor, B.; Khalid, A.; Araby, S. Influence of Interface on Epoxy/clay Nanocomposites: 2. Mechanical and Thermal Dynamic Properties. Procedia Manuf. 2015, 2, 23–27. [Google Scholar] [CrossRef] [Green Version]
- Sand Chee, S.; Jawaid, M. The Effect of Bi-Functionalized MMT on Morphology, Thermal Stability, Dynamic Mechanical, and Tensile Properties of Epoxy/Organoclay Nanocomposites. Polymers 2019, 11, 2012. [Google Scholar] [CrossRef] [Green Version]
- Choudalakis, G.; Gotsis, A.D. Permeability of Polymer/clay Nanocomposites: A Review. Eur. Polym. J. 2009, 45, 967–984. [Google Scholar] [CrossRef]
- Singha, S.; Hedenqvist, M.S. A Review on Barrier Properties of Poly(Lactic Acid)/Clay Nanocomposites. Polymers 2020, 12, 1095. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Guo, Y.; Rafailovich, M.H. Flame Retardant Polymer Nanocomposites and Interfaces. In Flame Retardants; IntechOpen: London, UK, 2019; ISBN 9781789858792. [Google Scholar]
- Ray, S.S.; Yamada, K.; Okamoto, M.; Ueda, K. Polylactide-Layered Silicate Nanocomposite: A Novel Biodegradable Material. Nano Letters 2002, 2, 1093–1096. [Google Scholar]
- Ray, S.S.; Yamada, K.; Okamoto, M.; Ogami, A.; Ueda, K. New Polylactide/Layered Silicate Nanocomposites. 3. High-Performance Biodegradable Materials. Chem. Mater. 2003, 15, 1456–1465. [Google Scholar]
- Zeng, Q.H.; Yu, A.B.; Lu, G.Q. Multiscale Modeling and Simulation of Polymer Nanocomposites. Prog. Polym. Sci. 2008, 33, 191–269. [Google Scholar] [CrossRef]
- Allegra, G.; Raos, G.; Vacatello, M. Theories and Simulations of Polymer-Based Nanocomposites: From Chain Statistics to Reinforcement. Prog. Polym. Sci. 2008, 33, 683–731. [Google Scholar] [CrossRef]
- Ganesan, V.; Jayaraman, A. Theory and Simulation Studies of Effective Interactions, Phase Behavior and Morphology in Polymer Nanocomposites. Soft Matter 2014, 10, 13–38. [Google Scholar] [CrossRef]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A Review of Multiscale Computational Methods in Polymeric Materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef] [PubMed]
- Ginzburg, V.V.; Hall, L.M. Theory and Modeling of Polymer Nanocomposites; Springer Nature: Cham, Switzerland, 2020; ISBN 9783030604431. [Google Scholar]
- Odegard, G.M. 6.2 Computational Multiscale Modeling—Nanoscale to Macroscale. In Comprehensive Composite Materials II; Elsevier: Amsterdam, The Netherlands, 2018; pp. 28–51. ISBN 9780081005347. [Google Scholar]
- Jlassi, K.; Chehimi, M.M.; Thomas, S. Clay-Polymer Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 9780323461535. [Google Scholar]
- Jeyakumar, R.; Sampath, P.S.; Ramamoorthi, R.; Ramakrishnan, T. Structural, Morphological and Mechanical Behaviour of Glass Fibre Reinforced Epoxy Nanoclay Composites. Int. J. Adv. Manuf. Technol. 2017, 93, 527–535. [Google Scholar] [CrossRef]
- Hackett, E.; Manias, E.; Giannelis, E.P. Computer Simulation Studies of PEO/layer Silicate Nanocomposites. Chem. Mater. 2000, 12, 2161–2167. [Google Scholar] [CrossRef]
- Geysermans, P.; Noguera, C. Advances in Atomistic Simulations of Mineral Surfaces. J. Mater. Chem. 2009, 19, 7807. [Google Scholar] [CrossRef]
- Manzano, H.; Masoero, E.; Lopez-Arbeloa, I.; Jennings, H.M. Shear Deformations in Calcium Silicate Hydrates. Soft Matter 2013, 9, 7333. [Google Scholar] [CrossRef]
- Galmarini, S.; Kunhi Mohamed, A.; Bowen, P. Atomistic Simulations of Silicate Species Interaction with Portlandite Surfaces. J. Phys. Chem. C Nanomater. Interfaces 2016, 120, 22407–22413. [Google Scholar] [CrossRef]
- Komarov, P.V.; Yu-Tsung, C.; Shih-Ming, C.; Khalatur, P.G.; Reineker, P. Highly Cross-Linked Epoxy Resins: An Atomistic Molecular Dynamics Simulation Combined with a Mapping/reverse Mapping Procedure. Macromolecules 2007, 40, 8104–8113. [Google Scholar] [CrossRef]
- Hagita, K.; Morita, H.; Doi, M.; Takano, H. Coarse-Grained Molecular Dynamics Simulation of Filled Polymer Nanocomposites under Uniaxial Elongation. Macromolecules 2016, 49, 1972–1983. [Google Scholar] [CrossRef] [Green Version]
- Langner, K.M.; Sevink, G.J.A. Mesoscale Modeling of Block Copolymer Nanocomposites. Soft Matter 2012, 8, 5102. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. EPL 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Koelman, J.M.V.A.; Hoogerbrugge, P.J. Dynamic Simulations of Hard-Sphere Suspensions under Steady Shear. EPL 1993, 21, 363–368. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical Mechanics of Dissipative Particle Dynamics. EPL 1995, 30, 191–196. [Google Scholar] [CrossRef] [Green Version]
- Groot, R.D.; Warren, P.B. Dissipative Particle Dynamics: Bridging the Gap between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Markina, A.A.; Ivanov, V.A.; Komarov, P.V.; Khokhlov, A.R.; Tung, S.-H. Self-Assembly of Lecithin and Bile Salt in the Presence of Inorganic Salt in Water: Mesoscale Computer Simulation. J. Phys. Chem. B 2017, 121, 1520–6106. [Google Scholar] [CrossRef]
- Guseva, D.V.; Rudyak, V.Y.; Komarov, P.V.; Bulgakov, B.A.; Babkin, A.V.; Chertovich, A.V. Dynamic and Static Mechanical Properties of Cross-linked Polymer Matrices: Multiscale Simulations and Experiments. Polymers 2018, 10, 792–806. [Google Scholar] [CrossRef] [Green Version]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. Orientation of Anisometric Layered Silicate Particles in Uncompatibilized and Compatibilized Polymer Melts under Shear Flow: A Dissipative Particle Dynamics Study. Macromol. Theory Simul. 2016, 25, 85–98. [Google Scholar] [CrossRef]
- Yong, X.; Kuksenok, O.; Balazs, A.C. Modeling Free Radical Polymerization Using Dissipative Particle Dynamics. Polymer 2015, 72, 217–225. [Google Scholar] [CrossRef]
- Scocchi, G.; Posocco, P.; Fermeglia, M.; Pricl, S. Polymer-Clay Nanocomposites: A Multiscale Molecular Modeling Approach. J. Phys. Chem. B 2007, 111, 2143–2151. [Google Scholar] [CrossRef] [Green Version]
- Scocchi, G.; Posocco, P.; Handgraaf, J.-W.; Fraaije, J.G.E.M.; Fermeglia, M.; Pricl, S. A Complete Multiscale Modelling Approach for Polymer-Clay Nanocomposites. Chemistry 2009, 15, 7586–7592. [Google Scholar] [CrossRef] [PubMed]
- Toth, R.; Santese, F.; Pereira, S.P.; Nieto, D.R.; Pricl, S.; Fermeglia, M.; Posocco, P. Size and Shape Matter! A Multiscale Molecular Simulation Approach to Polymer Nanocomposites. J. Mater. Chem. 2012, 22, 5398. [Google Scholar] [CrossRef]
- Suter, J.L.; Groen, D.; Coveney, P.V. Chemically Specific Multiscale Modeling of Clay-Polymer Nanocomposites Reveals Intercalation Dynamics, Tactoid Self-Assembly and Emergent Materials Properties. Adv. Mater. 2015, 27, 966–984. [Google Scholar] [CrossRef] [Green Version]
- Laurini, E.; Posocco, P.; Fermeglia, M.; Pricl, S. Multiscale Molecular Modeling of Clay–Polymer Nanocomposites. In Clay-Polymer Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2017; pp. 83–112. ISBN 9780323461535. [Google Scholar]
- Jiang, M.; Alzebdeh, K.; Jasiuk, I.; Ostoja-Starzewski, M. Scale and Boundary Conditions Effects in Elastic Properties of Random Composites. Acta Mech. 2001, 148, 63–78. [Google Scholar] [CrossRef]
- Jiang, M.; Jasiuk, I.; Ostoja-Starzewski, M. Apparent Elastic and Elastoplastic Behavior of Periodic Composites. Int. J. Solids Struct. 2002, 39, 199–212. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Komarov, P.V.; Khalatur, P.G. Thermal Properties and Topology of Epoxy Networks: A Multiscale Simulation Methodology. Macromolecules 2015, 48, 206–212. [Google Scholar] [CrossRef]
- Komarov, P.V.; Khalatur, P.G.; Khokhlov, A.R. Magnetoresponsive Smart Nanocomposites with Highly Cross-linked Polymer Matrix. Polym. Adv. Technol. 2021, 32, 3922–3933. [Google Scholar] [CrossRef]
- Komarov, P.V.; Baburkin, P.O.; Ivanov, V.A.; Chen, S.-A.; Khokhlov, A.R. Controlling Morphology of the Polymer Photoactive Layer in Photovoltaic Elements: Mesoscopic Simulation. Dokl. Phys. Chem. 2019, 485, 39–42. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Chertovich, A.V.; Khalatur, P.G.; Khokhlov, A.R. Study of the Mechanisms of Filler Reinforcement in Elastomer Nanocomposites. Macromolecules 2014, 47, 5400–5408. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Chertovich, A.V.; Khalatur, P.G.; Khokhlov, A.R. Effect of Nanotube Size on the Mechanical Properties of Elastomeric Composites. Soft Matter 2013, 9, 4067. [Google Scholar] [CrossRef]
- Capelot, M.; Montarnal, D.; Tournilhac, F.; Leibler, L. Metal-Catalyzed Transesterification for Healing and Assembling of Thermosets. J. Am. Chem. Soc. 2012, 134, 7664–7667. [Google Scholar] [CrossRef]
- Rudyak, V.Y.; Gavrilov, A.A.; Guseva, D.V.; Tung, S.-H.; Komarov, P.V. Accounting for π–π Stacking Interactions in the Mesoscopic Models of Conjugated Polymers. Mol. Syst. Des. Eng. 2020, 5, 1137–1146. [Google Scholar] [CrossRef]
- Rogers, K.; Takacs, E.; Thompson, M.R. Contact angle measurement of select compatibilizers for polymer-silicate layer nanocomposites. Polym. Test. 2005, 24, 423–427. [Google Scholar] [CrossRef]
- Pegoretti, A.; Dorigato, A.; Brugnara, M.; Penati, A. Contact angle measurements as a tool to investigate the filler–matrix interactions in polyurethane–clay nanocomposites from blocked prepolymer. Eur. Polym. J. 2008, 44, 1662–1672. [Google Scholar] [CrossRef]
- Si, M.; Araki, T.; Ade, H.; Kilcoyne, A.L.D.; Fisher, R.; Sokolov, J.C.; Rafailovich, M.H. Compatibilizing Bulk Polymer Blends by Using Organoclays. Macromolecules 2006, 39, 4793–4801. [Google Scholar] [CrossRef]
- Hoshino, J.; Limpanart, S.; Khunthon, S.; Osotchana, T.; Traiphold, R.; Srikhirin, T. Adsorption of single-strand alkylammonium salts on bentonite, surface properties of the modified clay and polymer nanocomposites formation by a two-roll mill. Mater. Chem. Phys. 2010, 123, 706–713. [Google Scholar] [CrossRef]
- Akcora, P.; Kumar, S.K.; Moll, J.; Lewis, S.; Schadler, L.S.; Li, Y.; Benicewicz, B.C.; Sandy, A.; Narayanan, S.; Ilavsky, J.; et al. “Gel-Like” Mechanical Reinforcement in Polymer Nanocomposite Melts. Macromolecules 2010, 43, 1003–1010. [Google Scholar] [CrossRef]
- Moll, J.F.; Akcora, P.; Rungta, A.; Gong, S.; Colby, R.H.; Benicewicz, B.C.; Kumar, S.K. Mechanical Reinforcement in Polymer Melts Filled with Polymer Grafted Nanoparticles. Macromolecules 2011, 44, 7473–7477. [Google Scholar] [CrossRef]
- Kim, E.S.; Shim, J.H.; Woo, J.Y.; Yoo, K.S.; Yoon, J.S. Effect of the Silane Modification of Clay on the Tensile Properties of Nylon 6/Clay Nanocomposites. J. Appl. Polym. Sci. 2010, 117, 809–816. [Google Scholar] [CrossRef]
- Kango, S.; Kalia, S.; Celli, A.; Njuguna, J.; Habibi, Y.; Kumar, R. Surface Modification of Inorganic Nanoparticles for Development of Organic–inorganic nanocomposites—A Review. Prog. Polym. Sci. 2013, 38, 1232–1261. [Google Scholar] [CrossRef]
- Kockmann, A.; Porsiel, J.C.; Saadat, R.; Garnweitner, G. Impact of Nanoparticle Surface Modification on the Mechanical Properties of Polystyrene-Based Nanocomposites. RSC Adv. 2018, 8, 11109–11118. [Google Scholar] [CrossRef] [Green Version]
- Joussein, E.; Petit, S.; Churchman, J.; Theng, B.; Righi, D.; Delvaux, B. Halloysite Clay Minerals—A Review. Clay Miner. 2005, 40, 383–426. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of High Polymer Solutions. J. Chem. Phys. 1941, 9, 660. [Google Scholar] [CrossRef]
- Huggins, M.L. Solutions of Long Chain Compounds. J. Chem. Phys. 1941, 9, 440. [Google Scholar] [CrossRef]
- Komarov, P.; Markina, A.; Ivanov, V. Influence of Surface Modification of Halloysite Nanotubes on Their Dispersion in Epoxy Matrix: Mesoscopic DPD Simulation. Chem. Phys. Lett. 2016, 653, 24–29. [Google Scholar] [CrossRef]
- DPD_Chem Package for Modeling Polymers and Melts Using the Reaction Version of Dissipative Particle Dynamics. Available online: https://www.researchgate.net/project/DPDChem-Software (accessed on 1 November 2021).
- Pavlov, A.S.; Khalatur, P.G. Filler Reinforcement in Cross-Linked Elastomer Nanocomposites: Insights from Fully Atomistic Molecular Dynamics Simulation. Soft Matter 2016, 12, 5402–5419. [Google Scholar] [CrossRef] [PubMed]
- Gross, J.L.; Yellen, J.; Zhang, P. Handbook of Graph Theory, 2nd ed.; CRC Press: London, UK, 2013; ISBN 9781439880180. [Google Scholar]
- Velasco-Santos, C.; Martinez-Hernandez, A.L.; Castano, V.M. Carbon Nanotube-Polymer Nanocomposites: The Role of Interfaces. Compos. Interfaces 2005, 11, 567–586. [Google Scholar] [CrossRef] [Green Version]
- Geng, Y.; Liu, M.Y.; Li, J.; Shi, X.M.; Kim, J.K. Effects of Surfactant Treatment on Mechanical and Electrical Properties of CNT/epoxy Nanocomposites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1876–1883. [Google Scholar] [CrossRef]
- Jesson, D.A.; Watts, J.F. The Interface and Interphase in Polymer Matrix Composites: Effect on Mechanical Properties and Methods for Identification. Polym. Rev. 2012, 52, 321–354. [Google Scholar] [CrossRef]
- Bharadwaj, R.K.; Mehrabi, A.R.; Hamilton, C.; Trujillo, C.; Murga, M.; Fan, R.; Chavira, A.; Thompson, A.K. Structure–property Relationships in Cross-Linked Polyester–clay Nanocomposites. Polymer 2002, 43, 3699–3705. [Google Scholar] [CrossRef]
- Peeterbroeck, S.; Alexandre, M.; Jérôme, R.; Dubois, P. Poly(ethylene-Co-Vinyl Acetate)/clay Nanocomposites: Effect of Clay Nature and Organic Modifiers on Morphology, Mechanical and Thermal Properties. Polym. Degrad. Stab. 2005, 90, 288–294. [Google Scholar] [CrossRef]
- Alateyah, A.I.; Dhakal, H.N.; Zhang, Z.Y. Processing, Properties, and Applications of Polymer Nanocomposites Based on Layer Silicates: A Review. Adv. Polym. Technol. 2013, 32, 21368. [Google Scholar] [CrossRef]
- Sliozberg, Y.; Andzelm, J.; Hatter, C.B.; Anasori, B.; Gogotsi, Y.; Hall, A. Interface Binding and Mechanical Properties of MXene-Epoxy Nanocomposites. Compos. Sci. Technol. 2020, 192, 108124. [Google Scholar] [CrossRef]
- Zabihi, O.; Ahmadi, M.; Naebe, M. Self-Assembly of Quaternized Chitosan Nanoparticles within Nanoclay Layers for Enhancement of Interfacial Properties in Toughened Polymer Nanocomposites. Mater. Des. 2017, 119, 277–289. [Google Scholar] [CrossRef]
- Qi, B.; Zhang, Q.X.; Bannister, M.; Mai, Y.-W. Investigation of the Mechanical Properties of DGEBA-Based Epoxy Resin with Nanoclay Additives. Compos. Struct. 2006, 75, 514–519. [Google Scholar] [CrossRef]
- Ding, W.; Eitan, A.; Fisher, F.T.; Chen, X.; Dikin, D.A.; Andrews, R.; Brinson, L.C.; Schadler, L.S.; Ruoff, R.S. Direct Observation of Polymer Sheathing in Carbon Nanotube−Polycarbonate Composites. Nano Lett. 2003, 3, 1593–1597. [Google Scholar] [CrossRef]
- Rittigstein, P.; Priestley, R.D.; Broadbelt, L.J.; Torkelson, J.M. Model Polymer Nanocomposites Provide an Understanding of Confinement Effects in Real Nanocomposites. Nat. Mater. 2007, 6, 278–282. [Google Scholar] [CrossRef]
- Kropka, J.M.; Putz, K.W.; Pryamitsyn, V.; Ganesan, V.; Green, P.F. Origin of Dynamical Properties in PMMA−C60 Nanocomposites. Macromolecules 2007, 40, 5424–5432. [Google Scholar] [CrossRef]
- Valentín, J.L.; Mora-Barrantes, I.; Carretero-González, J.; López-Manchado, M.A.; Sotta, P.; Long, D.R.; Saalwächter, K. Novel Experimental Approach to Evaluate Filler−Elastomer Interactions. Macromolecules 2010, 43, 334–346. [Google Scholar] [CrossRef]
- Mortezaei, M.; Famili, M.H.N.; Kokabi, M. The Role of Interfacial Interactions on the Glass-Transition and Viscoelastic Properties of Silica/polystyrene Nanocomposite. Compos. Sci. Technol. 2011, 71, 1039–1045. [Google Scholar] [CrossRef]
- Mortezaei, M.; Farzi, G.; Kalaee, M.R.; Zabihpoor, M. Evaluation of Interfacial Layer Properties in the Polystyrene/silica Nanocomposite. J. Appl. Polym. Sci. 2011, 119, 2039–2047. [Google Scholar] [CrossRef]
- Mortezaei, M.; Famili, M.H.N.; Kalaee, M.R. Effect of Immobilized Interfacial Layer on the Maximum Filler Loading of Polystyrene/silica Nanocomposites. J. Reinf. Plast. Compos. 2011, 30, 593–599. [Google Scholar] [CrossRef]
- Robertson, C.G.; Rackaitis, M. Further Consideration of Viscoelastic Two Glass Transition Behavior of Nanoparticle-Filled Polymers. Macromolecules 2011, 44, 1177–1181. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Daoulas, K.C.; Mavrantzas, V.G. Molecular Dynamics Simulation of a Polymer Melt/solid Interface: Local Dynamics and Chain Mobility in a Thin Film of Polyethylene Melt Adsorbed on Graphite. Macromolecules 2005, 38, 5796–5809. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A.; Baschnagel, J. Simulation Studies on the Dynamics of Polymers at Interfaces. Annu. Rev. Mater. Sci. 1996, 26, 107–134. [Google Scholar] [CrossRef]
- Torres, J.A.; Nealey, P.F.; de Pablo, J.J. Molecular Simulation of Ultrathin Polymeric Films near the Glass Transition. Phys. Rev. Lett. 2000, 85, 3221–3224. [Google Scholar] [CrossRef] [PubMed]
- Ndoro, T.V.M.; Böhm, M.C.; Müller-Plathe, F. Interface and Interphase Dynamics of Polystyrene Chains near Grafted and Ungrafted Silica Nanoparticles. Macromolecules 2012, 45, 171–179. [Google Scholar] [CrossRef]
- Brown, D.; Mélé, P.; Marceau, S.; Albérola, N.D. A Molecular Dynamics Study of a Model Nanoparticle Embedded in a Polymer Matrix. Macromolecules 2003, 36, 1395–1406. [Google Scholar] [CrossRef]
- Borodin, O.; Smith, G.D.; Bandyopadhyaya, R.; Byutner, O. Molecular Dynamics Study of the Influence of Solid Interfaces on Poly(ethylene Oxide) Structure and Dynamics. Macromolecules 2003, 36, 7873–7883. [Google Scholar] [CrossRef]
- Barbier, D.; Brown, D.; Grillet, A.-C.; Neyertz, S. Interface between End-Functionalized PEO Oligomers and a Silica Nanoparticle Studied by Molecular Dynamics Simulations. Macromolecules 2004, 37, 4695–4710. [Google Scholar] [CrossRef]
- Vogel, M. Rotational and Conformational Dynamics of a Model Polymer Melt at Solid Interfaces. Macromolecules 2009, 42, 9498–9505. [Google Scholar] [CrossRef]
- Eslami, H.; Müller-Plathe, F. Structure and Mobility of Nanoconfined Polyamide-6,6 Oligomers: Application of a Molecular Dynamics Technique with Constant Temperature, Surface Area, and Parallel Pressure. J. Phys. Chem. B 2009, 113, 5568–5581. [Google Scholar] [CrossRef]
- Yelash, L.; Virnau, P.; Binder, K.; Paul, W. Slow Process in Confined Polymer Melts: Layer Exchange Dynamics at a Polymer Solid Interface. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010, 82, 050801. [Google Scholar] [CrossRef] [Green Version]
- Eslami, H.; Müller-Plathe, F. Viscosity of Nanoconfined Polyamide-6,6 Oligomers: Atomistic Reverse Nonequilibrium Molecular Dynamics Simulation. J. Phys. Chem. B 2010, 114, 387–395. [Google Scholar] [CrossRef] [PubMed]
- Sadovnichy, V.; Tikhonravov, A.; Voevodin, V.; Opanasenko, V. “Lomonosov”: Supercomputing at Moscow State University. In Contemporary High Performance Computing: From Petascale toward Exascale (Chapman & Hall/CRC Computational Science); CRC Press: Boca Raton, CA, USA, 2013; pp. 283–307. [Google Scholar]


| System | −2] | −2] | −2] | Average |
|---|---|---|---|---|
| Unfilled network | 1.67 ± 0.03 | 1.66 ± 0.03 | 1.67 ± 0.02 | 1.67 ± 0.03 |
| i | 1.08 ± 0.11 | 1.14 ± 0.04 | 1.11 ± 0.035 | 1.11 ± 0.03 |
| ii | 1.14 ± 0.07 | 1.17 ± 0.01 | 1.13 ± 0.05 | 1.15 ± 0.02 |
| iii | 1.18 ± 0.02 | 1.09 ± 0.07 | 1.08 ± 0.14 | 1.12 ± 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malyshev, M.D.; Guseva, D.V.; Vasilevskaya, V.V.; Komarov, P.V. Effect of Nanoparticles Surface Bonding and Aspect Ratio on Mechanical Properties of Highly Cross-Linked Epoxy Nanocomposites: Mesoscopic Simulations. Materials 2021, 14, 6637. https://doi.org/10.3390/ma14216637
Malyshev MD, Guseva DV, Vasilevskaya VV, Komarov PV. Effect of Nanoparticles Surface Bonding and Aspect Ratio on Mechanical Properties of Highly Cross-Linked Epoxy Nanocomposites: Mesoscopic Simulations. Materials. 2021; 14(21):6637. https://doi.org/10.3390/ma14216637
Chicago/Turabian StyleMalyshev, Maxim D., Daria V. Guseva, Valentina V. Vasilevskaya, and Pavel V. Komarov. 2021. "Effect of Nanoparticles Surface Bonding and Aspect Ratio on Mechanical Properties of Highly Cross-Linked Epoxy Nanocomposites: Mesoscopic Simulations" Materials 14, no. 21: 6637. https://doi.org/10.3390/ma14216637
APA StyleMalyshev, M. D., Guseva, D. V., Vasilevskaya, V. V., & Komarov, P. V. (2021). Effect of Nanoparticles Surface Bonding and Aspect Ratio on Mechanical Properties of Highly Cross-Linked Epoxy Nanocomposites: Mesoscopic Simulations. Materials, 14(21), 6637. https://doi.org/10.3390/ma14216637







