Effect of Ground Granulated Blast Furnace Slag Replacement Ratio on Structural Performance of Precast Concrete Beams
Abstract
:1. Introduction
2. Experimental Program
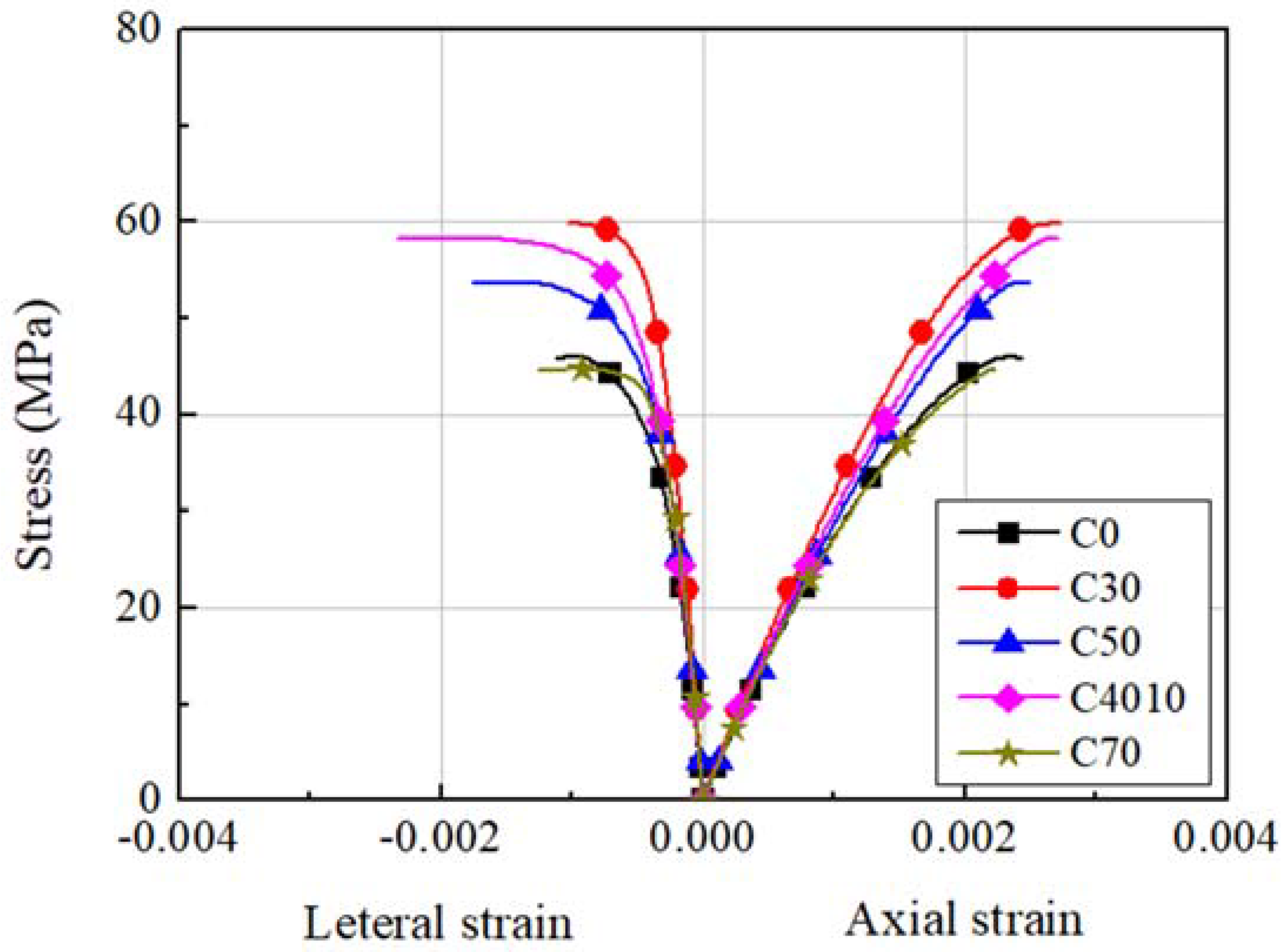
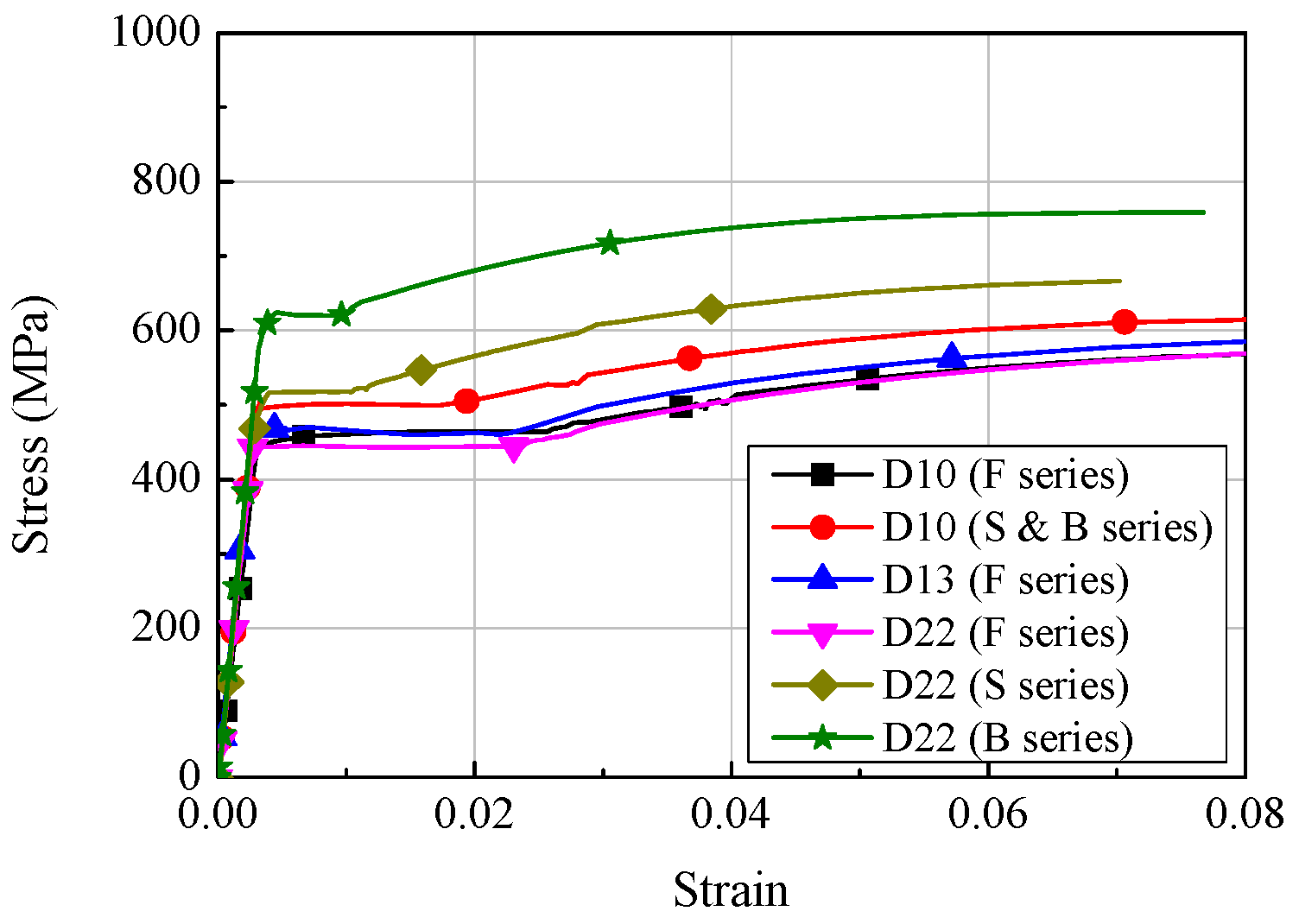
2.1. Materials
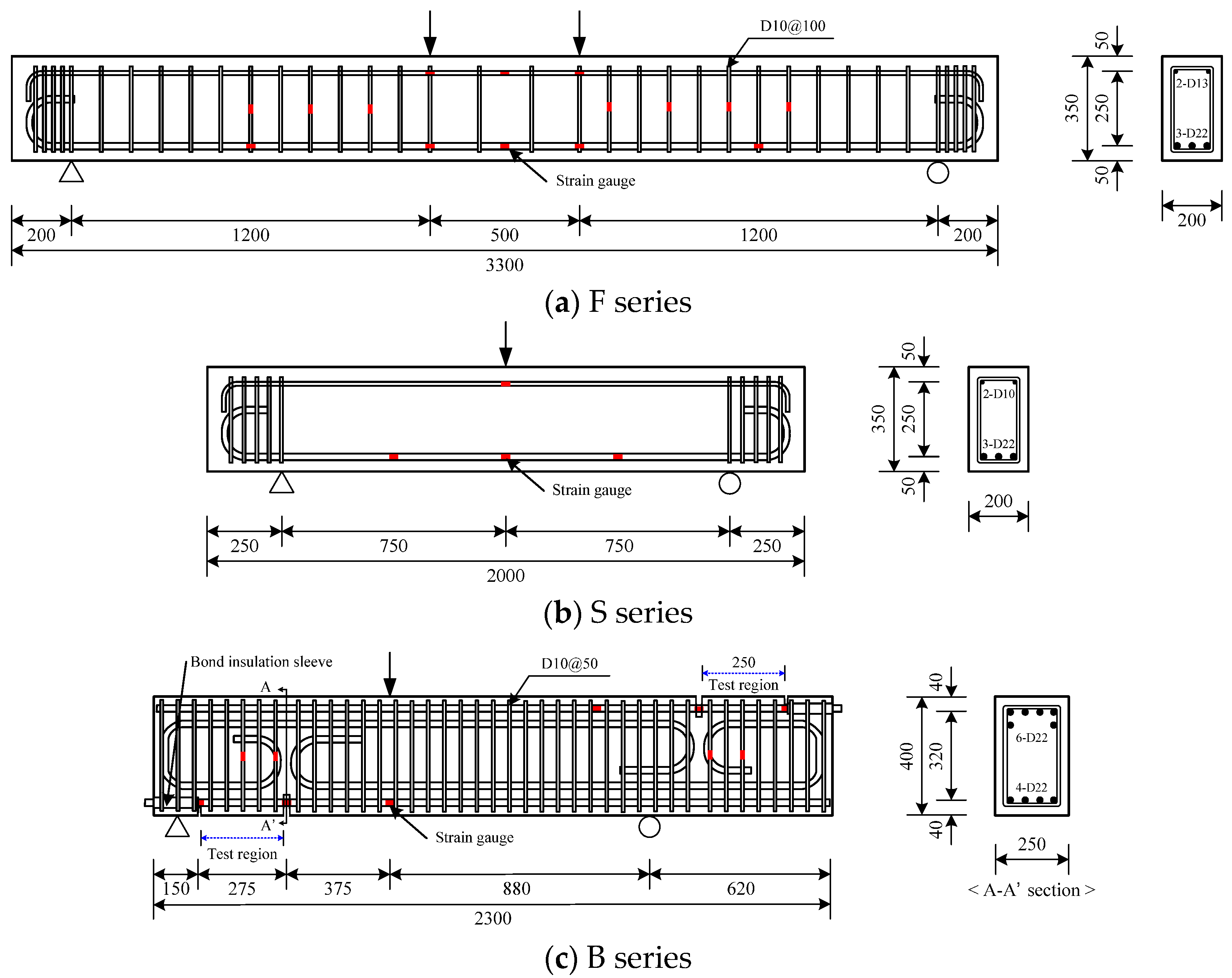
2.2. Specimens
2.3. Loading and Measurement Methods
3. Evaluation of Flexural Performance
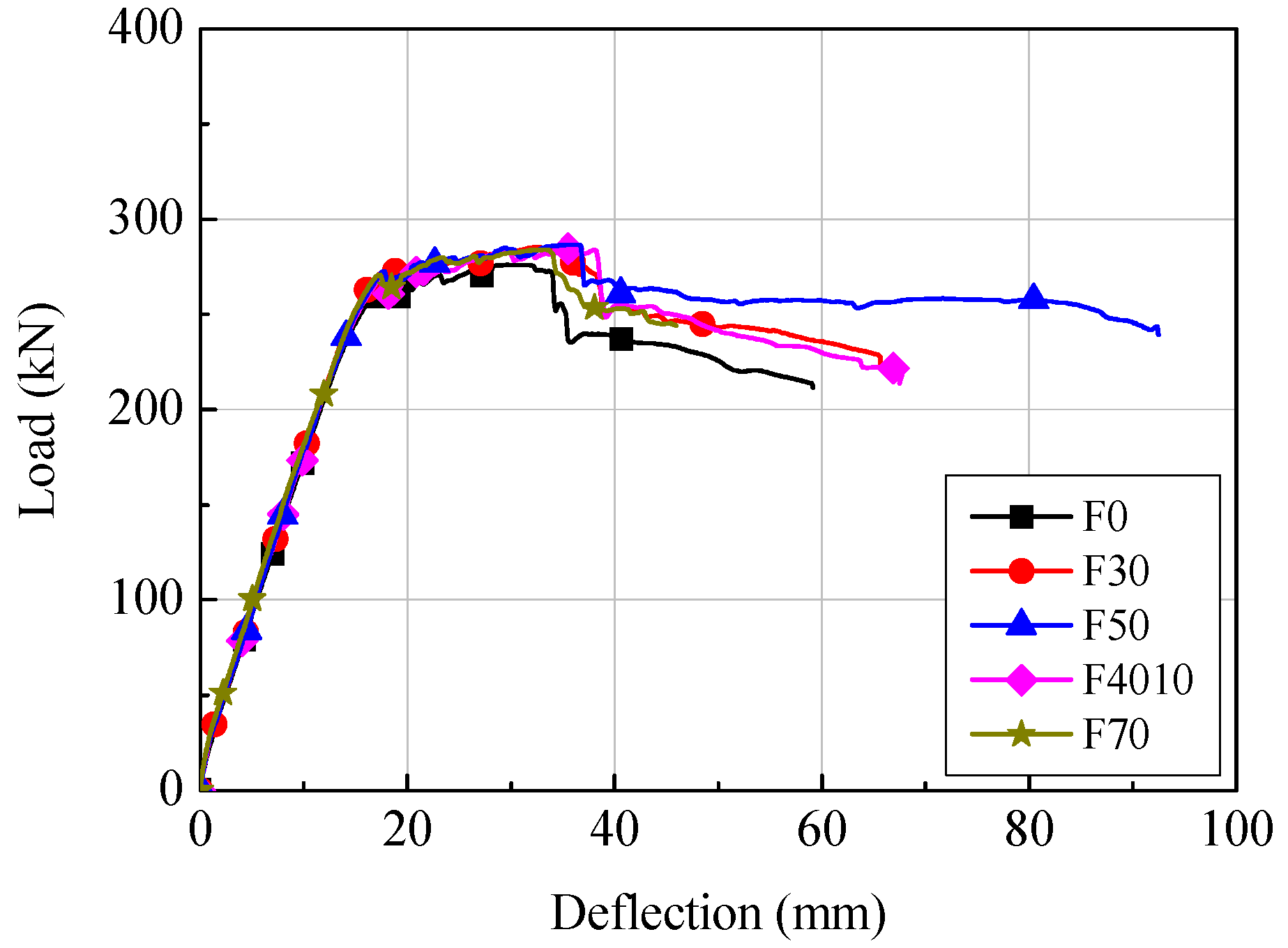
3.1. Load-Deflection Relationships
3.2. Flexural Strength
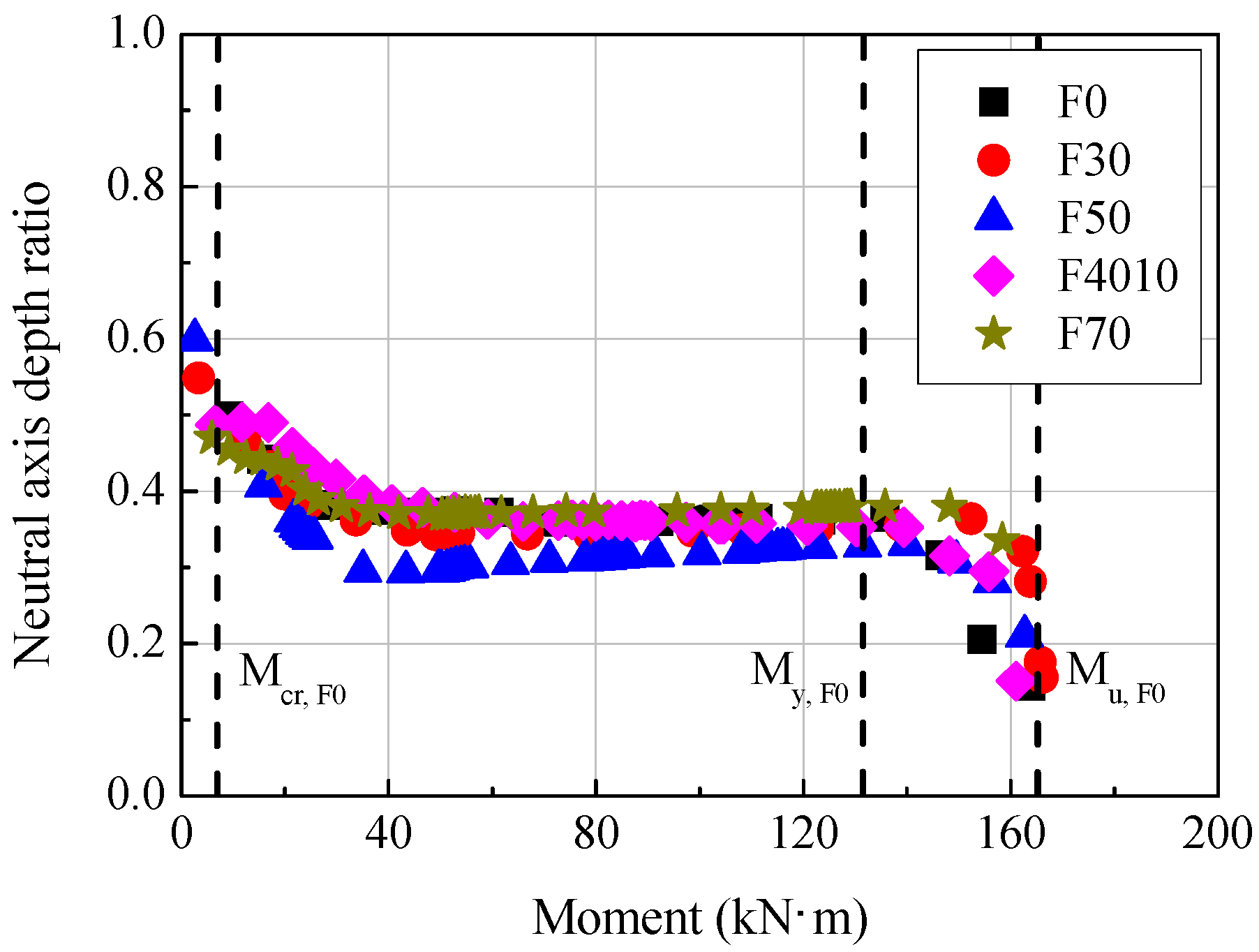
3.3. Neutral Axis Depth Ratio
3.4. Ductility Factors
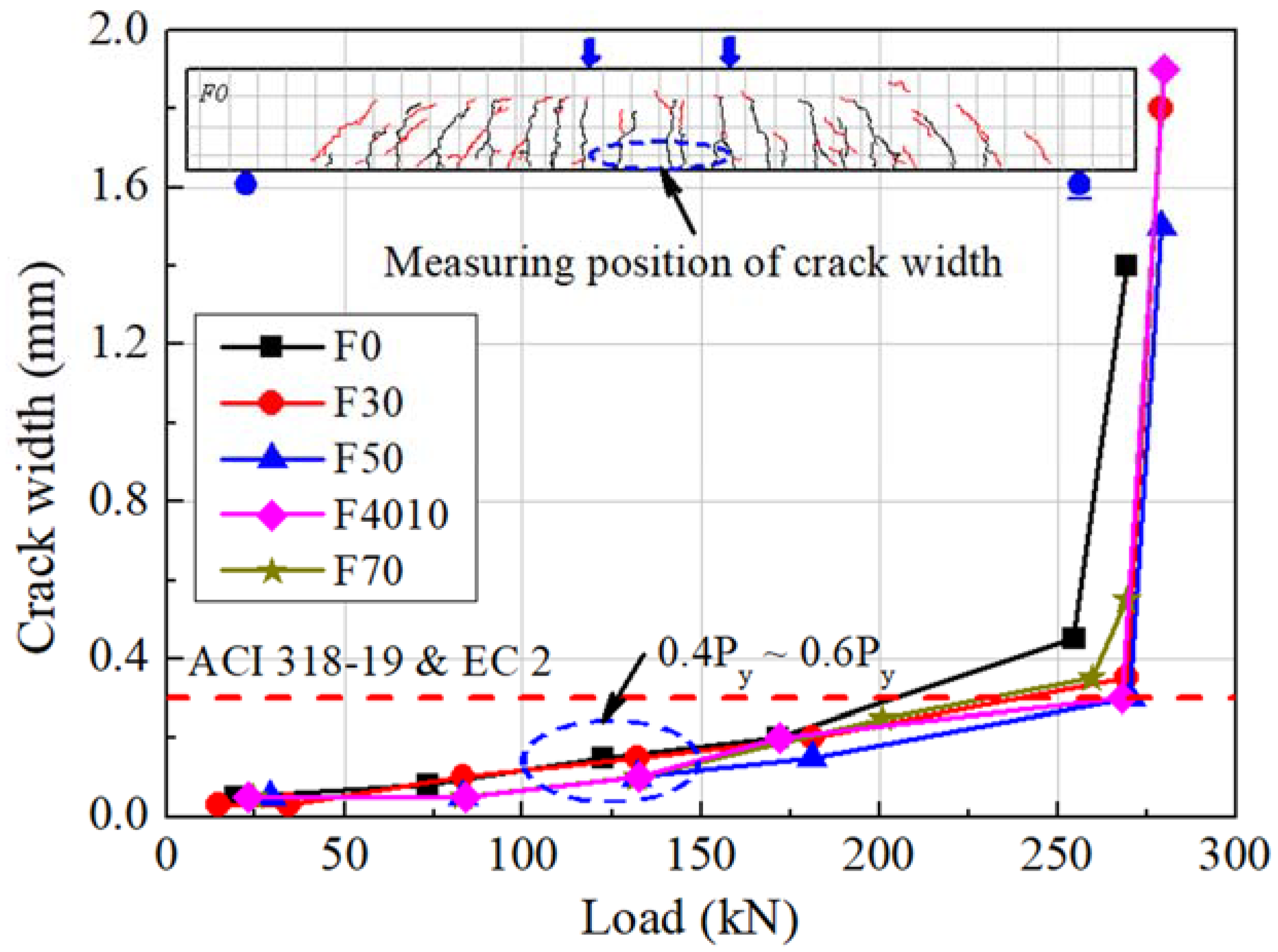
3.5. Serviceability
4. Evaluation of Shear Performance
4.1. Shear Force-Deflection Relationships
4.2. Comparison of Shear Strength
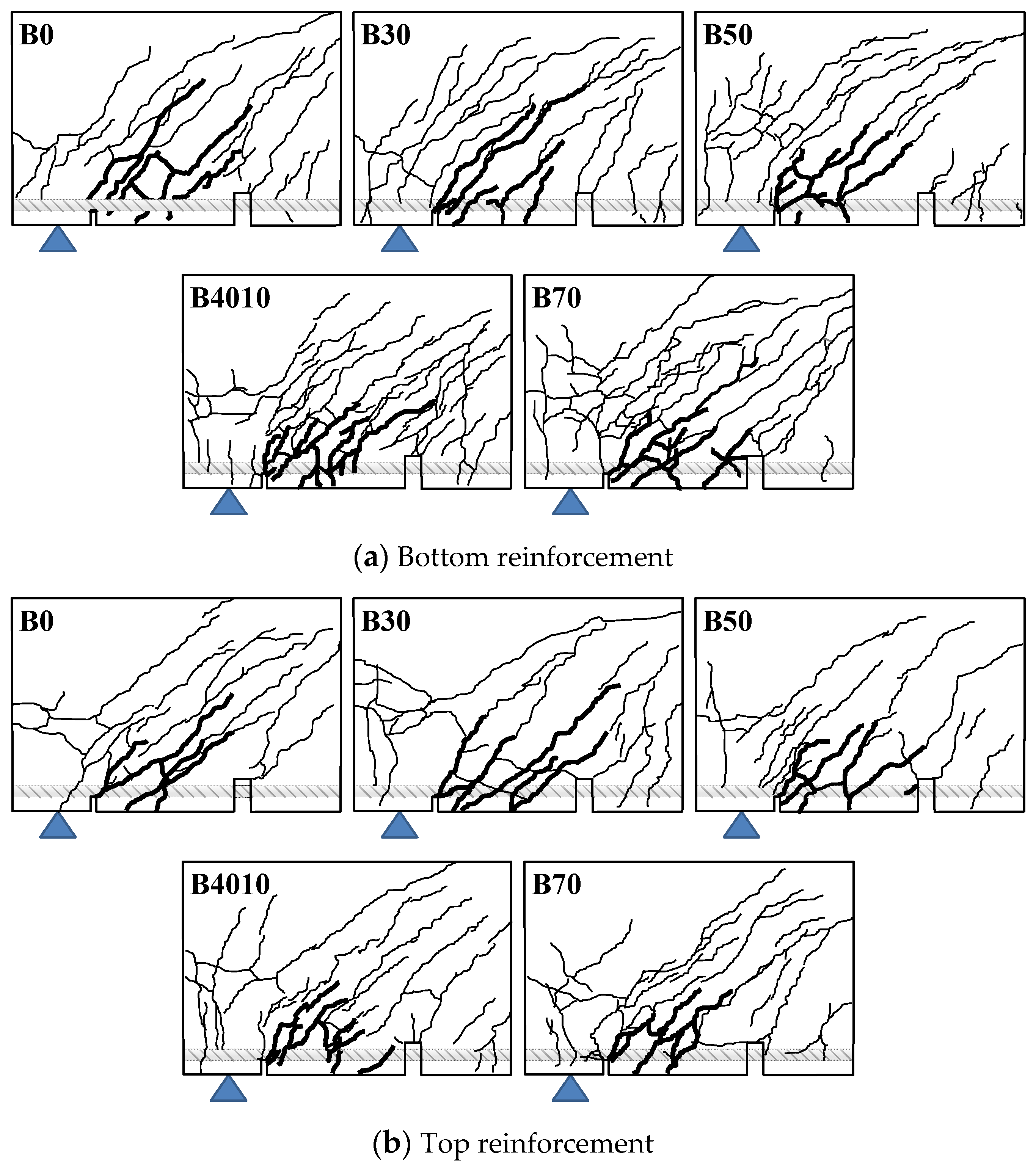
5. Evaluation of Bond Performance
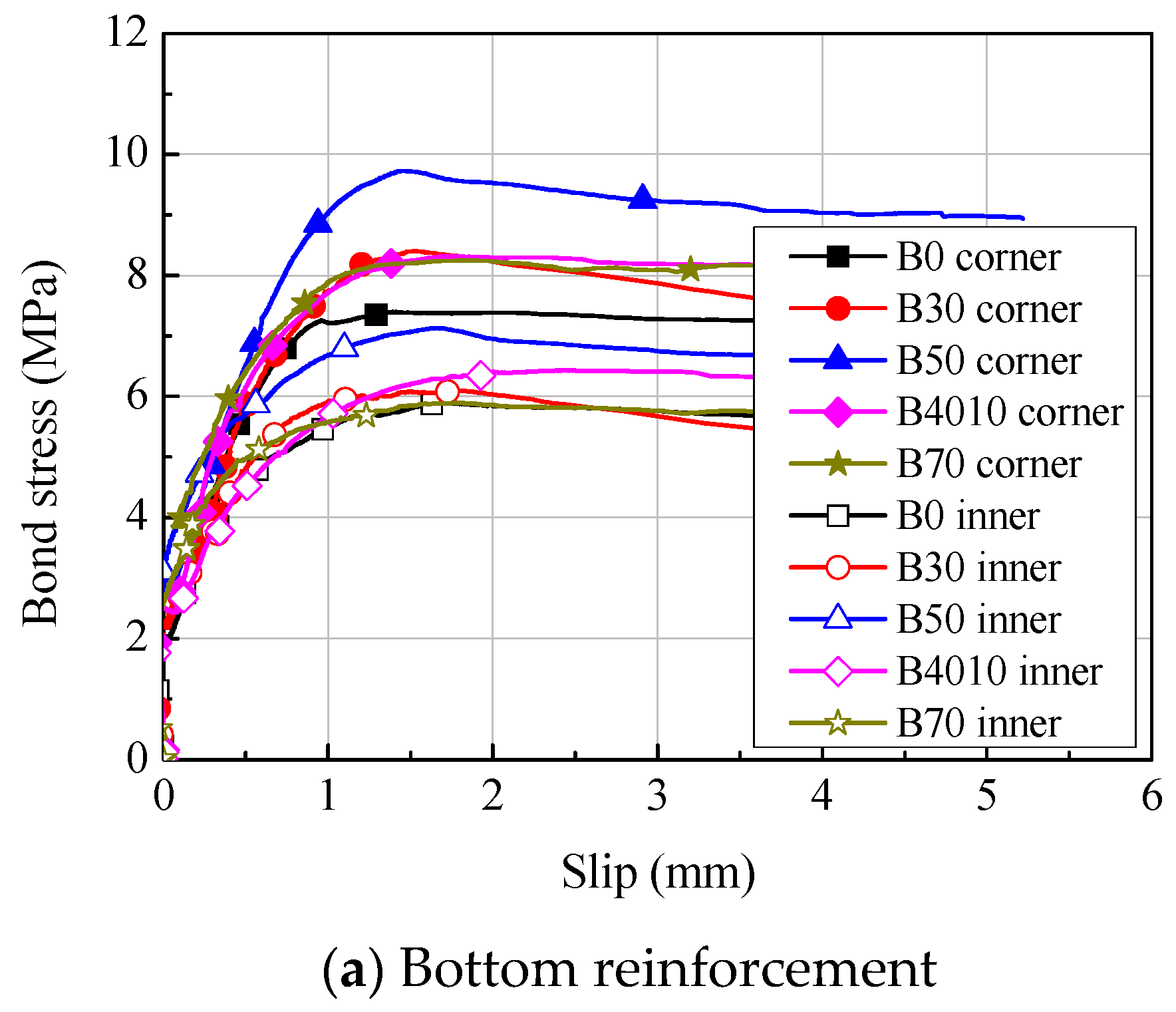
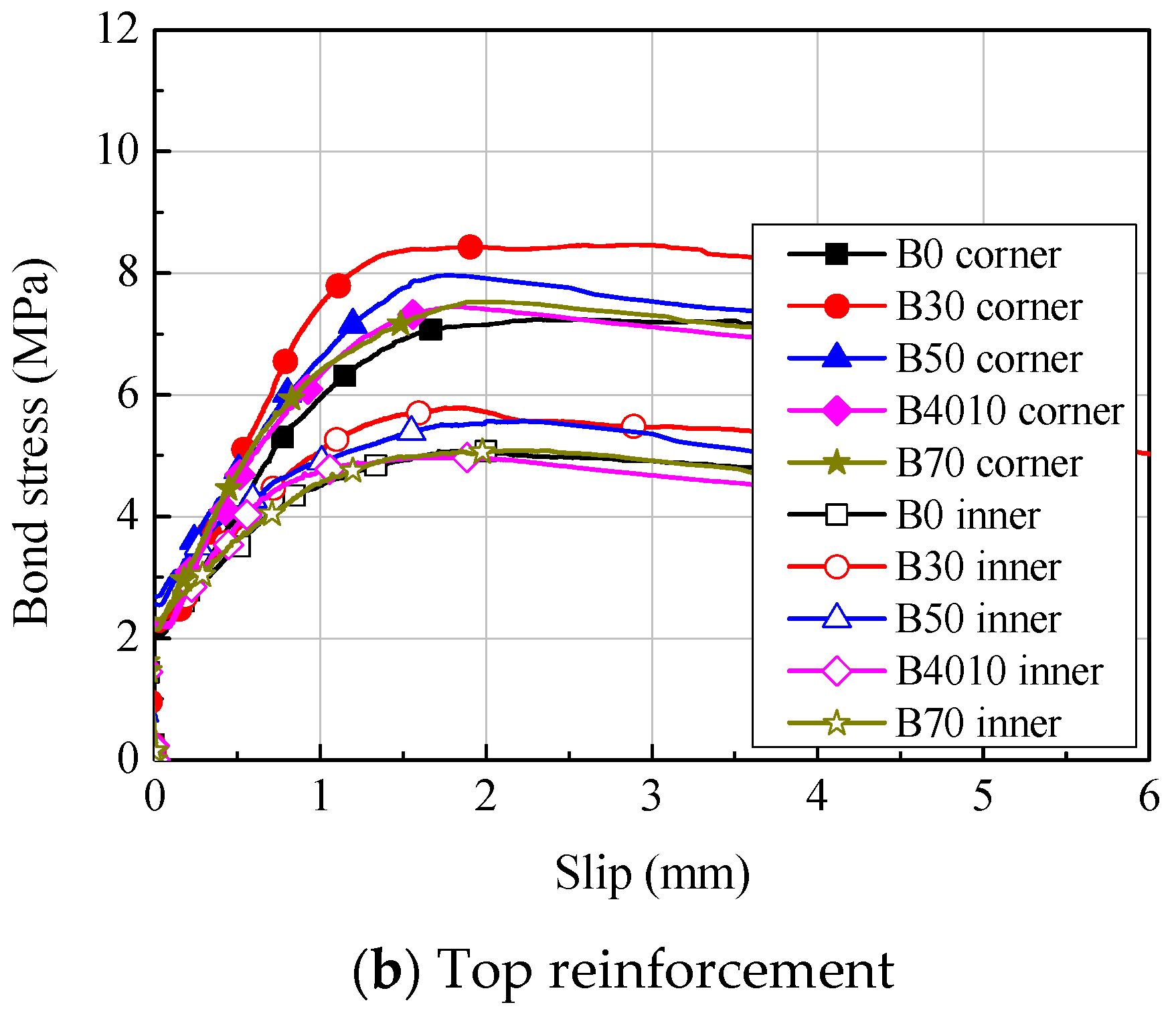
5.1. Bond Stress-Slip Relationships
5.2. Comparison of Bond Strength
6. Conclusions
- The flexural strength of the F series specimens was predicted by ACI 318-19 and EC 2. The mean ratio of the yield moment of the experimental results to that of the prediction results was 0.99, and the mean ratios of the ultimate moment were 1.21 and 1.19, respectively. This showed that the experimental results were predicted conservatively;
- The mean shear strengths of the S series specimens, measured experimentally, were 1.43 times and 1.71 times higher than the shear strength required by the ACI 318-19 and EC 2 standards, regardless of the replacement ratio of ground granulated blast furnace slag. However, in consideration of the concrete compressive strength, the shear strength of the S series specimens decreased as the replacement ratio of ground granulated blast furnace slag increased. Therefore, consideration is needed to determine the appropriate replacement ratio that can secure the required shear performance;
- The bond strengths of the B series specimens, measured experimentally, were 1.26 to 1.57 times higher than the values predicted by the formulas of ACI 318-19, Fujii-Morita and Maeda, regardless of the replacement ratio of ground granulated blast furnace slag. Therefore, the required bond strength was sufficiently satisfied. The formula proposed by Maeda predicted the experimental results at a mean experimental/analytical ratio of 1.26 with a coefficient of variation of 8.8%, indicating that the prediction was better than those obtained using formulas according to ACI 318-19 and Fujii-Morita;
- In consideration of the experimental results, in using the ground granulated blast furnace slag as an admixture for precast concrete, the cement replacement ratio may be increased up to 70% without causing any problems in securing the structural performance. However, in order to ensure sufficient safety of precast concrete members, it is considered reasonable to apply the replacement ratio of ground granulated blast furnace slag to 50% or less.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, K.-H.; Lim, J.-Y.; Ryu, D.-H.; Choi, S.-W. The present situation of production and it’s utilization of electronic arc furnace oxidizing slag in Korea and other countries. Mag. Korea Concr. Inst. 2007, 19, 51–57. [Google Scholar]
- Majhi, R.K.; Nayak, A.N.; Mukharjee, B.B. Characterization of lime activated recycled aggregate concrete with high-volume ground granulated blast furnace slag. Constr. Build. Mater. 2020, 259, 119882. [Google Scholar] [CrossRef]
- DePree, P.J.; Ferry, C.T. Mitigation of expansive electric arc furnace slag in brownfield redevelopment. In Proceedings of the GeoCongress 2008: Geosustainability and Geohazard Mitigation, New Orleans, LA, USA, 9–12 March 2008; pp. 271–278. [Google Scholar]
- Lee, Y.-J.; Kim, H.-G.; Kim, M.-J.; Kim, D.-H.; Kim, D.-S.; Kim, K.-H. Bond performance of reinforced concrete beams with electric arc furnace slag aggregates. Constr. Build. Mater. 2020, 244, 118366. [Google Scholar] [CrossRef]
- Gencel, O.; Munir, M.J.; Kazmi, S.M.S.; Sutcu, M.; Erdogmus, E.; Velasco, P.M.; Quesada, D.E. Recycling industrial slags in production of fired clay bricks for sustainable manufacturing. Ceram. Int. 2021, 47, 30425–30438. [Google Scholar] [CrossRef]
- Wang, K.; Zhi, G. Evaluating Properties of Blended Cements for Concrete Pavements; No. Final Report; Department of Civil, Construction and Environmental Engineering, Iowa State University: Ames, IA, USA, 2003. [Google Scholar]
- Macphee, D.E.; Cao, H.T. Theoretical description of impact of blast furnace slag on steel passivation in concrete. Mag. Concr. Res. 1993, 45, 63–69. [Google Scholar] [CrossRef]
- Ramezanianpour, A.A. Fly ash. In Cement Replacement Materials; Springer: Berlin, Germany, 2014; pp. 47–156. [Google Scholar]
- Rashad, A.M. An overview on rheology, mechanical properties and durability of high-volume slag used as a cement replacement in paste, mortar and concrete. Constr. Build. Mater. 2018, 187, 89–117. [Google Scholar] [CrossRef]
- Jiang, Y.; Ling, T.-C.; Shi, C.; Pan, S.-Y. Characteristics of steel slags and their use in cement and concrete-A review. Resour. Conserv. Recycl. 2018, 136, 187–197. [Google Scholar] [CrossRef]
- Haha, M.B.; Lothenbach, B.; Le Saout, G.; Winnefeld, F. Influence of slag chemistry on the hydration of alkali-activated blast-furnace slag-Part II: Effect of Al2O3. Cem. Concr. Res. 2012, 42, 4274–4283. [Google Scholar] [CrossRef]
- Song, H.-W.; Saraswathy, V. Studies on the corrosion resistance of reinforced steel in concrete with ground granulated blast-furnace slag-an overview. J. Hazard. Mater. 2006, 138, 226–233. [Google Scholar] [CrossRef]
- Caijun, S.; Yinyu, L. Investigation on some factors affecting the characteristics of alkali-phosphorus slag cement. Cem. Concr. Res. 1989, 19, 527–533. [Google Scholar] [CrossRef]
- Gruskovnjak, A.; Lothenbach, B.; Winnefeld, F.; Figi, R.; Ko, S.C.; Adler, M.; Mäder, U. Hydration mechanisms of super sulphated slag cement. Cem. Concr. Res. 2008, 38, 983–992. [Google Scholar] [CrossRef] [Green Version]
- Taylor, H.F.W. Cement Chemistry; Thomas Telford Publishing: London, UK, 1997. [Google Scholar]
- Shi, D.; Ye, J.; Zhang, W. Effects of activator content on properties, mineralogy, hydration and microstructure of alkali-activated materials synthesized from calcium silicate slag and ground granulated blast furnace slag. J. Build. Eng. 2020, 32, 101791. [Google Scholar] [CrossRef]
- Duży, P.; Sitarz, M.; Adamczyk, M.; Choińska, M.; Hager, I. Chloride ions’ penetration of fly ash and ground granulated blast furnace slags-based alkali-activated mortars. Materials 2021, 14, 6583. [Google Scholar] [CrossRef] [PubMed]
- Yue, Y.; Wang, J.J.; Basheer, P.A.M.; Bai, Y. Establishing the carbonation profile with Raman spectroscopy: Effects of fly ash and ground granulated blast furnace slag. Materials 2021, 14, 1798. [Google Scholar] [CrossRef] [PubMed]
- Özbay, E.; Erdemir, M.; Durmus, H.I. Utilization and efficiency of ground granulated blast furnace slag on concrete properties-A review. Constr. Build. Mater. 2016, 105, 423–434. [Google Scholar] [CrossRef]
- Kim, S.-W.; Lee, Y.-J.; Lee, J.-Y.; Kim, K.-H. Application of electric arc furnace oxidizing slag for environmental load reduction. Asian J. Chem. 2014, 26, 5867–5870. [Google Scholar] [CrossRef]
- Yazıcı, H.; Yardımcı, M.Y.; Yiğiter, H.; Aydın, S.; Türkel, S. Mechanical properties of reactive powder concrete containing high volumes of ground granulated blast furnace slag. Cem. Concr. Compos. 2010, 32, 639–648. [Google Scholar] [CrossRef]
- Escalante-Garcia, J.I.; Sharp, J.H. Effect of temperature on the hydration of the main clinker phases in Portland cements: Part II, blended cements. Cem. Concr. Res. 1998, 28, 1259–1274. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Lee, B.-S.; Lee, J.-S.; Kim, S.-W.; Kim, K.-H. Bond performance of precast RC beams according to replacement ratio of ground granulated blast furnace slag. J. Arch. Inst. Korea 2013, 29, 61–68. [Google Scholar]
- Lee, Y.-J.; Kim, H.-G.; Jeong, C.-Y.; Kim, D.-H.; Han, S.-P.; Kim, K.-H. Effect of surface roughness characteristics on structural performance of hollow core slabs. Materials 2021, 14, 2610. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19); American Concrete Institute (ACI): Farmington Hills, MI, USA, 2019.
- British Standard Institution. Eurocode 2: Design of Concrete Structures (BS EN 1992-1-1:2004); British Standard Institution (BSI): London, UK, 2004. [Google Scholar]
- Fujii, S.; Morita, S. Effect of transverse reinforcement on splitting bond strength. Trans. Jpn. Concr. Inst. 1981, 3, 237–244. [Google Scholar]
- Maeda, M. Study on Bond Splitting Failure of Reinforced Concrete Members. Master’s Thesis, The University of Tokyo, Tokyo, Japan, 1994. [Google Scholar]




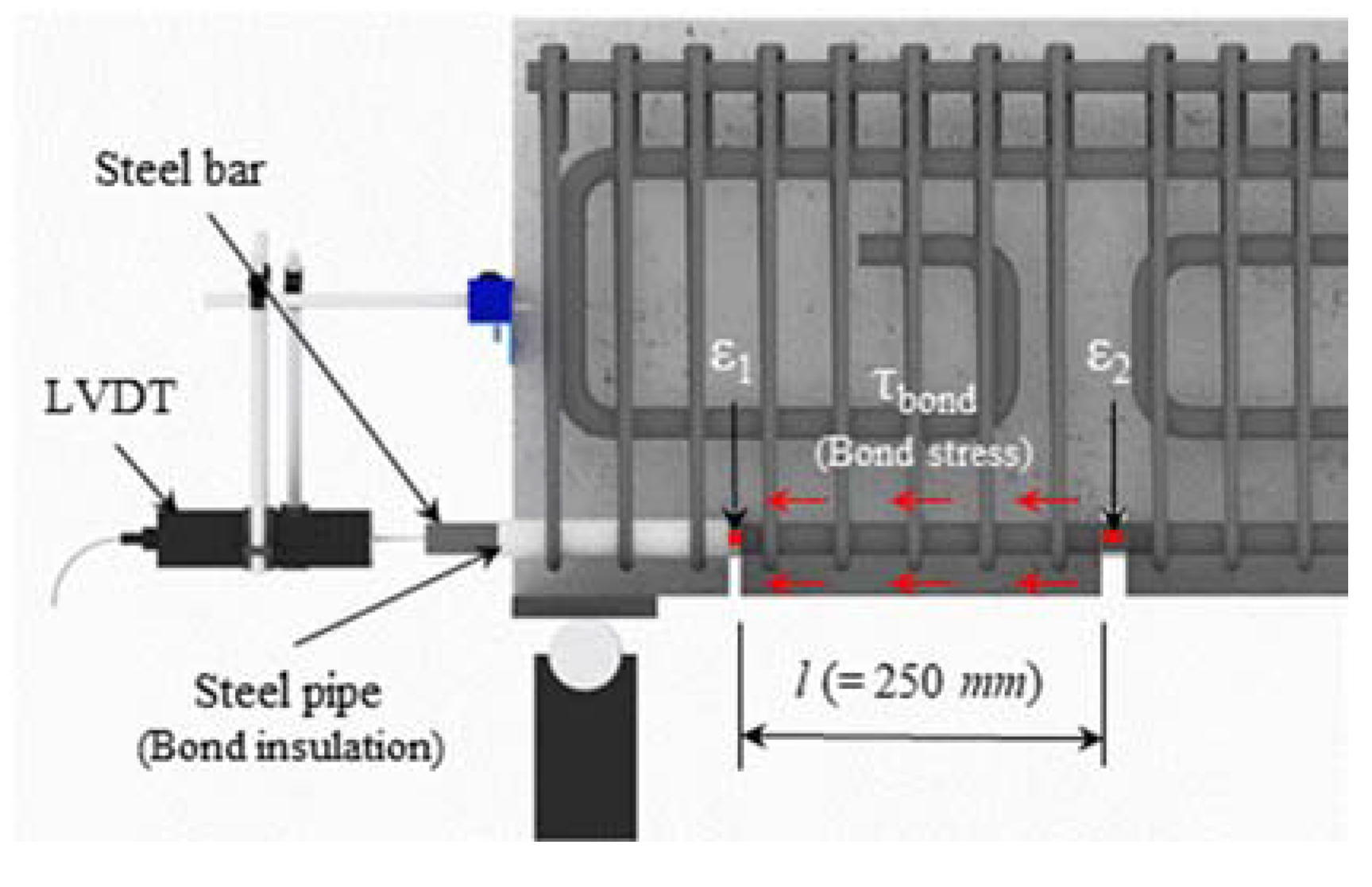
| Specimens | fck (MPa) | W/B (%) | S/a (%) | Unit Weight (kg/m3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| W | C | GGBS | FA | S | G | AE | AD | ||||
| C0 | 45 | 36.0 | 47.9 | 180 | 500 | - | - | 812 | 883 | 1.25 | 3.00 |
| C30 | 34.4 | 172 | 350 | 150 | - | 817 | 888 | 1.75 | |||
| C50 | 32.4 | 162 | 250 | 250 | - | 827 | 899 | 2.00 | |||
| C4010 | 32.4 | 162 | 250 | 200 | 50 | 821 | 892 | 2.50 | |||
| C70 | 30.4 | 152 | 150 | 350 | - | 836 | 909 | 2.50 | |||
| Specimens | f’c (MPa) | Size (mm) | a/d | Reinforcement (MPa) | |||||
|---|---|---|---|---|---|---|---|---|---|
| h | b | l | Tension | Compression | Shear | ||||
| F series | F0 | 46.7 | 200 | 350 | 3300 | 4.0 | 3-D22 fy = 448.7 | 2-D13 fy = 471.0 | D10@100 mm fwy = 496.6 |
| F30 | 58.0 | ||||||||
| F50 | 53.1 | ||||||||
| F4010 | 56.9 | ||||||||
| F70 | 45.2 | ||||||||
| S series | S0 | 46.7 | 200 | 350 | 2000 | 2.5 | 3-D22 fy = 544.0 | 2-D10 fy = 496.6 | - |
| S30 | 58.0 | ||||||||
| S50 | 53.1 | ||||||||
| S4010 | 56.9 | ||||||||
| S70 | 45.2 | ||||||||
| B series | B0 | 46.7 | 250 | 400 | 2300 | 2.0 | 6-D22 fy = 626.8 | D10@50 mm fwy = 517.3 | |
| B30 | 58.0 | ||||||||
| B50 | 53.1 | ||||||||
| B4010 | 56.9 | ||||||||
| B70 | 45.2 | ||||||||
| Specimens | f’c (MPa) | Experimental Result | Experimental/Analytical | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Moment | Curvature | Deflection | My,exp/My, ana | Mu, exp/Mu, ACI | Mu, exp/Mu, EC2 | |||||||
| My (kN·m) | Mu (kN·m) | φy (mm−1) | φu (mm−1) | φu/φy | Δy (mm) | Δu (mm) | Δu/Δy | |||||
| F0 | 46.7 | 133.4 | 165.7 | 1.34 | 8.46 | 6.45 | 13.1 | 29.7 | 2.27 | 0.97 | 1.18 | 1.17 |
| F30 | 58.0 | 133.3 | 171.4 | 1.33 | 12.58 | 9.46 | 12.8 | 34.4 | 2.69 | 0.97 | 1.20 | 1.19 |
| F50 | 53.1 | 130.1 | 172.4 | 1.31 | 12.92 | 9.86 | 12.5 | 36.0 | 2.88 | 0.94 | 1.22 | 1.20 |
| F4010 | 56.9 | 139.0 | 170.8 | 1.36 | 11.24 | 8.26 | 13.6 | 35.6 | 2.62 | 1.01 | 1.20 | 1.19 |
| F70 | 45.2 | 144.9 | 170.4 | 1.40 | - | - | 14.1 | 33.2 | 2.35 | 1.05 | 1.22 | 1.20 |
| Mean | 0.99 | 1.21 | 1.19 | |||||||||
| COV (%) | 4.32 | 1.26 | 1.25 | |||||||||
| Specimens | f’c (MPa) | Experimental Result | Experimental/Analytical | ||||||
|---|---|---|---|---|---|---|---|---|---|
| At Flexural Crack | At Diagonal Tension Crack | At Peak | Vu, exp/Vu, ACI | Vu, exp/Vu, EC2 | |||||
| Vcr (kN) | Δcr (mm) | Vd (kN) | Δd (mm) | Vu (kN) | Δu (mm) | ||||
| S0 | 46.7 | 34.5 | 0.51 | 52.6 | 0.86 | 111.2 | 2.40 | 1.61 | 1.89 |
| S30 | 58.0 | 33.8 | 0.57 | 49.2 | 0.79 | 97.2 | 2.49 | 1.26 | 1.54 |
| S50 | 53.1 | 28.2 | 0.41 | 49.4 | 0.80 | 110.2 | 2.58 | 1.49 | 1.80 |
| S4010 | 56.9 | 35.4 | 0.48 | 49.4 | 0.76 | 112.8 | 3.10 | 1.48 | 1.80 |
| S70 | 45.2 | 26.7 | 0.39 | 38.2 | 0.60 | 88.8 | 2.01 | 1.30 | 1.53 |
| Mean | 1.43 | 1.71 | |||||||
| COV (%) | 10.03 | 9.73 | |||||||
| Specimens | f’c (MPa) | Experimental Result (MPa) | Experimental/Analytical | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACI 318-19 (Considering Ktr) | Fujii-Morita | Maeda | |||||||||||
| τcorner | τinner | τmean | τcorner/τana | τinner/τana | τmean/τana | τcorner/τana | τinner/τana | τmean/τana | τcorner/τana | τinner/τana | τmean/τana | ||
| B0-B | 46.7 | 7.40 | 5.90 | 6.65 | 1.58 | 1.26 | 1.42 | 1.54 | 1.22 | 1.38 | 1.33 | 1.06 | 1.20 |
| B30-B | 58.0 | 7.69 | 6.00 | 6.85 | 1.47 | 1.15 | 1.31 | 1.43 | 1.12 | 1.27 | 1.31 | 1.03 | 1.17 |
| B50-B | 53.1 | 9.73 | 7.13 | 8.43 | 1.95 | 1.43 | 1.69 | 1.89 | 1.39 | 1.64 | 1.70 | 1.25 | 1.47 |
| B4010-B | 56.9 | 6.89 | 5.82 | 6.36 | 1.33 | 1.12 | 1.23 | 1.30 | 1.09 | 1.19 | 1.18 | 1.00 | 1.09 |
| B70-B | 45.2 | 7.74 | 5.76 | 6.75 | 1.68 | 1.25 | 1.46 | 1.63 | 1.22 | 1.42 | 1.40 | 1.05 | 1.23 |
| B0-T | 46.7 | 7.24 | 5.08 | 6.16 | 2.01 | 1.41 | 1.71 | 1.83 | 1.29 | 1.56 | 1.49 | 1.05 | 1.27 |
| B30-T | 58.0 | 8.46 | 5.76 | 7.11 | 2.10 | 1.43 | 1.77 | 1.92 | 1.31 | 1.62 | 1.62 | 1.10 | 1.36 |
| B50-T | 53.1 | 7.97 | 5.57 | 6.77 | 2.07 | 1.45 | 1.76 | 1.89 | 1.32 | 1.61 | 1.57 | 1.10 | 1.34 |
| B4010-T | 56.9 | 7.32 | 4.97 | 6.15 | 1.83 | 1.25 | 1.54 | 1.68 | 1.14 | 1.41 | 1.41 | 0.96 | 1.18 |
| B70-T | 45.2 | 7.53 | 5.09 | 6.31 | 2.12 | 1.43 | 1.78 | 1.94 | 1.31 | 1.62 | 1.57 | 1.06 | 1.31 |
| Mean | 1.81 | 1.32 | 1.57 | 1.71 | 1.24 | 1.47 | 1.46 | 1.06 | 1.26 | ||||
| COV (%) | 15.7 | 9.6 | 13.0 | 13.3 | 7.9 | 10.8 | 10.9 | 7.3 | 8.8 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-J.; Kim, H.-G.; Kim, K.-H. Effect of Ground Granulated Blast Furnace Slag Replacement Ratio on Structural Performance of Precast Concrete Beams. Materials 2021, 14, 7159. https://doi.org/10.3390/ma14237159
Lee Y-J, Kim H-G, Kim K-H. Effect of Ground Granulated Blast Furnace Slag Replacement Ratio on Structural Performance of Precast Concrete Beams. Materials. 2021; 14(23):7159. https://doi.org/10.3390/ma14237159
Chicago/Turabian StyleLee, Yong-Jun, Hyeong-Gook Kim, and Kil-Hee Kim. 2021. "Effect of Ground Granulated Blast Furnace Slag Replacement Ratio on Structural Performance of Precast Concrete Beams" Materials 14, no. 23: 7159. https://doi.org/10.3390/ma14237159
APA StyleLee, Y.-J., Kim, H.-G., & Kim, K.-H. (2021). Effect of Ground Granulated Blast Furnace Slag Replacement Ratio on Structural Performance of Precast Concrete Beams. Materials, 14(23), 7159. https://doi.org/10.3390/ma14237159







