Estimating of Bending Force and Curvature of the Bending Plate in a Three-Roller Bending System Using Finite Element Simulation and Analytical Modeling
Abstract
:1. Introduction
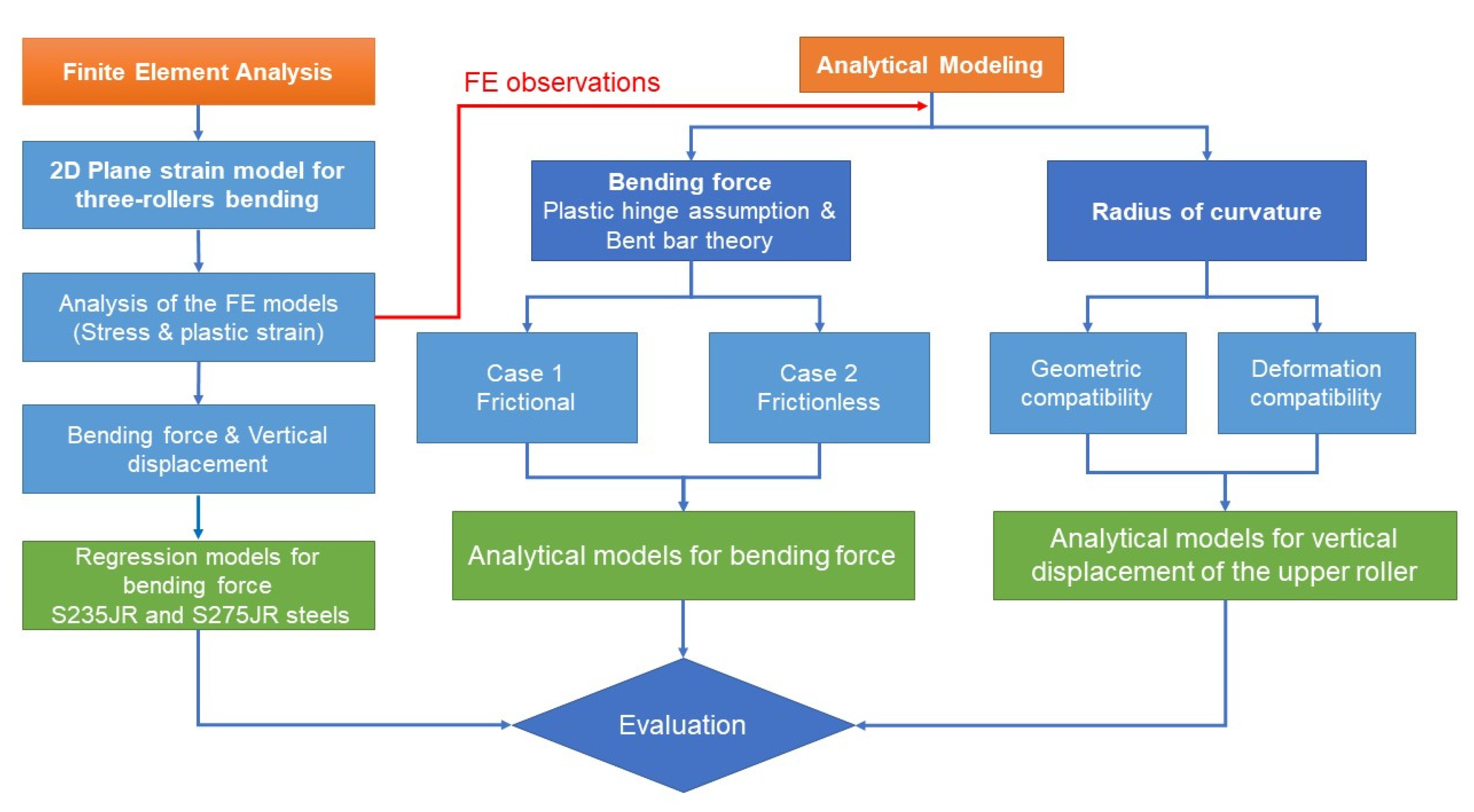
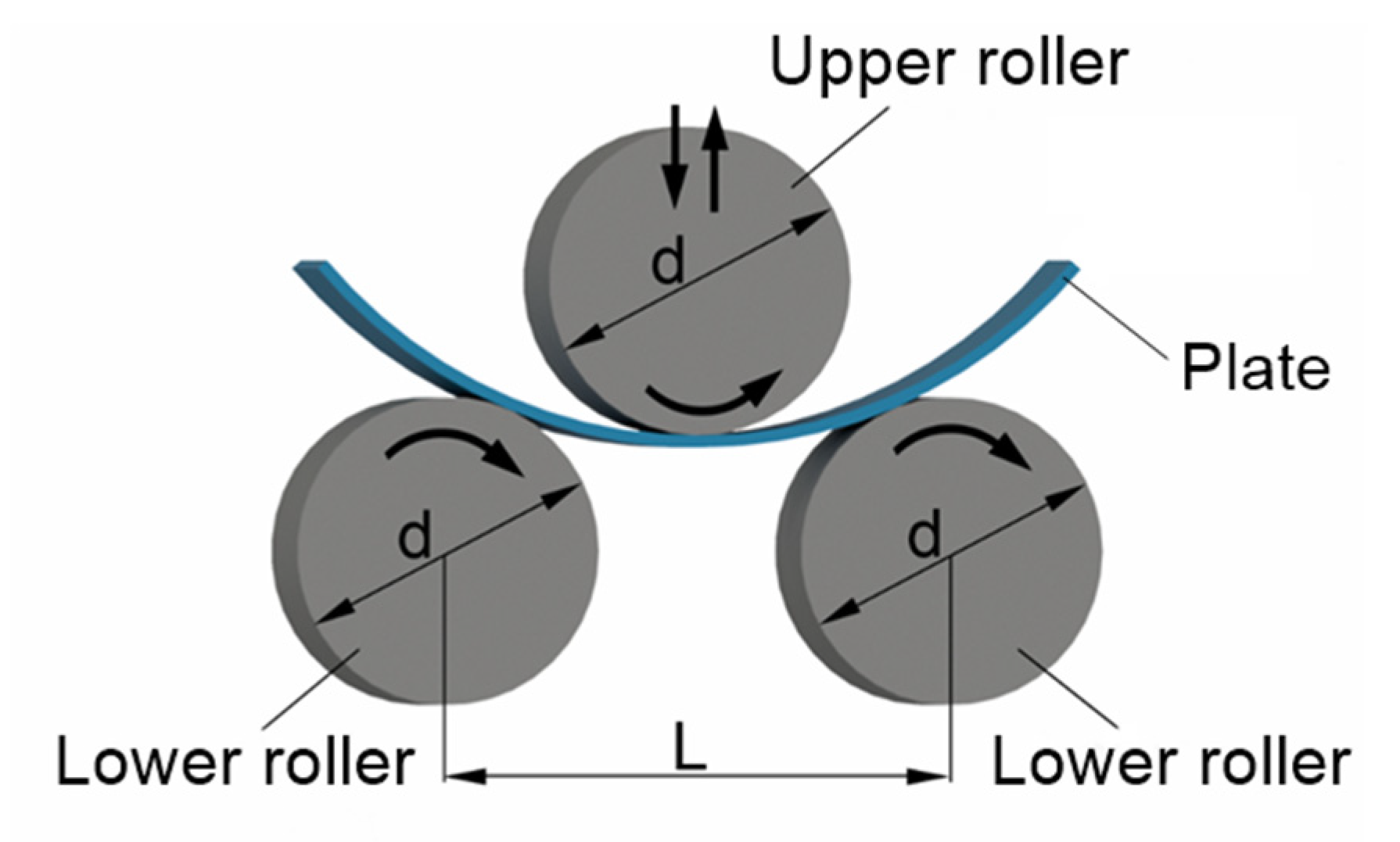
2. Numerical Simulation of the Three-Roller Banding Process
2.1. Research Methodology
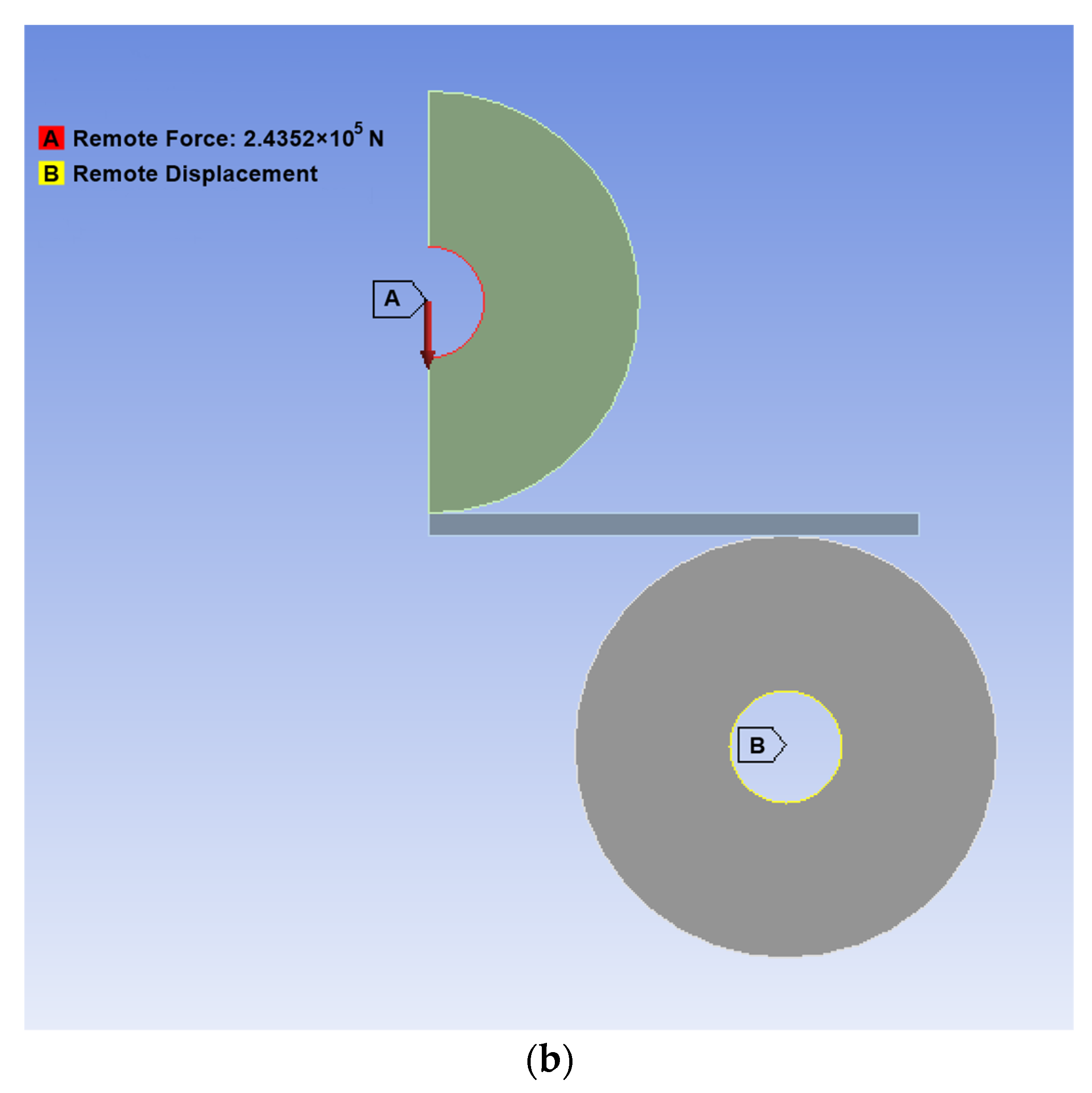
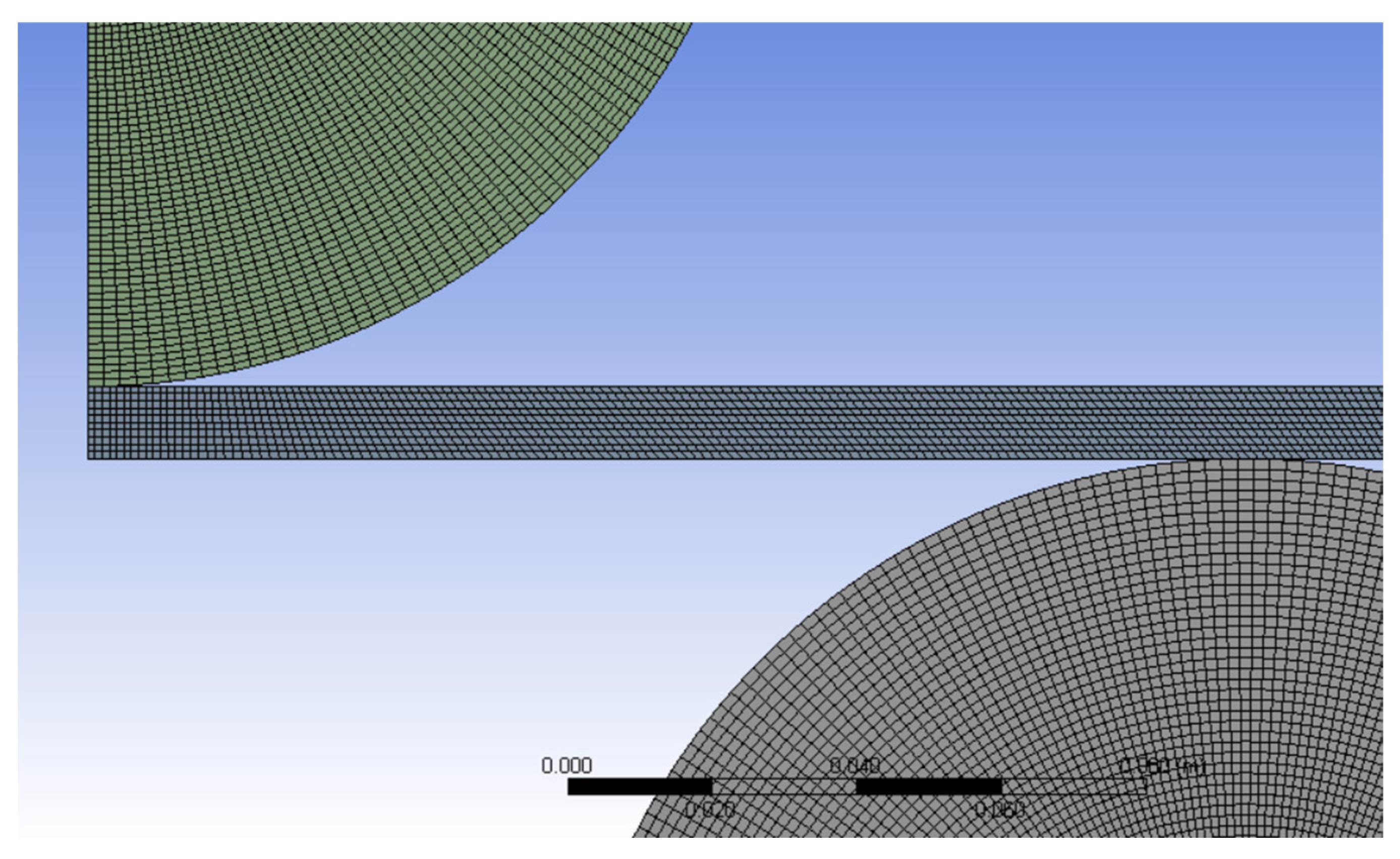
2.2. Finite Element Model
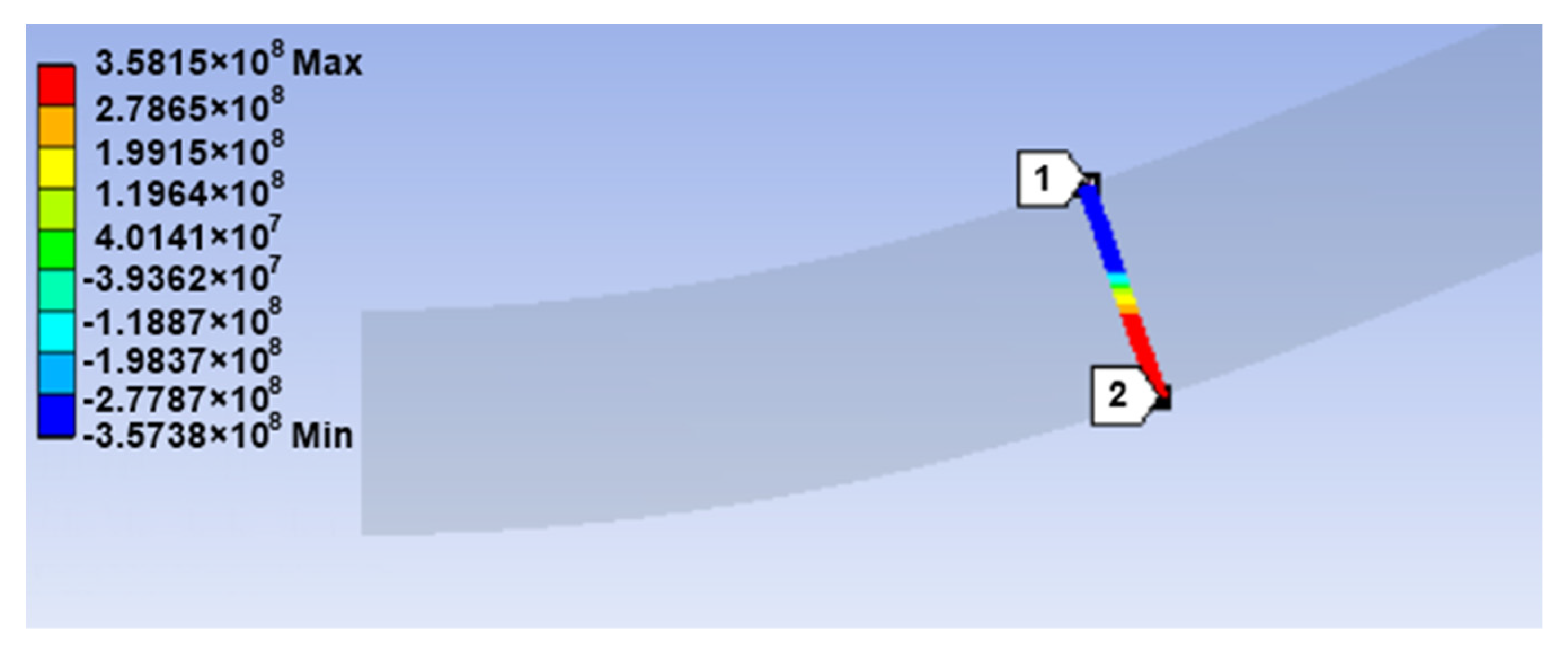
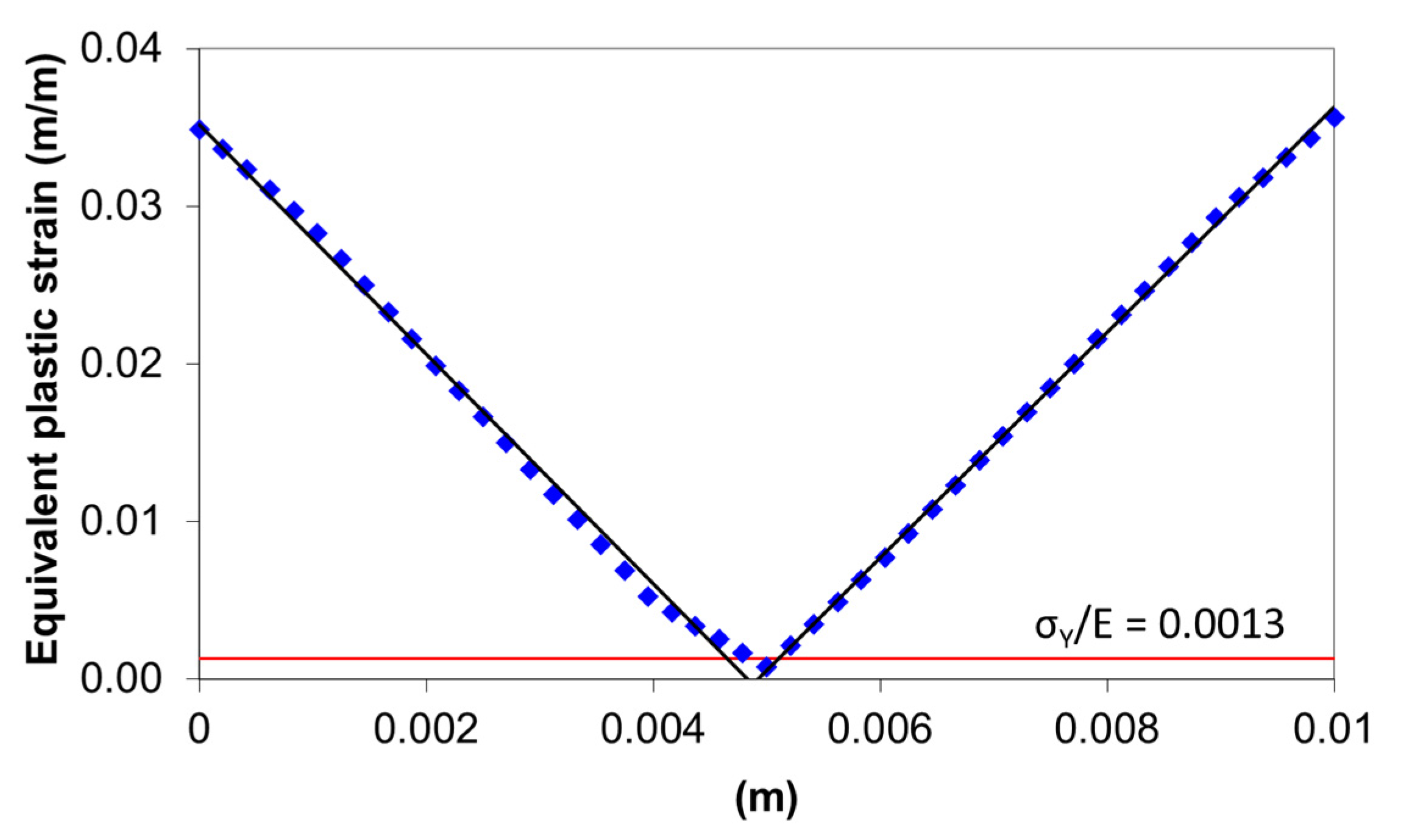
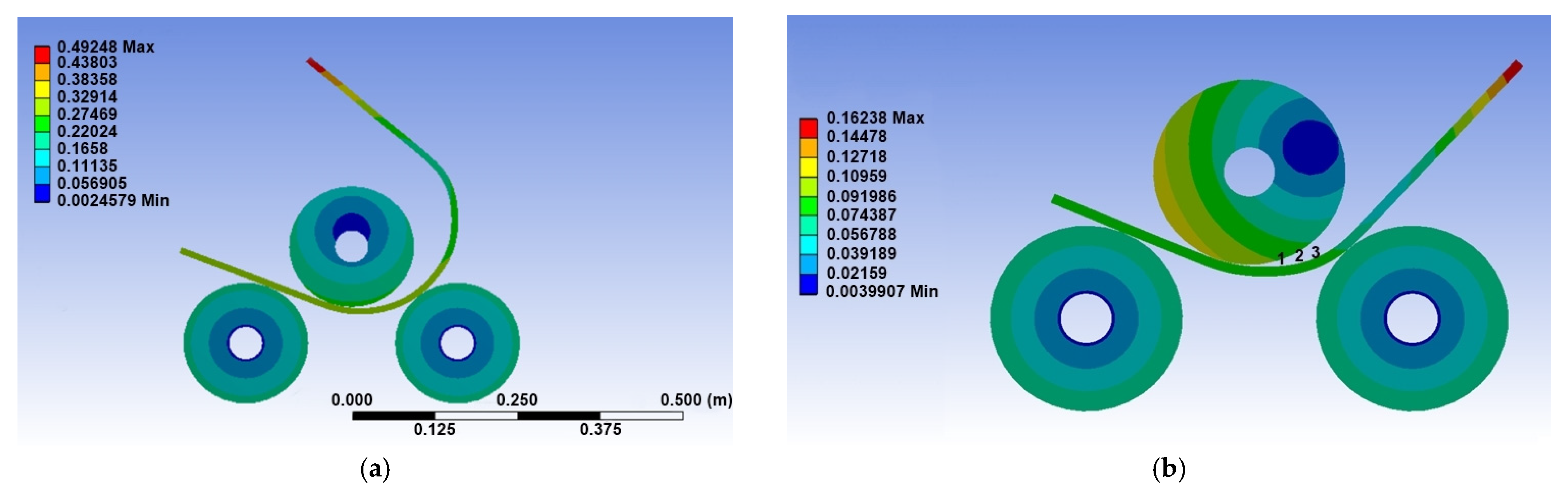
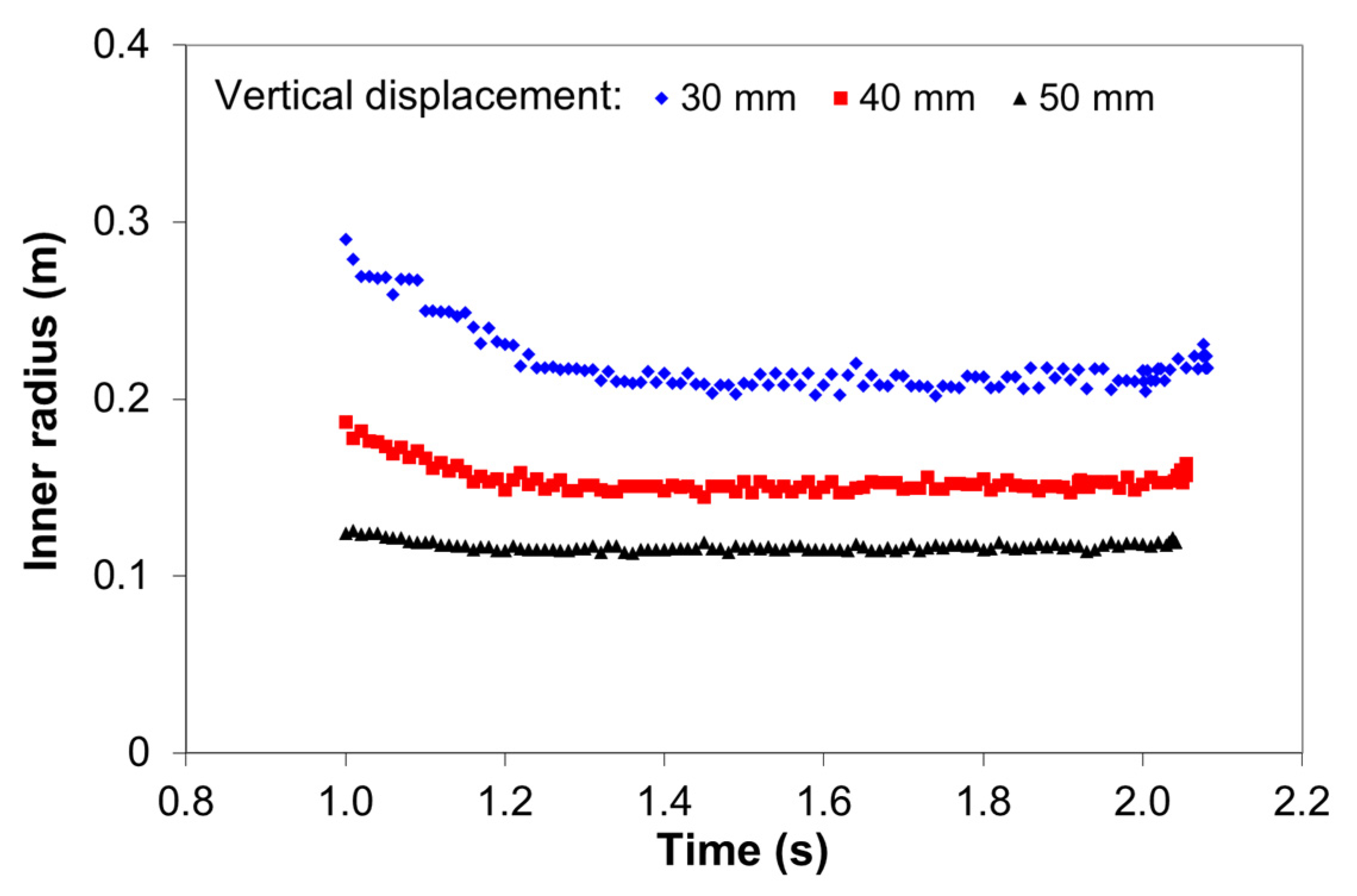
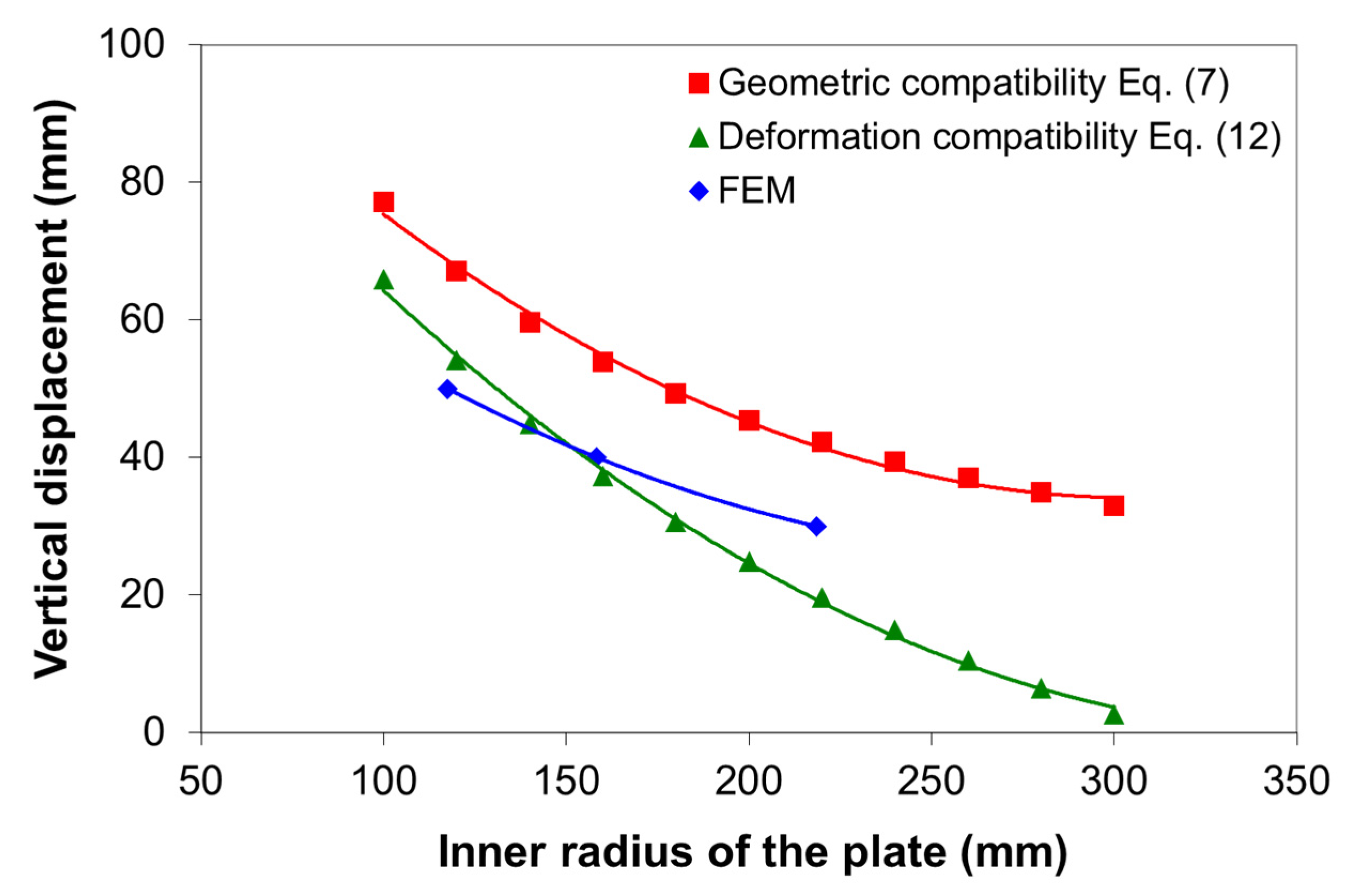
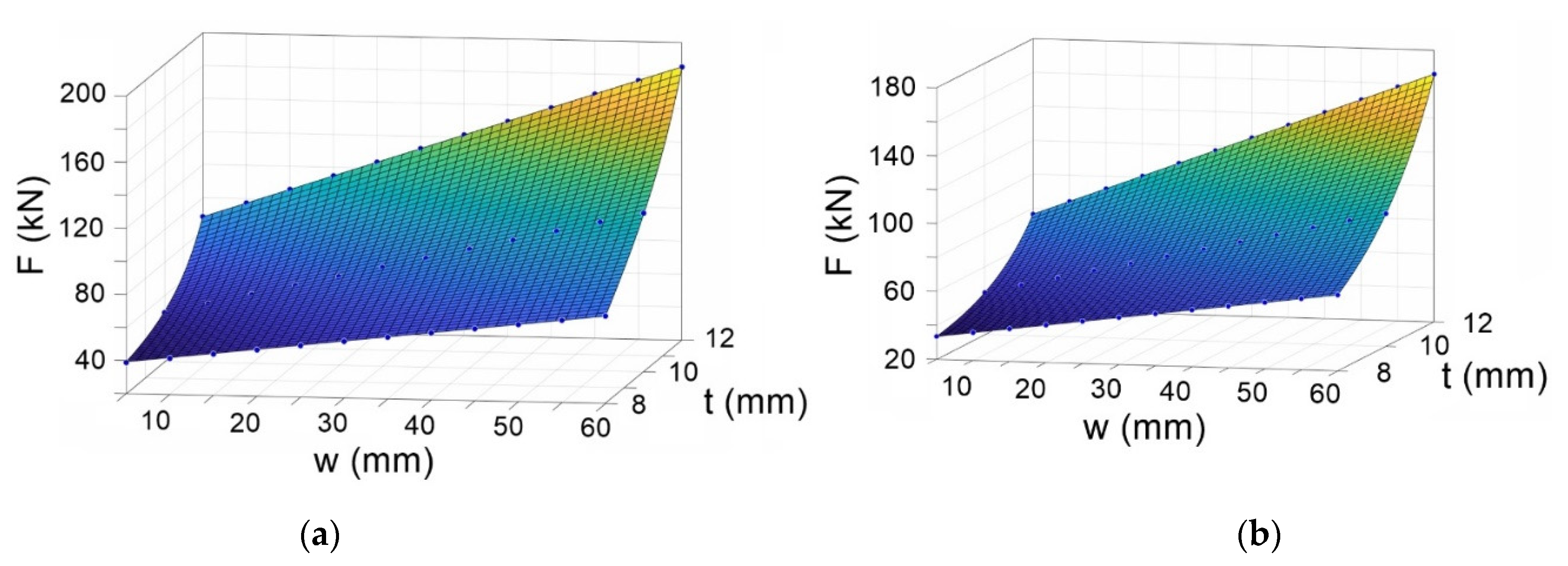
2.3. Numerical Simulation Results
3. Analytical Modeling of the Three-Roller Bending Process
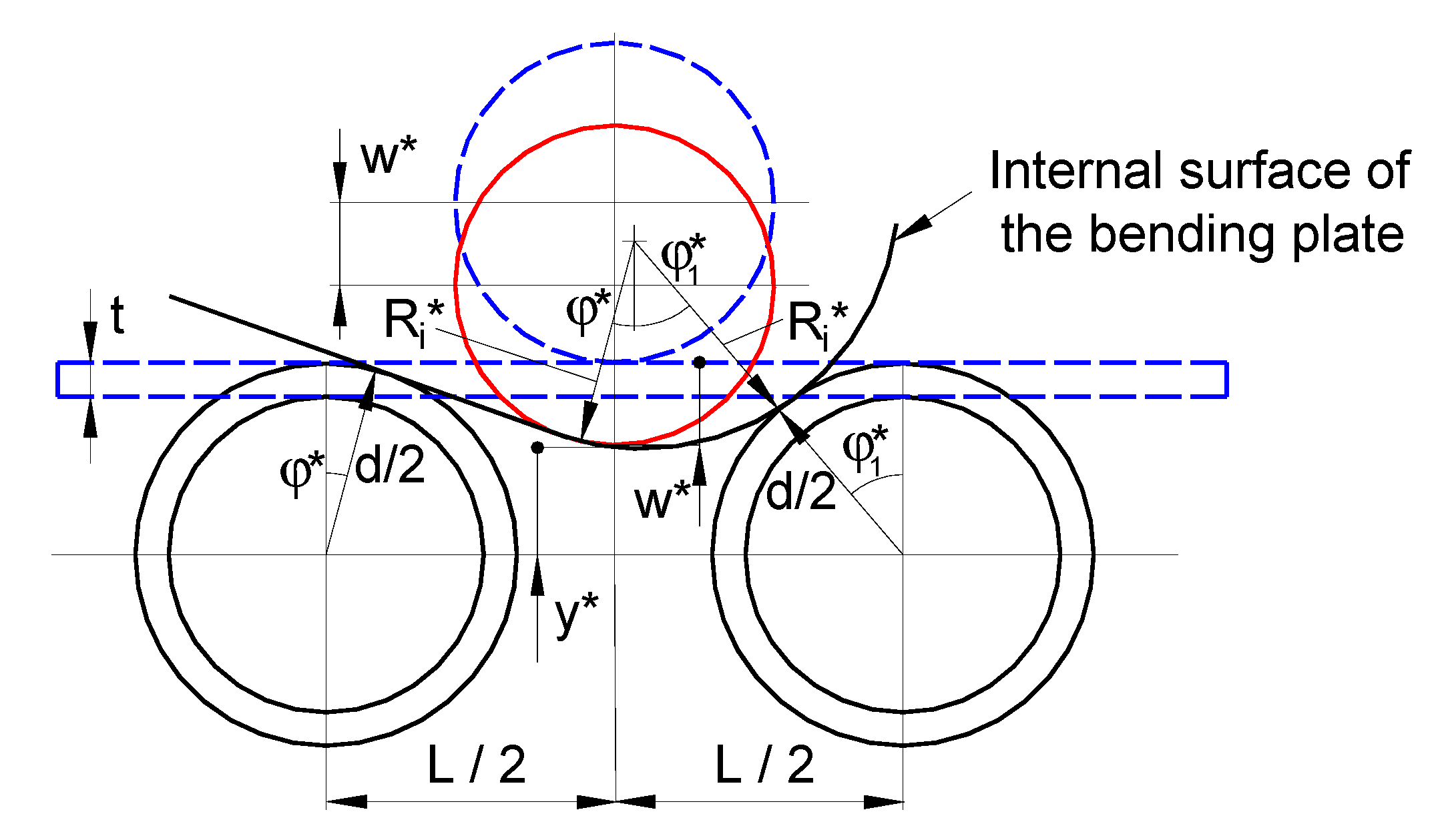
3.1. Radius of the Bending Plate
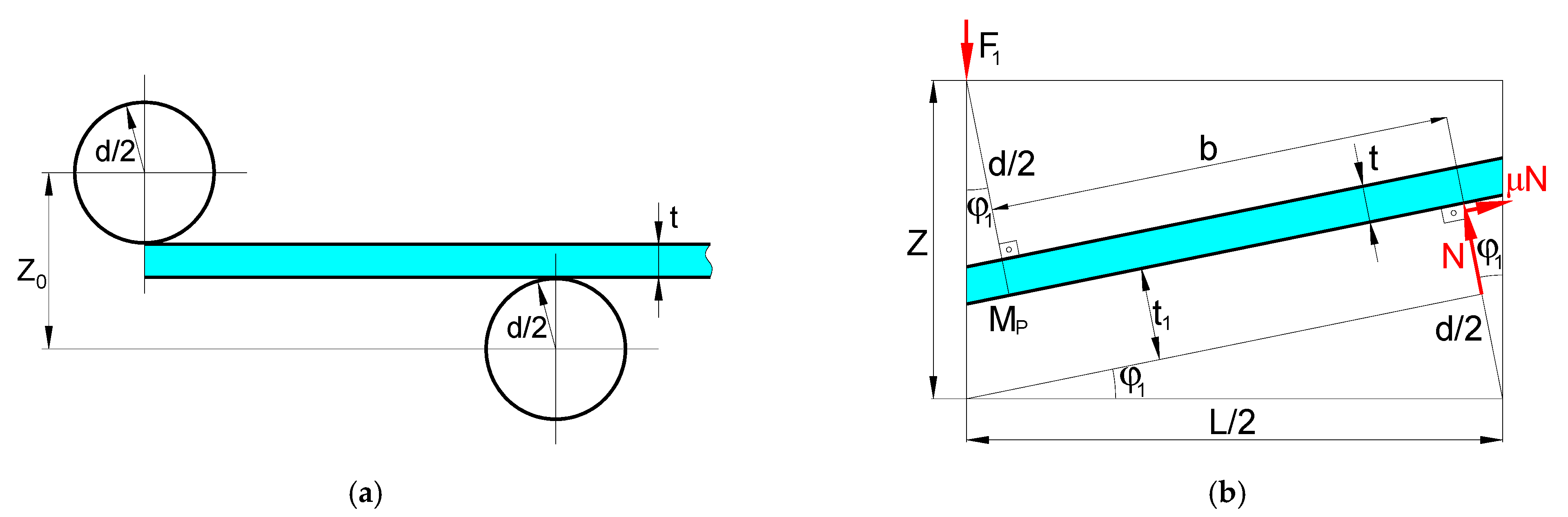
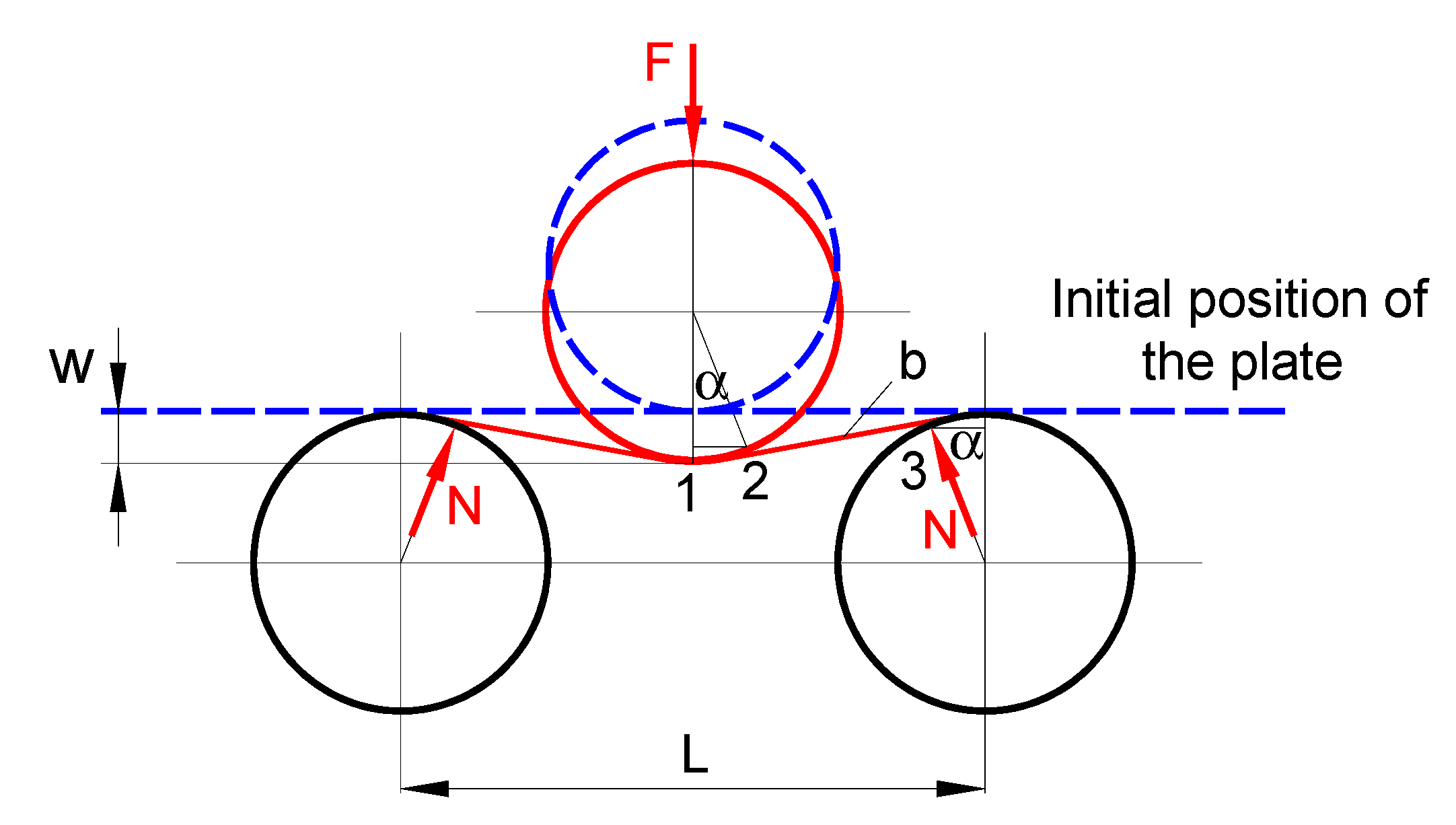
3.2. Bending Force
3.2.1. Case 1 Scenario (C1)
3.2.2. Case 2 Scenario (C2)
4. Predictive Models for Bending Force
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roggendorff, S.; Haeusler, J. Plate bending: Three rolls and four rolls compared. Weld. Met. Fabr. 1979, 47, 353–357. [Google Scholar]
- Hua, M.; Lin, Y.H. Large deflection analysis of elastoplastic plate in steady continuous four-roll bending process. Int. J. Mech. Sci. 1999, 41, 1461–1483. [Google Scholar] [CrossRef]
- Shin, J.G.; Lee, J.H.; Kim, Y.I.; Yim, H. Mechanics-based determination of the center roller displacement in three-roll bending for smoothly curved rectangular plates. J. Mech. Sci. Technol. 2001, 1, 1655–1663. [Google Scholar] [CrossRef]
- Chudasama, M.K.; Raval, H.K. Analytical model for prediction of force during 3 Roller multipass conical bending and its experimental verification. Int. J. Mech. Eng. Robot. Res. 2012, 1, 91–105. [Google Scholar]
- Chudasama, M.K.; Rava, H.K. An approximate bending force prediction for 3-roller conical bending process. Int J. Mater. Form. 2013, 6, 303–314. [Google Scholar] [CrossRef]
- Padgan, N.P.; Deshpande, P.D.; Sakhale, C.N. Force Analysis of Metal Sheet in Bending Operation on Sheet Bending Machine. Int J. Eng. Res. Tech. 2015, 4, 267–270. [Google Scholar]
- Jadhav, C.S.; Talmale, P.S. Verification and Analysis of Stress-Strain Curve of Sheet Metal by using Three Roller Bending Machine. Int. J. Eng. Dev. Res. 2017, 5, 368–374. [Google Scholar]
- Tran, H.Q. Asymmetrical Roll Bending Process Study: Dynamic Finite Element Modeling and Experiments. Ph.D. Thesis, Université du Québec, Québec, QC, Canada, November 2014. [Google Scholar]
- Feng, Z.; Champliaud, H. Modeling and simulation of asymmetrical three-roll bending process. Simul. Model. Pract. Theory 2011, 19, 1913–1917. [Google Scholar] [CrossRef]
- Feng, Z.; Champliaud, H. Three stage process for improving roll bending quality. Simul. Model. Pract. Theory 2011, 19, 887–898. [Google Scholar] [CrossRef]
- Ktari, A.; Antar, Z.; Haddar, N.; Elleuch, K. Modeling and computation of the three-roller bending process of steel sheets. J. Mech. Sci. Technol. 2012, 26, 123–128. [Google Scholar] [CrossRef]
- Taylor, V.K.; Gandhim, A.H.; Moliya, R.D.; Raval, H.K. Finite element analysis of deformed geometry in three-roller plate bending process. In Proceedings of the ASME 2008 International Manufacturing Science and Engineering Conference, Illinois, IL, USA, 7–10 October 2008; Evanston: Illinois, IL, USA, 2008; pp. 1–7. [Google Scholar]
- Neto, D.M.; Martins, J.M.P.; Oliveira, M.C.; Menezes, L.F.; Alves, J.L. Evaluation of strain and stress states in the single point incremental forming process. Int J. Adv. Manuf. Tech. 2016, 85, 521–534. [Google Scholar] [CrossRef] [Green Version]
- Patel, B.N.; Pandit, D.; Srinivasan, S.M. Large elaso-plastic deflection of micro-beams using strain gradient plasticity theory. Procedia Eng. 2017, 173, 1064–1070. [Google Scholar] [CrossRef]
- Pandit, D.; Srinivasan, S.M. Large Elasto-Plastic Deflection of Thin Beams with Roller Support Contact, 11th International Symposium on Plasticity and Impact Mechanics. Procedia Eng. 2017, 173, 1079–1084. [Google Scholar] [CrossRef]
- Fu, Z.; Tian, X.; Hu, B.; Yao, X. Analytical modeling and numerical simulation for three-roll bending forming of sheet metal. Int. J. Adv. Manuf. Technol. 2013, 69, 1639–1647. [Google Scholar] [CrossRef]
- Ansys Workbench 2018, Version 19; Software For Technical Computation; Ansys, Inc.: Canonsburg, PA, USA, 2018.
- Gavrilescu, I.; Boazu, D. Simulation of roll bending with three rollers pyramid system using FEM. Ann. Univ. Dunarea de Jos of Galati Fascicle VI 2017, 35, 21–28. [Google Scholar]
- Hardt, D.E.; Constantine, E.; Wright, A. A model of a sequential bending process for manufacturing simulation. J. Eng. Ind. Trans. ASME 1992, 114/181, 181–187. [Google Scholar] [CrossRef]
- MATLAB 2018, Version R2018a; Software For Technical Computation; The MathWorks, Inc.: Natick, MA, USA, 2018.
- Kamiński, K.; Solecka, M. Optimization of the truss-type structures using the generalized perturbation-based Stochastic Finite Element Method. Finite Elem. Anal. Des. 2013, 63, 69–79. [Google Scholar] [CrossRef]




| Parameters | S235JR | S275JR |
|---|---|---|
| Yield strength (MPa) | 235 | 275 |
| Young modulus (Pa) | 2.1 × 1011 | 2.1 × 1011 |
| Tangent modulus (Pa) | 2.1 × 109 | 2.1 × 109 |
| Poisson ratio (-) | 0.3 | 0.3 |
| Sheet thickness (mm) | 8, 10, 12 | 8, 10, 12 |
| Maximum vertical displacement (mm) | 50 | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavrilescu, I.; Boazu, D.; Stan, F. Estimating of Bending Force and Curvature of the Bending Plate in a Three-Roller Bending System Using Finite Element Simulation and Analytical Modeling. Materials 2021, 14, 1204. https://doi.org/10.3390/ma14051204
Gavrilescu I, Boazu D, Stan F. Estimating of Bending Force and Curvature of the Bending Plate in a Three-Roller Bending System Using Finite Element Simulation and Analytical Modeling. Materials. 2021; 14(5):1204. https://doi.org/10.3390/ma14051204
Chicago/Turabian StyleGavrilescu, Ionel, Doina Boazu, and Felicia Stan. 2021. "Estimating of Bending Force and Curvature of the Bending Plate in a Three-Roller Bending System Using Finite Element Simulation and Analytical Modeling" Materials 14, no. 5: 1204. https://doi.org/10.3390/ma14051204
APA StyleGavrilescu, I., Boazu, D., & Stan, F. (2021). Estimating of Bending Force and Curvature of the Bending Plate in a Three-Roller Bending System Using Finite Element Simulation and Analytical Modeling. Materials, 14(5), 1204. https://doi.org/10.3390/ma14051204





