Superionic Solid Electrolyte Li7La3Zr2O12 Synthesis and Thermodynamics for Application in All-Solid-State Lithium-Ion Batteries
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
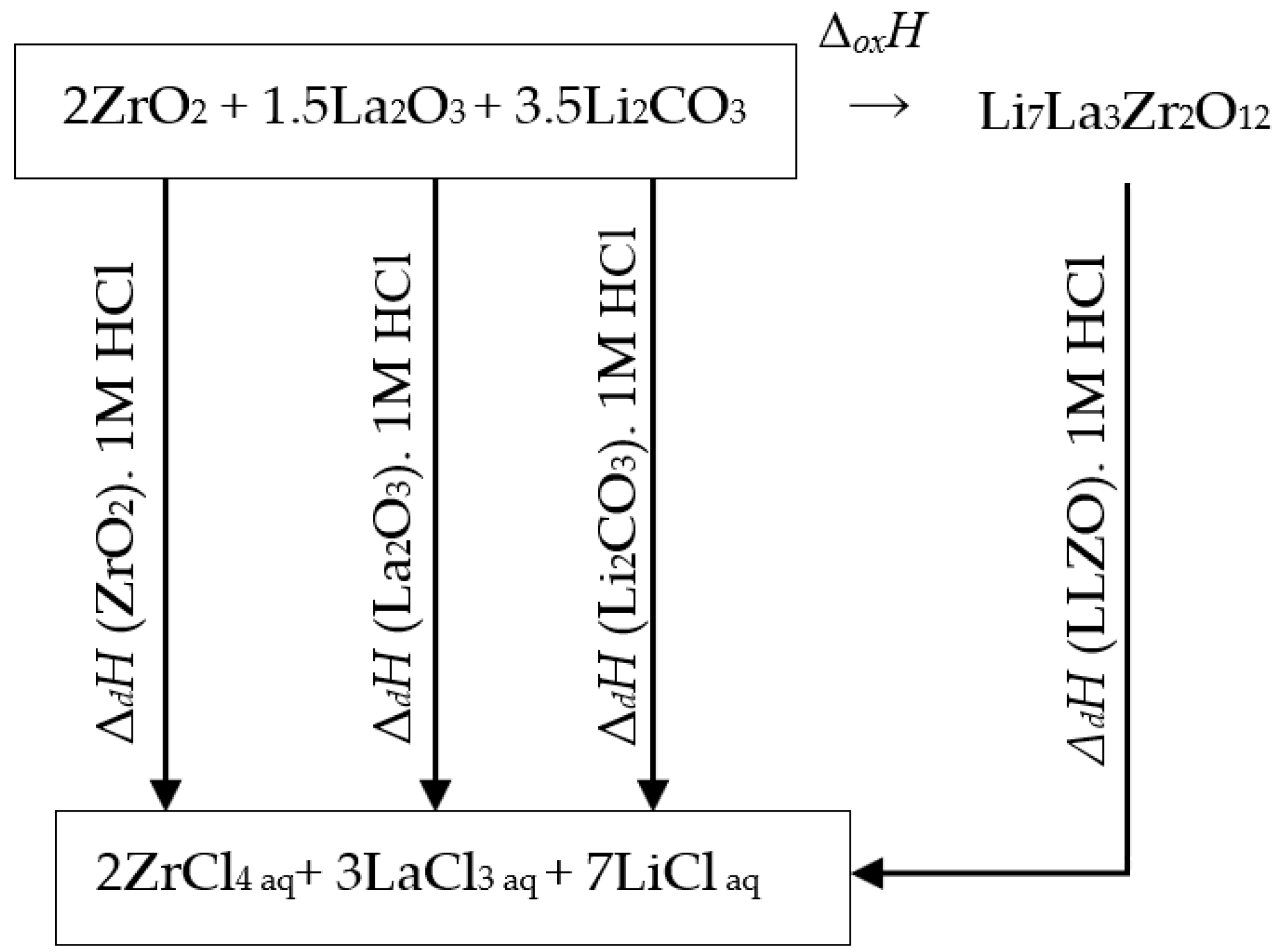
4.1. The Standard Formation Enthalpy
4.2. The Isobaric Heat Capacity
| T, K | Cp(exp.), J·K−1·mol−1 | Cp(rec.), J·K−1·mol−1 | Cp(N-K), J·K−1·mol−1 |
|---|---|---|---|
| 300 | - | - | 621.1 |
| 400 | 778.6 | 709.7 | 708.1 |
| 500 | 851.8 | 784.7 | 778.8 |
| 600 | 936.7 | 857.4 | 843.1 |
| 700 | 1002.8 | 925.0 | 904.3 |
| 800 | 1035.4 | 971.1 | 964.0 |
4.3. Entropy
4.4. The Standard Gibbs Free Energy
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nishi, Y. Lithium-ion secondary batteries; past 10 years and the future. J. Power Sources 2001, 100, 101–106. [Google Scholar] [CrossRef]
- Ma, J.; Li, Y.; Grundish, N.S.; Goodenough, J.B.; Chen, Y.; Guo, L.; Peng, Z.; Qi, X.; Yang, F.; Qie, L.; et al. The 2021 battery technology roadmap. J. Phys. D Appl. Phys. 2021, 54, 183001. [Google Scholar] [CrossRef]
- Horowitz, Y.; Schmidt, C.; Yoon, D.H.; Riegger, L.M.; Katzenmeier, L.; Bosch, G.M.; Noked, M.; Ein-Eli, Y.; Janek, J.; Zeier, W.G.; et al. Between Liquid and All Solid: A Prospect on Electrolyte Future in Lithium-Ion Batteries for Electric Vehicles. Energy Technol. 2020, 8, 2000580. [Google Scholar] [CrossRef]
- Han, L.; Lehmann, M.L.; Zhu, J.; Liu, T.; Zhou, Z.; Tang, X.; Heish, C.T.; Sokolov, A.P.; Cao, P.; Chen, X.C.; et al. Recent Developments and Challenges in Hybrid Solid Electrolytes for Lithium-Ion Batteries. Front. Energy Res. 2020, 8, 202. [Google Scholar] [CrossRef]
- Tan, D.H.; Chen, Y.T.; Yang, H.; Bao, W.; Sreenarayanan, B.; Doux, J.M.; Li, W.; Lu, B.; Ham, S.Y.; Sayahpour, B.; et al. Carbon-free high-loading silicon anodes enabled by sulfide solid electrolytes. Science 2021, 373, 1494–1499. [Google Scholar] [CrossRef] [PubMed]
- Byeon, Y.W.; Kim, H. Review on Interface and Interphase Issues in Sulfide Solid-State Electrolytes for All-Solid-State Li-Metal Batteries. Electrochem 2021, 2, 30. [Google Scholar] [CrossRef]
- Tripathi, A.K. Ionic liquid based solid electrolytes (ionogels) for application in rechargeable lithium battery. Mater. Today Energy 2021, 20, 100643. [Google Scholar] [CrossRef]
- Yu, T.; Yang, X.; Yang, R.; Bai, X.; Xu, G.; Zhao, S.; Duan, Y.; Wu, Y.; Wang, J. Progress and perspectives on typical inorganic solid-state electrolytes. J. Alloys Compd. 2021, 885, 161013. [Google Scholar] [CrossRef]
- Chan, C.K.; Yang, T.; Weller, J.M. Nanostructured garnet-type Li7La3Zr2O12: Synthesis, properties, and opportunities as electrolytes for Li-ion batteries. Electrochim. Acta 2017, 253, 268–280. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, W.; Zhu, G.; Huang, Y.; Feng, Q.; Lu, Y. Design Principles of the Anode–Electrolyte Interface for All Solid-State Lithium Metal Batteries. Small Methods 2020, 4, 1900592. [Google Scholar] [CrossRef]
- Tikekar, M.D.; Choudhury, S.; Tu, Z.; Archer, L.A. Design principles for electrolytes and interfaces for stable lithium-metal batteries. Nat. Energy 2016, 1, 16114. [Google Scholar] [CrossRef]
- Wang, H.; Yu, D.; Kuang, C.; Cheng, L.; Li, W.; Feng, X.; Zhang, Z.; Zhang, X.; Zhang, Y. Alkali metal anodes for rechargeable batteries. Chem 2019, 5, 313–338. [Google Scholar] [CrossRef] [Green Version]
- Famprikis, T.; Canepa, P.; Dawson, J.A.; Islam, M.S.; Masquelier, C. Fundamentals of inorganic solid-state electrolytes for batteries. Nat. Mater. 2019, 18, 1278–1291. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Shao, Y.; Lotsch, B.; Hu, Y.S.; Li, H.; Janek, J.; Nazar, L.F.; Nan, C.W.; Maier, J.; Armand, M.; et al. New horizons for inorganic solid state ion conductors. Energy Environ. Sci. 2018, 11, 1945–1976. [Google Scholar] [CrossRef] [Green Version]
- Park, K.; Yu, B.C.; Jung, J.W.; Li, Y.; Zhou, W.; Gao, H.; Son, S.; Goodenough, J.B. Electrochemical nature of the cathode interface for a solid-state lithium-ion battery: Interface between LiCoO2 and garnet-Li7La3Zr2O12. Chem. Mater. 2016, 28, 8051–8059. [Google Scholar] [CrossRef]
- Murugan, R.; Thangadurai, V.; Weppner, W. Fast lithium ion conduction in garnet-type Li7La3Zr2O12. Angewandte Chemie. Int. Ed. 2007, 46, 7778–7781. [Google Scholar] [CrossRef]
- Bai, Y.X.; Zhang, J.; Yang, Y.B.; Yang, R.; Yan, Y.L.; Wang, J. Enhance electrochemical performance of LiFePO4 cathode material by Al-doped Li7La3Zr2O12 and carbon co-coating surface modification. J. Alloy. Compd. 2020, 843, 154915. [Google Scholar] [CrossRef]
- Matsui, M.; Takahashi, K.; Sakamoto, K.; Hirano, A.; Takeda, Y.; Yamamoto, O.; Imanishi, N. Phase stability of a garnet-type lithium ion conductor Li7La3Zr2O12. Dalton Trans. 2014, 43, 1019–1024. [Google Scholar] [CrossRef]
- Dermenci, K.B.; Çekiç, E.; Turan, S. Al stabilized Li7La3Zr2O12 solid electrolytes for all-solid state Li-ion batteries. Int. J. Hydrog. Energy 2016, 41, 9860–9867. [Google Scholar] [CrossRef]
- Kotobuki, M.; Hanc, E.; Yan, B.; Molenda, J.; Lu, L. Stabilization of cubic Li7La3Zr2O12 by Al substitution in various atmospheres. Solid State Ion. 2020, 350, 115323. [Google Scholar] [CrossRef]
- Polizos, G.; Sharma, J.; Jafta, C.J.; Muralidharan, N.; Veith, G.M.; Keum, J.K.; Kukay, A.; Sahore, R.; Wood, D.L., III. Nanostructured ligament and fiber Al–doped Li7La3Zr2O12 scaffolds to mediate cathode-electrolyte interface chemistry. J. Power Sources 2021, 513, 230551. [Google Scholar] [CrossRef]
- Liu, X.; Gao, M.; Liu, Y.; Xiong, L.; Chen, J. Improving the room temperature ionic conductivity of Al-Li7La3Zr2O12 ceramics by Ba and Y or Ba and W co-doping. Ceram. Int. 2019, 45, 13488–13495. [Google Scholar] [CrossRef]
- PPosch, P.; Lunghammer, S.; Berendts, S.; Ganschow, S.; Redhammer, G.J.; Wilkening, A.; Lerch, M.; Gadermaier, B.; Rettenwander, D.; Wilkening, H.M.R. Ion dynamics in Al-stabilized Li7La3Zr2O12 single crystals–Macroscopic transport and the elementary steps of ion hopping. Energy Storage Mater. 2020, 24, 220–228. [Google Scholar] [CrossRef]
- Matsuki, Y.; Noi, K.; Suzuki, K.; Sakuda, A.; Hayashi, A.; Tatsumisago, M. Microstructure and conductivity of Al-substituted Li7La3Zr2O12 ceramics with different grain sizes. Solid State Ion. 2019, 342, 115047. [Google Scholar] [CrossRef]
- Wolfenstine, J.; Ratchford, J.; Rangasamy, E.; Sakamoto, J.; Allen, J.L. Synthesis and high Li-ion conductivity of Ga-stabilized cubic Li7La3Zr2O12. Mater. Chem. Phys. 2012, 134, 571–575. [Google Scholar] [CrossRef]
- Jalem, R.; Rushton, M.J.D.; Manalastas, W., Jr.; Nakayama, M.; Kasuga, T.; Kilner, J.A.; Grimes, R.W. Effects of gallium doping in garnet-type Li7La3Zr2O12 solid electrolytes. Chem. Mater. 2015, 27, 2821–2831. [Google Scholar] [CrossRef] [Green Version]
- Bernuy-Lopez, C.; Manalastas, W., Jr.; Lopez del Amo, J.M.; Aguadero, A.; Aguesse, F.; Kilner, J.A. Atmosphere controlled processing of Ga-substituted garnets for high Li-ion conductivity ceramics. Chem. Mater. 2014, 26, 3610–3617. [Google Scholar] [CrossRef]
- El Shinawi, H.; Janek, J. Stabilization of cubic lithium-stuffed garnets of the type “Li7La3Zr2O12” by addition of gallium. J. Power Sources 2013, 225, 13–19. [Google Scholar] [CrossRef]
- Huang, X.; Su, J.; Song, Z.; Xiu, T.; Jin, J.; Badding, M.E.; Wen, Z. Synthesis of Ga-doped Li7La3Zr2O12 solid electrolyte with high Li+ ion conductivity. Ceram. Int. 2021, 47, 2123–2130. [Google Scholar] [CrossRef]
- Su, J.; Huang, X.; Song, Z.; Xiu, T.; Badding, M.E.; Jin, J.; Wen, Z. Overcoming the abnormal grain growth in Ga-doped Li7La3Zr2O12 to enhance the electrochemical stability against Li metal. Ceram. Int. 2019, 45, 14991–14996. [Google Scholar] [CrossRef]
- Shen, L.; Wang, L.; Wang, Z.; Jin, C.; Peng, L.; Pan, X.; Sun, J.; Yang, R. Preparation and characterization of Ga and Sr co-doped Li7La3Zr2O12 garnet-type solid electrolyte. Solid State Ion. 2019, 339, 114992. [Google Scholar] [CrossRef]
- Tian, Y.; Zhou, Y.; Wang, W.; Zhou, Y. Effects of Ga–Ba Co-doping on the morphology and conductivity of Li7La3Zr2O12 electrolyte synthesized by sol-gel method. Ceram. Int. 2021, 48, 963670. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, J.; Hu, D.; Chen, F.; Shen, Q.; Zhang, L.; Dong, S. Synergistic regulation of garnet-type Ta-doped Li7La3Zr2O12 solid electrolyte by Li+ concentration and Li+ transport channel size. Electrochim. Acta 2019, 296, 823–829. [Google Scholar] [CrossRef]
- Wang, Y.; Lai, W. Phase transition in lithium garnet oxide ionic conductors Li7La3Zr2O12: The role of Ta substitution and H2O/CO2 exposure. J. Power Sources 2015, 275, 612–620. [Google Scholar] [CrossRef]
- Chen, X.; Wang, T.; Lu, W.; Cao, T.; Xue, M.; Li, B.; Zhang, C. Synthesis of Ta and Ca doped Li7La3Zr2O12 solid-state electrolyte via simple solution method and its application in suppressing shuttle effect of Li-S battery. J. Alloy. Compd. 2018, 744, 386–394. [Google Scholar] [CrossRef]
- Chen, X.; Cao, T.; Xue, M.; Lv, H.; Li, B.; Zhang, C. Improved room temperature ionic conductivity of Ta and Ca doped Li7La3Zr2O12 via a modified solution method. Solid State Ion. 2018, 314, 92–97. [Google Scholar] [CrossRef]
- Guo, H.; Su, J.; Zha, W.; Xiu, T.; Song, Z.; Badding, M.E.; Jin, J.; Wen, Z. Achieving high critical current density in Ta-doped Li7La3Zr2O12/MgO composite electrolytes. J. Alloy. Compd. 2021, 856, 157222. [Google Scholar] [CrossRef]
- Hosokawa, H.; Takeda, A.; Inada, R.; Sakurai, Y. Tolerance for Li dendrite penetration in Ta-doped Li7La3Zr2O12 solid electrolytes sintered with Li2.3C0.7B0.3O3 additive. Mater. Lett. 2020, 279, 128481. [Google Scholar]
- Huang, X.; Xiu, T.; Badding, M.E.; Wen, Z. Two-step sintering strategy to prepare dense Li-Garnet electrolyte ceramics with high Li+ conductivity. Ceram. Int. 2018, 44, 5660–5667. [Google Scholar] [CrossRef]
- He, M.; Cui, Z.; Chen, C.; Li, Y.; Guo, X. Formation of self-limited, stable and conductive interfaces between garnet electrolytes and lithium anodes for reversible lithium cycling in solid-state batteries. J. Mater. Chem. A 2018, 6, 11463–11470. [Google Scholar] [CrossRef]
- Xue, W.; Yang, Y.; Yang, Q.; Liu, Y.; Wang, L.; Chen, C.; Cheng, R. The effect of sintering process on lithium ionic conductivity of Li6.4Al0.2La3Zr2O12 garnet produced by solid-state synthesis. RSC Adv. 2018, 8, 13083–13088. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Song, Z.; Xiu, T.; Badding, M.E.; Wen, Z. Sintering, micro-structure and Li+ conductivity of Li7−xLa3Zr2-xNbxO12/MgO (x = 0.2−0.7) Li-Garnet composite ceramics. Ceram. Int. 2019, 45, 56–63. [Google Scholar] [CrossRef]
- Yang, T.; Li, Y.; Wu, W.; Cao, Z.; He, W.; Gao, Y.; Liu, J.; Li, G. The synergistic effect of dual substitution of Al and Sb on structure and ionic conductivity of Li7La3Zr2O12 ceramic. Ceram. Int. 2018, 44, 1538–1544. [Google Scholar] [CrossRef]
- Xiang, X.; Chen, F.; Shen, Q.; Zhang, L.; Chen, C. Effect of the lithium ion concentration on the lithium ion conductivity of Ga-doped LLZO. Mater. Res. Express 2019, 6, 085546. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, Y.; Hu, Q.; Cao, S.; Song, S.; Lu, X.; Shen, Q. S/MWCNt/LLZO Composite Electrode with e-/S/Li+ Conductive Network for All-Solid-State Lithium–Sulfur Batteries. J. Solid State Chem. 2021, 301, 122341. [Google Scholar] [CrossRef]
- Goswami, N.; Indu, M.S.; Murugan, R.; Kant, R. Experimental corroboration of theory for impedance response of solid electrolytes: Doped cubic garnet LLZO. J. Electroanal. Chem. 2021, 897, 115611. [Google Scholar] [CrossRef]
- Aravinth, K.; Ramasamy, P.; Sen, S.; Arumugam, R. Tunable photoluminescence properties of Dy3+ doped LLZO phosphors for WLED and dosimetry applications. Ceram. Int. 2021, 48, 1402–1407. [Google Scholar]
- Samui, P.; Modi, K.B.; Phapale, S.; Parida, S.C.; Mishra, R. Calorimetric investigations on lithium based ceramics. J. Chem. Thermodyn. 2021, 163, 106590. [Google Scholar] [CrossRef]
- Wyers, G.P.; Cordfunke, E.H.P.; Ouweltjes, W. The standard molar enthalpies of formation of the lithium zirconates. J. Chem. Thermodyn. 1989, 21, 1095–1100. [Google Scholar] [CrossRef]
- Bolech, M.; Cordfunke, E.H.P.; van Genderen, A.C.G.; van Der Laan, R.R.; Janssen, F.J.J.G.; Van Miltenburg, J.C. The heat capacity and derived thermodynamic functions of La2Zr2O7 and Ce2Zr2O7 from 4 to 1000 K. J. Phys. Chem. Solids 1997, 58, 433–439. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Navrotsky, A.; Venkatraman, S.; Manthiram, A. Enthalpy of Formation of LixCoO2 (0.5 ≤ x ≤ 1.0). J. Electrochem. Soc. 2005, 152, J82. [Google Scholar] [CrossRef]
- Huntelaar, M.E.; Booij, A.S.; Cordfunke, E.H.P. The standard molar enthalpies of formation of BaZrO3 (s) and SrZrO3 (s). J. Chem. Thermodyn. 1994, 26, 1095–1101. [Google Scholar] [CrossRef]
- Glushko, V.P.; Gurvich, L.V.; Bergman, G.A.; Veits, I.V.; Medvedev, V.A.; Khachkuruzov, G.A.; Yungman, V.S. Thermodinamicheskie Svoitsva Individual’nykh Veshchestv; Nauka: Moscow, Russia, 1978. [Google Scholar]
- Millard, E.B. Physical Chemistry for Colleges; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1921; ISBN-10: 1146961987. [Google Scholar]
- Pankratz, L.B. Thermodynamic Properties of Carbides, Nitrides, and Other Selected Substances; Bureau of Mines: Washington, DC, USA, 1995; ISBN-10: 9995679329. [Google Scholar]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 86th ed.; 2005–2006; CRC Press: Boca Raton, FL, USA, 2005; pp. 4–70. ISBN 0849304865 9780849304866. [Google Scholar]
- Samsonov, G.V. The Oxide Handbook; Springer: Boston, MA, USA, 1973; ISBN 978-1-4615-9597-7. [Google Scholar] [CrossRef]
- Awaka, J.; Kijima, N.; Hayakawa, H.; Akimoto, J. Synthesis and structure analysis of tetragonal Li7La3Zr2O12 with the garnet-related type structure. J. Solid State Chem. 2009, 182, 2046–2052. [Google Scholar] [CrossRef]
- Morachevskiy, A.G.; Sladkov, I.B.; Firsova, Y.G. Termodinamicheskiye Raschety v Khimii i Metallurgii; Lan’: St. Petersburg, Russia, 2018; ISBN 978-5-8114-3023-9. [Google Scholar]
- Il’ina, E.A.; Raskovalov, A.A.; Reznitskikh, O.G. Thermodynamic properties of solid electrolyte Li7La3Zr2O12. J. Chem. Thermodyn. 2019, 128, 68–73. [Google Scholar] [CrossRef]




| Element | Mass, wt.% |
|---|---|
| Lanthanum | 53.19 |
| Oxygen | 22.59 |
| Zirconium | 24.22 |
| Compound | Molar Mass, g·mol−1 | Specific Enthalpy, J·g−1 | Molar Enthalpy of Dissolution, kJ·mol−1 | Ref. |
|---|---|---|---|---|
| ZrO2 | 123.222 | −2186 ± 19 | −269.4 ± 2.34 | this work |
| La2O3 | 325.837 | −1927 ± 13 | −627.9 ± 4.23 | this work |
| Li2CO3 | 73.89 | −683 ± 9 | −50.5 ± 0.67 | this work |
| Li7La3Zr2O12 (with La2O3 impurity) | - | −1758 ± 34 | - | this work |
| Li7La3Zr2O12 | 839.741 | −1752.6 ± 35 | −1471.73 ± 29.39 | this work (recalculated) |
| Compound | ΔoxH°298.15, kJ·mol−1 | Reference |
|---|---|---|
| Li7La3Zr2O12 (s) | −186.4 ± 7.3 | this work |
| Li2ZrO3 (s) | −304.1 ± 1.4 | [48] |
| Li6Zr2O7 (s) | −112.86 | [49] |
| La2Zr2O7 (s) | −135.6 | [50] |
| Li2TiO3 (s) | −238.5 ± 1.5 | [48] |
| LiAlO2 (s) | −209.0 ± 3.2 | [4] |
| LiCoO2 (s) | −143.99 ± 1.38 | [51] |
| BaZrO3 (s) | −114.6 | [52] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aleksandrov, D.; Novikov, P.; Popovich, A.; Wang, Q. Superionic Solid Electrolyte Li7La3Zr2O12 Synthesis and Thermodynamics for Application in All-Solid-State Lithium-Ion Batteries. Materials 2022, 15, 281. https://doi.org/10.3390/ma15010281
Aleksandrov D, Novikov P, Popovich A, Wang Q. Superionic Solid Electrolyte Li7La3Zr2O12 Synthesis and Thermodynamics for Application in All-Solid-State Lithium-Ion Batteries. Materials. 2022; 15(1):281. https://doi.org/10.3390/ma15010281
Chicago/Turabian StyleAleksandrov, Daniil, Pavel Novikov, Anatoliy Popovich, and Qingsheng Wang. 2022. "Superionic Solid Electrolyte Li7La3Zr2O12 Synthesis and Thermodynamics for Application in All-Solid-State Lithium-Ion Batteries" Materials 15, no. 1: 281. https://doi.org/10.3390/ma15010281
APA StyleAleksandrov, D., Novikov, P., Popovich, A., & Wang, Q. (2022). Superionic Solid Electrolyte Li7La3Zr2O12 Synthesis and Thermodynamics for Application in All-Solid-State Lithium-Ion Batteries. Materials, 15(1), 281. https://doi.org/10.3390/ma15010281






