Spectral and Angular Characteristics of the High-Contrast Dielectric Grating under the Resonant Interaction of a Plane Wave and a Gaussian Beam
Abstract
:1. Introduction
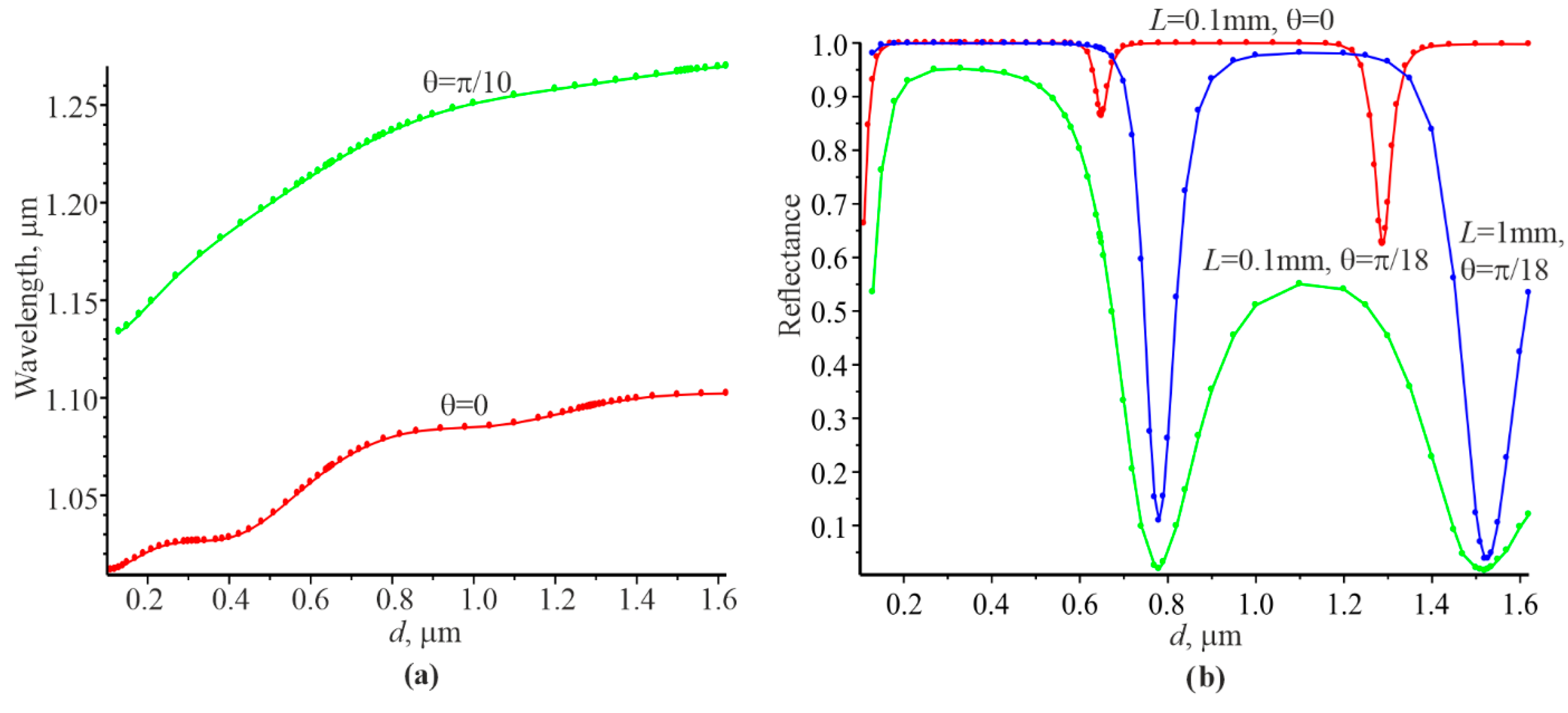
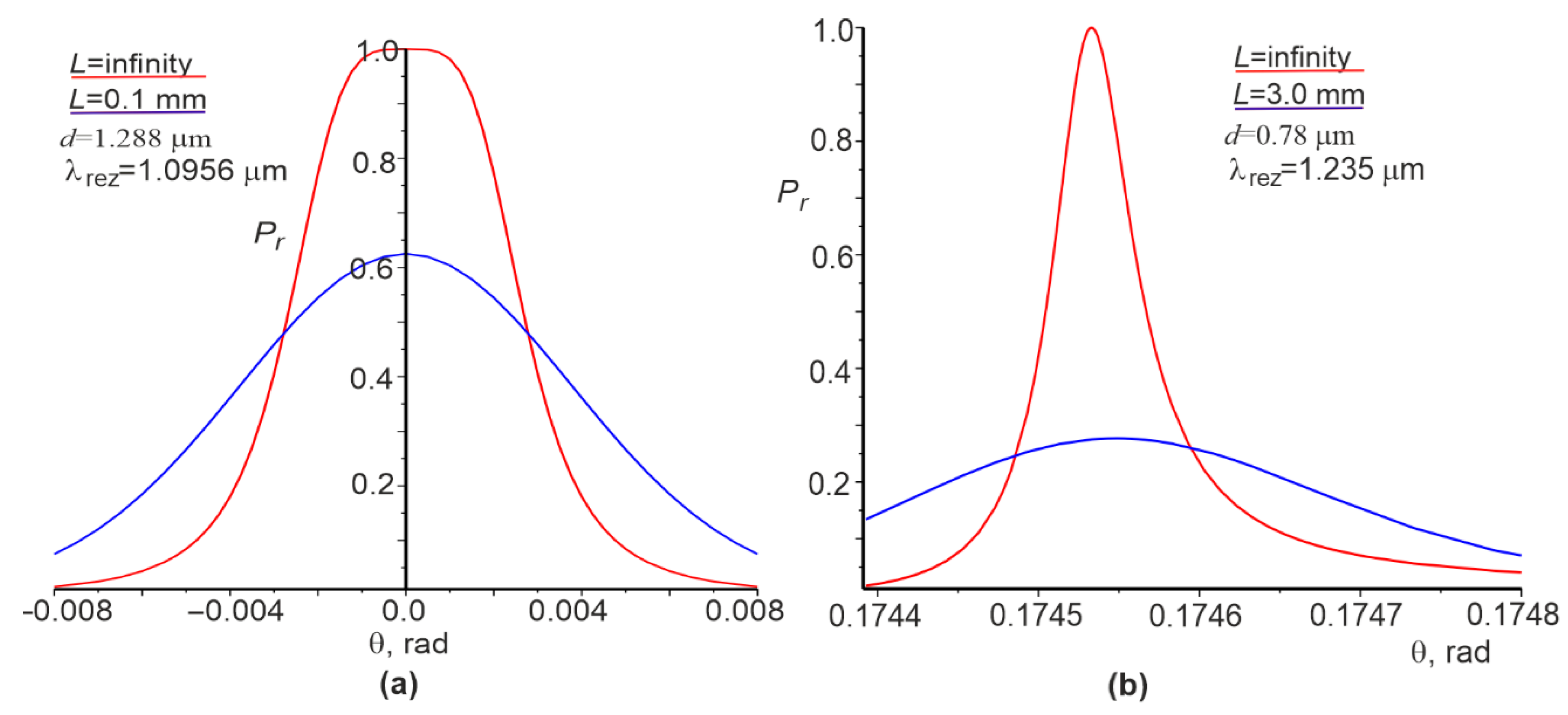
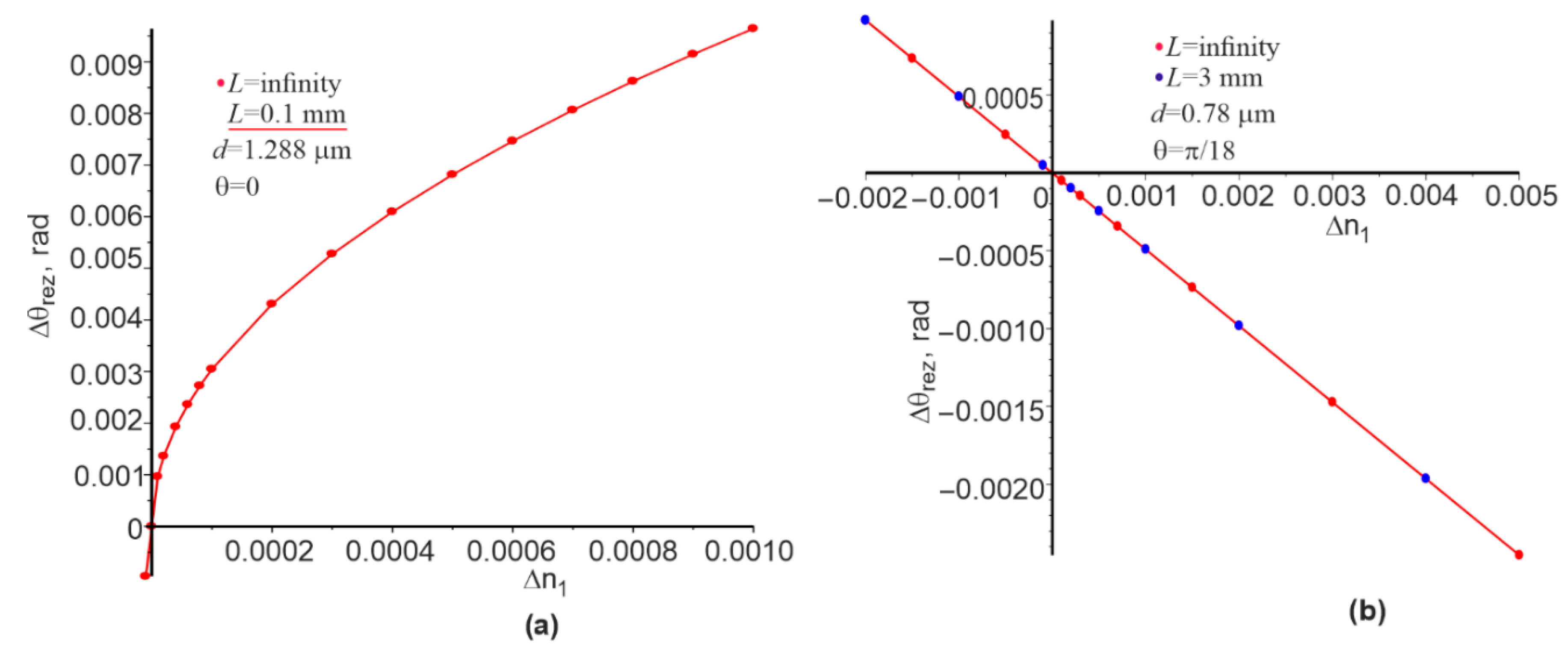
2. Results of Numerical Modeling and Discussions
3. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.-K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]
- Smirnova, T.; Fitio, V.; Sakhno, O.; Yezhov, P.; Bendziak, A.; Hryn, V.; Bellucci, S. Resonant and Sensing Performance of Volume Waveguide Structures Based on Polymer Nanomaterials. Nanomaterials 2020, 10, 2114. [Google Scholar] [CrossRef] [PubMed]
- Quaranta, G.; Basset, G.; Martin, O.J.F.; Gallinet, B. Recent Advances in Resonant Waveguide Gratings. Laser Photonics Rev. 2018, 12, 1800017. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, B.; Guo, Z.; Wu, X. Guided Mode Resonance Sensors with Optimized Figure of Merit. Nanomaterials 2019, 9, 837. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.S.; Magnusson, R. Theory and applications of guided-mode resonance filters. Appl. Opt. 1993, 32, 2606–2613. [Google Scholar] [CrossRef]
- Magnusson, R.; Ko, Y.H. Guided-Mode Resonance Nanophotonics: Fundamentals and Applications. In Nanoengineering: Fabrication, Properties, Optics, and Devices XIII; SPIE: Bellingham, WA, USA, 2016; Volume 9927, p. 992702. [Google Scholar]
- Norton, S.M.; Morris, G.M.; Erdogan, T. Experimental investigation of resonant-grating filter lineshapes in comparison with theoretical models. J. Opt. Soc. Am. A 1998, 15, 464–472. [Google Scholar] [CrossRef]
- Destouches, N.; Pommier, J.-C.; Parriaux, O.; Clausnitzer, T.; Lyndin, N.; Tonchev, S. Narrow band resonant grating of 100% reflection under normal incidence. Opt. Express 2006, 14, 12613. [Google Scholar] [CrossRef] [Green Version]
- Tamulevičius, T.; Šeperys, R.; Andrulevičius, M.; Tamulevičius, S. Total internal reflection based sub-wavelength grating sensor for the determination of refractive index of liquids. Photonics Nanostruct. Fundam. Appl. 2011, 9, 140–148. [Google Scholar] [CrossRef]
- Anderson, B.B.; Brodsky, A.M.; Burgess, L.W. Threshold effects in light scattering from a binary diffraction grating. Phys. Rev. E 1996, 54, 912–923. [Google Scholar] [CrossRef]
- Bellucci, S.; Fitio, V.M.; Yaremchuk, I.; Vernyhor, O.; Bendziak, A.; Bobitski, Y. Comparison of the Optical Planar Waveguide Sensors’ Characteristics Based on Guided-Mode Resonance. Symmetry 2020, 12, 1315. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of grating diffraction—E-mode polarization and losses. J. Opt. Soc. Am. 1983, 73, 451–455. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K.; Grann, E.B.; Pommet, D.A. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J. Opt. Soc. Am. A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- Li, L. Formulation and comparison of two recursive matrix algorithms for modeling layered diffraction gratings. J. Opt. Soc. Am. A 1996, 13, 1024–1035. [Google Scholar] [CrossRef] [Green Version]
- Yaremchuk, I.; Tamulevičius, T.; Fitio, V.; Gražulevičiūte, I.; Bobitski, Y.; Tamulevičius, S. Numerical implementation of the S-matrix algorithm for modeling of relief diffraction gratings. J. Mod. Opt. 2013, 60, 1781–1788. [Google Scholar] [CrossRef]
- Fitio, V.M.; Sakhno, O.V.; Smirnova, T.N. Analysis of the diffraction by the gratings generated in the materials with a nonlinear response. Optik 2008, 119, 236–246. [Google Scholar] [CrossRef]
- Fitio, V.M. Transmissions of Metallic Gratings with Narrow Slots. In Proceedings of the 2006 International Workshop on Laser and Fiber-Optical Networks Modeling, Kharkiv, Ukraine, 29 June–1 July 2006; Volume 4018, pp. 113–116. [Google Scholar] [CrossRef]
- Dansas, P.; Paraire, N. Fast modeling of fotonic bandgap structures by use of diffraction-grating approach. J. Opt. Soc. Am. A 1998, 15, 1586–1597. [Google Scholar] [CrossRef]
- Yaremchuk, I.; Tamulevičius, T.; Fitio, V.; Gražulevičiute, I.; Bobitski, Y.B.; Tamulevičius, S. Guide-mode resonance characteristics of periodic structure on base of diamond-like carbon film. Opt. Commun. 2013, 301–302, 1–6. [Google Scholar] [CrossRef]
- Fitio, V.; Bendziak, A.; Yezhov, P.; Hryn, V.; Sakhno, O.; Smirnova, T. Diffraction of a finite-cross-section light beam by the grating: Theoretical analysis and experimental verification. Opt. Int. J. Light Electron Opt. 2022, 252, 168550–168562. [Google Scholar] [CrossRef]
- Wu, S.-D.; Glytsis, E.N. Finite-number-of-periods holographic gratings with finite-width incident beams: Analysis using the finite-difference frequency-domain method. J. Opt. Soc. Am. A 2002, 19, 2018–2029. [Google Scholar] [CrossRef]
- Bendickson, J.M.; Glytsis, E.N.; Gaylord, T.K.; Brundrett, D.L. Guided-mode resonant subwavelength gratings: Effects of finite beams and finite gratings. J. Opt. Soc. Am. A 2001, 18, 1912–1928. [Google Scholar] [CrossRef]
- Harvey, J.E.; Nevis, E.A. Angular grating anomalies: Effects of finite beam size on wide-angle diffraction phenomena. Appl. Opt. 1992, 31, 6783–6788. [Google Scholar] [CrossRef] [PubMed]
- Ren, F.; Kim, K.-Y.; Chong, X.; Wang, A.X. Effect of finite metallic grating size on Rayleigh anomaly-surface plasmon polariton resonances. Opt. Express 2015, 23, 28868–28873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niederer, G.; Herzig, H.P.; Shamir, J.; Thiele, H.; Schnieper, M.; Zschokke, C. Tunable, oblique incidence resonant grating filter for telecommunications. Appl. Opt. 2004, 43, 1683–1694. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Tamir, T. Spatial modifications of Gaussian beams diffracted by reflection gratings. J. Opt. Soc. Am. A 1989, 6, 1368–1381. [Google Scholar] [CrossRef]
- Tao, S.; Wang, B.; Burr, G.W.; Chen, J. Diffraction efficiency of volume gratings with finite size: Corrected analytical solution. J. Mod. Opt. 2004, 51, 1115–1122. [Google Scholar] [CrossRef]
- Loktev, S.M.; Lyndin, N.M.; Parriaux, O.; Sychugov, V.A.; Tishchenko, A.V. Reflection of a finite light beam from a finite waveguide grating. Quantum Electron. 1997, 27, 445–449. [Google Scholar] [CrossRef]
- Pisarenco, M.; Setija, I.D. On the complexity of aperiodic Fourier modal methods for finite periodic structures. J. Comput. Phys. 2014, 261, 130–144. [Google Scholar] [CrossRef]
- Guizal, B.; Barchiesi, D.; Felbacq, D. Electromagnetic beam diffraction by a finite lamellar structure: An aperiodic coupled-wave method. J. Opt. Soc. Am. A 2003, 20, 2274–2280. [Google Scholar] [CrossRef]
- Lalanne, P.; Silberstein, E. Fourier-modal methods applied to waveguide computational problems. Opt. Lett. 2000, 25, 1092–1094. [Google Scholar] [CrossRef]
- Lecamp, G.; Hugonin, J.P.; Lalanne, P. Theoretical and computational concepts for periodic optical waveguides. Opt. Express 2007, 15, 11042–11060. [Google Scholar] [CrossRef]
- Avrutsky, I.A.; Sychugov, V.A. Reflection of a beam of finite size from a corrugated waveguide. J. Mod. Opt. 1989, 36, 1527–1539. [Google Scholar] [CrossRef]
- Fitio, V.; Yaremchuk, I.; Bendziak, A.; Marchewka, M.; Bobitski, Y. Diffraction of a Gaussian Beam with Limited cross Section by a Volume Phase Grating under Waveguide Mode Resonance. Materials 2021, 14, 2252. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill Book Company: San Francisco, CA, USA, 1967. [Google Scholar]
- Whittaker, E.T. On the functions which are represented by the expansions of the interpolation-theory. Proc. R. Soc. Sect. A Math. 1915, 35, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. Communication in the presence of noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Russell, P.S.J. Power conservation and field structures in uniform dielectric gratings. J. Opt. Soc. Am. A 1984, 1, 293–299. [Google Scholar] [CrossRef]
- Lu, H.; Huang, M.; Kang, X.B.; Liu, W.X.; Dong, C.; Zhang, J.; Xia, S.Q.; Zhang, X.Z. Improving the sensitivity of compound waveguide grating biosensor via modulated wavevector. Appl. Phys. Express 2018, 11, 082202. [Google Scholar] [CrossRef]
- Bellucci, S.; Fitio, V.; Yaremchuk, I.; Vernyhor, O.; Bobitski, Y. Features of the Resonance in a Rectangular Dielectric Surace-Relief Gratings Illuminated with a Limited Cross Section Gaussian Beam. Nanomaterials 2022, 12, 72. [Google Scholar] [CrossRef]
- Meade, R.D.; Winn, J.N.; Joannopoulos, J. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Yaremchuk, Y.; Fitio, V.; Bobitski, Y. Prediction of a region with high transmission (reflectance) for bandpass interferential filters by using the method of pointer function. Semicond. Phys. Quantum Electron. Optoelectron. 2008, 11, 50–53. [Google Scholar] [CrossRef]



| Parameters | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | 0.78 | 1.23496 | 0.037 | - | 0.0624 | 291 | 7865 | 0.491 | 7869 | ||
| 2 | 0.78 | 1.23496 | 0.186 | 0.1540 | 0.321 | 291 | 1556 | 0.491 | 1544 | 3.0 | |
| 3 | 1.52 | 1.26754 | 0.01186 | - | 0.01944 | 300.1 | 25,304 | 0.492 | 25,309 | ||
| 4 | 1.52 | 1.26754 | 0.0595 | 0.04709 | 0.09763 | 300.1 | 5044 | 0.492 | 5039 | 10 | |
| 5 | 1.288 | 0.0 | 1.09557 | 0.071 | - | 0.00543 | 456 | 6423 | - | - | |
| 6 | 1.288 | 0.0 | 1.09557 | 0.101 | 11.059 | 0.0090 | 456 | 4515 | - | - | 0.1 |
| 7 | 0.65 | 0.0 | 1.06449 | 0.24 | - | - | 405 | 1688 | - | - | |
| 8 | 0.65 | 0.0 | 1.06449 | 0.28 | 22.07 | - | 405 | 1446 | - | - | |
| 9 | 1.0 | 0.0 | 1.08490 | 11.5 | - | - | 480 | 41.7 | - | - | |
| 10 | 1.0 | 0.0 | 1.08490 | 11.5 | - | - | 480 | 41.7 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellucci, S.; Fitio, V.; Smirnova, T.; Yaremchuk, I.; Vernyhor, O.; Bobitski, Y. Spectral and Angular Characteristics of the High-Contrast Dielectric Grating under the Resonant Interaction of a Plane Wave and a Gaussian Beam. Materials 2022, 15, 3529. https://doi.org/10.3390/ma15103529
Bellucci S, Fitio V, Smirnova T, Yaremchuk I, Vernyhor O, Bobitski Y. Spectral and Angular Characteristics of the High-Contrast Dielectric Grating under the Resonant Interaction of a Plane Wave and a Gaussian Beam. Materials. 2022; 15(10):3529. https://doi.org/10.3390/ma15103529
Chicago/Turabian StyleBellucci, Stefano, Volodymyr Fitio, Tatiana Smirnova, Iryna Yaremchuk, Oleksandr Vernyhor, and Yaroslav Bobitski. 2022. "Spectral and Angular Characteristics of the High-Contrast Dielectric Grating under the Resonant Interaction of a Plane Wave and a Gaussian Beam" Materials 15, no. 10: 3529. https://doi.org/10.3390/ma15103529






