Numerical Study on the Laser Annealing of Silicon Used in Advanced V-NAND Device
Abstract
:1. Introduction
2. Development of a Numerical Model
2.1. Model Geometry and Process Conditions
2.2. Governing Equation and Boundary and Initial Conditions
2.3. Material Properties
3. Results and Discussion
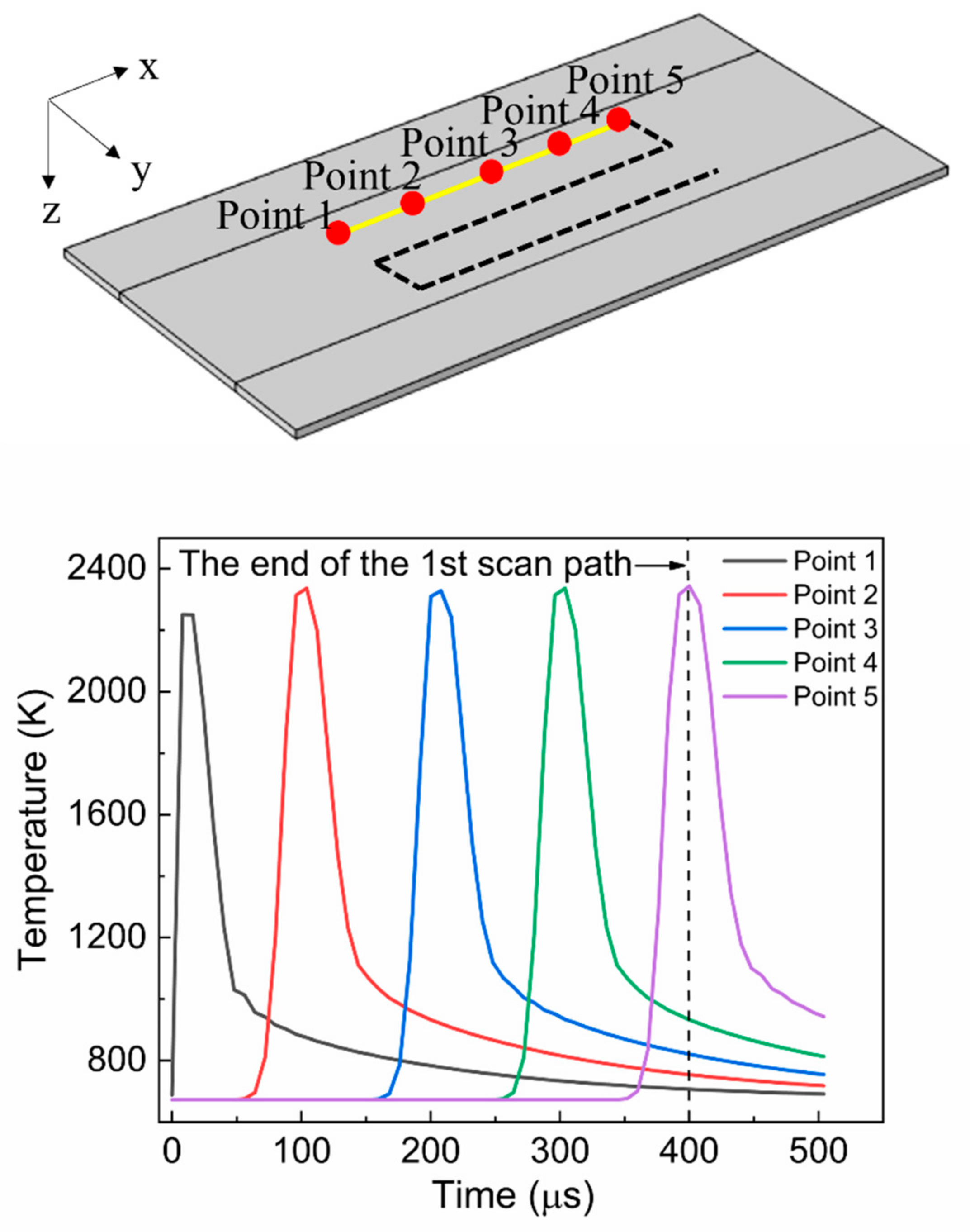
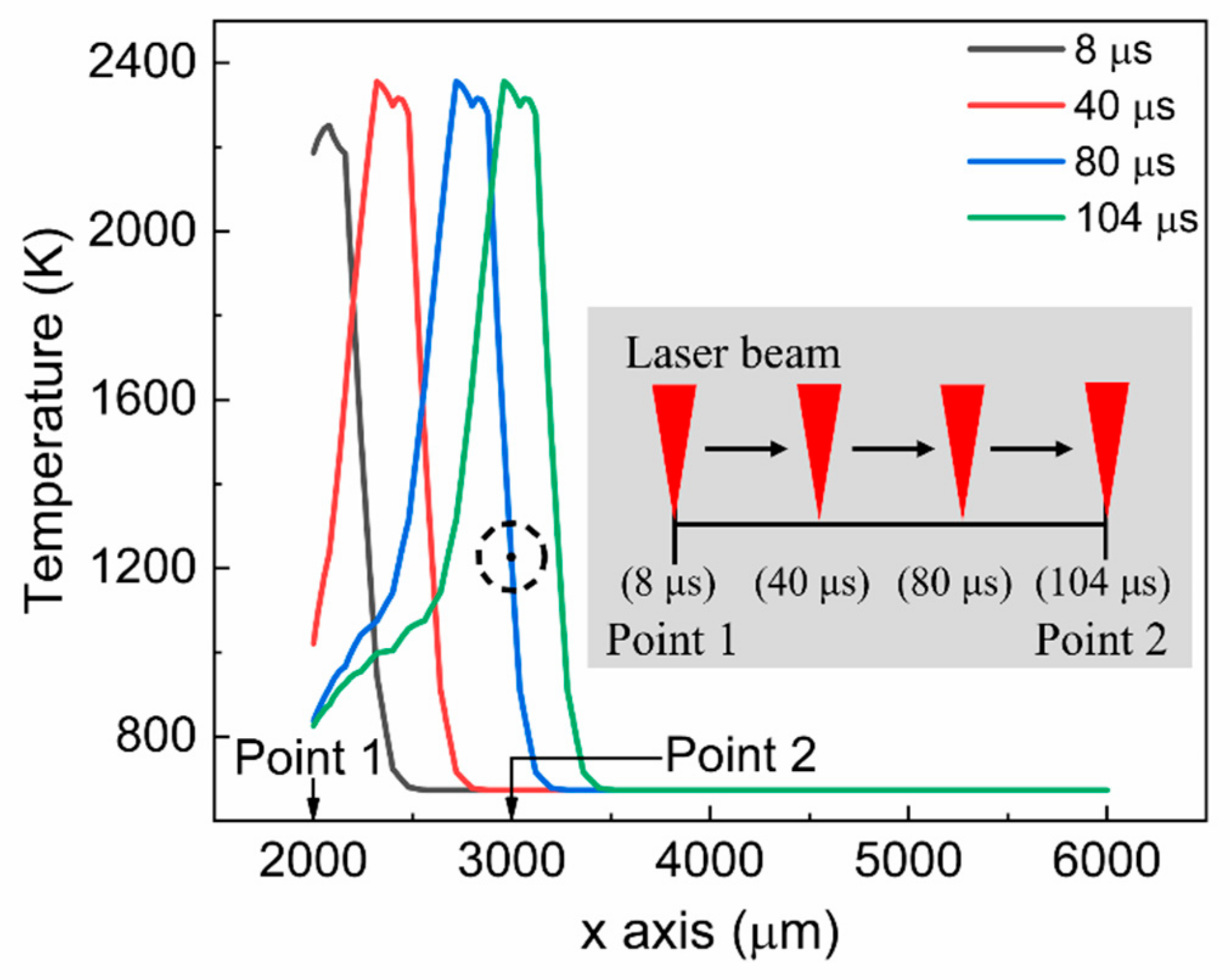
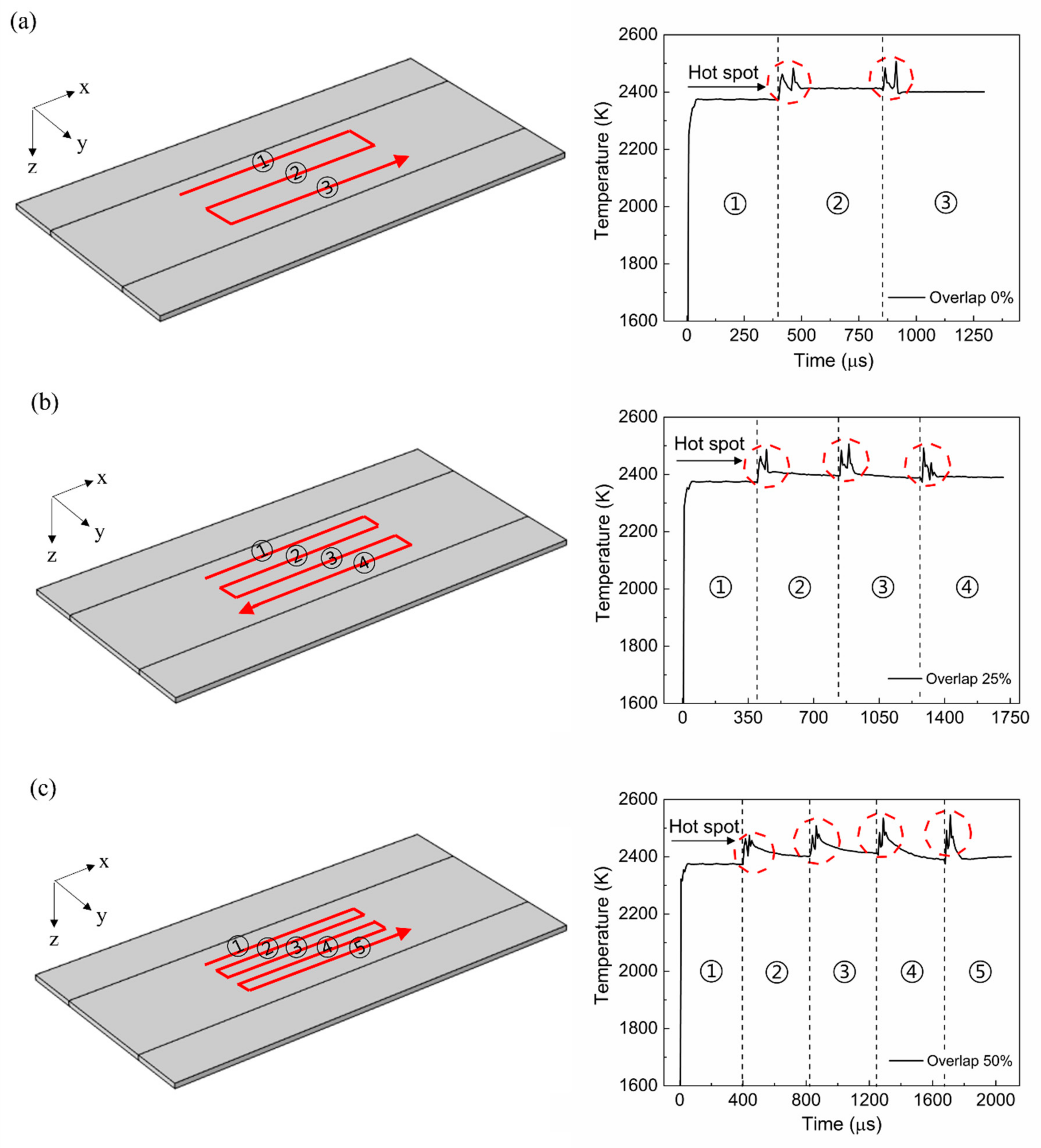
3.1. Temporal Profile of the Surface Temperature
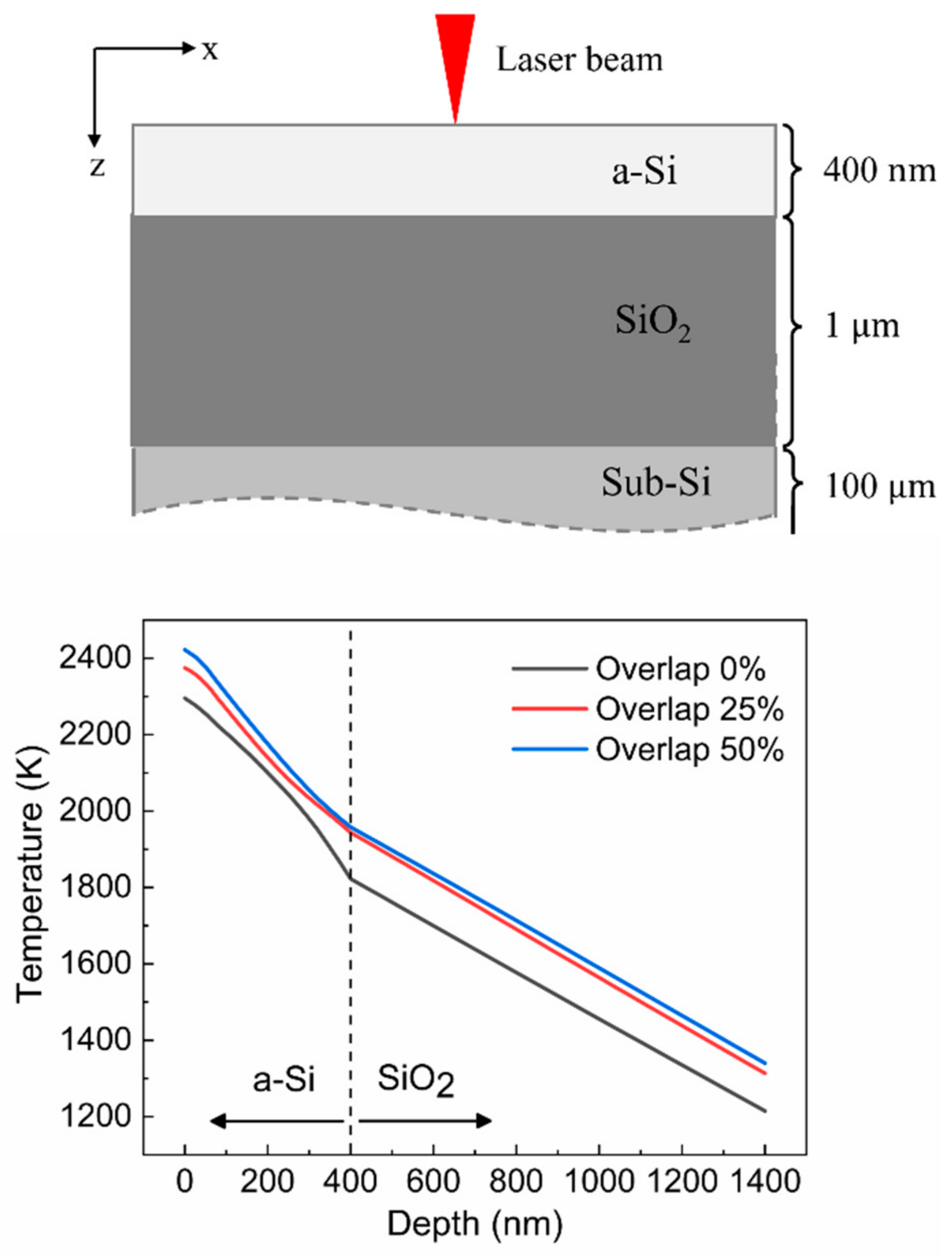
3.2. Temperature Distribution in the Depth Direction
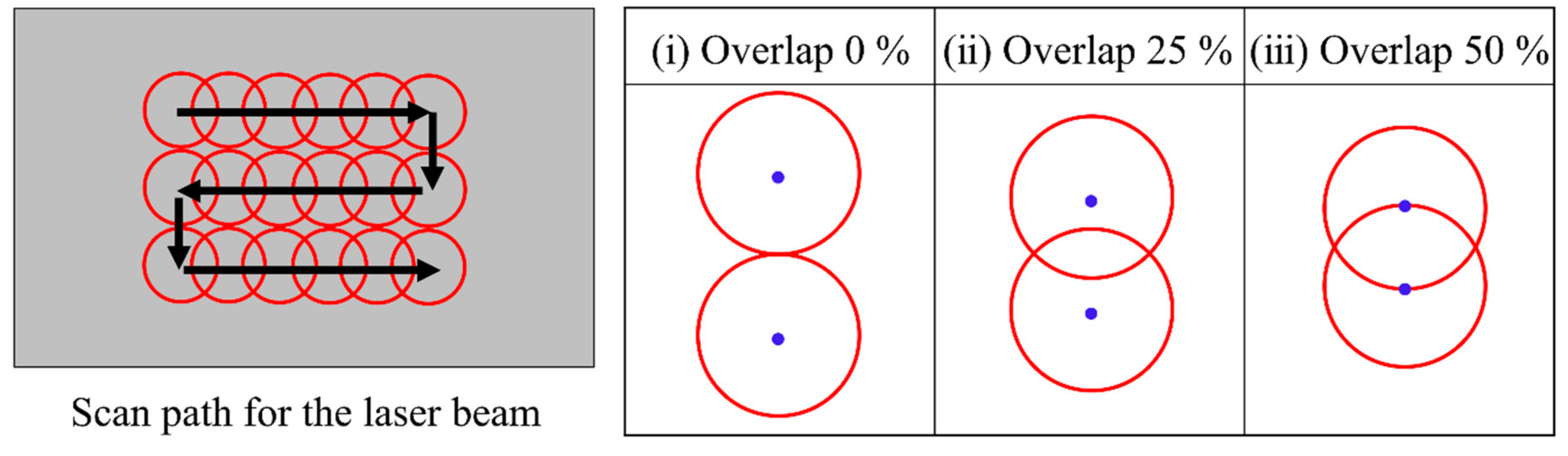
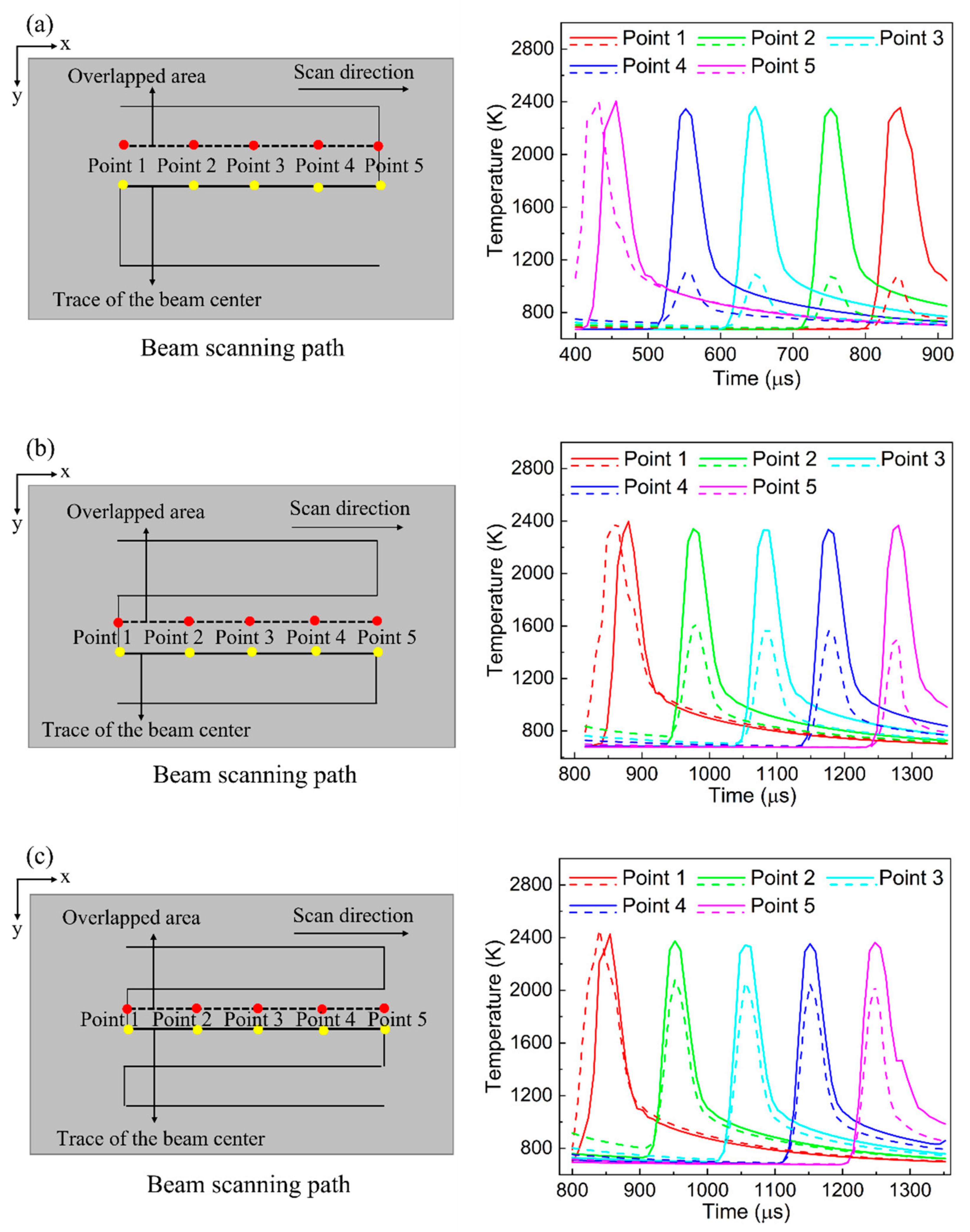
3.3. Analysis of the Temperature Uniformity with Different Overlap Ratios
3.4. Analysis of Melt Duration
4. Conclusions
- (1)
- The annealed surface was subjected to rapid heating and cooling. The heating and cooling rates after temperature stabilization were 4.7 × 107 K/s and 2.04 ×107 K/s, respectively.
- (2)
- The surface temperature gradually increased with time and beam overlap ratio because of the preheating effect and greater heat accumulation per unit area. More heat accumulation per unit area also induced hot spots at every corner of the scanning path.
- (3)
- Under the process conditions used in the simulation, the entire a-Si area was completely melted. The temperatures (1822–1958 K) at the interface between a-Si and SiO2 were lower than the melting point (1983 K) of SiO2. Thus, the SiO2 layer remained sufficiently solid to support the melted Si at the top
- (4)
- The temperature uniformity in the annealed area was considerably improved via beam overlapping. It was also found that the melt duration of the annealed a-Si increased with an increase in the overlap ratio. This indicated that a considerable increase in grain size could be achieved using beam overlapping.
- (5)
- In present study, the experimental work to validate the numerical model was not conducted, and this is the weakness of this study. As a future study, we are planning to develop a relevant validation method for our numerical model (i.e., the measurement of surface reflectivity or grain size for molten Si layer).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Masuoka, F.; Momodomi, M.; Iwata, Y.; Shirota, R. New ultra high density eprom and flash eeprom with nand structure cell. In Proceedings of the 1987 International Electron Devices Meeting, Washington, DC, USA, 6–9 December 1987; pp. 552–555. [Google Scholar] [CrossRef]
- Jang, J.; Kim, H.; Cho, W.; Cho, H.; Kim, J.; Shim, S.; Jang, Y.; Jeong, J.; Son, B.; Kim, D.; et al. Vertical cell array using TCAT (Terabit Cell Array Transistor) technology for ultra high density NAND flash memory. In Proceedings of the 2009 Symposium on VLSI Technology, Kyoto, Japan, 16–18 June 2009; pp. 192–193. [Google Scholar]
- Katsumata, R.; Kito, M.; Fukuzumi, Y.; Kido, M.; Tanaka, H.; Komori, Y.; Ishiduki, M.; Matsunami, J.; Fujiwara, T.; Nagata, Y.; et al. Pipe-shaped BiCS flash memory with 16 stacked layers and multi-level-cell operation for ultra high density storage devices. In Proceedings of the 2009 Symposium on VLSI Technology, Kyoto, Japan, 15–17 June 2009; pp. 136–137. [Google Scholar]
- Yun, J.G.; Kim, G.R.; Lee, J.E.; Kim, Y.; Shim, W.B.; Lee, J.H.; Shin, H.C.; Lee, J.D.; Park, B.G. Single-crystalline Si STacked ARray (STAR) NAND flash memory. IEEE Trans. Electron. Devices 2011, 58, 1006–1014. [Google Scholar]
- Parat, K.; Dennison, C. A Floating Gate Based 3D NAND Technology with CMOS Under Array. In Proceedings of the 2015 IEEE International Electron Devices Meeting, Washington, DC, USA, 4–5 June 2015; pp. 48–51. [Google Scholar] [CrossRef]
- Yoon, K.J.; Kim, Y.M.; Hwang, C.S. What Will Come After V-NAND Vertical Resistive Switching Memory. Adv. Electron. Mater. 2019, 5, 1800914. [Google Scholar] [CrossRef]
- Lerch, W.; Paul, S.; Niess, J.; McCoy, S.; Selinger, T.; Gelpey, J.; Cristiano, F.; Severac, F.; Gavelle, M.; Boninelli, S.; et al. Advanced activation of ultra-shallow junctions using flash assisted RTP. Mater. Sci. Eng. B 2005, 124, 24–31. [Google Scholar] [CrossRef]
- Kakkad, R.; Smith, J.; Lau, W.; Fonash, S. Crystallized Si films by low temperature rapid thermal annealing of amorphous silicon. J. Appl. Phys. 1989, 65, 2069–2072. [Google Scholar] [CrossRef] [Green Version]
- Pecz, B.; Dobos, L.; Panknin, D.; Skorupa, W.; Lioutas, C.; Vouroutzis, N. Crystallization of amorphous Si films by flash lamp annealing. Appl. Surf. Sci. 2005, 242, 185–191. [Google Scholar] [CrossRef]
- Ohdaira, K.; Fujiwara, T.; Endo, Y.; Nishizaki, S.; Matsumura, H. Explosive crystallization of amorphous silicon films by flash lamp annealing. J. Appl. Phys. 2009, 106, 044907. [Google Scholar] [CrossRef]
- Li, X.; Deng, J.; Ge, D.; Yue, H. Rapid crystallization of electrohydrodynamically atomized ZrO2 thin films by laser annealing. Appl. Surf. Sci. 2020, 510, 145510. [Google Scholar] [CrossRef]
- Zhechao, F.; Hongwei, F. Study on selective laser melting and heat treatment of Ti-6Al-4V alloy. Results Phys. 2018, 10, 660–664. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, H.; Liu, Y. Effect of laser surface remelting on the fatigue crack propagation rate of 40Cr steel. Results Phys. 2019, 12, 424–431. [Google Scholar] [CrossRef]
- Liu, B.; Li, B.Q.; Li, Z. Selective laser remelting of an additive layer manufacturing process on AlSi10Mg. Results Phys. 2019, 12, 982–988. [Google Scholar] [CrossRef]
- Shin, H.; Lee, M.; Ko, E.; Ryu, H.; Park, S.; Kim, E.; Ko, D. Dopant Activation of In Situ Phosphorus-Doped Silicon Using Multi-Pulse Nanosecond Laser Annealing. Phys. Status Solidi A 2020, 217, 1900988. [Google Scholar] [CrossRef]
- Tabata, T.; Karim, H.; Rozé, F.; Mazzamuto, F.; Sermage, B.; Kopalidis, P.; Roh, D. Dopant Redistribution and Activation in Ga Ion-Implanted High Ge Content SiGe by Explosive Crystallization during UV Nanosecond Pulsed Laser Annealing. ECS J. Solid State Sci. Technol. 2021, 10, 023005. [Google Scholar] [CrossRef]
- Kim, J.; Shin, I.; Park, T.; Kim, J.; Choi, S.; Lee, S.; Hong, S.; Lee, H.; Jung, Y.; Kim, T.; et al. Pt-dpoed Ni-silicide films formed by pulsed-laser annealing: Microstructural evolution and thermally robust Ni1-xPtxSi2 formation. J. Alloys Compd. 2019, 788, 1013–1020. [Google Scholar] [CrossRef]
- Park, M.; Vangelatos, Z.; Rho, Y.; Park, H.K.; Jang, J.; Grigoropoulos, C.P. Comprehensive analysis of blue diode laser annealing of amorphous silicon films. Thin Solid Film. 2020, 696, 137779. [Google Scholar] [CrossRef]
- Sakaike, K.; Higashi, S.; Murakami, H.; Miyazaki, S. Crystallization of amorphous Ge films induced by semiconductor diode laser annealing. Thin Solid Film. 2008, 516, 3595–3600. [Google Scholar] [CrossRef]
- Kim, C.H.; Song, I.H.; Nam, W.J.; Han, M.K. A Poly-Si TFT Fabricated by Excimer Laser Recrystallization on Floating Active Structure. IEEE Electron. Device. Lett. 2002, 23, 315–317. [Google Scholar] [CrossRef]
- Chowdhury, S.; Park, J.S.; Kim, J.M.; Kim, S.H.; Kim, Y.K.; Cho, E.C.; Cho, Y.H.; Yi, J.S. Crystallization of Amorphous Silicon via Excimer Laser Annealing and Evaluation of Its Passivation Properties. Energies 2020, 13, 3335. [Google Scholar] [CrossRef]
- Shih, C.J.; Fang, C.H.; Lu, C.C. Phase field modeling of excimer laser crystallization of thin silicon films on amorphous substrates. J. Appl. Phys. 2006, 100, 053504. [Google Scholar] [CrossRef]
- Theodorakos, I.; Zergioti, I.; Vamvakas, V.; Tsoukalas, D.; Raptis, Y.S. Picosecond and nanosecond laser annealing and simulation of amorphous silicon thin films for solar cell applications. J. Appl. Phys. 2014, 115, 043108. [Google Scholar] [CrossRef]
- Garcia, O.; Garcia-Ballesteros, J.J.; Munoz-Martin, D.; Nunez-Sanchez, S.; Morales, M.; Carabe, J.; Torres, I.; Gandia, J.J.; Molpeceres, C. Analysis of wavelength influence on a-Si crystallization processes with nanosecond laser sources. Appl. Surf. Sci. 2013, 278, 214–218. [Google Scholar] [CrossRef]
- Degorce, J.Y.; Gillet, J.N.; Magny, F.; Meunier, M. Three dimensional transient temperature field model for laser annealing. J. Appl. Phys. 2005, 97, 033520. [Google Scholar] [CrossRef] [Green Version]
- Said-Bacar, Z.; Leroy, Y.; Antoni, F.; Slaoui, A.; Fogarassy, E. Modeling of CW laser diode irradiation of amorphous silicon films. Appl. Surf. Sci. 2011, 257, 5127–5131. [Google Scholar] [CrossRef]
- Chang, C.H.; Chao, L.S. Modeling analysis of melting and solidifying processes in excimer laser crystallization of a-Si films with effective specific heat enthalpy method. Int. Heat. Mass Transf. 2008, 35, 571–576. [Google Scholar] [CrossRef]
- Yuan, Z.; Lou, Q.; Zhou, J.; Dong, J.; Wei, Y.; Wang, Z.; Zhao, H.; Wu, G. Numerical and experimental analysis on green laser crystallization of amorphous silicon thin films. Opt. Laser Technol. 2009, 41, 380–383. [Google Scholar] [CrossRef] [Green Version]
- Lowndes, D.H.; Wood, R.F.; Westbrook, R.D. Pulsed neodymium: Yttrium aluminum garnet laser (532 nm) melting of crystalline silicon: Experiment and theory. J. Appl. Phys. 1983, 43, 258. [Google Scholar] [CrossRef]
- Webber, H.C.; Cullis, A.G.; Chew, N.G. Computer simulation of high speed melting of amorphous silicon. Appl. Phys. Lett. 1983, 43, 669–671. [Google Scholar] [CrossRef]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead Publishing Limited: Cambridge, UK, 2002. [Google Scholar]
- Endo, R.K.; Fujihara, Y.; Susa, M. Calculation of density and heat capacity of silicon by molecular dynamics simulation. High Temp. High Press. 2003, 35, 505–511. [Google Scholar] [CrossRef] [Green Version]
- Rezek, B.; Nebel, C.E.; Stutzmann, M. Laser beam induced currents in polycrystalline silicon thin films prepared by interference laser crystallization. J. Appl. Phys. 2002, 91, 4220–4228. [Google Scholar] [CrossRef]
- Azuma, H.; Takeuchi, A.; Ito, T.; Fukushima, H.; Motohiro, T.; Yamaguchi, M. Pulsed KrF excimer laser annealing of silicon solar cell. Sol. Energy Mater. Sol. Cells 2002, 74, 289–294. [Google Scholar] [CrossRef]
- Hatano, M.; Moon, S.; Lee, M.; Suzuki, K.; Grigoropoulos, C.P. In Situ and ex situ diagnostics on melting and resolidification dynamics of amorphous and polycrystalline silicon thin films during excimer laser annealing. J. Non Cryst. Solids 2000, 266, 654–658. [Google Scholar] [CrossRef]
- Xu, X.; Grigoropoulos, C.P.; Russo, R.E. Nanosecond-time-resolution thermal emission measurement during pulsed excimer-laser interaction with materials. Appl. Phys. A 1996, 62, 51–59. [Google Scholar] [CrossRef]
- Miyasaka, M.; Stoemenos, J. Excimer laser annealing of amorphous and solid-phase-crystallized silicon films. J. Appl. Phys. 1999, 86, 5556–5565. [Google Scholar] [CrossRef]
- Im, J.S.; Kim, H.J.; Thompson, M.O. Phase transformation mechanisms involved in excimer laser crystallization of amorphous silicon films. Appl. Phys. Lett. 1993, 63, 1969. [Google Scholar] [CrossRef]
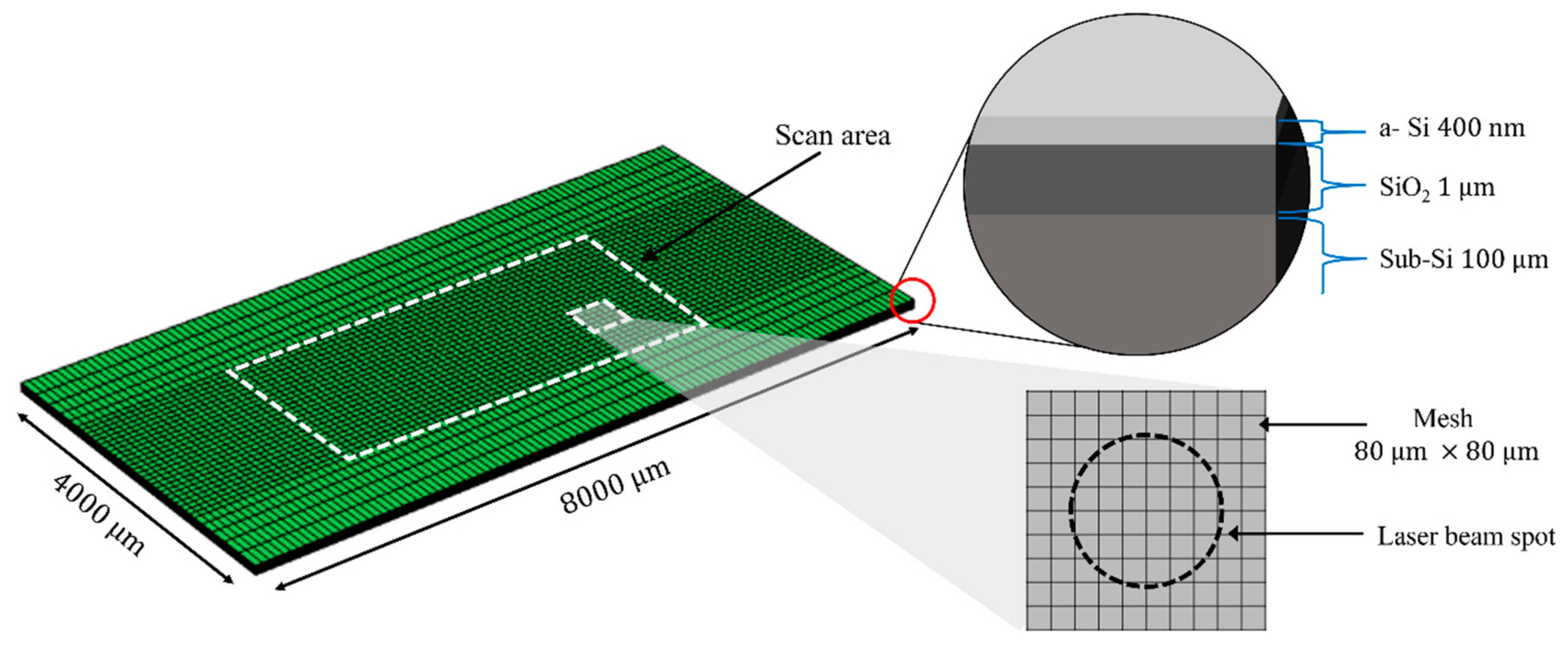

| Process Condition | Symbol | Unit | Value |
|---|---|---|---|
| Beam radius | 250 | ||
| Scan speed | 10 | ||
| Laser power | 300 | ||
| Average beam intensity |
| Constant | Unit | Value | Description |
|---|---|---|---|
| 2 | Convective heat transfer coefficient | ||
| – | 0.4 | Surface emissivity | |
| Stefan-Boltzmann constant |
| Property | Symbol | Unit | a-Si | SiO2 | Sub-Si |
|---|---|---|---|---|---|
| Melting temperature | K | 1440 | – | – | |
| Latent heat of fusion | [22] | – | – | ||
| Thermal conductivity | 1.3+ 1.3+ 1+ 1 for (298 < < ), 0.7 for (< < 2500) [30] | 1.4 | 34 | ||
| Specific heat | 852.28 + 0.08791− 0.0014751(1/) for (298 < < ), 852.28 + 0.08791− 0.0014751(1/) + g(T) for (< < + ), 968.22 for (+ < < 2500) [31,32] | 730 | 678 | ||
| Density | 2440–0.0544T for (298 < < 1000), 2524 for (1000 < < ) 2524–0.3487 (− 1683) for (< ) [32] | 2200 | 2320 | ||
| Absorption coefficient (at 532 nm) | for (298 < < ), for (< < 2500) [29,33] | – | – | ||
| Reflectivity (at 532 nm) | – | 0.4 for (298 < < ), 0.73 for (< < 2500) [33] | – | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, Y.-I.; Shin, J. Numerical Study on the Laser Annealing of Silicon Used in Advanced V-NAND Device. Materials 2022, 15, 4201. https://doi.org/10.3390/ma15124201
Son Y-I, Shin J. Numerical Study on the Laser Annealing of Silicon Used in Advanced V-NAND Device. Materials. 2022; 15(12):4201. https://doi.org/10.3390/ma15124201
Chicago/Turabian StyleSon, Yeong-Il, and Joonghan Shin. 2022. "Numerical Study on the Laser Annealing of Silicon Used in Advanced V-NAND Device" Materials 15, no. 12: 4201. https://doi.org/10.3390/ma15124201
APA StyleSon, Y.-I., & Shin, J. (2022). Numerical Study on the Laser Annealing of Silicon Used in Advanced V-NAND Device. Materials, 15(12), 4201. https://doi.org/10.3390/ma15124201







