Multi-Scale Crystal Plasticity Model of Creep Responses in Nickel-Based Superalloys
Abstract
:1. Introduction
2. Materials and Methods
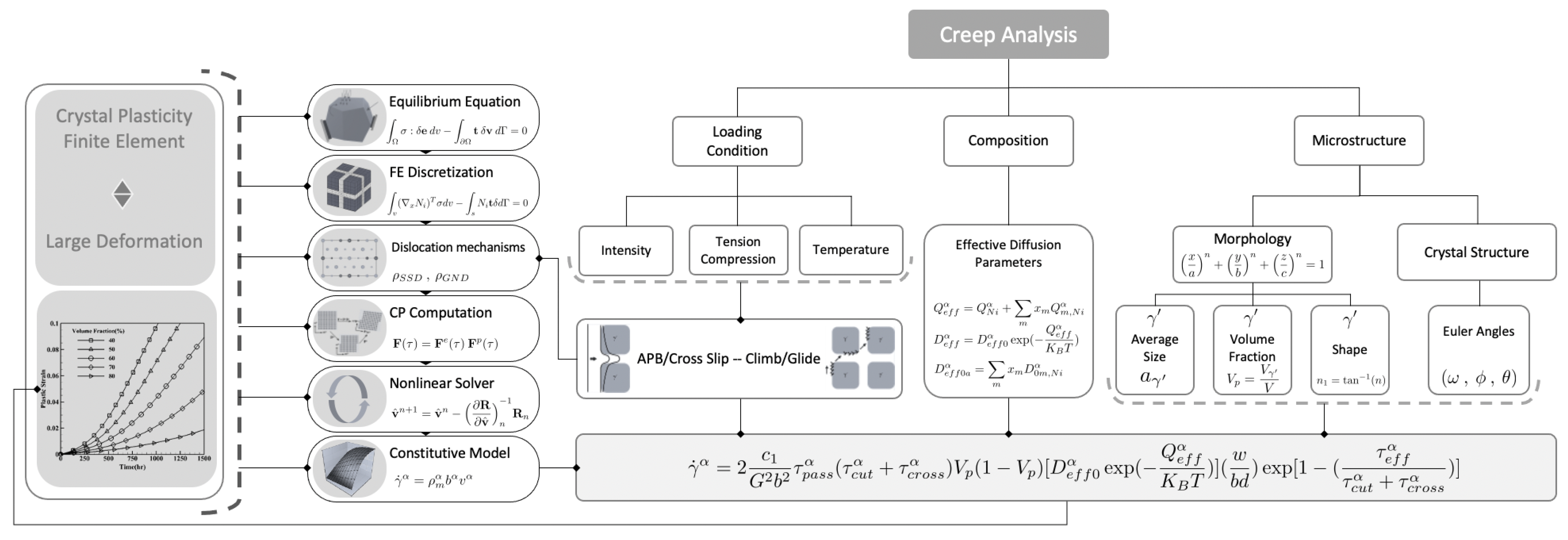
2.1. Plastic Deformation Kinematics
2.2. Entropic Kinetics and Constitutive Model at the Sub-Grain Scale
2.3. Constitutive Model at the Homogenized Scale
Calibration and Effective Parameters
3. Results and Discussions
3.1. Arithmetic Method to Calculate Diffusion Coefficients
3.2. Homogenized Constitutive Model Validations
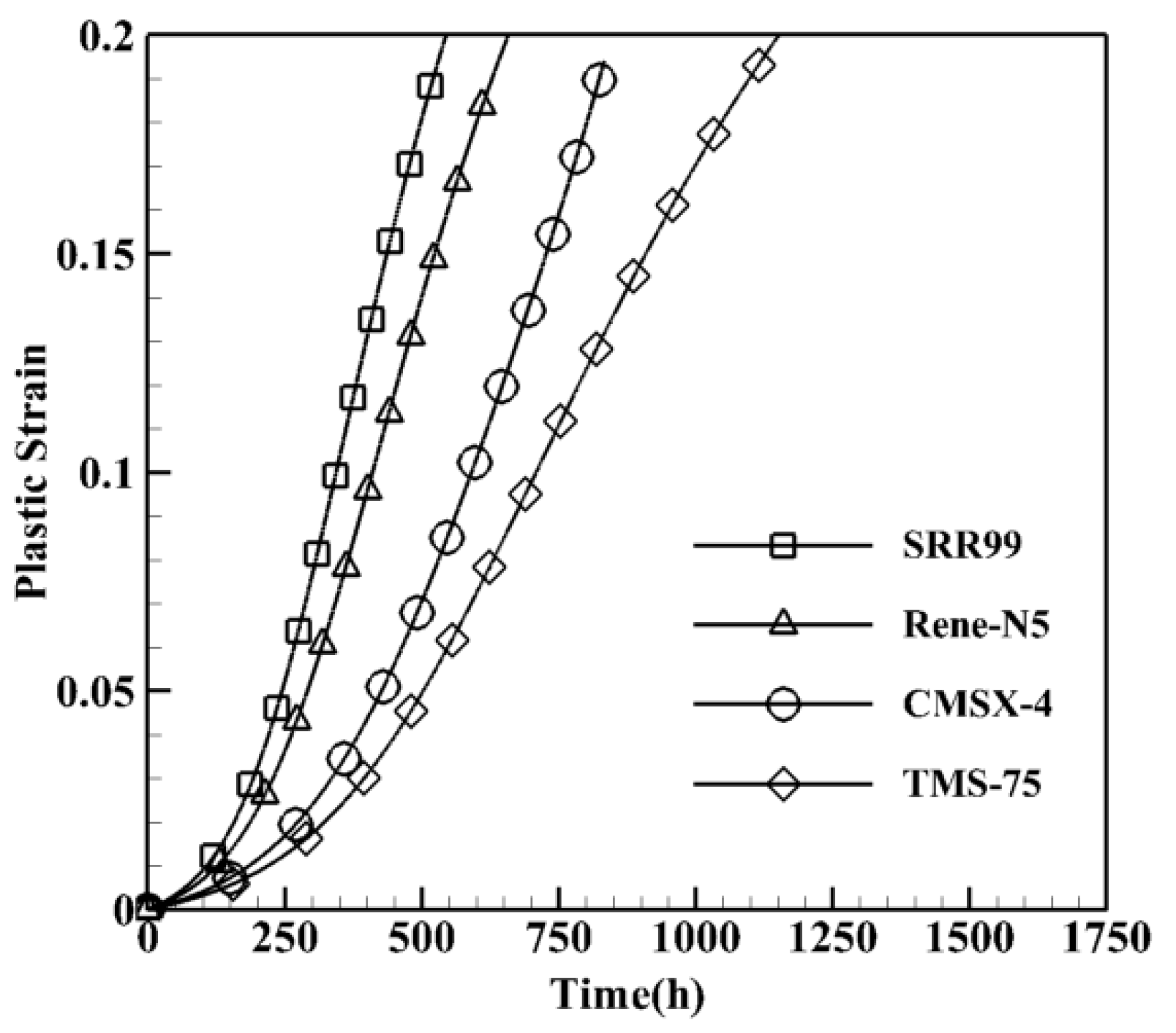
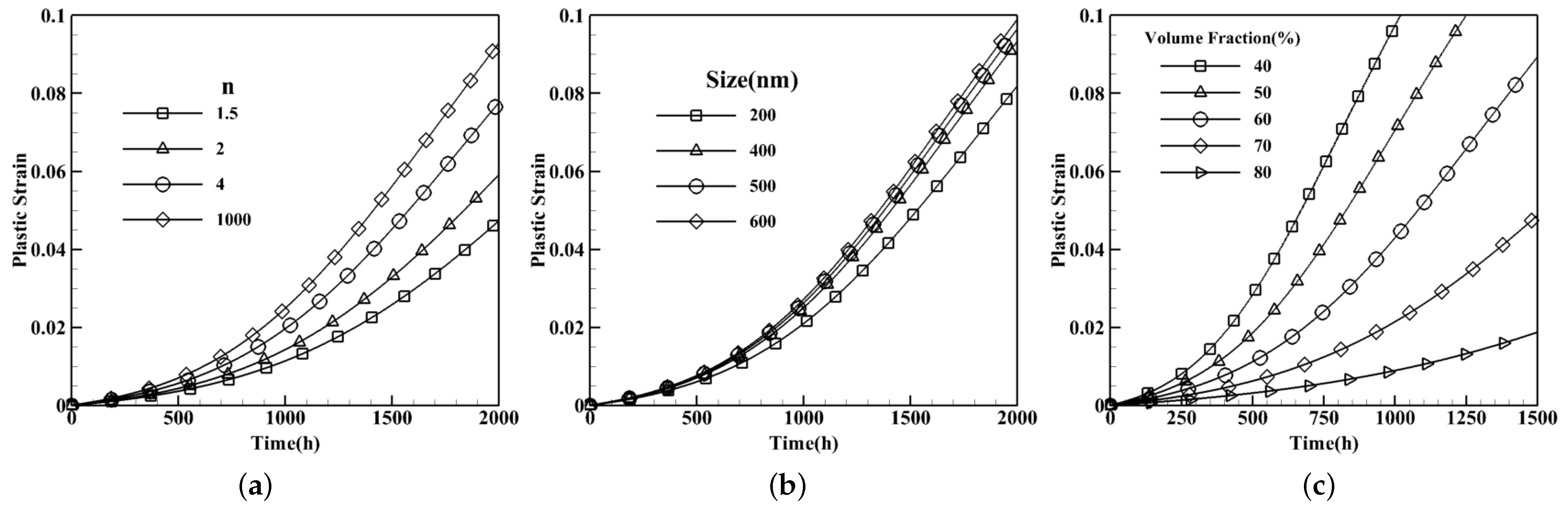
3.2.1. Composition Effects on Creep Curves
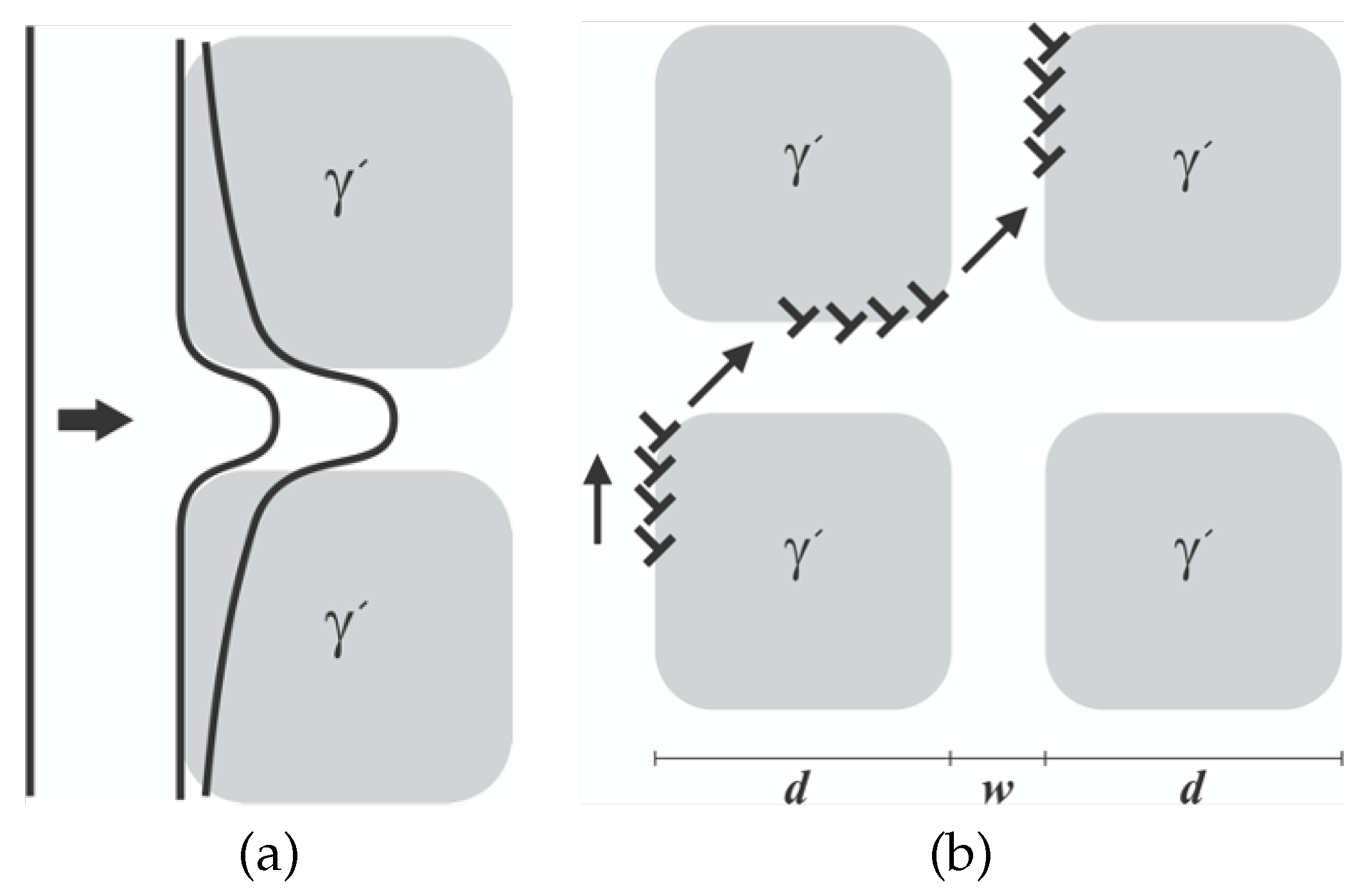
3.2.2. Morphology Effects on Creep Curves
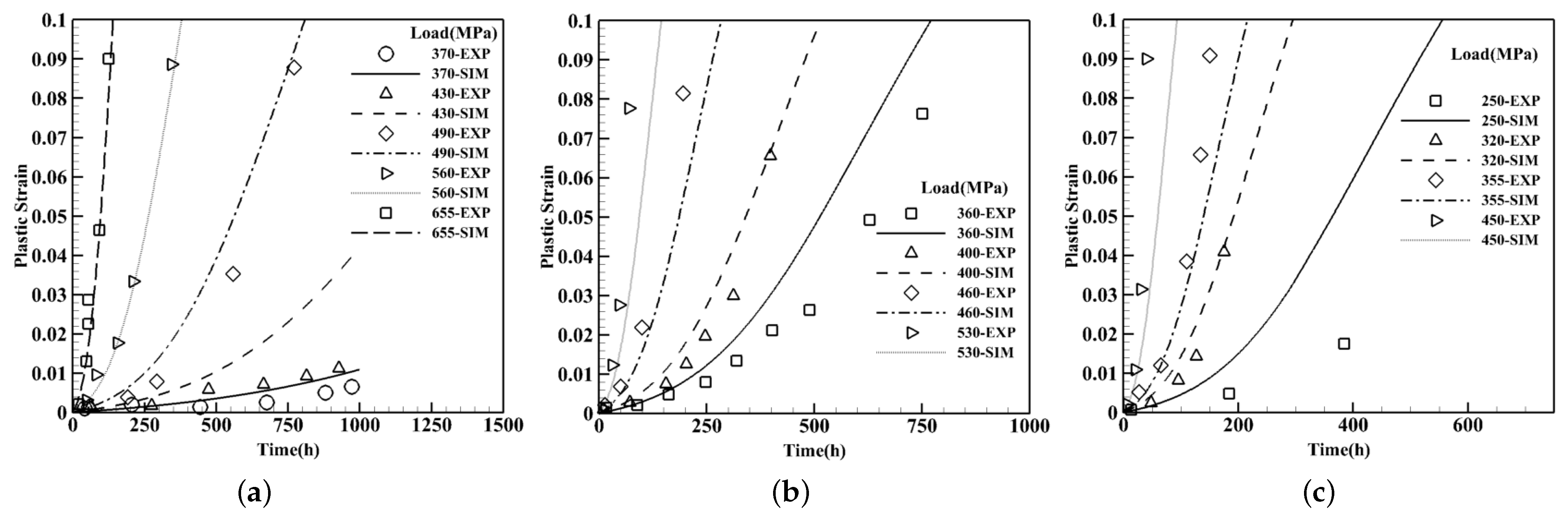
3.2.3. Temperature Effects on Creep Curves—Low to Medium Load Intensities
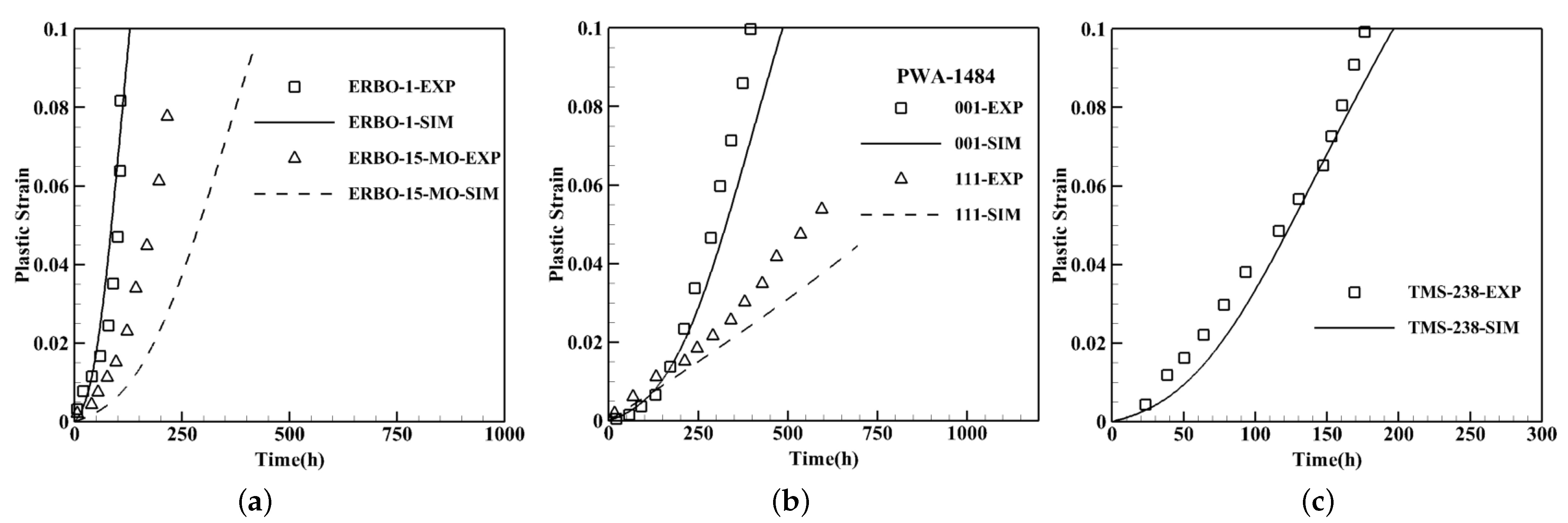
3.2.4. Crystal Orientation Effects on Creep Curves—Low to High Load Intensities
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McLean, M. Nickel-base superalloys: Current status and potential. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1995, 351, 419–433. [Google Scholar]
- Sugui, T.; Jun, X.; Xiaoming, Z.; Benjiang, Q.; Jianwei, L.; Lili, Y.; Wuxiang, W. Microstructure and creep behavior of FGH95 nickel-base superalloy. Mater. Sci. Eng. A 2011, 528, 2076–2084. [Google Scholar] [CrossRef]
- Epishin, A.; Link, T.; Brückner, U.; Portella, P. Kinetics of the topological inversion of the γ/γ′-microstructure during creep of a nickel-based superalloy. Acta Mater. 2001, 49, 4017–4023. [Google Scholar] [CrossRef]
- Pollock, T.M.; Tin, S. Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure and properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar]
- Ignat, M.; Buffiere, J.Y.; Chaix, J. Microstructures induced by a stress gradient in a nickel-based superalloy. Acta Metall. Mater. 1993, 41, 855–862. [Google Scholar] [CrossRef]
- Viswanathan, G.; Sarosi, P.M.; Whitis, D.H.; Mills, M.J. Deformation mechanisms at intermediate creep temperatures in the Ni-base superalloy René 88 DT. Mater. Sci. Eng. A 2005, 400, 489–495. [Google Scholar] [CrossRef]
- Unocic, R.R.; Zhou, N.; Kovarik, L.; Shen, C.; Wang, Y.; Mills, M.J. Dislocation decorrelation and relationship to deformation microtwins during creep of a γ′ precipitate strengthened Ni-based superalloy. Acta Mater. 2011, 59, 7325–7339. [Google Scholar] [CrossRef]
- Chatterjee, D.; Hazari, N.; Das, N.; Mitra, R. Microstructure and creep behavior of DMS4-type nickel based superalloy single crystals with orientations near < 0 0 1> and < 0 1 1>. Mater. Sci. Eng. A 2010, 528, 604–613. [Google Scholar]
- Cormier, J.; Milhet, X.; Mendez, J. Non-isothermal creep at very high temperature of the nickel-based single crystal superalloy MC2. Acta Mater. 2007, 55, 6250–6259. [Google Scholar] [CrossRef]
- Torster, F.; Baumeister, G.; Albrecht, J.; Lütjering, G.; Helm, D.; Daeubler, M. Influence of grain size and heat treatment on the microstructure and mechanical properties of the nickel-base superalloy U 720 LI. Mater. Sci. Eng. A 1997, 234, 189–192. [Google Scholar] [CrossRef]
- Hong, H.; Kim, I.; Choi, B.; Kim, M.; Jo, C. The effect of grain boundary serration on creep resistance in a wrought nickel-based superalloy. Mater. Sci. Eng. A 2009, 517, 125–131. [Google Scholar] [CrossRef]
- Fedelich, B.; Epishin, A.; Link, T.; Klingelhöffer, H.; Künecke, G.; Portella, P.D. Rafting during high temperature deformation in a single crystal superalloy: Experiments and modeling. Superalloys 2012 2012, 6, 491. [Google Scholar]
- Barba, D.; Smith, T.; Miao, J.; Mills, M.; Reed, R. Segregation-assisted plasticity in Ni-based superalloys. Metall. Mater. Trans. A 2018, 49, 4173–4185. [Google Scholar] [CrossRef] [Green Version]
- Beyerlein, I.; Tomé, C. A dislocation-based constitutive law for pure Zr including temperature effects. Int. J. Plast. 2008, 24, 867–895. [Google Scholar] [CrossRef]
- Knezevic, M.; Beyerlein, I.J.; Lovato, M.L.; Tomé, C.N.; Richards, A.W.; McCabe, R.J. A strain-rate and temperature dependent constitutive model for BCC metals incorporating non-Schmid effects: Application to tantalum–tungsten alloys. Int. J. Plast. 2014, 62, 93–104. [Google Scholar] [CrossRef] [Green Version]
- Pollock, T.; Argon, A. Creep resistance of CMSX-3 nickel base superalloy single crystals. Acta Metall. Mater. 1992, 40, 1–30. [Google Scholar] [CrossRef]
- Busso, E.; Meissonnier, F.; O’dowd, N. Gradient-dependent deformation of two-phase single crystals. J. Mech. Phys. Solids 2000, 48, 2333–2361. [Google Scholar] [CrossRef]
- Probst-Hein, M.; Dlouhy, A.; Eggeler, G. Interface dislocations in superalloy single crystals. Acta Mater. 1999, 47, 2497–2510. [Google Scholar] [CrossRef]
- Fedelich, B. A microstructural model for the monotonic and the cyclic mechanical behavior of single crystals of superalloys at high temperatures. Int. J. Plast. 2002, 18, 1–49. [Google Scholar] [CrossRef]
- Shenoy, M.; Kumar, R.; McDowell, D. Modeling effects of nonmetallic inclusions on LCF in DS nickel-base superalloys. Int. J. Fatigue 2005, 27, 113–127. [Google Scholar] [CrossRef]
- Fromm, B.S.; Chang, K.; McDowell, D.L.; Chen, L.Q.; Garmestani, H. Linking phase-field and finite-element modeling for process–structure–property relations of a Ni-base superalloy. Acta Mater. 2012, 60, 5984–5999. [Google Scholar] [CrossRef]
- Keshavarz, S.; Ghosh, S. Multi-scale crystal plasticity finite element model approach to modeling nickel-based superalloys. Acta Mater. 2013, 61, 6549–6561. [Google Scholar] [CrossRef]
- Moleinia, Z.; Bahr, D.F. Multi-Scale Analyses and Modeling of Metallic Nano-Layers. Materials 2021, 14, 450. [Google Scholar] [CrossRef] [PubMed]
- Nabarro, F.R.N. Theory of Crystal Dislocations; Dover Publications: Mignola, NY, USA, 1987. [Google Scholar]
- Keshavarz, S.; Ghosh, S.; Reid, A.C.; Langer, S.A. A non-Schmid crystal plasticity finite element approach to multi-scale modeling of nickel-based superalloys. Acta Mater. 2016, 114, 106–115. [Google Scholar] [CrossRef] [Green Version]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Keshavarz, S.; Molaeinia, Z.; Reid, A.; Langer, S. Morphology Dependent Flow Stress in Nickel-Based Superalloys in the Multi-Scale Crystal Plasticity Framework. Crystals 2017, 7, 334. [Google Scholar] [CrossRef] [Green Version]
- Birosca, S.; Liu, G.; Ding, R.; Jiang, J.; Simm, T.; Deen, C.; Whittaker, M. The dislocation behaviour and GND development in a nickel based superalloy during creep. Int. J. Plast. 2019, 118, 252–268. [Google Scholar] [CrossRef] [Green Version]
- Keshavarz, S.; Ghosh, S. Hierarchical crystal plasticity FE model for nickel-based superalloys: Sub-grain microstructures to polycrystalline aggregates. Int. J. Solids Struct. 2015, 55, 17–31. [Google Scholar] [CrossRef]
- Lours, P.; Coujou, A.; Coulomb, P. On the deformation of the <100> orientated γ′ strengthening phase of the CMSX2 superalloy. Acta Metall. Mater. 1991, 39, 1787–1797. [Google Scholar]
- Zhu, Z.; Basoalto, H.; Warnken, N.; Reed, R. A model for the creep deformation behaviour of nickel-based single crystal superalloys. Acta Mater. 2012, 60, 4888–4900. [Google Scholar] [CrossRef]
- Friedel, J. Dislocations: International Series of Monographs on Solid State Physics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Maier, K.; Mehrer, H.; Lessmann, E.; Schüle, W. Self-diffusion in nickel at low temperatures. Phys. Status Solidi 1976, 78, 689–698. [Google Scholar] [CrossRef]
- Han, G.; Yu, J.; Sun, Y.; Sun, X.; Hu, Z. Anisotropic stress rupture properties of the nickel-base single crystal superalloy SRR99. Mater. Sci. Eng. A 2010, 527, 5383–5390. [Google Scholar] [CrossRef]
- Shang, Z.; Wei, X.; Song, D.; Zou, J.; Liang, S.; Liu, G.; Nie, L.; Gong, X. Microstructure and mechanical properties of a new nickel-based single crystal superalloy. J. Mater. Res. Technol. 2020, 9, 11641–11649. [Google Scholar] [CrossRef]
- Vattré, A.; Fedelich, B. On the relationship between anisotropic yield strength and internal stresses in single crystal superalloys. Mech. Mater. 2011, 43, 930–951. [Google Scholar] [CrossRef]
- Murakumo, T.; Koizumi, Y.; Kobayashi, K.; Harada, H. Creep strength of Ni-base single-crystal superalloys on the γ/γ′ tie-line. Superalloys 2004, 155–162. Available online: https://www.tms.org/Superalloys/10.7449/2004/Superalloys_2004_155_162.pdf (accessed on 5 May 2022).
- Horst, O.; Adler, D.; Git, P.; Wang, H.; Streitberger, J.; Holtkamp, M.; Jöns, N.; Singer, R.; Körner, C.; Eggeler, G. Exploring the fundamentals of Ni-based superalloy single crystal (SX) alloy design: Chemical composition vs. microstructure. Mater. Des. 2020, 195, 108976. [Google Scholar] [CrossRef]
- Staroselsky, A.; Cassenti, B.N. Combined rate-independent plasticity and creep model for single crystal. Mech. Mater. 2010, 42, 945–959. [Google Scholar] [CrossRef]
- Celel, A.; Duhl, D. Second-generation nickel-base single crystal superalloy. In Proceedings of the International Symposium on Superalloys, Champion, PA, USA, 18–22 September 1988. [Google Scholar]
- Yuan, Y.; Kawagishi, K.; Koizumi, Y.; Kobayashi, T.; Yokokawa, T.; Harada, H. Creep deformation of a sixth generation Ni-base single crystal superalloy at 800 C. Mater. Sci. Eng. A 2014, 608, 95–100. [Google Scholar] [CrossRef]
- Matan, N.; Cox, D.; Carter, P.; Rist, M.; Rae, C.; Reed, R. Creep of CMSX-4 superalloy single crystals: Effects of misorientation and temperature. Acta Mater. 1999, 47, 1549–1563. [Google Scholar] [CrossRef]
- Knowles, D.; Gunturi, S. The role of <112>{111} slip in the asymmetric nature of creep of single crystal superalloy CMSX-4. Mater. Sci. Eng. A 2002, 328, 223–237. [Google Scholar]



| Alloy | Cr | Co | Mo | Re | W | Al | Ti | Ta | Ni |
|---|---|---|---|---|---|---|---|---|---|
| SRR99 | 0.08 | 0.05 | - | - | 0.10 | 0.055 | 0.022 | 0.03 | Bal |
| RENE-N5 | 0.07 | 0.075 | 0.015 | 0.03 | 0.05 | 0.062 | - | 0.06 | Bal |
| CMSX-4 | 0.065 | 0.09 | 0.006 | 0.03 | 0.06 | 0.056 | 0.01 | 0.065 | Bal |
| TMS-75 | 0.03 | 0.12 | 0.02 | 0.05 | 0.06 | 0.06 | - | 0.06 | Bal |
| Element | Cr | Co | Mo | Re | W | Al | Ti | Ta | Ni |
|---|---|---|---|---|---|---|---|---|---|
| 52 | 7.5 | 11.5 | 0.082 | 1.15 | 10 | 14 | 1.29 | 19 | |
| Q | 289 | 271.7 | 281.3 | 255 | 303 | 260 | 263.8 | 257.5 | 284 |
| Alloy | Cr | Co | Mo | Re | Ru | W | Al | Ti | Ta | Hf | Ni |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ERBO-1 | 0.075 | 0.10 | 0.004 | 0.01 | - | 0.021 | 0.126 | 0.013 | 0.022 | 0.0003 | Bal |
| ERBO-15-MO | 0.076 | 0.031 | 0.013 | - | - | 0.025 | 0.113 | 0.04 | - | - | Bal |
| PWA-1484 | 0.05 | 0.10 | 0.02 | 0.03 | - | 0.06 | 0.056 | - | 0.09 | 0.001 | Bal |
| TMS-238 | 0.046 | 0.065 | 0.011 | 0.064 | 0.05 | 0.04 | 0.059 | - | 0.076 | 0.0002 | Bal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshavarz, S.; Campbell, C.E.; Reid, A.C.E. Multi-Scale Crystal Plasticity Model of Creep Responses in Nickel-Based Superalloys. Materials 2022, 15, 4447. https://doi.org/10.3390/ma15134447
Keshavarz S, Campbell CE, Reid ACE. Multi-Scale Crystal Plasticity Model of Creep Responses in Nickel-Based Superalloys. Materials. 2022; 15(13):4447. https://doi.org/10.3390/ma15134447
Chicago/Turabian StyleKeshavarz, Shahriyar, Carelyn E. Campbell, and Andrew C. E. Reid. 2022. "Multi-Scale Crystal Plasticity Model of Creep Responses in Nickel-Based Superalloys" Materials 15, no. 13: 4447. https://doi.org/10.3390/ma15134447
APA StyleKeshavarz, S., Campbell, C. E., & Reid, A. C. E. (2022). Multi-Scale Crystal Plasticity Model of Creep Responses in Nickel-Based Superalloys. Materials, 15(13), 4447. https://doi.org/10.3390/ma15134447





