Experimental Investigation of the Mechanical Properties of the Sand–Concrete Pile Interface Considering Roughness and Relative Density
Abstract
:1. Introduction
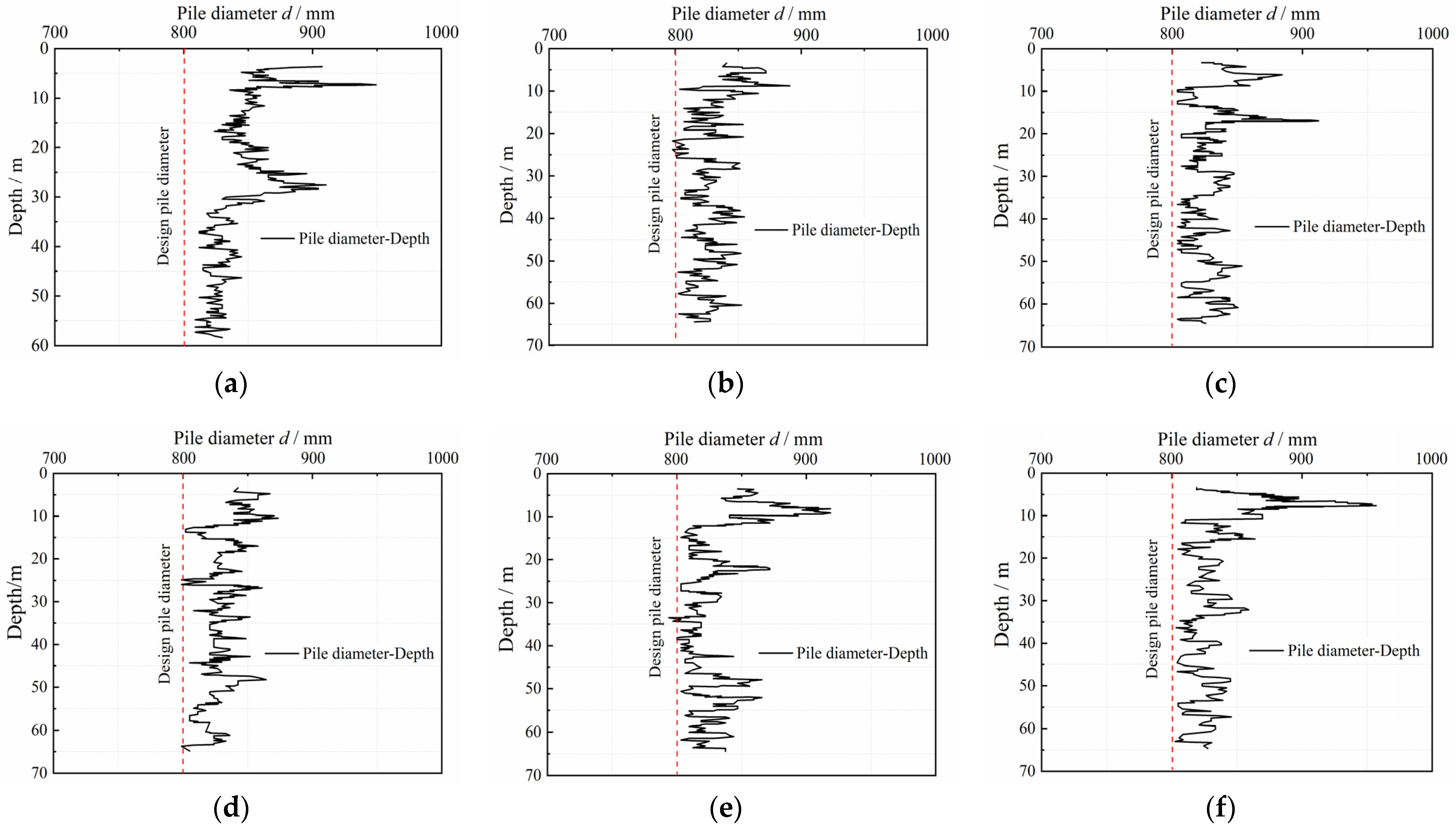
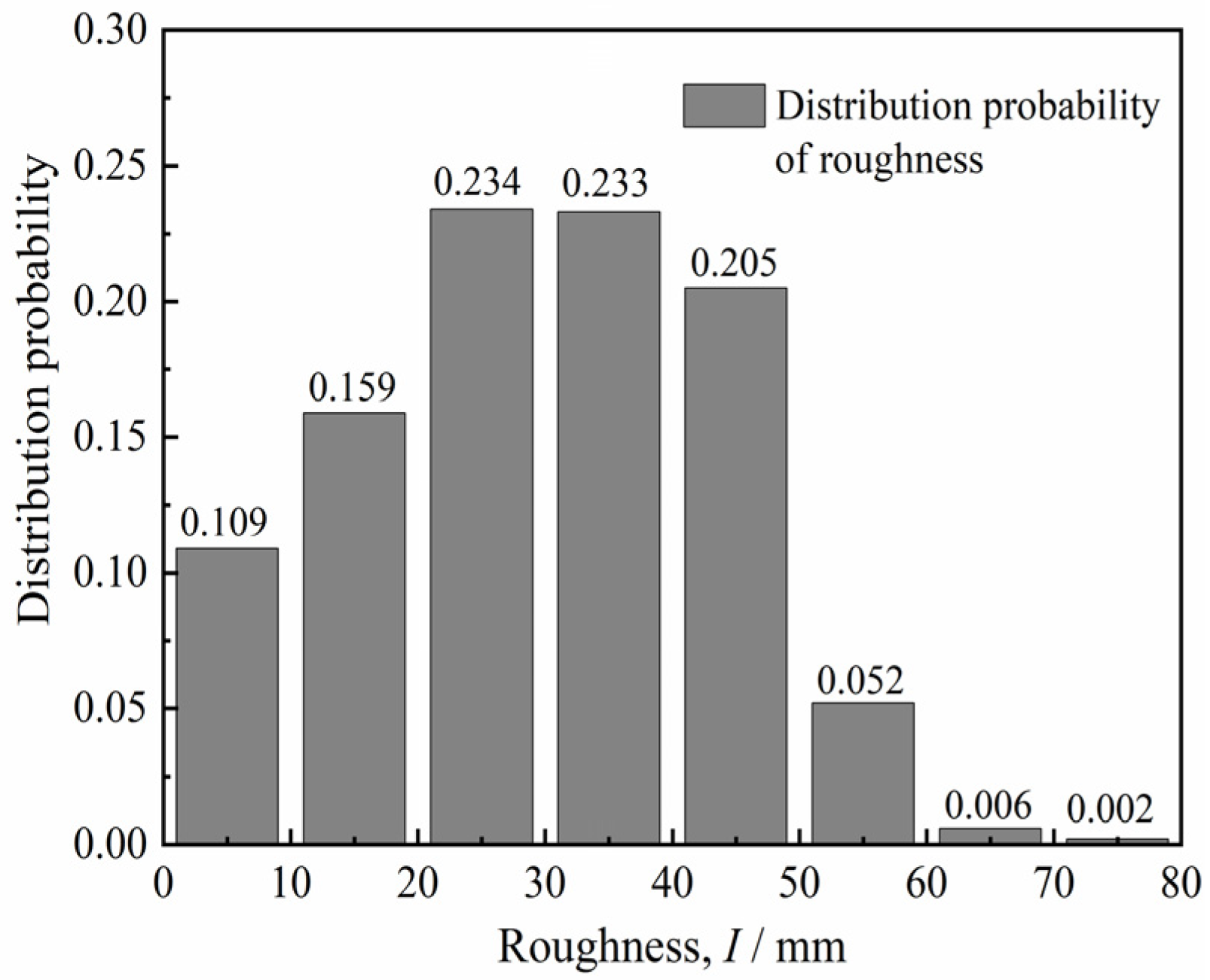
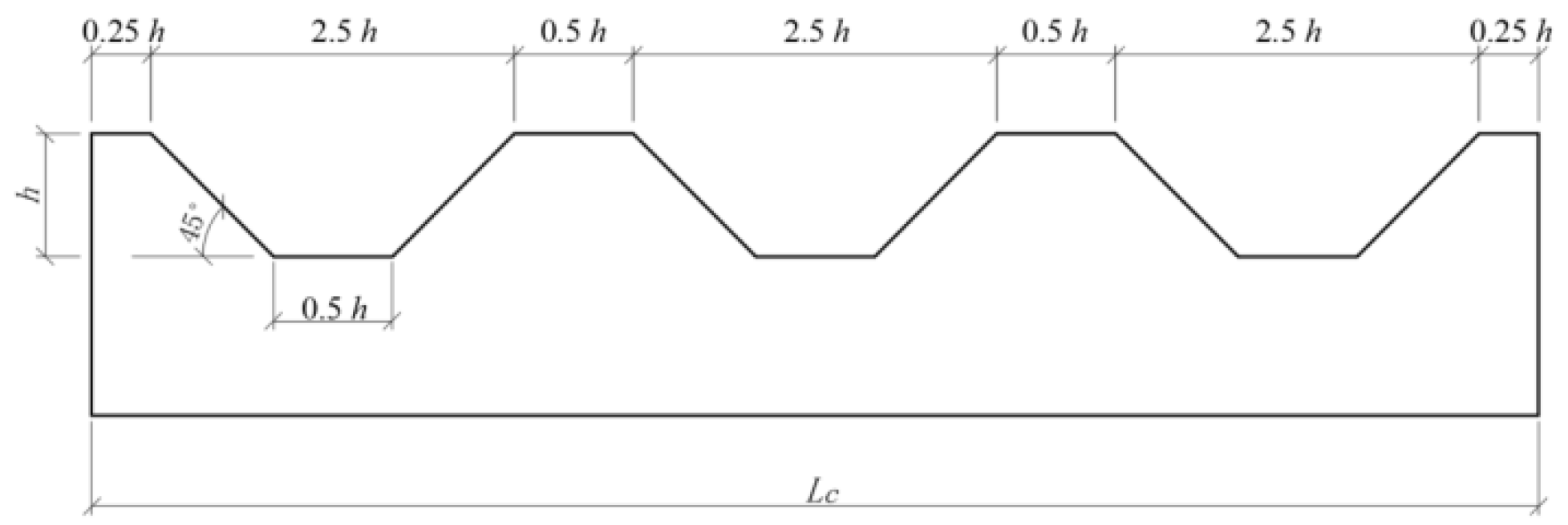
2. Roughness Design and Evaluation
3. Experiments
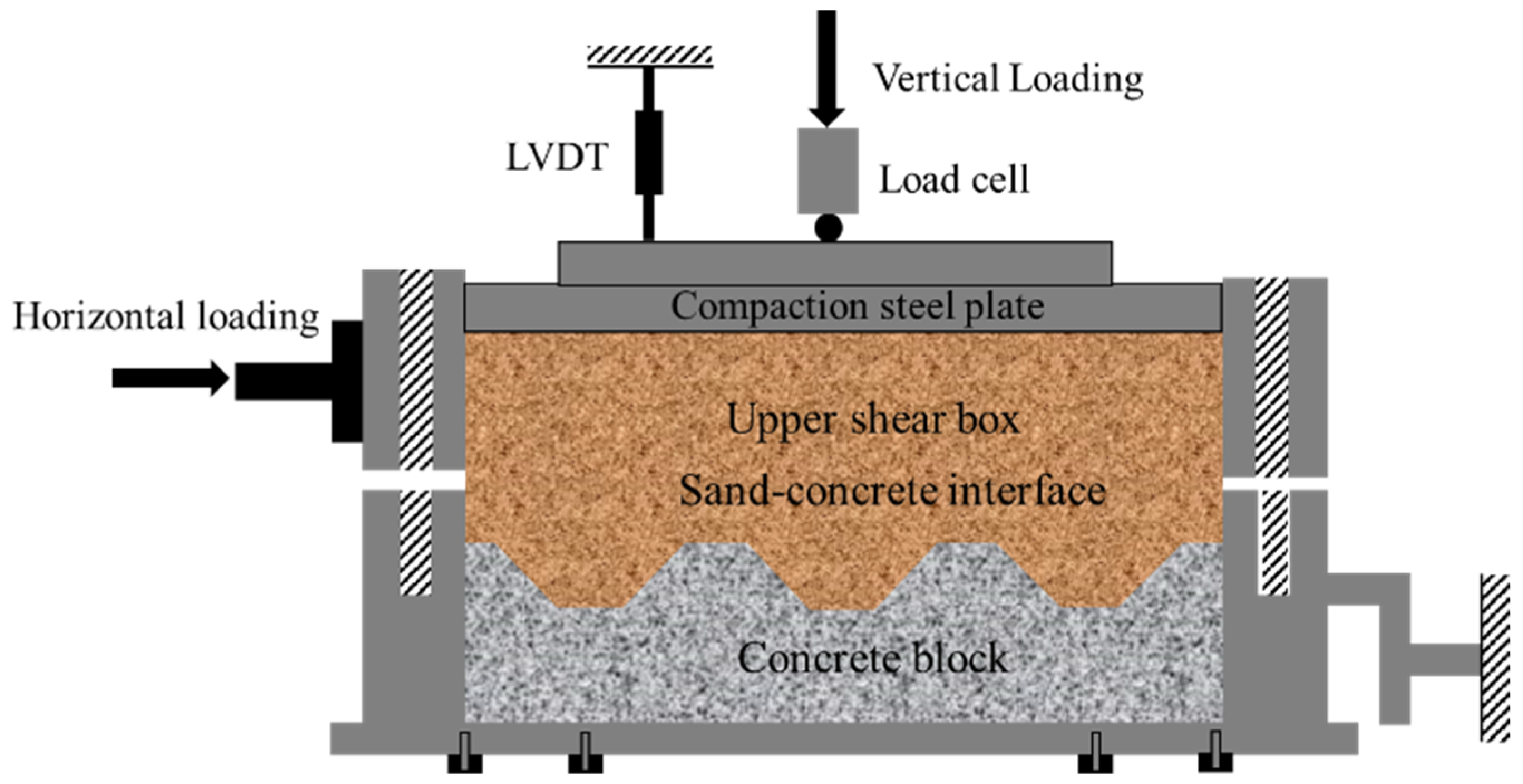
3.1. Test Apparatus
3.2. Test Materials
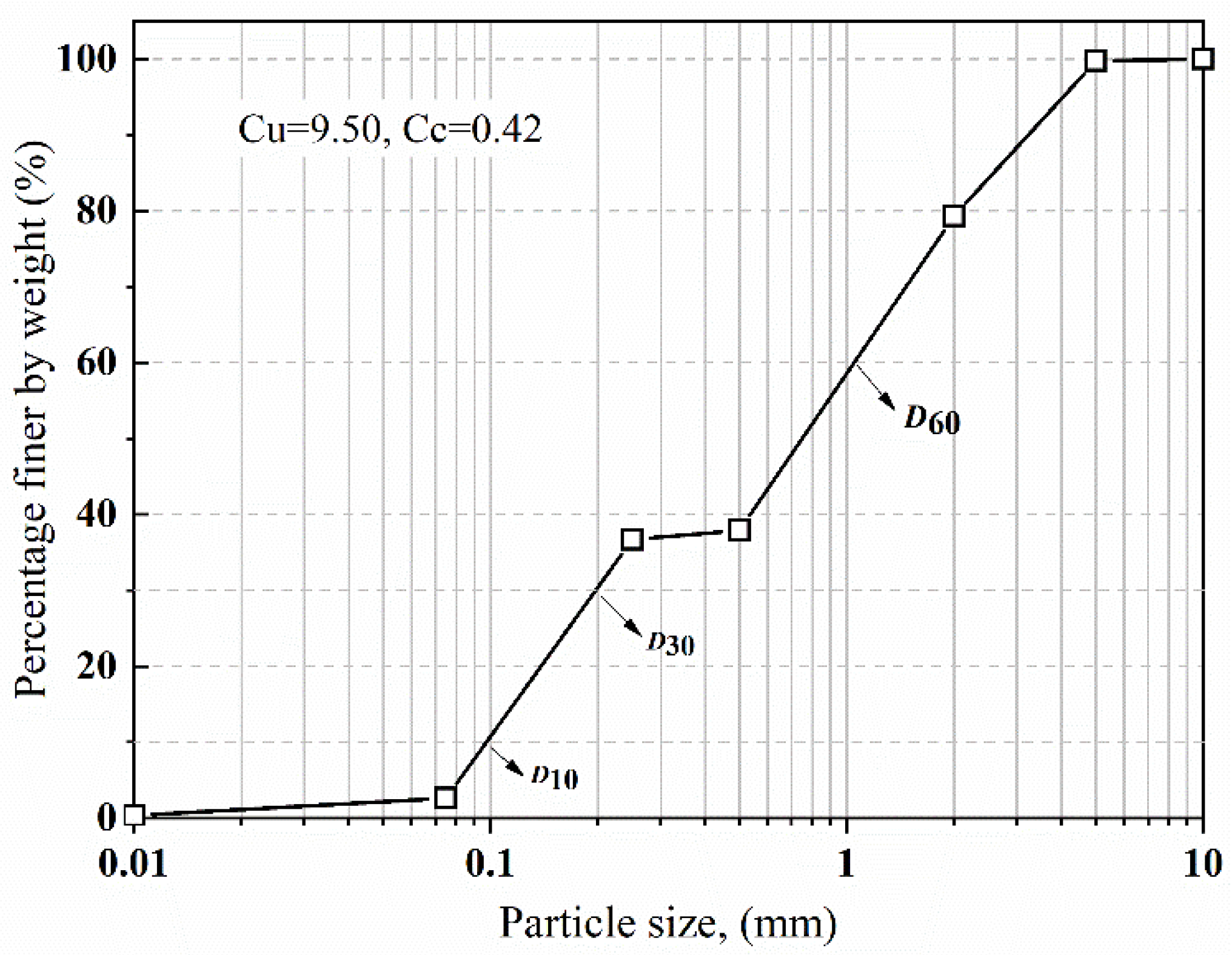
3.2.1. Soil Materials
3.2.2. Concrete Block
3.3. Test Program
4. Results and Analyses
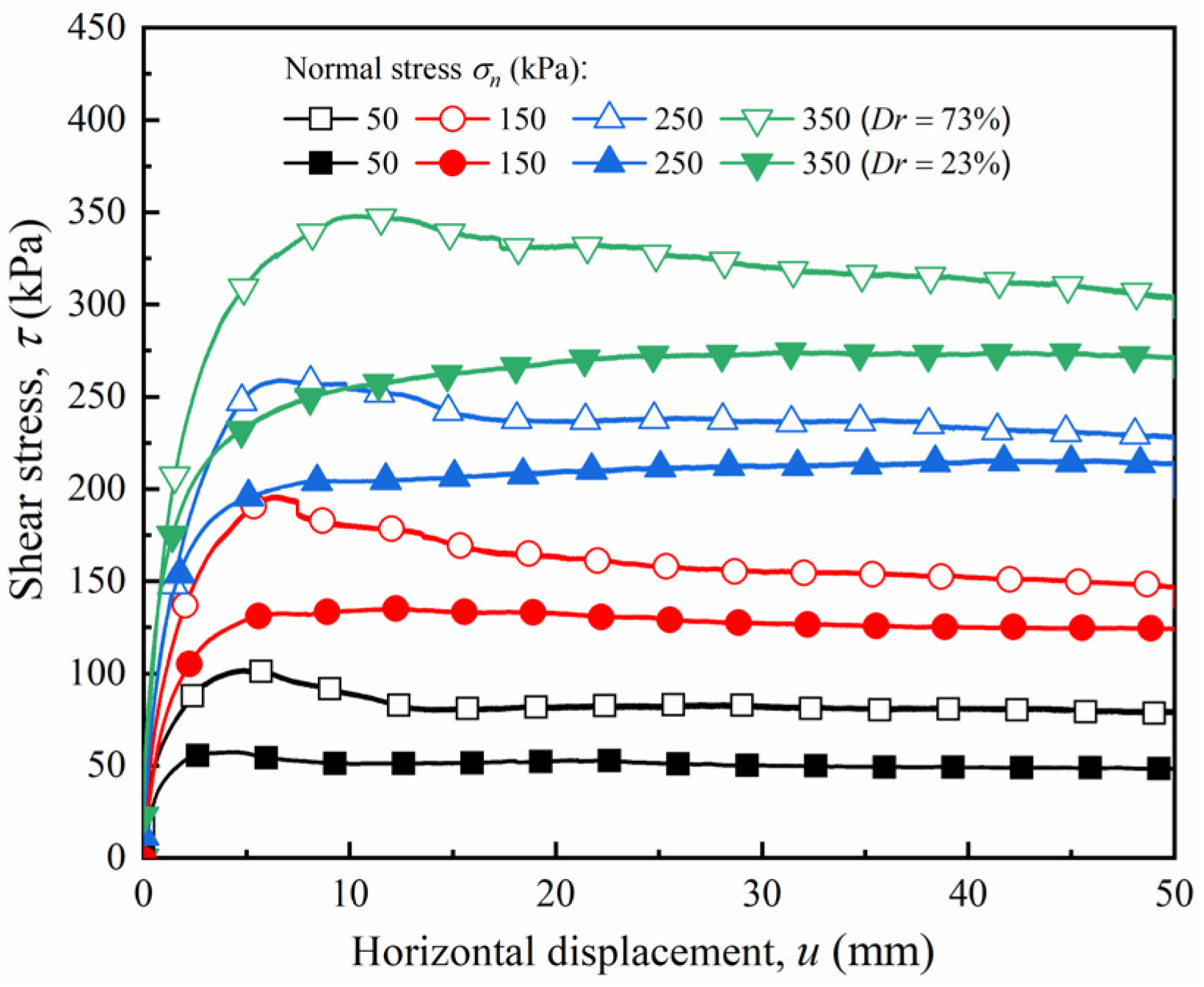
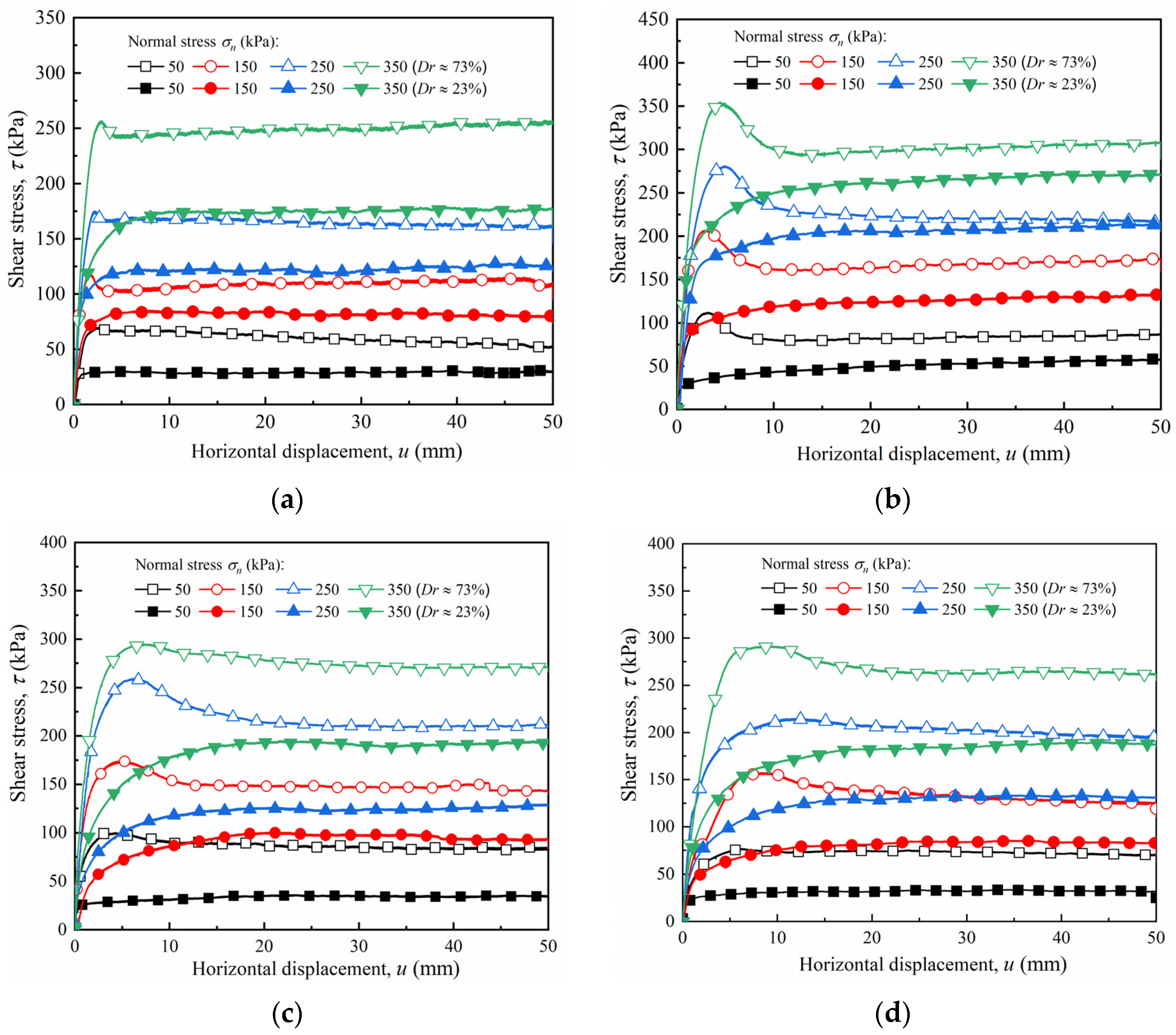
4.1. Shear Stress–Horizontal Displacemenet Relationship
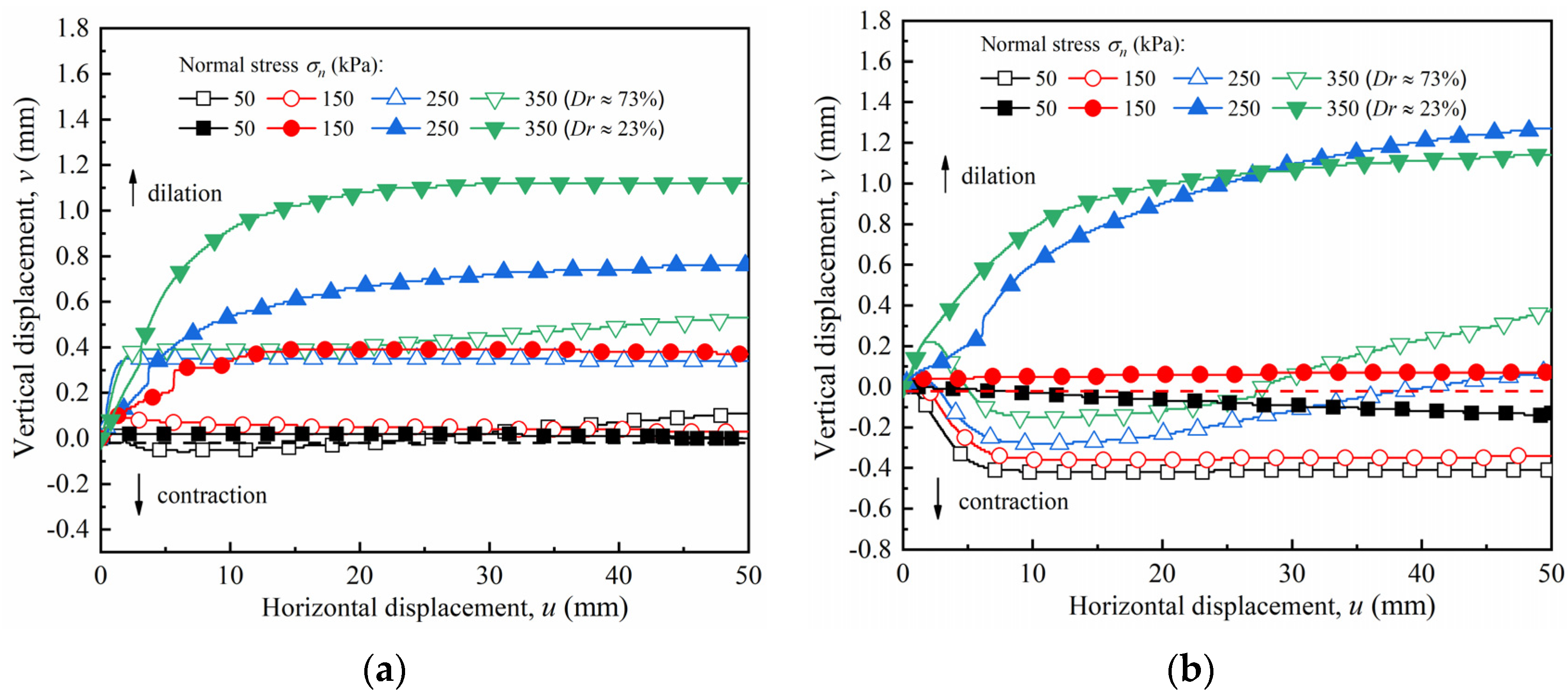
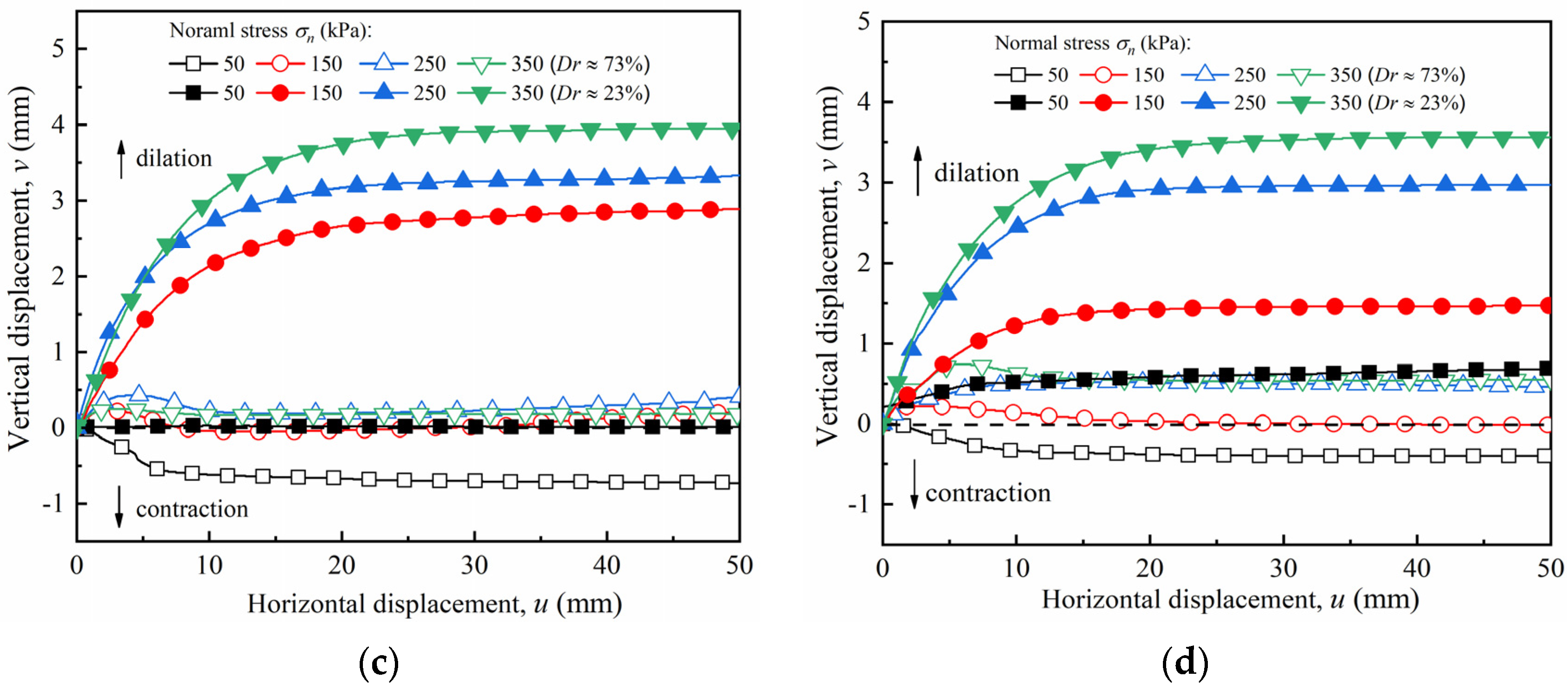
4.2. Vertical–Horizontal Displacement Relationship
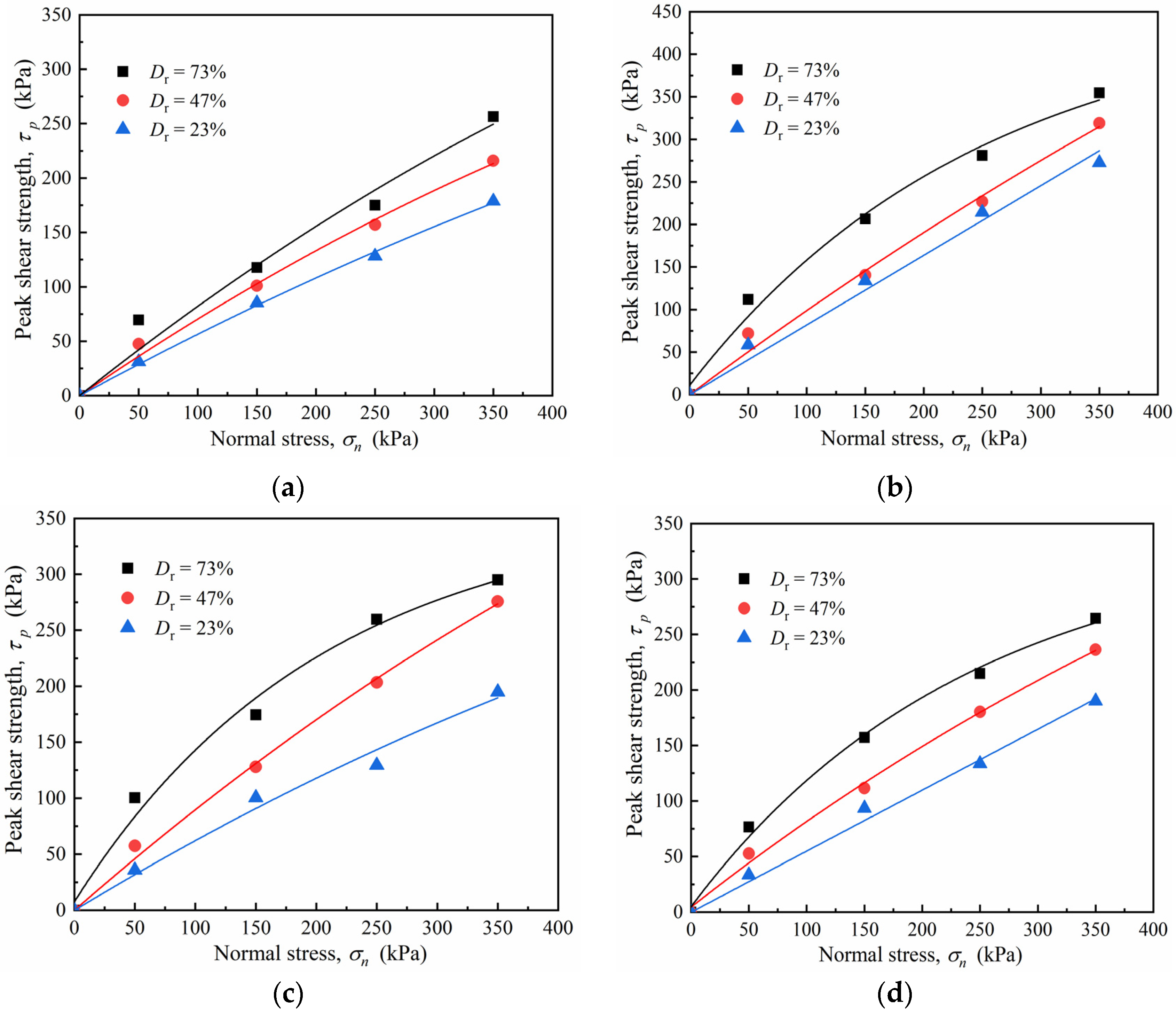
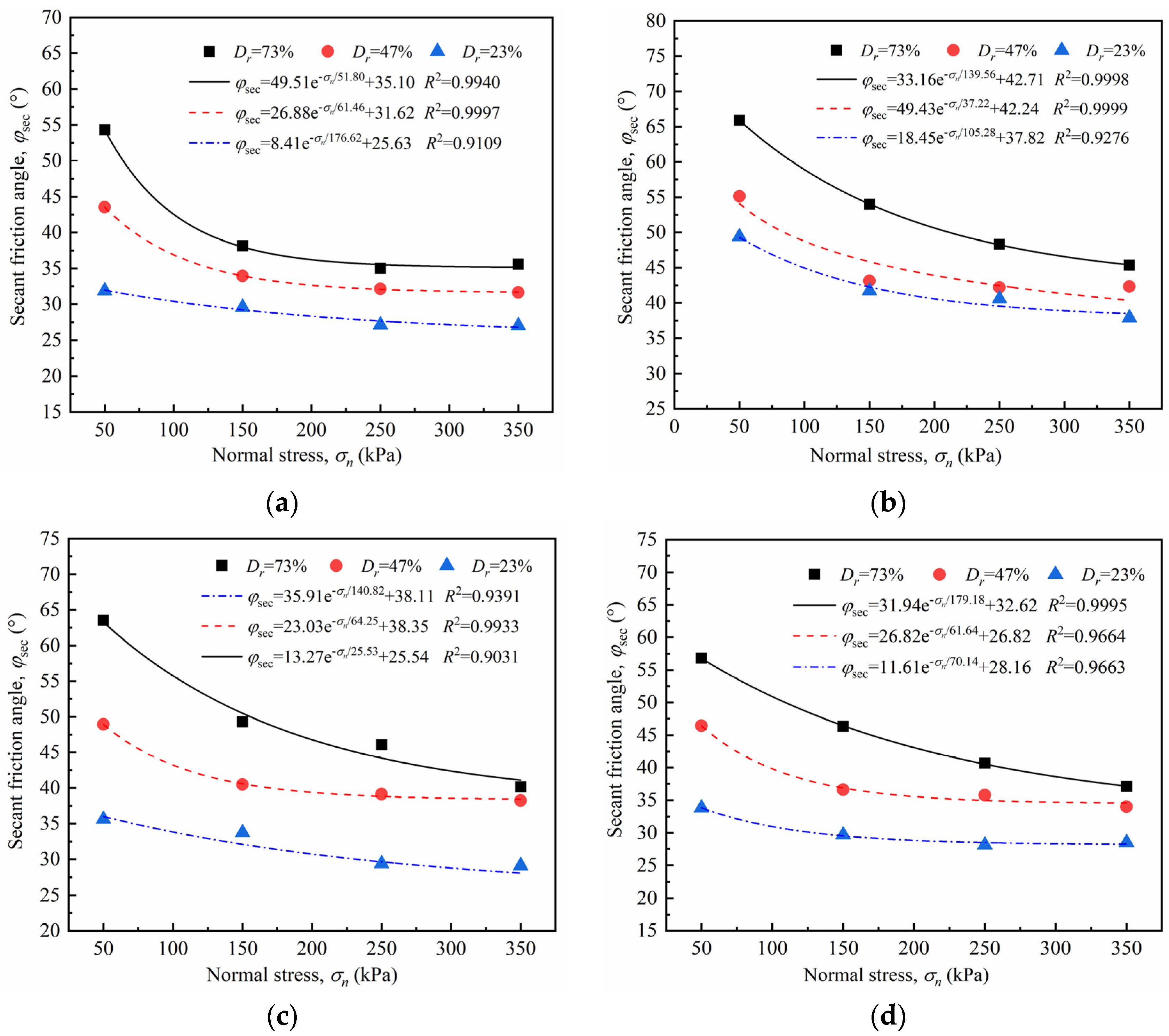
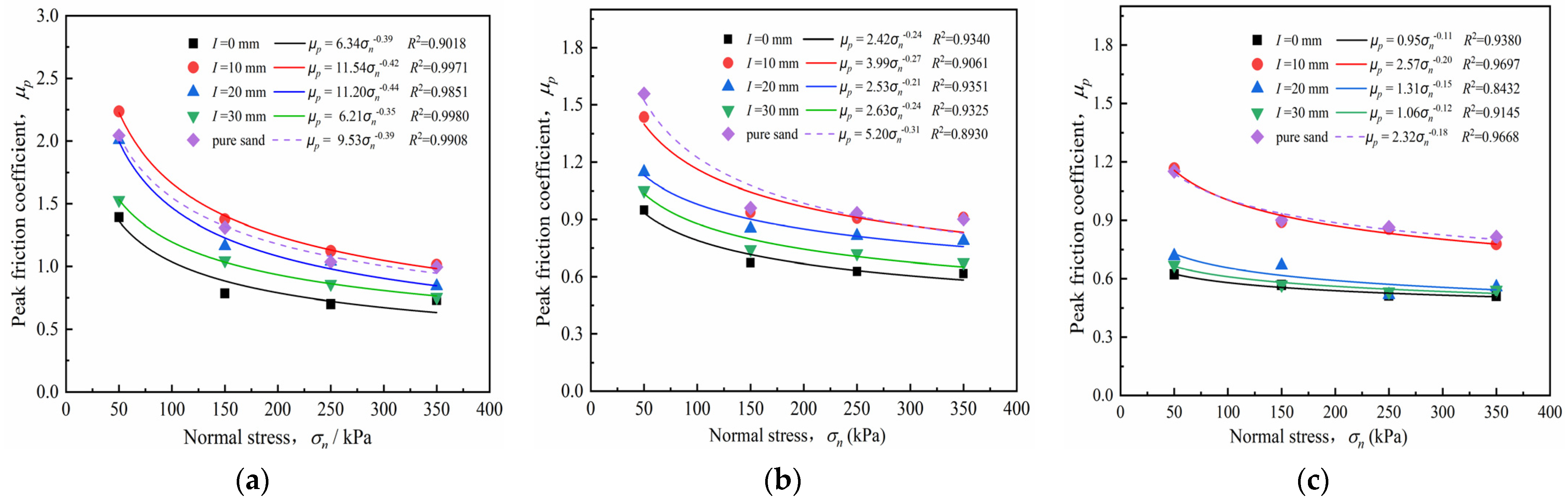
4.3. Strength Parameters of Sand–Concrete Interface
4.3.1. Peak Shear Strength
4.3.2. Secant Friction Angle
4.3.3. Peak Friction Coefficient
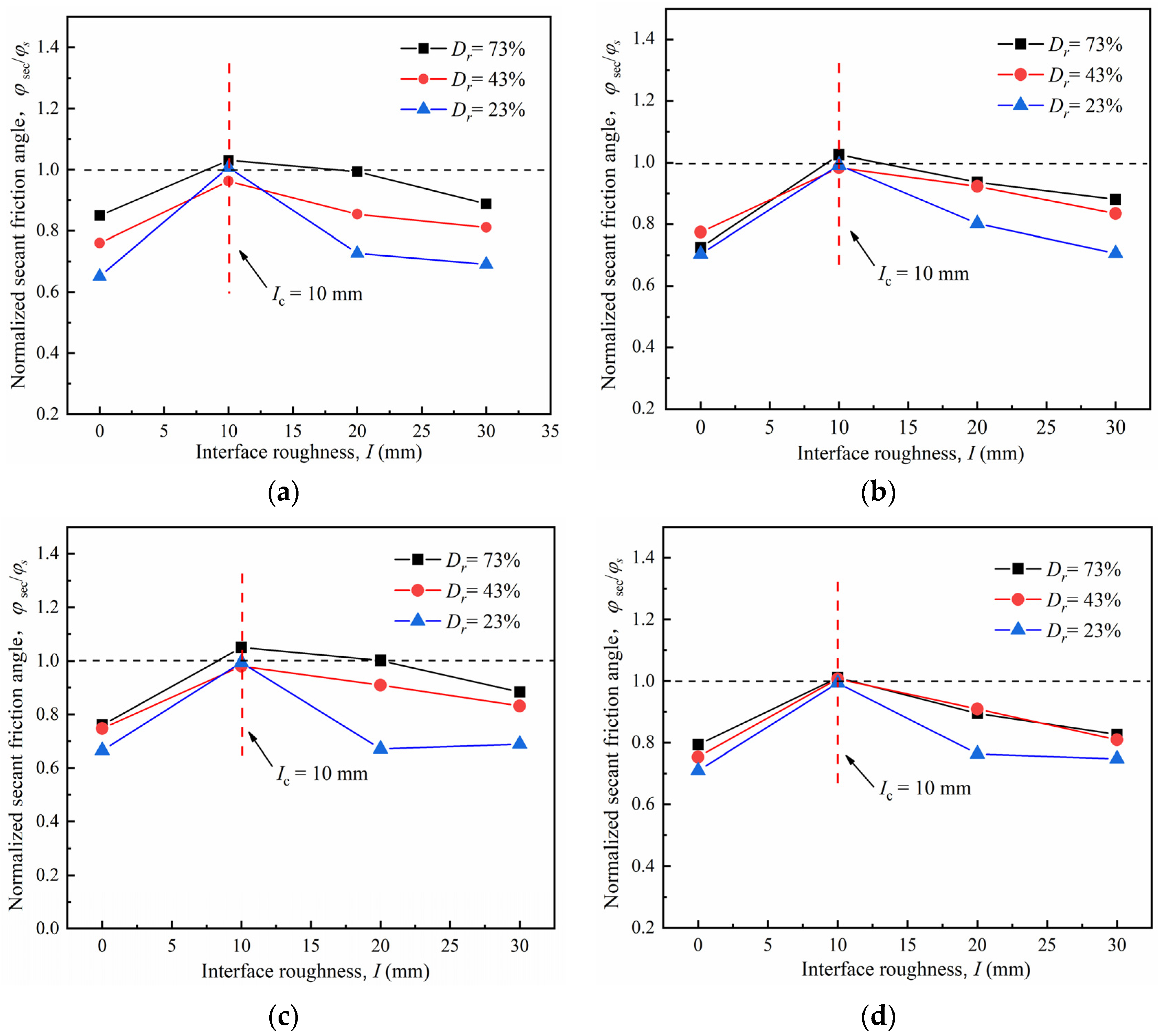
4.4. Effect of Surface Roughness
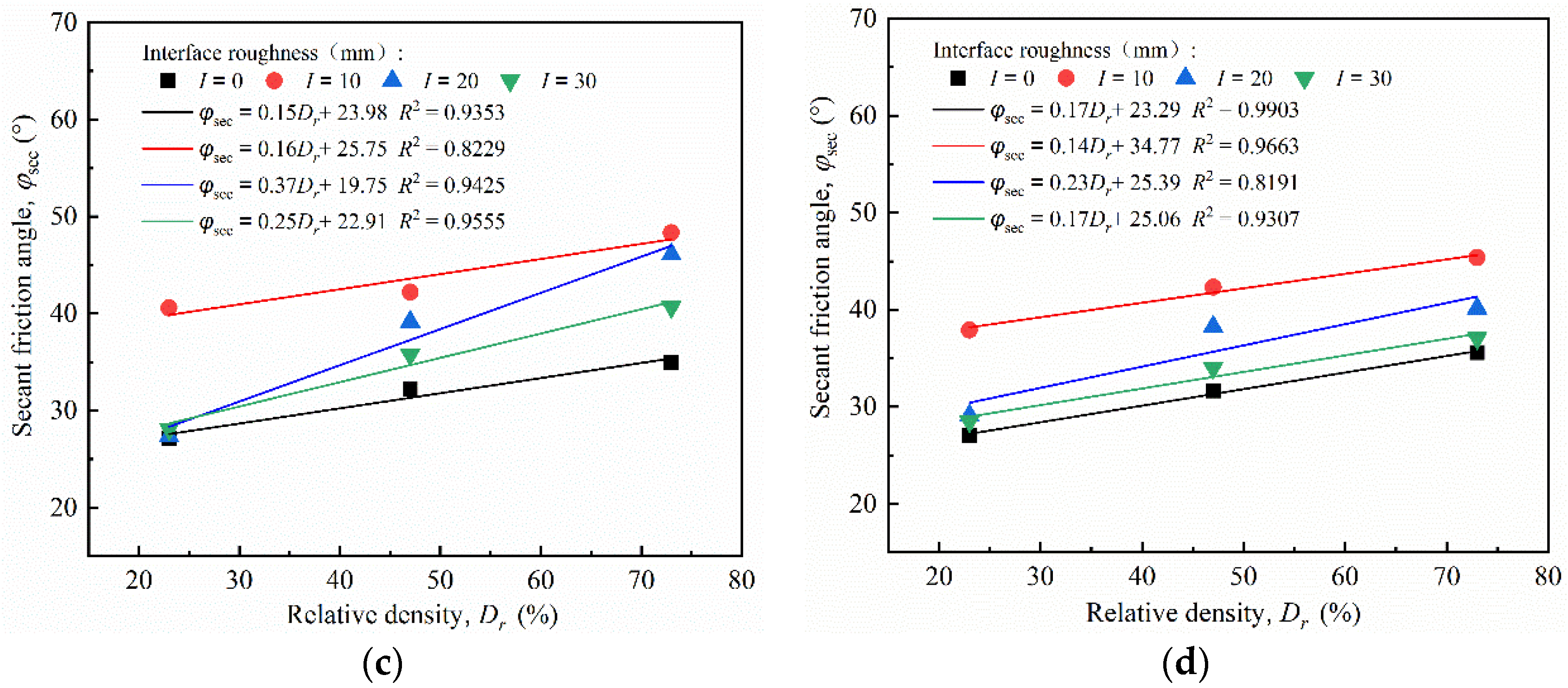
4.5. Effect of Relative Density
5. Conclusions
- For the smooth interface, the shear stress–horizontal displacement curves of the dense sand exhibited a softening reaction, whereas the curves of the loose sand consistently exhibited a hardening reaction. The relative density had a dominant effect on the curve development form. In contrast, the roughness had a more considerable influence on the curve development degree.
- The smooth interface with dense sand exhibited a slight dilatancy under low normal stress, and shear contraction was apparent as normal stress increased. As roughness increased, the dense sand first contracted and then dilated under low normal stress, and the shear contraction became more evident as the normal stress increased. The loose sand retained its original shear properties despite the state of roughness.
- The peak shear strength of the interface increased nonlinearly as the normal stress increased. The greater the relative density was, the more intense the nonlinear growth became. The secant friction angle reduced exponentially as the normal stress increased, but increased linearly as the relative density increased. The peak friction coefficient μp decreased as a power function as the normal stress increased.
- A critical roughness value Icr = 10 mm was identified in this study. When I < Icr, the peak friction coefficient μp and normalized secant friction angle φsec/φs initially increased with increasing roughness I, but gradually decreased as I ≥ Icr. When I attained Icr, φsec/φs of the interface with dense sand exceeded 1.0, and shear failure was more likely to occur in the soil.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, R.Y.; Hua, D.J.; Chen, K.J. Experimental study on interaction between rock granular flow and different structural forms of rigid retaining walls. Structures 2021, 34, 3557–3566. [Google Scholar] [CrossRef]
- Zhou, W.H.; Yin, J.H. A simple mathematical model for soil nail and soil interaction analysis. Comput. Geotech. 2008, 35, 479–488. [Google Scholar] [CrossRef]
- Ye, X.; Wang, Q.; Wang, S.; Scott, S.; Sheng, D. Performance of a compaction-grouted soil nail in laboratory tests. Acta Geotech. 2018, 14, 1049–1063. [Google Scholar] [CrossRef]
- Abdi, M.R.; Mirzaeifar, H. Experimental and PIV evaluation of grain size and distribution on soil-geogrid interactions in pullout test. Soils Found. 2017, 57, 1045–1058. [Google Scholar] [CrossRef]
- Lam, C.; Jefferis, S.A.; Martin, C.M. Effects of polymer and bentonite support fluids on concrete–sand interface shear strength. Géotechnique 2014, 64, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Leng, W.M.; Qi, Y.; Jin, Z.H.; Nie, R.S.; Qiu, J. Experimental study of mechanical properties of concrete pile-slurry-sand interface. Rock Soil Mech. 2018, 39, 2461–2472. [Google Scholar] [CrossRef]
- Abu-Farsakh, M.; Coronel, J.; Tao, M.J. Effect of soil moisture content and dry density on cohesive soil-geosynthetic interactions using large direct shear tests. J. Mater. Civ. Eng. 2007, 19, 540–549. [Google Scholar] [CrossRef]
- Dejong, J.T.; Westgate, Z.J. Role of Initial State, Material Properties, and Confinement Condition on Local and Global Soil-Structure Interface Behavior. J. Geotech. Geoenviron. Eng. 2009, 135, 1646–1660. [Google Scholar] [CrossRef]
- Martinez, A.; Frost, J.D. The influence of surface roughness form on the strength of sand-structure interfaces. Géotechnique Lett. 2017, 7, 104–111. [Google Scholar] [CrossRef]
- Jing, X.Y.; Zhou, W.H.; Zhu, H.X.; Yin, Z.Y.; Li, Y.M. Analysis of soil-structural interface behavior using three-dimensional DEM simulations. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 339–357. [Google Scholar] [CrossRef]
- Kou, H.L.; Diao, W.Z.; Zhang, W.C.; Zheng, J.B.; Ni, P.P.; Jang, B.A.; Wu, C.Z. Experimental Study of Interface Shearing between Calcareous Sand and Steel Plate Considering Surface Roughness and Particle Size. Appl. Ocean. 2021, 107, 9. [Google Scholar] [CrossRef]
- Morimichi, U.; Hideaki, K.; Yuichiro, U. Friction between dry sand and concrete under monotonic and repeated loading. Soils Found. 2008, 30, 115–128. [Google Scholar] [CrossRef] [Green Version]
- Frost, J.D.; Han, J. Behavior of Interfaces between Fiber-Reinforced Polymers and Sands. J. Geotech. Geoenviron. Eng. 1999, 125, 633–640. [Google Scholar] [CrossRef]
- Dove, J.E.; Frost, J.D. Peak friction behavior of smooth geomembrane-particle interfaces. J. Geotech. Geoenviron. Eng. 1999, 125, 544–555. [Google Scholar] [CrossRef]
- Han, F.; Ganju, E.; Salgado, R.; Prezzi, M. Effects of Interface Roughness, Particle Geometry, and Gradation on the Sand-Steel Interface Friction Angle. J. Geotech. Geoenviron. Eng. 2018, 144, 12. [Google Scholar] [CrossRef]
- Hryciw, R.D.; Student, M.I. Behavior of Sand Particles Around Rigid Ribbed Inclusions During Shear-ScienceDirect. Soils Found. 1993, 33, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.B.; Zhang, J.S.; Xiao, Y.J.; Li, J. Effect of roughness on shear behavior of red clay-concrete interface in large-scale direct shear tests. Can. Geotech. J. 2015, 52, 1122–1135. [Google Scholar] [CrossRef]
- Su, L.J.; Zhou, W.H.; Chen, W.B.; Jie, X.X. Effects of relative roughness and mean particle size on the shear strength of sand-steel interface. Measurement 2018, 122, 339–346. [Google Scholar] [CrossRef]
- Puech, A. Advances in axial cyclic pile design: Contribution of the SOLCYP project. In Proceedings of the ISSMGE Conference, TC 209 Workshop, Design for Cyclic Loading: Piles and Other Foundations, Paris, France, 4 September 2013; pp. 45–57. [Google Scholar]
- Kou, H.L.; Guo, W.; Zhang, M.Y.; Xu, Y.Q. Axial resistance of long rock-socketed bored piles in stratified soils. Ocean Eng. 2016, 114, 58–65. [Google Scholar] [CrossRef]
- Han, F.; Ganju, E.; Salgado, R.; Prezzi, M. Comparison of the load response of closed-ended and open-ended pipe piles driven in gravelly sand. Acta Geotech. 2019, 14, 1785–1803. [Google Scholar] [CrossRef]
- Fakharian, K.; Vafaei, N. Effect of density on skin friction response of piles embedded in sand by simple shear interface tests. Can. Geotech. J. 2021, 58, 619–636. [Google Scholar] [CrossRef]
- O’’Rourke, T.D.; Druschel, S.J.; Netravali, A.N. Shear Strength Characteristics of Sand-Polymer Interfaces. J. Geotech. Eng. 1990, 116, 451–469. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Liu, F.Y.; Hu, X.Q.; Ca, I.Y.Q. Cyclic and post-cyclic direct shear behaviors of geogrid-sand interface with different soil densities. Chin. J. Geotech. Eng. 2016, 38, 342–349. [Google Scholar] [CrossRef]
- Jin-xian, X. Research on Pore Diameter Variation Rule of Cast-in-Place Pile. Ph.D. Thesis, Tongji University, Shanghai, China, 2007. [Google Scholar]
- Jiang, D.H. Research on Quality of Drilled Holes for Cast-in-Place Piles in Shanghai District. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- ASTM (ASTM D2487–17e1); Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM: West Conshohocken, PA, USA, 2020.
- Taha, A.; Fall, M. Shear behavior of sensitive marine clay-steel interfaces. Acta Geotech. 2014, 9, 969–980. [Google Scholar] [CrossRef]
- ASTM. D5321; Standard test method for determining the coefficient of soil and geosynthetic or geosynthetic and geosynthetic friction by the direct shear method. ASTM Designation: West Conshohocken, PA, USA, 2012. [CrossRef]
- Cheng, H.; Wang, X.; Zhang, J.; Liu, Q.; Liu, W. Large-scale Direct Shear Tests of Interfaces Between Different Soils and Concrete Considering Roughness Effect. Adv. Eng. Sci. 2019, 51, 117–125. [Google Scholar] [CrossRef]
- Uesugi, M.; Engineering, H.K.O.G. Frictional Resistance at Yield between Dry Sand and Mild Steel. Soils Found. 1986, 26, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Namjoo, A.M.; Jafari, K.; Toufigh, V. Effect of particle size of sand and surface properties of reinforcement on sand-geosynthetics and sand-carbon fiber polymer interface shear behavior. Transp. Geotech. 2020, 24, 18. [Google Scholar] [CrossRef]
- Jia, L.; Yao, Y.P. Dilatancy behavior of soil-structure interfaces and its simulation. Ind. Constr. 2006, 36, 36–38. [Google Scholar] [CrossRef]
- Bishop, A.W. The Strength of Soils as Engineering Materials. Geotechnique 1966, 16, 91–130. [Google Scholar] [CrossRef] [Green Version]
- Bolton, M. The strength and dilatancy of sands. Geotechnique 1987, 36, 219–226. [Google Scholar] [CrossRef]
- Pang, L.; Jiang, C.; Ding, X.; Chen, H.; Deng, L. A parameter calibration method in two-surface elastoplastic model for sand-structure interface under monotonic shear loading. Comput. Geotech. 2021, 134, 104115. [Google Scholar] [CrossRef]
- Saberi, M.; Annan, C.D.; Konrad, J.-M.; Lashkari, A. A critical state two-surface plasticity model for gravelly soil-structure interfaces under monotonic and cyclic loading. Comput. Geotech. 2016, 80, 71–82. [Google Scholar] [CrossRef]
- Mortara, G.; Mangiola, A.; Ghionna, V.N. Cyclic shear stress degradation and post-cyclic behavior from sand-steel interface direct shear tests. Can. Geotech. J. 2007, 44, 739–752. [Google Scholar] [CrossRef]
- Zhou, G.Q.; Xia, H.C.; Zhao, G.S.; Zhou, J. Nonlinear Elastic Constitutive Model of Soil-Structure Interfaces Under Relatively High Normal Stress. J. China Univ. Min. Technol. 2007, 17, 301–305. [Google Scholar] [CrossRef]
- Hosseini, S.M.R.; Jesmani, M. Effect of normal stress and relative compaction on secant friction angle of sands. Turk. J. Eng. Environ. Sci. 2014, 38, 382–391. [Google Scholar] [CrossRef]
- Dove, J.E.; Jarrett, J.B. Behavior of dilative sand interfaces in a geotribology framework. J. Geotech. Geoenviron. Eng. 2002, 128, 25–37. [Google Scholar] [CrossRef]
- Wang, J.Q.; Zhou, J.; Huang, L.Y.; Huang, S.B. Macroscopic and mesoscopic studies of interface interaction on geosynthetics by use of large direct shear tests. Yantu Gongcheng Xuebao/Chin. J. Geotech. Eng. 2013, 35, 908–915. [Google Scholar]
- Zhang, L.; Xu, Z.Y.; Yao, P.; Zhao, M.H.; Chen, L. Experimental study and discrete element simulation on interface friction of geo-encased stone columns. Chin. J. Geotech. Eng. 2022, 44, 72–81. [Google Scholar] [CrossRef]
- Jin, Z.H.; Yang, Q.; Chen, C.; Leng, W.M.; Guo, F.Q.; Zhao, C.Y. Experimental study on effects of the roughness on mechanical behaviors of concrete-sand interface. Chin. J. Rock Mech. Eng. 2018, 37, 754–765. [Google Scholar] [CrossRef]
- Qian, J.G.; Gao, Q.; Xue, J.F.; Chen, H.W.; Huang, M.S. Soil and ribbed concrete slab interface modeling using large shear box and 3D FEM. Geomech. Eng. 2017, 12, 295–312. [Google Scholar] [CrossRef]
- Qian, J.G.; Chen, H.W.; Huang, M.S.; Hu, Y.Y.; Kong, D.Z. Numerical Modeling Pile-Soil Interface of Grouting Screw Uplift Pile. In Proceedings of the International Symposium on Advances in Foundation Engineering, Singapore, 5–6 December 2013. [Google Scholar] [CrossRef]






| Property | Value |
|---|---|
| D10 (mm) | 0.11 |
| D30 (mm) | 0.198 |
| D50 (mm) | 0.75 |
| D60 (mm) | 1.24 |
| Uniformity coefficient (Cu) | 9.50 |
| Coefficient of curvature (Cc) | 0.42 |
| Maximum void ratio emax | 0.73 |
| Minimum void ratio emin | 0.43 |
| Specific gravity Gs | 2.55 |
| Moisture content ω (%) | 12 |
| Constituent | Quantity: kg/m3 | Remarks |
|---|---|---|
| Cement | 317 | Cement strength = 49.3 MPa. Cementing material strength = 37.0 MPa Water/cement ratio = 0.40 Slump value of concrete = 180 mm Maximum water glue ratio = 0.55 |
| Fly ash | 138 | |
| Sharp sand | 596 | |
| Coarse aggregate | 1210 | |
| Water | 184 | |
| Admixture | 4.60 | |
| Density | 2450 |
| Interface Group | Groove Height h (mm) | Interface Roughness I (mm) | Relative Density Dr (%) | Total Testing Specimens | |
|---|---|---|---|---|---|
| I | 0 | 0 | 73, 47, 23 | 50, 150, 250, 350 | 12 |
| II | 20 | 10 | 73, 47, 23 | 50, 150, 250, 350 | 12 |
| III | 40 | 20 | 73, 47, 23 | 50, 150, 250, 350 | 12 |
| IV | 60 | 30 | 73, 47, 23 | 50, 150, 250, 350 | 12 |
| V | - | Sand–sand | 73, 47, 23 | 50, 150, 250, 350 | 12 |
| Roughness I/mm | Relative Density Dr | Maximum Volume Change Values under Different Normal Stresses v (Maximum Dilation or Contraction)/mm | |||
|---|---|---|---|---|---|
| 50 kPa | 150 kPa | 250 kPa | 350 kPa | ||
| 0 | 73% | −0.06 | 0.1 | 0.51 | 0.53 |
| 23% | 0.02 | 0.76 | 1.12 | 1.75 | |
| 10 | 73% | −0.42 | −0.36 | −0.28/0.08 | −0.15/0.38 |
| 23% | −0.14 | 0.07 | 1.27 | 1.14 | |
| 20 | 73% | −0.73 | −0.05 | 0.43 | 0.19 |
| 23% | 0.03 | 2.89 | 3.33 | 3.95 | |
| 30 | 73% | −0.4 | −0.01 | 0.52 | 0.74 |
| 23% | 0.69 | 1.47 | 2.97 | 3.56 | |
| Roughness I/mm | Relative Density Dr | Peak Shear Strength under Different Normal Stress Conditions σn/kPa | |||
|---|---|---|---|---|---|
| 50 kPa | 150 kPa | 250 kPa | 350 kPa | ||
| 0 | 73% | 69.6 | 117.76 | 175 | 256.48 |
| 43% | 47.52 | 100.96 | 157.12 | 215.84 | |
| 23% | 31.12 | 85.2 | 128.2 | 178.68 | |
| 10 | 73% | 111.8 | 206.36 | 280.96 | 354.6 |
| 43% | 71.8 | 140.52 | 226.68 | 318.88 | |
| 23% | 58.32 | 133.76 | 214.24 | 272.52 | |
| 20 | 73% | 100.36 | 174.44 | 259.8 | 295.12 |
| 43% | 57.4 | 128 | 203.48 | 275.68 | |
| 23% | 35.84 | 100.32 | 129.4 | 194.84 | |
| 30 | 73% | 76.44 | 157.24 | 214.92 | 264.52 |
| 43% | 52.6 | 111.44 | 180.2 | 236.24 | |
| 23% | 33.52 | 85.44 | 133.56 | 190.04 | |
| Roughness I/mm | Relative Density Dr | Interface Peak Friction Coefficient μp | |||
|---|---|---|---|---|---|
| 50 kPa | 150 kPa | 250 kPa | 350 kPa | ||
| 0 | 73% | 1.39 | 0.78 | 0.70 | 0.73 |
| 47% | 0.95 | 0.67 | 0.62 | 0.61 | |
| 23% | 0.62 | 0.57 | 0.51 | 0.51 | |
| 10 | 73% | 2.23 | 1.37 | 1.12 | 1.01 |
| 47% | 1.43 | 0.93 | 0.90 | 0.91 | |
| 23% | 1.17 | 0.89 | 0.85 | 0.78 | |
| 20 | 73% | 2.01 | 1.16 | 1.03 | 0.84 |
| 47% | 1.14 | 0.85 | 0.81 | 0.78 | |
| 23% | 0.72 | 0.67 | 0.52 | 0.56 | |
| 30 | 73% | 1.53 | 1.04 | 0.86 | 0.75 |
| 47% | 1.05 | 0.74 | 0.72 | 0.67 | |
| 23% | 0.67 | 0.57 | 0.53 | 0.54 | |
| sand | 73% | 2.04 | 1.31 | 1.04 | 0.99 |
| 47% | 1.56 | 0.96 | 0.93 | 0.90 | |
| 23% | 1.15 | 0.90 | 0.86 | 0.81 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Yang, Q.; Leng, W.; Dong, J.; Xu, F.; Wei, L.; Ruan, B. Experimental Investigation of the Mechanical Properties of the Sand–Concrete Pile Interface Considering Roughness and Relative Density. Materials 2022, 15, 4480. https://doi.org/10.3390/ma15134480
Chen C, Yang Q, Leng W, Dong J, Xu F, Wei L, Ruan B. Experimental Investigation of the Mechanical Properties of the Sand–Concrete Pile Interface Considering Roughness and Relative Density. Materials. 2022; 15(13):4480. https://doi.org/10.3390/ma15134480
Chicago/Turabian StyleChen, Chen, Qi Yang, Wuming Leng, Junli Dong, Fang Xu, Limin Wei, and Bo Ruan. 2022. "Experimental Investigation of the Mechanical Properties of the Sand–Concrete Pile Interface Considering Roughness and Relative Density" Materials 15, no. 13: 4480. https://doi.org/10.3390/ma15134480
APA StyleChen, C., Yang, Q., Leng, W., Dong, J., Xu, F., Wei, L., & Ruan, B. (2022). Experimental Investigation of the Mechanical Properties of the Sand–Concrete Pile Interface Considering Roughness and Relative Density. Materials, 15(13), 4480. https://doi.org/10.3390/ma15134480





