The Heat Partition Ratio during Braking in a Functionally Graded Friction Couple
Abstract
:1. Introduction
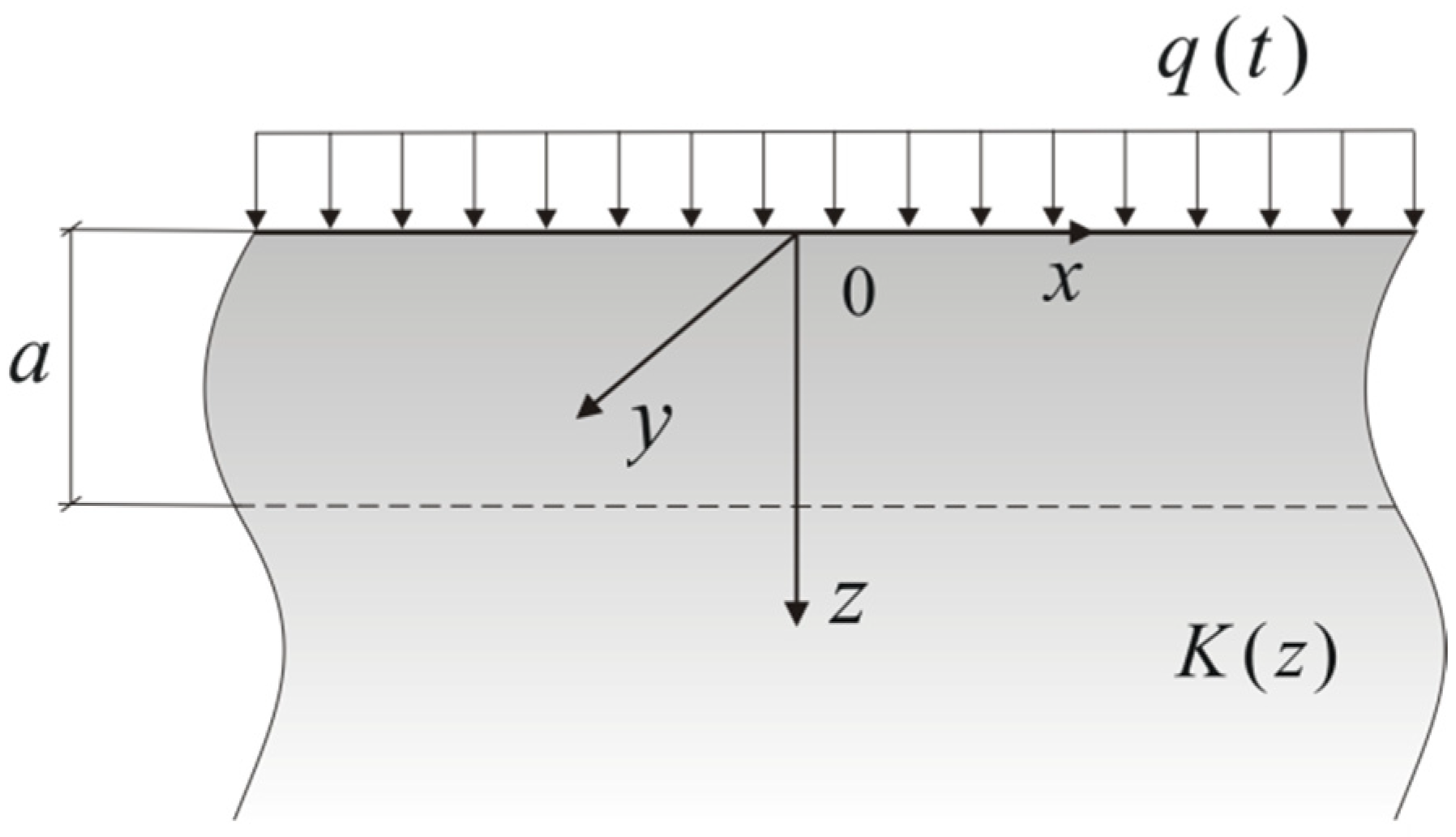
2. Heating of the FGM Semi-Space by the Heat Flux with Constant Intensity
3. Heating of the FGM Semi-Space by Heat Flux with the Intensity Linearly Decreasing in Time
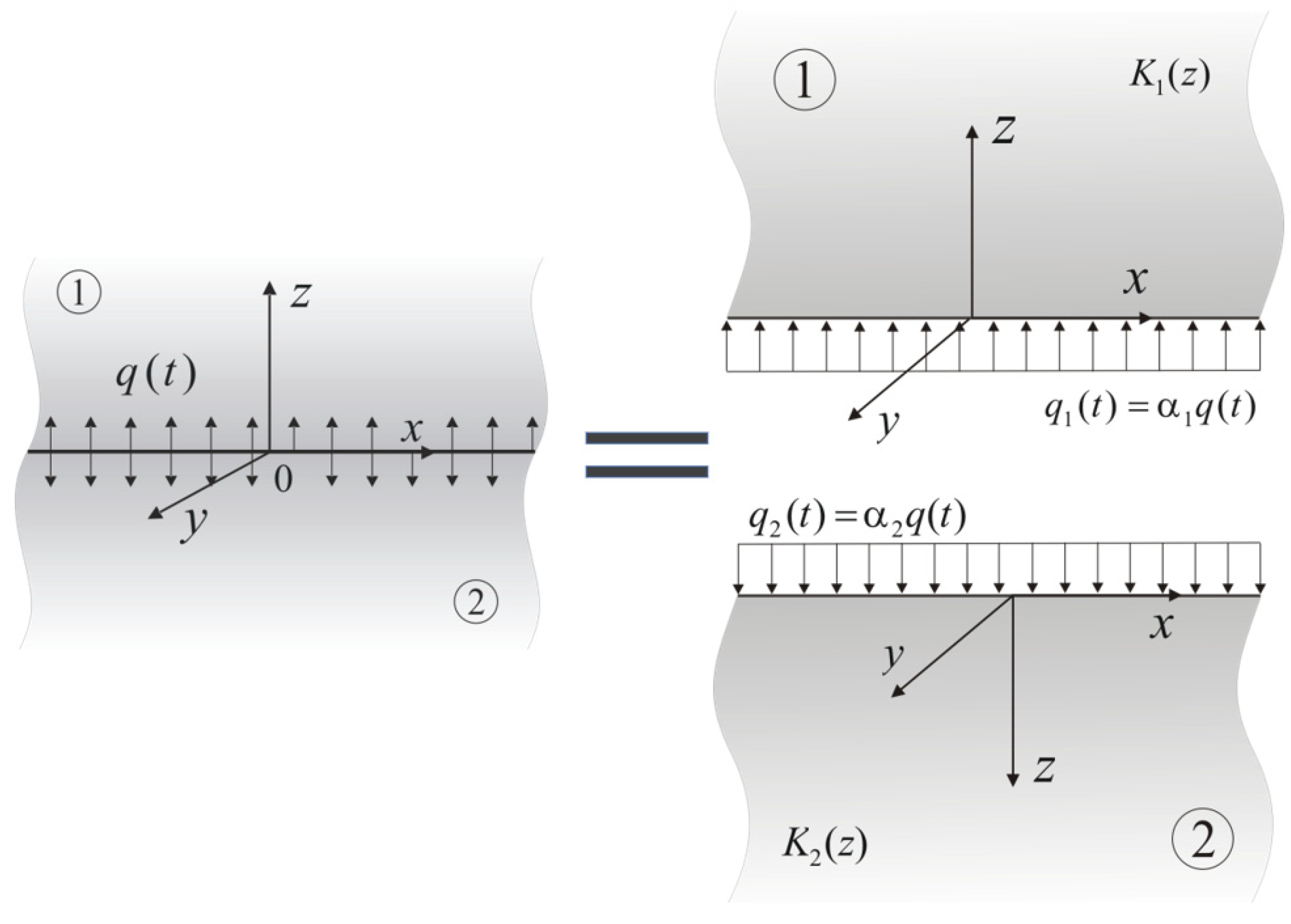
4. The Heat Partition Ratio
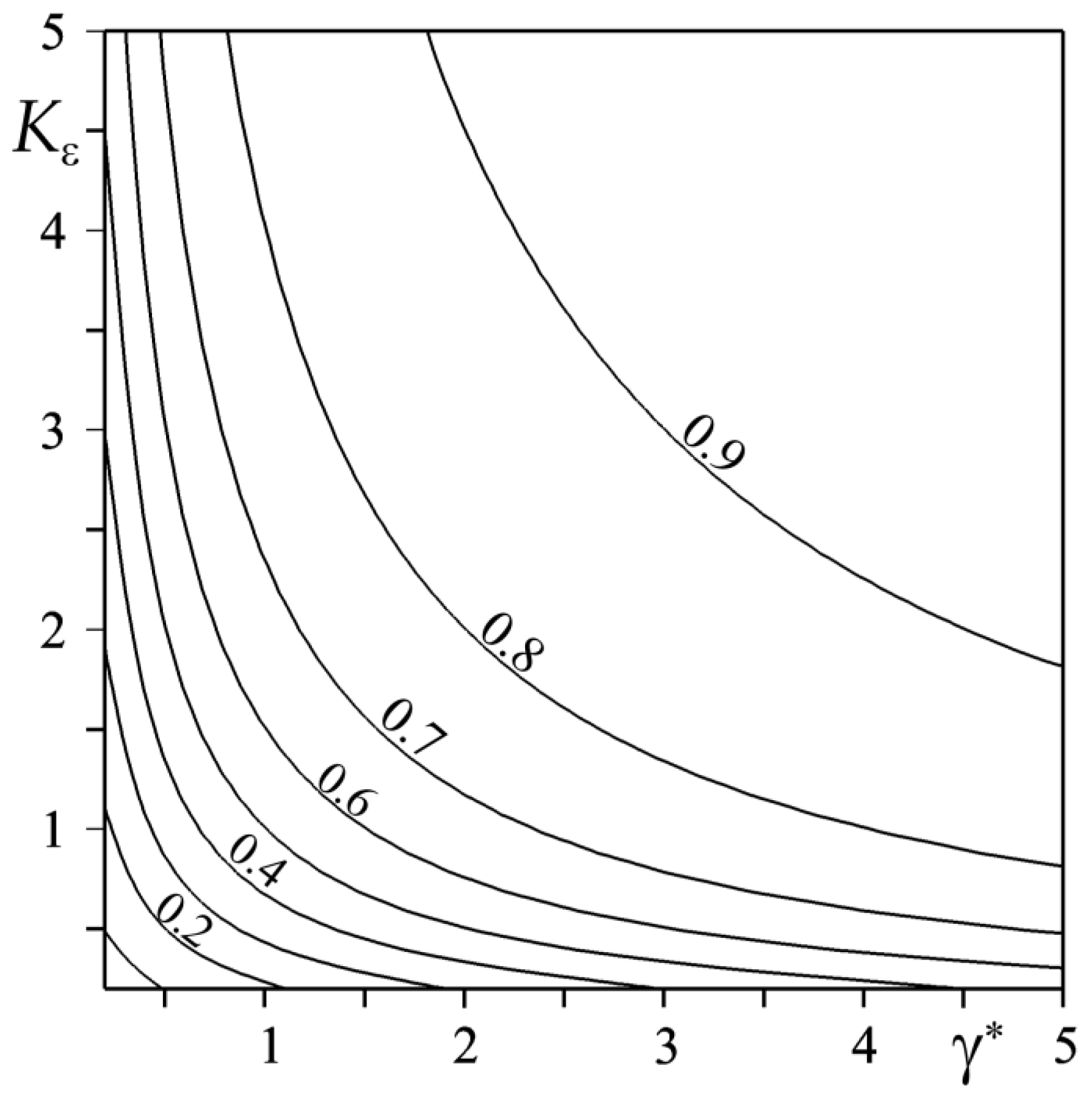
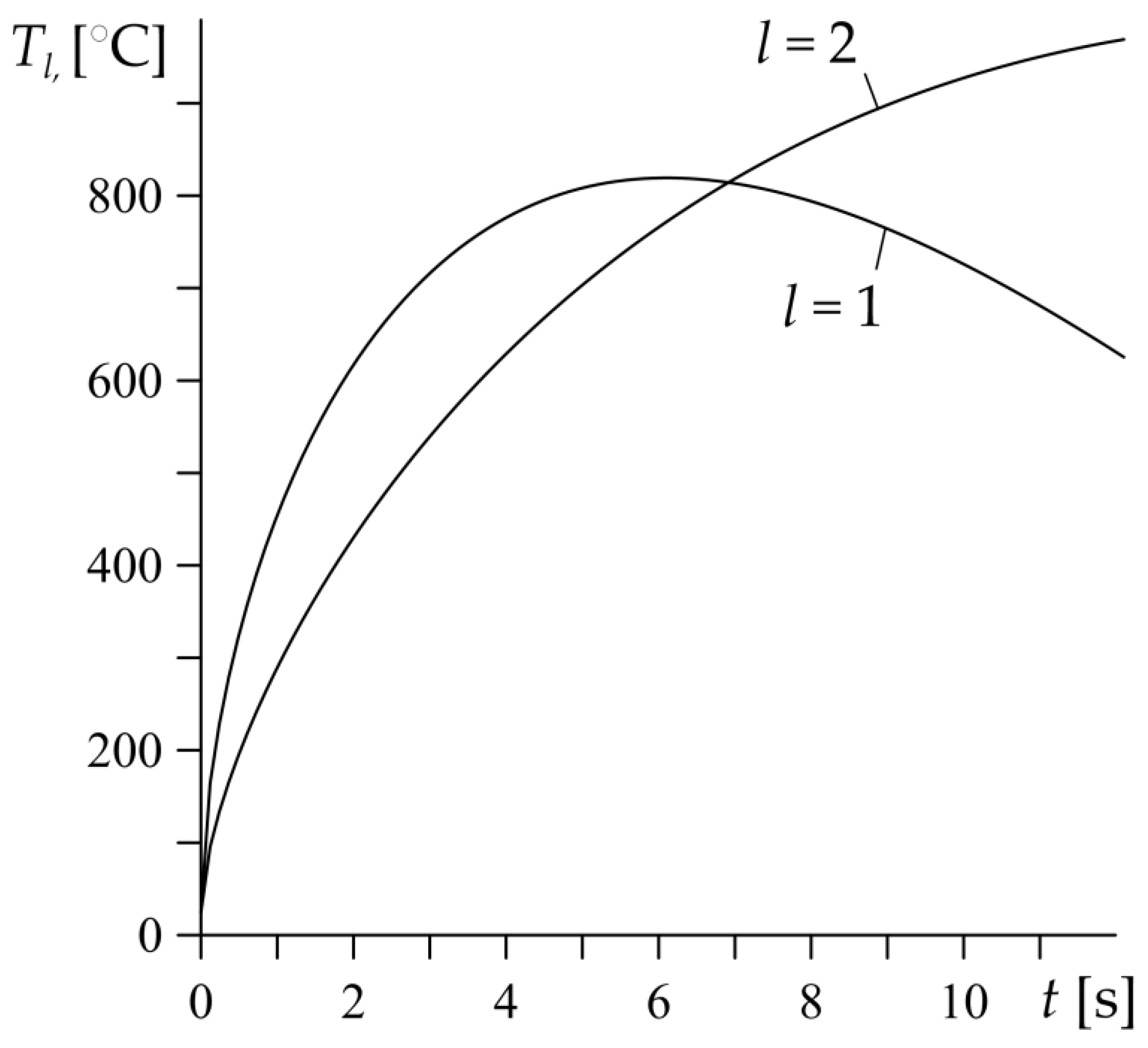
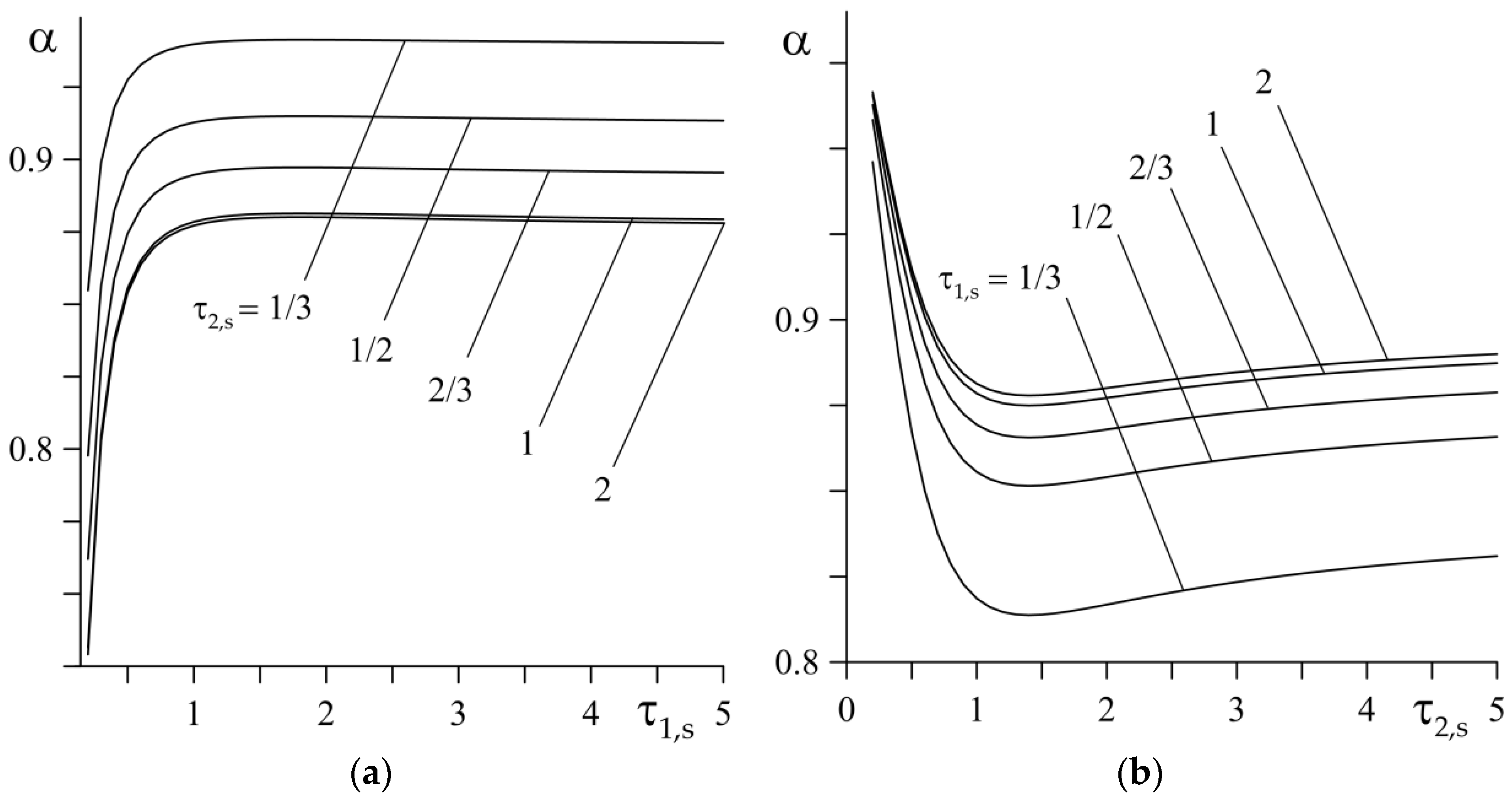
5. Example of Calculation of the Heat Partition Ratio for an FGM Couple
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Effective depth of heat penetration () | |
| Specific heat capacity () | |
| Coefficient of friction | |
| Modified Bessel functions of the first kind of the kth order | |
| Bessel functions of the first kind of the kth order | |
| Thermal diffusivity () | |
| Thermal conductivity () | |
| Dimensionless coefficient of thermal activity of friction couple | |
| Dimensionless parameter of the Laplace integral transform | |
| Intensity of heat flux () | |
| Nominal intensity of the heat flux () | |
| Time () | |
| Braking time () | |
| Temperature () | |
| Initial temperature () | |
| Volume fraction of the material phases (dimensionless) | |
| Spatial coordinate in axial direction () | |
| Heat partition ratio | |
| Parameter of material gradient () | |
| FGMs gradient ratio | |
| Temperature rise () | |
| Dimensionless temperature rise | |
| Scaling factor of temperature rise () | |
| Density () | |
| Dimensionless time | |
| Dimensionless braking time | |
| Dimensionless spatial coordinate in axial direction |
References
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal Barrier Coatings for Gas-Turbine Engine Applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Mahamood, R.M.; Akinlabi, E.T. Functionally Graded Materials; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Zhou, W.; Ai, S.; Chen, M.; Zhang, R.; He, R.; Pei, Y.; Fang, D. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2 + Ni) functionally graded bolted joint. Compos. Part B Eng. 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, R.; Ai, S.; He, R.; Pei, Y.; Fang, D. Load distribution in trends of porous metal-ceramic functionally graded composite joints subjected to thermomechanical loading. Compos. Struct. 2015, 134, 680–688. [Google Scholar] [CrossRef] [Green Version]
- Mahmoud, D.; Elbestawi, M. Lattice Structures and Functionally Graded Materials. Applications in Additive Manufacturing of Orthopedic Implants: A Review. J. Manuf. Mater. Process. 2017, 1, 13. [Google Scholar] [CrossRef]
- Hovorun, T.P.; Berladir, K.V.; Pererva, V.I.; Rudenko, S.G.; Martynov, A.I. Modern Materials for Automotive Industry. J. Eng. Sci. 2017, 4, 8–18. [Google Scholar] [CrossRef] [Green Version]
- Strojny-Nędza, A.; Pietrzak, K.; Gili, F.; Chmielewski, M. FGM based on copper-alumina composites for brake disc applications. Arch. Civ. Mech. Eng. 2020, 20, 83. [Google Scholar] [CrossRef]
- Newcomb, T.P. Temperatures reached in disc brakes. J. Mech. Eng. Sci. 1960, 2, 167–177. [Google Scholar] [CrossRef]
- Chichinadze, A.V. Polymers in Friction Assembles of Machines and Devices: A Handbook; Allerton Press Inc.: New York, NY, USA, 1984. [Google Scholar]
- Day, A.J. Braking of Road Vehicles; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Ling, F.F. Surface Mechanics; John Wiley & Sons: New York, NY, USA, 1973. [Google Scholar]
- Barber, J.R.; Comninou, M. Thermoelastic contact problems. In Thermal Stresses, 3rd ed.; Hetnarsky, R.R., Ed.; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Awrejcewicz, J.; Pyryev, Y. Nonsmooth Dynamics of Contacting Thermoelastic Bodies; Springer: New York, NY, USA, 2009. [Google Scholar]
- Yevtushenko, A.A.; Kuciej, M. One-dimensional thermal problem of friction during braking: The history of development and actual state. Int. J. Heat Mass Transf. 2012, 55, 4148–4153. [Google Scholar] [CrossRef]
- Evtushenko, O.; Kuciej, M.; Topczewska, K. Determination of the maximal temperature of a pad-disk tribosystem during one-time braking. Mater. Sci. 2020, 56, 152–159. [Google Scholar] [CrossRef]
- Pyryev, Y.; Yevtushenko, A. The influence of the brakes friction elements thickness on the contact temperature and wear. Heat Mass Transf. 2000, 36, 319–323. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Grześ, P. The FEM-modeling of the frictional heating phenomen in the pad/disc tribosystem (a review). Num. Heat Trans. Part A-Appl. 2010, 58, 207–226. [Google Scholar] [CrossRef]
- Wasilewski, P. Frictional heating in railway brakes: A review of numerical models. Arch. Computat. Methods Eng. 2020, 27, 45–58. [Google Scholar] [CrossRef]
- Deressa, K.T.; Ambie, D.A. Thermal load simulations in railway disc brake: A systematic review of modelling temperature, stress and fatigue. Arch. Computat. Methods Eng. 2022, 29, 2271–2283. [Google Scholar] [CrossRef]
- Blok, H. Theoretical field study of temperature rise at surfaces of actual contact under oiliness lubricating conditions. Proc. Instn. Mech. Engrs. (Gen. Discuss. Lubr. Lubr.) 1937, 45, 222–235. [Google Scholar]
- Day, A.J.; Newcomb, T.P. Dissipation of frictional energy from the interface of an annular disc brake. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1984, 198, 201–209. [Google Scholar] [CrossRef]
- Grześ, P. Partition of heat in 2D finite element model of a disc brake. Acta Mech. Autom. 2011, 5, 35–41. [Google Scholar]
- Yevtushenko, A.A.; Grześ, P. Finite element analysis of heat partition ratio in a pad/disc brake system. Num. Heat Trans. Part A-Appl. 2011, 58, 521–542. [Google Scholar] [CrossRef]
- Qiu, L.Q.; Qi, H.S.; Wood, A. Two-dimensional finite element analysis of the heat partition ratio of a friction brake. Proc. Inst. Mech. Eng. Part J J. Eng. Trib. 2018, 232, 1489–1501. [Google Scholar] [CrossRef] [Green Version]
- Afzal, A.; Abdul Mujeebu, M. Thermo-Mechanical and Structural Performances of Automobile Disc Brakes: A Review of Numerical and Experimental Studies. Arch. Comput. Methods Eng. 2019, 26, 1489–1513. [Google Scholar] [CrossRef]
- Carslaw, H.C.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Hasselgruber, H. Der Schaltvorgang einer Trockenreibung Kupplung bei kleinster Erwärmung. Konstruction 1963, 15, 41–45. [Google Scholar]
- Ginzburg, A.G. Coefficient of distribution of the heat flows during braking. In Calculation and Testing of Friction Couples; Mechanical Engineering: Moscow, Russia, 1974. (In Russian) [Google Scholar]
- Yevtushenko, A.; Kuciej, M.; Topczewska, K. Effect of the Temporal Profile of the Friction Power on Temperature of a Pad-Disc Brake System. J. Theoret. Appl. Mech. 2019, 57, 461–473. [Google Scholar] [CrossRef]
- Xiong, C.; Chen, M.; Yu, L. Analytical model and material equivalent methods for steady state heat partition coefficient between two contact discs in multi-disc clutch. Proc. J. Mech. Eng. J. Automob. Eng. 2019, 234, 857–871. [Google Scholar] [CrossRef]
- Xia, Y.; Yano, A.; Hayashi, N.; Noraguchi, N.; Xie, G. Analysis of temperature and heat partitioning coefficient during friction between polymer and steel. Tribol. Int. 2022, 171, 107561. [Google Scholar] [CrossRef]
- Yevtushenko, A.; Topczewska, K.; Zamojski, P. Influence of Thermal Sensitivity of Functionally Graded Materials on Temperature during Braking. Materials 2022, 15, 963. [Google Scholar] [CrossRef]
- Yevtushenko, A.; Topczewska, K.; Kuciej, M. Analytical Determination of the Brake Temperature Mode during Repetitive Short-Term Braking. Materials 2021, 14, 1912. [Google Scholar] [CrossRef]
- Sneddon, I.N. The Use of Integral Transforms; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; United States Department of Commerce, National Bureau of Standards (NBS): Washington, DC, USA, 1964. [Google Scholar]
- Vashchenko-Zakharchenko, M.E. Symbolic Calculus and Its Application to Integration of Linear Differential Equations; University Press: Kiev, Ukraine, 1862. [Google Scholar]
- Yevtushenko, A.; Topczewska, K.; Zamojski, P. The Effect of Functionally Graded Materials on Temperature during Frictional Heating: Under Uniform Sliding. Materials 2021, 14, 4285. [Google Scholar] [CrossRef]
- Bateman, H.; Erdélyi, A. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume 1. [Google Scholar]
- Yevtushenko, A.; Topczewska, K.; Zamojski, P. The Effect of Functionally Graded Materials on Temperature during Frictional Heating at Single Braking. Materials 2021, 14, 6241. [Google Scholar] [CrossRef]
- Özişik, N.M. Heat Conduction; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Charron, F. Partage de la Chaleur Entre Deux Corps Frottants; Publications Scientifiques et Techniques; Blondel La Rougery: Paris, France, 1943; 182p. [Google Scholar]
- Talati, F.; Jalalifar, S. Analysis of heat conduction in a disk brake system. Heat Mass Transf. 2009, 45, 1047–1059. [Google Scholar] [CrossRef]
- Adamowicz, A.; Grześ, P. Analysis of disc brake temperature distribution during single braking under non-axisymmetric load. Appl. Therm. Eng. 2011, 31, 1003–1012. [Google Scholar] [CrossRef] [Green Version]
- Loizou, A.; Qi, H.S.; Day, A.J. A fundamental study on the heat partition ratio of vehicle disk brakes. J. Heat Transf. 2013, 135, 121302. [Google Scholar] [CrossRef]
- Yevtushenko, A.; Kuciej, M.; Topczewska, K. Analytical model for investigation of the effect of friction power on temperature in the disk brake. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Topczewska, K. Influence of the Time of Increase in Contact Pressure in the Course of Braking on the Temperature of a Pad–Disc Tribosystem. Mater. Sci. 2018, 54, 250–259. [Google Scholar] [CrossRef]
- Mao, J.J.; Ke, L.L.; Yang, J.; Kitipornchai, S.; Wang, Y.S. The coupled thermoelastic instability of FGM coatings with arbitrarily varying properties: In-plane sliding. Acta Mech. 2018, 229, 2979–2995. [Google Scholar] [CrossRef]
| Element Subscript | Material Subscript, m | Material | Thermal Conductivity | Specific Heat Capacity | |
|---|---|---|---|---|---|
| base, 0 | Al2O3 | 37.24 | 727.29 | 3990.92 | |
| core, 1 | Cu | 402.65 | 147.35 | 8947.92 | |
| base, 0 | ZrO2 | 1.94 | 452.83 | 6102.16 | |
| core, 1 | Ti-6Al-4V | 6.87 | 538.08 | 4431.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yevtushenko, A.; Topczewska, K.; Zamojski, P. The Heat Partition Ratio during Braking in a Functionally Graded Friction Couple. Materials 2022, 15, 4623. https://doi.org/10.3390/ma15134623
Yevtushenko A, Topczewska K, Zamojski P. The Heat Partition Ratio during Braking in a Functionally Graded Friction Couple. Materials. 2022; 15(13):4623. https://doi.org/10.3390/ma15134623
Chicago/Turabian StyleYevtushenko, Aleksander, Katarzyna Topczewska, and Przemysław Zamojski. 2022. "The Heat Partition Ratio during Braking in a Functionally Graded Friction Couple" Materials 15, no. 13: 4623. https://doi.org/10.3390/ma15134623
APA StyleYevtushenko, A., Topczewska, K., & Zamojski, P. (2022). The Heat Partition Ratio during Braking in a Functionally Graded Friction Couple. Materials, 15(13), 4623. https://doi.org/10.3390/ma15134623








