Effect of Shear and Pure Bending Spans on the Behaviour of Steel Beams with Corrugated Webs
Abstract
:1. Introduction
2. Experimental Program
2.1. Fabrication and Details of Specimens
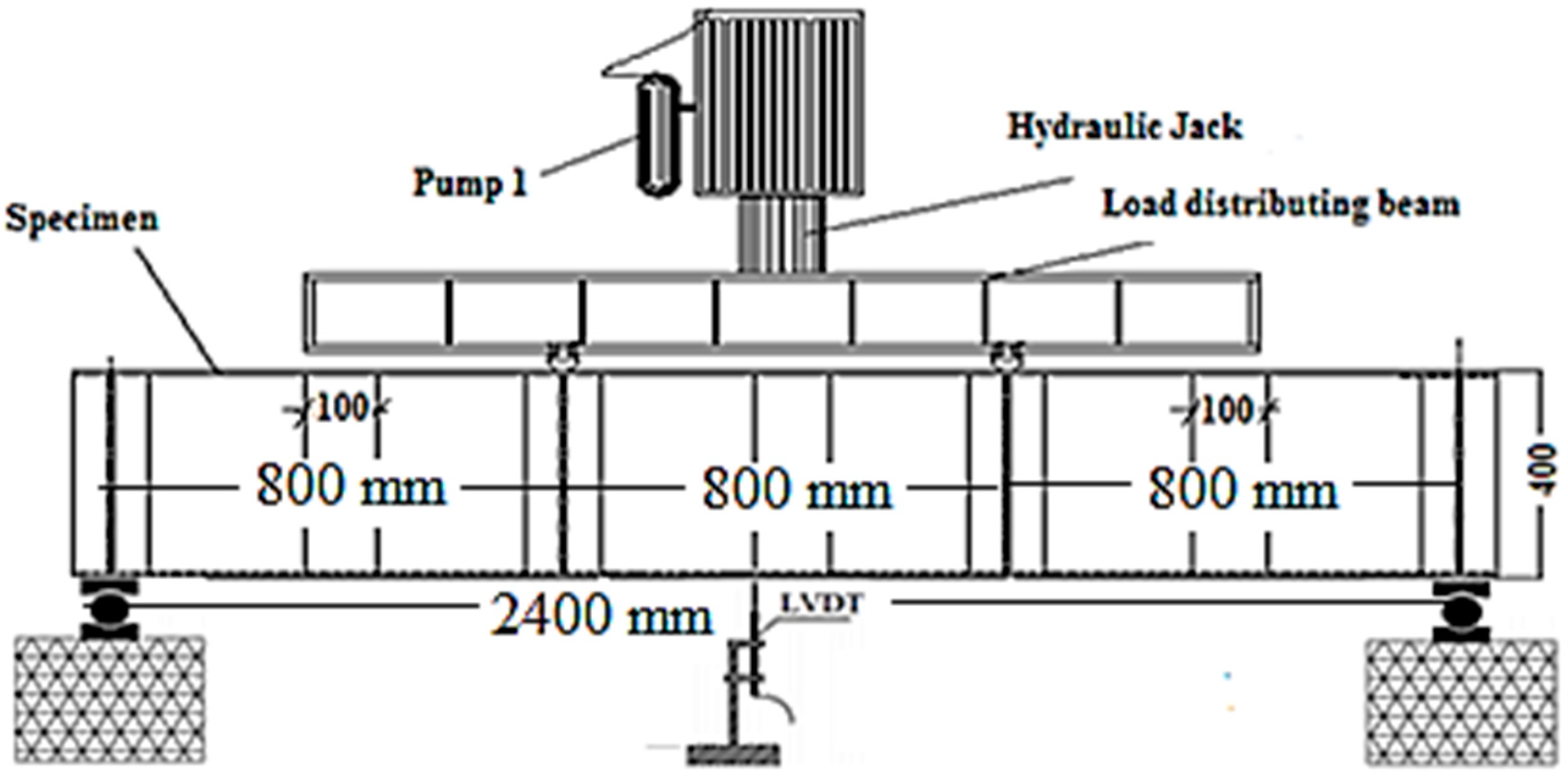
2.2. Testing Procedure and Instrumentations
2.3. Test Results and Discussion
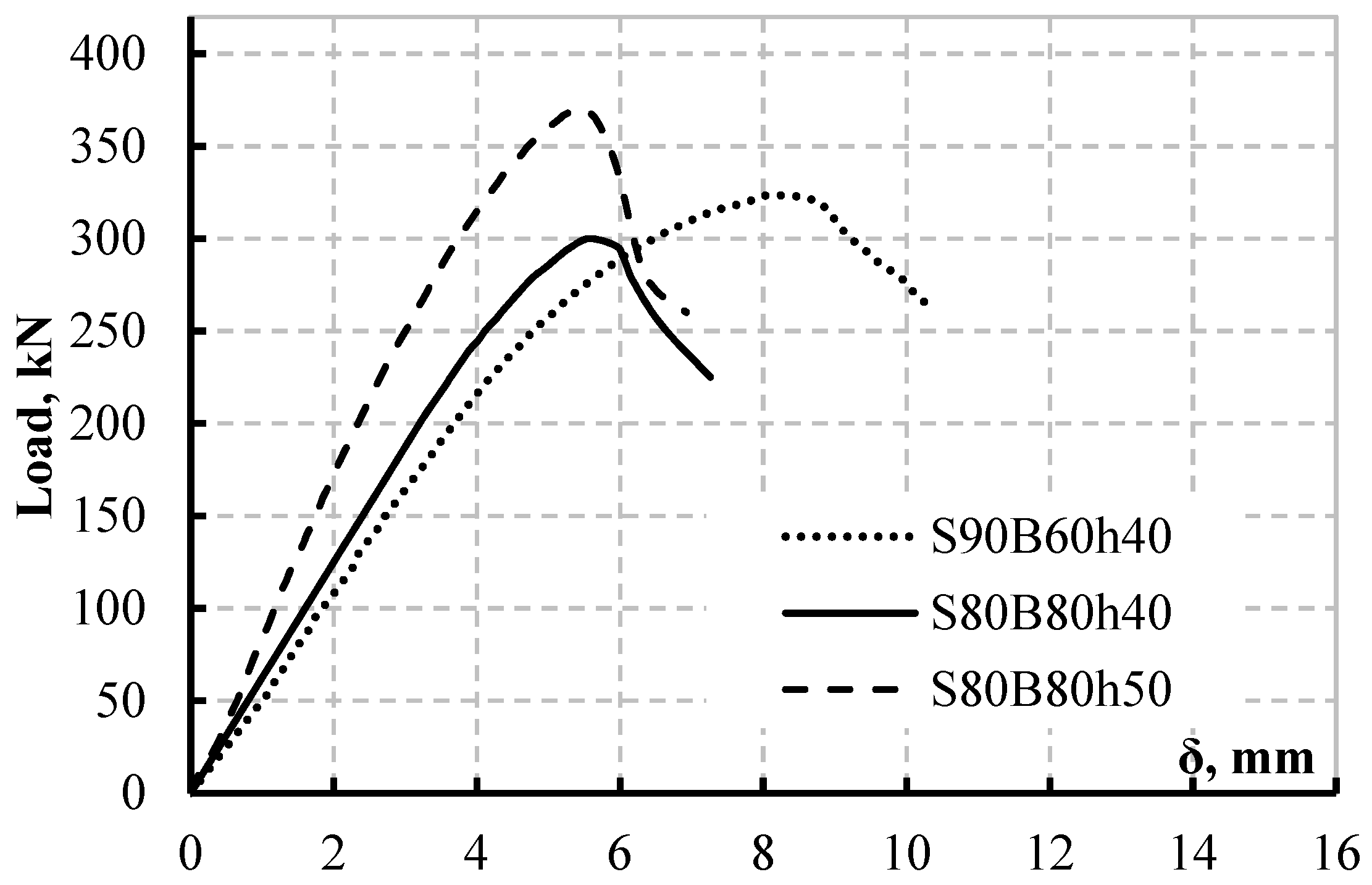
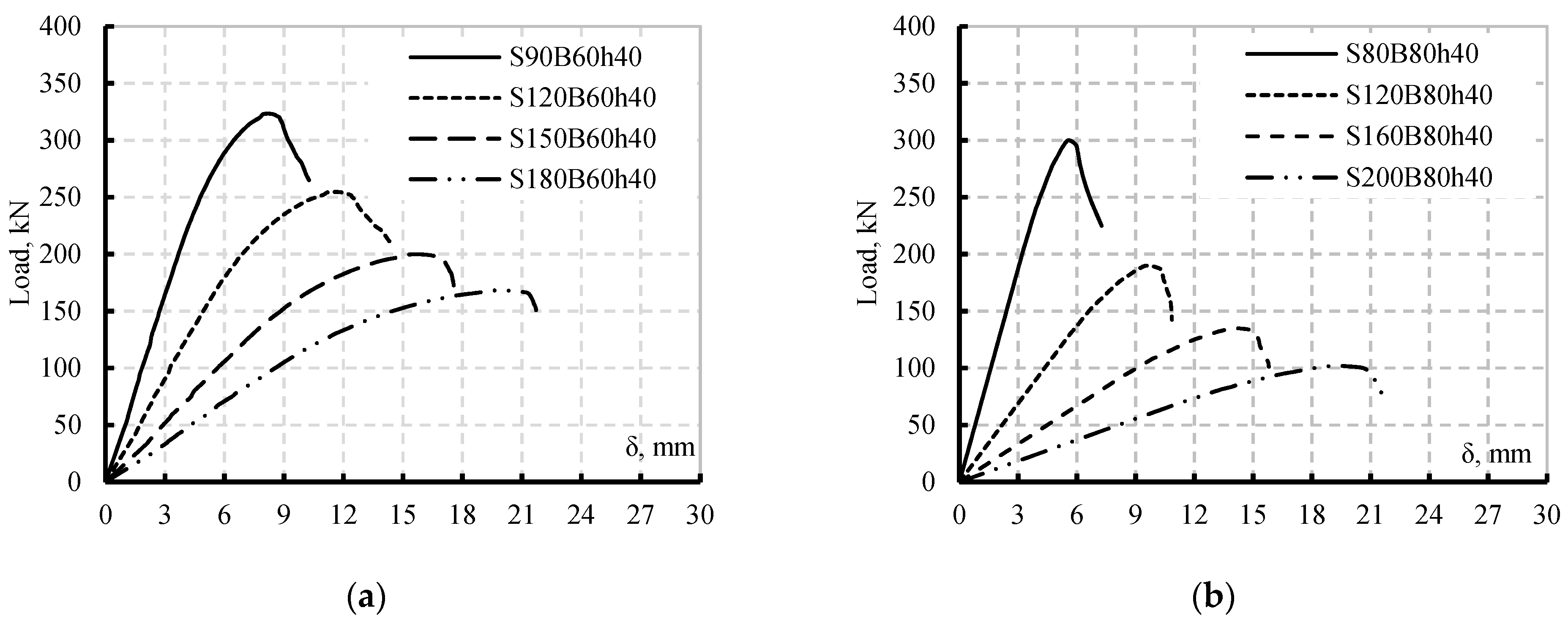
Load-Deflection Response
3. Theoretical Analysis
3.1. EN 1993-1-5 Standard
3.2. DASt-Richtlinie 015
4. Numerical Simulation
4.1. Modelling, Mesh Sensitivity, and Initial Imperfection
4.2. Parametric Study
5. Conclusions
- The ultimate load capacity and failure mechanism of SBCWs are not affected by pure bending span in both scenarios of loading (i.e., over inclined or horizontal folds); since the bending moment value does not change;
- Shear span is the most important component in determining the ultimate load capacity of the SBCW. On the other hand, shear span can only influence the failure load value, whereas the failure mode is the same and controlled by the maximum bending moment that the compression flange can withstand;
- The overall bending moment produced by the load multiplied by the moment arm, as well as the transversal bending moment formed by shear force, control the failure mode for SBCW governed by flange buckling modes;
- The increase in S.S lengths had higher effects than increasing the B.S lengths on the beam capacity and stiffness; in contrast there were no effects on the failure modes.
Author Contributions
Funding
Conflicts of Interest
References
- Elgaaly, M.; Seshadri, A.; Hamilton, R.W. Bending strength of steel beams with corrugated webs. J. Struct. Eng. 1997, 123, 772–782. [Google Scholar] [CrossRef]
- Aschinger, R.; Lindner, J. Zu besonderheiten bei Trapezstegtragern. Stahlbau 1997, 66, 136–142. (In Germanica) [Google Scholar]
- Abbas, H.H.; Sause, R.; Driver, R.G. Analysis of flange transverse bending of corrugated web I-girders under in-plane loads. J. Struct. Eng. 2007, 133, 347–355. [Google Scholar] [CrossRef]
- Elgaaly, M.; Hamilton, R.W.; Seshadri, A. Shear strength of beams with corrugated webs. J. Struct. Eng. 1996, 122, 390–398. [Google Scholar] [CrossRef]
- Abbas, H.H.; Sause, R.; Driver, R.G. Behavior of corrugated web I-girders under in- plane loads. J. Eng. Mech. 2006, 132, 806–814. [Google Scholar] [CrossRef]
- Sause, R.; Abbas, H.H.; Wassef, W.G.; Driver, R.G.; Elgaaly, M. Corrugated Web Girder Shape and Strength Criteria. In ATLSS Reports; Report No: 03–18; Leigh University: Bethlehem, PA, USA, 2003; Available online: http://preserve.lehigh.edu/engr-civil-environmental-atlss-reports/245 (accessed on 1 September 2003).
- Abbas, H.H.; Sauce, R.; Driver, R.G. Simplified analysis of flange transverse bending of corrugated web I-girders under in-plane moment and shear. Eng. Struct. 2007, 29, 2816–2824. [Google Scholar] [CrossRef]
- Lindner, J. Zur Bemessung von Trapezstegtragern. Stahlbau 1992, 61, 311–318. (In German) [Google Scholar]
- Elamary, A.S.; Alharthi, Y.; Sharaky, I.A. Behavior of steel beams with different web profiles along the beam length. J. Constr. Steel Res. 2021, 185, 106875. [Google Scholar] [CrossRef]
- Elamary, A.S. Cardiff theory: Web panel aspect ratio limits and their relation with inclination angle of membrane tensile yield strength. Int. J. Steel Struct. 2016, 16, 799–806. [Google Scholar] [CrossRef]
- Lindner, J.; Aschinger, R. Grenz schubtragfähigkeit von I-Trägern mit trapezförmig profillierten Stegen. Stahlbau 1988, 57, 377–380. (In German) [Google Scholar]
- Lee, S.C.; Lee, D.S.; Yoo, C.H. Ultimate shear strength of long web panels. J. Constr. Steel Res. 2008, 64, 1357–1365. [Google Scholar] [CrossRef]
- Luo, R.; Edlund, B. Shear capacity of plate girders with trapezoidally corrugated webs. Thin-Walled Struct. 1996, 26, 19–44. [Google Scholar] [CrossRef]
- Yi, J.; Gil, H.; Youm, K.; Lee, H. Interactive shear buckling behaviour of trapezoidally corrugated steel webs. Eng. Struct. 2008, 30, 1659–1666. [Google Scholar] [CrossRef]
- Alharthi, Y.; Sharaky, I.A.; Elamary, A.S. Numerical analysis of hybrid steel beams with trapezoidal corrugated-web non-welded inclined folds. Adv. Civ. Eng. 2021. [Google Scholar] [CrossRef]
- Moon, J.; Yi, J.; Choi, B.H.; Lee, H.E. Shear strength and design of trapezoidally corrugated steel webs. J. Constr. Steel Res. 2009, 65, 1198–1205. [Google Scholar] [CrossRef]
- Elamary, A.S.; Alharthi, Y.; Abdalla, O.; Alqurashi, M.; Sharaky, I.A. Failure mechanism of hybrid steel beams with trapezoidal corrugated-web non-welded inclined folds. Materials 2021, 14, 1424. [Google Scholar] [CrossRef]
- Eldib, M.E.A. Shear buckling strength and design of curved corrugated steel webs for bridges. J. Constr. Steel Res. 2009, 65, 2129–2139. [Google Scholar] [CrossRef]
- Kövesdi, B.; Jáger, B.; Dunai, L. Bending and shear interaction behavior of girders with trapezoidally corrugated webs. J. Constr. Steel Res. 2016, 121, 383–397. [Google Scholar] [CrossRef]
- Elamary, A.S.; Alharthi, Y.M.; Hassanein, M.F.; Sharaky, I.A. Trapezoidally corrugated web steel beams loaded over horizontal and inclined folds. J. Constr. Steel Res. 2022, 192, 107202. [Google Scholar] [CrossRef]
- Kövesdi, B.; Jáger, B.; Dunai, L. Stress distribution in the flanges of girders with corrugated webs. J. Constr. Steel Res. 2012, 79, 204–215. [Google Scholar] [CrossRef]
- Kövesdi, B. Patch Loading Resistance of Girders with Corrugated Webs. Ph.D. Thesis, Budapest University of Technology & Economics, and Institute of Structural Design, University of Stuttgart, Stuttgart, Germany, 2010. [Google Scholar]
- Koichi, W.; Masahiro, K. In-plane bending capacity of steel girders with corrugated web plates. J. Struct. Eng. JSCE 2006, 62, 323–336. (In Japanese) [Google Scholar]
- Jáger, B.; Dunai, L.; Kövesdi, B. Flange buckling behavior of girders with corrugated web part II: Numerical study and design method development. Thin-Walled Struct. 2017, 118, 238–252. [Google Scholar] [CrossRef]
- Dabon, M.; Elamary, A.S. Flange compactness effects on the behavior of steel beams with corrugated webs. JES. J. Eng. Sci. 2006, 34, 1507–1523. [Google Scholar] [CrossRef]
- EN 1993-1-5; Eurocode 3: Design of Steel Structures, Part 1–5: Plated Structural Elements. European Committee for Standardization: Brussels, Belgium, 2005.
- DIN-EN 1011-2; Recommendations for Welding of Metallic Materials, Part 2 Arc Welding of Ferritic Steels. Deutsches Institut fur Normung: Berlin, Germany, 2001.
- TS 138 EN 10002-1; Metallic Materials-Tensile Testing—Part 1: Method of Test at Ambient Temperature. Turkish Standards Institution: Ankara, Turkey, 2004.
- für Stahlbau, D.A. DASt-Richtlinie 015, Trager mit schlanken Stegen; Stahlbau Verlags- und Service GmbH: Düsseldorf, Germany, 1990. (In German) [Google Scholar]
- ANSYS® v19.2, ANSYS: Canonsburg, PA, USA, 2019.
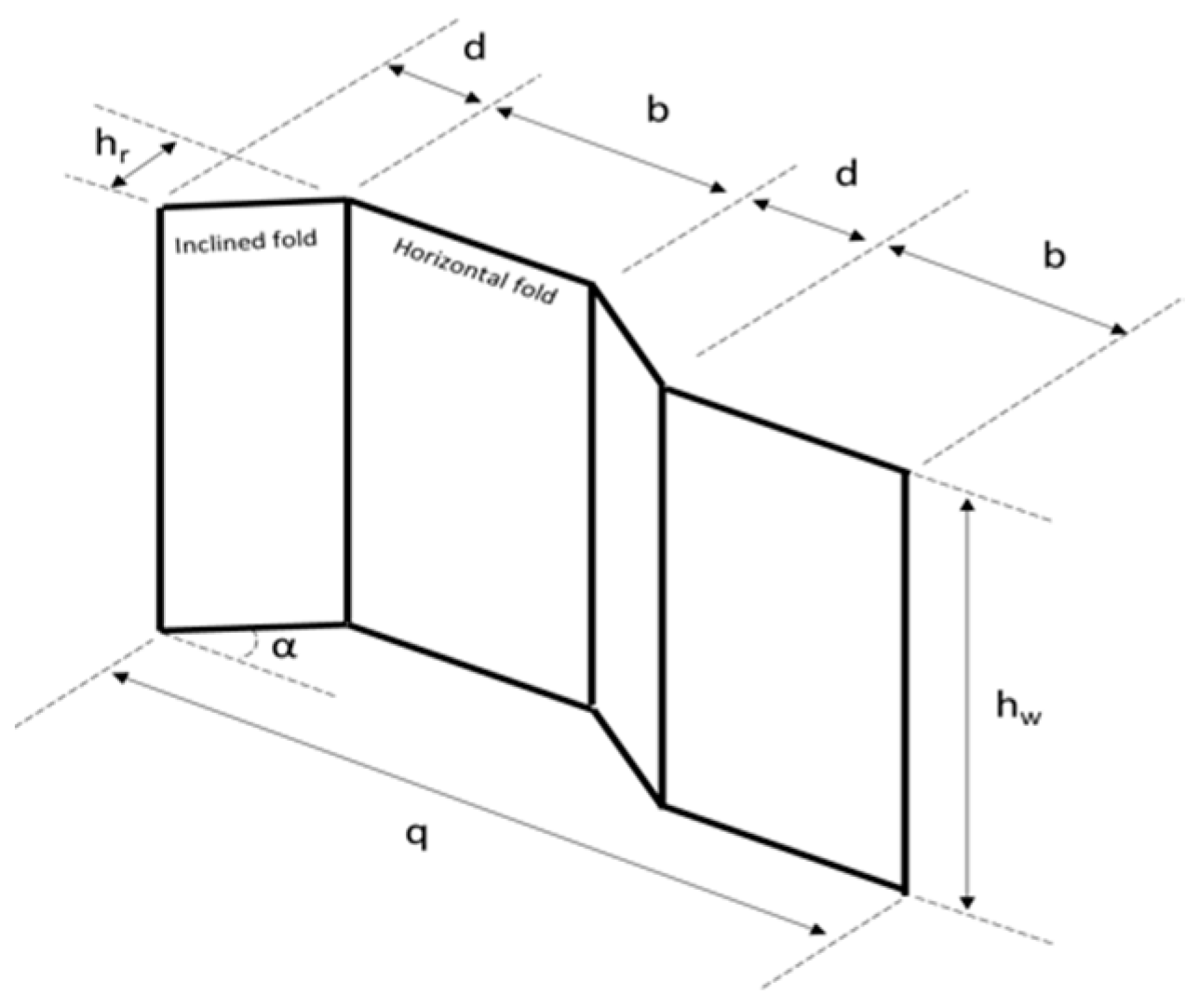

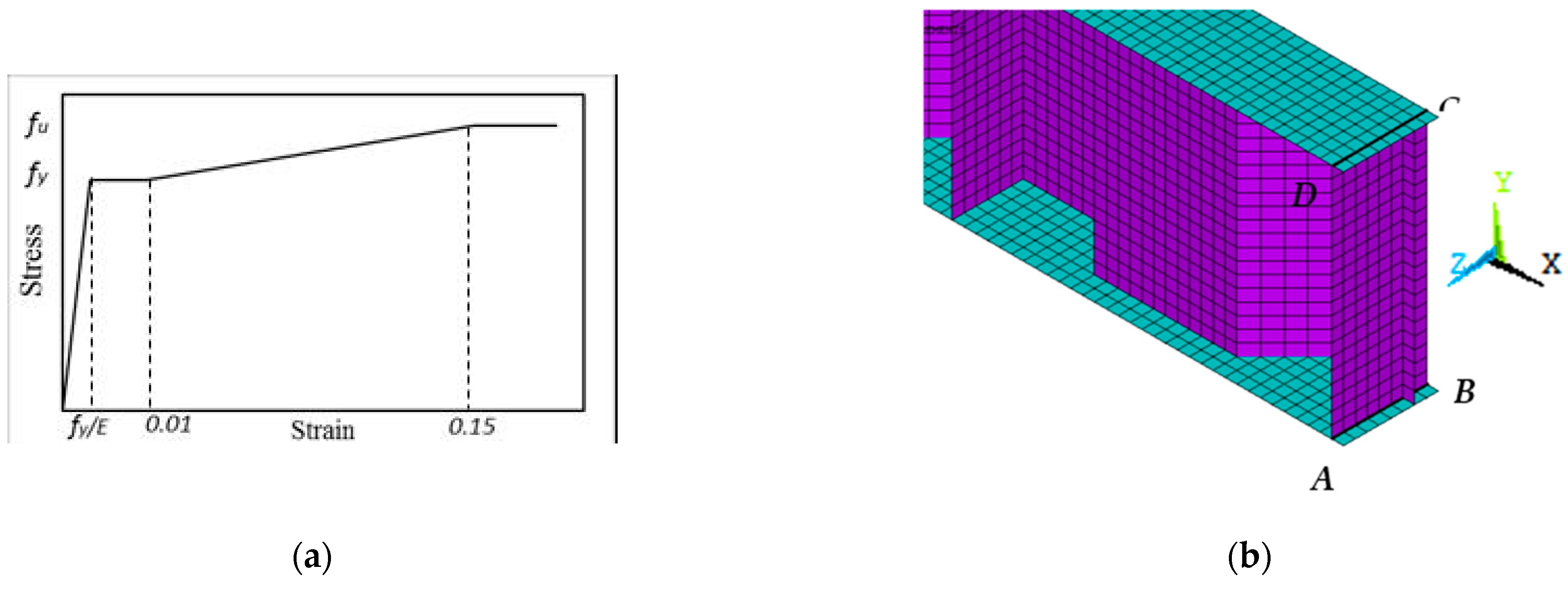
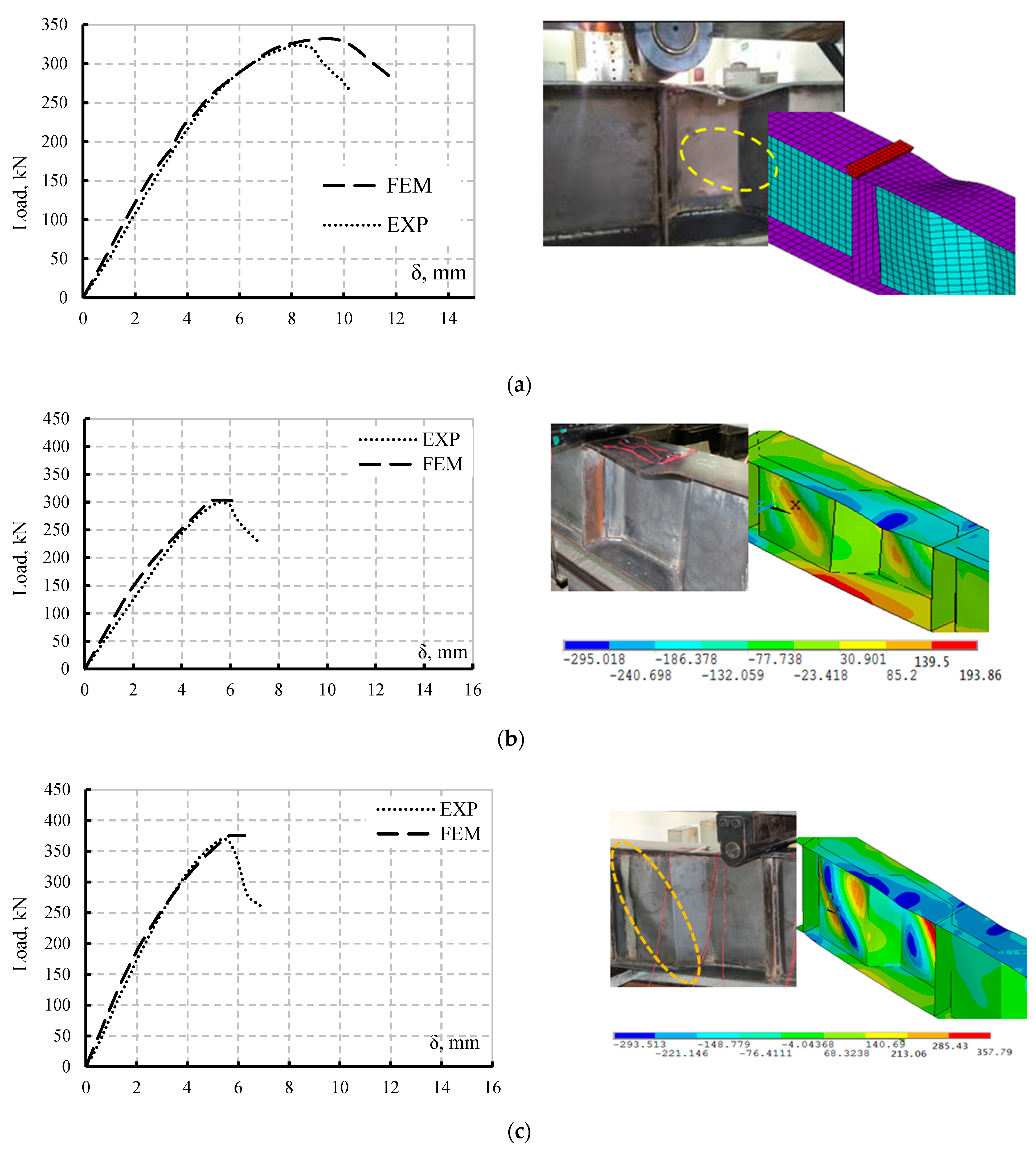
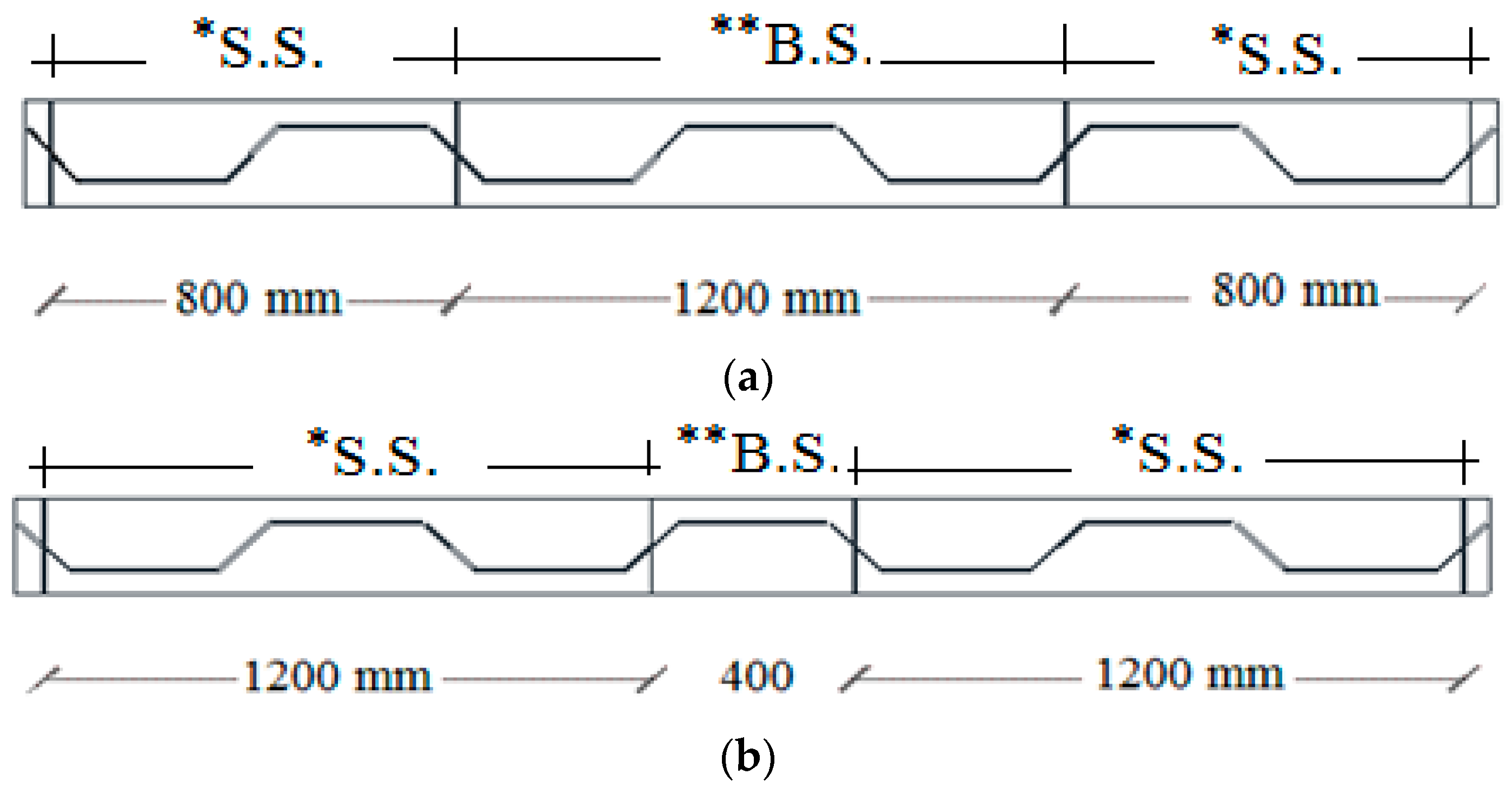
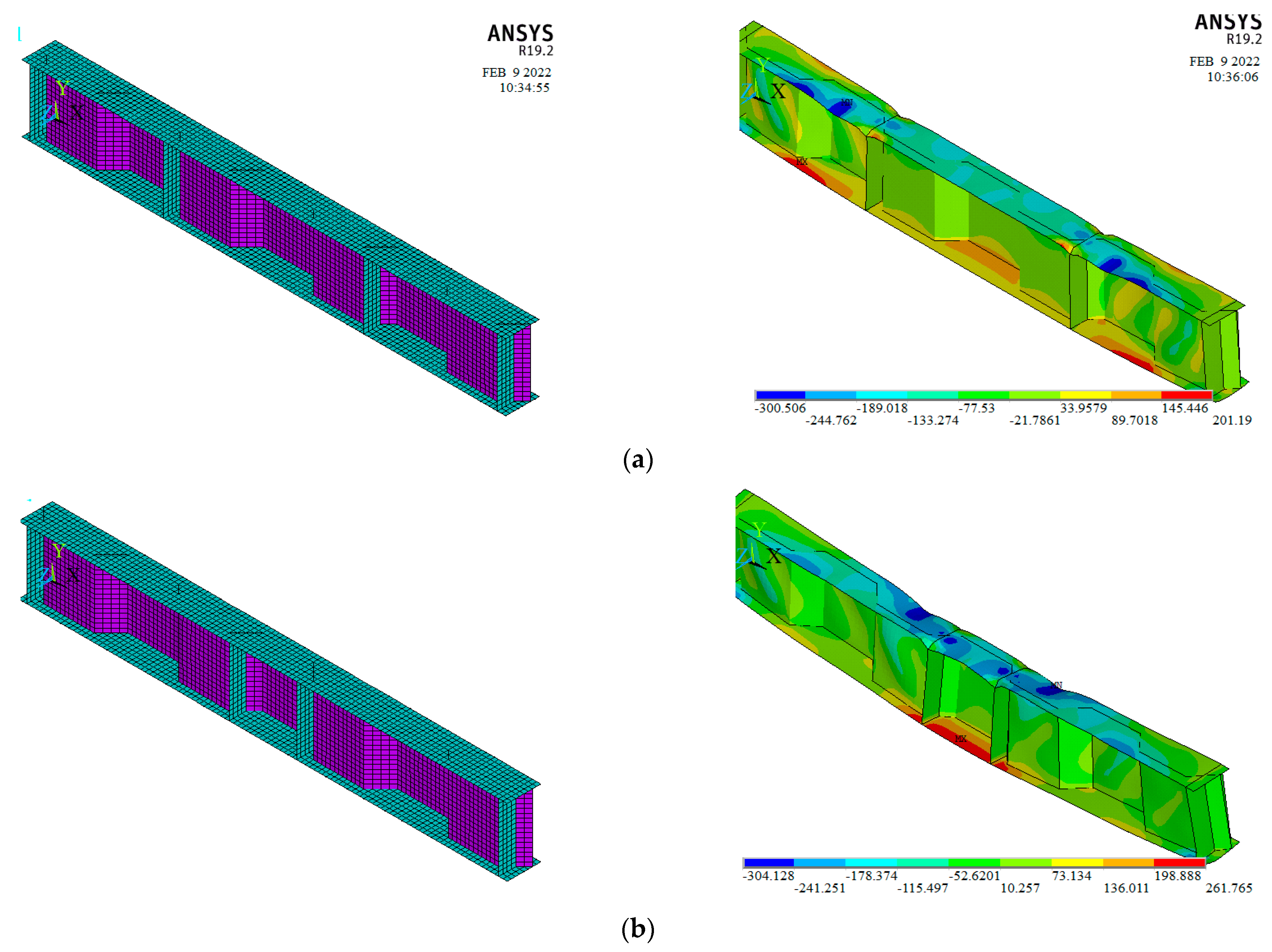


| Specimen ID | Shear and Bending Span (mm) | CW (mm) | hw (mm) | tw (mm) | bf (mm) | tf (mm) | |||
|---|---|---|---|---|---|---|---|---|---|
| * S. S. | ** B. S. Loads | b | d | hr | |||||
| S90B60h40 | 900 | 600 | 200 | 100 | 100 | 400 | 3 | 200 | 8.0 |
| S80B80h40 | 800 | 800 | 300 | 400 | |||||
| S80B80h50 | 800 | 800 | 300 | 500 | |||||
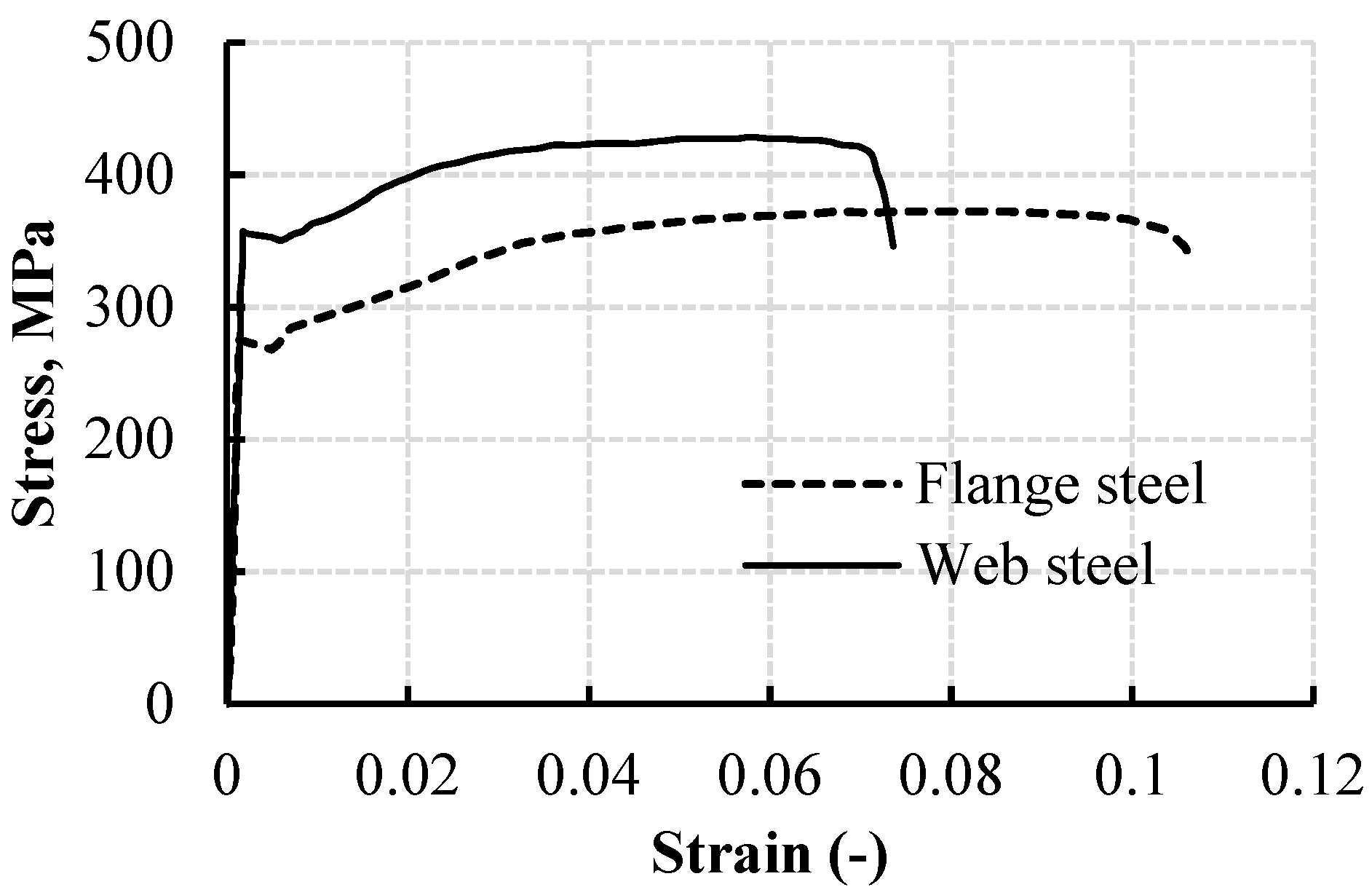
| Coupon Type | Average fy (MPa) | Average fu (MPa) | Average E (GPa) | Maximum Strain (−) |
|---|---|---|---|---|
| Web | 352 | 418 | 198 | 0.075 |
| Flange | 270 | 360 | 192 | 0.102 |
| Beam ID | Loads and Deflection | Failure Mechanisms | |||||
|---|---|---|---|---|---|---|---|
| Pu | δu | Web | Flange | ||||
| kN | mm | Mode | Position | Angle | Mode | Position | |
| S90B60h40 | 323 | 10.25 | -- | -- | -- | LB * | M + V |
| S80B80h40 | 305 | 5.58 | LB | M + V | |||
| S80B80h50 | 365 | 4.52 | LB | M + V | 30° | ||
| Specimen | Mexp (kN.m.) | EN1993-1-1 | DASt-R015 | ||
|---|---|---|---|---|---|
| M (kN.m.) | M (kN.m.) | Equation (10) | |||
| S90B60h40 | 145.35 | 117.10 | 0.81 | 172.48 | 1.19 |
| S80B80h40 | 122 | 114.05 | 0.93 | 172.48 | 1.41 |
| S80B80h50 | 146 | 143.14 | 0.98 | 216.48 | 1.48 |
| Degree of Freedom- Displacement | Degree of Freedom- Rotation | |||||
|---|---|---|---|---|---|---|
| Dx | Dy | Dz | Rx | Ry | Rz | |
| AB | C | R | R | R | R | -- |
| CD | C | -- | -- | -- | R | -- |
| Beams I.D | Ls (mm) | h (mm) | b (mm) | Shear Span (S.S) (mm) | Bending Span (B.S) (mm) | Test Factors |
|---|---|---|---|---|---|---|
| S90B60h40 | 2400 | 400 | 200 | 900 | 600 | Control beam (CB90) |
| S120B60h40 | 3000 | 1200 | 600 | Effect of S.S | ||
| S150B60h40 | 3600 | 400 | 200 | 1500 | 600 | |
| S180B60h40 | 4200 | 1800 | 600 | |||
| S90B90h40 | 3000 | 900 | 900 | Effect of B.S | ||
| S90B120h40 | 3600 | 400 | 200 | 900 | 1200 | |
| S900B150h40 | 4200 | 900 | 1500 | |||
| S80B80h40 | 2400 | 400 | 200 | 800 | 800 | Control beam (CB80) |
| S120B80h40 | 3200 | 1200 | 800 | |||
| S160B80h40 | 4000 | 400 | 200 | 1600 | 800 | Effect of S.S |
| S200B80h40 | 4800 | 2000 | 800 | |||
| S80B120h40 | 2800 | 800 | 1200 | |||
| S80B160h40 | 3200 | 400 | 200 | 800 | 1600 | Effect of B.S |
| S80B200h40 | 3600 | 800 | 2000 |
| Beams I.D | Ls (mm) | S.S (mm) | B.S (mm) | Yield load (kN) | Max. load (kN) | µu (%) | δu (mm) | Failure Mode (−) |
|---|---|---|---|---|---|---|---|---|
| S90B60h40 | 2400 | 900 | 600 | 284.24 | 323.0 | − | 8.42 | FB |
| S120B60h40 | 3000 | 1200 | 600 | 204.79 | 254.4 | 78.8 | 11.87 | FB |
| S150B60h40 | 3600 | 1500 | 600 | 167.07 | 199.6 | 61.8 | 16.12 | |
| S180B60h40 | 4200 | 1800 | 600 | 141.96 | 168.0 | 52.0 | 20.37 | |
| S90B90h40 | 2700 | 900 | 900 | 259.53 | 316.5 | 98.0 | 10.61 | FB |
| S90B120h40 | 3000 | 900 | 1200 | 260.04 | 313.3 | 97.0 | 12.83 | |
| S900B150h40 | 3300 | 900 | 1500 | 254.28 | 310.1 | 96.0 | 15.01 | |
| S80B80h40 | 2400 | 800 | 800 | 243.00 | 300.0 | − | 5.57 | FB |
| S120B80h40 | 3200 | 1200 | 800 | 161.50 | 190.0 | 63.3 | 9.58 | FB |
| S160B80h40 | 4000 | 1600 | 800 | 109.22 | 133.2 | 44.4 | 14.98 | |
| S200B80h40 | 4800 | 2000 | 800 | 84.66 | 102.0 | 34.0 | 19.17 | |
| S80B120h40 | 2800 | 800 | 1200 | 244.44 | 291.0 | 97.0 | 8.01 | FB |
| S80B160h40 | 3200 | 800 | 1600 | 236.16 | 288.0 | 96.0 | 10.44 | |
| S80B200h40 | 3600 | 800 | 2000 | 230.85 | 285.0 | 95.0 | 13.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharaky, I.A.; Alharthi, Y.M.; Elamary, A.S. Effect of Shear and Pure Bending Spans on the Behaviour of Steel Beams with Corrugated Webs. Materials 2022, 15, 4675. https://doi.org/10.3390/ma15134675
Sharaky IA, Alharthi YM, Elamary AS. Effect of Shear and Pure Bending Spans on the Behaviour of Steel Beams with Corrugated Webs. Materials. 2022; 15(13):4675. https://doi.org/10.3390/ma15134675
Chicago/Turabian StyleSharaky, Ibrahim A., Yasir M. Alharthi, and Ahmed S. Elamary. 2022. "Effect of Shear and Pure Bending Spans on the Behaviour of Steel Beams with Corrugated Webs" Materials 15, no. 13: 4675. https://doi.org/10.3390/ma15134675
APA StyleSharaky, I. A., Alharthi, Y. M., & Elamary, A. S. (2022). Effect of Shear and Pure Bending Spans on the Behaviour of Steel Beams with Corrugated Webs. Materials, 15(13), 4675. https://doi.org/10.3390/ma15134675






