First-Principles Study on the Effect of Lithiation in Spinel LixMn2O4 (0 ≤ x ≤ 1) Structure: Calibration of CASTEP and ONETEP Simulation Codes
Abstract
:1. Introduction
2. Materials and Methods
3. Results
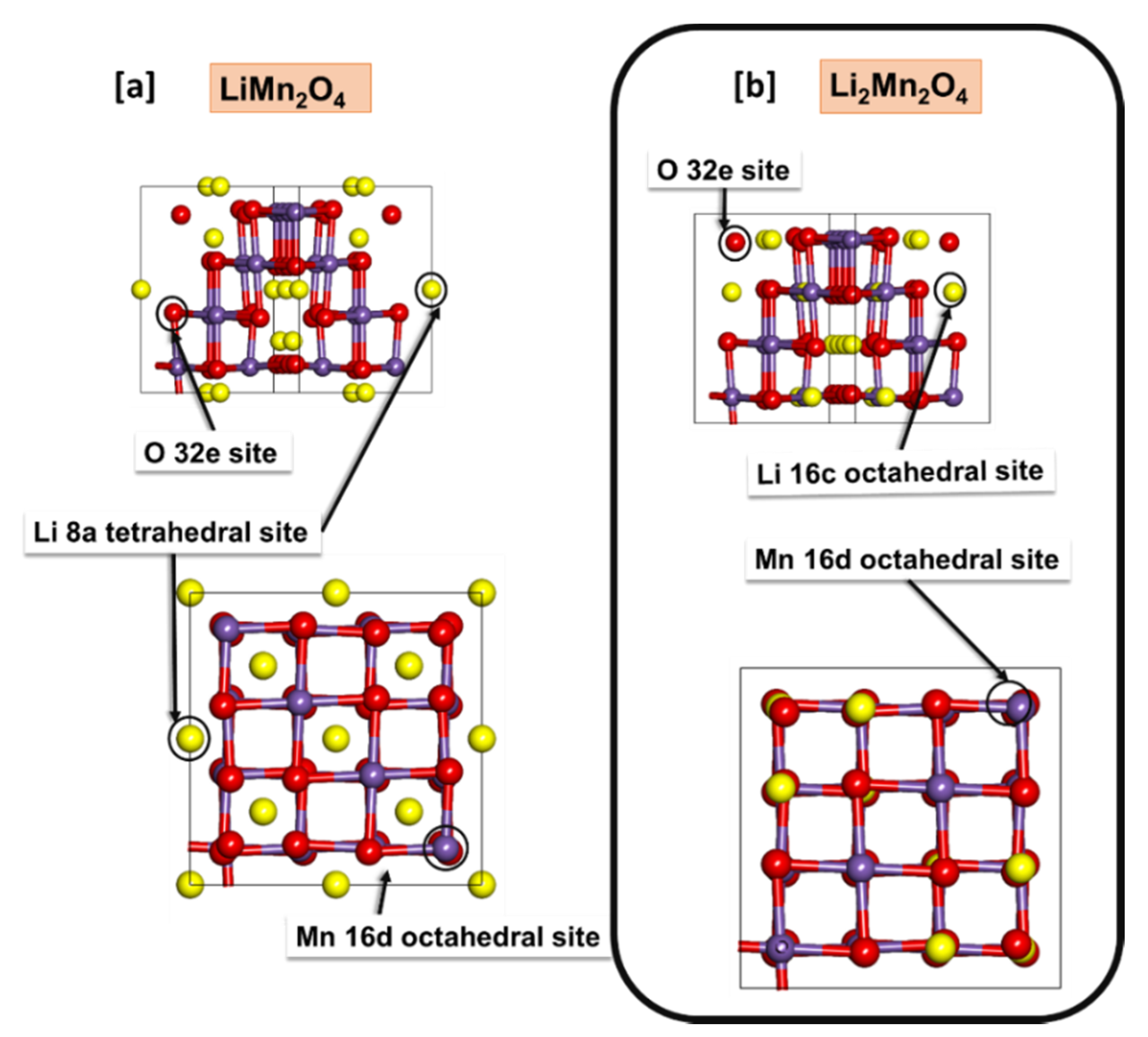
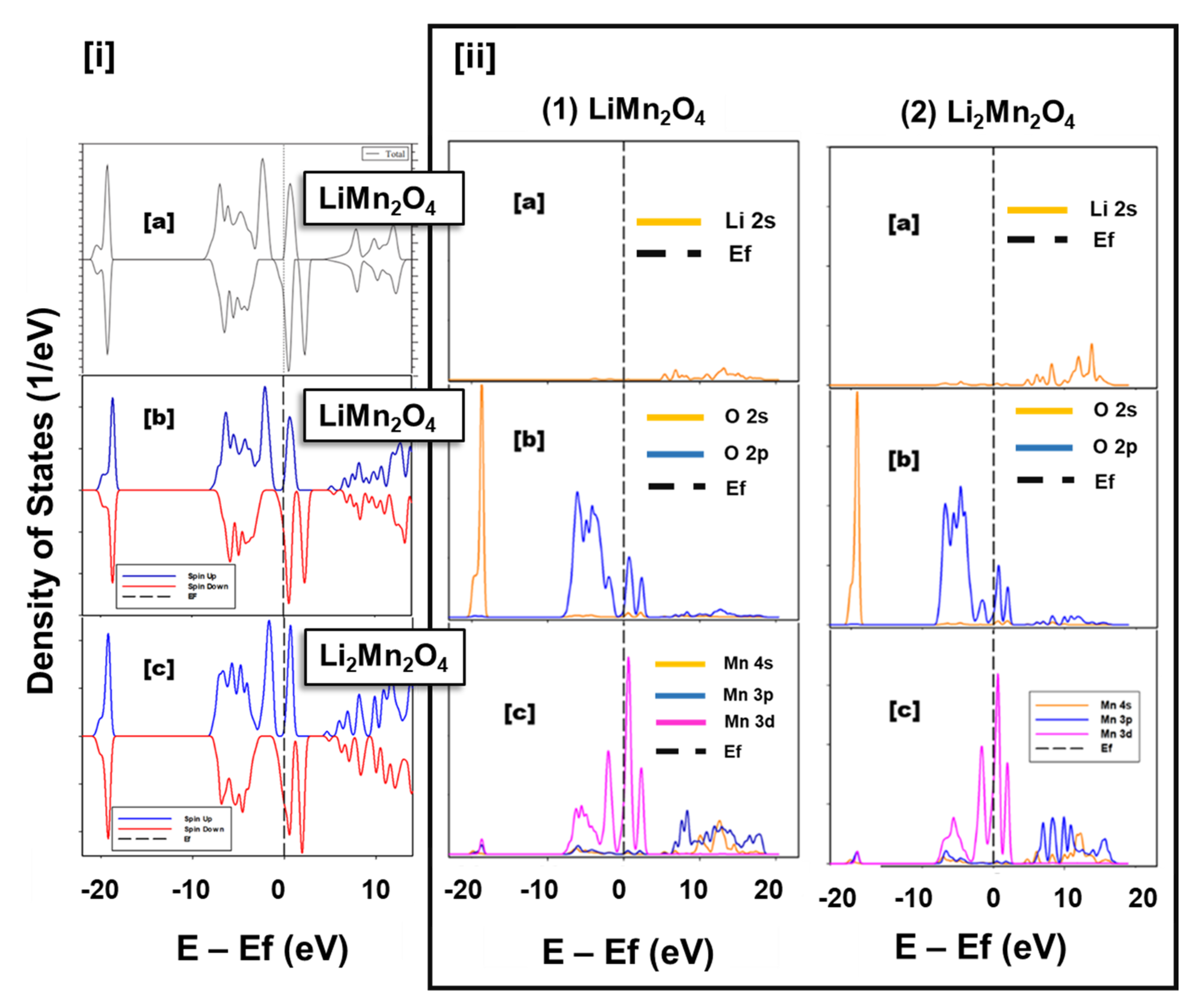
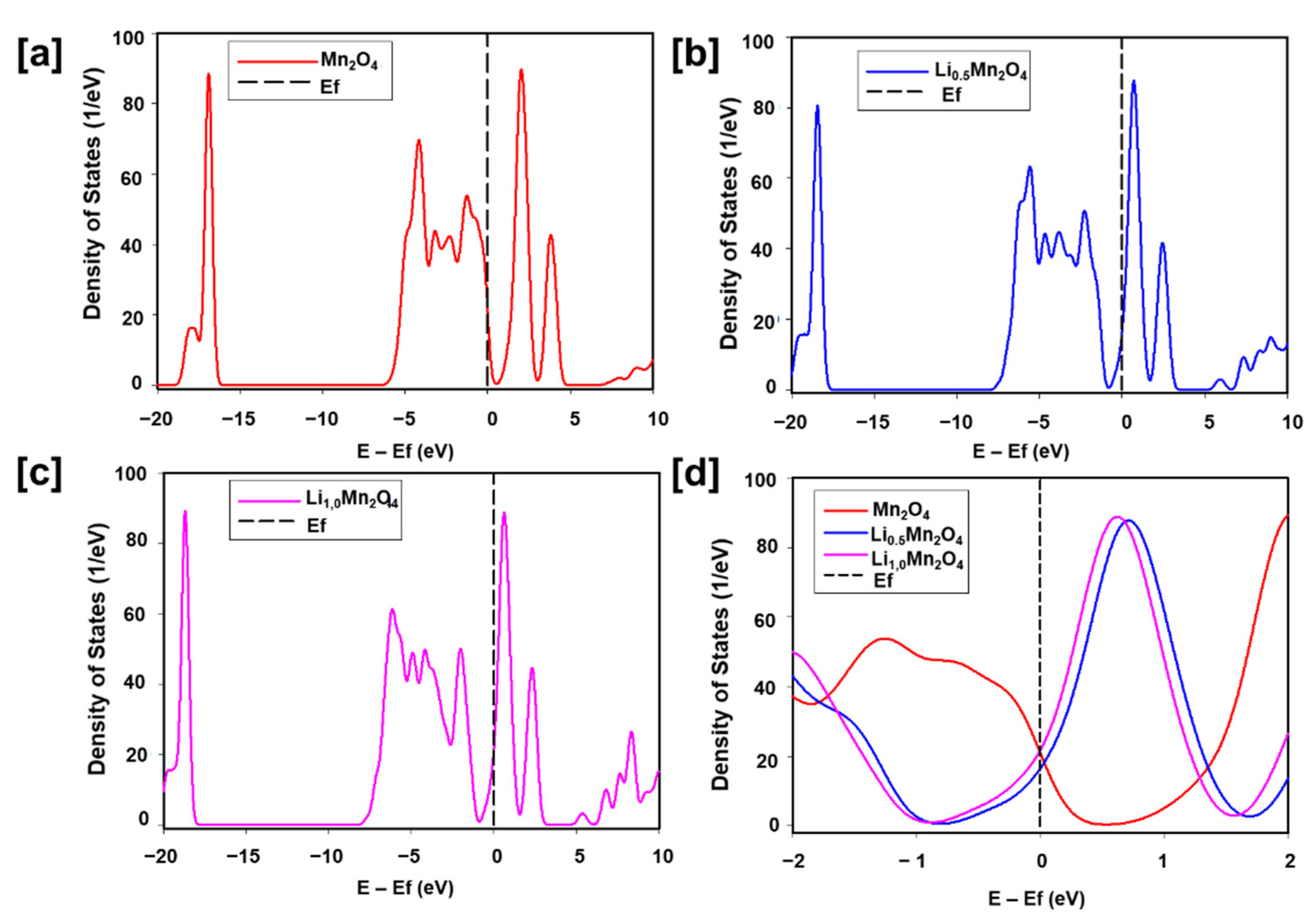
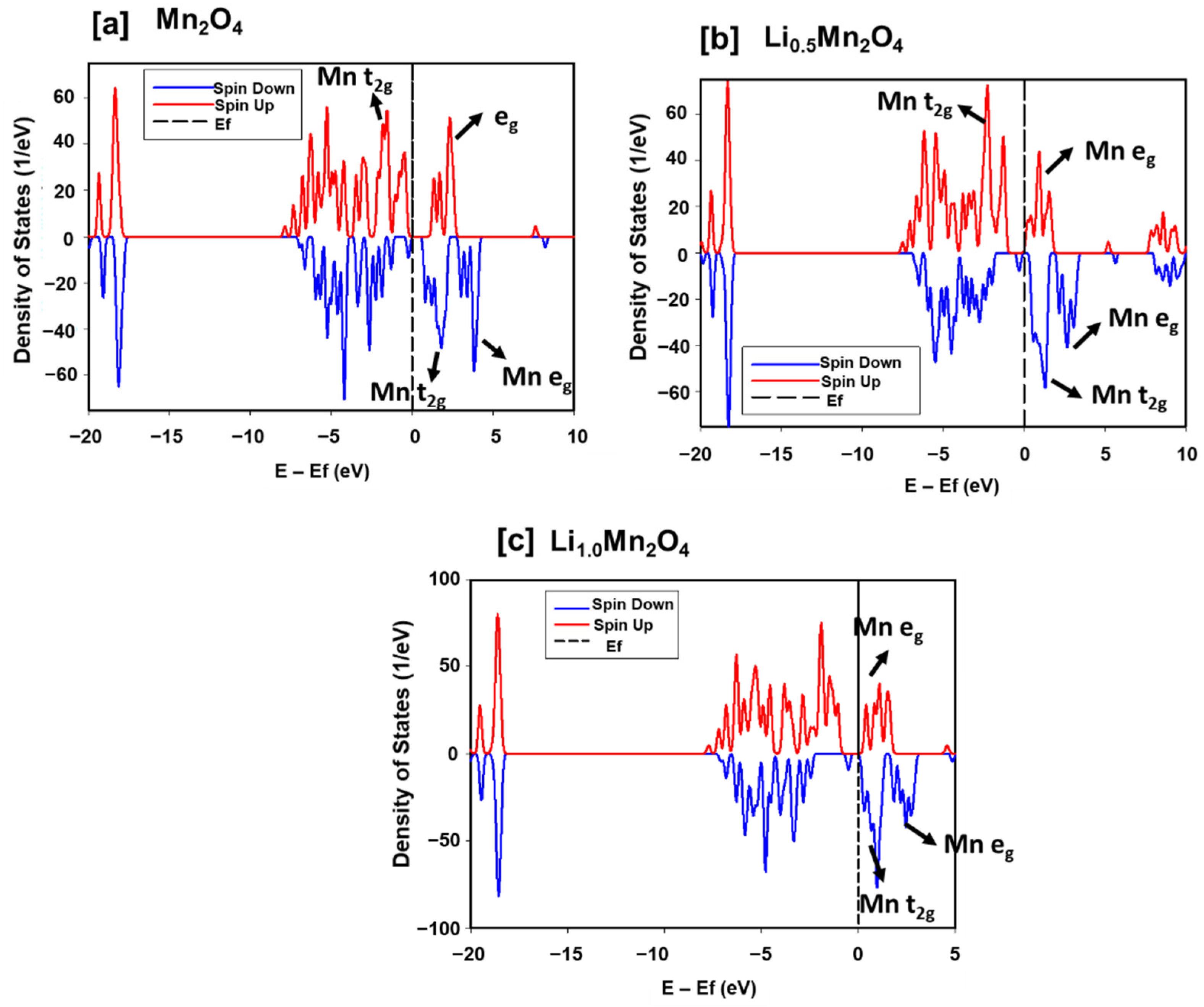
3.1. Structural Properties and Electronic Properties
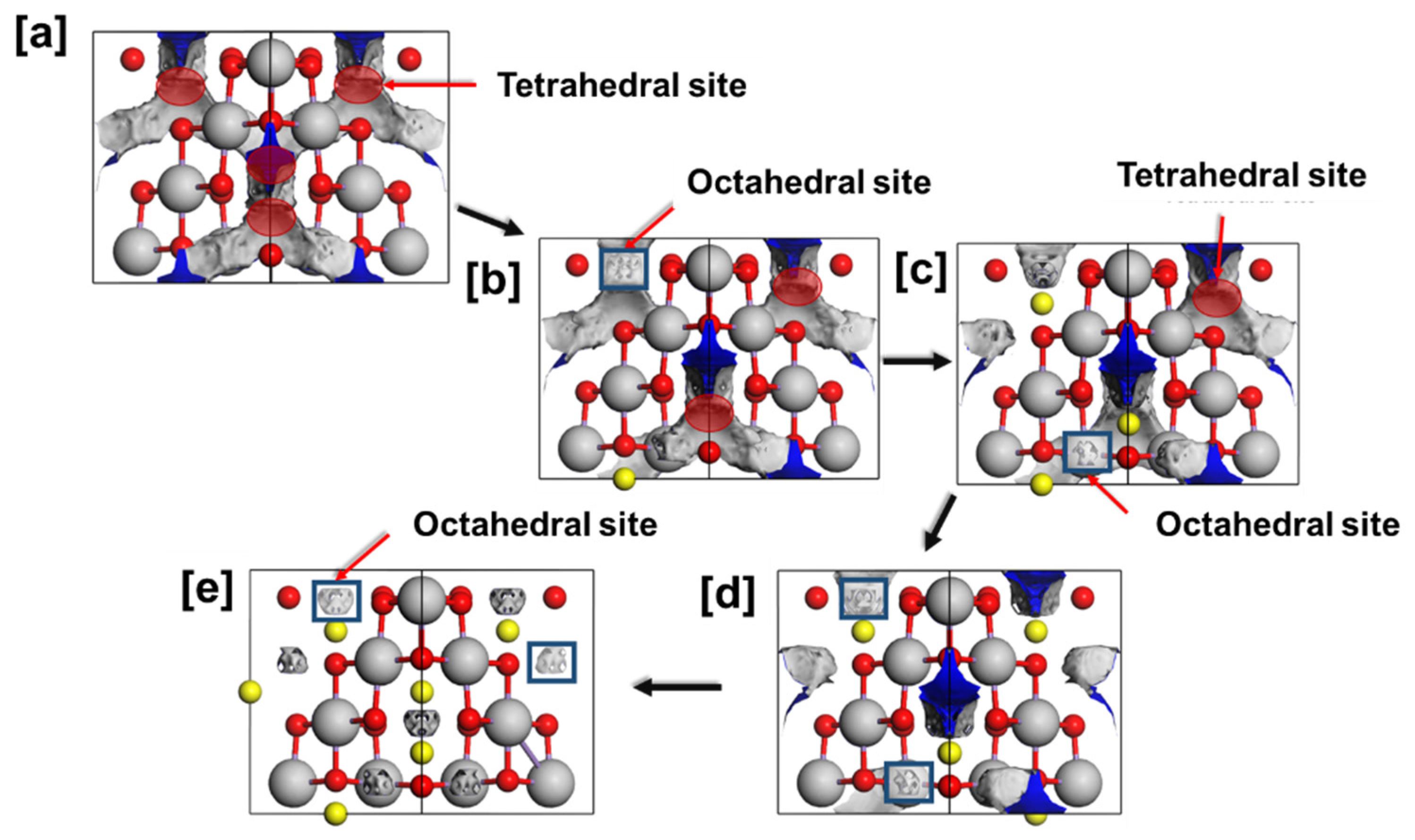
3.2. Discharging the LixMn2O4 (0 ≤ x ≤ 1) Spinel
3.3. CASTEP and ONETEP Open Cell Voltage (OCV) of the LixMn2O4 (0 ≤ x ≤ 1) Spinel

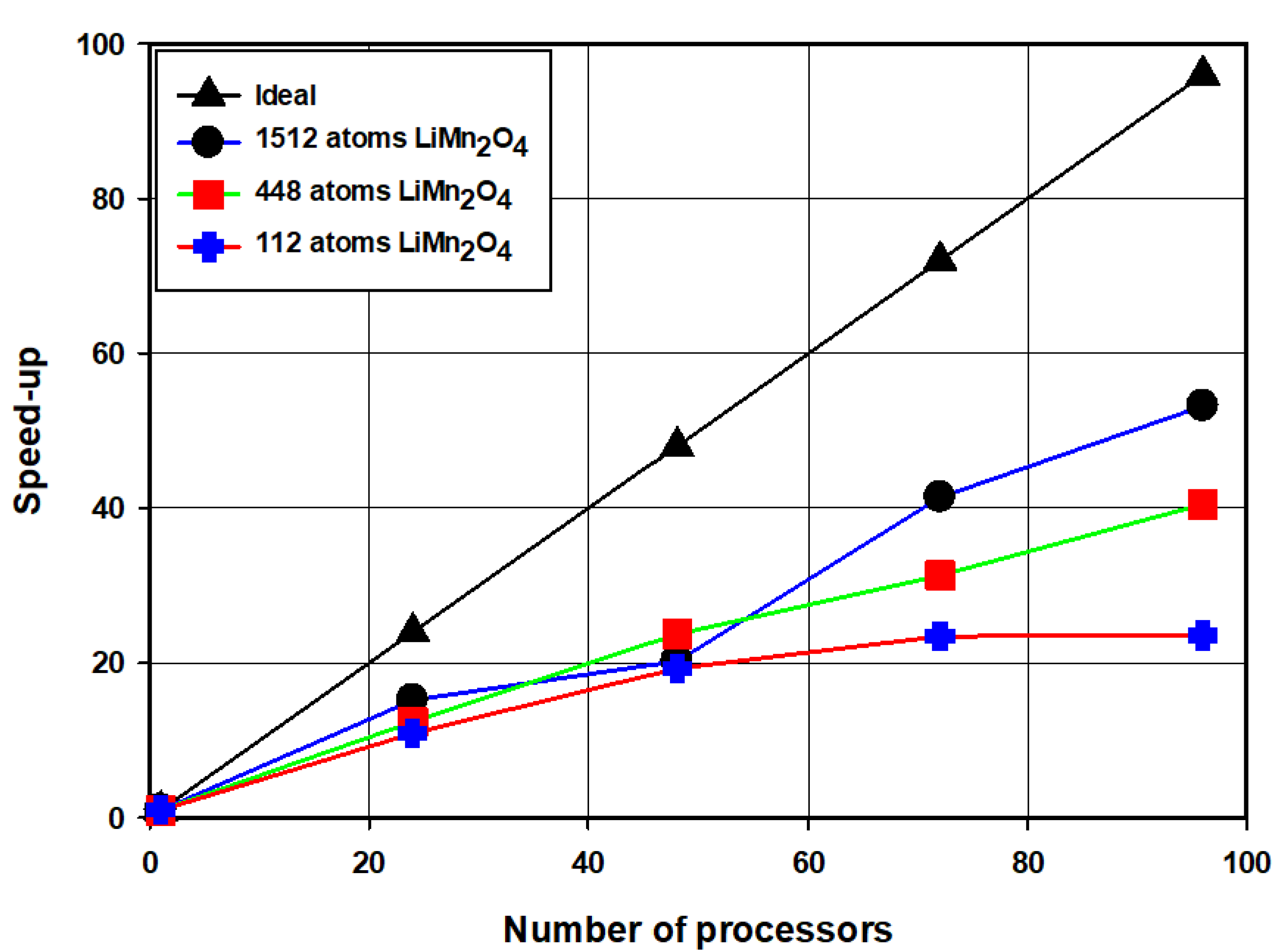
3.4. Scaling of the ONETEP Code South Africa’s CHPC
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franco, A.A.; Rucci, A.; Brandell, D.; Frayret, C.; Gaberscek, M.; Jankowski, P.; Johansson, P. Boosting rechargeable batteries R&D by multiscale modeling: Myth or reality? Chem. Rev. 2019, 119, 4569–4627. [Google Scholar] [CrossRef] [PubMed]
- Deng, D. Li-ion batteries: Basics, progress, and challenges. Energy Sci. Eng. 2015, 3, 385–418. [Google Scholar] [CrossRef]
- Yin, W.J.; Wei, S.H.; Al-Jassim, M.M.; Turner, J.; Yan, Y. Doping properties of monoclinic BiVO4 studied by first-principles density-functional theory. Phys. Rev. 2011, 83, 155102. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Baerends, E.J. Kohn-Sham density functional theory: Predicting and understanding chemistry. Rev. Comput. Chem. 2000, 15, 1–86. [Google Scholar] [CrossRef]
- Jain, A.; Shin, Y.; Persson, K.A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Aydinol, M.K.; Kohan, A.F.; Ceder, G.; Cho, K.; Joannopoulos, J. Ab initio study of lithium intercalation in metal oxides and metal dichalcogenides. Phys. Rev. B Condens. Matter. 1997, 56, 1354. [Google Scholar] [CrossRef]
- Walsh, A.; Wei, S.H.; Yan, Y.; Al-Jassim, M.M.; Turner, J.A.; Woodhouse, M.; Parkinson, B.A. Structural, magnetic, and electronic properties of the Co-Fe-Al oxide spinel system: Density-functional theory calculations. Phys. Rev. B Condens. Matter. 2007, 76, 165119. [Google Scholar] [CrossRef]
- Goedecker, S. Linear scaling electronic structure methods. Rev. Mod. Phys. 1999, 71, 1085. [Google Scholar] [CrossRef]
- Kohn, W. Analytic properties of Bloch waves and Wannier functions. Phys. Rev. Lett. 1959, 115, 809. [Google Scholar] [CrossRef]
- Kohn, W. Density functional and density matrix method scaling linearly with the number of atoms. Phys. Rev. Lett. 1996, 76, 3168. [Google Scholar] [CrossRef]
- Li, M.; Lu, J.; Chen, Z.; Amine, K. 30 years of lithium-ion batteries. Adv. Mater. 2018, 30, 1800561. [Google Scholar] [CrossRef]
- Huang, W.; Wang, G.; Luo, C.; Xu, Y.; Eckstein, B.J.; Chen, Y.; Wang, B.; Huang, J.; Kang, Y.; Wu, J. Controllable growth of LiMn2O4 by carbohydrate-assisted combustion synthesis for high performance Li-ion batteries. Nano Energy 2019, 64, 103936. [Google Scholar] [CrossRef]
- Han, C.G.; Zhu, C.; Saito, G.; Sheng, N.; Nomura, T.; Akiyama, T. Enhanced cycling performance of surface-doped LiMn2O4 modified by a Li2CuO2-Li2NiO2 solid solution for rechargeable lithium-ion batteries. Electrochim. Acta 2017, 224, 71–79. [Google Scholar] [CrossRef]
- Pan, B.; Feng, Z.; Sa, N.; Han, S.D.; Ma, Q.; Fenter, P.; Vaughey, J.T.; Zhang, Z.; Liao, C. Advanced hybrid battery with a magnesium metal anode and a spinel LiMn2O4 cathode. ChemComm 2016, 52, 9961–9964. [Google Scholar] [CrossRef] [PubMed]
- Tesfamhret, Y.; Liu, H.; Chai, Z.; Berg, E.; Younesi, R. On the Manganese Dissolution Process from LiMn2O4 Cathode Materials. ChemElectroChem 2021, 8, 1516–1523. [Google Scholar] [CrossRef]
- Cai, Z.; Ma, Y.; Huang, X.; Yan, X.; Yu, Z.; Zhang, S.; Song, G.; Xu, Y.; Wen, C.; Yang, W. High electrochemical stability Al-doped spinel LiMn2O4 cathode material for Li-ion batteries. J. Energy Storage 2020, 27, 101036. [Google Scholar] [CrossRef]
- Van der Ven, A.; Marianetti, C.; Morgan, D.; Ceder, G. Phase transformations and volume changes in spinel LixMn2O4. Solid State Ion. 2000, 135, 21–32. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Zhang, S.; Sun, L.; Zhang, W.; Dang, F.; Seifert, H.J.; Du, Y. Intrinsic Defects in LiMn2O4: First-Principles Calculations. ACS Omega 2021, 6, 21255–21264. [Google Scholar] [CrossRef]
- Ma, Y.; Dai, Y.; Zhou, Q.; Cheng, J.; Li, H.; Hu, W. A First-Principles Study on the Structure and Electronic Structure of Ti-Doped Spinel LiMn2O4 for Li-Ion Batteries. J. Electron. Mater. J. 2022, 51, 77–83. [Google Scholar] [CrossRef]
- Ledwaba, R.S.; Kgatwane, K.M.; Sayle, D.C.; Ngoepe, P.E. Structural characterisation and mechanical properties of nanosized spinel LiMn2O4 cathode investigated using atomistic simulation. Mater. Res. Bull. 2022, 146, 111611. [Google Scholar] [CrossRef]
- Shibiri, B.; Ledwaba, R.S.; Ngoepe, P.E. Discharge induced structural variation of simulated bulk Li1+xMn2O4 (0≤ x ≤ 1). Opt. Mater. 2019, 92, 67–70. [Google Scholar] [CrossRef]
- Ledwaba, R.S.; Sayle, D.C.; Ngoepe, P.E. Atomistic Simulation and Characterization of Spinel Li1+xMn2O4 (0≤ x ≤ 1) Nanoparticles. ACS Appl. Energy Mater. 2020, 3, 1429–1438. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. CASTEP 4.2 Academic version, licensed under the UKCP-MSI Agreement. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Skylaris, C.K.; Haynes, P.D.; Mostofi, A.A.; Payne, M.C. Introducing ONETEP: Linear-scaling density functional simulations on parallel computers. Chem. Phys. 2005, 122, 84119. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B Condens. Matter. 1990, 41, 7892. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Först, C.J.; Schimpl, J. Projector augmented wave method: Ab initio molecular dynamics with full wave functions. Bull. Mater. Sci. 2003, 26, 33–41. [Google Scholar] [CrossRef]
- Grechnev, G.E.; Ahuja, R.; Johansson, B.; Eriksson, O. Electronic structure, magnetic, and cohesive properties of LixMn2O4: Theory. Phys. Rev. B Condens. Matter. 2002, 65, 174408. [Google Scholar] [CrossRef]
- Chevrier, V.L.; Ong, S.P.; Armiento, R.; Chan, M.K.; Ceder, G. Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds. Phys. Rev. B Condens. Matter. 2010, 82, 075122. [Google Scholar] [CrossRef]
- Bagcı, S.; Tütüncü, H.M.; Duman, S.; Bulut, E.; Özacar, M.; Srivastava, G.P. Physical properties of the cubic spinel LiMn2O4. J. Phys. Chem. Solids 2014, 75, 463–469. [Google Scholar] [CrossRef]
- Rousse, G.; Masquelier, C.; Rodriguez-Carvajal, J.; Elkaim, E.; Lauriat, J.P.; Martinez, J.L. X-ray study of the spinel LiMn2O4 at low temperatures. Chem. Mater. 1999, 11, 3629–3635. [Google Scholar] [CrossRef]
- Mishra, S.K.; Ceder, G. Structural stability of lithium manganese oxides. Phys. Rev. B Condens. Matter. 1999, 59, 6120. [Google Scholar] [CrossRef]
- Xu, B.; Meng, S. Factors affecting Li mobility in spinel LiMn2O4—A first-principles study by GGA and GGA+ U methods. J. Power Sources 2010, 195, 4971–4976. [Google Scholar] [CrossRef]
- Thackeray, M.M.; Mansuetto, M.F.; Bates, J.B. Structural stability of LiMn2O4 electrodes for lithium batteries. J. Power Sources 1997, 68, 153–158. [Google Scholar] [CrossRef]
- Hon, Y.M.; Lin, S.P.; Fung, K.Z.; Hon, M.H. Synthesis and characterization of nano-LiMn2O4 powder by tartaric acid gel process. J. Eur. Ceram. Soc. 2002, 22, 653–660. [Google Scholar] [CrossRef]
- Ariyoshi, K.; Iwakoshi, Y.; Nakayama, N.; Ohzuku, T. Topotactic Two-Phase Reactions of Li[Ni1/2Mn3/2]O4 (P4332) in Nonaqueous Lithium Cells. J. Electrochem. Soc. 2004, 151, A296. [Google Scholar] [CrossRef]
- Xia, Y.; Yoshio, M. An investigation of lithium ion insertion into spinel structure Li-Mn-O compounds. J. Electrochem. Soc. 1996, 143, 825. [Google Scholar] [CrossRef]
- Julien, C.M.; Mauger, A.; Zaghib, K.; Groult, H. Comparative issues of cathode materials for Li-ion batteries. Inorganics 2014, 2, 132–154. [Google Scholar] [CrossRef]
- Bazito, F.F.; Torresi, R.M. Cathodes for lithium ion batteries: The benefits of using nanostructured materials. J. Braz. Chem. Soc. 2006, 17, 627–642. [Google Scholar] [CrossRef]
- Barker, J.; West, K..; Saidi, Y.; Pynenburg, R.; Zachau-Christiansen, B.; Koksbang, R. Kinetics and thermodynamics of the lithium insertion reaction in spinel phase LixMn2O4. J. Power Sources 1995, 54, 475–478. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hlungwani, D.; Ledwaba, R.S.; Ngoepe, P.E. First-Principles Study on the Effect of Lithiation in Spinel LixMn2O4 (0 ≤ x ≤ 1) Structure: Calibration of CASTEP and ONETEP Simulation Codes. Materials 2022, 15, 5678. https://doi.org/10.3390/ma15165678
Hlungwani D, Ledwaba RS, Ngoepe PE. First-Principles Study on the Effect of Lithiation in Spinel LixMn2O4 (0 ≤ x ≤ 1) Structure: Calibration of CASTEP and ONETEP Simulation Codes. Materials. 2022; 15(16):5678. https://doi.org/10.3390/ma15165678
Chicago/Turabian StyleHlungwani, Donald, Raesibe Sylvia Ledwaba, and Phuti Esrom Ngoepe. 2022. "First-Principles Study on the Effect of Lithiation in Spinel LixMn2O4 (0 ≤ x ≤ 1) Structure: Calibration of CASTEP and ONETEP Simulation Codes" Materials 15, no. 16: 5678. https://doi.org/10.3390/ma15165678
APA StyleHlungwani, D., Ledwaba, R. S., & Ngoepe, P. E. (2022). First-Principles Study on the Effect of Lithiation in Spinel LixMn2O4 (0 ≤ x ≤ 1) Structure: Calibration of CASTEP and ONETEP Simulation Codes. Materials, 15(16), 5678. https://doi.org/10.3390/ma15165678






