Experimental Study of Energy Evolution at a Discontinuity in Rock under Cyclic Loading and Unloading
Abstract
:1. Introduction
2. Test Equipment and Specimens
2.1. Test Equipment
2.2. Sample Preparation
3. Test Procedure
3.1. Uniaxial Compression Test
3.2. Direct Shear Test
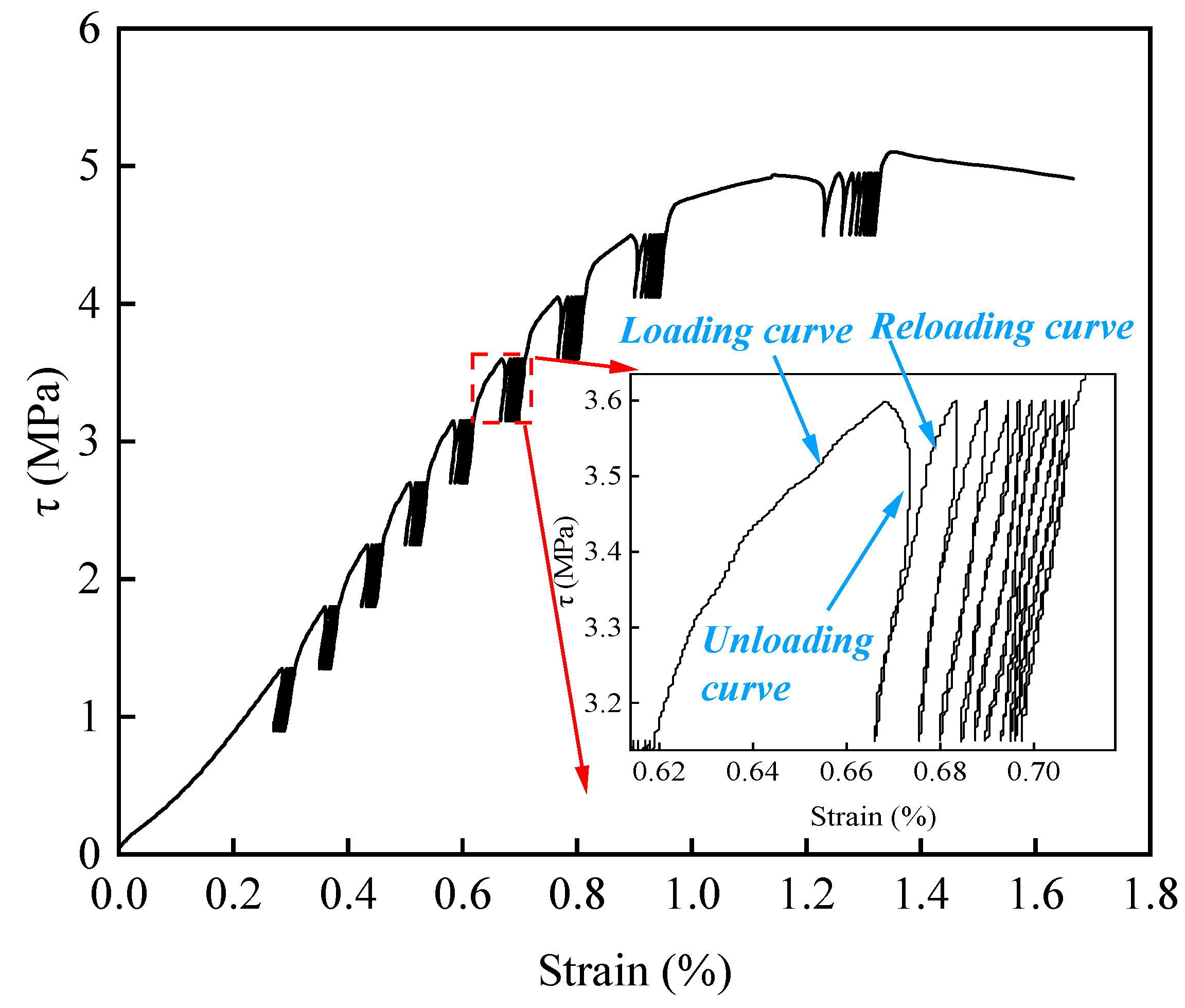
3.3. Graded Cyclic Shear Tests
4. Results and Discussion
4.1. Deformation Characteristics of Specimen during Failure
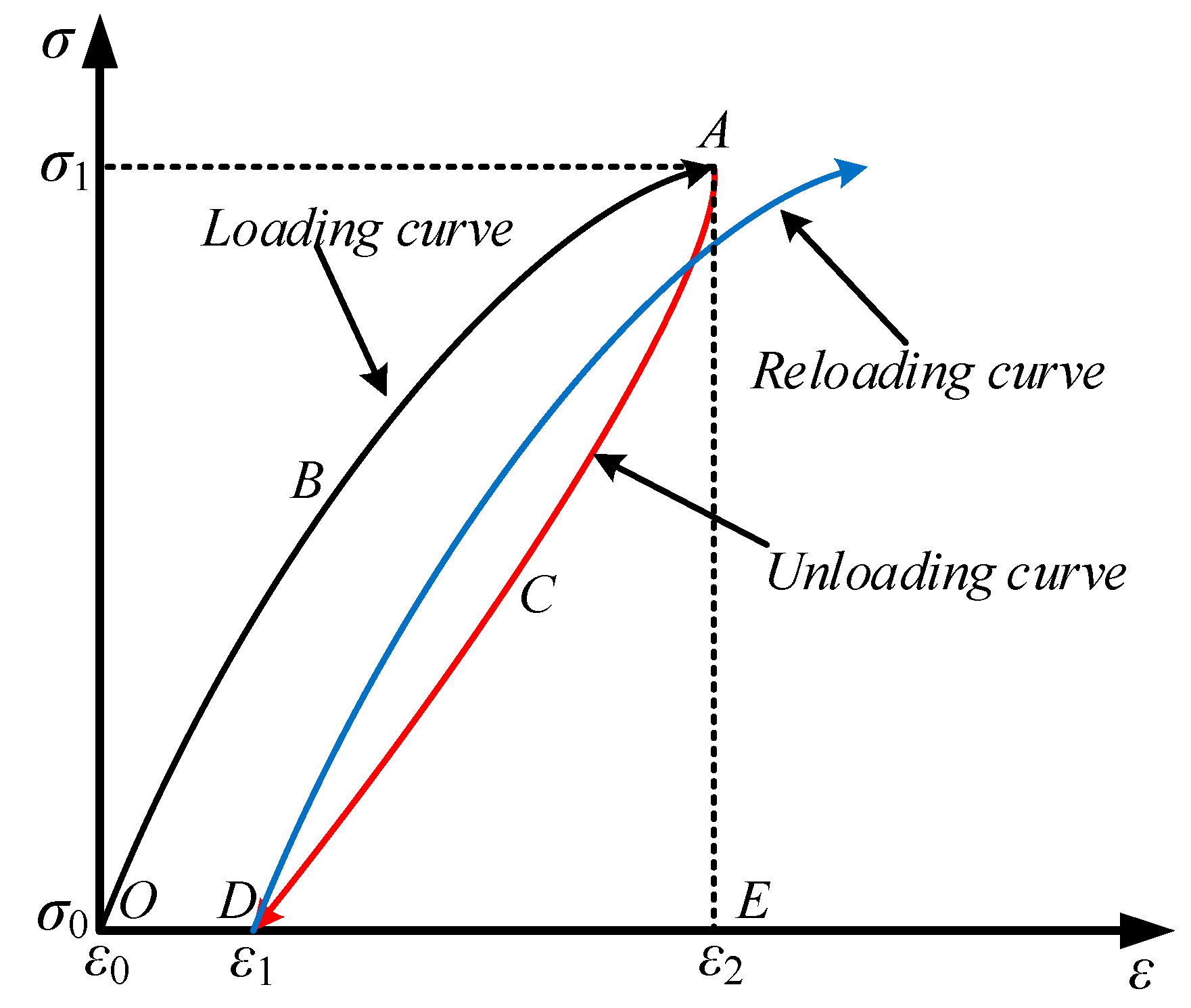
4.2. Energy Density Calculation Method
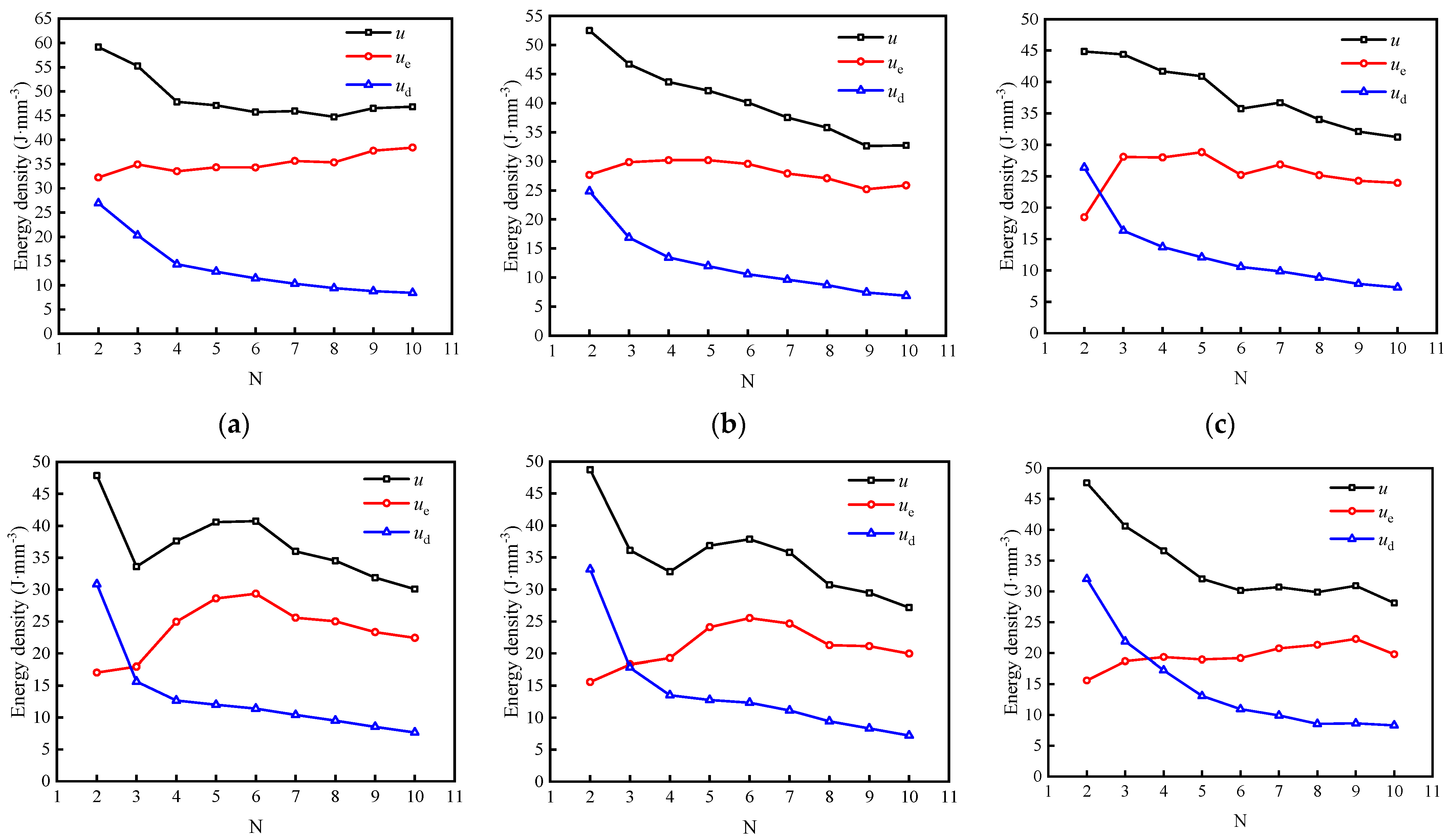
4.3. Energy Evolution Process in Samples
4.4. Energy Distribution in Samples
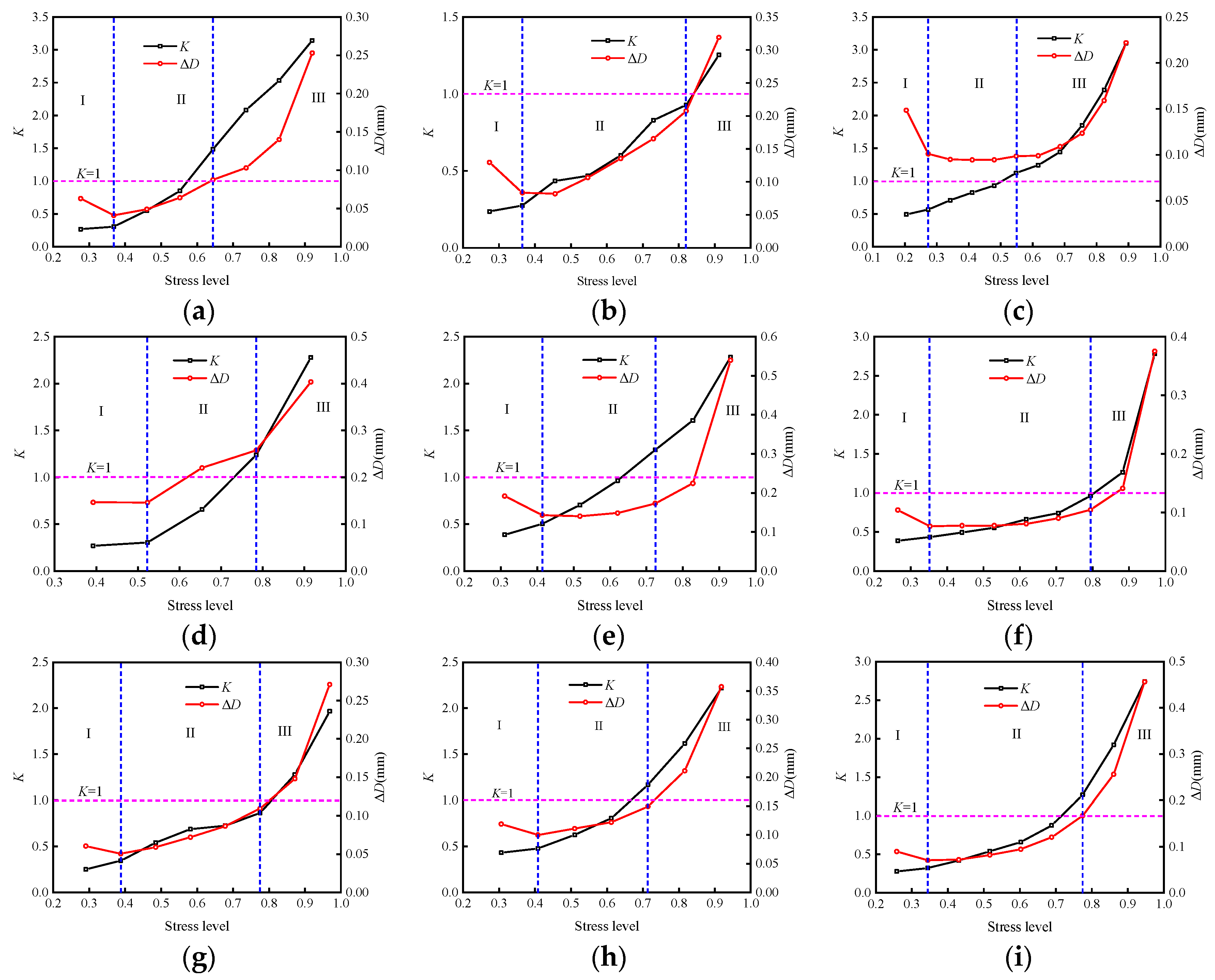
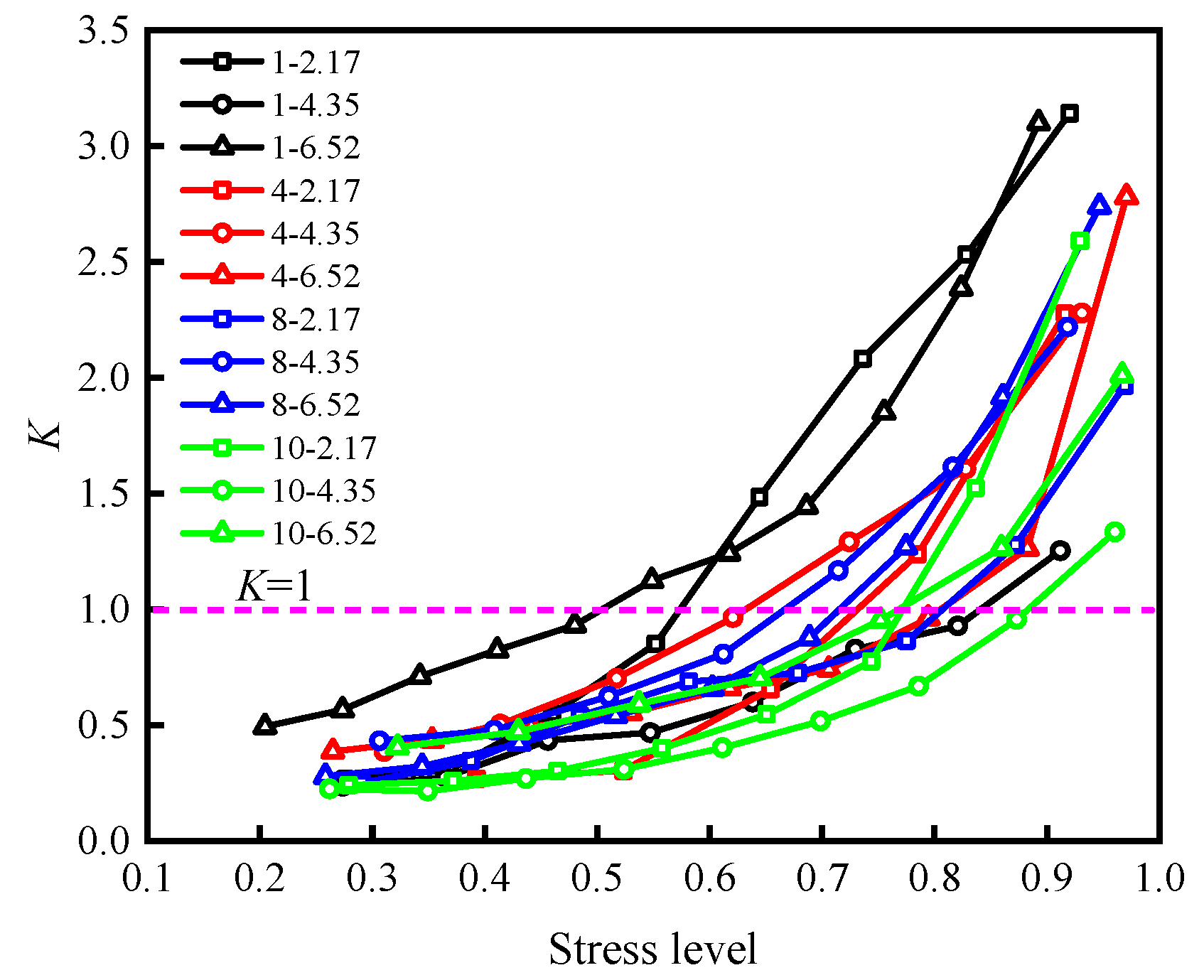
4.5. Energy Criterion for Rock Discontinuity Failure
5. Conclusions
- (1)
- Compared with the stress–strain curve, the energy density can clearly reflect the internal deterioration of the rock discontinuity, so as to predict the failure of the rock discontinuity more accurately.
- (2)
- Under the same cyclic stress, the specimen gradually hardens with the increase in the number of cycles. With the increase of cyclic stress, the dissipated energy density of each stage gradually exceeds the elastic energy density and occupies a dominant position and increases rapidly as failure becomes imminent.
- (3)
- With the increase of stress level, the elastic energy proportion of the sample presents a downward trend, with a slow rate in the early stage, but decreases significantly as the sample approaches failure; the variation in the proportion of energy dissipated shows the opposite trend.
- (4)
- The energy dissipation ratio can be used to characterize internal damage to the sample under load. In the initial stage of loading, the sample is in the extrusion and compaction stage, and the energy dissipation ratio remains unchanged. Then, the fracture develops steadily, the damage in the sample intensifies, and the energy dissipation ratio increases linearly (albeit at a low rate). Before the specimen is about to fail, the change rate is accelerated, and then a sudden change occurs, indicating that the rapid release of energy is the fundamental reason for the failure of the rock discontinuity.
- (5)
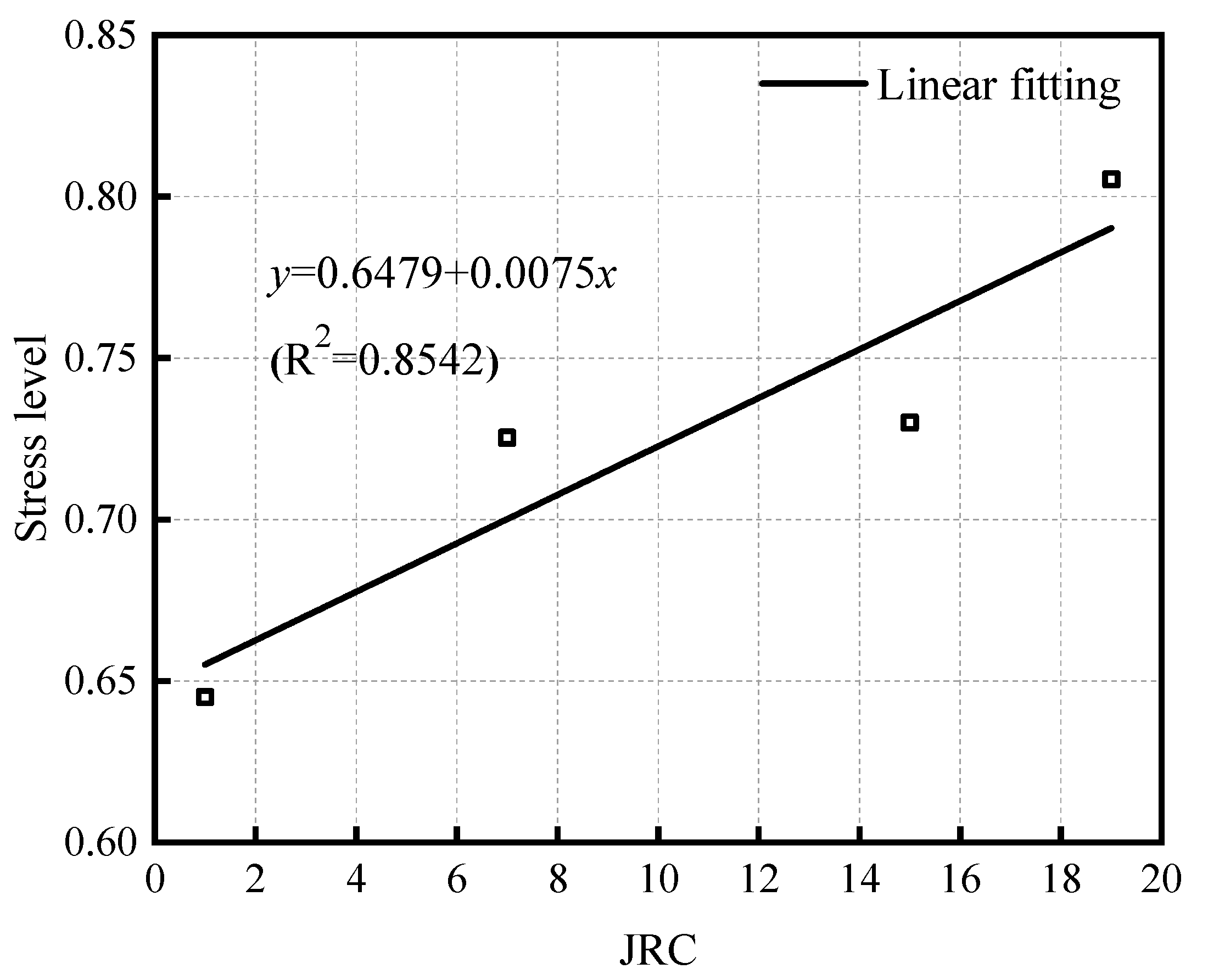
- The increase of the roughness of rock discontinuity samples will improve their energy storage capacity to a certain extent: the higher the JRC of the rock discontinuity, the greater the energy storage limit and stiffness of the specimen.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sagong, M.; Bobet, A. Coalescence of multiple flaws in a rock-model material in uniaxial compression. Int. J. Rock Mech. Min. Sci. 2002, 39, 229–241. [Google Scholar] [CrossRef]
- Meng, Q.B.; Zhang, M.W.; Han, L.J.; Pu, H.; Nie, T.Y. Effects of Acoustic Emission and Energy Evolution of Rock Specimens Under the Uniaxial Cyclic Loading and Unloading Compression. Rock Mech. Rock Eng. 2016, 49, 3873–3886. [Google Scholar] [CrossRef]
- Yang, S.Q.; Yin, P.F.; Zhang, Y.C.; Chen, M.; Zhou, X.P.; Jing, H.W.; Zhang, Q.Y. Failure behavior and crack evolution mechanism of a non-persistent jointed rock mass containing a circular hole. Int. J. Rock Mech. Min. Sci. 2019, 114, 101–121. [Google Scholar] [CrossRef]
- He, M.C.; Sousa, L.R.E.; Miranda, T.; Zhu, G.L. Rockburst laboratory tests database—Application of data mining techniques. Eng. Geol. 2015, 185, 116–130. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F.; Fan, P.; Dong, L. Experimental Investigation of the Influence of Joint Geometric Configurations on the Mechanical Properties of Intermittent Jointed Rock Models under Cyclic Uniaxial Compression. Rock Mech. Rock Eng. 2017, 50, 1453–1471. [Google Scholar] [CrossRef]
- Xie, H.P.; Li, L.Y.; Yang, J.; Peng, R.D.; Yang, Y.M. Energy analysis for damage and catastrophic failure of rocks. Sci. China Technol. Sci. 2011, 54, 199–209. [Google Scholar] [CrossRef]
- Sujatha, V.; Kishen, J. Energy Release Rate due to Friction at Bimaterial Interface in Dams. J. Eng. Mech. 2003, 129, 793–800. [Google Scholar] [CrossRef]
- Huang, D.; Li, Y.R. Conversion of strain energy in triaxial unloading tests on marble. Int. J. Rock Mech. Min. Sci. 2014, 66, 160–168. [Google Scholar] [CrossRef]
- Xie, H.P.; Peng, R.D.; Yang, J.U.; Zhou, H.W. On energy analysis of rock failure. Chin. J. Rock Mech. Eng. 2005, 15, 2603–2608. (In Chinese) [Google Scholar]
- Xie, H.P.; Ju, Y.; Li, L.Y.; Peng, R.D. Energy mechanism of deformation and failure of rock masses. Chin. J. Rock Mech. Eng. 2008, 27, 1729–1740. (In Chinese) [Google Scholar]
- Tu, Y.L.; Liu, X.R.; Zhong, Z.L.; Li, Y.Y. New criteria for defining slope failure using the strength reduction method. Eng. Geol. 2016, 212, 63–71. [Google Scholar] [CrossRef]
- Peng, K.; Wang, Y.Q.; Zou, Q.L.; Liu, Z.P.; Mou, J.H. Effect of crack angles on energy characteristics of sandstones under a complex stress path. Eng. Fract. Mech. 2019, 218, 106577. [Google Scholar] [CrossRef]
- Wang, J.A.; Park, H.D. Comprehensive prediction of rockburst based on analysis of strain energy in rocks. Tunn. Undergr. Space Technol. 2001, 16, 49–57. [Google Scholar] [CrossRef]
- Wu, Z.H.; Song, Z.Y.; Tan, J.; Zhang, Y.Z.; Qi, Z.J. The evolution law of rock energy under different graded cyclic loading and unloading modes. J. Min. Saf. Eng. 2020, 37, 836–844+851. (In Chinese) [Google Scholar]
- Wang, H.; Yang, T.H.; Liu, H.L.; Zhao, Y.C.; Deng, W.X.; Hou, X.G. Mechanical properties and energy evolution of dry and saturated sandstones under cyclic loading. Rock Soil Mech. 2017, 38, 1600–1608. (In Chinese) [Google Scholar]
- Jia, Z.Q.; Li, C.B.; Zhang, R.; Wang, M.; Gao, M.Z.; Zhang, Z.T.; Zhang, Z.P.; Ren, L.; Xie, J. Energy Evolution of Coal at Different Depths Under Unloading Conditions. Rock Mech. Rock Eng. 2019, 52, 4637–4649. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, M.; Jin, Y.; Zou, D.W. Theoretical analysis and experimental research on the energy dissipation of rock crushing based on fractal theory. J. Nat. Gas Sci. Eng. 2016, 33, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.Z.; Gao, F. Confining pressure effect on rock energy. Chin. J. Rock Mech. Eng. 2015, 34, 1–11. (In Chinese) [Google Scholar]
- Munoz, H.; Taheri, A.; Chanda, E.K. Rock Drilling Performance Evaluation by an Energy Dissipation Based Rock Brittleness Index. Rock Mech. Rock Eng. 2016, 49, 3343–3355. [Google Scholar] [CrossRef]
- Munoz, H.; Taheri, A.; Chanda, E.K. Fracture Energy-Based Brittleness Index Development and Brittleness Quantification by Pre-peak Strength Parameters in Rock Uniaxial Compression. Rock Mech. Rock Eng. 2016, 49, 4587–4606. [Google Scholar] [CrossRef]
- Song, D.Z.; Wang, E.Y.; Liu, J. Relationship between EMR and dissipated energy of coal rock mass during cyclic loading process. Saf. Sci. 2012, 50, 751–760. [Google Scholar] [CrossRef]
- Patton, F.D. Multiple modes of shear failure in rock. In Proceedings of the 1st ISRM Congress, Lisbon, Portugal, 25 September–1 October 1966; International Society for Rock Mechanics and Rock Engineering: Lisbon, Portugal, 1966. [Google Scholar]
- Wang, Z.; Gu, L.L.; Shen, M.R.; Zhang, F.; Zhang, G.K.; Wang, X. Shear stress relaxation behavior of rock discontinuities with different joint roughness coefficient and stress histories. J. Struct. Geol. 2019, 126, 272–285. [Google Scholar] [CrossRef]
- Barton, N. Suggested methods for the quantitative description of discontinuities in rock masses: International Society for Rock Mechanics. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 319–368. [Google Scholar]
- Liu, X.S.; Ning, J.G.; Tan, Y.L.; Gu, Q.H. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Meng, Q.B.; Zhang, M.W.; Zhang, Z.Z.; Han, L.J.; Pu, H. Research on non-linear characteristics of rock energy evolution under uniaxial cyclic loading and unloading conditions. Environ. Earth Sci. 2019, 78, 650. [Google Scholar] [CrossRef]
- Li, P.; Cai, M.F. Energy evolution mechanism and failure criteria of jointed surrounding rock under uniaxial compression. J. Cent. South Univ. 2021, 28, 1857–1874. [Google Scholar] [CrossRef]
- Zhang, M.W.; Meng, Q.B.; Liu, S.D. Energy Evolution Characteristics and Distribution Laws of Rock Materials under Triaxial Cyclic Loading and Unloading Compression. Adv. Mater. Sci. Eng. 2017, 2017, 5471571. [Google Scholar] [CrossRef] [Green Version]
- Li, T.T.; Pei, X.J.; Wang, D.P.; Huang, R.Q.; Tang, H. Nonlinear behavior and damage model for fractured rock under cyclic loading based on energy dissipation principle. Eng. Fract. Mech. 2019, 206, 330–341. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Gao, F. Experimental investigation on the energy evolution of dry and water-saturated red sandstones. Int. J. Min. Sci. Technol. 2015, 25, 383–388. [Google Scholar] [CrossRef]
- Meng, Q.B.; Zhang, M.W.; Han, L.J.; Pu, H.; Chen, Y.L. Acoustic Emission Characteristics of Red Sandstone Specimens under Uniaxial Cyclic Loading and Unloading Compression. Rock Mech. Rock Eng. 2018, 51, 969–988. [Google Scholar] [CrossRef]

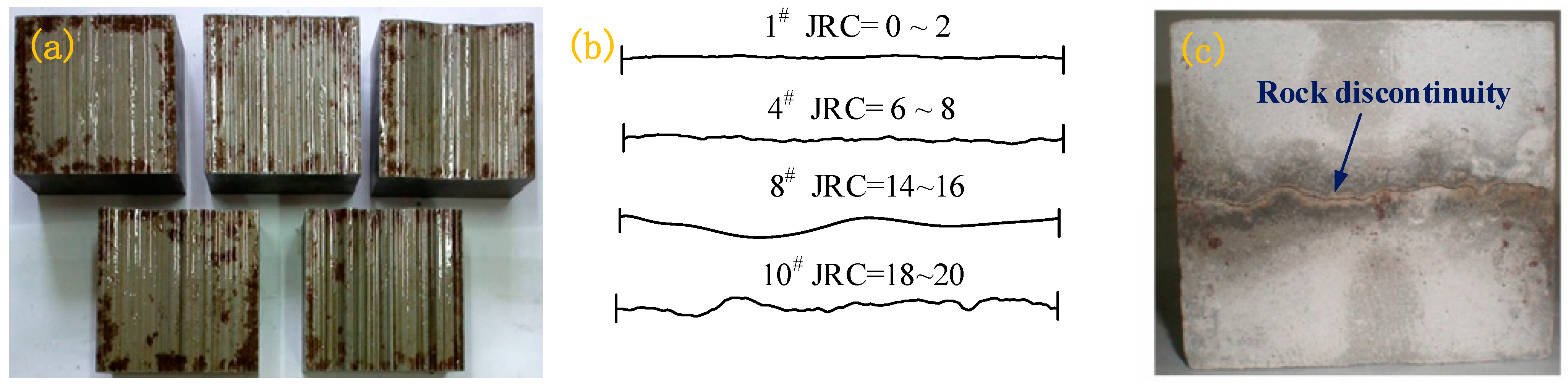





| Sample | Peak Stress/kN | σc/MPa |
|---|---|---|
| 1 | 228.47 | 22.85 |
| 2 | 233.44 | 23.34 |
| 3 | 177.69 | 17.77 |
| 4 | 248.37 | 24.84 |
| 5 | 198.55 | 19.86 |
| Average value | 217.30 | 21.73 |
| Sample | Peak Stress/kN | τc/MPa |
|---|---|---|
| 1–2.17 | 7.5 | 1.5 |
| 1–4.35 | 15.2 | 3.0 |
| 1–6.52 | 18.5 | 3.7 |
| 4–2.17 | 10.1 | 2.0 |
| 4–4.35 | 15.2 | 3.0 |
| 4–6.52 | 22.5 | 4.5 |
| 8–2.17 | 12.2 | 2.4 |
| 8–4.35 | 20.0 | 4.0 |
| 8–6.52 | 25.0 | 5.0 |
| 10–2.17 | 12.5 | 2.5 |
| 10–4.35 | 22.1 | 4.4 |
| 10–6.52 | 27.5 | 5.5 |
| Sample | Upper Limit of Loading Stress at First Stage/MPa | Amplitude/MPa |
|---|---|---|
| 1–2.17 | 0.45 | 0.15 |
| 1–4.35 | 0.90 | 0.30 |
| 1–6.52 | 1.10 | 0.37 |
| 4–2.17 | 0.60 | 0.20 |
| 4–4.35 | 0.90 | 0.30 |
| 4–6.52 | 1.35 | 0.45 |
| 8–2.17 | 0.72 | 0.24 |
| 8–4.35 | 1.20 | 0.40 |
| 8–6.52 | 1.50 | 0.50 |
| 10–2.17 | 0.75 | 0.25 |
| 10–4.35 | 1.32 | 0.44 |
| 10–6.52 | 1.65 | 0.55 |
| Sample | Stress Level |
|---|---|
| 1–2.17 | 0.28, 0.37, 0.46, 0.55, 0.64, 0.74, 0.83, 0.92 |
| 1–4.35 | 0.27, 0.36, 0.46, 0.55, 0.64, 0.73, 0.82, 0.91 |
| 1–6.52 | 0.20, 0.27, 0.34, 0.41, 0.48, 0.55, 0.62, 0.69, 0.75, 0.82, 0.89 |
| 4–2.17 | 0.39, 0.52, 0.65, 0.79, 0.92 |
| 4–4.35 | 0.31, 0.41, 0.52, 0.62, 0.72, 0.83, 0.93 |
| 4–6.52 | 0.26, 0.35, 0.44, 0.53, 0.62, 0.71, 0.79, 0.88, 0.97 |
| 8–2.17 | 0.29, 0.39, 0.48, 0.58, 0.68, 0.78, 0.87, 0.97 |
| 8–4.35 | 0.31, 0.41, 0.51, 0.61, 0.71, 0.82, 0.92 |
| 8–6.52 | 0.26, 0.34, 0.43, 0.52, 0.60, 0.69, 0.77, 0.86, 0.95 |
| 10–2.17 | 0.28, 0.37, 0.46, 0.56, 0.65, 0.74, 0.84, 0.93 |
| 10–4.35 | 0.26, 0.35, 0.44, 0.52, 0.61, 0.70, 0.79, 0.87, 0.96 |
| 10–6.52 | 0.32, 0.43, 0.54, 0.64, 0.75, 0.86, 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, W.; Gu, L.; Wang, Z.; Ma, J.; Li, H.; Zhou, H. Experimental Study of Energy Evolution at a Discontinuity in Rock under Cyclic Loading and Unloading. Materials 2022, 15, 5784. https://doi.org/10.3390/ma15165784
Zheng W, Gu L, Wang Z, Ma J, Li H, Zhou H. Experimental Study of Energy Evolution at a Discontinuity in Rock under Cyclic Loading and Unloading. Materials. 2022; 15(16):5784. https://doi.org/10.3390/ma15165784
Chicago/Turabian StyleZheng, Wei, Linlin Gu, Zhen Wang, Junnan Ma, Hujun Li, and Hang Zhou. 2022. "Experimental Study of Energy Evolution at a Discontinuity in Rock under Cyclic Loading and Unloading" Materials 15, no. 16: 5784. https://doi.org/10.3390/ma15165784
APA StyleZheng, W., Gu, L., Wang, Z., Ma, J., Li, H., & Zhou, H. (2022). Experimental Study of Energy Evolution at a Discontinuity in Rock under Cyclic Loading and Unloading. Materials, 15(16), 5784. https://doi.org/10.3390/ma15165784






