A Consolidation Curve Reproduction Based on Sigmoid Model: Evaluation and Statistical Assessment
Abstract
:1. Introduction
2. Overview of Stress–Strain Approximations for One-Dimensional Loading
3. Theoretical Background
4. Materials and Methods
4.1. Soil Material Used in the Present Study
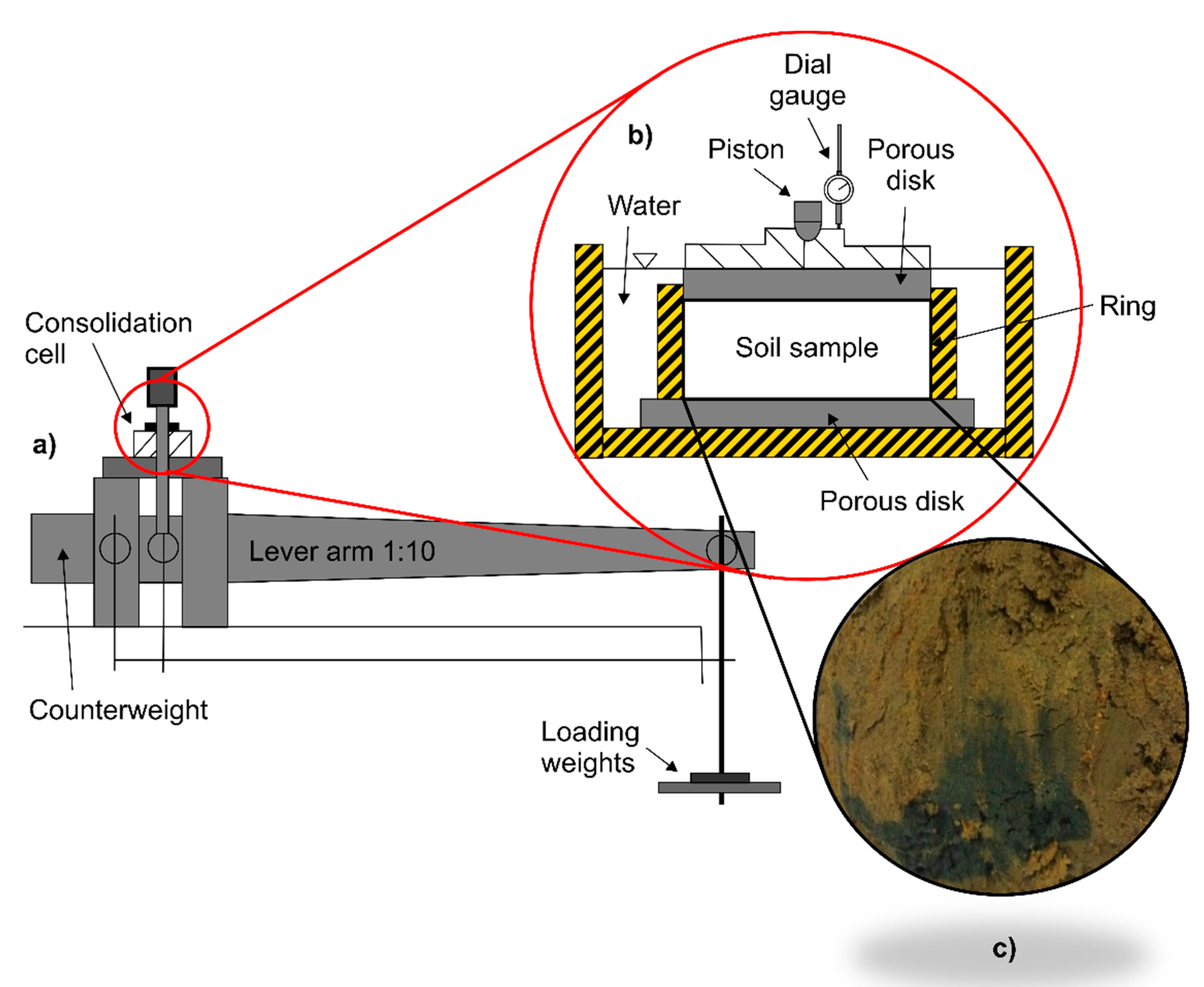
4.2. Testing Procedure
4.3. Statistical Analysis
5. Results
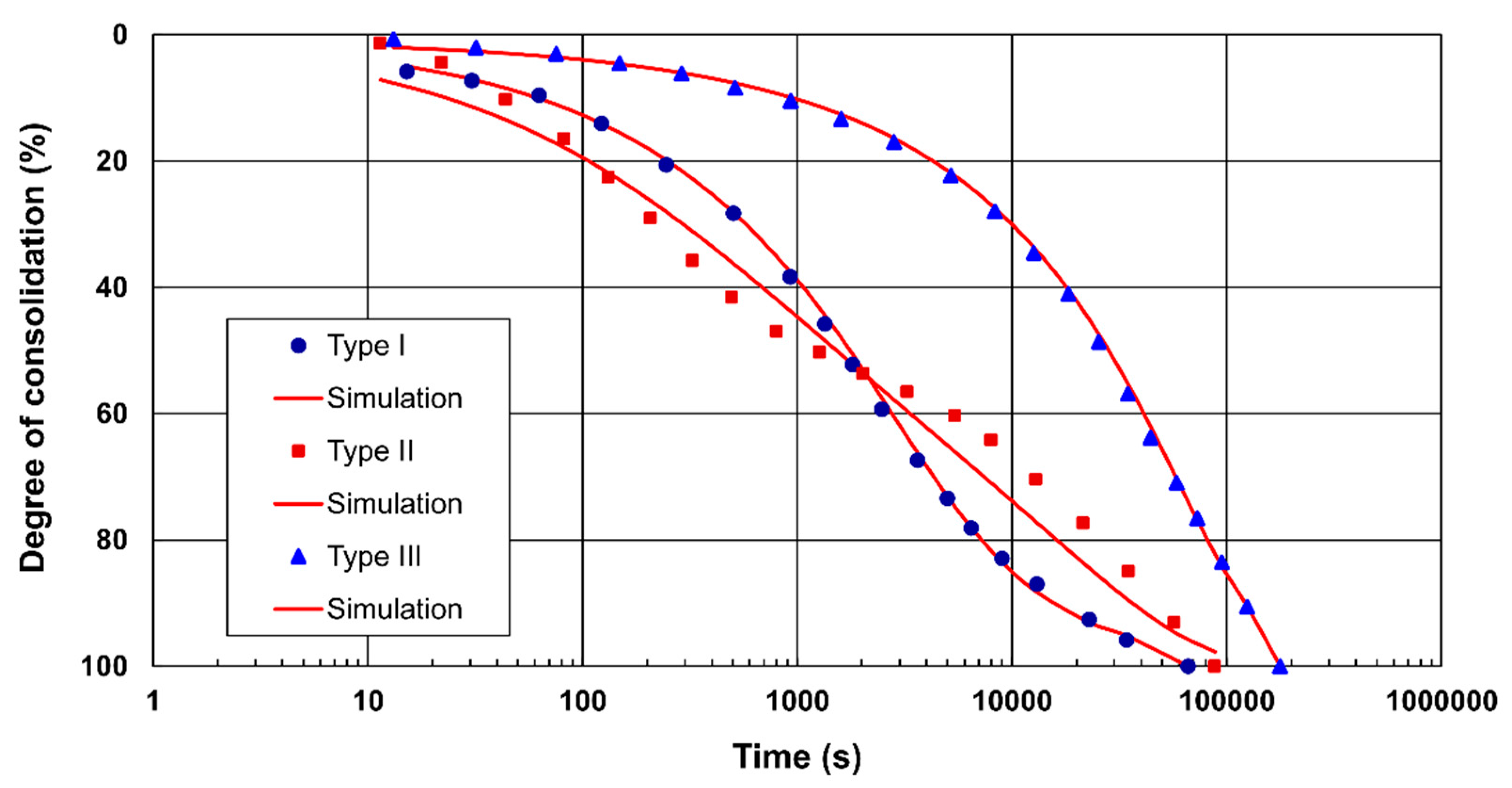
5.1. Marsal et al. Cases
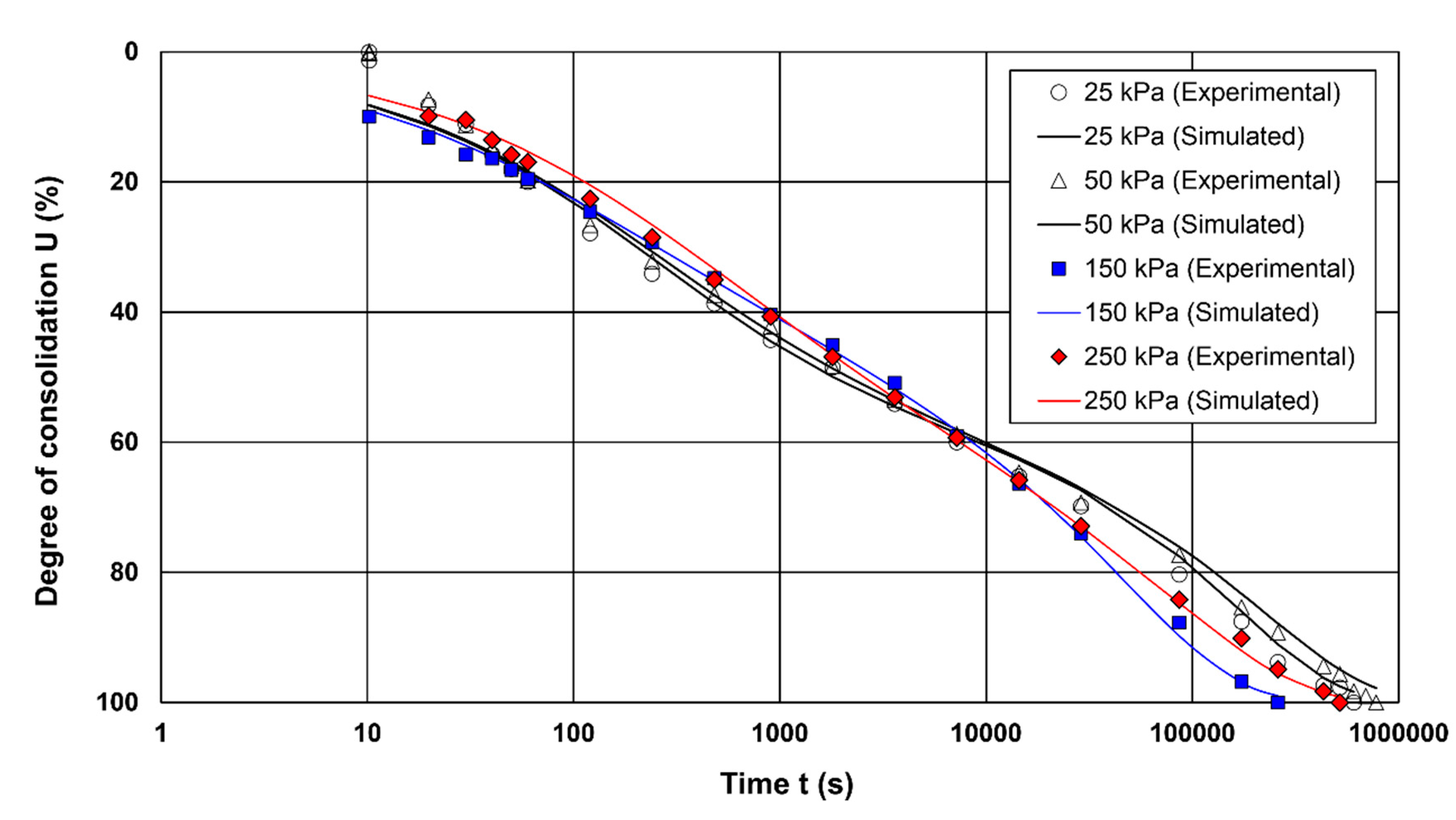
5.2. Soft Organic Soils
6. Conclusions
- A consolidation curve of various shapes usually represents the laboratory results of the consolidation test. The curve described as an exact mathematical function enables precise determination of any point in its course for any consolidation time. This provides an accurate indication of critical points on the curve, such as tangent to the inflection point, the end time of filtration consolidation, i.e., EOP point or specific time, and the compression necessary to compute the coefficient of consolidation;
- Optimizing the input data allows for the densification of measurement points, leading to increased accuracy in constitutive modelling when the observed and predicted consolidation courses are compared;
- In general, the graphical results obtained during calibration indicated adequate model prediction over the range of the average degree of consolidation, and the simulations mostly cover the measurements;
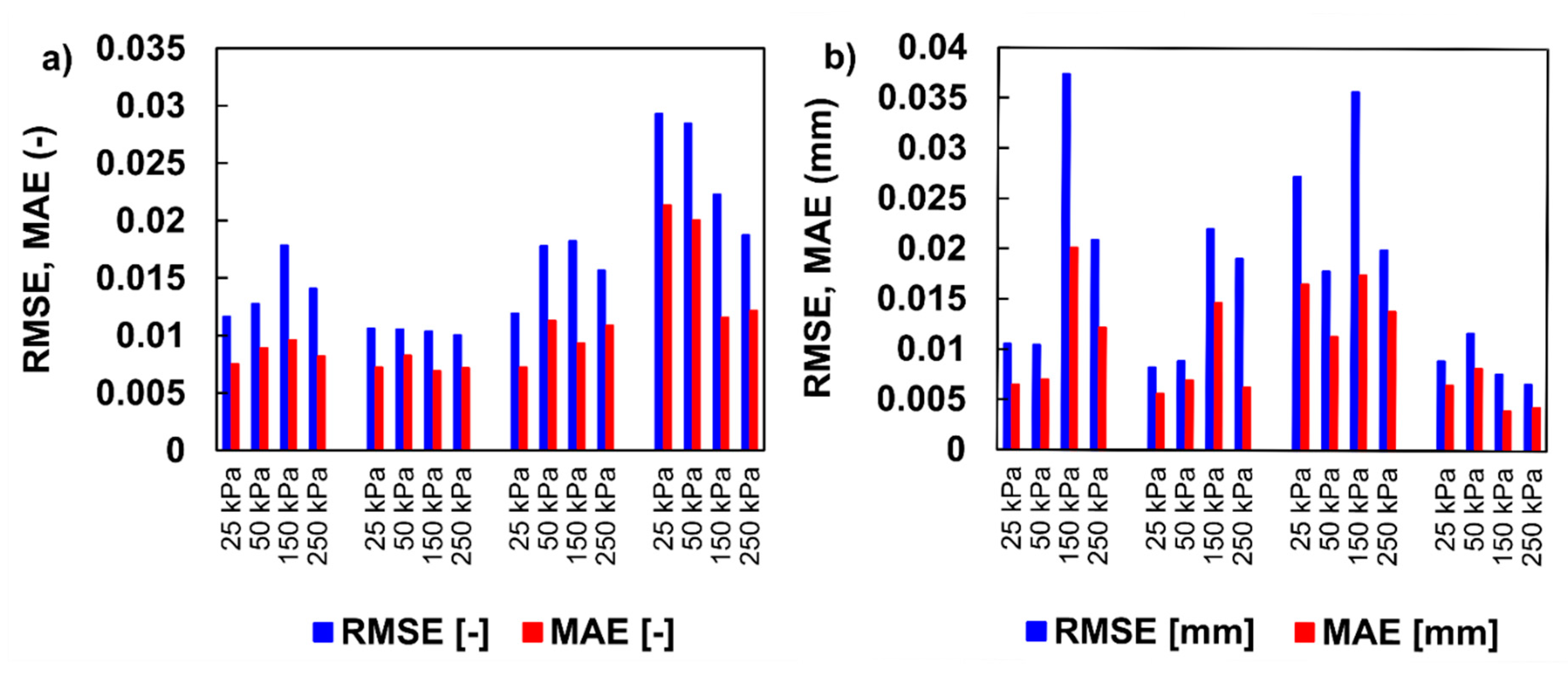
- Comparisons between observed and predicted data were assessed using various deviation statistics, such as mean error (E), root mean square error (RMSE), mean absolute error (MAE), weighted error (WE), the revised Nash–Sutcliffe efficiency index (CE1) and the refined index of model performance (dr). The weighted error (WE) was chosen as the optimization target because this normalized metric eliminates the scale effects on the fit between the experimental and simulated results;
- Although all the statistical measures indicated a perfect match between the experimental and simulated data, some exhibited illogical behaviour, i.e., CE1 and dr decreased increased simulated values, as assessed by the RMSE or MAE. A possible cause of the ambiguous results is the absence of extreme values in the input data. RMSE or MAE do not provide information about the level or degree of error; therefore, they should be linked to other statistical metrics. According to our statistical analysis, we recommended the use of RMSE or MAE in combination with WE to evaluate the optimization of laboratory data from consolidation studies. Combining these indicators resulted in correct and logical behaviour; WE decreased with decreased RMSE or MAE values;
- All findings based on statistical assessments demonstrate that the evaluated sigmoid model is efficient and applicable for accurate reproduction of various shapes of laboratory consolidation curves and is therefore a valuable tool for numerical analysis.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, Z.Y.; Jin, Y.F. Practice of Optimisation Theory in Geotechnical Engineering; Tongji University Press: Shanghai, China, 2019. [Google Scholar]
- Nie, W.; Guo, W. Applications of Chapman-Richards model to geotechnical engineering. J. Rock Mech. Geotech. Eng. 2019, 11, 1286–1292. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; John Wiley: New York, NY, USA, 1948. [Google Scholar]
- Butterfield, R.; Baligh, F. A new evaluation of loading cycles in an oedometer. Géotechnique 1996, 46, 547–553. [Google Scholar] [CrossRef]
- Liu, M.D.; Xu, K.J.; Horpibulsuk, S. A mathematical function to represent S-shaped relationships for geotechnical applications. Proc. Inst. Civ. Eng. Geotech. Eng. 2013, 166, 321–327. [Google Scholar] [CrossRef]
- Sun, R.; Peng, W.W.; Huang, H.Z.; Ling, D.; Yang, J. Improved reliability data curve fitting method by considering samples distinction. Eksploat. Niezawodn. 2012, 14, 62–71. [Google Scholar]
- Bayat, H.; Rastgo, M.; Zadeh, M.M.; Vereecken, H. Particle size distribution models, their characteristics and fitting capability. J. Hydrol. 2015, 529, 872–889. [Google Scholar] [CrossRef]
- Watabe, Y.; Leroueil, S. Modeling and implementation of the isotache concept for long-term consolidation behavior. Int. J. Geomech. 2015, 15, A4014006. [Google Scholar] [CrossRef]
- Ferrari, A.; Favero, V.; Laloui, L. One-dimensional compression and consolidation of shales. Int. J. Rock Mech. Min. Sci. 2016, 88, 286–300. [Google Scholar] [CrossRef]
- Le, T.M.; Fatahi, B.; Khabbaz, H.; Sun, W. Numerical optimization applying trust-region reflective least squares algorithm with constraints to optimize the non-linear creep parameters of soft soil. Appl. Math. Model. 2017, 41, 236–256. [Google Scholar] [CrossRef]
- Farnsworth, C. Evaluation of curve fitting techniques for estimating time of surcharge release in embankment construction over Soft Soils. In Proceedings of the Construction Research Congress 2018, New Orleans, LA, USA, 2–4 April 2018. [Google Scholar]
- Rastgou, M.; Bayat, H.; Mansoorizadeh, M. Fitting soil particle-size distribution (PSD) models by PSD curve fitting software. Pol. J. Soil Sci. 2019, 52, 211–223. [Google Scholar] [CrossRef]
- Fu, Y.; He, S.; Zhang, S.; Yong, Y. Parameter Analysis on Hardening Soil Model of Soft Soil for Foundation Pits Based on Shear Rates in Shenzhen Bay, China. Adv. Mater. Sci. Eng. 2020, 2020, 1687–8434. [Google Scholar] [CrossRef]
- Lai, Y.; Wang, L.; Zhang, Y.; Hong, Y. Site-specific soil reaction model for monopiles in soft clay based on laboratory element stress-strain curves. Ocean. Eng. 2021, 220, 108437. [Google Scholar] [CrossRef]
- Kovačević, M.S.; Bačić, M.; Librić, L.; Gavin, K. Evaluation of creep behavior of soft soils by utilizing multisensor data combined with machine learning. Sensors 2022, 22, 2888. [Google Scholar] [CrossRef] [PubMed]
- Handy, R. First-order rate equations in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2002, 128, 416–425. [Google Scholar] [CrossRef]
- Chan, A.H.C. Determination of the coefficient of consolidation using a least squares method. Géotechnique 2003, 53, 673–678. [Google Scholar] [CrossRef]
- Mesri, G. Primary compression and secondary compression. Geotech. Spec. Publ. 2003, 119, 122–166. [Google Scholar]
- King, G. How not to lie with statistics: Avoiding common mistakes in quantitative political science. Am. J. Political Sci. 1986, 30, 666–687. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of stress-strain curves by three parameters. Nat. Adv. Com. Aer. 1943, 902, 1–23. [Google Scholar]
- Graham, J.; Pinkney, R.B.; Lew, K.V.; Trainor, P.G. Curve-fitting and laboratory data. Can. Geotech. J. 1982, 19, 201–205. [Google Scholar] [CrossRef]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Chapman, D.G. Statistical problems in population dynamics. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960. [Google Scholar]
- Ayrton, W.E.; Perry, J. On struts. Engineering 1886, 62, 464–465. [Google Scholar]
- Southwell, R.V. On the analysis of experimental observations in problems of elastic stability. In Proceedings of the Royal Society of London; Royal Society: London, UK, 1932; Volume 135, pp. 601–616. [Google Scholar]
- Duncan, J.M.; Chang, C.M. Nonlinear analysis of stress and strain in soils. J. Soil Mech. Found. Div. 1970, 96, 1629–1653. [Google Scholar] [CrossRef]
- Chin, F.K. Discussion on Relation between strength and maturity of concrete. J. Am. Concr. Inst. 1971, 68, 728–729. [Google Scholar]
- Tan, S.B. Empirical method for estimating secondary and total settlement. In Proceedings of the 4th Asian Regional Conference on Soil Mechanics and Foundation Engineering, Bangkok, Thailand, 26 July–1 August 1971. [Google Scholar]
- Sridharan, A.; Rao, A. Rectangular hyperbola method for one dimensional consolidation. Geotech. Test. J. 1981, 4, 161–168. [Google Scholar] [CrossRef]
- Le, T.M.; Fatahi, B.; Khabbaz, H. Viscous behaviour of soft clay and inducing factors. Geotech. Geol. Eng. 2012, 30, 1069–1083. [Google Scholar] [CrossRef]
- Augustesen, A.; Liingaard, M.; Lade, P.V. Evaluation of time-dependent behavior of soils. Int. J. Geomech. 2004, 4, 137–156. [Google Scholar] [CrossRef] [Green Version]
- Leroueil, S. The isotache approach—Where are we 50 years after its development by Professor Suklje. In Proceedings of the 13th Danube-European Conference on Geotechnical Engineering, Ljubljana, Slovenia, 29 May–1 June 2006. [Google Scholar]
- Kaczmarek, Ł.; Dobak, P. Contemporary overview of soil creep phenomenon. Contemp. Trends Geosci. 2017, 6, 28–40. [Google Scholar] [CrossRef]
- Buisman, A.S. Results of long duration settlement tests. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering, Cambridge, MA, USA, 22–26 June 1936. [Google Scholar]
- Singh, A.; Mitchell, J.K. General stress-strain-time function for soils. J. Soil Mech. Found. Div. 1968, 94, 21–46. [Google Scholar] [CrossRef]
- Havel, F. Creep in Soft Soils. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2004. [Google Scholar]
- Kohlrausch, R. Theorie des elektrischen rückstandes in der leidener flasche. Ann. Phys. 1854, 167, 179–214. [Google Scholar] [CrossRef]
- Janbu, N. The resistance concept applied to deformations of soils. In Proceedings of the 7th International Soil Mechanics and Foundation Engineering Conference, Mexico City, Mexico, 29 August 1969. [Google Scholar]
- Feng, T.W. Some observations on the oedometric consolidation strain rate behaviors of saturated clay. J. GeoEngin. 2010, 5, 1–7. [Google Scholar]
- Marsal, R.J.; Sandoval, R.; Hiriart, F. Curvas deformación-tiempo en las arcillas del Valle de México. In Ingenieria Civil; Colegio de Ingenieros Civiles de Mexico: Mexico City, Mexico, 1950. [Google Scholar]
- Leonards, G.A.; Girault, P. A study of the one-dimensional consolidation test. In Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris, France, 17–22 July 1961. [Google Scholar]
- Lo, K.Y. Secondary Compression of Clays. J. Soil Mech. Found. Div. 1961, 87, 61–82. [Google Scholar] [CrossRef]
- Wahls, H.E. Analysis of primary and secondary consolidation. J. Soil Mech. Found. Div. 1962, 88, 207–231. [Google Scholar] [CrossRef]
- Majer, E.; Bialobrzeski, T. Oznaczanie pionowego współczynnika konsolidacji (Cv) namułów organicznych metodami IL i CL. Acta Sci. Pol. Arch. 2015, 14, 15–27. [Google Scholar]
- Zeng, L.L.; Hong, Z.S.; Cui, Y.J. On the volumetric strain-time curve patterns of dredged clays during primary consolidation. Géotechnique 2015, 65, 1023–1028. [Google Scholar] [CrossRef]
- Zhang, W.M. A simple method for rate of consolidation deformation and its applications. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Korea, 17–22 September 2017. [Google Scholar]
- Terzaghi, K.; Fröhlich, O.K. Theorie der Setzung von Tonschichte; Leipzig/Wien Deuticke: Vienna, Austria, 1936. [Google Scholar]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- ISO 17892-5:2017; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 5: Incremental Loading Oedometer Test. PKN: Warszawa, Poland, 2017.
- Huwaldt, J.; Steinhorst, S. Plot Digitizer (Version 2.6.9). Software. Available online: https://sourceforge.net/projects/plotdigitizer/files/ (accessed on 21 June 2022).
- Olek, B.S. Experimental insights into consolidation rates during one-dimensional loading with special reference to excess pore water pressure. Acta Geotech. 2020, 15, 3571–3591. [Google Scholar] [CrossRef]
- Jin, Y.F.; Yin, Z.Y.; Wu, Z.X.; Zhou, W.H. Identifying parameters of easily crushable sand and application to offshore pile driving. Ocean. Eng. 2018, 154, 416–429. [Google Scholar] [CrossRef]
- Helland, I.S. On the interpretation and use of R2 in regression analysis. Biometrics 1987, 43, 61–69. [Google Scholar] [CrossRef]
- Legates, D.R.; Davis, R.E. The continuing search for an anthropogenic climate change signal: Limitations of correlation-based approaches. Geophys. Res. Lett. 1997, 24, 2319–2322. [Google Scholar] [CrossRef]
- Azubuike, I.M. On the misconception of R2 for (r)2 in a regression model. Int. J. Res. Sci. Innov. 2019, 6, 71–76. [Google Scholar]
- Addiscott, T.M.; Whitmore, A.P. Computer simulation of changes of soil mineral nitrogen and crop nitrogen during autumn, winter and spring. J. Agric. Sci. 1987, 109, 141–157. [Google Scholar] [CrossRef]
- Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
- Levasseur, S.; Malécot, Y.; Boulon, M.; Flavigny, E. Soil parameter identification using a genetic algorithm. Int. J. Numer. Anal. Methods. Geomech. 2008, 32, 89–213. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- McCuen, R.H.; Snyder, W.M. A proposed index for comparing hydrographs. Water Resour. Res. 1975, 11, 1021–1024. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in waters head simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. A refined index of model performance: A rejoinder. Int. J. Climatol. 2013, 33, 1053–1056. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. Short communication: A refined index of model performance. Int. J. Climatol. 2011, 32, 2088–2094. [Google Scholar] [CrossRef]
- Ladson, A.R. Hydrology: An Australian Introduction; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Ali, M.H.; Abustan, I. A new novel index for evaluating model performance. J. Nat. Resour. Develop. 2014, 4, 1–9. [Google Scholar]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]


| Particle Size | Atterberg Limits | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Soil Type | Sample | Sand (%) | Silt (%) | Clay (%) | Natural Water Content (%) | Liquid Limit (%) | Plastic Limit (%) | Plasticity Index (%) | Organic Content (%) | Specific Gravity (-) |
| Organic silty clay | O1 | 13 | 68 | 19 | 60.30 | 82.96 | 33.33 | 49.63 | 7.00 | 2.56 |
| Organic clayey silt | O2 | 2 | 56 | 42 | 84.00 | 109.50 | 54.22 | 55.28 | 11.30 | 2.62 |
| Organic clayey silt | O3 | 23 | 60 | 17 | 55.22 | 66.11 | 32.80 | 33.31 | 5.00 | 2.61 |
| Organic clayey silt | O4 | 18 | 61 | 21 | 51.75 | 75.22 | 37.50 | 37.72 | 6.80 | 2.63 |
| a1 | a2 | x0 | n | R2 | E | RMSE | MAE | WE | CE1 | dr |
|---|---|---|---|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] |
| Type I | ||||||||||
| 0.012807 | 0.000372 | 9982.806 | 0.991025 | 0.998 | −0.0017 | 0.0110 | 0.0080 | 0.0211 | 0.968 | 0.991 |
| Type II | ||||||||||
| 0.036131 | 0.000902 | 648.8058 | 0.79307 | 0.981 | 0.448297 | 0.0443 | 0.0094 | 0.119 | 0.826 | 0.926 |
| Type III | ||||||||||
| 0.002755 | 0.000663 | 22.80575 | 0.670025 | 0.999 | 0.006929 | 0.0084 | 0.0069 | 0.027 | 0.931 | 0.982 |
| σ | A1 | A2 | x0 | p | R2 | E | RMSE | MAE | WE | CE1 | dr |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [kPa] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] | [-] |
| Sample O1 | |||||||||||
| 25 | 0.03087 | 0.000262 | 2999.806 | 1.004025 | 0.99914 | 0.0009 | 0.01133 | 0.00699 | 0.017 | 0.977 | 0.997 |
| 50 | 0.02807 | 0.000472 | 2082.806 | 0.970025 | 0.99875 | −0.0036 | 0.01275 | 0.00889 | 0.019 | 0.989 | 0.996 |
| 150 | 0.04180 | 0.000252 | 1282.806 | 0.970025 | 0.99758 | 0.0027 | 0.01784 | 0.00960 | 0.021 | 0.942 | 0.984 |
| 250 | 0.02280 | 0.000222 | 1882.806 | 0.985025 | 0.99866 | 0.0009 | 0.01406 | 0.00819 | 0.015 | 0.983 | 0.988 |
| Sample O2 | |||||||||||
| 25 | 0.02194 | 0.000632 | 5952.806 | 1.220703 | 0.99925 | 0.0012 | 0.01059 | 0.00720 | 0.022 | 0.976 | 0.986 |
| 50 | 0.00689 | 1.82 × 10−5 | 12992.81 | 0.848267 | 0.99918 | −0.0003 | 0.01052 | 0.00824 | 0.025 | 0.984 | 0.998 |
| 150 | 0.01160 | 0.000272 | 5382.806 | 0.999025 | 0.99945 | 0.0048 | 0.01033 | 0.00688 | 0.016 | 0.920 | 0.976 |
| 250 | 0.01010 | 0.000202 | 5312.806 | 0.999025 | 0.99924 | −0.0002 | 0.01002 | 0.00716 | 0.025 | 0.986 | 0.998 |
| Sample O3 | |||||||||||
| 25 | 0.02797 | 0.000568 | 3982.806 | 1.180054 | 0.99920 | 0.0036 | 0.01191 | 0.00722 | 0.020 | 0.978 | 0.981 |
| 50 | 0.02807 | 0.000524 | 1099.806 | 0.870025 | 0.99727 | −0.0011 | 0.01776 | 0.01127 | 0.022 | 0.976 | 0.990 |
| 150 | 0.04780 | 0.000292 | 1222.806 | 0.970025 | 0.99746 | 0.0027 | 0.01820 | 0.00929 | 0.017 | 0.965 | 0.983 |
| 250 | 0.02790 | 0.000195 | 1492.862 | 0.999925 | 0.99814 | 0.0002 | 0.01564 | 0.01083 | 0.031 | 0.978 | 0.996 |
| Sample O4 | |||||||||||
| 25 | 0.05423 | 0.000182 | 368.8058 | 0.89707 | 0.99465 | 0.0003 | 0.02925 | 0.02134 | 0.061 | 0.984 | 0.997 |
| 50 | 0.05413 | 0.000112 | 320.6058 | 0.85707 | 0.99585 | 0.0047 | 0.02846 | 0.02003 | 0.056 | 0.989 | 0.998 |
| 150 | 0.07013 | 0.000452 | 141.9958 | 0.77207 | 0.99464 | 0.0032 | 0.02224 | 0.01157 | 0.019 | 0.961 | 0.986 |
| 250 | 0.03673 | 0.000202 | 448.8058 | 0.79207 | 0.99671 | −0.0004 | 0.01872 | 0.01217 | 0.030 | 0.982 | 0.997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olek, B.S. A Consolidation Curve Reproduction Based on Sigmoid Model: Evaluation and Statistical Assessment. Materials 2022, 15, 6188. https://doi.org/10.3390/ma15186188
Olek BS. A Consolidation Curve Reproduction Based on Sigmoid Model: Evaluation and Statistical Assessment. Materials. 2022; 15(18):6188. https://doi.org/10.3390/ma15186188
Chicago/Turabian StyleOlek, Bartłomiej Szczepan. 2022. "A Consolidation Curve Reproduction Based on Sigmoid Model: Evaluation and Statistical Assessment" Materials 15, no. 18: 6188. https://doi.org/10.3390/ma15186188
APA StyleOlek, B. S. (2022). A Consolidation Curve Reproduction Based on Sigmoid Model: Evaluation and Statistical Assessment. Materials, 15(18), 6188. https://doi.org/10.3390/ma15186188




