A Mesoscale Study on the Dilation of Actively Confined Concrete under Axial Compression
Abstract
:1. Introduction
2. Mesoscale Model of Concrete
2.1. Random Aggregate Structure
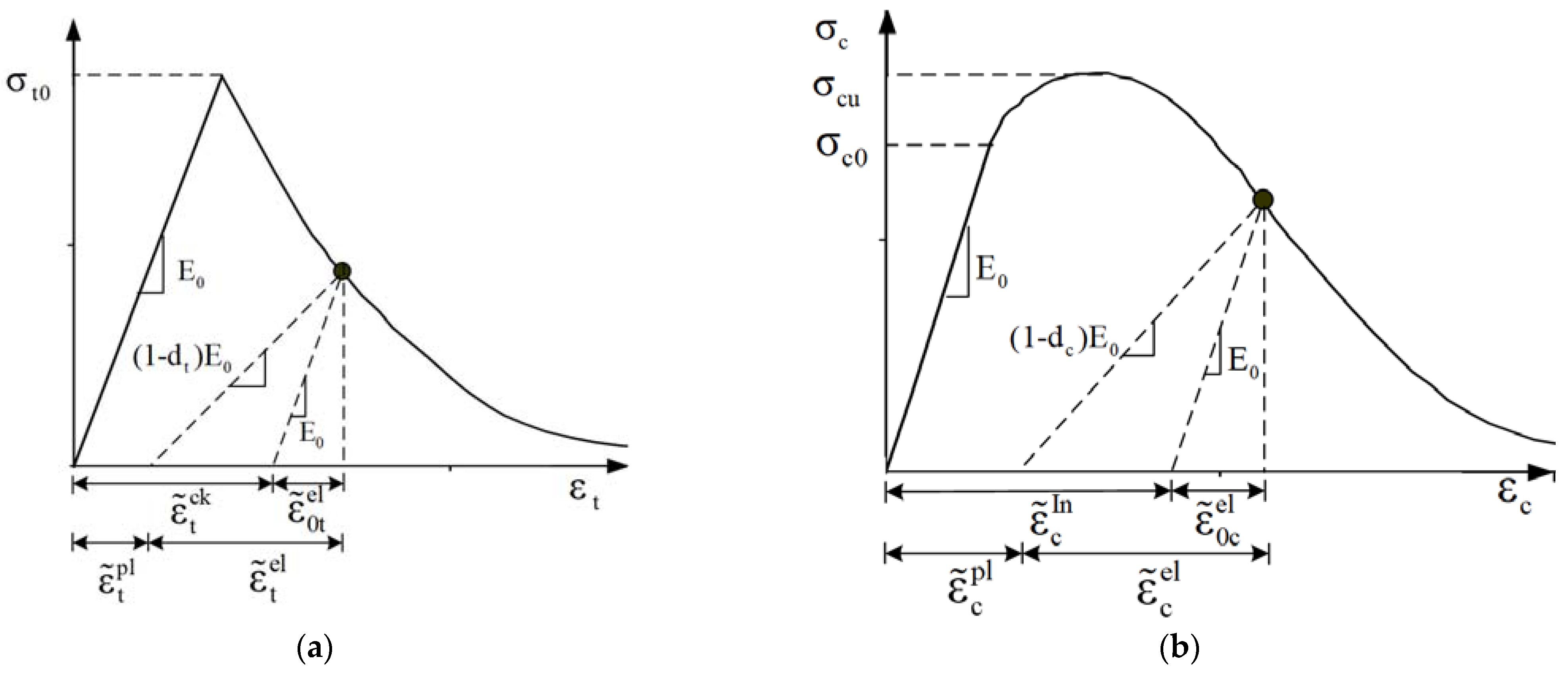
2.2. Material Model
2.3. Strength Relationship between Concrete and Mortar
3. Validation of the Mesoscale Model
3.1. Stress–Strain Curve
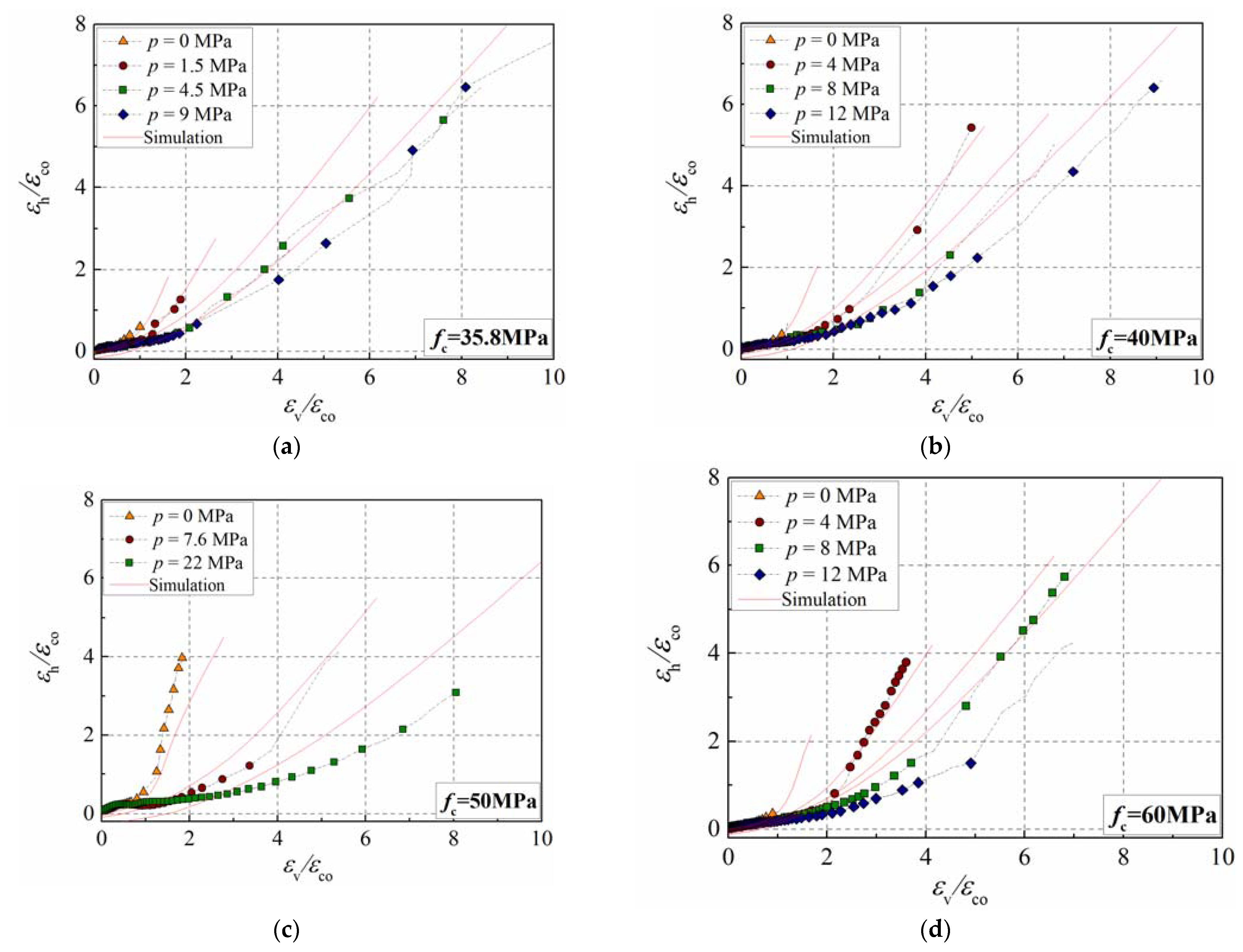
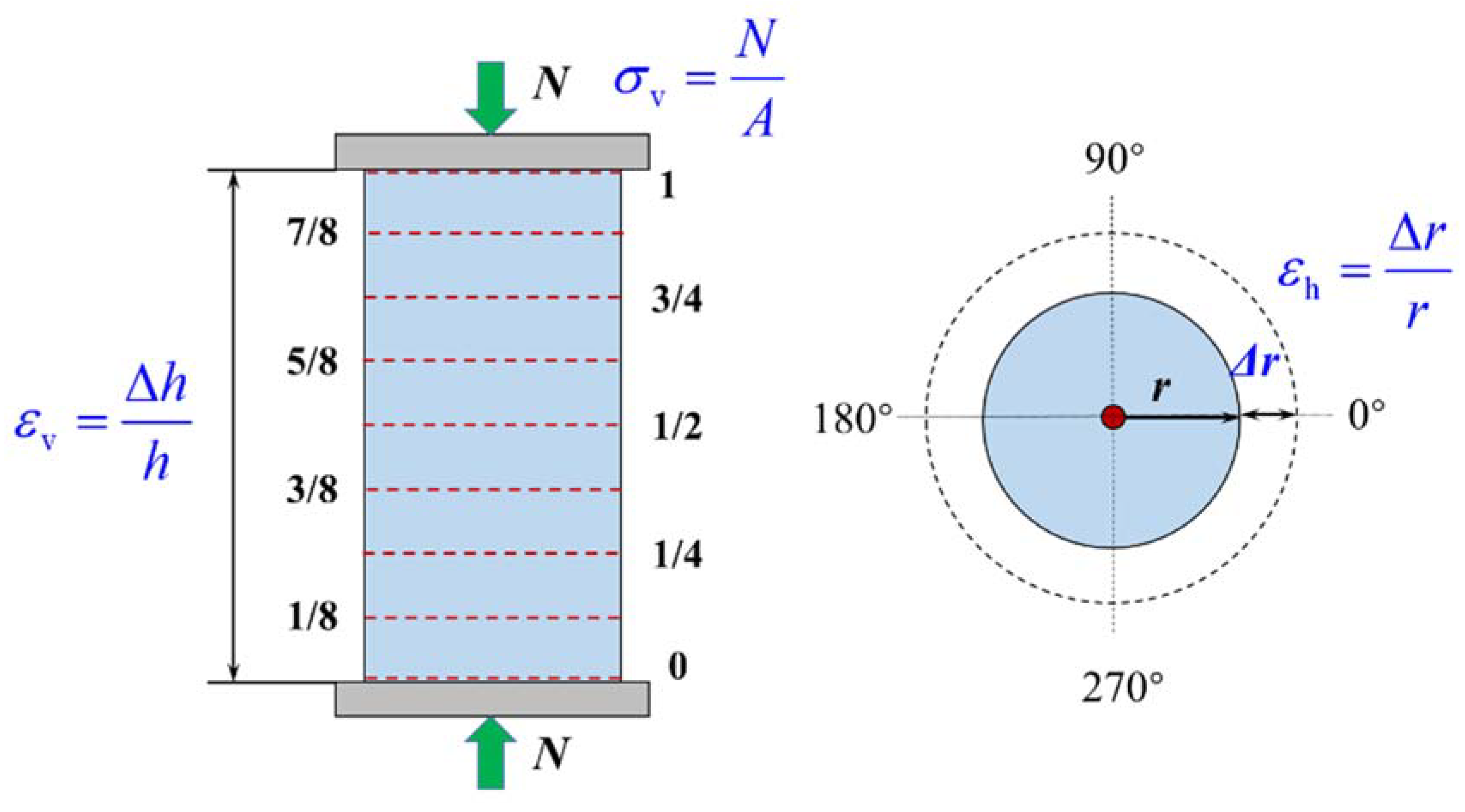
3.2. Lateral–Axial Strain Curve
4. Parameter Analysis
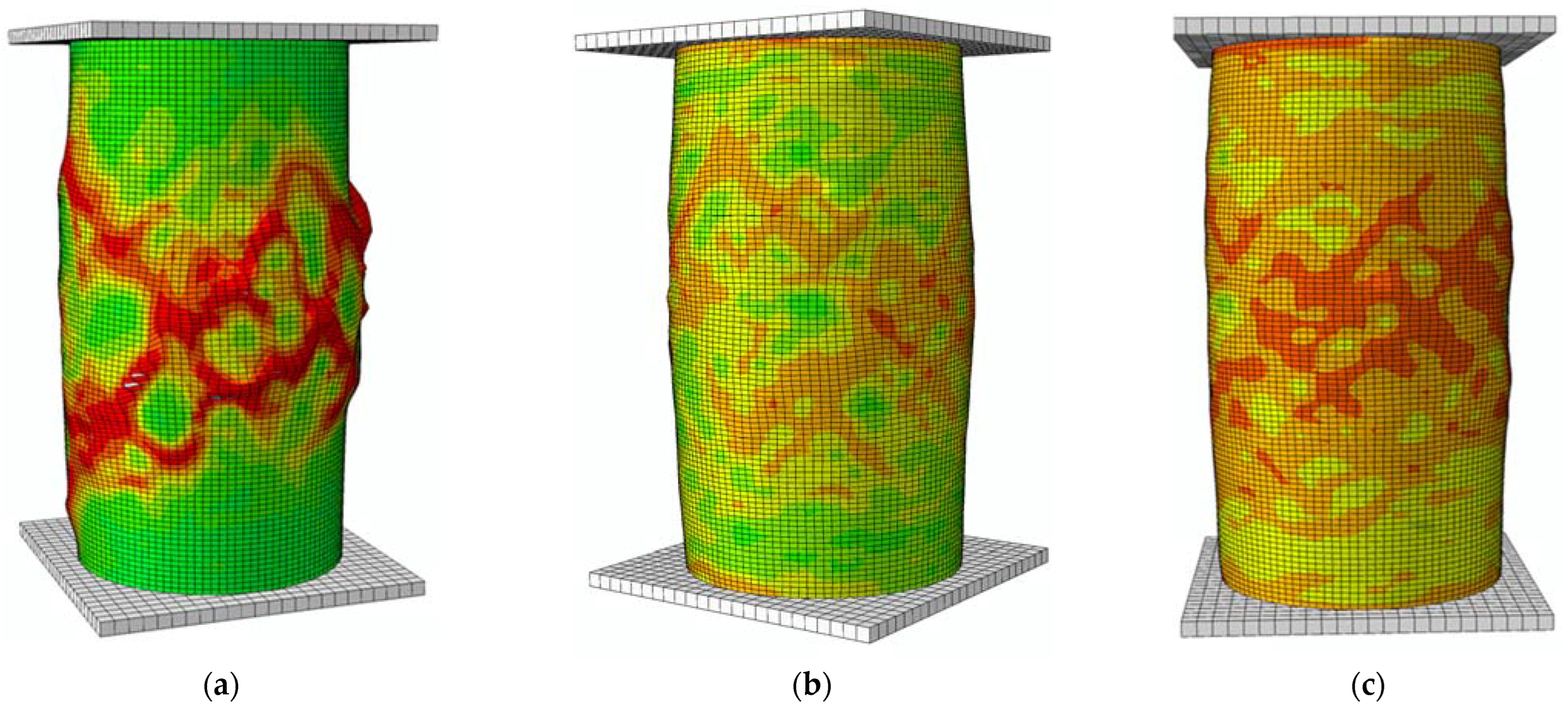
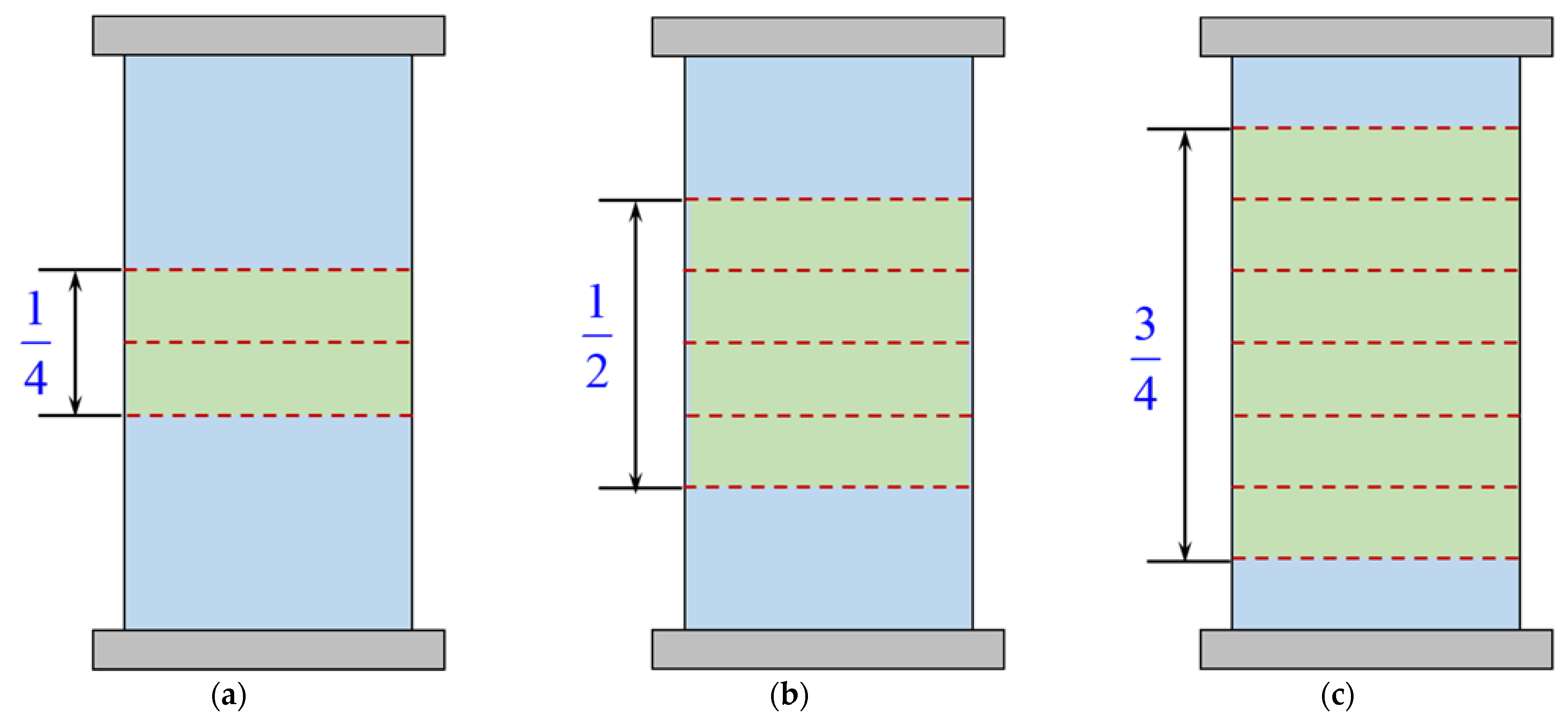
4.1. Failure Mode and Strain Distribution
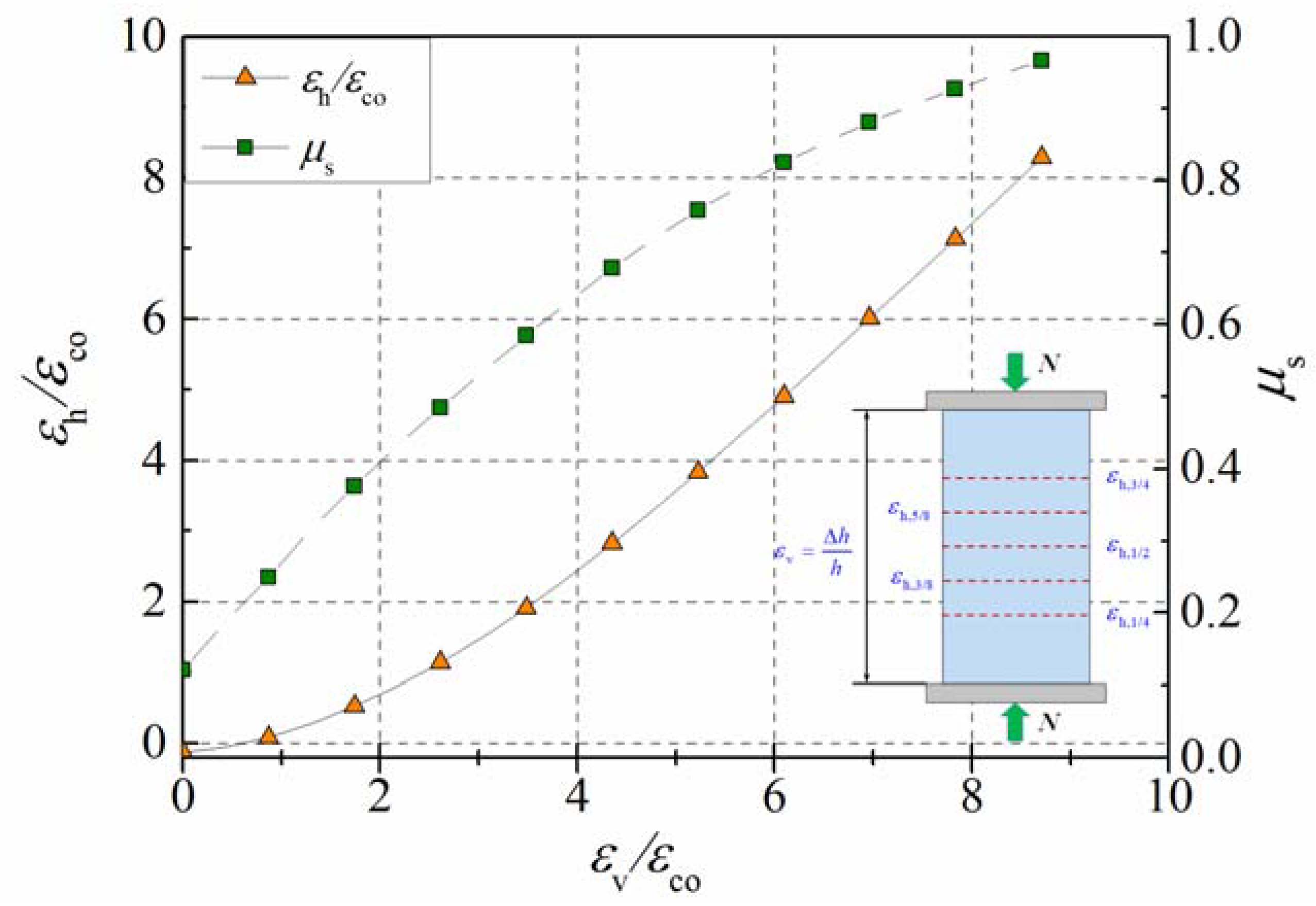
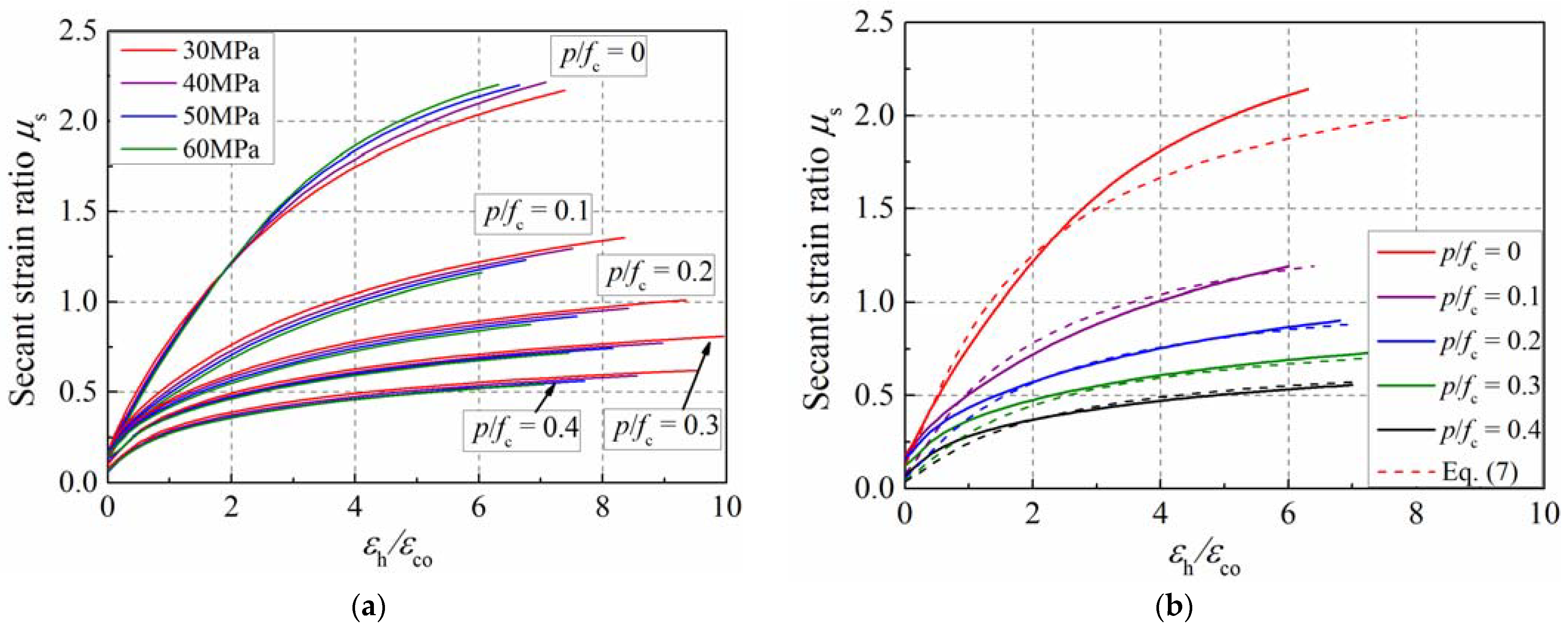
4.2. Secant Strain Ratio of The Specimen
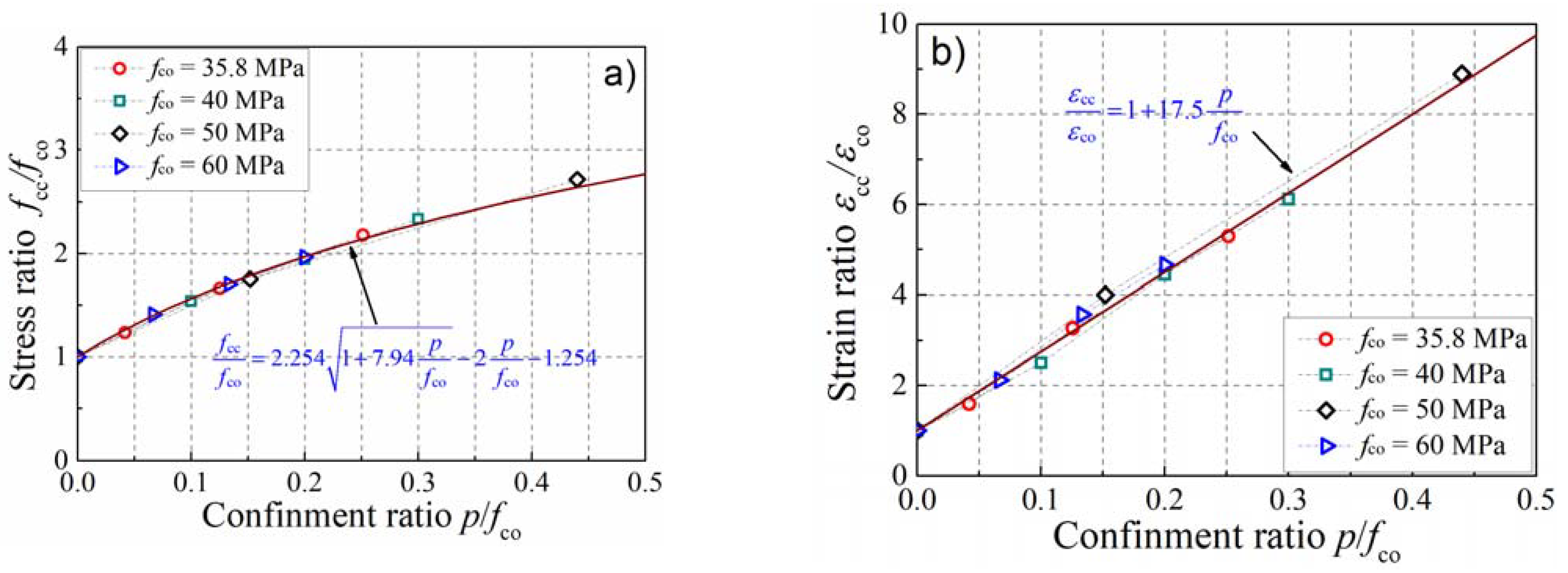
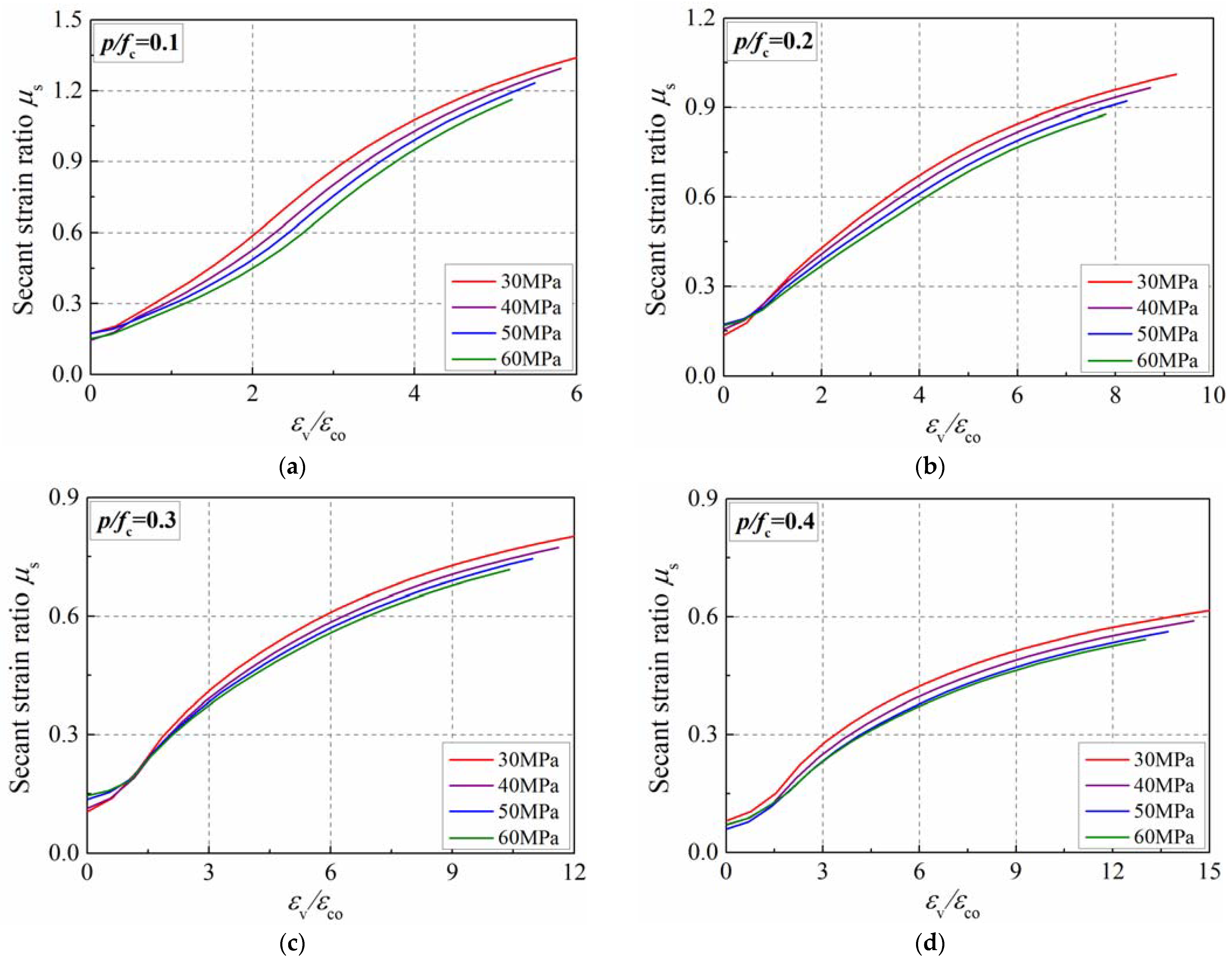
4.3. Influence of the Compressive Strength
4.4. Influence of the Confinement Ratio
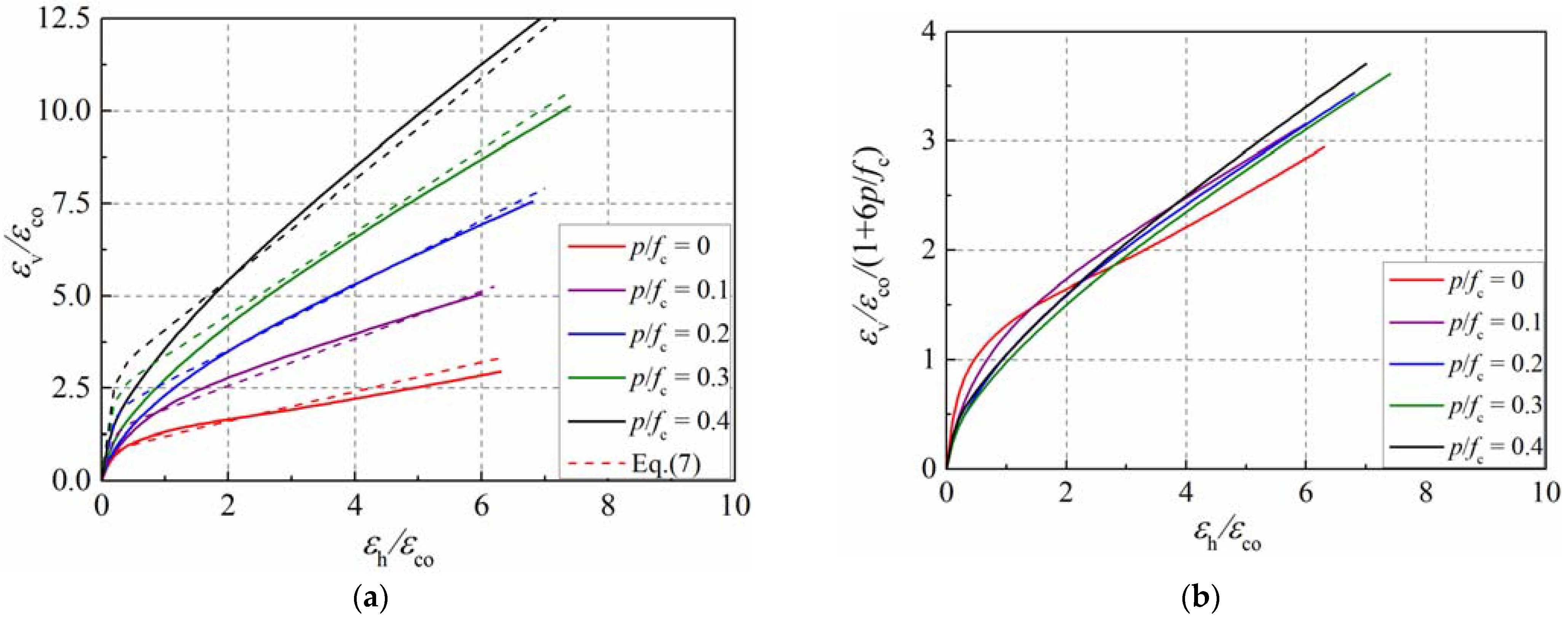
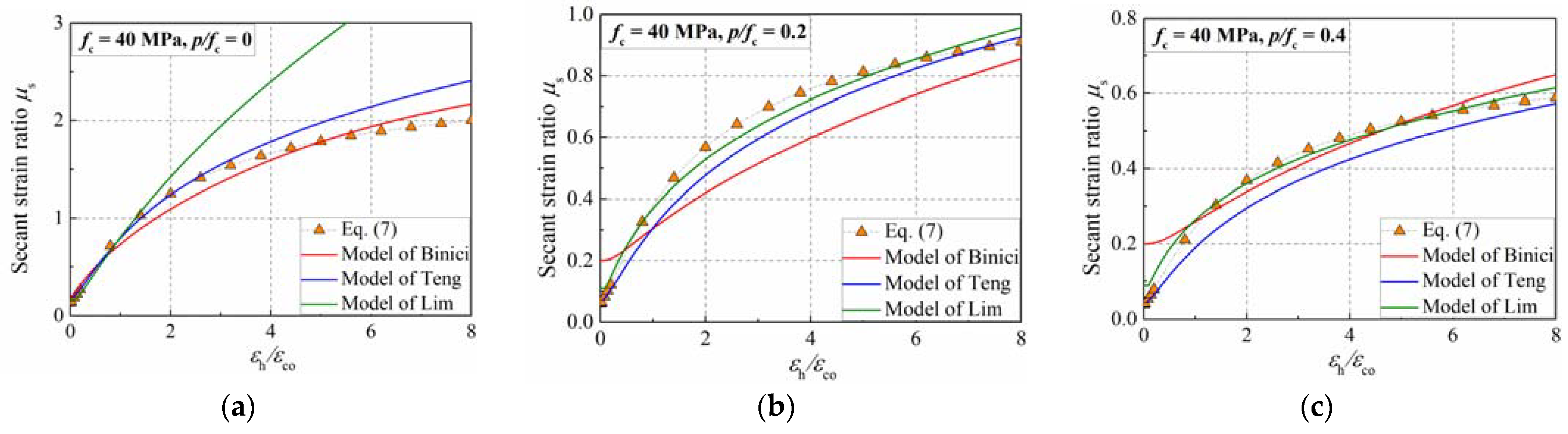
4.5. Dilation Model for Actively Confined Concrete
5. Conclusions
- The simulation results of the mesoscale model were in good agreement with the stress–strain curves of the plain concrete from codes, based on which the strength relationship between the concrete and mortar was established.
- The mesoscale model made a good estimation of the stress–strain and lateral–axial strain curves of the concrete in active confinement, illustrating that it was an efficient tool for investigating the concrete’s mechanical and deformational behavior.
- The distribution of the lateral strain along the circumference and the height of the specimen was not uniform when compressive failure occurred in the concrete.
- The confinement ratio had a more significant influence on the transverse dilation than that of the concrete’s strength. With the increase in the confinement ratio, the transverse dilation was inhibited, and then the concrete’s secant strain ratio slowly developed.
- An expression of the lateral–axial strain curve of the concrete in active confinement was proposed, which can reflect the simulation results of the mesoscale model, and it was consistent with the prediction of the existing formulas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mirmiran, A.; Shahawy, M. Dilation characteristics of confined concrete. Mech. Cohesive-Frict. Mater. 1997, 2, 237–249. [Google Scholar] [CrossRef]
- Mirmiran, A.; Shahawy, M. A new concrete-filled hollow FRP composite column. Compos. B. Eng. 1996, 27, 263–268. [Google Scholar] [CrossRef]
- Binici, B. An analytical model for stress-strain behavior of confined concrete. Eng. Struct. 2005, 27, 1040–1051. [Google Scholar] [CrossRef]
- Jiang, T.; Teng, J.G. Analysis-oriented stress-strain models for FRP-confined concrete. Eng. Struct. 2007, 29, 2968–2986. [Google Scholar] [CrossRef]
- Sfer, D.; Carol, I.; Gettu, R.; Etse, G. Study of the behavior of concrete under triaxial compression. J. Eng. Mech. 2002, 128, 156–163. [Google Scholar] [CrossRef]
- Harries, K.A.; Kharel, G. Experimental investigation of the behavior of variably confined concrete. Cem. Concr. Res. 2003, 33, 873–880. [Google Scholar] [CrossRef]
- Spoelstra, M.R.; Monti, G. FRP-confined concrete model. J. Compos. Constr. 1999, 3, 143–150. [Google Scholar] [CrossRef]
- Fam, A.Z.; Rizkalla, S.H. Confinement model for axially loaded concrete confined by circular fiber-reinforced tubes. Struct. J. 2001, 98, 451–461. [Google Scholar]
- Lahlou, K.; Aitcin, P.C.; Chaallal, O. Behavior of high-strength concrete under confined stresses. Cem. Concr. Compos. 1992, 14, 185–193. [Google Scholar] [CrossRef]
- Imran, I.; Pantazopoulou, S.J. Experimental study of plain concrete under triaxial stress. ACI Mater. J. 1996, 93, 589–601. [Google Scholar] [CrossRef]
- Lu, X.; Hsu, C.T. Stress-strain relations of high-strength concrete under triaxial compression. J. Mater. Civ. Eng. 2007, 19, 261–268. [Google Scholar] [CrossRef]
- Candappa, D.C.; Sanjayan, J.G.; Setunge, S. Complete triaxial stress-strain curves of high-strength concrete. J. Mater. Civil Eng. 2001, 13, 209–215. [Google Scholar] [CrossRef]
- Teng, J.; Huang, Y.L.; Lam, L.; Ye, L.P. Theoretical model for fiber-reinforced polymer-confined concrete. J. Compos. Constr. 2007, 11, 201–210. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Lateral strain-to-axial strain relationship of confined concrete. J. Struct. Eng. 2015, 141, 04014141. [Google Scholar] [CrossRef]
- Nguyen, D.; Lawrence, C.; Borderie, C.; Matallah, M.; Nahas, G. A mesoscopic model for a better understanding of the transition from diffuse damage to localized damage. Eur. J. Environ. Civ. Eng. 2010, 14, 751–776. [Google Scholar] [CrossRef]
- Caballero, A.; Carol, I.; Lopez, C.M. 3D meso-mechanical analysis of concrete specimens under biaxial loading. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 877–886. [Google Scholar] [CrossRef]
- Dupray, F.; Malecot, Y.; Daudeville, L.; Buzaud, E. A mesoscopic model for the behavior of concrete under high confinement. Int. J. Num. Methods Geomech. 2009, 33, 1407–1423. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Q.; Wang, Z.; Zhang, J.; Wang, Z.; Li, Z. 3D mesoscale fracture analysis of concrete under complex loading. Eng. Fract. Mech. 2019, 220, 106646. [Google Scholar] [CrossRef]
- Jin, L.; Du, M.; Li, D.; Du, X.; Xu, H. Effects of cross section size and transverse rebar on the behavior of short squared RC columns under axial compression. Eng. Struct. 2017, 142, 223–239. [Google Scholar] [CrossRef]
- Jin, L.; Yu, W.; Du, X.; Yang, W. Dynamic size effect of concrete under tension: A numerical study. Int. J. Impact Eng. 2019, 132, 103318. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S.O. Mesoscale models for concrete: Homogenisation and damage behavior. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Du, X.; Jin, L.; Ma, G. Numerical simulation of dynamic tensile-failure of concrete at mesoscale. Int. J. Impact Eng. 2014, 66, 5–17. [Google Scholar] [CrossRef]
- Fuller, W.B.; Thompson, S.E. The laws of proportioning concrete. Trans. Am. Soc. Civ. Eng. 1907, 59, 67–143. [Google Scholar] [CrossRef]
- Jin, L.; Xia, H.; Jiang, X.; Du, X. Size effect on shear failure of CFRP-strengthened concrete beams without web reinforcement: Mesoscale simulation and formulation. Compos. Struct. 2020, 236, 111895. [Google Scholar] [CrossRef]
- Donza, H.; Cabrera, O.; Irassar, E.F. High-strength concrete with different fine aggregate. Cem. Concr. Res. 2022, 32, 1755–1761. [Google Scholar] [CrossRef]
- Meddah, M.S.; Zitouni, S.; Belâabes, S. Effect of content and particle size distribution of coarse aggregate on the compressive strength of concrete. Constr. Build. Mater. 2010, 24, 505–512. [Google Scholar] [CrossRef]
- Jin, L.; Fan, L.; Li, P.; Du, X. Size effect of axial-loaded concrete-filled steel tubular columns with different confinement coefficients. Eng. Struct. 2019, 198, 109503. [Google Scholar] [CrossRef]
- Jin, L.; Chen, H.; Wang, Z.; Du, X. Size effect on axial compression failure of CFRP-wrapped square concrete columns: Tests and simulations. Compos. Struct. 2020, 254, 112843. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Grote, D.L.; Park, S.W.; Zhou, M. Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization. Int. J. Impact Eng. 2001, 25, 869–886. [Google Scholar] [CrossRef]
- Mondal, P.; Shah, S.P.; Marks, L.D. Nanomechanical Properties of Interfacial Transition Zone in Concrete; Nanotechnology in Construction 3; Springer: Berlin/Heidelberg, Germany, 2009; pp. 315–320. [Google Scholar]
- Chen, H.; Xu, B.; Mo, Y.L.; Zhou, T. Behavior of mesoscale heterogeneous concrete under uniaxial tensile and compressive loadings. Constr. Build. Mater. 2018, 178, 418–431. [Google Scholar] [CrossRef]
- Prokopski, G.; Halbiniak, J. Interfacial transition zone in cementitious materials. Cem. Concr. Res. 2000, 30, 579–583. [Google Scholar] [CrossRef]
- Su, J. The Research on the Size Effect of Concrete Behavior in Compression and Tension; Hunan University: Hunan, China, 2013. (In Chinese) [Google Scholar]
- Chen, P.; Liu, J.; Cui, X.; Si, S. Mesoscale analysis of concrete under axial compression. Constr. Build. Mater. 2022, 337, 127580. [Google Scholar] [CrossRef]
- Huang, Y.J.; Yang, Z.J.; Chen, X.W.; Liu, G.H. Monte Carlo simulations mesoscale dynamic compressive behavior of concrete based on X-ray computed tomography images. Int. J. Impact Eng. 2016, 97, 102–115. [Google Scholar] [CrossRef]
- CEB. CEB-FIP Model Code 1990; CEB Bulletin D’information: London, UK, 1990; pp. 35–37. [Google Scholar]
- Mander, J.B.; Priestley, M.J.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Chen, P.; Cui, X.; Zheng, H.; Si, S. Mesoscale study on dilation behavior of plain concrete under axial compression. Buildings 2022, 12, 908. [Google Scholar] [CrossRef]
- Marques, S.P.; Marques, D.C.; Lins, S.J.; Cavalcante, M.A. Model for analysis of short columns of concrete confined by fiber-reinforced polymer. J. Compos. Constr. 2004, 8, 332–340. [Google Scholar] [CrossRef]







| Aggregate | Mortar Matrix | ITZ | |
|---|---|---|---|
| Mass density (kg/m3) | 2400 | 2400 | 2400 |
| Compressive strength | - | fm | 0.8 fm |
| Tensile strength | - | ||
| Elastic modulus (GPa) | 60 | ||
| Fracture energy (N/mm) | - | ||
| Poisson’s ratio | 0.20 | 0.20 | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Cui, X.; Zheng, H.; Si, S. A Mesoscale Study on the Dilation of Actively Confined Concrete under Axial Compression. Materials 2022, 15, 6490. https://doi.org/10.3390/ma15186490
Chen P, Cui X, Zheng H, Si S. A Mesoscale Study on the Dilation of Actively Confined Concrete under Axial Compression. Materials. 2022; 15(18):6490. https://doi.org/10.3390/ma15186490
Chicago/Turabian StyleChen, Peng, Xiaomeng Cui, Huijun Zheng, and Shengpu Si. 2022. "A Mesoscale Study on the Dilation of Actively Confined Concrete under Axial Compression" Materials 15, no. 18: 6490. https://doi.org/10.3390/ma15186490
APA StyleChen, P., Cui, X., Zheng, H., & Si, S. (2022). A Mesoscale Study on the Dilation of Actively Confined Concrete under Axial Compression. Materials, 15(18), 6490. https://doi.org/10.3390/ma15186490




