Optimization and Predictive Modeling of Reinforced Concrete Circular Columns
Abstract
:1. Introduction
2. Dataset Generation and Analysis
3. Results
3.1. Ensemble Learning Model Predictions
3.2. SHAP Analysis
3.3. Four-Level Factorial Analysis
3.4. Development of an Equation for the Prediction of the Optimum Reinforcement Area
4. Discussion
5. Conclusions
- Four different machine learning models were developed using the XGBoost, LightGBM, Random Forest, and CatBoost algorithms. All of these algorithms performed well on the dataset with an R2 score greater than 0.99. Among these models, the Random Forest algorithm performed best in terms of both accuracy and computational speed whereas the CatBoost algorithm was nearly an order of magnitude slower than the rest of the algorithms.
- The results of the SHAP analysis showed that the outer diameter of the circular column has the greatest impact on the machine learning model predictions. The impacts of the applied axial loading (N) and bending moment (M) were found to be dependent on the value of D. At smaller values of D, N was shown to have a larger impact on the model output.
- After dividing the dataset into four segments for each variable the four-level factorial analysis showed that a 59% increase in the outer diameter can lead to a 143% increase in the optimal value of . was also found to be highly sensitive to variations in N and M. Doubling the magnitude of N was observed to cause a 68% increase in the optimal value of whereas doubling the magnitude of M led to a 41% increase in the optimal value of .
- A closed-form equation with an R2 score of 0.9985 was proposed which predicts the optimal value for as a function of column outer diameter, axial loading, bending moment, column length, and the unit prices of concrete and steel.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Root mean square error (RMSE) | |
| Coefficient of determination (R2): | |
| Mean absolute error (MAE): | |
| Pearson correlation coefficient: | |
References
- Bekdaş, G.; Cakiroglu, C.; Islam, K.; Kim, S.; Geem, Z.W. Optimum Design of Cylindrical Walls Using Ensemble Learning Methods. Appl. Sci. 2022, 12, 2165. [Google Scholar] [CrossRef]
- Bekdaş, G. Harmony Search Algorithm Approach for Optimum Design of Post-Tensioned Axially Symmetric Cylindrical Reinforced Concrete Walls. J. Optim. Theory Appl. 2015, 164, 342–358. [Google Scholar] [CrossRef]
- Bekdaş, G.; Cakiroglu, C.; Kim, S.; Geem, Z.W. Optimal Dimensioning of Retaining Walls Using Explainable Ensemble Learning Algorithms. Materials 2022, 15, 4993. [Google Scholar] [CrossRef]
- Arama, Z.A.; Kayabekir, A.E.; Bekdaş, G.; Kim, S.; Geem, Z.W. The Usage of the Harmony Search Algorithm for the Optimal Design Problem of Reinforced Concrete Retaining Walls. Appl. Sci. 2021, 11, 1343. [Google Scholar] [CrossRef]
- Kayabekir, A.E.; Arama, Z.A.; Bekdaş, G.; Nigdeli, S.M.; Geem, Z.W. Eco-Friendly Design of Reinforced Concrete Retaining Walls: Multi-objective Optimization with Harmony Search Applications. Sustainability 2020, 12, 6087. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Bekdaş, G.; Kim, S.; Geem, Z.W. Optimisation of Shear and Lateral–Torsional Buckling of Steel Plate Girders Using Meta-Heuristic Algorithms. Appl. Sci. 2020, 10, 3639. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Bekdaş, G. Buckling Analysis and Stacking Sequence Optimization of Symmetric Laminated Composite Plates. In Advances in Structural Engineering—Optimization. Studies in Systems, Decision and Control; Nigdeli, S.M., Bekdaş, G., Kayabekir, A.E., Yucel, M., Eds.; Springer: Cham, Switzerland, 2021; Volume 326. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Bekdaş, G.; Geem, Z.W. Harmony Search Optimisation of Dispersed Laminated Composite Plates. Materials 2020, 13, 2862. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Islam, K.; Bekdaş, G.; Kim, S.; Geem, Z.W. Metaheuristic Optimization of Laminated Composite Plates with Cut-Outs. Coatings 2021, 11, 1235. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Islam, K.; Bekdaş, G.; Billah, M. CO2 emission and cost optimization of concrete-filled steel tubular (CFST) columns using metaheuristic algorithms. Sustainability 2021, 13, 8092. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Islam, K.; Bekdaş, G.; Kim, S.; Geem, Z.W. CO2 Emission Optimization of Concrete-Filled Steel Tubular Rectangular Stub Columns Using Metaheuristic Algorithms. Sustainability 2021, 13, 10981. [Google Scholar] [CrossRef]
- Toklu, Y.C.; Temur, R.; Bekdaş, G. Teaching learning based optimization algorithm for analyses of trusses considering elastoplastic behavior. In Fluids, Heat and Mass Transfer, Mechanical and Civil Engineering; Recent Advances in Mechanical Engineering Series 17; WSEAS Press: Athens, Greece, 2015; ISBN 978-1-61804-358-0. [Google Scholar]
- Ulusoy, S. Optimum design of timber structures under fire using metaheuristic algorithm. Građevinar 2022, 74, 115–124. [Google Scholar] [CrossRef]
- Ocak, A.; Nigdeli, S.M.; Bekdaş, G.; Kim, S.; Geem, Z.W. Adaptive Harmony Search for Tuned Liquid Damper Optimization under Seismic Excitation. Appl. Sci. 2022, 12, 2645. [Google Scholar] [CrossRef]
- Ocak, A.; Bekdaş, G.; Nigdeli, S.M.; Kim, S.; Geem, Z.W. Optimization of Tuned Liquid Damper Including Different Liquids for Lateral Displacement Control of Single and Multi-Story Structures. Buildings 2022, 12, 377. [Google Scholar] [CrossRef]
- Ulusoy, S.; Nigdeli, S.M.; Bekdaş, G. Introduction and Review on Active Structural Control. In Optimization of Tuned Mass Dampers. Studies in Systems, Decision and Control; Bekdaş, G., Nigdeli, S.M., Eds.; Springer: Cham, Switzerland, 2022; Volume 432. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. An efficient hybrid algorithm based on Water Cycle and Moth-Flame Optimization algorithms for solving numerical and constrained engineering optimization problems. Soft Comput. 2019, 23, 1699–1722. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. -Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Harifi, S.; Mohammadzadeh, J.; Khalilian, M.; Ebrahimnejad, S. Giza Pyramids Construction: An ancient-inspired metaheuristic algorithm for optimization. Evol. Intel. 2021, 14, 1743–1761. [Google Scholar] [CrossRef]
- Holland, H.; Reitman, J.S. Cognitive systems based on adaptive algorithms. ACM SIGART Bull. 1977, 63, 49. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Fogel, D.B. Artificial Intelligence through Simulated Evolution. In Evolutionary Computation: The Fossil Record; IEEE: Piscataway, NJ, USA, 1998; pp. 227–296. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; ISBN 0-262-11170-5. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V.R. Colliding bodies optimization method for optimum discrete design of truss structures. Comput. Struct. 2014, 139, 43–53. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simmulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Du, H.; Wu, X.; Zhuang, J. Small-World Optimization. In Advances in Natural Computation. ICNC 2006: Lecture Notes in Computer Science; Jiao, L., Wang, L., Gao, X., Liu, J., Wu, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4222. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Soft. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Harifi, S.; Khalilian, M.; Mohammadzadeh, J. Emperor Penguins Colony: A new metaheuristic algorithm for optimization. Evol. Intel. 2019, 12, 211–226. [Google Scholar] [CrossRef]
- Li, M.D.; Zhao, H.; Weng, X.W.; Han, T. A novel nature-inspired algorithm for optimization: Virus colony search. Adv. Eng. Soft. 2016, 92, 65–88. [Google Scholar] [CrossRef]
- Salimi, H. Stochastic fractal search: A powerful metaheuristic algorithm. Knowl. -Based Syst. 2015, 75, 1–18. [Google Scholar] [CrossRef]
- Kashan, A.H. League Championship Algorithm (LCA): An algorithm for global optimization inspired by sport championships. Appl. Soft Comput. 2014, 16, 171–200. [Google Scholar] [CrossRef]
- Geem, Z.W.; Lee, K.S.; Park, Y. Application of harmony search to vehicle routing. Am. J. Appl. Sci. 2005, 2, 1552–1557. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, R.; Zhang, Y.; Gammana Guruge, N.S. A Multi-Bus Dispatching Strategy Based on Boarding Control. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5029–5043. [Google Scholar] [CrossRef]
- Villalobos, O.A.R.; Rojas, E.J.R.; Velandia, J.B.; Cuchango, H.E.E. Application of the Harmonic Search Algorithm for Identification of Model Parameters of Traffic Lights for a High Way of Bogotá. Int. J. Eng. Res. Technol. 2020, 13, 240–246. [Google Scholar] [CrossRef]
- Ganeshkumar, N.; Kumar, S. QoS Aware Modified Harmony Search Optimization for Route Selection in VANETs. Indian J. Comput. Sci. Eng. (IJCSE) 2022, 13, 2. [Google Scholar] [CrossRef]
- You, C.-H.; Suh, S.-H.; Jung, W.; Kim, H.-J.; Lee, D.-I. Dual-Polarization Radar-Based Quantitative Precipitation Estimation of Mountain Terrain Using Multi-Disdrometer Data. Remote Sens. 2022, 14, 2290. [Google Scholar] [CrossRef]
- Loy-Benitez, J.; Li, Q.; Nam, K.; Nguyen, H.T.; Kim, M.; Park, D.; Yoo, C. Multi-objective optimization of a time-delay compensated ventilation control system in a subway facility—A harmony search strategy. Build. Environ. 2021, 190, 107543. [Google Scholar] [CrossRef]
- Abdulkhaleq, M.T.; Rashid, T.A.; Alsadoon, A.; Hassan, B.A.; Mohammadi, M.; Abdullah, J.M.; Vimal, S. Harmony search: Current studies and uses on healthcare systems. Artif. Intell. Med. 2022, 131, 102348. [Google Scholar] [CrossRef]
- Taghipour, S.; Zarrineh, P.; Ganjtabesh, M. Improving protein complex prediction by reconstructing a high-confidence protein-protein interaction network of Escherichia coli from different physical interaction data sources. BMC Bioinform. 2017, 18, 10. [Google Scholar] [CrossRef]
- Li, X.; Wang, B.; Lv, H.; Yin, Q.; Zhang, Q.; Wei, X. Constraining DNA Sequences With a Triplet-Bases Unpaired. IEEE Trans. NanoBiosci. 2020, 19, 299–307. [Google Scholar] [CrossRef]
- Mohsen, A.M.; Khader, A.T.; Ramachandram, D. HSRNAFold: A harmony search algorithm for RNA secondary structure prediction based on minimum free energy. In Proceedings of the 2008 International Conference on Innovations in Information Technology, Al Ain, United Arab Emirates, 16–18 December 2008; pp. 11–15. [Google Scholar] [CrossRef]
- Bibartiu, O.; Dürr, F.; Rothermel, K. Optimal Refinement for Component-based Architectures. In Proceedings of the 2021 IEEE 25th International Enterprise Distributed Object Computing Conference (EDOC), Gold Coast, Australia, 25–29 October 2021; pp. 142–151. [Google Scholar] [CrossRef]
- Schofield, J.S.; Evans, K.R.; Hebert, J.S.; Marasco, P.D.; Carey, J.P. The effect of biomechanical variables on force sensitive resistor error: Implications for calibration and improved accuracy. J. Biomech. 2016, 49, 786–792. [Google Scholar] [CrossRef]
- Feng, D.C.; Liu, Z.T.; Wang, X.D.; Jiang, Z.M.; Liang, S.X. Failure mode classification and bearing capacity prediction for reinforced concrete columns based on ensemble machine learning algorithm. Adv. Eng. Inform. 2020, 45, 101126. [Google Scholar] [CrossRef]
- Dogan, G.; Arslan, M.H.; Baykan, O.K. Determination of damage levels of RC columns with a smart system oriented method. Bull. Earthquake Eng. 2020, 18, 3223–3245. [Google Scholar] [CrossRef]
- Nasrollahzadeh, K.; Nouhi, E. Fuzzy inference system to formulate compressive strength and ultimate strain of square concrete columns wrapped with fiber-reinforced polymer. Neural Comput. Appl. 2018, 30, 69–86. [Google Scholar] [CrossRef]
- Naderpour, H.; Nagai, K.; Fakharian, P.; Haji, M. Innovative models for prediction of compressive strength of FRP-confined circular reinforced concrete columns using soft computing methods. Compos. Struct. 2019, 215, 69–84. [Google Scholar] [CrossRef]
- Bossio, A.; Lignola, G.P.; Fabbrocino, F.; Monetta, T.; Prota, A.; Bellucci, F.; Manfredi, G. Nondestructive assessment of corrosion of reinforcing bars through surface concrete cracks. Struct. Concr. 2017, 18, 104–117. [Google Scholar] [CrossRef]
- Bossio, A.; Fabbrocino, F.; Monetta, T.; Lignola, G.P.; Prota, A.; Manfredi, G.; Bellucci, F. Corrosion effects on seismic capacity of reinforced concrete structures. Corros. Rev. 2019, 37, 45–56. [Google Scholar] [CrossRef]
- Fabbrocino, F.; Funari, M.F.; Greco, F.; Lonetti, P.; Luciano, R.; Penna, R. Dynamic crack growth based on moving mesh method. Compos. Part B Eng. 2019, 174, 107053. [Google Scholar] [CrossRef]
- Kayabekir, A.E.; Bekdaş, G.; Yücel, M.; Nigdeli, S.M.; Geem, Z.W. Harmony Search Algorithm for Structural Engineering Problems. In Nature-Inspired Metaheuristic Algorithms for Engineering Optimization Applications; Springer Tracts in Nature-Inspired Computing, Carbas, S., Toktas, A., Ustun, D., Eds.; Springer: Singapore, 2021. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Feng, D.C.; Wang, W.J.; Mangalathu, S.; Taciroglu, E. Interpretable XGBoost-SHAP machine-learning model for shear strength prediction of squat RC walls. J. Struct. Eng. 2021, 147, 04021173. [Google Scholar] [CrossRef]
- Rahman, J.; Ahmed, K.S.; Khan, N.I.; Islam, K.; Mangalathu, S. Data-driven shear strength prediction of steel fiber reinforced concrete beams using machine learning approach. Eng. Struct. 2021, 233, 111743. [Google Scholar] [CrossRef]
- Degtyarev, V.V.; Naser, M.Z. Boosting machines for predicting shear strength of CFS channels with staggered web perforations. Structures 2021, 34, 3391–3403. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Gulin, A. Catboost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Lee, S.; Vo, T.P.; Thai, H.T.; Lee, J.; Patel, V. Strength prediction of concrete-filled steel tubular columns using Categorical Gradient Boosting algorithm. Eng. Struct. 2021, 238, 112109. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Nguyen, Q.H.; Ly, H.B.; Ho, L.S.; Al-Ansari, N.; Le, H.V.; Tran, V.Q.; Prakash, I.; Pham, B.T. Influence of data splitting on performance of machine learning models in prediction of shear strength of soil. Math. Probl. Eng. 2021, 2021, 4832864. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]

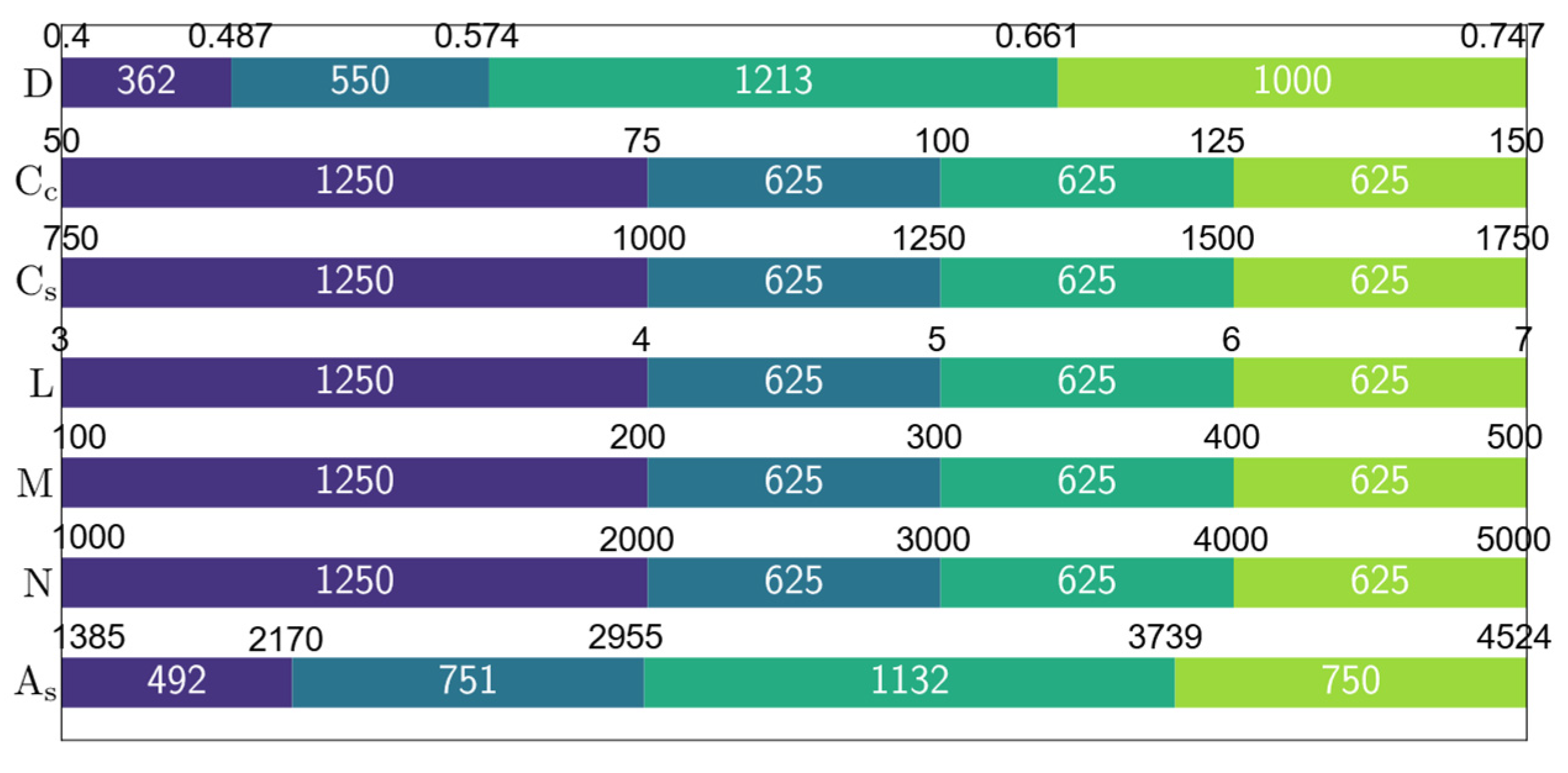










| Variable | Min | Max | Average | Standard Deviation | Variance | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Actual | Normalized | Actual | Normalized | Actual | Normalized | Actual | Normalized | Actual | Normalized | |
| D [m] | 0.4 | 0.647 | 0.747 | 1.209 | 0.618 | 1 | 0.087 | 0.141 | 0.0076 | 0.02 |
| Cc [USD/m3] | 50 | 0.5 | 150 | 1.5 | 100 | 1 | 35.4 | 0.354 | 1250 | 0.125 |
| Cs [USD/ton] | 750 | 0.6 | 1750 | 1.4 | 1250 | 1 | 354 | 0.283 | 125,000 | 0.08 |
| L [m] | 3 | 0.6 | 7 | 1.4 | 5 | 1 | 1.41 | 0.283 | 2 | 0.08 |
| M [kNm] | 100 | 0.333 | 500 | 1.667 | 300 | 1 | 141 | 0.471 | 20,000 | 0.222 |
| N [kN] | 1000 | 0.333 | 5000 | 1.667 | 3000 | 1 | 1414 | 0.471 | 2,000,000 | 0.222 |
| As [mm2] | 1385 | 0.447 | 4524 | 1.459 | 3101 | 1 | 799 | 0.258 | 639,080 | 0.067 |
| Algorithm | Variable | R2 | MAE | RMSE | Duration [s] | |||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |||
| XGBoost | As | 0.9999 | 0.9995 | 1.998 | 7.523 | 3.839 | 17.072 | 5.14 |
| Random Forest | As | 0.9999 | 0.9996 | 2.593 | 7.111 | 6.095 | 15.929 | 3.71 |
| LightGBM | As | 0.9994 | 0.9988 | 9.962 | 12.767 | 19.673 | 27.157 | 6.07 |
| CatBoost | As | 0.9998 | 0.9994 | 7.579 | 10.788 | 12.440 | 18.940 | 28.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekdaş, G.; Cakiroglu, C.; Kim, S.; Geem, Z.W. Optimization and Predictive Modeling of Reinforced Concrete Circular Columns. Materials 2022, 15, 6624. https://doi.org/10.3390/ma15196624
Bekdaş G, Cakiroglu C, Kim S, Geem ZW. Optimization and Predictive Modeling of Reinforced Concrete Circular Columns. Materials. 2022; 15(19):6624. https://doi.org/10.3390/ma15196624
Chicago/Turabian StyleBekdaş, Gebrail, Celal Cakiroglu, Sanghun Kim, and Zong Woo Geem. 2022. "Optimization and Predictive Modeling of Reinforced Concrete Circular Columns" Materials 15, no. 19: 6624. https://doi.org/10.3390/ma15196624
APA StyleBekdaş, G., Cakiroglu, C., Kim, S., & Geem, Z. W. (2022). Optimization and Predictive Modeling of Reinforced Concrete Circular Columns. Materials, 15(19), 6624. https://doi.org/10.3390/ma15196624








