Development of a Computational Model of the Mechanical Behavior of the L4–L5 Lumbar Spine: Application to Disc Degeneration
Abstract
1. Introduction
2. Materials and Methods
2.1. Method of Movable Cellular Automata
2.2. Model of the Lumbar Spine Segment
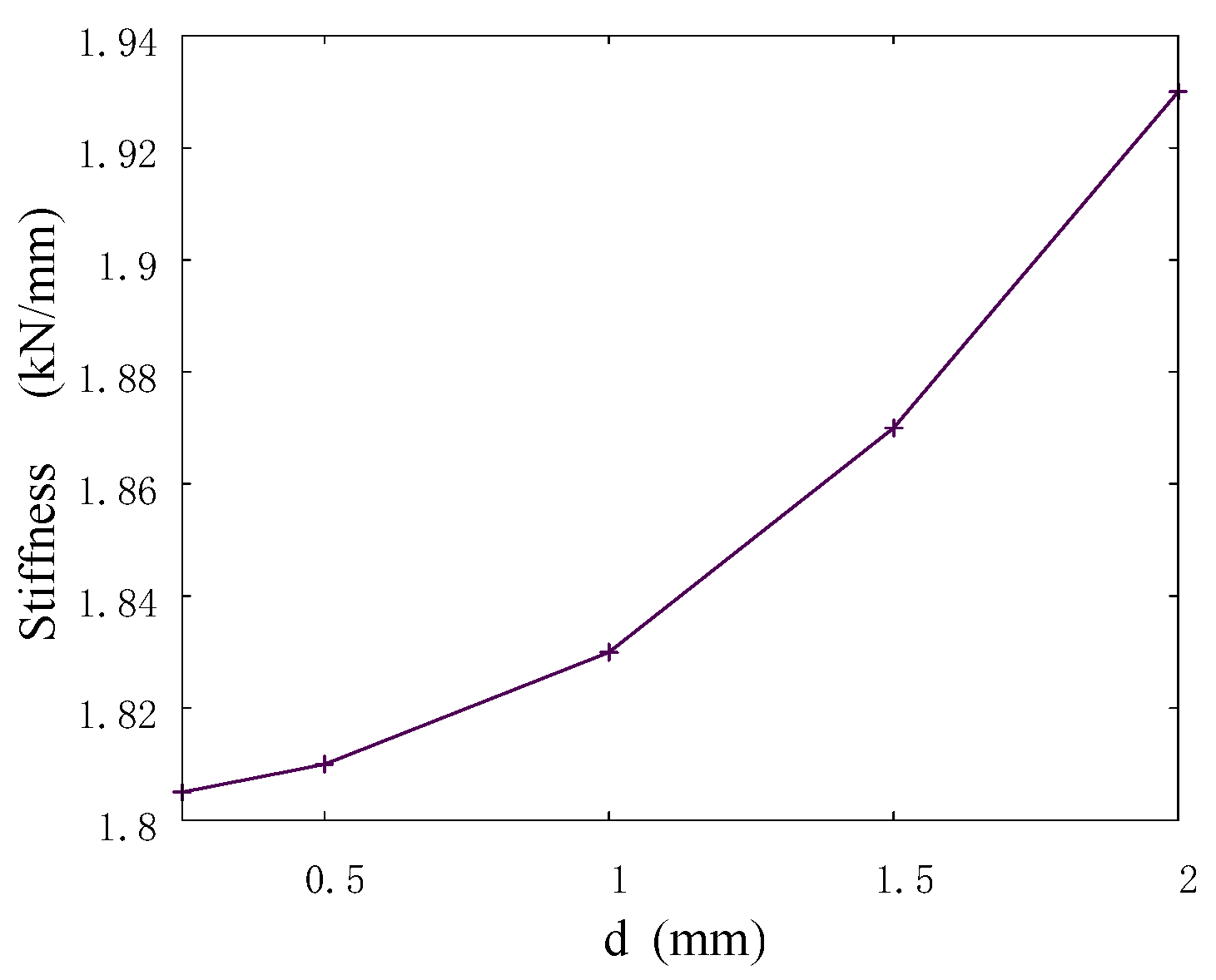
2.3. Model Verification
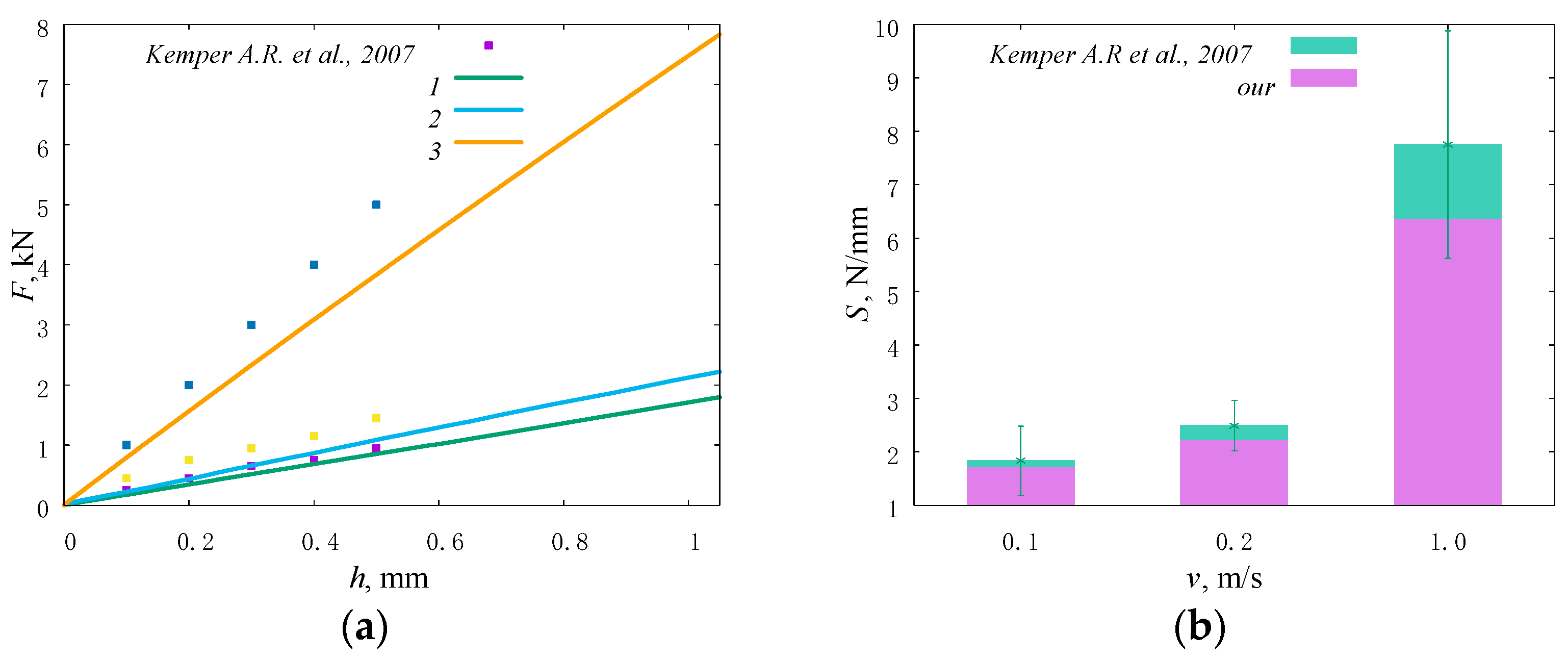
2.4. Model Validation
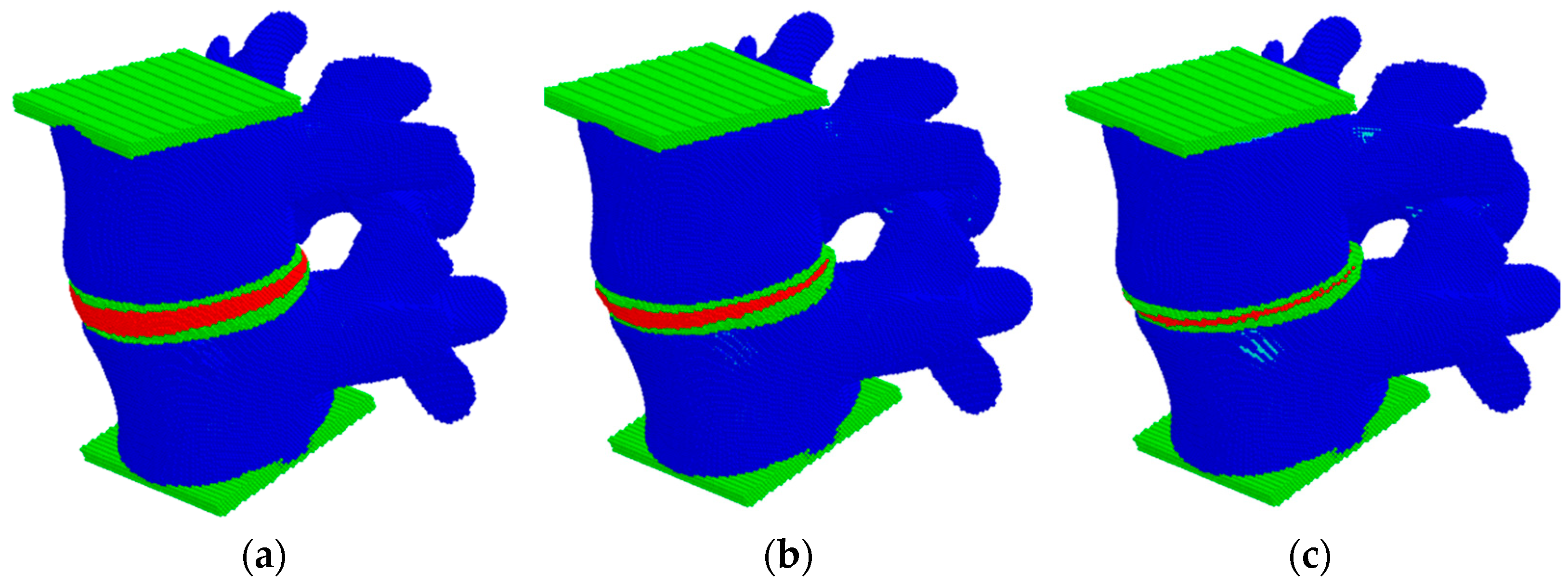
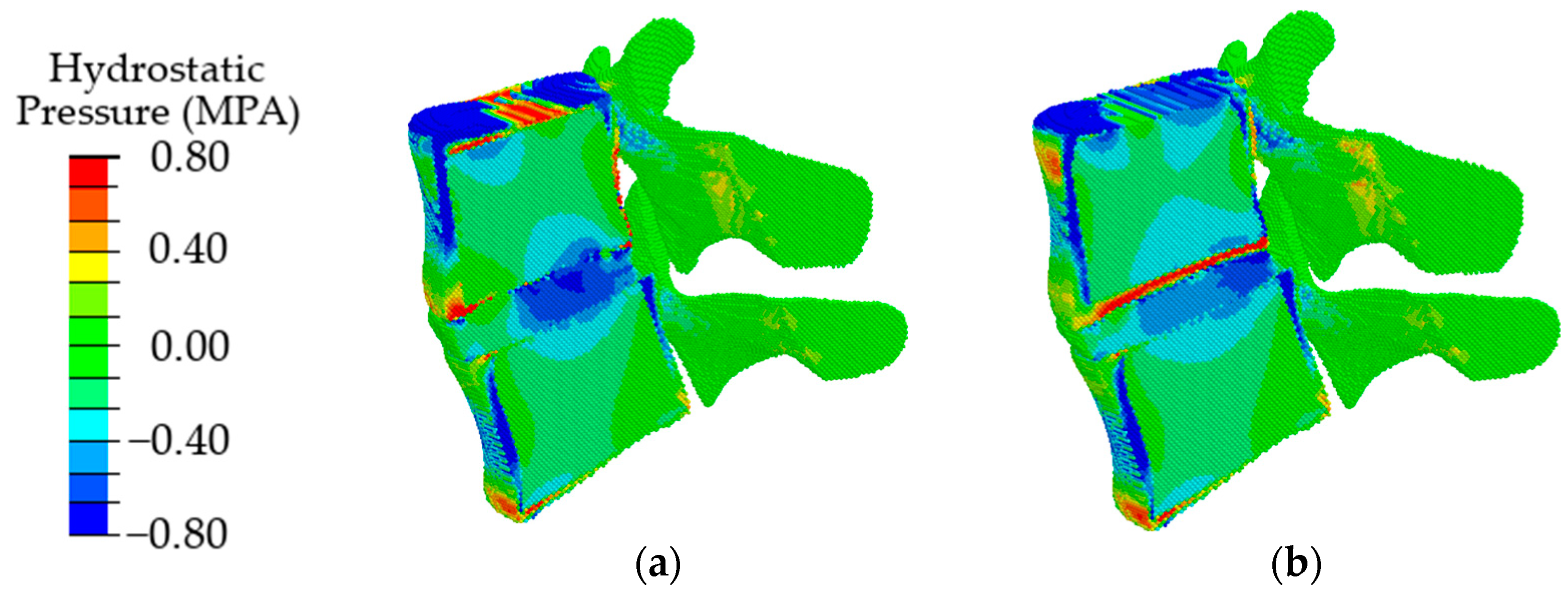
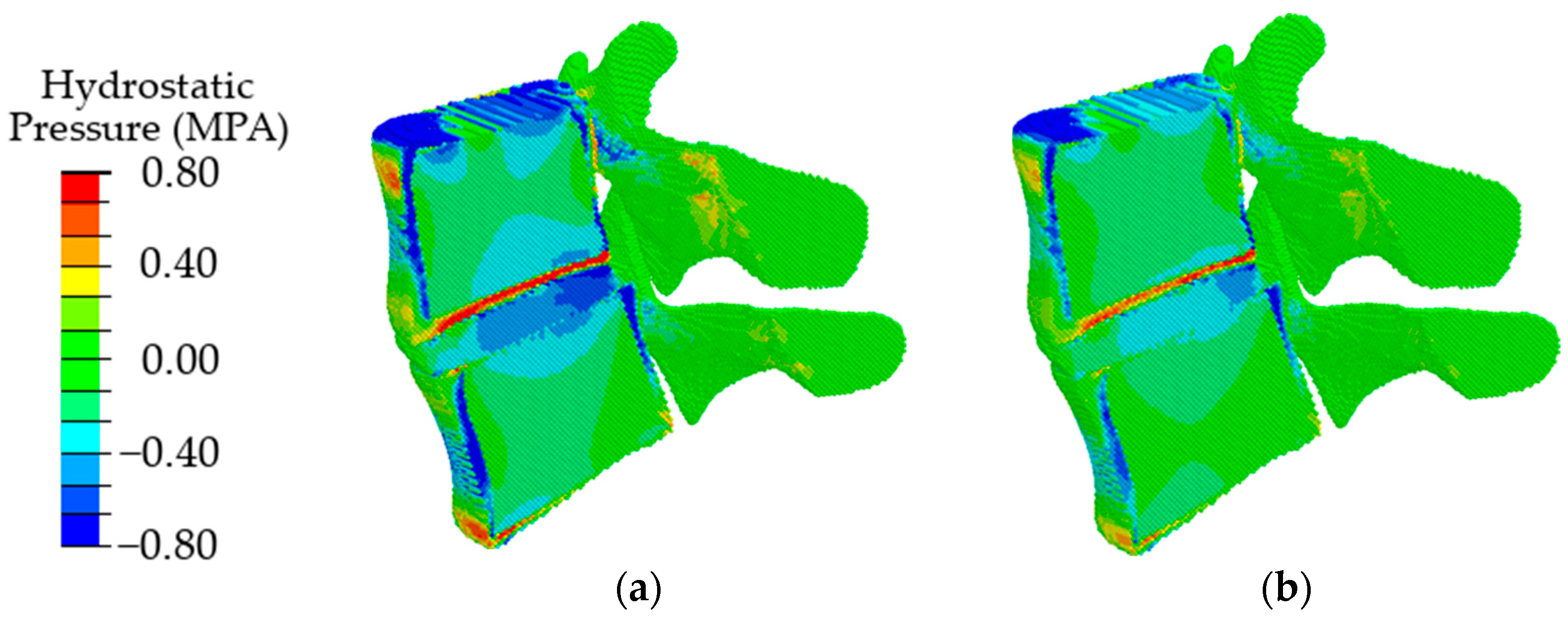
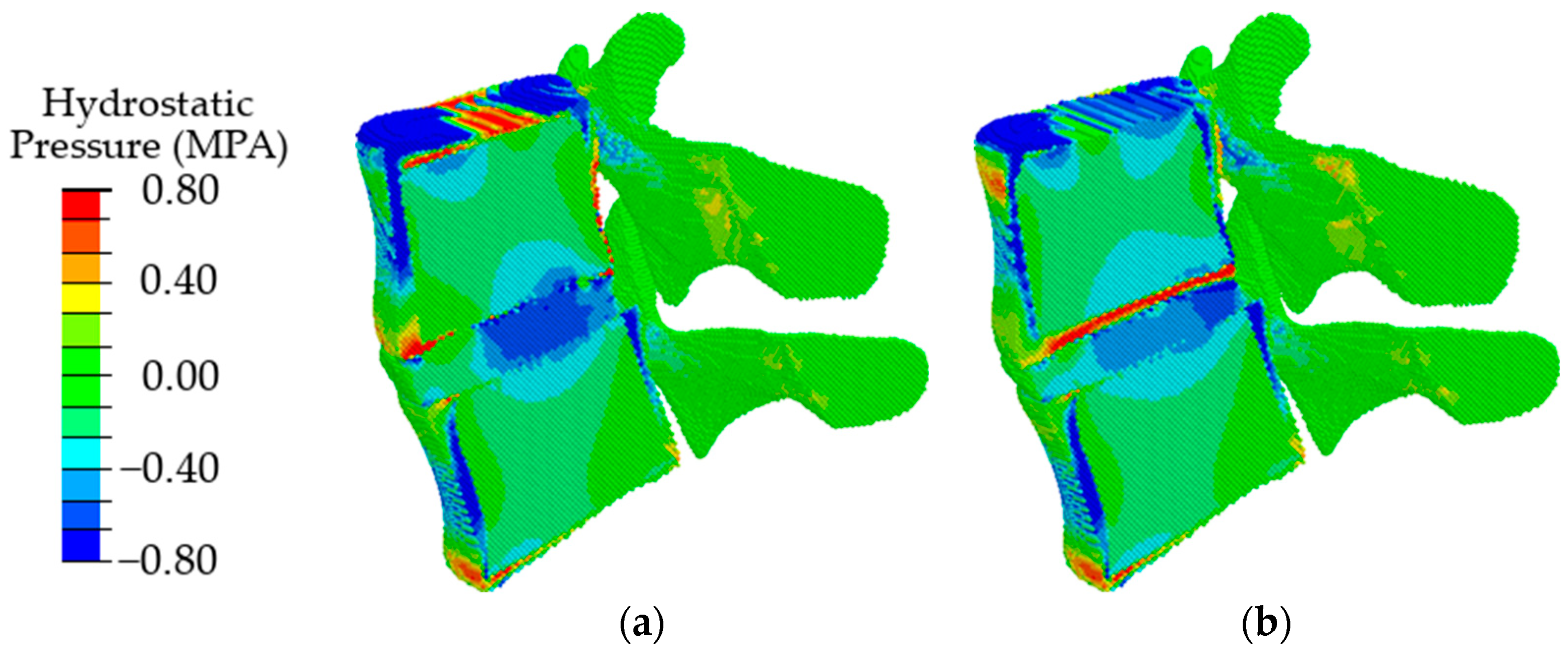
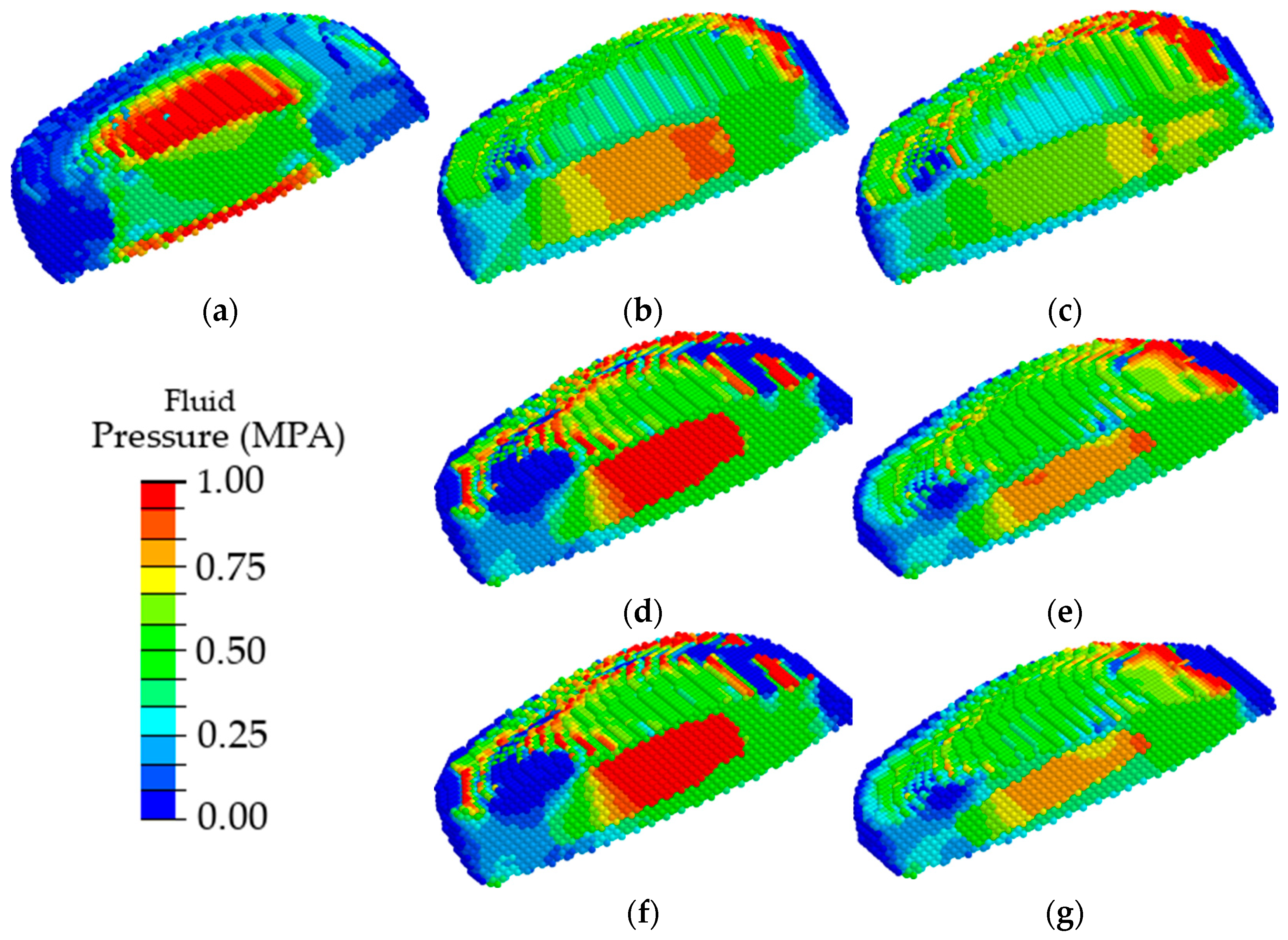
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rustenburg, C.M.E.; Emanuel, K.S.; Peeters, M.; Lems, W.F.; Vergroesen, P.A.; Smit, T.H. Osteoarthritis and intervertebral disc degeneration: Quite different, quite similar. JOR Spine 2018, 1, e1033. [Google Scholar] [CrossRef] [PubMed]
- Hickman, T.; Rathan-Kumar, S.; Peck, S.H. Development, pathogenesis, and regeneration of the intervertebral disc: Current and future insights spanning traditional to omics methods. Front. Cell Dev. Biol. 2022, 10, 841831. [Google Scholar] [CrossRef] [PubMed]
- Ge, C.Y.; Hao, D.J.; Yan, L.; Shan, L.Q.; Zhao, Q.P.; He, B.R.; Hui, H. Intradural lumbar disc herniation: A case report and literature review. Clin. Interv. Aging 2019, 14, 2295–2299. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Du, H.; Zhao, W.; Ma, S.; Zhang, M.; Guan, M.; Liu, M. Inhibition of both endplate nutritional pathways results in intervertebral disc degeneration in a goat model. J. Orthop. Surg. Res. 2019, 14, 138. [Google Scholar] [CrossRef]
- Urban, J.P.; Holm, S.; Maroudas, A.; Nachemson, A. Nutrition of the intervertebral disk. An in vivo study of solute transport. Clin. Orthop. Relat. Res. 1977, 129, 101–114. [Google Scholar] [CrossRef]
- Volz, M.; Elmasry, S.; Jackson, A.R.; Travascio, F. Computational modeling intervertebral disc pathophysiology: A review. Front. Physiol. 2022, 12, 750668. [Google Scholar] [CrossRef]
- Hadjipavlou, A.T.M.; Bogduk, N.; Zindrick, M. The pathophysiology of disc degeneration: A critical review. J. Bone Jt. Surg. 2008, 90, 1261–1270. [Google Scholar] [CrossRef]
- Elmasry, S.; Asfour, S.; de Rivero Vaccari, J.P.; Travascio, F. Effects of Tobacco Smoking on the Degeneration of the Intervertebral Disc: A Finite Element Study. PLoS ONE 2015, 10, e0136137. [Google Scholar] [CrossRef]
- Boxberger, J.I.; Auerbach, J.D.; Sen, S.; Elliott, D.M. An in vivo model of reduced nucleus pulposus glycosaminoglycan content in the rat lumbar intervertebral disc. Spine 2008, 33, 146–154. [Google Scholar] [CrossRef]
- Nerurkar, N.L.; Mauck, R.L.; Elliott, D.M. ISSLS prize winner: Integrating theoretical and experimental methods for functional tissue engineering of the annulus fibrosus. Spine 2008, 33, 2691–2701. [Google Scholar] [CrossRef]
- Mainardi, A.; Cambria, E.; Occhetta, P.; Martin, I.; Barbero, A.; Schären, S.; Mehrkens, A.; Krupkova, O. Intervertebral disc-on-a-chip as advanced in vitro model for mechanobiology research and drug testing: A review and perspective. Front. Bioeng. Biotechnol. 2022, 9, 826867. [Google Scholar] [CrossRef] [PubMed]
- Lao, L.; Daubs, M.D.; Scott, T.P.; Lord, E.L.; Cohen, J.R.; Yin, R.; Zhong, G.; Wang, J.C. Effect of disc degeneration on lumbar segmental mobility analyzed by kinetic magnetic resonance imaging. Spine 2015, 40, 316–322. [Google Scholar] [CrossRef] [PubMed]
- Kaya Ayvaz, D.; Kervancıoğlu, P.; Bahşi, A.; Bahşi, İ. A radiological evaluation of lumbar spinous processes and interspinous spaces, including clinical implications. Cureus 2021, 13, e19454. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hao, L.; Suyou, L.; Shan, Z.; Maiwulanjiang, M.; Li, S.; Wang, C.; Fan, S.; Zhao, F. Biomechanical properties of lumbar endplates and their correlation with MRI findings of lumbar degeneration. J. Biomech. 2016, 49, 586–593. [Google Scholar] [CrossRef] [PubMed]
- Mantell, M.; Cyriac, M.; Haines, C.M.; Gudipally, M.; O’Brien, J.R. Biomechanical analysis of an expandable lateral cage and a static transforaminal lumbar interbody fusion cage with posterior instrumentation in an in vitro spondylolisthesis model. J. Neurosurg. Spine 2016, 24, 32–38. [Google Scholar] [CrossRef]
- Daniels, A.H.; Paller, D.J.; Koruprolu, S.; Palumbo, M.A.; Crisco, J.J. Dynamic biomechanical examination of the lumbar spine with implanted total spinal segment replacement (TSSR) utilizing a pendulum testing system. PLoS ONE 2013, 8, e57412. [Google Scholar] [CrossRef]
- Xiang, X.; Yamada, Y.; Akiyama, Y.; Tao, Z.; Kudo, N. Validation of Lumbar Compressive Force Simulation in Forward Flexion Condition. Appl. Sci. 2021, 11, 726. [Google Scholar] [CrossRef]
- Baumgartner, L.; Wuertz-Kozak, K.; Le Maitre, C.L.; Wignall, F.; Richardson, S.M.; Hoyland, J.; Wills, C.R.; González Ballester, M.A.; Neidlin, M.; Alexopoulos, L.G.; et al. Multiscale Regulation of the Intervertebral Disc: Achievements in Experimental, In Silico, and Regenerative Research. Int. J. Mol. Sci. 2021, 22, 703. [Google Scholar] [CrossRef]
- Naoum, S.; Vasiliadis, A.V.; Koutserimpas, C.; Mylonakis, N.; Kotsapas, M.; Katakalos, K. Finite Element Method for the Evaluation of the Human Spine: A Literature Overview. J. Funct. Biomater. 2021, 12, 43. [Google Scholar] [CrossRef]
- Cai, X.Y.; Sun, M.S.; Huang, Y.P.; Liu, Z.X.; Liu, C.J.; Du, C.F.; Yang, Q. Biomechanical Effect of L4 -L5 Intervertebral Disc Degeneration on the Lower Lumbar Spine: A Finite Element Study. Orthop. Surg. 2020, 12, 917–930. [Google Scholar] [CrossRef]
- Ibarz, E.; Herrera, A.; Más, Y.; Rodríguez-Vela, J.; Cegoñino, J.; Puértolas, S.; Gracia, L. Development and Kinematic Verification of a Finite Element Model for the Lumbar Spine: Application to Disc Degeneration. Biomed. Res. Int. 2013, 2013, 705185. [Google Scholar] [CrossRef] [PubMed]
- Rayudu, N.M.; Subburaj, K.; Mohan, R.E.; Sollmann, N.; Dieckmeyer, M.; Kirschke, J.S.; Baum, T. Patient-Specific Finite Element Modeling of the Whole Lumbar Spine Using Clinical Routine Multi-Detector Computed Tomography (MDCT) Data-A Pilot Study. Biomedicines 2022, 10, 1567. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, J.; Tu, S.; Li, S.; Yi, J.; Han, Z.; Ren, B.; Zhang, L.; Ma, C.; Liu, J.; et al. Finite Element Analysis of a Novel Fusion Strategy in Minimally Invasive Transforaminal Lumbar Interbody Fusion. Biomed Res. Int. 2022, 2022, 4266564. [Google Scholar] [CrossRef]
- Zhao, H.; Qiao, H.; Yan, K.; Liao, B. Biomechanical Evaluation of an Oblique Lateral Locking Plate System for Oblique Lumbar Interbody Fusion: A Finite Element Analysis. World Neurosurg. 2022, 160, e126–e141. [Google Scholar] [CrossRef]
- Amiri, S.; Naserkhaki, S.; Parnianpour, M. Modeling and validation of a detailed FE viscoelastic lumbar spine model for vehicle occupant dummies. Comput. Biol. Med. 2018, 99, 191–200. [Google Scholar] [CrossRef]
- Lerchl, T.; El Husseini, M.; Bayat, A.; Sekuboyina, A.; Hermann, L.; Nispel, K.; Baum, T.; Löffler, M.T.; Senner, V.; Kirschke, J.S. Validation of a Patient-Specific Musculoskeletal Model for Lumbar Load Estimation Generated by an Automated Pipeline From Whole Body CT. Front. Bioeng. Biotechnol. 2022, 10, 862804. [Google Scholar] [CrossRef]
- Kandil, K.; Zaïri, F.; Messager, T.; Zaïri, F. A microstructure-based model for a full lamellar-interlamellar displacement and shear strain mapping inside human intervertebral disc core. Comput. Biol. Med. 2021, 135, 104629. [Google Scholar] [CrossRef]
- Yang, B.; O’Connell, G.D. Intervertebral disc swelling maintains strain homeostasis throughout the annulus fibrosus: A finite element analysis of healthy and degenerated discs. Acta Biomater. 2019, 100, 61–74. [Google Scholar] [CrossRef]
- Nikkhoo, M.; Lu, M.-L.; Chen, W.C.; Fu, C.-J.; Niu, C.-C.; Lin, Y.-H.; Cheng, C.-H. Biomechanical Investigation Between Rigid and Semirigid Posterolateral Fixation During Daily Activities: Geometrically Parametric Poroelastic Finite Element Analyses. Front. Bioeng. Biotechnol. 2021, 9, 646079. [Google Scholar] [CrossRef]
- Wan, S.; Xue, B.; Xiong, Y. Three-Dimensional Biomechanical Finite Element Analysis of Lumbar Disc Herniation in Middle Aged and Elderly. J. Healthc. Eng. 2022, 2022, 7107702. [Google Scholar] [CrossRef]
- Li, J.; Xu, C.; Zhang, X.; Xi, Z.; Liu, M.; Fang, Z.; Wang, N.; Xie, L.; Song, Y. TELD with limited foraminoplasty has potential biomechanical advantages over TELD with large annuloplasty: An in-silico study. BMC Musculoskelet. Disord. 2021, 22, 616. [Google Scholar] [CrossRef] [PubMed]
- Qasim, M.; Natarajan, R.N.; An, H.S.; Andersson, G.B.J. Damage accumulation location under cyclic loading in the lumbar disc shifts from inner annulus lamellae to peripheral annulus with increasing disc degeneration. J. Biomech. 2014, 47, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Smolinski, P. Dynamic finite element modeling of poroviscoelastic soft tissue. Comput. Methods Biomech. Biomed. Eng. 2006, 9, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Castro, A.P.G.; Alves, J.L. Numerical implementation of an osmo-poro-visco-hyperelastic finite element solver: Application to the intervertebral disc. Comput. Methods Biomech. Biomed. Eng. 2020, 5, 538–550. [Google Scholar] [CrossRef] [PubMed]
- Veisari, S.F.; Haghpanahi, M.; Saberi, H. A Modified finite element model of a poroviscoelastic intervertebral disc. Biomed.Eng. Appl. Basis Commun. 2022, 2022, 2250038. [Google Scholar] [CrossRef]
- Hassan, C.R.; Lee, W.; Komatsu, D.E.; Qin, Y.-X. Evaluation of nucleus pulposus fluid velocity and pressure alteration induced by cartilage endplate sclerosis using a poro-elastic finite element analysis. Biomech. Model. Mechanobiol. 2021, 20, 281–291. [Google Scholar] [CrossRef]
- Mengoni, M. Biomechanical modelling of the facet joints: A review of methods and validation processes in finite element analysis. Biomech. Model. Mechanobiol. 2021, 20, 389–401. [Google Scholar] [CrossRef]
- Psakhie, S.G.; Horie, Y.; Ostermeyer, G.P.; Korostelev, S.Y.; Smolin, A.Y.; Shilko, E.V.; Dmitriev, A.I.; Blatnik, S.; Špegel, M.; Zavšek, S. Movable cellular automata method for simulating materials with mesostructure. Theor. Appl. Fract. Mech. 2001, 37, 311–334. [Google Scholar] [CrossRef]
- Shilko, E.V.; Psakhie, S.G.; Schmauder, S.; Popov, V.L.; Astafurov, S.V.; Smolin, A.Y. Overcoming the limitations of distinct element method for multiscale modeling of materials with multimodal internal structure. Comput. Mater. Sci. 2015, 102, 267–285. [Google Scholar] [CrossRef]
- Eremina, G.M.; Smolin, A.Y. Risk assessment of resurfacing implant loosening and femur fracture under low-energy impacts taking into account degenerative changes in bone tissues. Computer simulation. Comput. Methods Progr. Biomed. 2021, 200, 105929. [Google Scholar] [CrossRef]
- Smolin, A.Y.; Eremina, G.M.; Shilko, E.V. A tool for studying the mechanical behavior of the bone–endoprosthesis system based on multi-scale simulation. In Multiscale Biomechanics and Tribology of Inorganic and Organic Systems; Ostermeyer, G.-P., Popov, V.L., Shilko, E.V., Vasiljeva, O., Eds.; Springer: Singapore, 2021; pp. 91–126. [Google Scholar] [CrossRef]
- Psakhie, S.G.; Dimaki, A.V.; Shilko, E.V.; Astafurov, S.V. A coupled discrete element-finite difference approach for modeling mechanical response of fluid-saturated porous material. Int. J. Numer. Methods Eng. 2016, 106, 623–643. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–190. [Google Scholar] [CrossRef]
- Eremina, G.; Smolin, A.; Martyshina, I. Convergence analysis and validation of a discrete element model of the human lumbar spine. Rep. Mech. Eng. 2022, 3, 62–70. [Google Scholar] [CrossRef]
- Eremina, G.; Smolin, A. Verification and validation of numerical models for the materials of the lumbar spine. Proc. Struct. Int. 2022, 35, 115–123. [Google Scholar] [CrossRef]
- Fan, R.X.; Liu, J.; Li, Y.L.; Liu, J.; Gao, J.Z. Finite element investigation of the effects of the low-frequency vibration generated by vehicle driving on the human lumbar mechanical properties. BioMed Res. Int. 2018, 2018, 7962414. [Google Scholar] [CrossRef] [PubMed]
- Dall’Ara, E.; Karl, C.; Mazza, G.; Franzoso, G.; Vena, P.; Pretterklieber, M.; Pahr, D.; Zysset, P. Tissue properties of the human vertebral body sub-structures evaluated by means of microindentation. J. Mech. Behav. Biomed. Mater. 2013, 25, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Haj-Ali, R.; Massarwa, E.; Aboudi, J.; Galbusera, F.; Wolfram, U.; Wilke, H.-J. A new multiscale micromechanical model of vertebral trabecular bones. Biomech. Model. Mechanobiol. 2017, 16, 933–946. [Google Scholar] [CrossRef]
- Freeman, A.L.; Buttermann, G.R.; Beaubien, B.P.; Rochefort, W.E. Compressive properties of fibrous repair tissue compared to nucleus and annulus. J. Biomech. 2013, 46, 1714–1721. [Google Scholar] [CrossRef]
- Cortes, D.H.; Han, W.M.; Smith, L.J.; Elliott, D.M. Mechanical properties of the extra-fibrillar matrix of human annulus fibrosus are location and age dependent. J. Orthop. Res. 2013, 31, 1725–1732. [Google Scholar] [CrossRef]
- Ogurkowska, M.B.; Błaszczyk, A. Distribution of Young’s modulus at various sampling points in a human lumbar spine vertebral body. Spine J. 2020, 20, 1861–1875. [Google Scholar] [CrossRef]
- Jacobs, N.T.; Cortes, D.H.; Peloquin, J.M.; Vresilovic, E.J.; Elliott, D.M. Validation and application of an intervertebral disc finite element model utilizing independently constructed tissue-level constitutive formulations that are nonlinear, anisotropic, and time-dependent. J. Biomech. 2014, 47, 2540–2546. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.C.; Wilcox, R.K. Finite element analysis of the spine: Towards a framework of verification, validation and sensitivity analysis. Med. Eng. Phys. 2008, 30, 1287–1304. [Google Scholar] [CrossRef] [PubMed]
- Nikkhoo, M.; Wang, J.L.; Parnianpour, M.; El Rich, M.; Khalaf, K. Biomechanical response of intact, degenerated and repaired intervertebral discs under impact loading—Ex-vivo and In-Silico investigation. J. Biomech. 2018, 70, 26–32. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Yang, J.; Lieberman, I.H.; Haddas, R. Lumbar spine finite element model for healthy subjects: Development and validation. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1–15. [Google Scholar] [CrossRef]
- Zahari, S.N.; Latif, M.; Rahim, N.; Kadir, M.; Kamarul, T. The effects of physiological biomechanical loading on intradiscal pressure and annulus stress in lumbar spine: A finite element analysis. J. Healthc. Eng. 2017, 2017, 9618940. [Google Scholar] [CrossRef]
- Cowin, S.C.; Doty, B. Tissue Mechanics; Springer: New York, NY, USA, 2007; pp. 247–288. [Google Scholar]
- Kemper, A.R.; McNally, C.; Duma, S.M. The influence of strain rate on the compressive stiffness properties of human lumbar intervertebral discs. Biomed. Sci. Instrum. 2007, 43, 176–181. [Google Scholar]
- Costi, J.J.; Stokes, I.A.; Gardner-Morse, M.; Label, J.P.; Scoffone, H.M.; Yatridis, J.K. Direct measurement of maximum intervertebral disc shear strain at six degrees of freedom: Movements in which disc tissue is at risk of injury. J. Biomech. 2007, 40, 2457–2466. [Google Scholar] [CrossRef]
- Claus, A.; Hides, J.; Moseley, G.L.; Hodges, P. Sitting versus standing: Does the intradiscal pressure cause disc degeneration or low back pain? J. Electromyogr. Kinesiol. 2008, 18, 550–558. [Google Scholar] [CrossRef]
- Han, K.-S.; Rohlmann, A.; Zander, T.; Taylor, W.R. Lumbar spinal loads vary with body height and weight. Med. Eng. Phys. 2013, 35, 969–977. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Xue, J.; Li, Y.; Yang, G.; Wang, G.; Wang, J. Combined Effects of Graded Foraminotomy and Annular Defect on Biomechanics after Percutaneous Endoscopic Lumbar Decompression: A Finite Element Study. J. Health. Eng. 2020, 2020, 8820228. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, C.; Guo, R.; Cha, T.; Li, G. Prediction of biomechanical responses of human lumbar discs-a stochastic finite element model analysis. Comp. Meth. Biomech. Biomed. Eng. 2021, 24, 1730–1741. [Google Scholar] [CrossRef] [PubMed]
- Dreischarf, M.; Shirazi-Adl, A.; Arjmand, N.; Rohlmann, A.; Schmidt, H. Estimation of loads on human lumbar spine: A review of in vivo and computational model studies. J. Biomech. 2016, 49, 833–845. [Google Scholar] [CrossRef] [PubMed]
- Honegger, J.D.; Actis, J.A.; Gates, D.H. Development of a multiscale model of the human lumbar spine for investigation of tissue loads in people with and without a transtibial amputation during sit-to-stand. Biomech. Model. Mechanobiol. 2021, 20, 339–358. [Google Scholar] [CrossRef] [PubMed]
- Hui, Y.; Zhou, Z.; Du, J.; Wu, B.; Huang, W. Finite element mechanics analysis of lumbar spine with normal and varying degrees of herniated lesions under different working conditions and material properties. Mech. Adv. Mat. Struct. 2021, 2021, 1–18. [Google Scholar] [CrossRef]
- Hamidrad, S.; Abdollahi, M.; Badali, V.; Nikkhoo, M.; Naserkhaki, S. Biomechanical modeling of spinal ligaments: Finite element analysis of L4-L5 spinal segment. Comput. Methods Biomech. Biomed. Engin. 2021, 24, 1807–1818. [Google Scholar] [CrossRef]
- Chagnon, A.; Aubin, C.E.; Villemure, I. Biomechanical influence of disk properties on the load transfer of healthy and degenerated disks using a poroelastic finite element model. J. Biomech. Eng. 2010, 132, 111006. [Google Scholar] [CrossRef]
- Du, C.F.; Cai, X.Y.; Gui, W.; Sun, M.S.; Liu, Z.X.; Liu, C.J.; Zhang, C.Q.; Huang, Y.P. Does oblique lumbar interbody fusion promote adjacent degeneration in degenerative disc disease: A finite element analysis. Comput. Biol. Med. 2021, 128, 104122. [Google Scholar] [CrossRef]
- Ratish, S.; Gao, Z.-X.; Prasad, H.M.; Pei, Z.; Bijendra, D. Percutaneous Endoscopic Lumbar Spine Surgery for Lumbar Disc Herniation and Lumbar Spine Stenosis: Emphasizing on Clinical Outcomes of Transforaminal Technique. Surg. Sci. 2018, 9, 63–84. [Google Scholar] [CrossRef]
- Kurutz, M.; Oroszváry, L. Finite element analysis of weightbath hydrotraction treatment of degenerated lumbar spine segments in elastic phase. J. Biomech. 2010, 43, 433–441. [Google Scholar] [CrossRef]
- Adams, M.A.; Roughley, P.J. What is intervertebral disc degeneration, and what causes it? Spine 2006, 31, 2151–2161. [Google Scholar] [CrossRef]
- Du, Y.; Tavana, S.; Rahman, T.; Baxan, N.; Hansen, U.N.; Newell, N. Sensitivity of Intervertebral Disc Finite Element Models to Internal Geometric and Non-geometric Parameters. Front. Bioeng. Biotechnol. 2021, 9, 660013. [Google Scholar] [CrossRef] [PubMed]
- Ayotte, D.C.; Ito, K.; Perren, S.M.; Tepic, S. Direction-dependent constriction flow in a poroelastic solid: The intervertebral disc valve. J. Biomech. Eng. 2000, 122, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Adams, M.; McNally, D.; Dolan, P. ‘Stress’ distribution inside intervertebral discs. J. Bone Joint Surg. Br. 1996, 78, 965–972. [Google Scholar] [CrossRef]
- Fields, A.J.; Ballatori, A.; Liebenberg, E.C.; Lotz, J.C. Contribution of the endplates to disc degeneration. Curr. Mol. Biol. Rep. 2018, 4, 151–160. [Google Scholar] [CrossRef] [PubMed]
- Jackson, A.R.; Huang, C.-Y.; Gu, W.Y. Effect of endplate calcification and mechanical deformation on the distribution of glucose in intervertebral disc: A 3D finite element study. Comput. Methods Biomech. Biomed. Engin. 2011, 14, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yi, X.D.; Li, C.D. The influence of artificial nucleus pulposus replacement on stress distribution in the cartilaginous endplate in a 3-dimensional finite element model of the lumbar intervertebral disc. Medicine 2017, 96, e9149. [Google Scholar] [CrossRef]
- Zhao, L.; Yan, G.H.; Ju, D.B.; Shi, Z.G.; Zhang, M.C. Finite element analysis of lumbar disc degeneration on the biomechanical properties of the cartilage endplate effects. Chin. J. Clin. Anat. 2015, 33, 455–460. [Google Scholar]
- Cannella, M.; Isaacs, J.L.; Allen, S.; Orana, A.; Vresilovic, E.; Marcolongo, M. Nucleus implantation: The biomechanics of augmentation versus replacement with varying degrees of nucleotomy. J. Biomech. Eng. 2014, 136, 051001. [Google Scholar] [CrossRef]
- Näther, P.; Kersten, J.F.; Kaden, I.; Irga, K.; Nienhaus, A. Distribution Patterns of Degeneration of the Lumbar Spine in a Cohort of 200 Patients with an Indication for Lumbar MRI. Int. J. Environ. Res. Public Health 2022, 19, 3721. [Google Scholar] [CrossRef]




| Type of Tissue | Density of the Matrix, ρ, kg/m3 | Young’s of the Matrix, E, GPa | Poisson’s Ratio ν | Bulk Modulus of the Solid, Ks, GPa | Porosity, θ | Permeability k, m2 |
|---|---|---|---|---|---|---|
| AF | 1060 | 0.0025 | 0.20 | 3.4 | 0.8 | 3 × 10−19 |
| NP | 1060 | 0.0015 | 0.30 | 5 | 0.8 | 3 × 10−19 |
| CEP | 1000 | 0.005 | 0.46 | 9 | 0.8 | 7 × 10−18 |
| Cortical | 1850 | 10 | 0.30 | 17 | 0.04 | 1 × 10−16 |
| Cancellous | 700 | 0.1 | 0.20 | 10 | 0.7 | 1 × 10−19 |
| Stage of Degradation | Young’s Modulus E, MPa | Porosity θ | Permeability k, m2 |
|---|---|---|---|
| AF 0 | 2.5 | 0.82 | 1.52 × 10−19 |
| AF 1 | 2.7 | 0.72 | 1.25 × 10−19 |
| AF 2 | 2.9 | 0.62 | 1.00 × 10−19 |
| NP 0 | 1.5 | 0.78 | 2.42 × 10−19 |
| NP 1 | 1.7 | 0.68 | 2.20 × 10−19 |
| NP 2 | 2.0 | 0.58 | 2.00 × 10−19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eremina, G.; Smolin, A.; Xie, J.; Syrkashev, V. Development of a Computational Model of the Mechanical Behavior of the L4–L5 Lumbar Spine: Application to Disc Degeneration. Materials 2022, 15, 6684. https://doi.org/10.3390/ma15196684
Eremina G, Smolin A, Xie J, Syrkashev V. Development of a Computational Model of the Mechanical Behavior of the L4–L5 Lumbar Spine: Application to Disc Degeneration. Materials. 2022; 15(19):6684. https://doi.org/10.3390/ma15196684
Chicago/Turabian StyleEremina, Galina, Alexey Smolin, Jing Xie, and Vladimir Syrkashev. 2022. "Development of a Computational Model of the Mechanical Behavior of the L4–L5 Lumbar Spine: Application to Disc Degeneration" Materials 15, no. 19: 6684. https://doi.org/10.3390/ma15196684
APA StyleEremina, G., Smolin, A., Xie, J., & Syrkashev, V. (2022). Development of a Computational Model of the Mechanical Behavior of the L4–L5 Lumbar Spine: Application to Disc Degeneration. Materials, 15(19), 6684. https://doi.org/10.3390/ma15196684








