Research on Splitting-Tensile Properties and Failure Mechanism of Steel-Fiber-Reinforced Concrete Based on DIC and AE Techniques
Abstract
1. Introduction
2. Materials and Methods
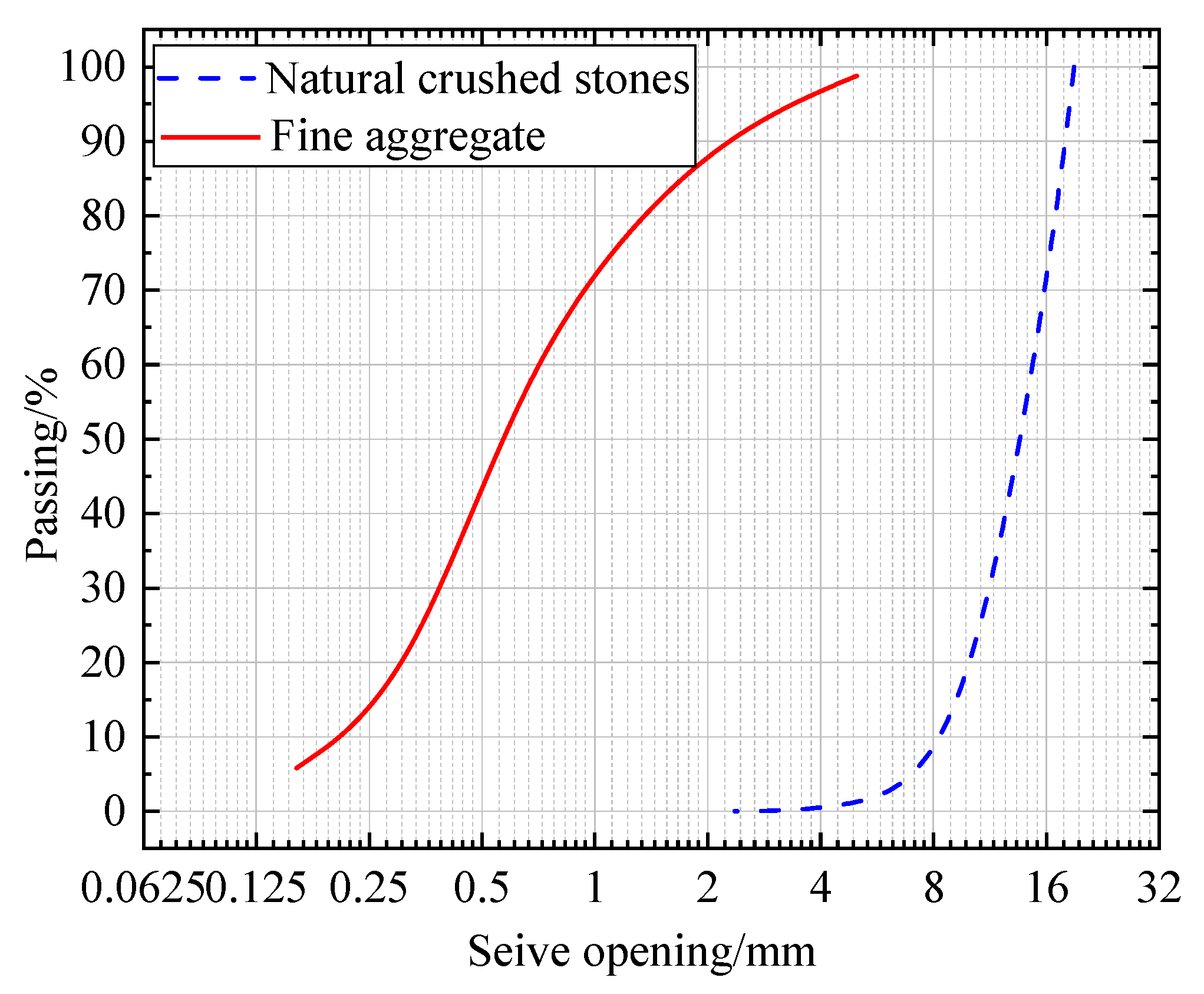
2.1. Materials
2.2. Workability of Fresh Concrete
2.3. Preparation of Specimens
- (1)
- Firstly, the premixed mortar with a water-binder ratio of 0.4 was used to paint the HJS-60 double-horizontal axis concrete mixer manufactured by Cangzhou Yixuan Test Instrument Co., Ltd. (Cangzhou, China) to avoid water absorption.
- (2)
- Cement, fly ash, sand, coarse aggregates, and water reducer agent were added into the mixer and mixed at a low speed of 62 rpm for 30 s. After that, steel fibers were dispersed manually into the mixer and blended at a high speed of 125 rpm for 60 s. Finally, the air-entraining agent was dissolved into water and then the liquid was added into the mixer and mixed for 120 s.
- (3)
- The fresh concrete mixture was poured into moulds. The molds were then placed on a vibrating table and vibrated for 30 s to avoid segregation of fresh concrete. The specimens were demolded 24 h after casting and then cured for 28 days in a curing box with a temperature of 20 ± 2 °C and a relative humidity of 95%.
- (4)
- After 28 days’ curing, the specimens were taken out and painted by white-black speckles. The typical specimens prepared are shown in Figure 3. A, B, C and D represent concrete with steel fiber content of 0.0%,1.0%,1.5% and 2.0%, respectively. There are three specimens for each mix group, “A-1” represents the first specimen in the mix group with steel fiber content of 0.0%.
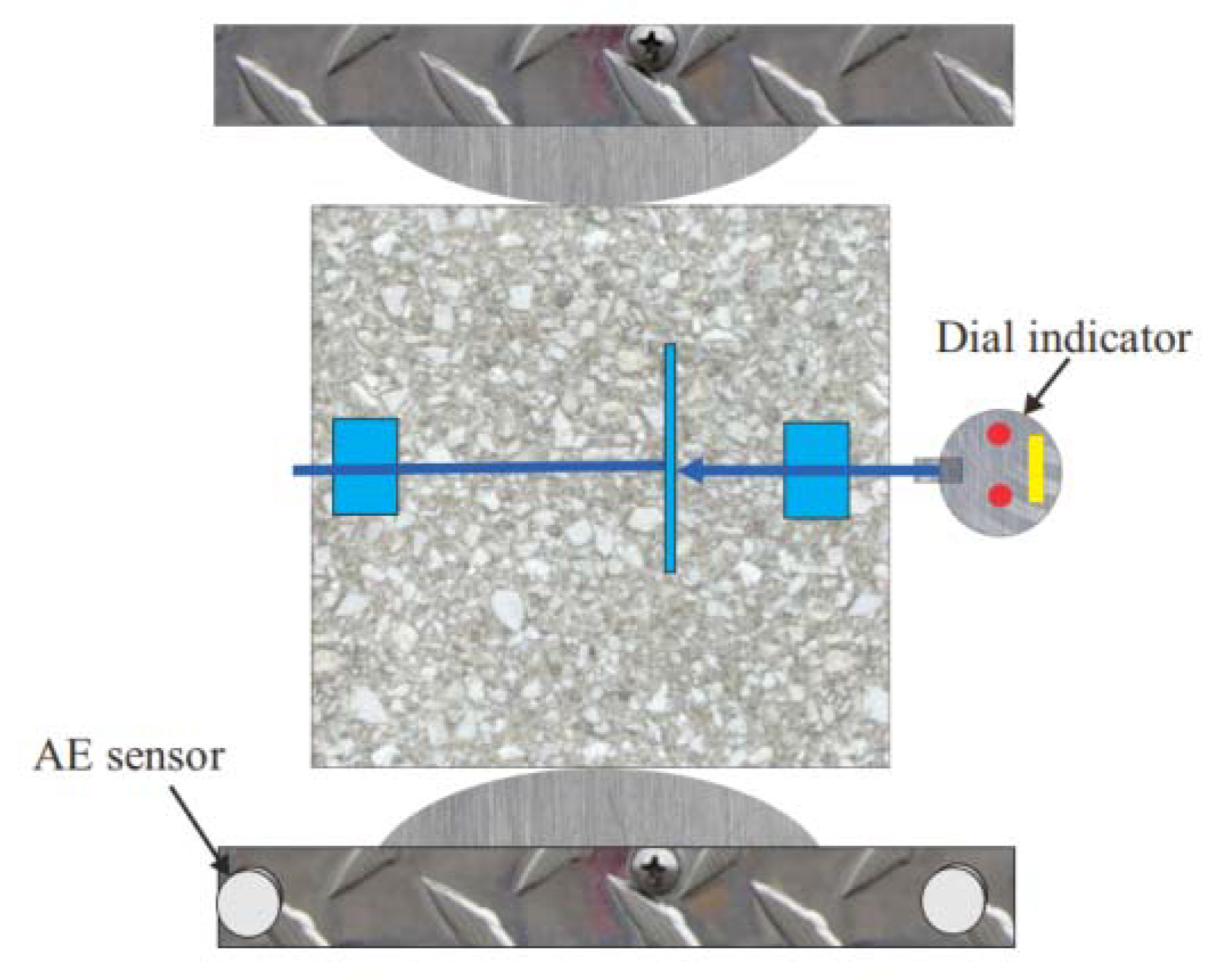
2.4. Testing Procedure
3. Results
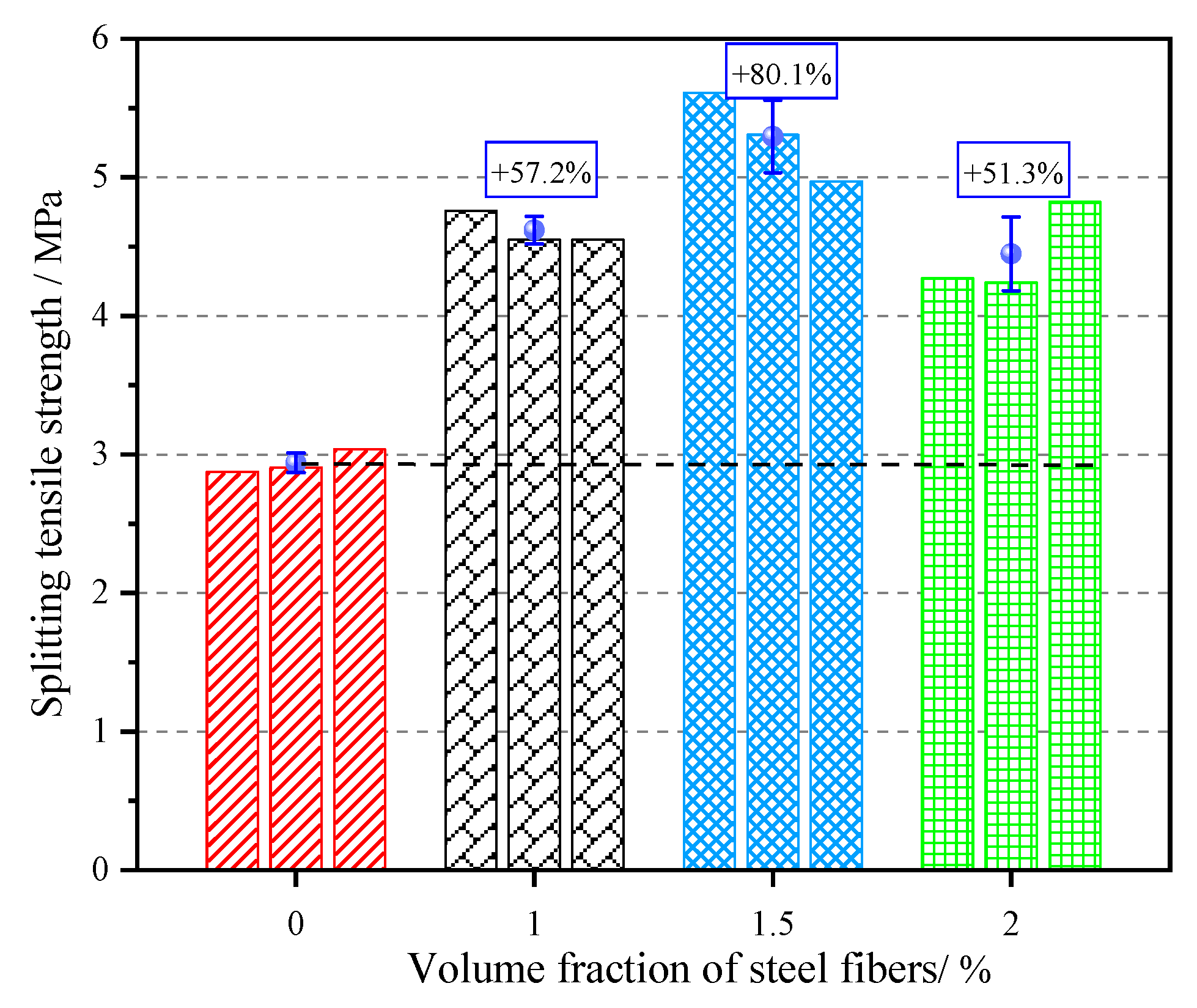
3.1. Splitting-Tensile Strength of SFRC
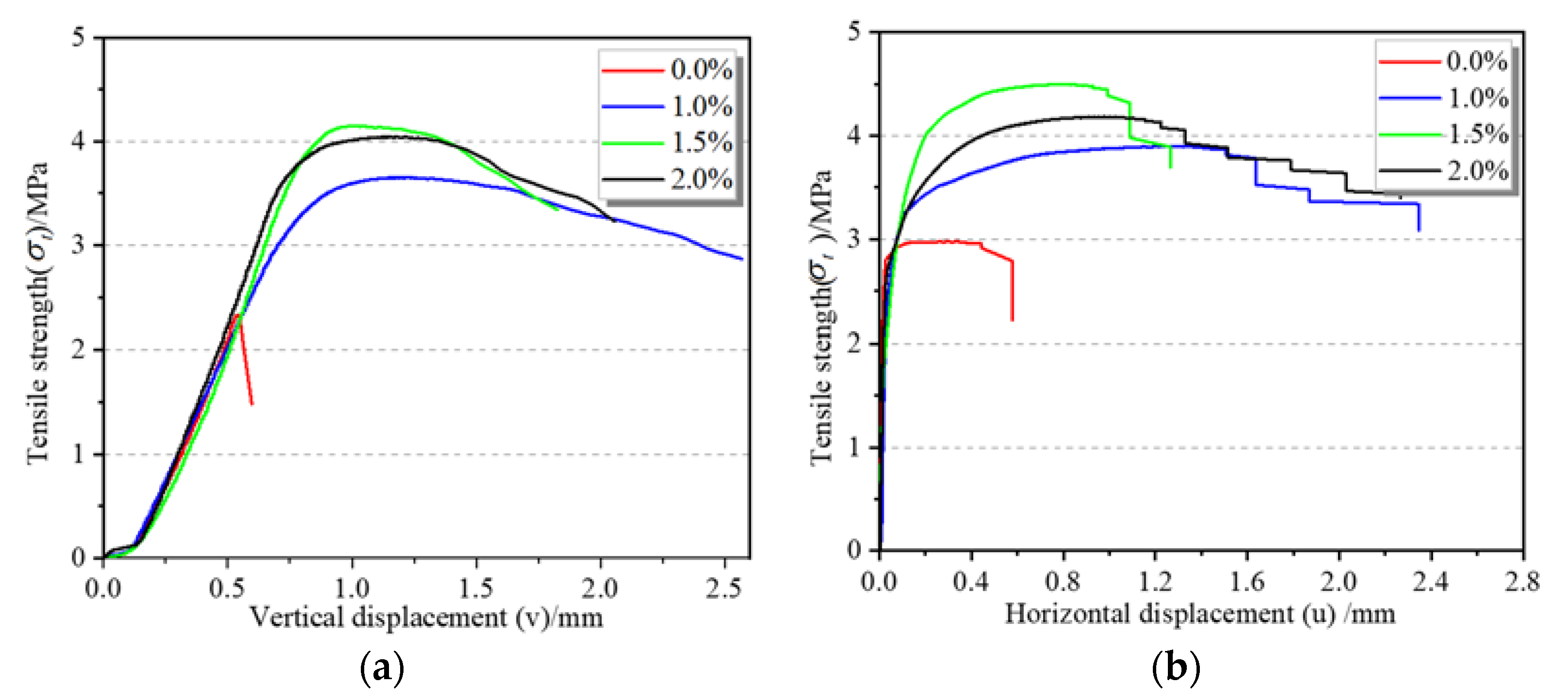
3.2. Tensile Stress Displacement Relationship during Loading
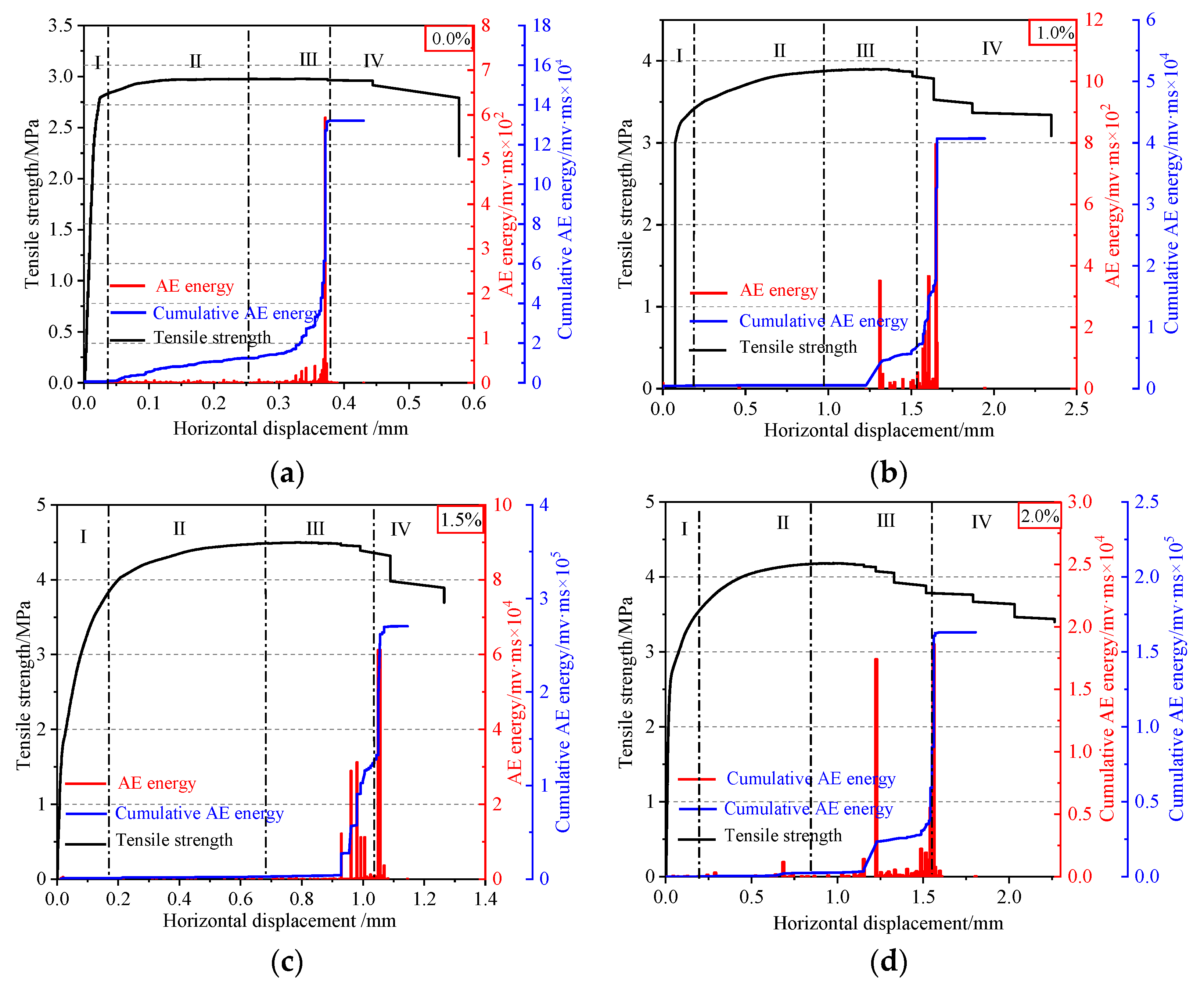
3.3. AE Energy Evolution Law in the Test
4. Discussion
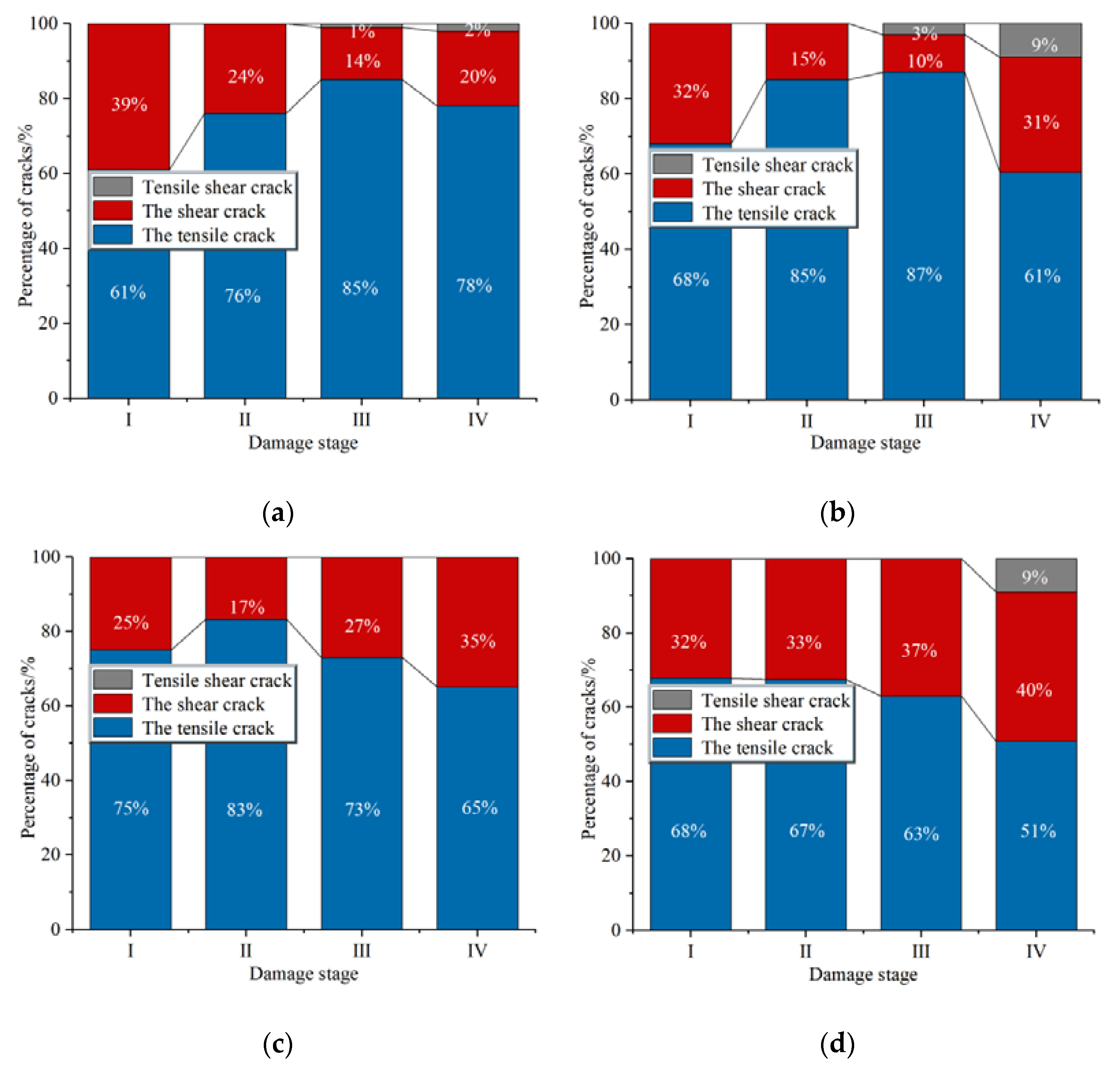
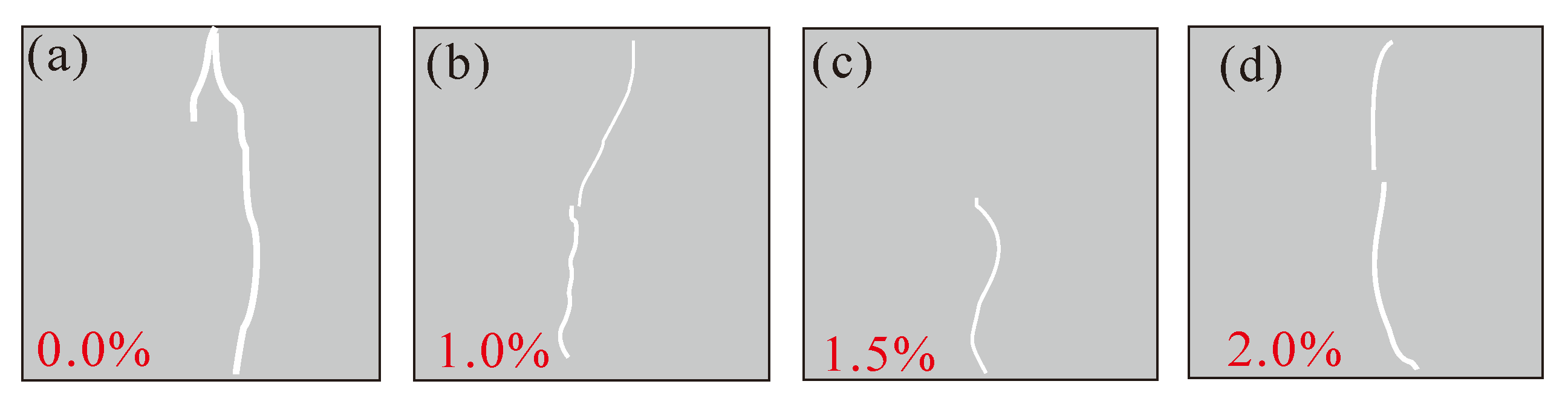
4.1. Crack Evolution during Splitting-Tensile Failure of SFRC
4.2. Pull-Shear Failure Mechanism Based on RA and AF
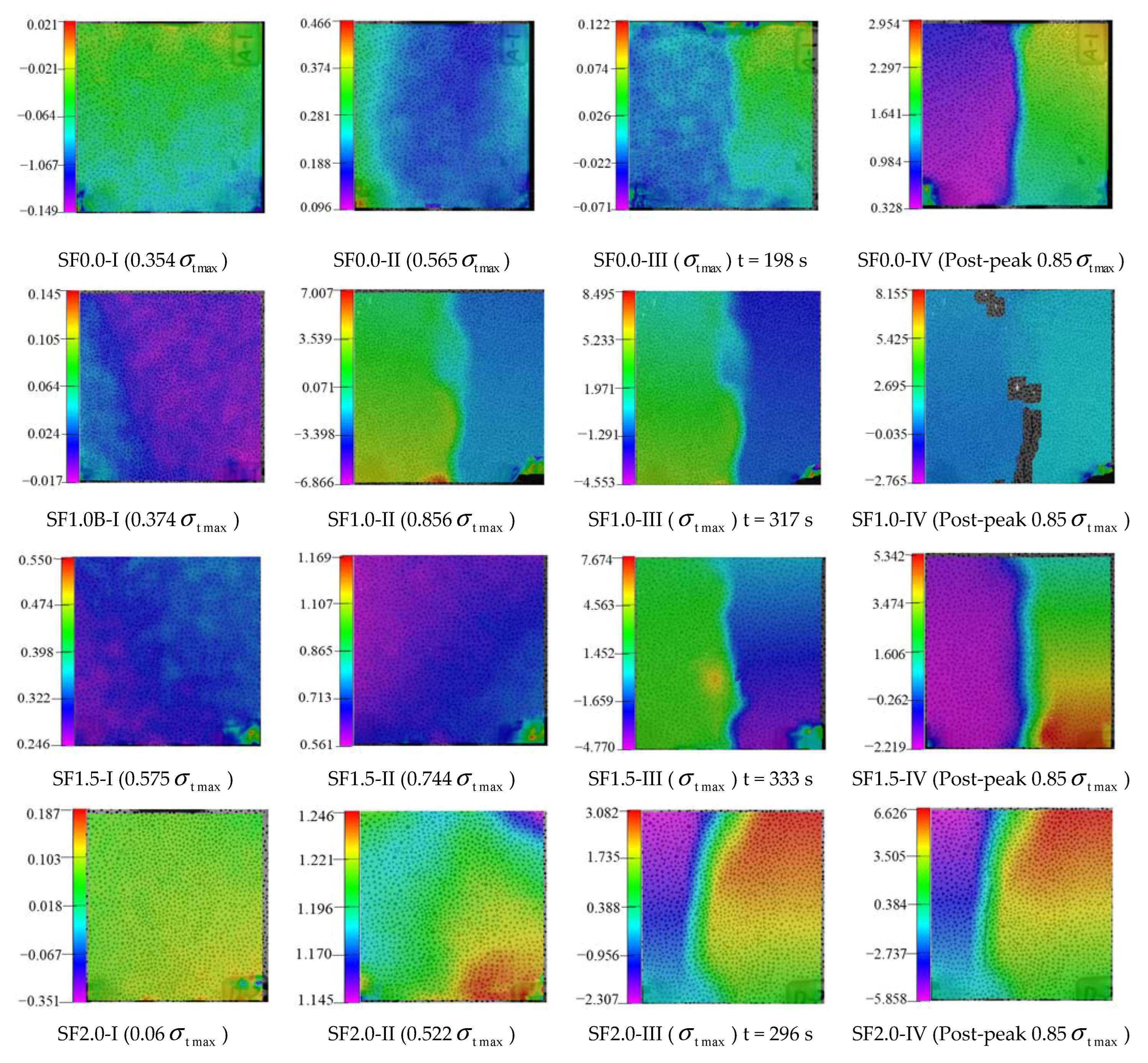
4.3. Variation Law of Full-Field Horizontal Displacement during Splitting-Tensile Process of SFRC
5. Conclusions
- (1)
- The addition of steel fibers significantly improved the splitting-tensile strength of concrete. With the increase of the volume fraction of steel fibers, the splitting-tensile strength of concrete increased first and then decreased, and reached the maximum value of 5.294 MPa when the content was 1.5%.
- (2)
- AE energy can reflect the four stages of concrete fracture characteristics; the critical state of instability can be judged effectively by the sudden increase of accumulated AE energy. The splitting-tensile process of SFRC mainly included the following four stages: Stage I (0 < < 0.85), where there is almost no AE signal; Stage II (0.85 < < ), which produces a small amount of AE signal; Stage III ( < < post-peak 0.9 ), which produces a dense and intense AE energy; Stage IV (post-peak 0.9 < ), where AE signals are no longer generated. Stage III could be regarded as a precursor to the failure of the specimen.
- (3)
- Tensile cracks dominated the whole process of splitting and tensile failure of SFRC. The percentage of shear cracks in SFRC with volume fractions of steel fibers of 0.0% was high in stage I, 1.0%, and 1.5% was high in stage I and stage IV. However, the proportion of shear cracks in concrete with volume fractions of steel fibers of 2.0% is between 30–40% at every stage.
- (4)
- DIC is possible to measure and accurately determine parameters of crack, such as its actual length, shape, and trajectory of propagation. The combination of AE and DIC is an effective experimental research method, which has great development potential in the field of non-destructive monitoring of SFRC structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.H.; Liu, J.Z.; Liu, J.P.; Zhang, Q.Q.; Han, F.Y. Effect of Steel Fiber on Flexural Toughness and Fracture Mechanics Behavior of Ultrahigh-Performance Concrete with Coarse Aggregate. J. Mater. Civ. Eng. 2018, 30, 04018323. [Google Scholar] [CrossRef]
- Venkateshwaran, A.; Tan, K.H.; Li, Y. Residual flexural strengths of steel fiber reinforced concrete with multiple hooked-end fibers. Struct. Concr. 2018, 19, 352–365. [Google Scholar] [CrossRef]
- Dhanapal, J.; Jeyaprakash, S. Mechanical properties of mixed steel fiber reinforced concrete with the combination of micro and macro steel fibers. Struct. Concr. 2020, 21, 458–467. [Google Scholar] [CrossRef]
- Wu, Z.M.; Shi, C.J.; He, W.; Wu, L.M. Effects of steel fiber content and shape on mechanical properties of ultra high performance concrete. Constr. Build. Mater. 2016, 103, 8–14. [Google Scholar] [CrossRef]
- Bhosale, A.; Rasheed, M.A.; Prakash, S.S.; Raju, J. A study on the efficiency of steel vs. synthetic vs. hybrid fibers on fracture behavior of concrete in flexure using acoustic emission. Constr. Build. Mater. 2019, 199, 256–268. [Google Scholar] [CrossRef]
- Biscaia, H.; Franco, N.; Chastre, C. Stainless Steel Bonded to Concrete: An Experimental Assessment using the DIC Technique. Int. J. Concr. Struct. Mater. 2018, 12, 9. [Google Scholar] [CrossRef]
- Su, C.D.; Lin, H.X. Mechanical performances of steel fiber reinforced high strength concrete disc under cyclic loading. Constr. Build. Mater. 2017, 146, 276–282. [Google Scholar] [CrossRef]
- Shi, X.J.; Park, P.; Rew, Y.; Huang, K.; Sim, C. Constitutive behaviors of steel fiber reinforced concrete under uniaxial compression and tension. Constr. Build. Mater. 2020, 233, 117316. [Google Scholar] [CrossRef]
- Wu, H.Y.; Lin, X.S.; Zhou, A.N.; Zhang, Y.X. A temperature-dependent material model for numerical simulation of steel fibre reinforced concrete. Constr. Build. Mater. 2022, 320, 126329. [Google Scholar] [CrossRef]
- Zhang, S.L.; Zhang, C.S.; Liao, L.; Wang, C.L. Investigation into the effect of fibre distribution on the post-cracking tensile strength of SFRC through physical experimentation and numerical simulation. Constr. Build. Mater. 2020, 248, 118433. [Google Scholar] [CrossRef]
- Han, J.H.; Zhao, M.M.; Chen, J.Y. Effects of steel fiber length and coarse aggregate maximum size on mechanical properties of steel fiber reinforced concrete. Constr. Build. Mater. 2019, 209, 577–591. [Google Scholar] [CrossRef]
- Fotouhi, F.; Ashkezari, G.D.; Razmara, M. Experimental relationships between steel fiber volume fraction and mechanical properties of ultra-high performance fiber-reinforced concrete. J. Build. Eng. 2020, 32, 101613. [Google Scholar] [CrossRef]
- Ruan, T.; Poursaee, A. Fiber-Distribution Assessment in Steel Fiber–Reinforced UHPC Using Conventional Imaging, X-Ray CT Scan, and Concrete Electrical Conductivity. J. Mater. Civ. Eng. 2019, 31, 04019133. [Google Scholar] [CrossRef]
- Kazemi, M.T.; Golsorkhtabar, H.; Beygi, M.H.A. Gholamitabar, M. Fracture properties of steel fiber reinforced high strength concrete using work of fracture and size effect methods. Constr. Build. Mater. 2017, 142, 482–489. [Google Scholar] [CrossRef]
- Ding, X.X.; Li, C.Y.; Zhao, M.L.; Li, J.; Geng, H.B.; Lian, L. Tensile Behavior of Self-Compacting Steel Fiber Reinforced Concrete Evaluated by Different Test Methods. Crystals 2021, 11, 251. [Google Scholar] [CrossRef]
- Kachouh, N.; El-Maaddawy, T.; El-Hassan, H. Numerical Modeling of Concrete Deep Beams Made with Recycled Aggregates and Steel Fibers. Buildings 2022, 12, 529. [Google Scholar] [CrossRef]
- Lehner, P.; Horňáková, M. Effect of Amount of Fibre and Damage Level on Service Life of SFR Recycled Concrete in Aggressive Environment. Buildings 2021, 11, 489. [Google Scholar] [CrossRef]
- Golewski, G.L. Evaluation of fracture processes under shear with the use of DIC technique in fly ash concrete and accurate measurement of crack path lengths with the use of a new crack tip tracking method. Measurement 2021, 181, 109632. [Google Scholar] [CrossRef]
- Li, S.T.; Chen, X.D.; Guo, S.S. Evaluation of Fracture Process Zone in the Flexural Response of Different Concrete Materials Using DIC Method. J. Mater. Civ. Eng. 2020, 24, 2435–2438. Available online: https://www.researchgate.net/publication/342566291 (accessed on 25 July 2022). [CrossRef]
- Alam, S.Y.; Loukili, A. Transition from energy dissipation to crack openings during continuum-discontinuum fracture of cocrete. Int. J. Fract. 2017, 206, 49–66. [Google Scholar] [CrossRef]
- Tu, J.C.; Zhao, D.; Zhao, J. Experimental study on in situ monitoring of the evolution law of cracks in wood components with transverse cracks based on acoustic emission and image correlation. J. Beijing For. Univ. 2020, 42, 142–148. (In Chinese) [Google Scholar]
- Sayadi, A.; Neitzert, T.R.; Clifton, G.C. Ultra-lightweight concrete containing expanded poly-lactic acid as lightweight aggregate. KSCE J. Civ. Eng. 2018, 22, 4083–4094. [Google Scholar] [CrossRef]
- Rouchiera, S.; Forayb, G.; Godinb, N.; Woloszyn, M.; Roux, J.J. Damage monitoring in fibre reinforced mortar by combined digital image correlation and acoustic emission. Constr. Build. Mater. 2013, 38, 371–380. [Google Scholar] [CrossRef]
- Liu, X.L.; Dai, S.H.; Nawnit, K. Experimental study on the fracture process zone characteristics in concrete utilizing DIC and AE Methods. Appl. Sci. 2019, 9, 1346. [Google Scholar] [CrossRef]
- Alam, S.Y.; Saliba, J.; Loukili, A. Fracture examination in concrete through combined digital image correlation and acoustic emision techniques. Constr. Build. Mater. 2014, 69, 232–242. [Google Scholar] [CrossRef]
- Skarżyński, Ł.; Tejchman, J. Experimental investigations of fracture process using DIC in plain and reinforced concrete beams under bending. Strain 2013, 49, 521–543. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Test Method Standard for Physical and Mechanical Properties of Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019. (In Chinese)
- Jiao, Y.B.; Zhang, L.D.; Guo, Q.L. Acoustic Emission-Based Reinforcement Evaluation of Basalt and Steel Fibers on Low-Temperature Fracture Resistance of Asphalt Concrete. J. Mater. Civ. Eng. 2020, 32, 04020104. [Google Scholar] [CrossRef]
- Li, S.T.; Fan, X.Q.; Chen, X.D. Development of fracture process zone in full-graded dam concrete under three-point bending by DIC and acoustic emission. Eng. Fract. Mech. 2020, 230, 106972. [Google Scholar] [CrossRef]
- Iliopoulos, S.; Aggelis., D.G.; Pyl, L.; Vantomme, J. Detection and evaluation of cracks in the concrete buffer of the Belgian Nuclear Waste container using combined NDT techniques. Constr. Build. Mater. 2015, 78, 369–378. [Google Scholar] [CrossRef]
- Gao, D.Y.; Wang, F.H. Effects of recycled fine aggregate and steel fiber on compressive and splitting tensile properties of concrete. J. Build. Eng. 2021, 44, 102631. [Google Scholar] [CrossRef]
- Xia, D.T.; Xie, S.J.; Fu, M.; Zhu, F. Effects of maximum particle size of coarse aggregates and steel fiber content on the mechanical properties and impact resistance of recycled aggregate concrete. Adv. Struct. Eng. 2021, 24, 3085–3098. [Google Scholar] [CrossRef]
- Xie, T.C. Mechanism Study of Crack Initiation and Propagation in a Rock Mass with Complicated Cracks under Compression. Master’s Thesis, China University of Geosciences, Wuhan, China, 2020. (In Chinese). [Google Scholar]
- Makhutov, N.A.; Matvienko, Y.G. Griffith theory and development of fracture mechanics criteria. Mater. Sci. 1993, 29, 216–319. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, D.S.; Song, Q.H. Reliability analysis for propagation of rock crack based on Griffith theory. Eng. Mech. 2008, 9, 156–161. (In Chinese) [Google Scholar]
- Gross, D.; Seelig, T. Fracture Mechanics, with An Introduction to Micromechanics; Springer: Berlin/Heidelberg, Germay, 2006; Available online: https://www.researchgate.net/publication/43184929_Fracture_Mechanics_With_an_Introduction_to_Micromechanics (accessed on 25 July 2022).
- Fan, T.Y. Theoretical Basis of Fracture; Science Press: Beijing, China, 2003. [Google Scholar]
- Amara, B. Griffith Energy Balance Model for Crack-Growth Prediction in Reinforced Concrete. J. Eng. Mech. 1996, 122, 683. [Google Scholar] [CrossRef]
- Wang, J.; Fu, J.X.; Song, W.D.; Zhang, Y.F.; Wu, Y. Mechanical behavior, acoustic emission properties and damage evolution of cemented paste backfifill considering structural feature. Constr. Build. Mater. 2020, 261, 119958. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, X.; Gu, Y. Effects of off-axis angle on shear progressive damage of 3D woven composites with X-ray micro-computed tomography. Compos. Part A Appl. Sci. Manuf. 2018, 115, 311–320. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Soulioti, D.V.; Gatselou, E.A.; Barkoulab, N.M.; Matikasb, T.E. Monitoring of the mechanical behavior of concrete with chemically treated steel fibers by acoustic emission. Constr. Build. Mater. 2013, 48, 55–60. [Google Scholar] [CrossRef]
- Fan, X.Q.; Hu, S.W.; Lu, J.; Wei, C.J. Acoustic emission properties of concrete on dynamic tensile test. Constr. Build. Mater. 2016, 114, 66–75. [Google Scholar] [CrossRef]
- Wang, C.Y.; Chang, X.K.; Liu, Y.L.; Gong, F.Q. Experimental Study on Fracture Patterns and Crack Propagation of Sandstone Based on Acoustic Emission. Adv. Civ. Eng. 2021, 2021, 8847158. [Google Scholar] [CrossRef]
- Colombo, I.S.; Main, I.G.; Forde, M.C. Assessing Damage of Reinforced Concrete Beam Using “b-value” Analysis of Acoustic Emission Signals. J. Mater. Civ. Eng. 2003, 15, 280–286. [Google Scholar] [CrossRef]





| Cement Type | Stability | Setting Time/min | Compressive Strength/MPa | Flexural Strength/MPa | |||
|---|---|---|---|---|---|---|---|
| Initial | Final | 3 Days | 28 Days | 3 Days | 28 Days | ||
| P.O 42.5 | Qualified | 229 | 282 | 28.9 | 45.0 | 5.1 | 7.7 |
| Material | SiO2 | Al2O3 | CaO | Fe2O3 | MgO | SO3 | Ignition Loss |
|---|---|---|---|---|---|---|---|
| Cement | 22.81% | 5.62% | 61.43% | 3.36% | 1.35% | 2.17% | 2.60% |
| SiO2 | Al2O3 | CaO | Fe2O3 | MgO | SO3 | Ignition Loss |
|---|---|---|---|---|---|---|
| 49.02% | 31.56% | 4.88% | 6.97% | 0.83% | 1.2% | 4.70% |
| Water Reduction Ratio (%) | Air-Inducing Ratio (%) | Air Volume Fraction (%) | Compressive Strength Ratio (%) | |||
|---|---|---|---|---|---|---|
| 1 Day | 3 Days | 7 Days | 28 Days | |||
| 14 | 29 | 5.0~7.0 | 220 | 183 | 180 | 165 |
| Mix Groups | Composition/kg/m3 | |||||||
|---|---|---|---|---|---|---|---|---|
| Cement | Fly Ash | Fine Aggregate | Coarse Aggregate | Water | Water Reducer | Air-Entraining Agent | Steel Fibers | |
| 0.0% | 282 | 18 | 544 | 1240 | 150 | 2.1 | 0.03 | 0 |
| 1.0% | 282 | 18 | 544 | 1240 | 150 | 2.1 | 0.03 | 78 |
| 1.5% | 282 | 18 | 544 | 1240 | 150 | 2.1 | 0.03 | 117 |
| 2.0% | 282 | 18 | 544 | 1240 | 150 | 2.1 | 0.03 | 156 |
| Mix Groups | Slump (mm) | Air Content (%) |
|---|---|---|
| 0.0% | 148 | 5.2 |
| 1.0% | 128 | 2.2 |
| 1.5% | 116 | 1.5 |
| 2.0% | 103 | 1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, T.; Pan, X.; Tang, L.; Sun, Q.; Pan, J. Research on Splitting-Tensile Properties and Failure Mechanism of Steel-Fiber-Reinforced Concrete Based on DIC and AE Techniques. Materials 2022, 15, 7150. https://doi.org/10.3390/ma15207150
Luo T, Pan X, Tang L, Sun Q, Pan J. Research on Splitting-Tensile Properties and Failure Mechanism of Steel-Fiber-Reinforced Concrete Based on DIC and AE Techniques. Materials. 2022; 15(20):7150. https://doi.org/10.3390/ma15207150
Chicago/Turabian StyleLuo, Tao, Xiaofeng Pan, Liyun Tang, Qiang Sun, and Jiaojiao Pan. 2022. "Research on Splitting-Tensile Properties and Failure Mechanism of Steel-Fiber-Reinforced Concrete Based on DIC and AE Techniques" Materials 15, no. 20: 7150. https://doi.org/10.3390/ma15207150
APA StyleLuo, T., Pan, X., Tang, L., Sun, Q., & Pan, J. (2022). Research on Splitting-Tensile Properties and Failure Mechanism of Steel-Fiber-Reinforced Concrete Based on DIC and AE Techniques. Materials, 15(20), 7150. https://doi.org/10.3390/ma15207150







