Piston Wear Detection and Feature Selection Based on Vibration Signals Using the Improved Spare Support Vector Machine for Axial Piston Pumps
(This article belongs to the Section Manufacturing Processes and Systems)
Abstract
1. Introduction
2. Materials and Methods
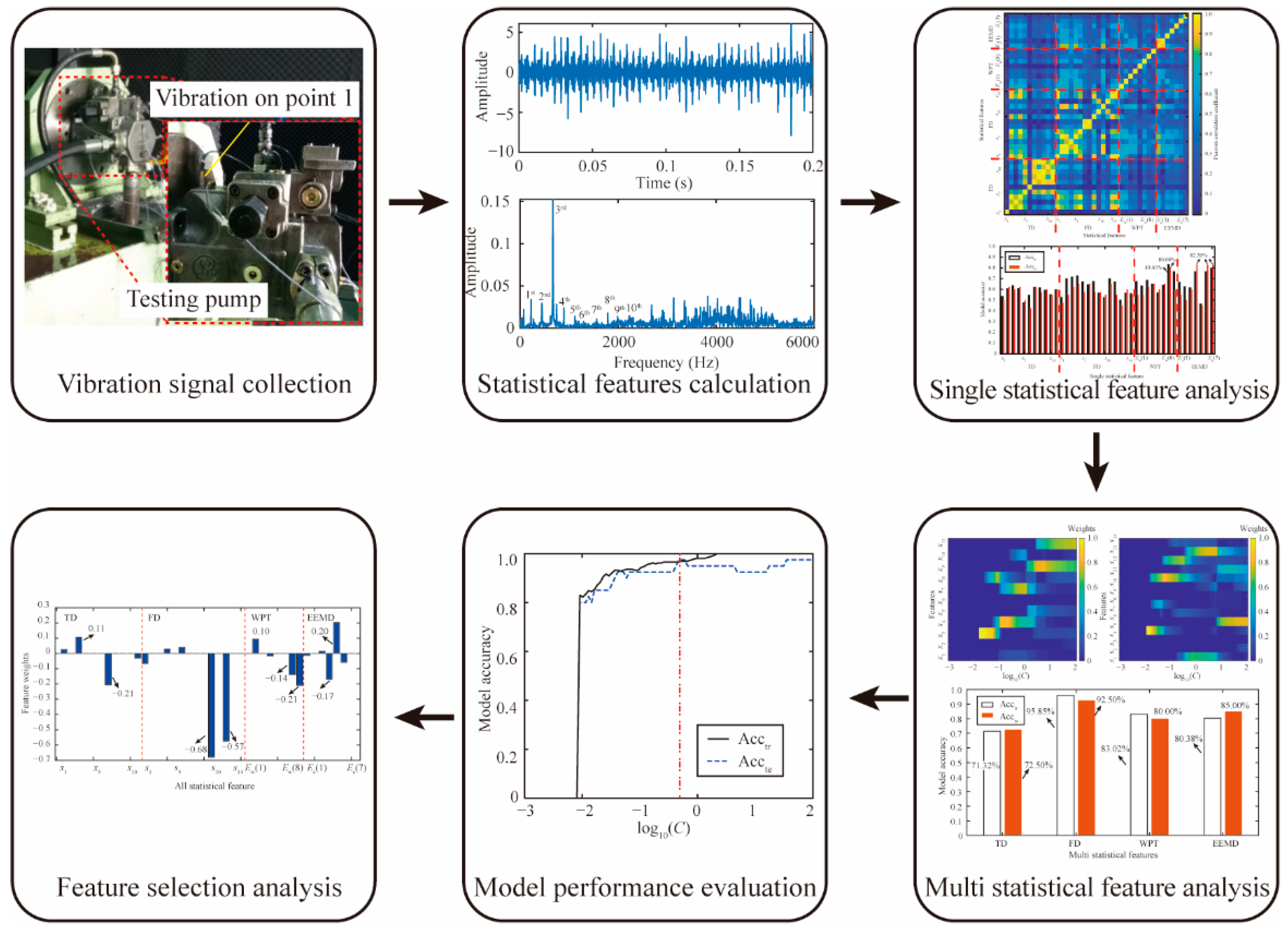
2.1. Experimental Setup and Procedure
2.2. Improved SPARE-SVM Based Methodology
3. Results and Discussion
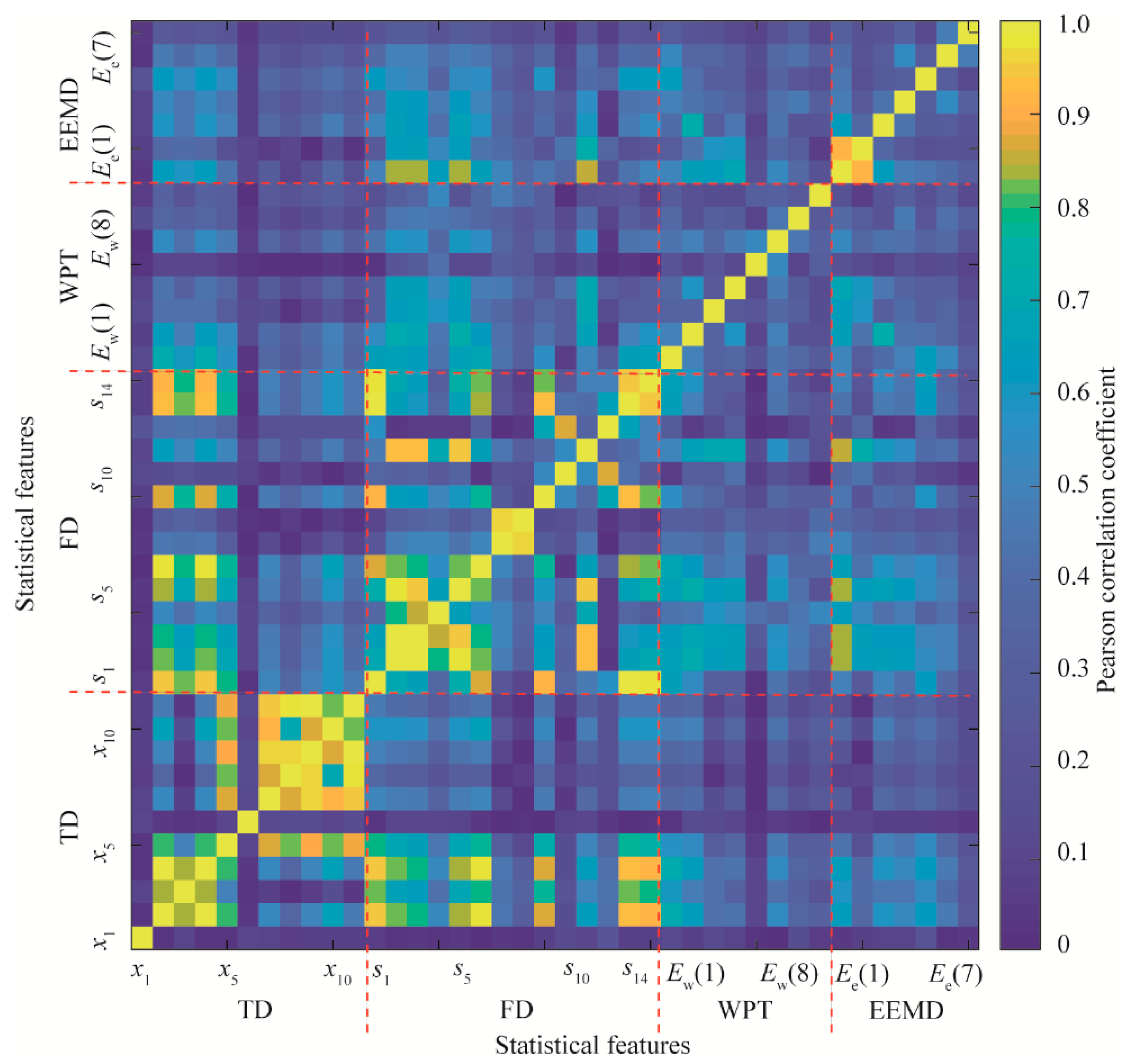
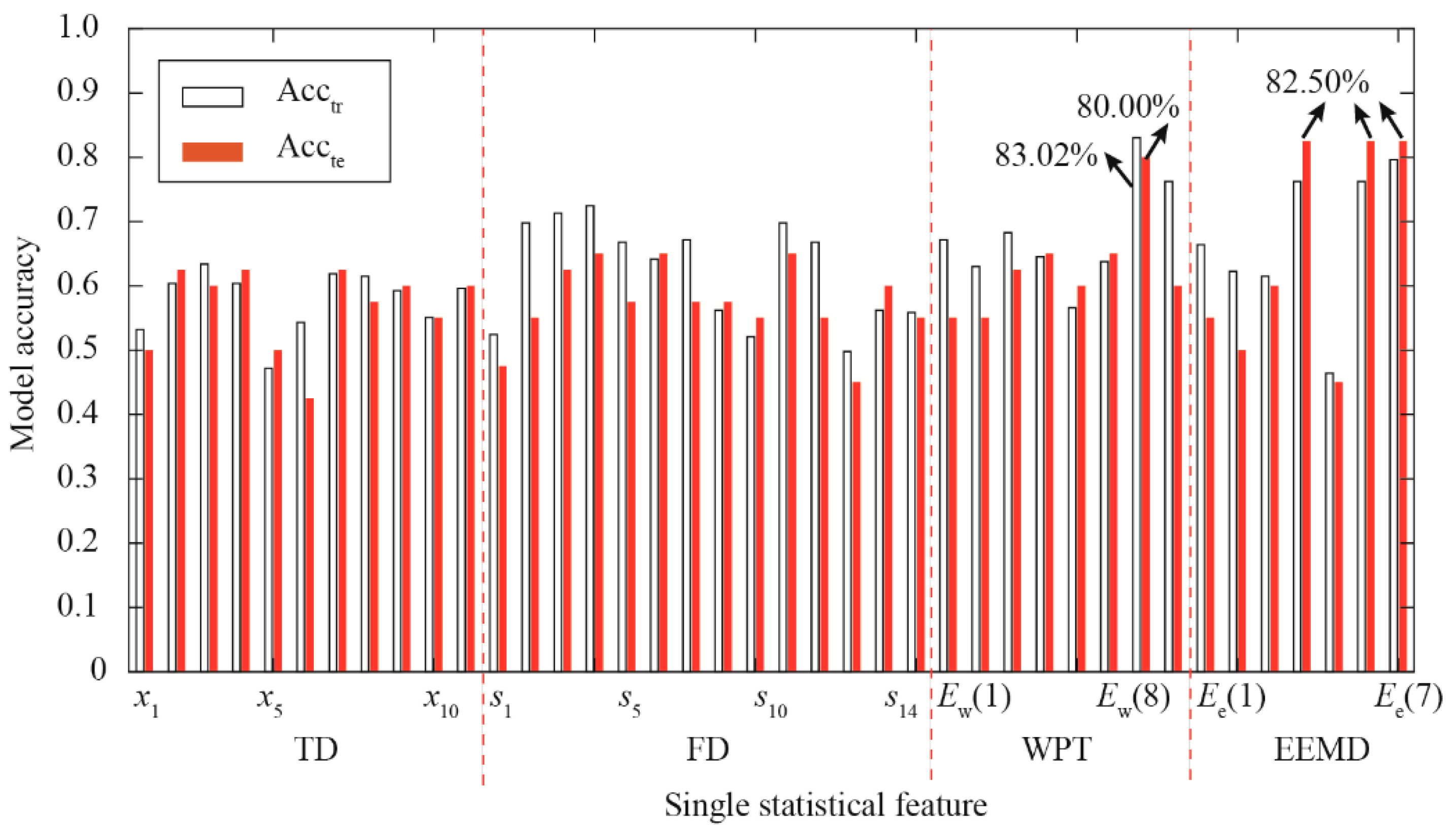
3.1. Single Statistical Feature Analysis
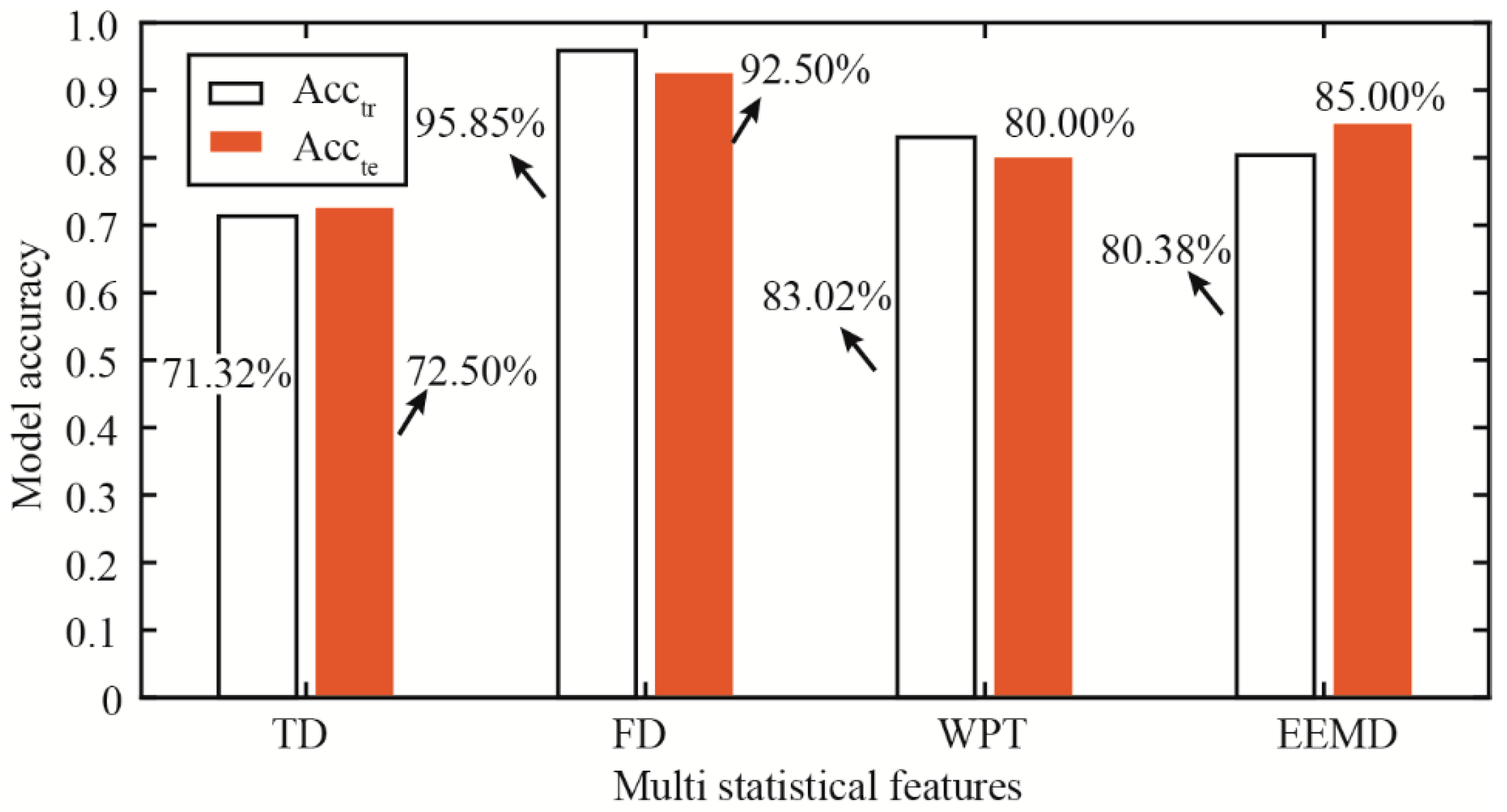
3.2. Multiple Statistical Feature Analysis
3.3. Model Performance Evaluation
3.4. Feature Selection Analysis
4. Conclusions
- The proposed methodology can integrate feature selection during the machine learning process of piston wear detection.
- A large set of features is constructed in the TD, FD, and TFD. Single and multiple feature analysis are utilized to illustrate the relevance and impact of sparsity in the comprehensive set of features.
- Feature effects on the model accuracy are analyzed. The maximum model testing and training accuracy values are 97.50% and 96.60%, respectively.
- Spare features s10, s12, Ew(8), x7, Ee(5), and Ee(4) are selected and validated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault diagnosis of hydraulic piston pump based on deep learning and Bayesian optimization. ISA Trans. 2022, 129 Pt A, 555–563. [Google Scholar] [CrossRef]
- Zhang, C.C.; Zhu, C.H.; Meng, B.; Li, S. Challenges and Solutions for High-Speed Aviation Piston Pumps: A Review. Aerospace 2021, 8, 392–398. [Google Scholar] [CrossRef]
- Xiao, C.; Tang, H.; Ren, Y.; Xiang, J.; Kumar, A. Adaptive MOMEDA based on improved advance-retreat algorithm for fault features extraction of axial piston pump. ISA Trans. 2022, 128 Pt B, 503–520. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, X.; Li, H.; Liu, Y.; Zhang, B.; Dong, Q. A New Approach for Modeling Mixed Lubricated Piston-Cylinder Pairs of Variable Lengths in Swash-Plate Axial Piston Pumps. Materials 2021, 14, 5836–5841. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.Q.; Xia, Y.M.; Xiang, J.W. Modelling and Fault Detection for Specific Cavitation Damage Based on the Discharge Pressure of Axial Piston Pumps. Mathematics 2022, 10, 2461–2469. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.H.; Xu, B.; Wang, Q.N.; Lyu, F.; Li, K. Integrated slipper retainer mechanism to eliminate slipper wear in high-speed axial piston pumps. Front. Mech. Eng. 2022, 17, 1. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Luo, H.; Zhang, J. An Empirical Model for the Churning Losses Prediction of Fluid Flow Analysis in Axial Piston Pumps. Micromachines 2021, 12, 398–402. [Google Scholar] [CrossRef] [PubMed]
- Chao, Q.; Xu, Z.; Tao, J.; Liu, C. Capped piston: A promising design to reduce compressibility effects, pressure ripple and cavitation for high-speed and high-pressure axial piston pumps. Alex. Eng. J. 2023, 62, 509–521. [Google Scholar] [CrossRef]
- Qi, B.; Yong, Z. Tribological study of piston–cylinder interface of radial piston pump in high-pressure common rail system considering surface topography effect. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 234, 1381–1395. [Google Scholar] [CrossRef]
- Huayong, Y.; Jian, Y.; Hua, Z. Research on materials of piston and cylinder of water hydraulic pump. Ind. Lubr. Tribol. 2003, 55, 38–43. [Google Scholar] [CrossRef]
- Zhang, J.; Qiu, X.; Gong, X.; Kong, X. Wear behavior of friction pairs of different materials for ultra-high-pressure axial piston pump. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2018, 233, 945–953. [Google Scholar] [CrossRef]
- D’Andrea, D.; Epasto, G.; Bonanno, A.; Guglielmino, E.; Benazzi, G. Failure analysis of anti-friction coating for cylinder blocks in axial piston pumps. Eng. Fail. Anal. 2019, 104, 126–138. [Google Scholar] [CrossRef]
- Gao, Q.; Xiang, J.W.; Hou, S.M.; Tang, H.S.; Zhong, Y.T.; Ye, S.G. Method using L-kurtosis and enhanced clustering-based segmentation to detect faults in axial piston pumps. Mech. Syst. Signal Process. 2021, 147, 107130. [Google Scholar] [CrossRef]
- Chaoang, X.; Hesheng, T.; Yan, R. Compressed sensing reconstruction for axial piston pump bearing vibration signals based on adaptive sparse dictionary model. Meas. Control 2020, 53, 649–661. [Google Scholar] [CrossRef]
- Maradey Lázaro, J.G.; Borrás Pinilla, C. A methodology for detection of wear in hydraulic axial piston pumps. Int. J. Interact. Des. Manuf. 2020, 14, 1103–1119. [Google Scholar] [CrossRef]
- Dong, M.; He, D. A segmental hidden semi-Markov model (HSMM)-based diagnostics and prognostics framework and methodology. Mech. Syst. Signal Process. 2007, 21, 2248–2266. [Google Scholar] [CrossRef]
- Wang, S.H.; Xiang, J.W.; Zhong, Y.T.; Tang, H.S. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Signal Process. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- Hou, X.; Guo, W.; Ren, S.; Li, Y.; Si, Y.; Su, L. Bolt-Loosening Detection Using 1D and 2D Input Data Based on Two-Stream Convolutional Neural Networks. Materials 2022, 15, 6757–6762. [Google Scholar] [CrossRef]
- Li, H.; Tian, S.; Yang, Z. A Novel Blade Vibration Monitoring Experimental System Based on Blade Tip Sensing. Materials 2022, 15, 6987–6995. [Google Scholar] [CrossRef] [PubMed]
- Said, Z.; Sharma, P.; Elavarasan, R.M.; Tiwari, A.K.; Rathod, M.K. Exploring the specific heat capacity of water-based hybrid nanofluids for solar energy applications: A comparative evaluation of modern ensemble machine learning techniques. J. Energy Storage 2022, 54, 105230. [Google Scholar] [CrossRef]
- Kim, D.; Heo, T.Y. Anomaly Detection with Feature Extraction Based on Machine Learning Using Hydraulic System IoT Sensor Data. Sensors 2022, 22, 2479. [Google Scholar] [CrossRef] [PubMed]
- Said, Z.; Sharma, P.; Aslfattahi, N.; Ghodbane, M. Experimental analysis of novel ionic liquid-MXene hybrid nanofluid’s energy storage properties: Model-prediction using modern ensemble machine learning methods. J. Energy Storage 2022, 52, 104858. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y.; Li, G. An Integrated Deep Learning Method towards Fault Diagnosis of Hydraulic Axial Piston Pump. Sensors 2020, 20, 6576. [Google Scholar] [CrossRef] [PubMed]
- Cui, M.L.; Wang, Y.Q.; Lin, X.S.; Zhong, M.Y. Fault Diagnosis of Rolling Bearings Based on an Improved Stack Autoencoder and Support Vector Machine. IEEE Sens. J. 2021, 21, 4927–4937. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Chen, G.; Ding, J. Modified multiscale weighted permutation entropy and optimized support vector machine method for rolling bearing fault diagnosis with complex signals. ISA Trans. 2021, 114, 470–484. [Google Scholar] [CrossRef]
- Kecik, K.; Smagala, A.; Lyubitska, K. Ball Bearing Fault Diagnosis Using Recurrence Analysis. Materials 2022, 15, 5940–5952. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Wang, W. Fault Diagnosis of Permanent Magnet DC Motors Based on Multi-Segment Feature Extraction. Sensors 2021, 21, 7505. [Google Scholar] [CrossRef]
- Dhiman, H.; Deb, D.; Muyeen, S.M.; Kamwa, I. Wind Turbine Gearbox Anomaly Detection Based on Adaptive Threshold and Twin Support Vector Machines. IEEE Trans. Energy Convers. 2021, 36, 3462–3469. [Google Scholar] [CrossRef]
- Gelman, L.; Solinski, K.; Ball, A. Novel Instantaneous Wavelet Bicoherence for Vibration Fault Detection in Gear Systems. Energies 2021, 14, 6811–6820. [Google Scholar] [CrossRef]
- Ranawat, N.S.; Kankar, P.K.; Miglani, A. Fault Diagnosis in Centrifugal Pump using Support Vector Machine and Artificial Neural Network. J. Eng. Res. 2021, 9, 99–111. [Google Scholar] [CrossRef]
- Kshirsagar, P.R.; Joshi, K.A.; Hendre, V.S.; Paliwal, K.K.; Akojwar, S.G.; Atauurahman, S. Mental task classification using wavelet transform and support vector machine. Int. J. Biomed. Eng. Technol. 2021, 37, 368–381. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, Z.P. A new hybrid model of sparsity empirical wavelet transform and adaptive dynamic least squares support vector machine for fault diagnosis of gear pump. Adv. Mech. Eng. 2020, 12, 168781402092204. [Google Scholar] [CrossRef]
- Chen, S.L.; Gao, Z.H.; Zhu, X.Q.; Du, Y.M.; Pang, C. Unstable unsteady aerodynamic modeling based on least squares support vector machines with general excitation. Chin. J. Aeronaut. 2020, 33, 2499–2509. [Google Scholar] [CrossRef]
- Wang, Y.J.; Kang, S.Q.; Jiang, Y.C.; Yang, G.X.; Song, L.X.; Mikulovich, V.I. Classification of fault location and the degree of performance degradation of a rolling bearing based on an improved hyper-sphere-structured multi-class support vector machine. Mech. Syst. Signal Process. 2012, 29, 404–414. [Google Scholar] [CrossRef]
- Li, G.; Yang, L.; Wu, Z.; Wu, C. D.C. Programming for sparse proximal support vector machines. Inf. Sci. 2021, 547, 187–201. [Google Scholar] [CrossRef]
- Ye, Z.; Yu, J.B. Multi-level features fusion network-based feature learning for machinery fault diagnosis. Appl. Soft Comput. 2022, 122, 108900. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, S.Q.; Hu, M.F.; Zhang, L.G.; Liu, H.T. Intelligent fault diagnosis of wind turbine gearboxes based on refined generalized multi-scale state joint entropy and robust spectral feature selection. Nonlinear Dyn. 2022, 107, 2485–2517. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Li, S.M.; Lu, J.T.; Xin, Y.; Ma, H.J. Intrinsic component filtering for fault diagnosis of rotating machinery. Chin. J. Aeronaut. 2021, 34, 397–409. [Google Scholar] [CrossRef]
- Spilka, J.; Frecon, J.; Leonarduzzi, R.; Pustelnik, N.; Abry, P.; Doret, M. Sparse Support Vector Machine for Intrapartum Fetal Heart Rate Classification. IEEE J. Biomed. Health Inform. 2017, 21, 664–671. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Yang, Z.; Tian, S.; Li, H.; Jin, R.; Yan, R.; Chen, X. Biprobes Blade Tip Timing Method for Frequency Identification Based on Active Aliasing Time-Delay Estimation and Dealiasing. IEEE Trans. Ind. Electron. 2022, 70, 1939–1948. [Google Scholar] [CrossRef]
- Tang, H.B.; Fu, Z.; Huang, Y. A fault diagnosis method for loose slipper failure of piston pump in construction machinery under changing load. Appl. Acoust. 2021, 172, 107634. [Google Scholar] [CrossRef]
- Zheng, Z.; Xin, G. Fault Feature Extraction of Hydraulic Pumps Based on Symplectic Geometry Mode Decomposition and Power Spectral Entropy. Entropy 2019, 21, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.L.; Zheng, Z.; Zhu, Y.; Li, Y. Demodulation for hydraulic pump fault signals based on local mean decomposition and improved adaptive multiscale morphology analysis. Mech. Syst. Signal Process. 2015, 58–59, 179–205. [Google Scholar] [CrossRef]
- Gao, Z.; Lin, J.; Wang, X.; Xu, X. Bearing Fault Detection Based on Empirical Wavelet Transform and Correlated Kurtosis by Acoustic Emission. Materials 2017, 10, 571–579. [Google Scholar] [CrossRef] [PubMed]
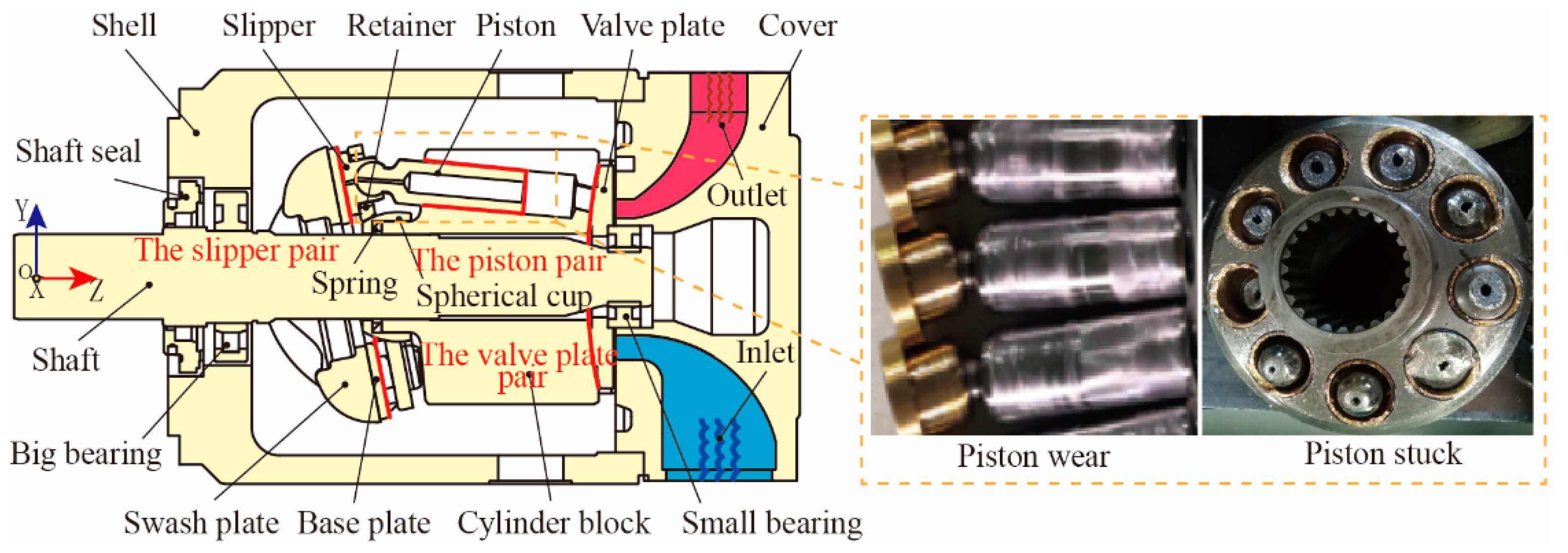









| No. | Parameters | Values |
|---|---|---|
| 1 | Rated speed | 1500 r/min |
| 2 | Maximum value of the displacement | 40 cm3/r |
| 3 | Maximum value of the discharge pressure | 35 MPa |
| 4 | Piston diameter | 17 mm |
| 5 | Piston number | 9 |
| No. | Description | Expression | No. | Description | Expression |
|---|---|---|---|---|---|
| 1 | Mean value | 2 | Standard deviation | ||
| 3 | Root amplitude | 4 | Root mean square | ||
| 5 | Peak value | 6 | Skewness value | ||
| 7 | Kurtosis value | 8 | Crest factor | ||
| 9 | Clearance factor | 10 | Shape factor | ||
| 11 | Impulse factor |
| No. | Description | Expression | No. | Description | Expression |
|---|---|---|---|---|---|
| 1 | Mean frequency | 2 | Frequency center | ||
| 3 | Root 2 order weighting | 4 | Root 4-2 order weighting | ||
| 5 | 2-4 order weighting | 6 | 2 order center moment | ||
| 7 | 3 order center moment | 8 | 4 order center moment | ||
| 9 | Root 2 order center moment | 10 | Root 2 order center moment convergence index | ||
| 11 | 3 order convergence index | 12 | 4 order convergence index | ||
| 13 | 1/2 order convergence index | 14 | Root 2 order convergence index |
| No. | Description | Expression |
|---|---|---|
| 1 | Frequency band energy ratio | |
| 2 | IMF energy ratio |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, S.; Xia, Y.; Xiang, J. Piston Wear Detection and Feature Selection Based on Vibration Signals Using the Improved Spare Support Vector Machine for Axial Piston Pumps. Materials 2022, 15, 8504. https://doi.org/10.3390/ma15238504
Xia S, Xia Y, Xiang J. Piston Wear Detection and Feature Selection Based on Vibration Signals Using the Improved Spare Support Vector Machine for Axial Piston Pumps. Materials. 2022; 15(23):8504. https://doi.org/10.3390/ma15238504
Chicago/Turabian StyleXia, Shiqi, Yimin Xia, and Jiawei Xiang. 2022. "Piston Wear Detection and Feature Selection Based on Vibration Signals Using the Improved Spare Support Vector Machine for Axial Piston Pumps" Materials 15, no. 23: 8504. https://doi.org/10.3390/ma15238504
APA StyleXia, S., Xia, Y., & Xiang, J. (2022). Piston Wear Detection and Feature Selection Based on Vibration Signals Using the Improved Spare Support Vector Machine for Axial Piston Pumps. Materials, 15(23), 8504. https://doi.org/10.3390/ma15238504







