Geotechnical and Shear Behavior of Novel Lunar Regolith Simulants TUBS-M, TUBS-T, and TUBS-I
Abstract
:1. Introduction
1.1. Space Exploration and In Situ Resource Utilization
1.2. The Lunar Surface
1.3. Regolith Processing Technologies
1.4. Lunar Regolith Simulants and Their Requirements
1.5. Adaptable Lunar Regolith Simulants TUBS-M, TUBS-T, and TUBS-I
- Base simulants: They consist entirely of lithic particles and are suitable for general applications, simple processing experiments, and geotechnical investigations.
- Chemically adapted simulants (CAS): Compared to base simulants, CAS additionally contain different proportions of minerals found in lunar rocks like ilmenite or olivine. This type is particularly suitable for the extraction of chemical components within the scope of in situ resource utilization (ISRU) research or for the production of thermally altered particles such as agglutinates and glasses.
- Physically adapted simulants (PAS): They contain agglutinates and glass particles, which were produced from CAS by thermal adaptation processes. This type can be used for advanced and highly specific applications.
1.6. Mission Risks and Relevance of Data Acquisition
2. Materials and Methods
2.1. Processing of the Raw Material
2.2. Particle Size Distribution Measurement
2.3. Measurement of Particle Morphology and Surface Structure
2.4. Bulk and Flow Properties
3. Influence of Measurement System on Particle Size Distribution
3.1. Methodological Background of Relevant Measurement Procedures
3.2. Particle Size Measurement of TUBS-M
4. Properties of Lunar Regolith Simulants
4.1. Chemistry and Morphology of Lunar Regolith and Simulants
4.2. Particle Size Fractions in the Broadly Distributed Lunar Regolith
4.3. Bulk Density and Consolidation
4.4. Shear Tests and Flowability
- the lower their aspect ratio is,
- the smaller the porosity in the bulk material is and
- the greater the friction coefficient between the particles.
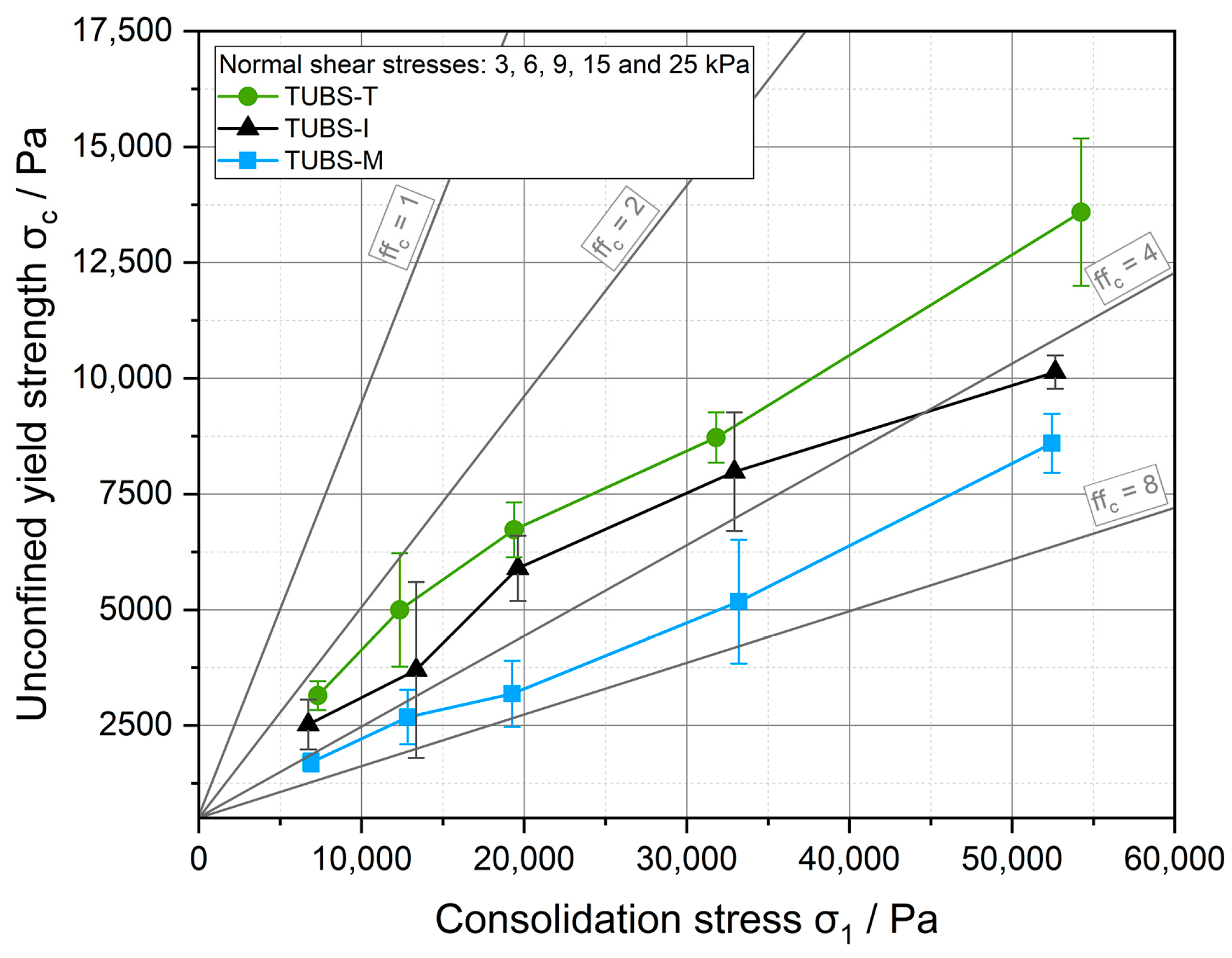
4.5. Cohesion
4.6. Geotechnical Behavior of TUBS-M, TUBS-T, and TUBS-I
4.7. Comparison of the Data with Real Lunar Regolith
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| TUBS-M | TUBS-T | |||||
|---|---|---|---|---|---|---|
| Grain Size Fraction µm | Bulk Density g cm−3 | Tapped Density g cm−3 | Hausner Ratio - | Bulk Density g cm−3 | Tapped Density g cm−3 | Hausner Ratio- |
| 1000–2000 | 1.27 | 1.49 | 1.17 | 1.25 | 1.34 | 1.08 |
| 500–1000 | 1.25 | 1.42 | 1.13 | 1.20 | 1.32 | 1.11 |
| 250–500 | 1.25 | 1.35 | 1.09 | 1.24 | 1.31 | 1.05 |
| 160–250 | 1.29 | 1.36 | 1.06 | 1.27 | 1.30 | 1.03 |
| 90–160 | 1.33 | 1.42 | 1.07 | 1.28 | 1.30 | 1.01 |
| 45–90 | 1.35 | 1.45 | 1.08 | 1.25 | 1.28 | 1.02 |
| 25–45 | 1.32 | 1.47 | 1.11 | 1.20 | 1.32 | 1.10 |
| <25 | 1.20 | 1.32 | 1.10 | 1.10 | 1.15 | 1.04 |
| Cohesion/Pa | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TUBS-M | TUBS-T | |||||||||
| Grain Size Fraction µm | 3 kPa | 6 kPa | 9 kPa | 15 kPa | 25 kPa | 3 kPa | 6 kPa | 9 kPa | 15 kPa | 25 kPa |
| 1000–2000 | 43.00 | 93.00 | 98.33 | 488.33 | 507.33 | 52.33 | 135.67 | 131.67 | 845.67 | 997.00 |
| 500–1000 | 37.00 | 124.67 | 82.00 | 125.00 | 218.67 | 46.33 | 104.00 | 98.00 | 133.67 | 295.33 |
| 250–500 | 63.00 | 31.00 | 52.67 | 66.33 | 70.33 | 33.33 | 37.00 | 36.67 | 24.33 | 89.67 |
| 160–250 | 19.67 | 29.00 | 49.33 | 79.33 | 50.33 | 38.67 | 34.67 | 19.00 | 54.33 | 79.00 |
| 90–160 | 39.33 | 16.00 | 84.00 | 77.33 | 78.67 | 35.33 | 40.67 | 44.00 | 103.00 | 91.33 |
| 45–90 | 39.67 | 40.67 | 56.00 | 69.00 | 56.00 | 66.00 | 97.00 | 91.00 | 145.67 | 246.67 |
| 25–45 | 64.00 | 94.00 | 126.33 | 196.67 | 266.33 | 94.67 | 142.00 | 198.67 | 341.67 | 539.00 |
| <25 | 232.67 | 318.00 | 412.33 | 568.33 | 877.00 | 195.33 | 332.00 | 438.67 | 569.33 | 848.67 |
| Cohesion/Pa | |||||
|---|---|---|---|---|---|
| Regolith Simulant | 3 kPa | 6 kPa | 9 kPa | 15 kPa | 25 kPa |
| TUBS-M | 349.67 | 604.67 | 668.67 | 1023.67 | 1902.67 |
| TUBS-I | 584.33 | 717.00 | 1300.00 | 1749.33 | 2240.67 |
| TUBS-T | 642.67 | 1077.67 | 1360.67 | 1714.33 | 2793.67 |
| Bulk Densities/g cm−3 | |||||
|---|---|---|---|---|---|
| Regolith Simulant | 3 kPa | 6 kPa | 9 kPa | 15 kPa | 25 kPa |
| TUBS-M | 1.41 | 1.55 | 1.55 | 1.61 | 1.62 |
| TUBS-I | 1.43 | 1.49 | 1.51 | 1.56 | 1.58 |
| TUBS-T | 1.33 | 1.38 | 1.42 | 1.46 | 1.50 |
References
- Linke, S.; Windisch, L.; Kueter, N.; Voss, A.; Prziwara, P.; Stoll, E.; Schilde, C.; Kwade, A. TUBS-M and TUBS-T—New Lunar Regolith Simulant adaptable to local Lunar surface characteristics. In Proceedings of the 69th International Astronautical Congress (IAC), Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Linke, S.; Windisch, L.; Kueter, N.; Wanvik, J.E.; Voss, A.; Stoll, E.; Schilde, C.; Kwade, A. TUBS-M and TUBS-T based modular Regolith Simulant System for the support of lunar ISRU activities. Planet. Space Sci. 2019, 180, 104747. [Google Scholar] [CrossRef]
- Indyk, S.J.; Benaroya, H. A structural assessment of unrefined sintered lunar regolith simulant. Acta Astronaut. 2017, 140, 517–536. [Google Scholar] [CrossRef]
- Meurisse, A.; Makaya, A.; Willsch, C.; Sperl, M. Solar 3D printing of lunar regolith. Acta Astronaut. 2018, 152, 800–810. [Google Scholar] [CrossRef]
- Taylor, L.A.; Meek, T.T. Microwave Sintering of Lunar Soil: Properties, Theory, and Practice. J. Aerosp. Eng. 2005, 18, 188–196. [Google Scholar] [CrossRef] [Green Version]
- Benaroya, H.; Indyk, S.; Mottaghi, S. Advanced Systems Concept for Autonomous Construction and Self-repair of Lunar Surface ISRU Structures. In Moon: Prospective Energy and Material Resources; Badescu, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 641–660. ISBN 978-3-642-27968-3. [Google Scholar]
- Benaroya, H.; Bernold, L. Engineering of lunar bases. Acta Astronaut. 2008, 62, 277–299. [Google Scholar] [CrossRef]
- Gerdes, N.; Fokken, L.G.; Linke, S.; Kaierle, S.; Suttmann, O.; Hermsdorf, J.; Stoll, E.; Trentlage, C. Selective Laser Melting for processing of regolith in support of a lunar base. J. Laser Appl. 2018, 30, 32018. [Google Scholar] [CrossRef]
- Cesaretti, G.; Dini, E.; de Kestelier, X.; Colla, V.; Pambaguian, L. Building components for an outpost on the Lunar soil by means of a novel 3D printing technology. Acta Astronaut. 2014, 93, 430–450. [Google Scholar] [CrossRef]
- Fateri, M.; Gebhardt, A. Process Parameters Development of Selective Laser Melting of Lunar Regolith for On-Site Manufacturing Applications. Int. J. Appl. Ceram. Technol. 2015, 12, 46–52. [Google Scholar] [CrossRef]
- Sanders, G.B. Overview of Past Lunar In Situ Resource Utilization (ISRU) Development by NASA. In Presentation to European Space Agency (ESA) Workshop: Towards the Use of Lunar Resources, Noordwijk, The Netherlands, 3 July 2018; NASA: Greenbel, MD, USA, 2018. [Google Scholar]
- Stenzel, C.; Weiss, L.; Rohr, T. Sustainable challenges on the moon. Curr. Opin. Green Sustain. Chem. 2018, 9, 8–12. [Google Scholar] [CrossRef]
- Taylor, L.A.; Carrier, W.D. Oxygen production on the moon: An overview and evaluation. In Resources of Near-Earth Space; The University of Arizona Press: Tucson, AZ, USA, 1993; p. 69. [Google Scholar]
- Schwandt, C.; Hamilton, J.A.; Fray, D.J.; Crawford, I.A. The production of oxygen and metal from lunar regolith. Planet. Space Sci. 2012, 74, 49–56. [Google Scholar] [CrossRef]
- Curreri, P.A.; Ethridge, E.C.; Hudson, S.B. Process Demonstration For Lunar In Situ Resource Utilization—Molten Oxide Electrolysis; NASA/TM-2006-214600; NASA: Greenbel, MD, USA, 2006.
- Caruso, J.; Spina, D.; Greer, L.; John, W.; Michele, C. Excavation on the Moon: Regolith Collection for Oxygen Production and Outpost Site Preparation. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. ISBN 978-1-62410-128-1. [Google Scholar]
- Lomax, B.A.; Conti, M.; Khan, N.; Bennett, N.S.; Ganin, A.Y.; Symes, M.D. Proving the viability of an electrochemical process for the simultaneous extraction of oxygen and production of metal alloys from lunar regolith. Planet. Space Sci. 2020, 180, 104748. [Google Scholar] [CrossRef]
- Troisi, I.; Lunghi, P.; Lavagna, M. Oxygen extraction from lunar dry regolith: Thermodynamic numerical characterization of the carbothermal reduction. Acta Astronaut. 2022, 199, 113–124. [Google Scholar] [CrossRef]
- Schlüter, L.; Cowley, A.; Pennec, Y.; Roux, M. Gas purification for oxygen extraction from lunar regolith. Acta Astronaut. 2021, 179, 371–381. [Google Scholar] [CrossRef]
- Wamelink, G.W.W.; Frissel, J.Y.; Krijnen, W.H.J.; Verwoert, M.R.; Goedhart, P.W. Can Plants Grow on Mars and the Moon: A Growth Experiment on Mars and Moon Soil Simulants. PLoS ONE 2014, 9, e103138. [Google Scholar] [CrossRef] [Green Version]
- Sanders, G.B.; Paz, A.; Oryshchyn, L.; Araghi, K.; Muscatello, A.; Linne, D.L.; Kleinhenz, J.E.; Peters, T. Mars ISRU for Production of Mission Critical Consumables—Options, Recent Studies, and Current State of the Art. In Proceedings of the AIAA SPACE 2015 Conference and Exposition, Pasadena, CA, USA, 31 August–2 September 2015; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015. ISBN 978-1-62410-334-6. [Google Scholar]
- Nakamura, T.; Senior, C.L. Solar Thermal Power for Lunar Materials Processing. J. Aerosp. Eng. 2008, 21, 91–101. [Google Scholar] [CrossRef]
- Rodriguez, G.; Good, W. Silicon moon—The foundations of a cislunar economy. In Proceedings of the AIAA Space 2001 Conference and Exposition, Albuquerque, NM, USA, 28–30 August 2001; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; p. 08282001. [Google Scholar]
- Ellery, A. Generating and storing power on the moon using in situ resources. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 1045–1063. [Google Scholar] [CrossRef]
- Rapp, D. (Ed.) Lunar ISRU technology. In Use of Extraterrestrial Resources for Human Space Missions to Moon or Mars; Springer: Berlin/Heidelberg, Germany, 2013; pp. 91–111. ISBN 978-3-642-32761-2. [Google Scholar]
- Sanders, G. NASA Lunar ISRU Strategy. In Proceedings of the What Next for Space Resource Utilization? Workshop, Luxembourg, Germany, 10 October 2019. [Google Scholar]
- Eckart, P.; Aldrin, B. (Eds.) The Lunar Base Handbook: An Introduction to Lunar Base Design, Development, and Operations, 2nd ed.; McGraw-Hill: Boston, MA, USA, 2006; ISBN 9780073294445. [Google Scholar]
- Heiken, G.H. (Ed.) Lunar Sourcebook: A User’s Guide to the Moon; Univ. Press: Cambridge, UK, 1991; ISBN 0521334446. [Google Scholar]
- Gaier, J.R. The Need for High Fidelity Lunar Regolith Simulants; National Aeronautics and Space Administration NASA/TM-2008-215261; Glenn Research Center: Cleveland, OH, USA, 2008.
- Jolliff, B.L.; Wieczorek, M.A.; Shearer, C.K.; Neal, C.R. (Eds.) New Views of the Moon; Mineralogical Society of America: Chantilly, VA, USA, 2006; ISBN 0939950723. [Google Scholar]
- Sibille, L.; Carpenter, P.; Schlagheck, R.; French, R.A. Lunar Regolith Simulant Materials: Recommendations for Standardization, Production, and Usage; NASA/TP-2006-214605; NASA: Washington, DC, USA, 2006.
- Arslan, H.; Batiste, S.; Sture, S. Engineering Properties of Lunar Soil Simulant JSC-1A. J. Aerosp. Eng. 2010, 23, 70–83. [Google Scholar] [CrossRef]
- Cadenhead, D.; Wagner, N.J.; Jones, B.R.; Stetter, J.R. Some surface characteristics and gas interactions of Apollo 14 fines and rock fragments. Proc. Third Lunar Sci. Conf. 1972, 3, 2243–2257. [Google Scholar]
- Cadenhead, D.A.; Mikhail, R.S. Water vapor weathering of Taurus-Littrow orange soil—A pore-structure analysis. In Proceedings of the 6th Lunar and Planetary Science Conference Proceedings, Houston, TX, USA, 17–21 March 1975; pp. 3317–3331. [Google Scholar]
- Holmes, H.F.; Gammage, R.B. Interaction of gases with lunar materials—Revised results for Apollo 11. In Proceedings of the 6th Lunar and Planetary Science Conference Proceedings, Houston, TX, USA, 17–21 March 1975; pp. 3343–3350. [Google Scholar]
- Gammage, R.B.; Holmes, H.F. Blocking of the water-lunar fines reaction by air and water concentration effects. In Proceedings of the 6th Lunar and Planetary Science Conference Proceedings, Houston, TX, USA, 17–21 March 1975. [Google Scholar]
- Kuhns, M.; Metzger, P.; Hasnain, Z.; Zacny, K. Instant Landing Pads for Lunar Missions. In Earth and Space 2021, Space Exploration, Utilization, Engineering, and Construction in Extreme Environments, Proceedings of the 17th Biennial International Conference on Engineering, Science, Construction, and Operations in Challenging Environments, Virtual Conference, 19–23 April 2021; van Susante, P.J., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 1027–1032. ISBN 9780784483374. [Google Scholar]
- Mueller, R.P.; King, R.H.; El-Genk, M.S. Trade Study of Excavation Tools and Equipment for Lunar Outpost Development and ISRU. In AIP Conference Proceedings, Albuquerque, New Mexico, Mexico, 10–14 February 2008; AIP: Woodbury, NY, USA, 2008; pp. 237–244. [Google Scholar]
- Sanders, G.; Larson, W.; Sacksteder, K.; Mclemore, C. NASA In-Situ Resource Utilization (ISRU) Project: Development and Implementation. In Proceedings of the AIAA SPACE 2008 Conference & Exposition, San Diego, CA, USA, 9–11 September 2008; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. ISBN 978-1-62410-002-4. [Google Scholar]
- Voß, A.; Freund, R.; Linke, S.; Stoll, E. (Eds.) MIRA3D—A Terrestrial Robotic Prototype for Additive Layer Manufacturing of Lunar Regolith: IAC-18-A3.2B.11,x43642. In Proceedings of the 69th International Astronautical Congress, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Wilcox, B.H.; Litwin, T.; Biesiadecki, J.; Matthews, J.; Heverly, M.; Morrison, J.; Townsend, J.; Ahmad, N.; Sirota, A.; Cooper, B. Athlete: A cargo handling and manipulation robot for the moon. J. Field Robot. 2007, 24, 421–434. [Google Scholar] [CrossRef]
- Lim, S.; Prabhu, V.L.; Anand, M.; Taylor, L.A. Extra-terrestrial construction processes—Advancements, opportunities and challenges. Adv. Space Res. 2017, 60, 1413–1429. [Google Scholar] [CrossRef] [Green Version]
- Farries, K.W.; Visintin, P.; Smith, S.T.; van Eyk, P. Sintered or melted regolith for lunar construction: State-of-the-art review and future research directions. Constr. Build. Mater. 2021, 296, 123627. [Google Scholar] [CrossRef]
- Urbina, D.; Madakashira, H.; Salini, J.; Govindaraj, S.; Bjoerstad, R.; Gancet, J.; Sperl, M.; Meurisse, A.; Fateri, M.; Imhof, B.; et al. Robotic Prototypes for the Solar Sintering of Regolith on the Lunar Surface Developed within the Regolight Project. In Proceedings of the 68th International Astronautical Congress (IAC), Adelaide, Australia, 13 November 2017. [Google Scholar]
- Fateri, M.; Gebhardt, A.; Gabrielli, R.A.; Herdrich, G.; Fasoulas, S.; Großmann, A.; Schnauffer, P.; Middendorf, P. Additive Manufacturing of Lunar Regolith for Extra-terrestrial Industry Plant. In Proceedings of the International Symposium on Space Technology and Science (ICTS), Kobe, Japan, 4–10 July 2015. [Google Scholar]
- Voss, A.; Kuhr, L.; Freund, R.; Linke, S.; Stoll, E. Requirements for a mobile lunar prototype for additive layer manufacturing. In Proceedings of the i-Sairas 2018, Madrid, Spain, 4–6 June 2018. [Google Scholar]
- Beyer, L.A. Lunarcrete-A Novel Approach to Extraterrestrial Construction. In Proceedings of the Seventh Princeton/AIAA/SSI Conference, Princeton, NJ, USA, 8–11 May 1985; pp. 165–171. [Google Scholar]
- Lin, T.D.; Love, H.; Stark, D. Physical properties of concrete made with Apollo 16 lunar soil samples. In Proceedings of the Second Conference on Lunar Bases and Space Activities of the 21st Century, Houston, TX, USA, 5–7 April 1988; NASA: Greenbelt, MD, USA, 1992; pp. 483–487. [Google Scholar]
- Toutanji, H.; Fiske, M.R.; Bodiford, M.P. Development and Application of Lunar “Concrete” for Habitats. In Engineering, Construction, and Operations in Challenging Environments, Earth & Space 2006, Proceedings of the 10th Biennial International Conference on Engineering, Construction, and Operations in Challenging Environments and Second NASA/ARO/ASCE Workshop on Granular Materials in Lunar and Martian Exploration, League City/Houston, TX, USA, 5–8 March 2006; Malla, R.B., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 1–8. ISBN 9780784408308. [Google Scholar]
- Happel, J.A. Indigenous Materials for Lunar Construction. Appl. Mech. Rev. 1993, 46, 313–325. [Google Scholar] [CrossRef]
- Ruess, F.; Schaenzlin, J.; Benaroya, H. Structural Design of a Lunar Habitat. J. Aerosp. Eng. 2006, 19, 133–157. [Google Scholar] [CrossRef]
- Wang, K.-T.; Lemougna, P.N.; Tang, Q.; Li, W.; Cui, X.-M. Lunar regolith can allow the synthesis of cement materials with near-zero water consumption. Gondwana Res. 2017, 44, 1–6. [Google Scholar] [CrossRef]
- Collins, P.J.; Edmunson, J.; Fiske, M.; Radlińska, A. Materials characterization of various lunar regolith simulants for use in geopolymer lunar concrete. Adv. Space Res. 2022, 69, 3941–3951. [Google Scholar] [CrossRef]
- Altun, A.A.; Ertl, F.; Marechal, M.; Makaya, A.; Sgambati, A.; Schwentenwein, M. Additive manufacturing of lunar regolith structures. Open Ceram. 2021, 5, 100058. [Google Scholar] [CrossRef]
- Oh, K.; Chen, T.; Kou, R.; Yi, H.; Qiao, Y. Ultralow-binder-content thermoplastic composites based on lunar soil simulant. Adv. Space Res. 2020, 66, 2245–2250. [Google Scholar] [CrossRef]
- Baasch, J.; Windisch, L.; Koch, F.; Linke, S.; Stoll, E.; Schilde, C. Regolith as substitute mold material for aluminum casting on the Moon. Acta Astronaut. 2021, 182, 1–12. [Google Scholar] [CrossRef]
- Wilkinson, A.; DeGennaro, A. Digging and pushing lunar regolith: Classical soil mechanics and the forces needed for excavation and traction. J. Terramech. 2007, 44, 133–152. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Xu, K.; Ding, X.; Wei, H.; Chao, C.; Wang, B.; Wang, B. Robotic drilling tests in simulated lunar regolith environment. J. Field Robot. 2021, 38, 1011–1035. [Google Scholar] [CrossRef]
- Simulant Working Group. Status of Lunar Regolith Simulants and Demand for Apollo Lunar Samples; Report from the Simulant Working Group of the Lunar Exploration Analysis Group and Curation and Analysis Planning Team for Extraterrestrial Materials to the Planetary Science Subcommittee of the NASA Advisory Council, December; NASA Langley Research Center: Hampton, VA, USA, 2010.
- Schrader, C.; Rickman, D.; Mclemore, C.; Fikes, J.; Wilson, S.; Stoeser, D.; Butcher, A.; Botha, P. Extant and Extinct Lunar Regolith Simulants: Modal Analyses of NU-LHT-1M and -2m, OB-1, JSC-1, JSC-1A and -1AF, FJS-1, and MLS-1. In Proceedings of the Planetary and Terrestrial Mining Symposium (PTMSS)/Northern Centre for Advanced Technology, Inc. (NORCAT), Montreal, QC, Canada, 12–15 June 2008. [Google Scholar]
- Manick, K.; Gill, S.-J.; Najorka, J.; Smith, C.L.; Duvet, L. Fundamental properties characterization of lunar regolith simulants at the european space agency (ESA) sample analogue curation facility. In Proceedings of the 49th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–23 March 2018. [Google Scholar]
- Taylor, L.A.; Pieters, C.M.; Britt, D. Evaluations of lunar regolith simulants. Planet. Space Sci. 2016, 126, 1–7. [Google Scholar] [CrossRef]
- Just, G.H.; Joy, K.H.; Roy, M.J.; Smith, K.L. Geotechnical characterisation of two new low-fidelity lunar regolith analogues (UoM-B and UoM-W) for use in large-scale engineering experiments. Acta Astronaut. 2020, 173, 414–424. [Google Scholar] [CrossRef]
- Engelschiøn, V.S.; Eriksson, S.R.; Cowley, A.; Fateri, M.; Meurisse, A.; Kueppers, U.; Sperl, M. EAC-1A: A novel large-volume lunar regolith simulant. Sci. Rep. 2020, 10, 5473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Isachenkov, M.; Chugunov, S.; Landsman, Z.; Akhatov, I.; Metke, A.; Tikhonov, A.; Shishkovsky, I. Characterization of novel lunar highland and mare simulants for ISRU research applications. Icarus 2022, 376, 114873. [Google Scholar] [CrossRef]
- Patel, Z.S.; Brunstetter, T.J.; Tarver, W.J.; Whitmire, A.M.; Zwart, S.R.; Smith, S.M.; Huff, J.L. Red risks for a journey to the red planet: The highest priority human health risks for a mission to Mars. NPJ Microgravity 2020, 6, 33. [Google Scholar] [CrossRef]
- Kuwata, Y.; Balaram, B. Combined EDL-Mobility Planning for Planetary Missions. In Infotech@Aerospace 2011, St. Louis, MO, USA, 29–31 March 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011; ISBN 978-1-60086-944-0. [Google Scholar]
- Salotti, J.-M.; Doche, J. Preliminary study of rescue systems for Mars landing. Acta Astronaut. 2021, 188, 81–88. [Google Scholar] [CrossRef]
- Dahlstrom, E.; Pozza, M.A. New Risks of Future Lunar Landings. In Risk Management in Outer Space Activities: An Australian and New Zealand Perspective; Pozza, M.A., Dennerley, J.A., Eds.; Springer: Singapore, 2022; pp. 221–239. ISBN 978-981-16-4755-0. [Google Scholar]
- Bourke, R.D. Surface knowledge and risks to landing and roving: The scale problem. In The Environmental Model of Mars: Proceedings of the 2nd COSPAR Colloquium, Sopron, Hungary, 22–26 January 1990; Szego, K., Ed.; Elsevier Science: Burlington, MA, USA, 1991; pp. 147–153. ISBN 9780080407876. [Google Scholar]
- Menon, M.S.; Kothandhapani, A.; Sundaram, N.S.; Raghavan, V.; Nagaraj, S. Terrain-based Analysis as a Design and Planning Tool for Operations of a Lunar Exploration Rover for the TeamIndus Lunar Mission. In Proceedings of the 15th International Conference on Space Operations (SpaceOps 2018), Marseille, France, 28 May–1 June 2018; Curran Associates Inc.: Red Hook, NY, USA, 2018. ISBN 978-1-62410-562-3. [Google Scholar]
- Ono, M.; Fuchs, T.J.; Steffy, A.; Maimone, M.; Yen, J. Risk-aware planetary rover operation: Autonomous terrain classification and path planning. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–10, ISBN 978-1-4799-5379-0. [Google Scholar]
- Spiessbach, A.; Clark, B.; Larimer, S.; Tobey, B.; Lindauer, B.; Koenig, R.; Lisec, T. Issues And Options For A Mars Rover. In Mobile Robots II, Robotics and IECON ‘87 Conferences, Cambridge, CA, Monday, 2 November 1987; Chun, W.H., Wolfe, W.J., Eds.; SPIE: Bellingham, WA, USA, 1987; p. 164. [Google Scholar]
- Anand, M.; Crawford, I.A.; Balat-Pichelin, M.; Abanades, S.; van Westrenen, W.; Péraudeau, G.; Jaumann, R.; Seboldt, W. A brief review of chemical and mineralogical resources on the Moon and likely initial in situ resource utilization (ISRU) applications. Planet. Space Sci. 2012, 74, 42–48. [Google Scholar] [CrossRef]
- Coloma, S.; Martinez, C.; Yalcn, B.C.; Olivares-Mendez, M.A. Enhancing Rover Teleoperation on the Moon With Proprioceptive Sensors and Machine Learning Techniques. IEEE Robot. Autom. Lett. 2022, 7, 11434–11441. [Google Scholar] [CrossRef]
- Carrier, W.D. Lunar soil grain size distribution. Moon 1973, 6, 250–263. [Google Scholar] [CrossRef]
- Monkul, M.M.; Dacic, A. Effect of grain size distribution on stress-strain behavior of lunar soil simulants. Adv. Space Res. 2017, 60, 636–651. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Yue, Z. NAO-1: Lunar Highland Soil Simulant Developed in China. J. Aerosp. Eng. 2009, 22, 53–57. [Google Scholar] [CrossRef]
- Yang, J.; Wei, L.M. Collapse of loose sand with the addition of fines: The role of particle shape. Géotechnique 2012, 62, 1111–1125. [Google Scholar] [CrossRef] [Green Version]
- Fonseca, J.; O’Sullivan, C.; Coop, M.R.; Lee, P.D. Non-invasive characterization of particle morphology of natural sands. Soils Found. 2012, 52, 712–722. [Google Scholar] [CrossRef]
- Grill, L.; Ostermeier, P.; Würth, M.; Reiss, P. Behaviour of lunar regolith simulants in fluidised bed reactors for in-situ resource utilisation. Planet. Space Sci. 2019, 180, 104757. [Google Scholar] [CrossRef]
- Schulze, D. Powders and Bulk Solids: Behavior, Characterization, Storage and Flow; Springer: Berlin, Germany, 2008; ISBN 9783540737681. [Google Scholar]
- Freeman, R.E.; Cooke, J.R.; Schneider, L.C.R. Measuring shear properties and normal stresses generated within a rotational shear cell for consolidated and non-consolidated powders. Powder Technol. 2009, 190, 65–69. [Google Scholar] [CrossRef]
- Leung, L.Y.; Mao, C.; Chen, L.P.; Yang, C.-Y. Precision of pharmaceutical powder flow measurement using ring shear tester: High variability is inherent to powders with low cohesion. Powder Technol. 2016, 301, 920–926. [Google Scholar] [CrossRef]
- Leturia, M.; Benali, M.; Lagarde, S.; Ronga, I.; Saleh, K. Characterization of flow properties of cohesive powders: A comparative study of traditional and new testing methods. Powder Technol. 2014, 253, 406–423. [Google Scholar] [CrossRef]
- Bernard-Granger, G.; Giraud, M.; Pascal, E.; Mailhan, L.; Larsson, T.; Valot, C.; Ablitzer, C.; Gatumel, C.; Berthiaux, H. Rheological properties of alumina powder mixtures investigated using shear tests. Powder Technol. 2019, 345, 300–310. [Google Scholar] [CrossRef] [Green Version]
- Schulze, D. Round robin test on ring shear testers. Adv. Powder Technol. 2011, 22, 197–202. [Google Scholar] [CrossRef]
- Bellmann, C.; Caspari, A.; Moitzi, C.; Babick, F. Dynamische und Elektrophoretische Lichtstreuung: Leitfaden zur Partikelgrößenanalyse und Zetapotentialbestimmung; Anton Paar GmbH: Graz, Austria, 2018; ISBN 978-3-200-04433-3. [Google Scholar]
- Stieß, M. (Ed.) Mechanische Verfahrenstechnik—Partikeltechnologie 1; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-32551-2. [Google Scholar]
- Eshel, G.; Levy, G.J.; Mingelgrin, U.; Singer, M.J. Critical Evaluation of the Use of Laser Diffraction for Particle-Size Distribution Analysis. Soil Sci. Soc. Am. J. 2004, 68, 736. [Google Scholar] [CrossRef]
- Taylor, L.; Schmitt, H.; Carrier, W.; Nakagawa, M. Lunar Dust Problem: From Liability to Asset. In Proceedings of the 1st Space Exploration Conference: Continuing the Voyage of Discovery, Orlando, FL, USA, 30 January–1 February 2005; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005. ISBN 978-1-62410-022-2. [Google Scholar]
- Peters, B. Dust/Regolith for Surface Exploration. In Proceedings of the NASA Extravehicular Activity (EVA) Technology Workshop 2017, Houston, TX, USA, 12 October 2017. [Google Scholar]
- Rickman, D.; Immer, C.; Metzger, P.; Dixon, E.; Pendleton, M.; Edmunson, J. Particle Shape in Simulants of the Lunar Regolith. J. Sediment. Res. 2012, 82, 823–832. [Google Scholar] [CrossRef]
- Görz, H.; White, E.W.; Johnson, G.G.; Pearson, M.W. (Eds.) Cesemi Studies of Apollo 14 and 15 Fines. In Proceedings of the Abstracts of the Lunar and Planetary Science Conference, Houston, TX, USA, 10–13 January 1972. [Google Scholar]
- Görz, H.; White, W.E.; Roy, R.; Johnson, G.G. (Eds.) Particle Size and Shape Distributions of Lunar Fines by CESEMI. In Proceedings of the Lunar Science Conference, Houston, TX, USA, 11–14 January 1971; Volume 2, pp. 2021–2025. [Google Scholar]
- Hadjittofis, E.; Das, S.C.; Zhang, G.G.Z.; Heng, J.Y.Y. Interfacial Phenomena. In Developing Solid Oral Dosage Forms: Pharmaceutical Theory & Practice, 2nd ed.; Qiu, Y., Chen, Y., Zhang, G.G.Z., Yu, L.X., Mantri, R.V., Eds.; Academic Press: London, UK, 2017; pp. 225–252. ISBN 9780128024478. [Google Scholar]
- Höber, D.; Taschner, A.; Fimbinger, E. Excavation and Conveying Technologies for Space Applications. Berg Huettenmaenn. Mon. 2021, 166, 95–103. [Google Scholar] [CrossRef]
- Schrunk, D.G.; Sharpe, B.L.; Cooper, B.L.; Thangavelu, M. The Moon; Praxis: New York, NY, USA, 2007; ISBN 978-0-387-36055-3. [Google Scholar]
- Liu, T.; Wei, C.; Liang, L.; Zhang, J.; Zhao, Y. Simulation and Analysis of the Lunar Regolith Sampling Process Based on the Discrete Element Method. Trans. Jpn. Soc. Aero. Space Sci. 2014, 57, 309–316. [Google Scholar] [CrossRef] [Green Version]
- Colwell, J.E.; Batiste, S.; Horányi, M.; Robertson, S.; Sture, S. Lunar surface: Dust dynamics and regolith mechanics. Rev. Geophys. 2007, 45, RG2006. [Google Scholar] [CrossRef]
- Monkul, M.M. On Some of the Factors Influencing the Fines’ Role on Liquefaction of Silty Sands. In Proceedings of the GeoCongress 2012, State of the Art and Practice in Geotechnical Engineering, Oakland, CA, USA, 25–29 March 2012; Yesiller, N., Athanasopoulos-Zekkos, A., Hryciw, R.D., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 799–808, ISBN 9780784412121. [Google Scholar]
- Hampe, E.; Molerus, O. Schüttgutmechanik, Grundlagen und Anwendungen in der Verfahrenstechnik. Berlin-Heidelberg-New York-Tokyo, Springer-Verlag 1985. XI, 310 S., 157 Abb., DM 98,—. ISBN 3-540-15428-0. Z. Angew. Math. Mech. 1986, 66, 633. [Google Scholar] [CrossRef]
- Schwedes, J. Fließverhalten von Schüttgütern in Bunkern. Chem. Ing. Tech. 1976, 48, 294–300. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Zhang, W.; Shao, J.; Wang, Z.; Wu, X. Experimental Study on the Basic Properties of a Green New Coal Mine Grouting Reinforcement Material. ACS Omega 2020, 5, 16722–16732. [Google Scholar] [CrossRef]
- Parrella, L.; Barletta, D.; Boerefijn, R.; Poletto, M. Comparison between a Uniaxial Compaction Tester and a Shear Tester for the Characterization of Powder Flowability. KONA 2008, 26, 178–189. [Google Scholar] [CrossRef] [Green Version]
- Schulze, D. Fließeigenschaften von Schüttgütern mit faser- und plättchenförmigen Partikeln. Schüttgut 2002, 8, 538–546. [Google Scholar]
- Jange, C.G.; Ambrose, R.K. Effect of surface compositional difference on powder flow properties. Powder Technol. 2019, 344, 363–372. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Gurappa, B. Particulate Solids in Bulk: Storage and Flow. In Coulson and Richardson’s Chemical Engineering: Volume 2A: Particulate Systems and Particle Technology, 6th ed.; Gurappa, B., Chhabra, R.P., Coulson, J.M., Richardson, J.F., Eds.; Butterworth-Heinemann: Amsterdam, The Netherlands, 2019; pp. 67–132. ISBN 9780081010983. [Google Scholar]
- Fu, X.; Huck, D.; Makein, L.; Armstrong, B.; Willen, U.; Freeman, T. Effect of particle shape and size on flow properties of lactose powders. Particuology 2012, 10, 203–208. [Google Scholar] [CrossRef]
- Janssen, P.H.M.; Depaifve, S.; Neveu, A.; Francqui, F.; Dickhoff, B.H.J. Impact of Powder Properties on the Rheological Behavior of Excipients. Pharmaceutics 2021, 13, 1198. [Google Scholar] [CrossRef] [PubMed]
- Stavrou, A.G.; Hare, C.; Hassanpour, A.; Wu, C.-Y. Investigation of powder flowability at low stresses: Influence of particle size and size distribution. Powder Technol. 2020, 364, 98–114. [Google Scholar] [CrossRef]
- Molerus, O.; Nywlt, M. The influence of the fine particle content of the flow behaviour of bulk materials. Powder Technol. 1984, 37, 145–154. [Google Scholar] [CrossRef]
- Schulze, D. Spezielle Eigenschaften und Einflüsse auf das Fließverhalten. In Pulver und Schüttgüter: Fließeigenschaften und Handhabung, 3rd ed.; Schulze, D., Ed.; Springer Vieweg: Berlin/Heidelberg, Germany, 2014; pp. 217–247. ISBN 978-3-642-53884-1. [Google Scholar]
- Castellanos, A. The relationship between attractive interparticle forces and bulk behaviour in dry and uncharged fine powders. Adv. Phys. 2005, 54, 263–376. [Google Scholar] [CrossRef]
- Carr, R.L. Evaluating flow properties of solids. Chem. Eng. 1965, 18, 163–168. [Google Scholar]

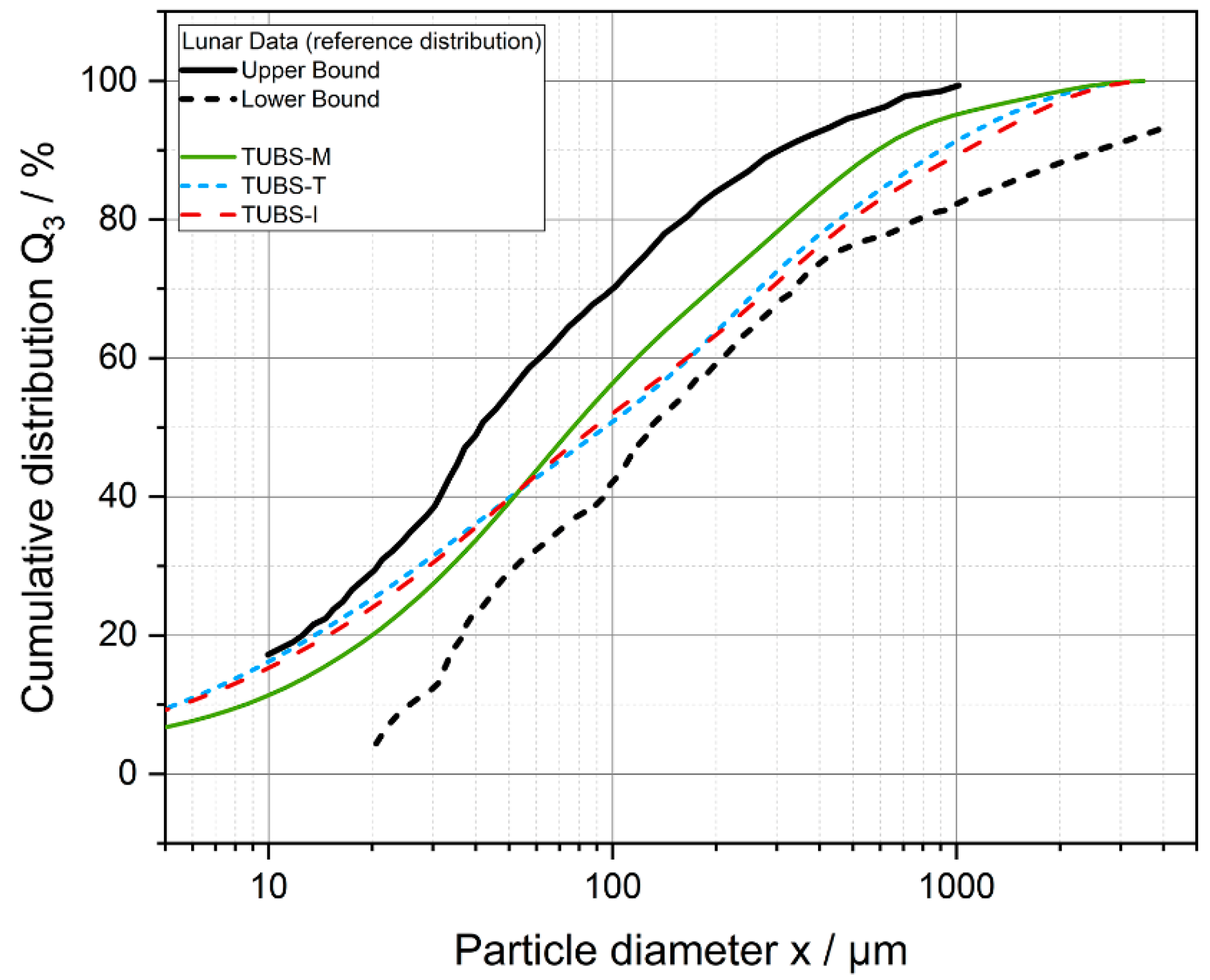


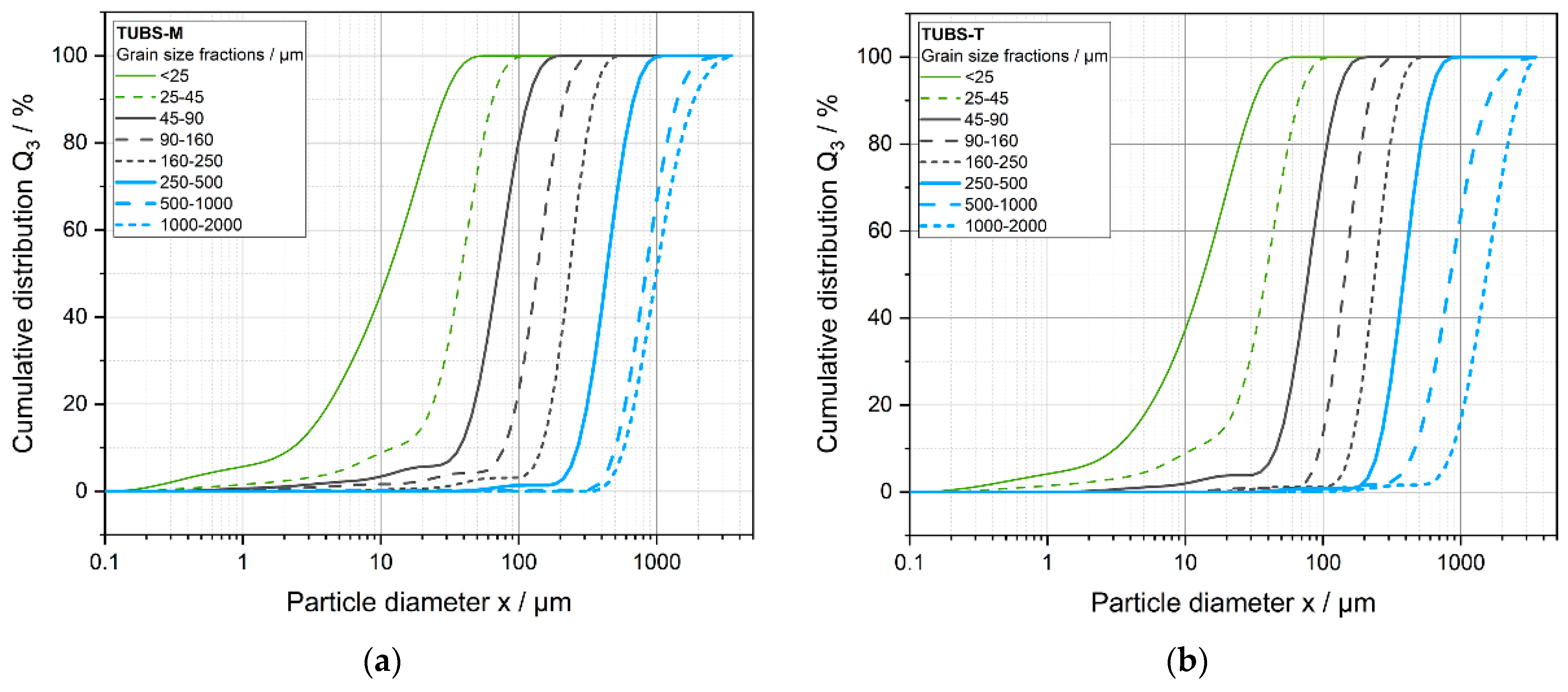
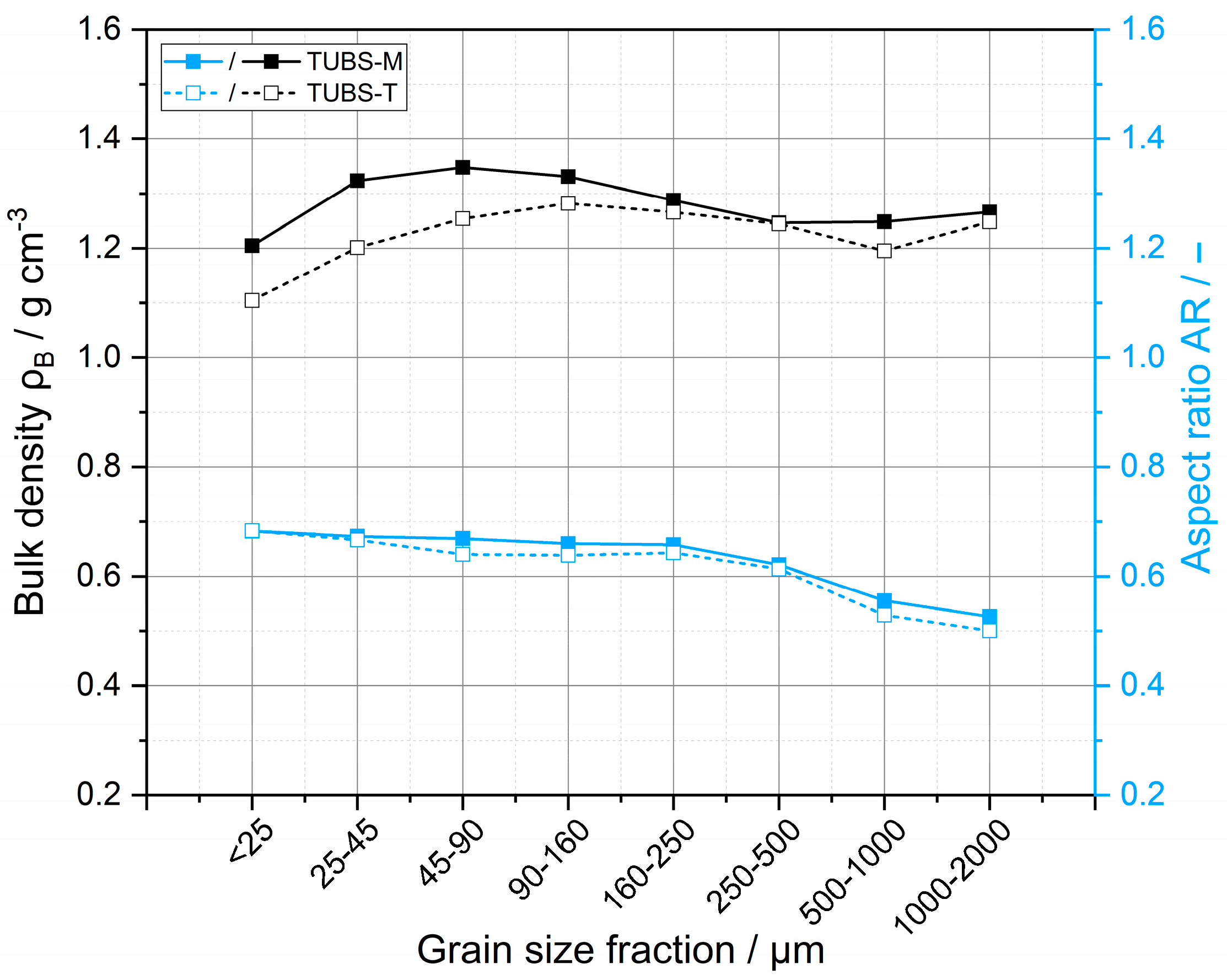
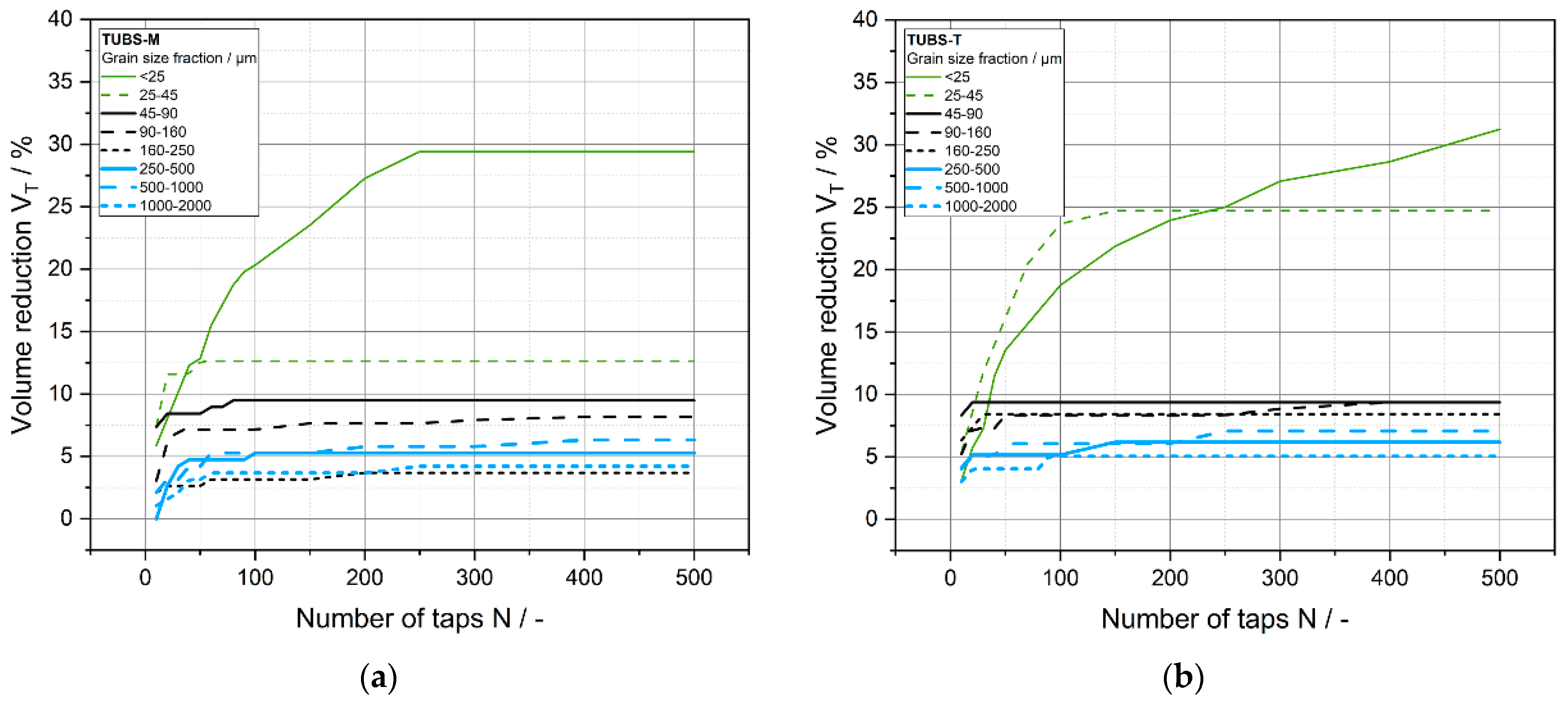
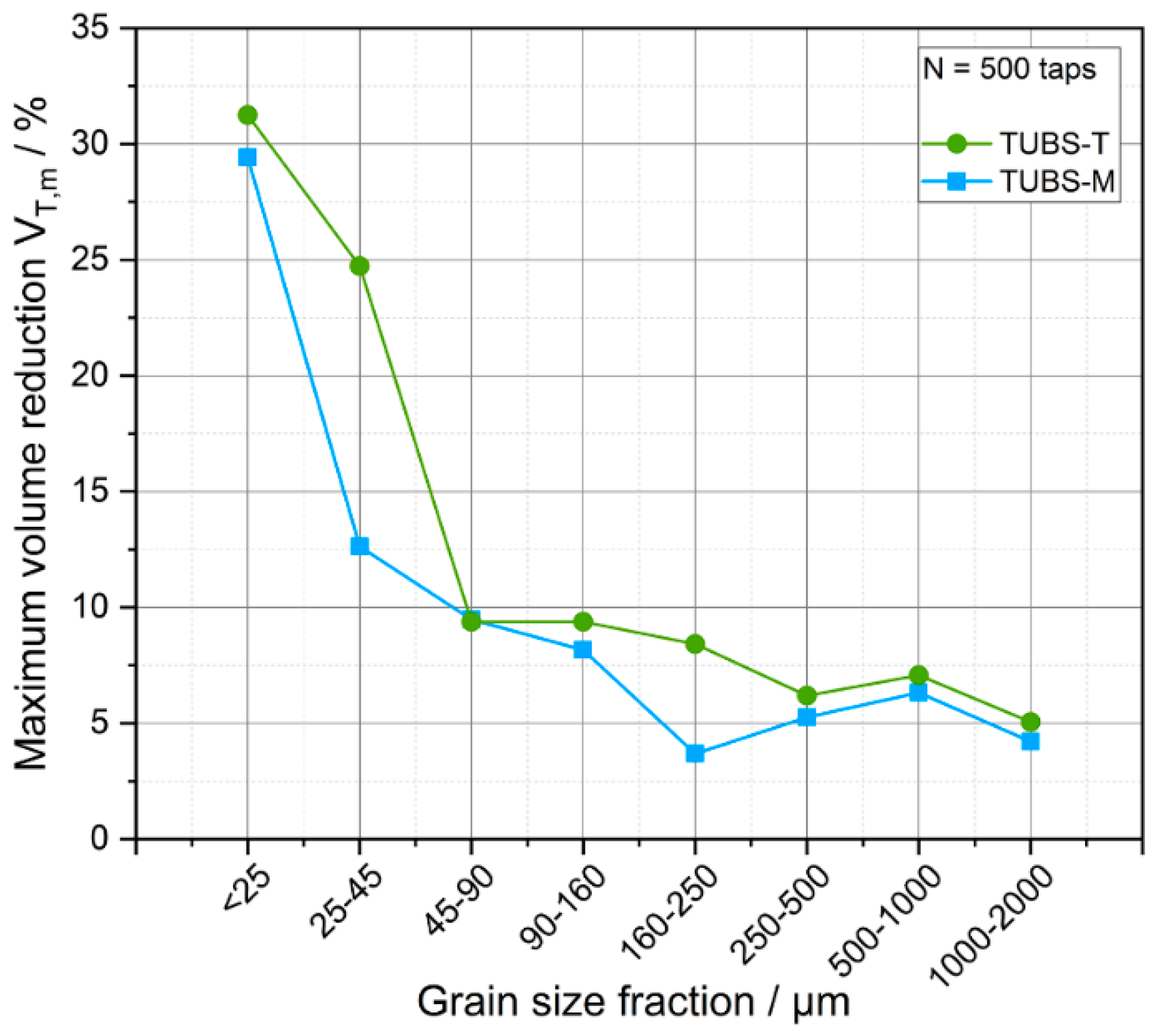



| TUBS-M | TUBS-T | |||||||
|---|---|---|---|---|---|---|---|---|
| Grain Size Fraction | x10 μm | x50 μm | x90 μm | PDI - | x10 μm | x50 μm | x90 μm | PDI - |
| 1000–2000 | 1057.69 | 1475.19 | 1696.85 | 0.43 | 379 | 1247.82 | 1469.35 | 0.87 |
| 500–1000 | 578.53 | 856.5 | 1259.44 | 0.79 | 479.61 | 707.48 | 994.66 | 0.73 |
| 250–500 | 267 | 431 | 681 | 0.96 | 252 | 388 | 588 | 0.87 |
| 160–250 | 146 | 232 | 349 | 0.88 | 159 | 238 | 349 | 0.80 |
| 90–160 | 78.1 | 135 | 215 | 1.01 | 94.6 | 145 | 217 | 0.84 |
| 45–90 | 37.1 | 70.3 | 118 | 1.15 | 45.7 | 78 | 125 | 1.02 |
| 25–45 | 12.40 | 37.90 | 64.80 | 1.38 | 11.7 | 38.7 | 66.3 | 1.41 |
| <25 | 2.28 | 11.30 | 28.60 | 2.33 | 3.12 | 13.6 | 31.6 | 2.09 |
| Property | TUBS-M | TUBS-I | TUBS-T | Lunar Regolith |
|---|---|---|---|---|
| Bulk density g cm−3 | 1.41–1.62 | 1.43–1.56 | 1.33–1.46 | 1.45–1.55 |
| Tapped density g cm−3 | 1.81 | 1.65 | 1.61 | na |
| Av. Hausner ratio - | 1.19 | 1.10 | 1.15 | na |
| Aspect ratio - | 0.53–0.68 | 0.50–0.68 | 0.50–0.68 | 0.4–0.7 [95] |
| Particle size | Acc. to distribution | |||
| µm | band | |||
| x10 | 8.5 | 5.5 | 5.3 | 5–25 |
| x50 | 76.7 | 88.6 | 96.0 | 41–130 |
| x90 | 593.6 | 1074.9 | 912.3 | 300–2600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Windisch, L.; Linke, S.; Jütte, M.; Baasch, J.; Kwade, A.; Stoll, E.; Schilde, C. Geotechnical and Shear Behavior of Novel Lunar Regolith Simulants TUBS-M, TUBS-T, and TUBS-I. Materials 2022, 15, 8561. https://doi.org/10.3390/ma15238561
Windisch L, Linke S, Jütte M, Baasch J, Kwade A, Stoll E, Schilde C. Geotechnical and Shear Behavior of Novel Lunar Regolith Simulants TUBS-M, TUBS-T, and TUBS-I. Materials. 2022; 15(23):8561. https://doi.org/10.3390/ma15238561
Chicago/Turabian StyleWindisch, Lisa, Stefan Linke, Magnus Jütte, Julian Baasch, Arno Kwade, Enrico Stoll, and Carsten Schilde. 2022. "Geotechnical and Shear Behavior of Novel Lunar Regolith Simulants TUBS-M, TUBS-T, and TUBS-I" Materials 15, no. 23: 8561. https://doi.org/10.3390/ma15238561
APA StyleWindisch, L., Linke, S., Jütte, M., Baasch, J., Kwade, A., Stoll, E., & Schilde, C. (2022). Geotechnical and Shear Behavior of Novel Lunar Regolith Simulants TUBS-M, TUBS-T, and TUBS-I. Materials, 15(23), 8561. https://doi.org/10.3390/ma15238561








