Prediction of the Sound Absorption Coefficient of Three-Layer Aluminum Foam by Hybrid Neural Network Optimization Algorithm
Abstract
:1. Introduction
2. Equilibrium Optimizer-Generalized Regression Neural Network
2.1. Generalized Regression Neural Network
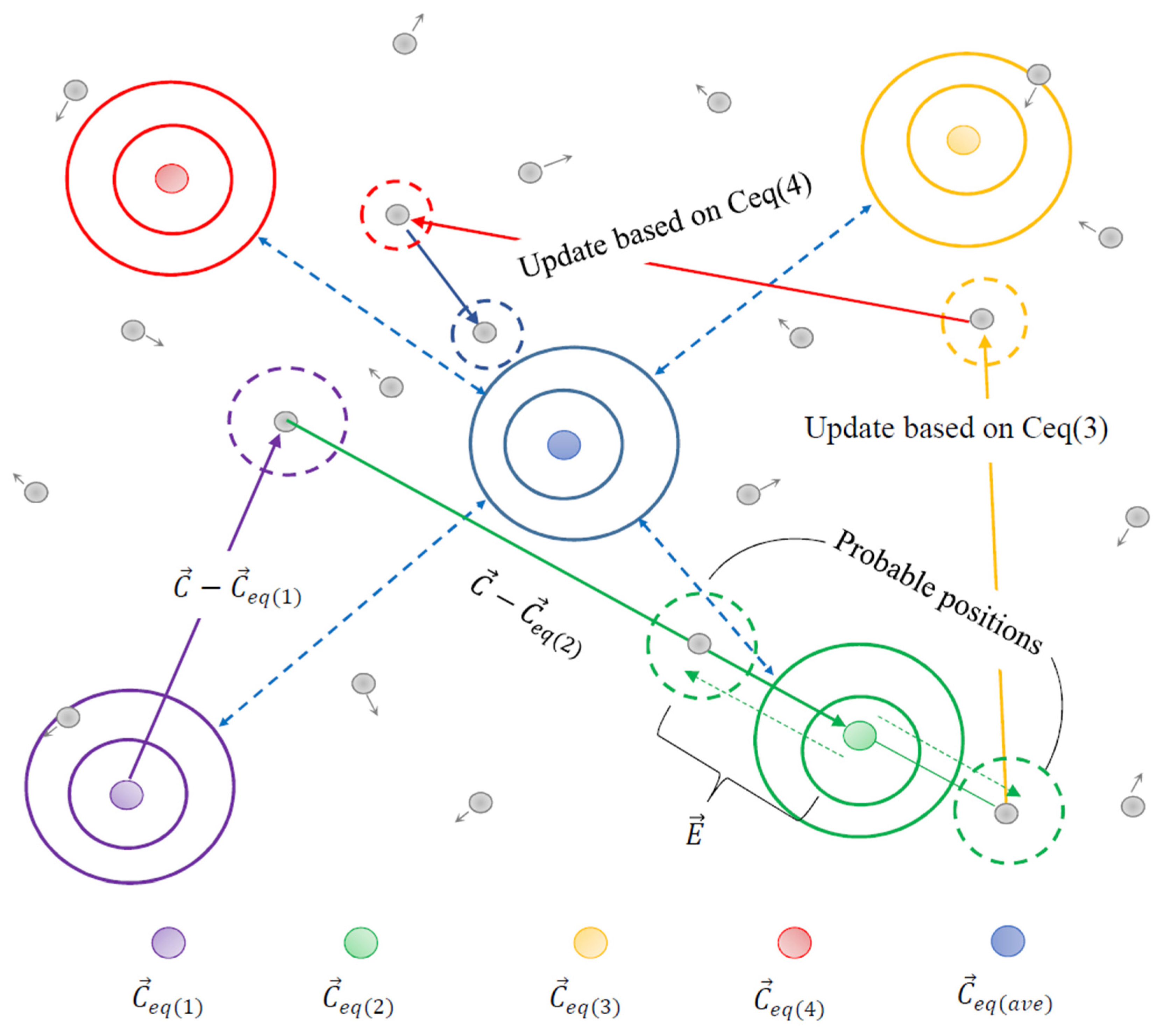
2.2. Equilibrium Optimizer Algorithm
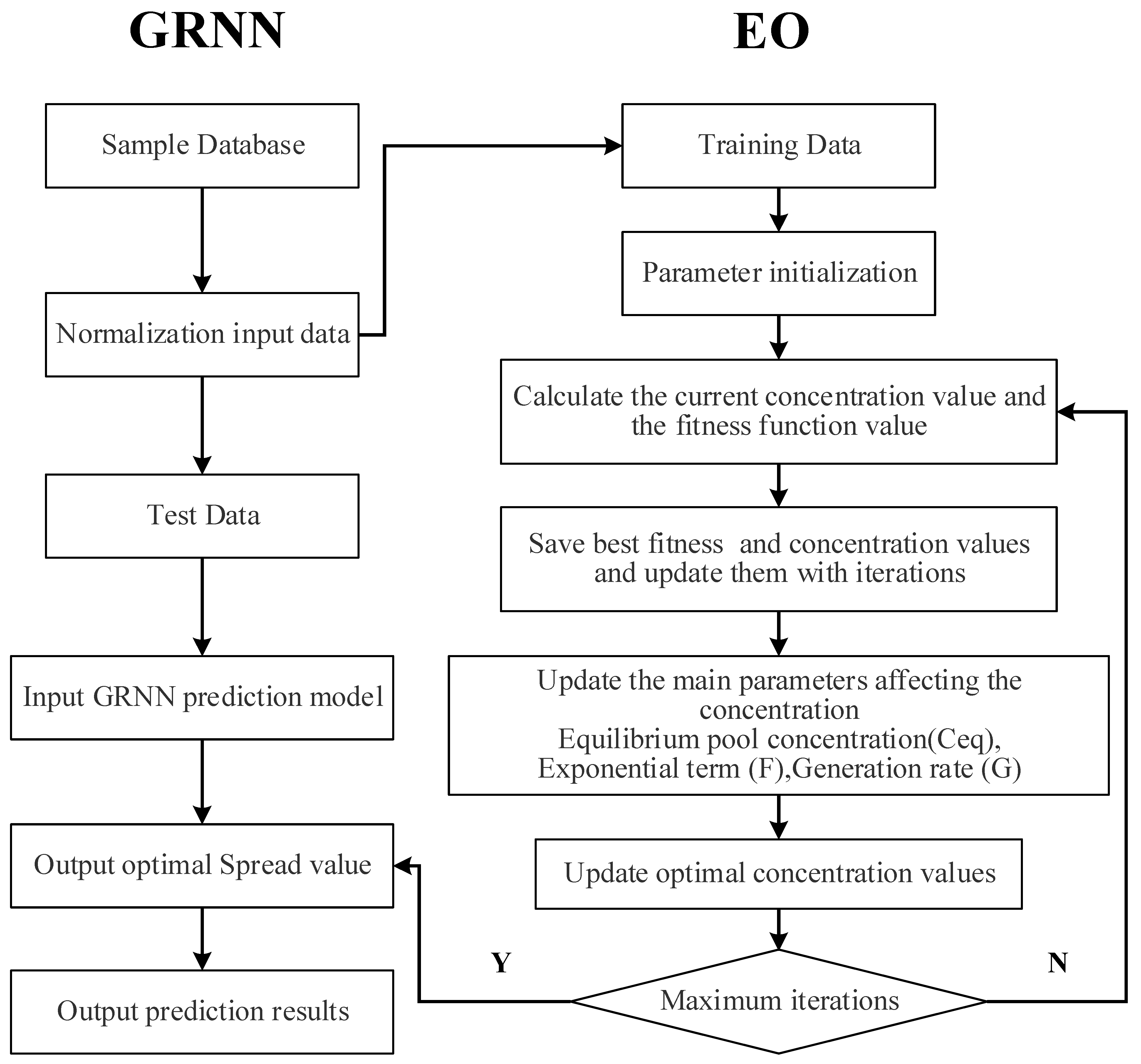
2.3. EO-GRNN for Predicting Sound Absorption Coefficient
3. Experimental
3.1. Experiment Data
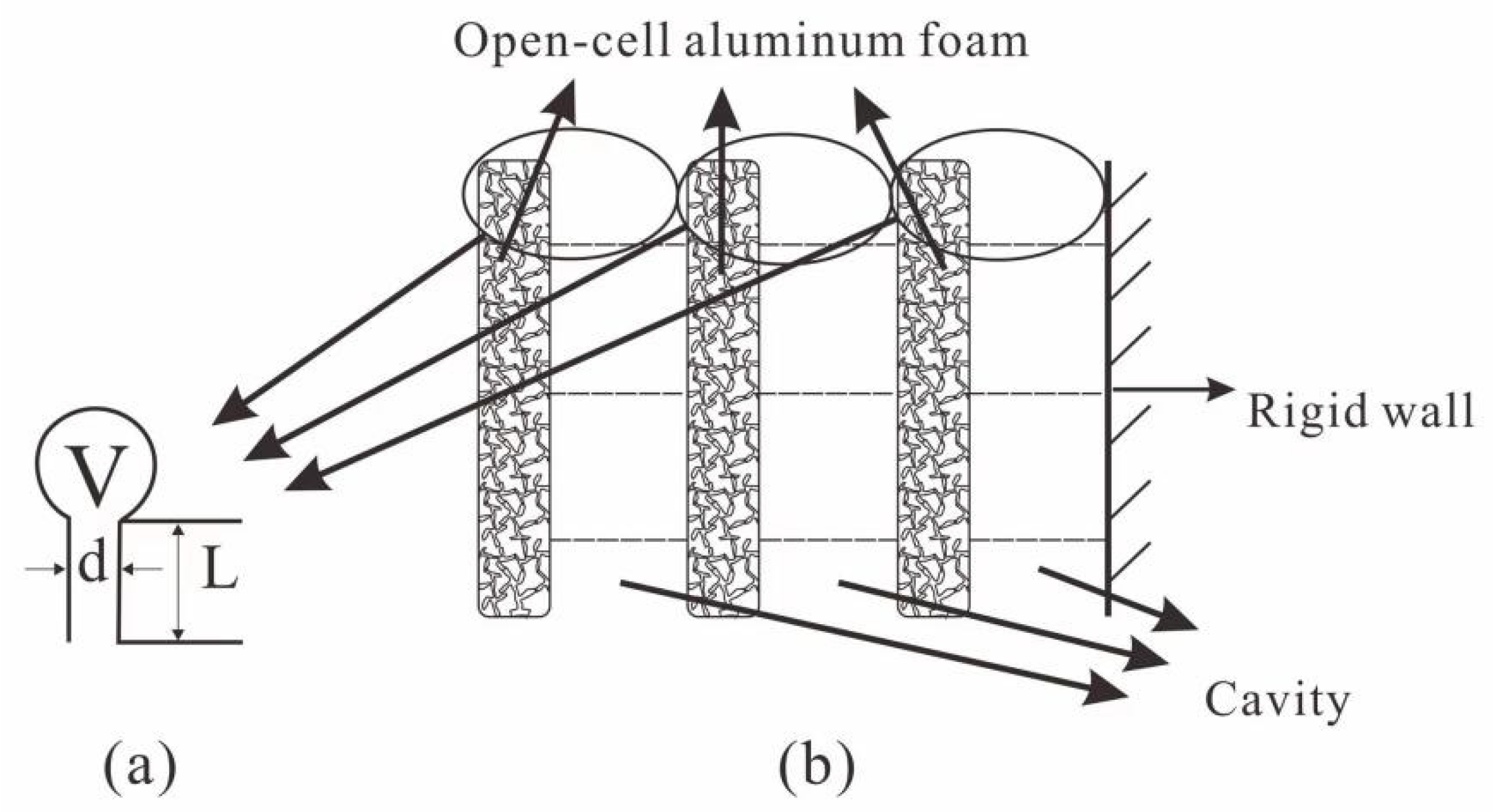
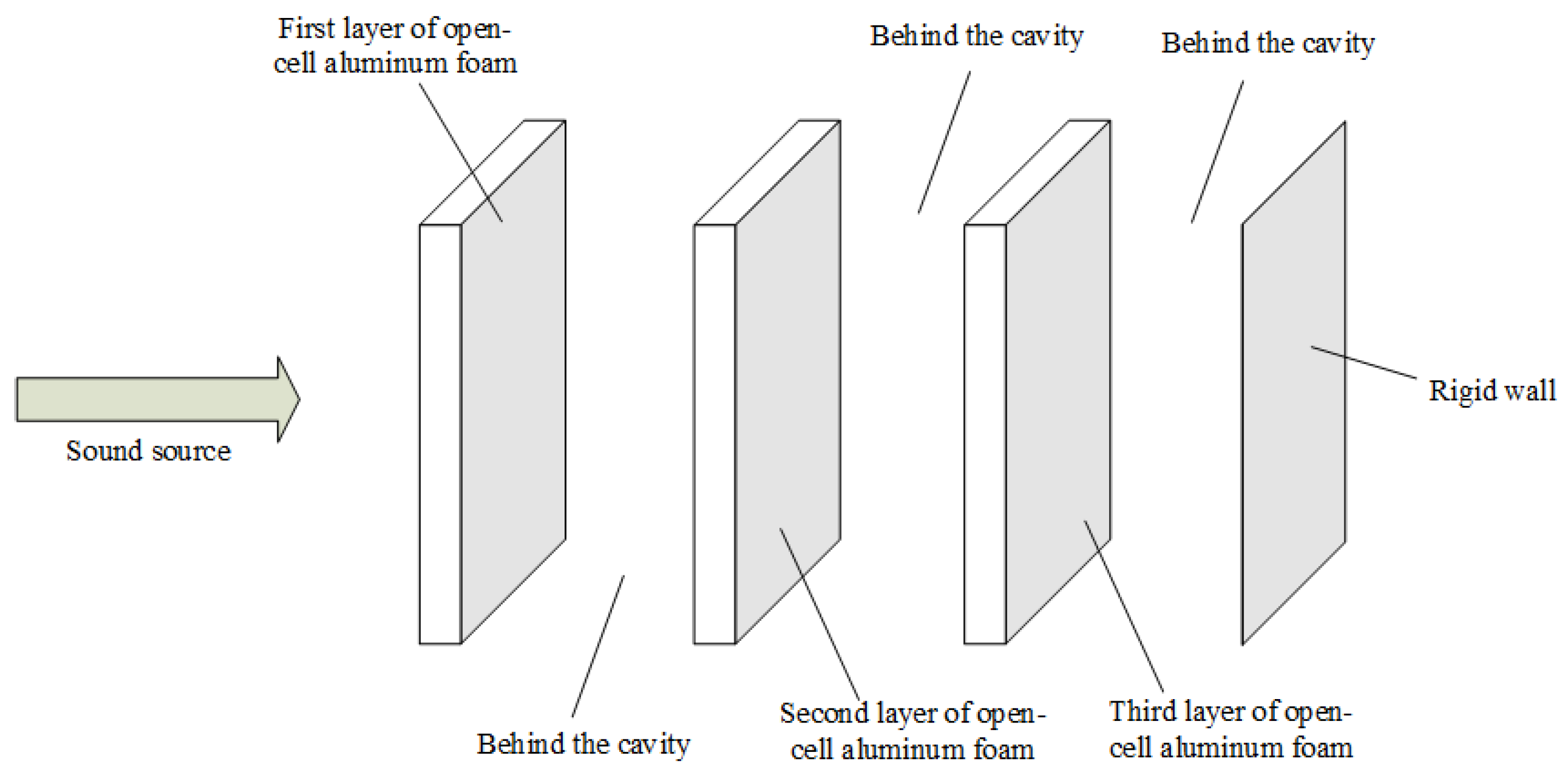
3.2. Measurement of the Sound Absorption Coefficient
3.3. Prediction of the Sound Absorption Coefficient
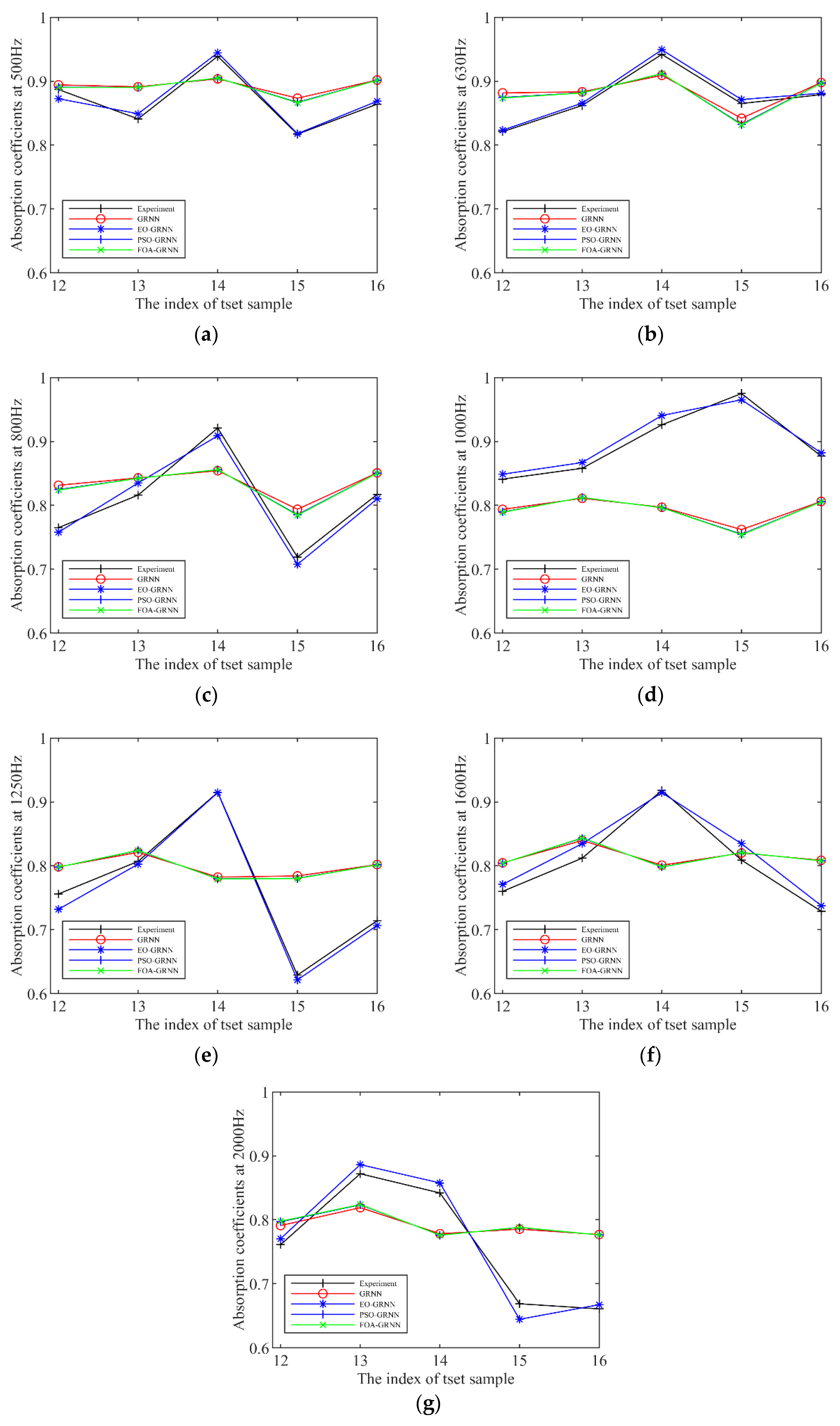
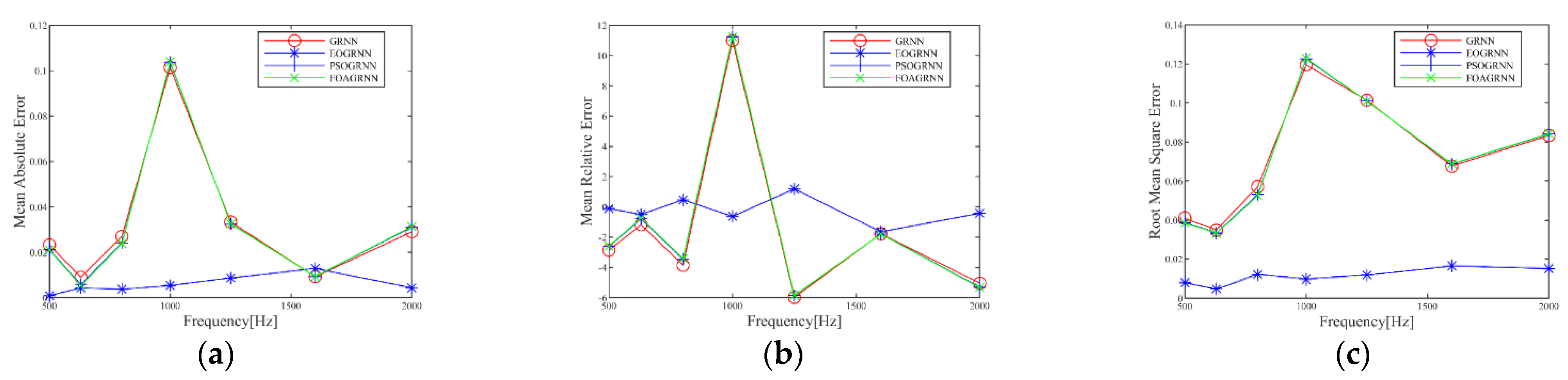
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giles-Corti, B.; Vernez-Moudon, A.; Reis, R.; Turrell, G.; Owen, N. City planning and population health: A global challenge: Urban design, transport, and health 1. Lancet 2016, 388, 2912. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.; Ketzel, M.; Kakosimos, K.; Sørensen, M.; Jensen, S.S. Road traffic air and noise pollution exposure assessment—A review of tools and techniques. Sci. Total Environ. 2018, 634, 661–676. [Google Scholar] [CrossRef] [PubMed]
- Markevych, I.; Schoierer, J.; Hartig, T.; Chudnovsky, A.; Hystad, P.; Dzhambov, A.M.; de Vries, S.; Triguero-Mas, M.; Brauer, M.; Nieuwenhuijsen, M.J.; et al. Exploring pathways linking greenspace to health: Theoretical and methodological guidance. Environ. Res. 2017, 158, 301–317. [Google Scholar] [CrossRef] [PubMed]
- Lisi, L.; Qi, S.; Manbo, L.; Junxue, Z.; Shiwei, L. Investigation of Sound Absorption Feature of Closed-Cell Aluminum Foams Combined with Porous Materials. Nanosci. Nanotechnol. Lett. 2017, 9, 392–397. [Google Scholar]
- Kumar, R.; Jain, H.; Sriram, S.; Chaudhary, A.; Khare, A.; Ch, V.A.; Mondal, D.P. Lightweight open cell aluminum foam for superior mechanical and electromagnetic interference shielding properties. Mater. Chem. Phys. 2020, 240, 122274. [Google Scholar] [CrossRef]
- Srinath, G.; Vadiraj, A.; Balachandran, G.; Sahu, S.N.; Gokhale, A.A. Characteristics of aluminium metal foam for automotive applications. Trans. Indian Inst. Met. 2010, 63, 765–772. [Google Scholar] [CrossRef]
- Ming-ying, C.; Zhen, J.; Cheng-chang, J.; Qiu-chi, W.; Chao, W.; Qian, Q.; Zhe, L. Research progress of aluminum foam and its composites. Powder Metall. Technol. 2019, 37, 68–73. [Google Scholar] [CrossRef]
- Liang, L.; Guo, W.; Zhang, Y.; Zhang, W.; Li, L.; Xing, X. Radial Basis Function Neural Network for prediction of medium-frequency sound absorption coefficient of composite structure open-cell aluminum foam. Appl. Acoust. 2020, 170, 107505. [Google Scholar] [CrossRef]
- Liang, L.; Mi, H.; Guo, W.; Zhang, Y.; Ma, H.; Zhang, Z.; Li, L. Estimation of sound absorption coefficient of composite structured aluminum foam by radial basis function neural network. Appl. Acoust. 2022, 185, 108414. [Google Scholar] [CrossRef]
- Cheng, W.; Duan, C.-Y.; Liu, P.-S.; Lu, M. Sound absorption performance of various nickel foam-base multi-layer structures in range of low frequency. Trans. Nonferrous Met. Soc. China 2017, 27, 1989–1995. [Google Scholar] [CrossRef]
- Liu, P.S.; Xu, X.B.; Cheng, W.; Chen, J.H. Sound absorption of several various nickel foam multilayer structures at aural frequencies sensitive for human ears. Trans. Nonferrous Met. Soc. China 2018, 28, 1334–1341. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Trupiano, S.; Vivio, F. Multiscale analysis and mechanical characterization of open-cell foams by simplified FE modeling. Eur. J. Mech. A/Solids 2021, 89, 104291. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, J.; Wang, Y.; Song, D.; Cao, R.; Yang, X. Enhanced sound absorption characteristic of aluminum-polyurethane interpenetrating phase composite foams. Mater. Lett. 2022, 323, 132595. [Google Scholar] [CrossRef]
- JingFeng, N.; GuiPing, Z. Sound absorption characteristics of multilayer porous metal materials backed with an air gap. J. Vib. Control 2014, 22, 2861–2872. [Google Scholar] [CrossRef]
- Lin, M.-D.; Tsai, K.-T.; Su, B.-S. Estimating the sound absorption coefficients of perforated wooden panels by using artificial neural networks. Appl. Acoust. 2009, 70, 31–40. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G.; Puyana-Romero, V.; Trematerra, A. A Comparison between Numerical Simulation Models for the Prediction of Acoustic Behavior of Giant Reeds Shredded. Appl. Sci. 2020, 10, 6881. [Google Scholar] [CrossRef]
- Khobotov, A.G.; Kalinina, V.I.; Khil’ko, A.I.; Malekhanov, A.I. Novel Neuron-like Procedure of Weak Signal Detection against the Non-Stationary Noise Background with Application to Underwater Sound. Remote Sens. 2022, 14, 4860. [Google Scholar] [CrossRef]
- Guy, R.W. A Preliminary Study Model for the Absorption or Transmission of Sound in Multi-Layer Systems. Noise Control Eng. J. 1989, 33, 117. [Google Scholar] [CrossRef]
- Delany, M.E.; Bazley, E.N. Acoustical properties of fibrous absorbent materials. J. Acoust. Soc. Am. 1970, 48, 105–116. [Google Scholar] [CrossRef]
- Allard, J.F.; Champoux, Y. New empirical equations for sound propagation in rigid frame fibrous materials. Acoust. Soc. Am. J. 1992, 91, 3346–3353. [Google Scholar] [CrossRef]
- Miki, Y. Acoustical properties of porous materials-Modeling of Delany_Bazley models. J. Acoust. Soc. Jpn. 1990, 11, 19–24. [Google Scholar] [CrossRef]
- Jeon, J.H.; Yang, S.S.; Kang, Y.J. Estimation of sound absorption coefficient of layered fibrous material using artificial neural networks. Appl. Acoust. 2020, 169, 107476. [Google Scholar] [CrossRef]
- Dong, G.; Wu, J.H.; Wu, J.; Jing, L.; Zhao, W. Acoustic performance of aluminum foams with semiopen cells. Appl. Acoust. 2015, 87, 103–108. [Google Scholar]
- Wang, F.; Chen, Z.; Wu, C.; Yang, Y.; Li, S. Analysis of acoustic performance of glass fiber felts after water absorption and their estimation results by artificial neural network. J. Text. Inst. 2019, 111, 1008–1016. [Google Scholar] [CrossRef]
- Choi, W.; Won, S.; Kim, G.S.; Kang, N. Artificial Neural Network Modelling of the Effect of Vanadium Addition on the Tensile Properties and Microstructure of High-Strength Tempcore Rebars. Materials 2022, 15, 3781. [Google Scholar] [CrossRef]
- Churyumov, A.; Kazakova, A.; Churyumova, T. Modelling of the Steel High-Temperature Deformation Behaviour Using Artificial Neural Network. Metals 2022, 12, 447. [Google Scholar] [CrossRef]
- Honysz, R. Modeling the Chemical Composition of Ferritic Stainless Steels with the Use of Artificial Neural Networks. Metals 2021, 11, 724. [Google Scholar] [CrossRef]
- Liu, J.; Bao, W.; Shi, L.; Zuo, B.; Gao, W. General regression neural network for prediction of sound absorption coefficients of sandwich structure nonwoven absorbers. Appl. Acoust. 2014, 76, 128–137. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, M.; Zhao, M.; Sun, J. Modification and Noise Reduction Design of Gear Transmission System of EMU Based on Generalized Regression Neural Network. Machines 2022, 10, 157. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S. Annual Energy Consumption Forecasting Based on PSOCA-GRNN Model. Abstr. Appl. Anal. 2014, 1, 217630. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Luo, Z.; Xie, C. Study and Application on Fruit Fly Optimization Algorithm Optimized General Regression Neural Network in Mined-out area Stability Analysis. World Sci-Tech RD 2015, 37, 230–234. [Google Scholar]
- Xie, X.; Fu, G.; Xue, Y.; Zhao, Z.; Chen, P.; Lu, B.; Jiang, S. Risk prediction and factors risk analysis based on IFOA-GRNN and apriori algorithms: Application of artificial intelligence in accident prevention. Process Saf. Environ. Prot. 2019, 122, 169–184. [Google Scholar] [CrossRef]
- Mian, H.R.; Hu, G.J.; Hewage, K.; Rodriguez, M.J.; Sadiq, R. Predicting unregulated disinfection by-products in water distribution networks using generalized regression neural networks. Urban Water J. 2021, 18, 711–724. [Google Scholar] [CrossRef]
- Zeng, L.; Liu, Q.; Jing, L.; Lan, L.; Feng, J. Using Generalized Regression Neural Network to Retrieve Bare Surface Soil Moisture From Radarsat-2 Backscatter Observations, Regardless of Roughness Effect. Front. Earth Sci. 2021, 9, 657206. [Google Scholar] [CrossRef]
- Preethi, R.; Sathiyapriya, G.; Shanthi, S.A. Radial basis function bipolar fuzzy neural network. Mater. Today Proc. 2022. [Google Scholar] [CrossRef]
- Leonard, J.A.; Kramer, M.A.; Ungar, L.H. Using radial basis functions to approximate a function and its error bounds. IEEE Trans. Neural Netw. 1992, 3, 624–627. [Google Scholar] [CrossRef]
- Reboucas, E.D.; de Medeiros, F.N.S.; Marques, R.C.P.; Chagas, J.V.S.; Guimaraes, M.T.; Santos, L.O.; Medeiros, A.G.; Peixoto, S.A. Level set approach based on Parzen Window and floor of log for edge computing object segmentation in digital images. Appl. Soft Comput. 2021, 105, 107273. [Google Scholar] [CrossRef]
- Han, F.; Seiffert, G.; Zhao, Y.; Gibbs, B. Acoustic absorption behaviour of an open-celled aluminium foam. J. Phys. D Appl. Phys. 2003, 36, 294–302. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Lu, T.J. Optimized acoustic properties of cellular solids. J. Acoust. Soc. Am. 1999, 106, 756–765. [Google Scholar] [CrossRef]
- Zainel, Q.M.; Darwish, S.M.; Khorsheed, M.B. Employing Quantum Fruit Fly Optimization Algorithm for Solving Three-Dimensional Chaotic Equations. Mathematics 2022, 10, 4147. [Google Scholar] [CrossRef]
- Yadav, A.; Hasan, M.K.; Joshi, D.; Kumar, V.; Aman, A.H.M.; Alhumyani, H.; Alzaidi, M.S.; Mishra, H. Optimized Scenario for Estimating Suspended Sediment Yield Using an Artificial Neural Network Coupled with a Genetic Algorithm. Water 2022, 14, 2815. [Google Scholar] [CrossRef]
- Wu, Y.; Al-Jumaili, S.J.; Al-Jumeily, D.; Bian, H. Prediction of the Nitrogen Content of Rice Leaf Using Multi-Spectral Images Based on Hybrid Radial Basis Function Neural Network and Partial Least-Squares Regression. Sensors 2022, 22, 8626. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Wang, Z.; Qi, X.; Bai, B.; Zhi, J. Prediction of Green Properties of Flux Pellets Based on Improved Generalized Regression Neural Network. Metals 2022, 12, 1840. [Google Scholar] [CrossRef]





| Material Code | Porosity (%) | Pore Size (10−6 m) | Thickness (10−3 m) | Density (g/cm3) | |
|---|---|---|---|---|---|
| A | A1 | 57.185 | 78 | 3 | 1.156 |
| A2 | 57.185 | 78 | 5 | 1.156 | |
| A3 | 57.185 | 78 | 6 | 1.156 | |
| A4 | 57.185 | 78 | 8 | 1.156 | |
| A5 | 57.185 | 78 | 10 | 1.156 | |
| B | B1 | 62.333 | 67 | 3 | 1.017 |
| B2 | 62.333 | 67 | 5 | 1.017 | |
| B3 | 62.333 | 67 | 6 | 1.017 | |
| B4 | 62.333 | 67 | 8 | 1.017 | |
| B5 | 62.333 | 67 | 10 | 1.017 |
| Sample Number | Sample Code | α500 | α630 | α800 | α100 | α1250 | α1600 | α2000 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | A1 | 0.036 | 0.036 | 0.083 | 0.078 | 0.070 | 0.095 | 0.131 | 0.076 |
| 2 | A2 | 0.060 | 0.055 | 0.087 | 0.109 | 0.092 | 0.118 | 0.154 | 0.096 |
| 3 | A3 | 0.067 | 0.072 | 0.139 | 0.121 | 0.127 | 0.179 | 0.250 | 0.136 |
| 4 | A4 | 0.071 | 0.068 | 0.106 | 0.132 | 0.151 | 0.211 | 0.307 | 0.149 |
| 5 | A5 | 0.077 | 0.077 | 0.156 | 0.166 | 0.206 | 0.299 | 0.432 | 0.202 |
| 6 | B1 | 0.052 | 0.043 | 0.060 | 0.086 | 0.079 | 0.114 | 0.165 | 0.086 |
| 7 | B2 | 0.063 | 0.061 | 0.083 | 0.106 | 0.103 | 0.143 | 0.198 | 0.108 |
| 8 | B3 | 0.061 | 0.052 | 0.109 | 0.120 | 0.121 | 0.163 | 0.228 | 0.122 |
| 9 | B4 | 0.073 | 0.060 | 0.121 | 0.146 | 0.169 | 0.242 | 0.356 | 0.167 |
| 10 | B5 | 0.072 | 0.064 | 0.146 | 0.167 | 0.203 | 0.298 | 0.439 | 0.198 |
| Sample Number | Sample Code | α500 | α630 | α800 | α100 | α1250 | α1600 | α2000 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | A4L20A3L40A4L10 | 0.942 | 0.924 | 0.825 | 0.744 | 0.677 | 0.709 | 0.690 | 0.787 |
| 2 | A5L30A3L30A1L20 | 0.899 | 0.944 | 0.892 | 0.811 | 0.815 | 0.841 | 0.851 | 0.865 |
| 3 | A5L40A5L30B2L50 | 0.961 | 0.937 | 0.920 | 0.947 | 0.990 | 0.985 | 0.936 | 0.954 |
| 4 | A5L30A4L40A3L10 | 0.936 | 0.902 | 0.818 | 0.750 | 0.737 | 0.754 | 0.703 | 0.800 |
| 5 | A4L40A5L20B4L10 | 0.816 | 0.776 | 0.720 | 0.685 | 0.715 | 0.790 | 0.737 | 0.748 |
| 6 | A4L40A5L50A4L0 | 0.889 | 0.859 | 0.774 | 0.720 | 0.726 | 0.765 | 0.680 | 0.773 |
| 7 | A5L20A2L20A3L20 | 0.850 | 0.952 | 0.965 | 0.906 | 0.832 | 0.827 | 0.859 | 0.884 |
| 8 | A5L30B4L30B5L30 | 0.850 | 0.797 | 0.777 | 0.767 | 0.830 | 0.872 | 0.885 | 0.825 |
| 9 | B4L20B5L30A4L30 | 0.954 | 0.966 | 0.926 | 0.909 | 0.890 | 0.780 | 0.636 | 0.866 |
| 10 | B4L30A5L30A5L20 | 0.867 | 0.832 | 0.788 | 0.771 | 0.803 | 0.812 | 0.841 | 0.816 |
| 11 | B4L40B5L30A1L20 | 0.931 | 0.926 | 0.888 | 0.847 | 0.863 | 0.889 | 0.850 | 0.885 |
| 12 | B5L30A5L30A5L10 | 0.887 | 0.821 | 0.765 | 0.841 | 0.756 | 0.760 | 0.761 | 0.799 |
| 13 | B5L30A2L20B2L20 | 0.841 | 0.862 | 0.816 | 0.858 | 0.807 | 0.812 | 0.872 | 0.838 |
| 14 | A5L30A5L30A4L40 | 0.939 | 0.942 | 0.921 | 0.926 | 0.915 | 0.918 | 0.842 | 0.915 |
| 15 | A2L40B2L50B4L30 | 0.817 | 0.865 | 0.719 | 0.975 | 0.629 | 0.809 | 0.669 | 0.783 |
| 16 | A5L20B5L30A5L10 | 0.864 | 0.879 | 0.817 | 0.877 | 0.714 | 0.729 | 0.661 | 0.792 |
| Models | Spread Value | Max RMSE | Min RMSE | Ave RMSE |
|---|---|---|---|---|
| GRNN | 2.4 | 0.120 | 0.035 | 0.072 |
| EO-GRNN | 0.7 | 0.017 | 0.005 | 0.011 |
| PSO-GRNN | 2.2 | 0.123 | 0.033 | 0.072 |
| FOA-GRNN | 2.2 | 0.123 | 0.033 | 0.072 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, H.; Guo, W.; Liang, L.; Ma, H.; Zhang, Z.; Gao, Y.; Li, L. Prediction of the Sound Absorption Coefficient of Three-Layer Aluminum Foam by Hybrid Neural Network Optimization Algorithm. Materials 2022, 15, 8608. https://doi.org/10.3390/ma15238608
Mi H, Guo W, Liang L, Ma H, Zhang Z, Gao Y, Li L. Prediction of the Sound Absorption Coefficient of Three-Layer Aluminum Foam by Hybrid Neural Network Optimization Algorithm. Materials. 2022; 15(23):8608. https://doi.org/10.3390/ma15238608
Chicago/Turabian StyleMi, Han, Wenlong Guo, Lisi Liang, Hongyue Ma, Ziheng Zhang, Yanli Gao, and Linbo Li. 2022. "Prediction of the Sound Absorption Coefficient of Three-Layer Aluminum Foam by Hybrid Neural Network Optimization Algorithm" Materials 15, no. 23: 8608. https://doi.org/10.3390/ma15238608
APA StyleMi, H., Guo, W., Liang, L., Ma, H., Zhang, Z., Gao, Y., & Li, L. (2022). Prediction of the Sound Absorption Coefficient of Three-Layer Aluminum Foam by Hybrid Neural Network Optimization Algorithm. Materials, 15(23), 8608. https://doi.org/10.3390/ma15238608






