Angle-Dependent Raman Scattering Studies on Anisotropic Properties of Crystalline Hexagonal 4H-SiC
Abstract
1. Introduction
2. Experimental
3. Results and Discussion
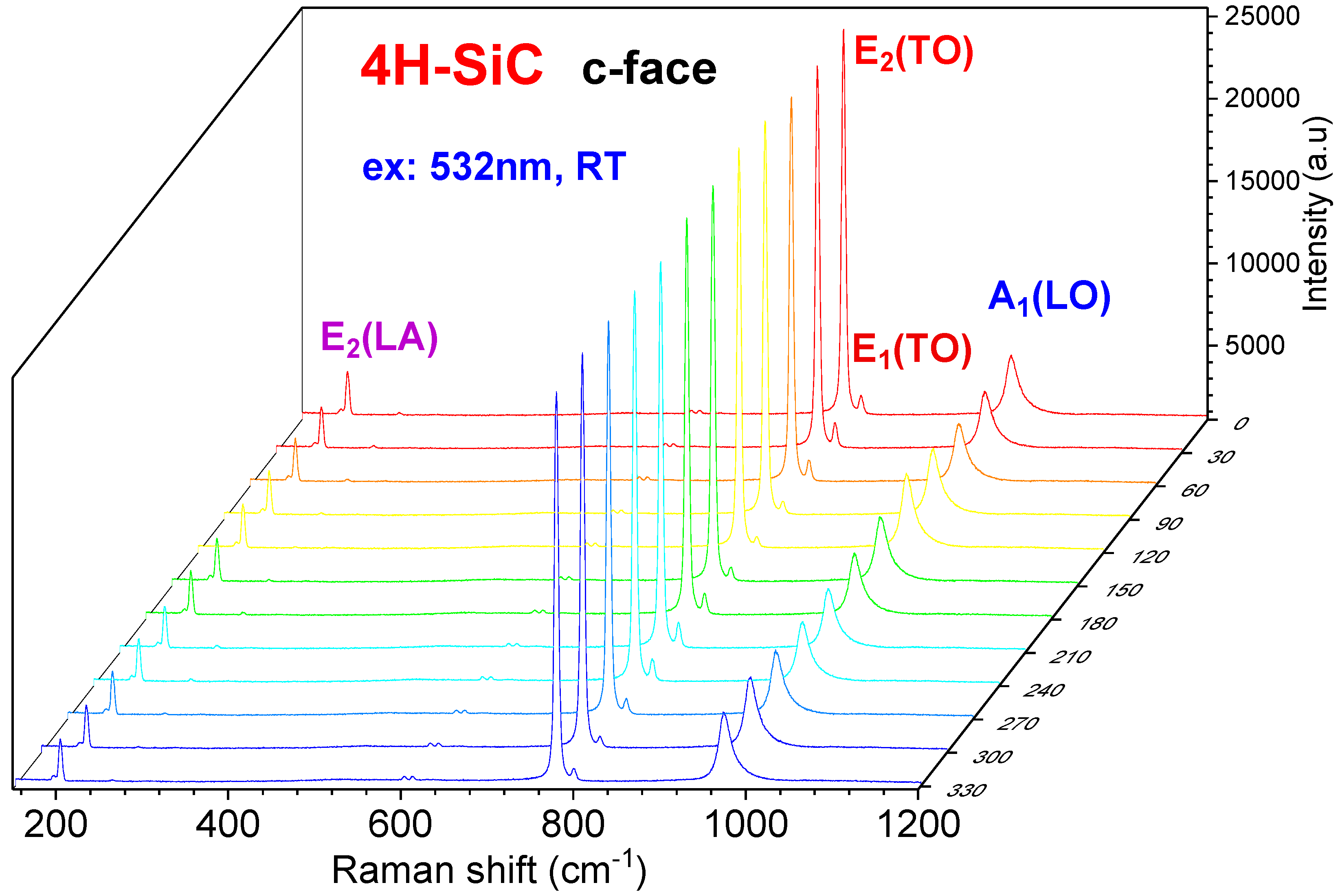
3.1. Angular-Dependent Raman Spectra from c-face 4H-SiC
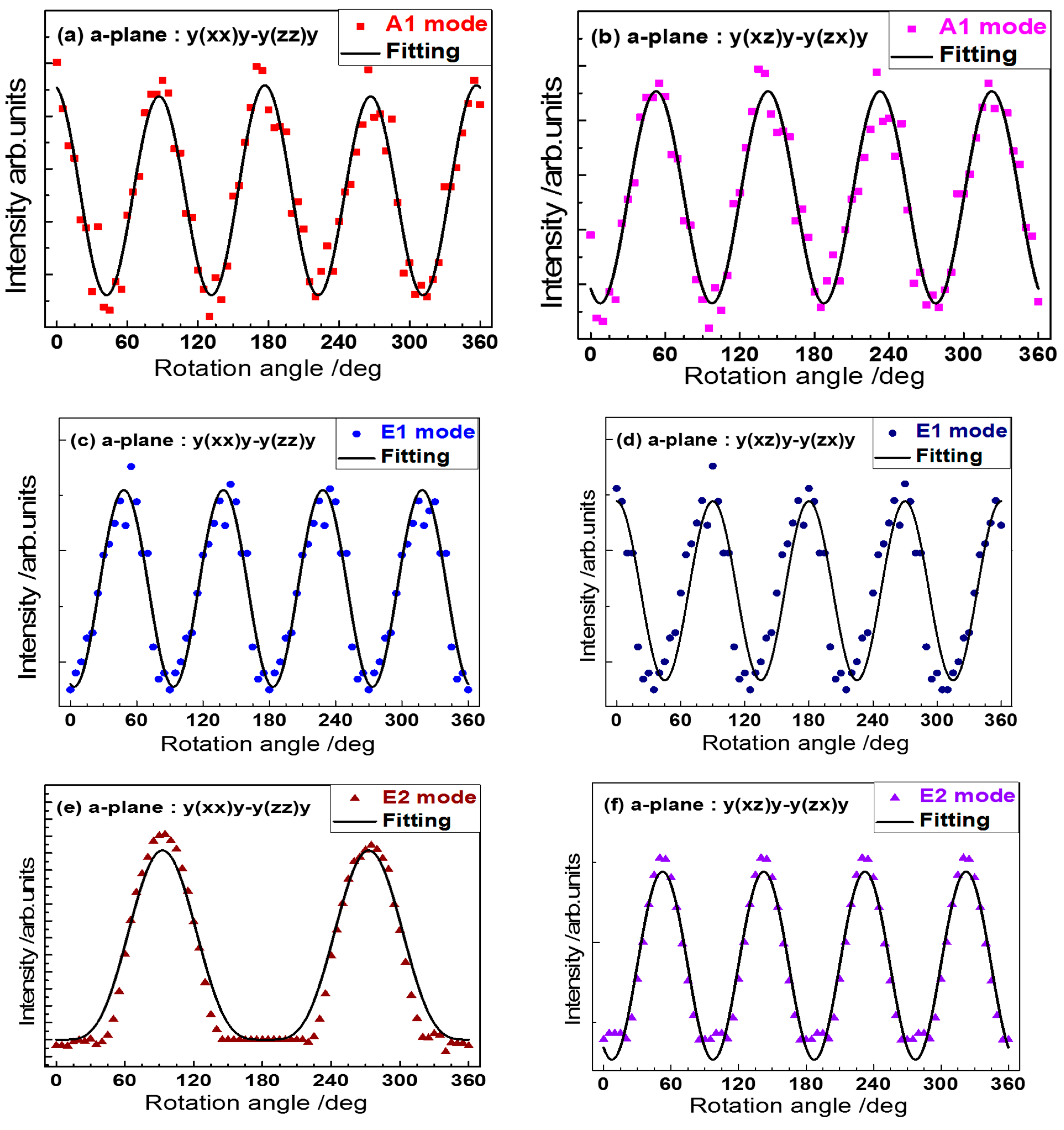
3.2. Angular-Dependent Raman Spectra from a-Face 4H-SiC
3.3. Raman Selection Rules
3.4. Rotation Raman Spectral Intensities and Analyses
3.5. Raman Tensor Element Analyses
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Choyke, W.J.; Matsunami, H.; Pensl, G. (Eds.) Silicon Carbide: Recent Major Advances; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Feng, Z.C. (Ed.) SiC Power Materials—Devices and Applications; Springer: Berlin, Germany, 2004. [Google Scholar]
- Friedrichs, P.; Kimoto, T.; Ley, L.; Pensl, G. (Eds.) Silicon Carbide: Volume 1: Growth, Defects, and Novel Applications (2009); Silicon Carbide: Volume 2: Power Devices and Sensors; WILEY-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Saddow, S.E. (Ed.) Silicon Carbide Biotechnology; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Kimoto, T.; Co, J.A. (Eds.) Fundamentals of Silicon Carbide Technology: Growth, Characterization, Devices and Applications; Wiley Publishing: Hoboken, NJ, USA, 2014. [Google Scholar]
- Feng, Z.C. (Ed.) Handbook of Silicon Carbide and Related Materials; Taylar & Francis, CRC Publishing: London, UK; New York, NY, USA, 2022; in press. [Google Scholar]
- Choyke, W.J.; Pensl, G. Physical properties of SiC. MRS Bull. 1997, 22, 25–29. [Google Scholar] [CrossRef]
- Wright, N.G.; Horsfall, A.B. SiC sensors: A review. J. Phys. D Appl. Phys. 2007, 40, 6345–6354. [Google Scholar] [CrossRef]
- Dhar, S.; Haney, S.; Cheng, L.; Ryu, S.R.; Agarwal, A.K.; Yu, L.C.; Cheung, K.P. Inversion layer carrier concentration and mobility in 4H–SiC metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2010, 108, 054509. [Google Scholar] [CrossRef]
- Saddow, S.E.; Frewin, C.L.; Nezafatil, M.; Oliveros, I.A.; Afroz, S.; Register, J.; Reyes, M.; Thomas, S. 3C-SiC on Si: A Bio- and Hemo-compatible Material for Advanced Nano-Bio Devices. In Proceedings of the IEEE Nanotechnology Materials and Devices Conference (NMDC), Aci Castello, Italy, 12–15 October 2014; pp. 46–53. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, F.; Wan, L.; Yang, Q.; Feng, Z.C. Raman scattering study on anisotropic property in wurtzite 4H-SiC. J. Light Scatt. 2018, 30, 37–42. [Google Scholar] [CrossRef]
- Klahold, W.M.; Choyke, W.J.; Devaty, R.P. Band structure properties, phonons, and exciton fine structure in 4H-SiC measured by wavelength-modulated absorption and low-temperature photoluminescence. Phys. Rev. B 2020, 102, 205203. [Google Scholar] [CrossRef]
- Han, L.; Liang, L.; Kang, Y.; Qiu, Y. Review of SiC IGBT: Models, Fabrications, Characteristics and Applications. IEEE Trans. Power Electron. 2021, 36, 2080–2093. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, T.; Fan, J.; Maddi, H.J.R.; White, M.H.; Agarwal, A.K. Effects of JFET Region Design and Gate Oxide Thickness on the Static and Dynamic Performance of 650 V SiC Planar Power MOSFETs. Materials 2022, 15, 5995. [Google Scholar] [CrossRef]
- Sultan, N.M.; Albarody, T.M.B.; Al-Jothery, H.K.M.; Abdullah, M.A.; Mohammed, H.G.; Obodo, K.O. Thermal Expansion of 3C-SiC Obtained from In-Situ X-ray Diffraction at High Temperature and First-Principal Calculations. Materials 2022, 15, 6229. [Google Scholar] [CrossRef] [PubMed]
- Harima, H.; Nakashima, S.I.; Uemura, T. Raman scattering from anisotropic LOphonon–plasmon–coupled mode in ntype 4H– and 6H–SiC. J. Appl. Phys. 1995, 78, 1996. [Google Scholar] [CrossRef]
- Nakashima, S.; Harima, H. Raman investigation of SiC polytypes. Phys. Status Solidi A 1997, 162, 37. [Google Scholar] [CrossRef]
- Burton, J.C.; Sun, L.; Pophristic, M.; Long, F.H.; Feng, Z.C.; Ferguson, I. Spatial characterization of doped SiC wafers by Raman spectroscopy. J. Appl. Phys. 1998, 84, 6268–6273. [Google Scholar] [CrossRef]
- Burton, J.C.; Sun, L.; Long, F.H.; Feng, Z.C.; Ferguson, I. First- and second-order Raman scattering from semi-insulating 4H-SiC. Phys. Rev. B 1999, 59, 7282–7284. [Google Scholar] [CrossRef]
- Han, R.; Han, B.; Wang, D.H.; Li, C. Temperature dependence of Raman scattering from 4H-SiC with hexagonal defects. Appl. Phys. Lett. 2011, 99, 011912. [Google Scholar] [CrossRef]
- Sun, H.Y.; Lien, S.C.; Qiu, Z.R.; Wang, H.C.; Mei, T.; Liu, C.W.; Feng, Z.C. Temperature dependence of Raman scattering in bulk 4H-SiC with different carrier concentration. Opt. Express 2013, 21, 26475–26482. [Google Scholar] [CrossRef] [PubMed]
- Tseng, Y.C.; Cheng, Y.C.; Lee, Y.C.; Ma, D.L.; Yu, B.Y.; Lin, B.C.; Chen, H.L. Using Visible Laser-Based Raman Spectroscopy to Identify the Surface Polarity of Silicon Carbide. J. Phys. Chem. C 2016, 120, 18228–18234. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D.; Wang, F.; Xu, G.; Tin, C.C.; Lin, T.; Feng, Z.; Feng, Z.C. Efficient quality analysis of homo-epitaxial 4H-SiC thin films by the forbidden Raman Scattering Mode. Opt. Mater. Express 2018, 8, 119–127. [Google Scholar] [CrossRef]
- Shimada, K.; Asada, K.; Yodo, M.; Ohtani, N. Raman scattering microscopy imaging of basal plane stacking faults and associated partial dislocations in 4H-SiC crystals. J. Appl. Phys. 2020, 127, 165704. [Google Scholar] [CrossRef]
- Song, Y.; Xu, Z.; Liu, T.; Rommel, M.; Wang, H.; Wang, Y.; Fang, F. Depth Profiling of Ion-Implanted 4H–SiC Using Confocal Raman Spectroscopy. Crystals 2020, 10, 131. [Google Scholar] [CrossRef]
- Chakravorty, A.; Singh, B.; Jatav, H.; Ojha, S.; Singh, J.; Kanjilal, D.; Kabiraj, D. Intense ionizing irradiation-induced atomic movement toward recrystallization in 4H-SiC. J. Appl. Phys. 2020, 128, 165901. [Google Scholar] [CrossRef]
- Huang, M.; Yang, Z.; Wang, S.; Liu, J.; Gong, M.; Ma, Y.; Liu, J.; Zhai, P.; Sun, Y.; Li, Y. Recrystallization effects in GeV Bi ion implanted 4H-SiC Schottky barrier diode investigated by cross-sectional Micro-Raman spectroscopy. Nucl. Inst. Methods Phys. Res. B 2020, 478, 5–10. [Google Scholar] [CrossRef]
- Wang, C.; Fang, Z.; Yi, A.; Yang, B.; Wang, Z.; Zhou, L.; Shen, C.; Zhu, Y.; Zhou, Y.; Bao, R.; et al. High-Q microresonators on 4H-silicon-carbide-oninsulator platform for nonlinear photonics. Light Sci. Appl. 2021, 10, 139. [Google Scholar] [CrossRef] [PubMed]
- Meli, A.; Muoio, A.; Trotta, A.; Meda, L.; Parisi, M.; La Via, F. Epitaxial Growth and Characterization of 4H-SiC for Neutron Detection Applications. Materials 2021, 14, 976. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Xiao, A.; Li, R.; Wang, M.; He, S.; Sun, M.; Wang, L.; Qu, C.; Qiu, W. Angle-Resolved Intensity of Polarized Micro-Raman Spectroscopy for 4H-SiC. Crystals 2021, 11, 626. [Google Scholar] [CrossRef]
- Steiner, J.; Wellmann, P.J. Impact of Mechanical Stress and Nitrogen Doping on the Defect Distribution in the Initial Stage of the 4H-SiC PVT Growth Process. Materials 2022, 15, 1897. [Google Scholar] [CrossRef] [PubMed]
- Usami, Y.; Imokawa, K.; Nohdomi, R.; Sunahara, A.; Mizoguchi, H. Phase Changes of 4H-SiC in Excimer Laser Doping. J. Electron. Mater. 2022, 51, 3766–3772. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Y.; Liu, H.; Chen, H.; Li, X.; Liu, D.; Zhu, F.; Liu, Z.; Cheng, Y. Investigation of the recovery behavior of irradiation defects induced by a neutron in 4H-SiC combining Raman scattering and lattice parameters. J. Mater. Res. 2022, 37, 2910–2919. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.C.; Wang, L.; Zhu, L.; Wang, Z.L. Highly Sensitive Photoelectric Detection and Imaging Enhanced by the Pyro-Phototronic Effect Based on a Photoinduced Dynamic Schottky Effect in 4H-SiC. Adv. Mater. 2022, 34, 2204363. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, S.; Yan, G.; Shen, Z.; Zhao, W.; Wang, L.; Liu, X. Investigation on Step-Bunched Homoepitaxial Layers Grown on On-Axis 4H-SiC Substrates via Molten KOH Etching. Crystals 2022, 12, 788. [Google Scholar] [CrossRef]
- Lin, H.C.; Feng, Z.C.; Chen, M.S.; Shen, Z.X.; Ferguson, I.T.; Lu, W. Raman Scattering Study on Anisotropic Property of Wurtzite GaN. J. Appl. Phys. 2009, 105, 036102. [Google Scholar] [CrossRef]
- Zheng, W.; Zheng, R.S.; Wu, H.L.; Li, F.D. Strongly anisotropic behavior of A1(TO) phonon mode in bulk AlN. J. Alloys Compd. 2014, 584, 374–376. [Google Scholar] [CrossRef]
- Jin, L.; Wu, H.L.; Zhang, Y.; Qin, Z.Y.; Shi, Y.Z.; Cheng, H.J.; Zheng, R.S.; Chen, W.H. The growth mode and Raman scattering characterization of m-AlN crystals grown by PVT method. J. Alloys Compd. 2020, 824, 153935. [Google Scholar] [CrossRef]
- Zheng, W.; Zheng, R.S.; Huang, F.; Wu, H.L.; Li, F.D. Raman tensor of AlN bulk single crystal. Photonics Res. 2015, 3, 38–43. [Google Scholar] [CrossRef]
- Zheng, W.; Yan, J.; Li, F.; Huang, F. Elucidation of “phase difference” in Raman tensor formalism. Photonics Res. 2018, 6, 709–712. [Google Scholar] [CrossRef]
- Zheng, W.; Yan, J.; Li, F.; Huang, F. Raman spectroscopy regulation in van der Waals crystals. Photonics Res. 2018, 6, 991–995. [Google Scholar] [CrossRef]
- Inui, T.; Tanabe, Y.; Onodera, Y. Group Theory and Its Applications in Physics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Olego, D.; Cardona, M. Raman scattering by coupled LO-phonon-plasmon modes and forbidden TO-phonon Raman scattering in heavily doped p-type GaAs. Phys. Rev. B 1981, 24, 7217–7232. [Google Scholar] [CrossRef]
- Strach, T.; Brunen, J.; Lederle, B.; Zegenhagen, J.; Cardona, M. Determination of the phase difference between the Raman tensor elements of the A1g-like phonons in SmBa2Cu3O7-δ. Phys. Rev. B 1998, 57, 1292–1297. [Google Scholar] [CrossRef]
- Shi, S.; Yu, Y.; Wang, N.; Zhang, Y.; Shi, W.; Liao, X.; Duan, N. Investigation of the Anisotropy of 4H-SiC Materials in Nanoindentation and Scratch Experiments. Materials 2022, 15, 2496. [Google Scholar] [CrossRef]

| A-Plane Tensor Element | |||
|---|---|---|---|
| A1 mode | |a/d| | 1.003 ± 0.024 | 0.198 ± 0.019 |
| A1 mode | |b/d| | 1.004 ± 0.023 | 0.198 ± 0.020 |
| 111.37° | 92.86° | ||
| E1 mode | |c/d| | 0.388 ± 0.029 | 0.292 ± 0.013 |
| E2 mode | |d/d| | 1.000 ± 0.007 | 1.000 ± 0.006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.C.; Zhao, D.; Wan, L.; Lu, W.; Yiin, J.; Klein, B.; Ferguson, I.T. Angle-Dependent Raman Scattering Studies on Anisotropic Properties of Crystalline Hexagonal 4H-SiC. Materials 2022, 15, 8751. https://doi.org/10.3390/ma15248751
Feng ZC, Zhao D, Wan L, Lu W, Yiin J, Klein B, Ferguson IT. Angle-Dependent Raman Scattering Studies on Anisotropic Properties of Crystalline Hexagonal 4H-SiC. Materials. 2022; 15(24):8751. https://doi.org/10.3390/ma15248751
Chicago/Turabian StyleFeng, Zhe Chuan, Dishu Zhao, Lingyu Wan, Weijie Lu, Jeffrey Yiin, Benjamin Klein, and Ian T. Ferguson. 2022. "Angle-Dependent Raman Scattering Studies on Anisotropic Properties of Crystalline Hexagonal 4H-SiC" Materials 15, no. 24: 8751. https://doi.org/10.3390/ma15248751
APA StyleFeng, Z. C., Zhao, D., Wan, L., Lu, W., Yiin, J., Klein, B., & Ferguson, I. T. (2022). Angle-Dependent Raman Scattering Studies on Anisotropic Properties of Crystalline Hexagonal 4H-SiC. Materials, 15(24), 8751. https://doi.org/10.3390/ma15248751






