Numerical Simulation of Elastic Wave Field in Viscoelastic Two-Phasic Porous Materials Based on Constant Q Fractional-Order BISQ Model
Abstract
:1. Introduction
2. Methods
2.1. Constant Q Fractional-Order Constitutive Relationship
2.2. Constant Q Wave Propagation Equations
2.3. Finite-Difference Numerical Solution
2.3.1. Discretisation of Fractional Order Time Derivatives
2.3.2. Stability and Absorption Boundary Conditions
3. Results and Discussion
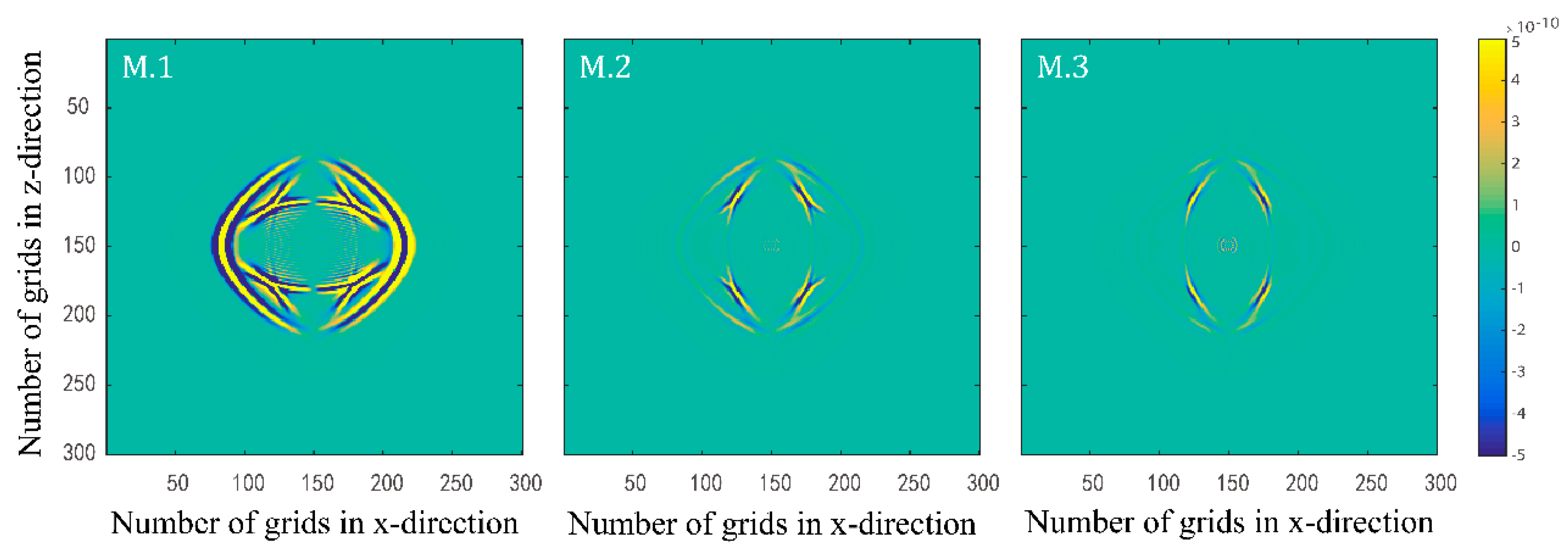
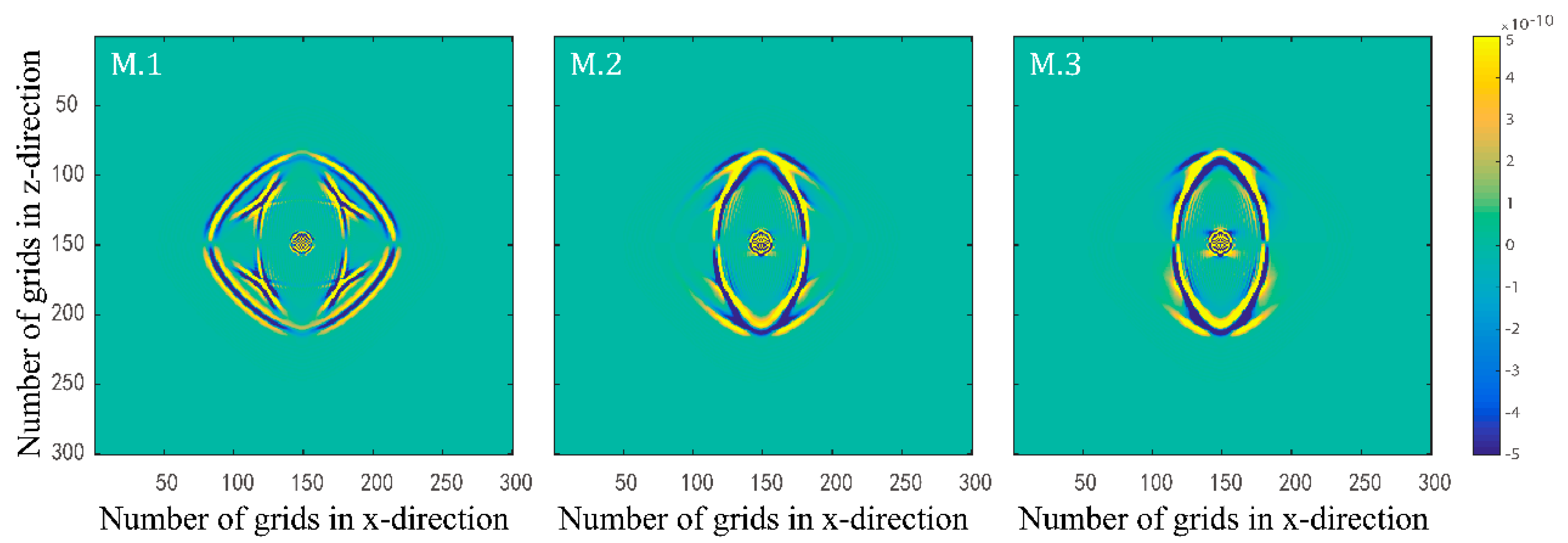
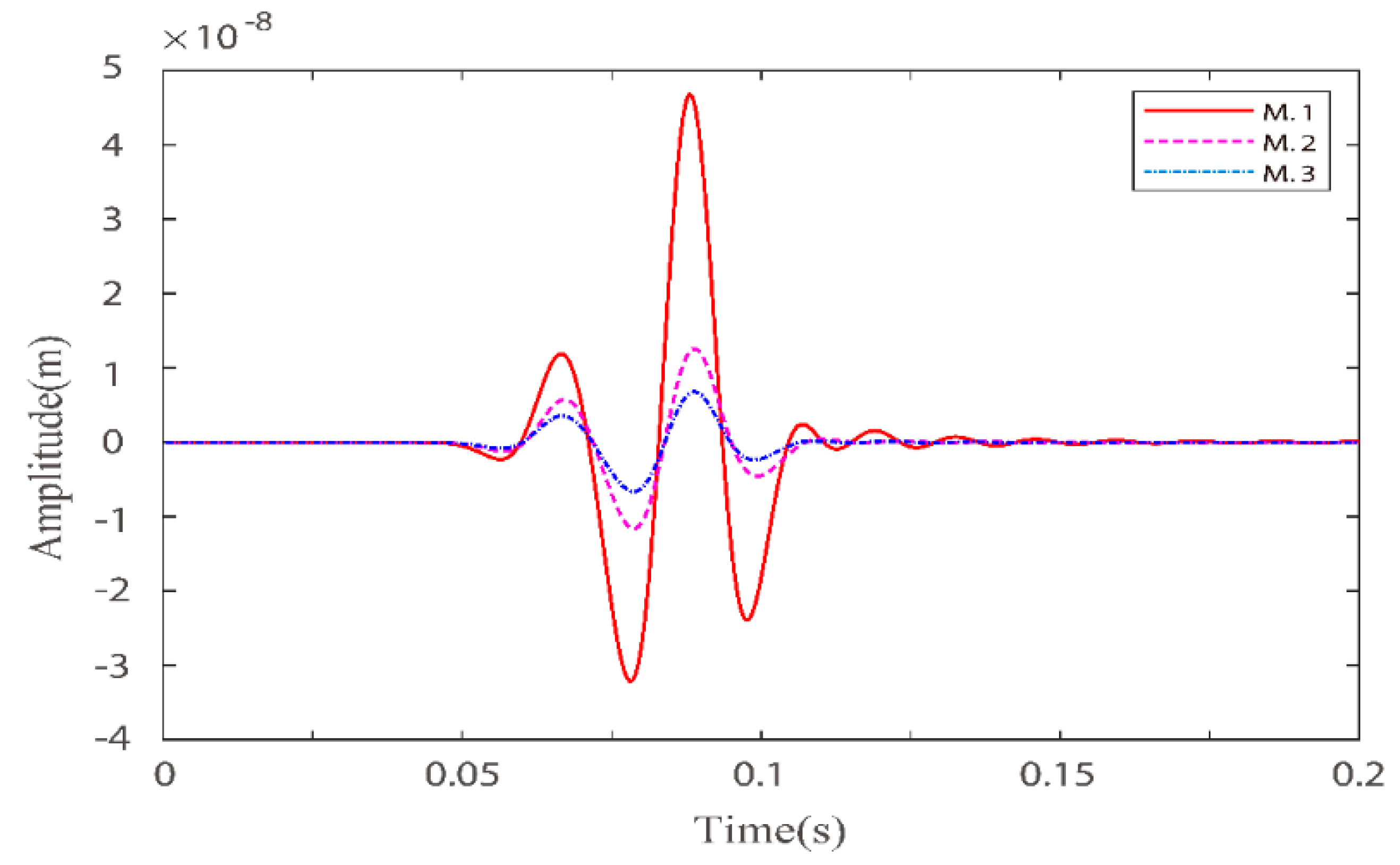
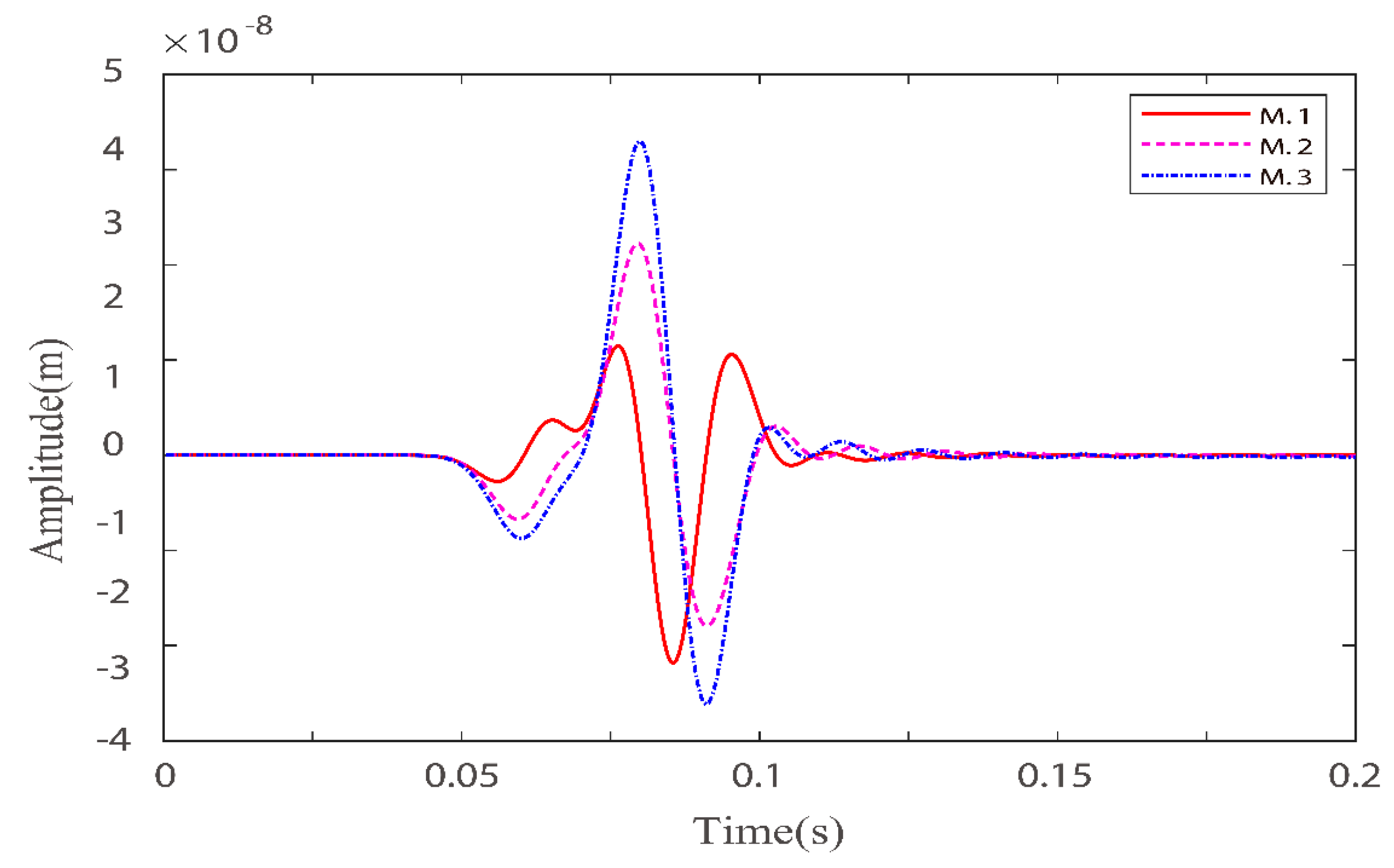
3.1. Single Layer Model with Different Phase Boundaries
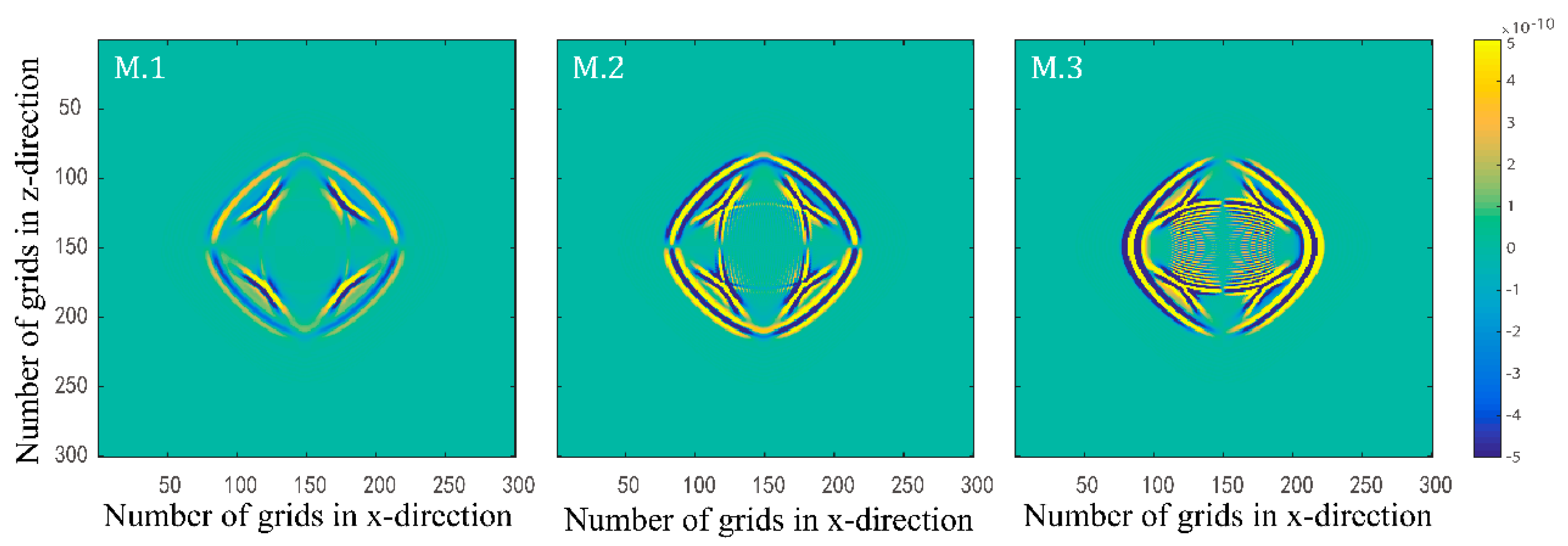
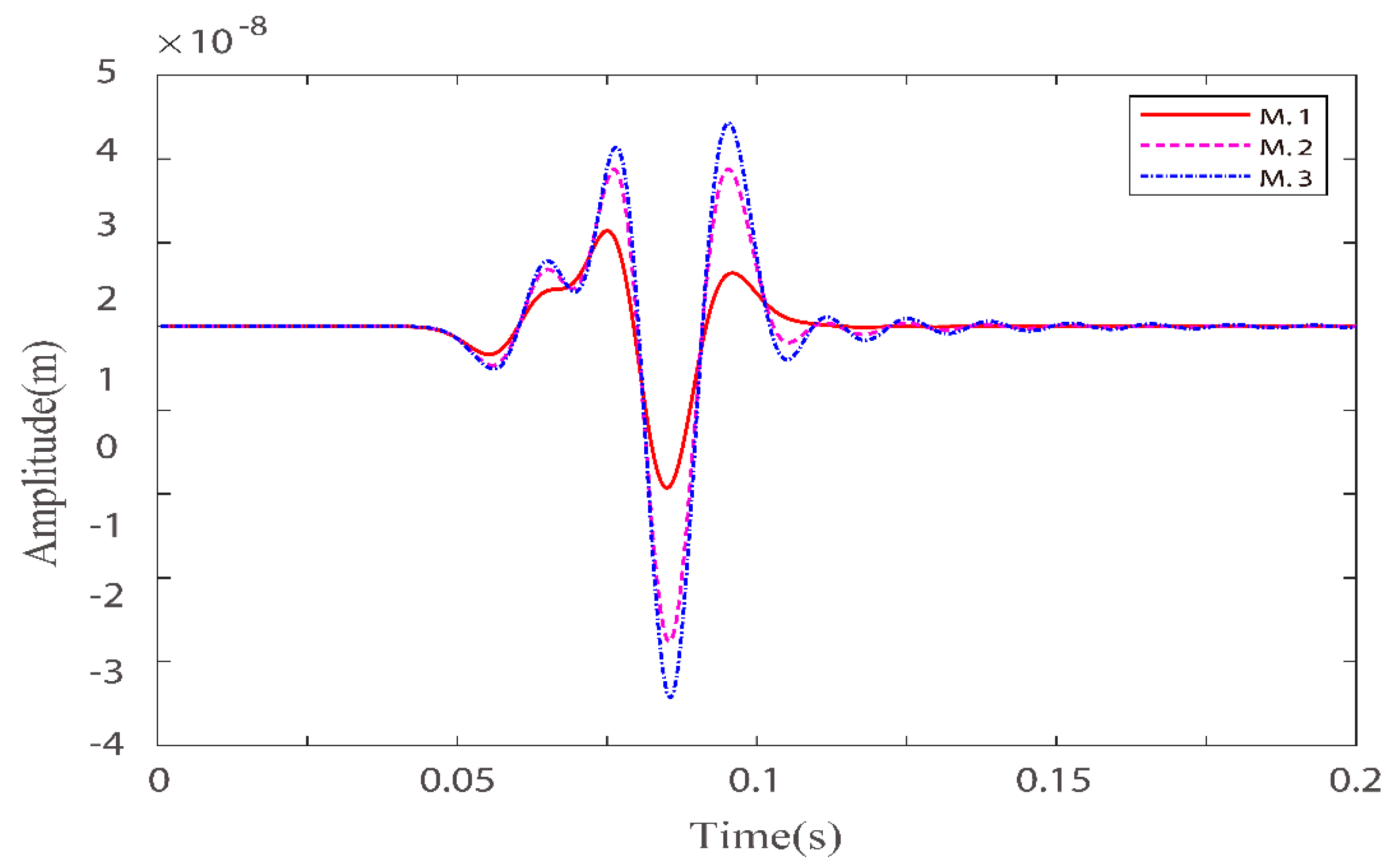
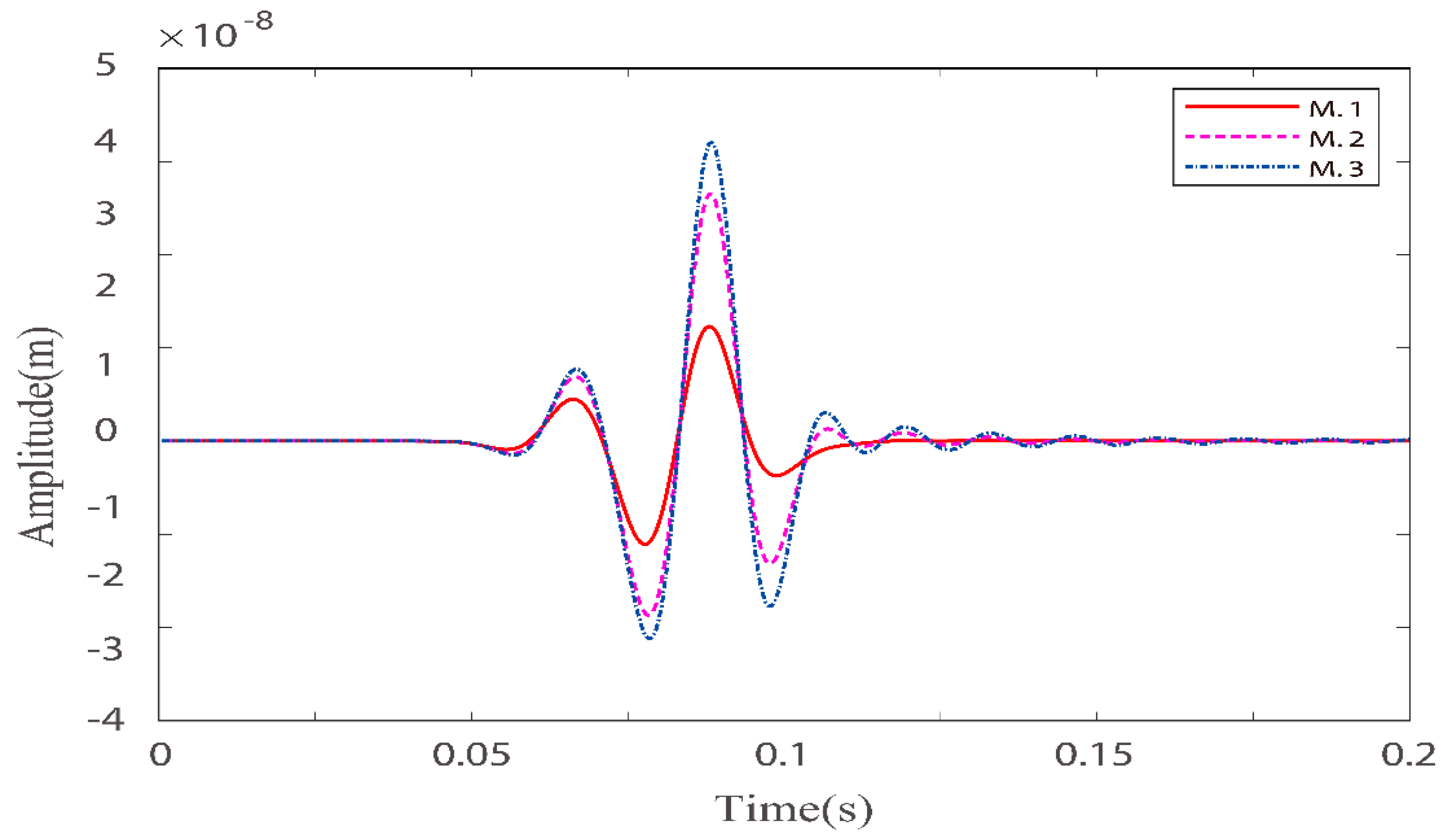
3.2. Single Layer Models with Different Quality Factor Groups
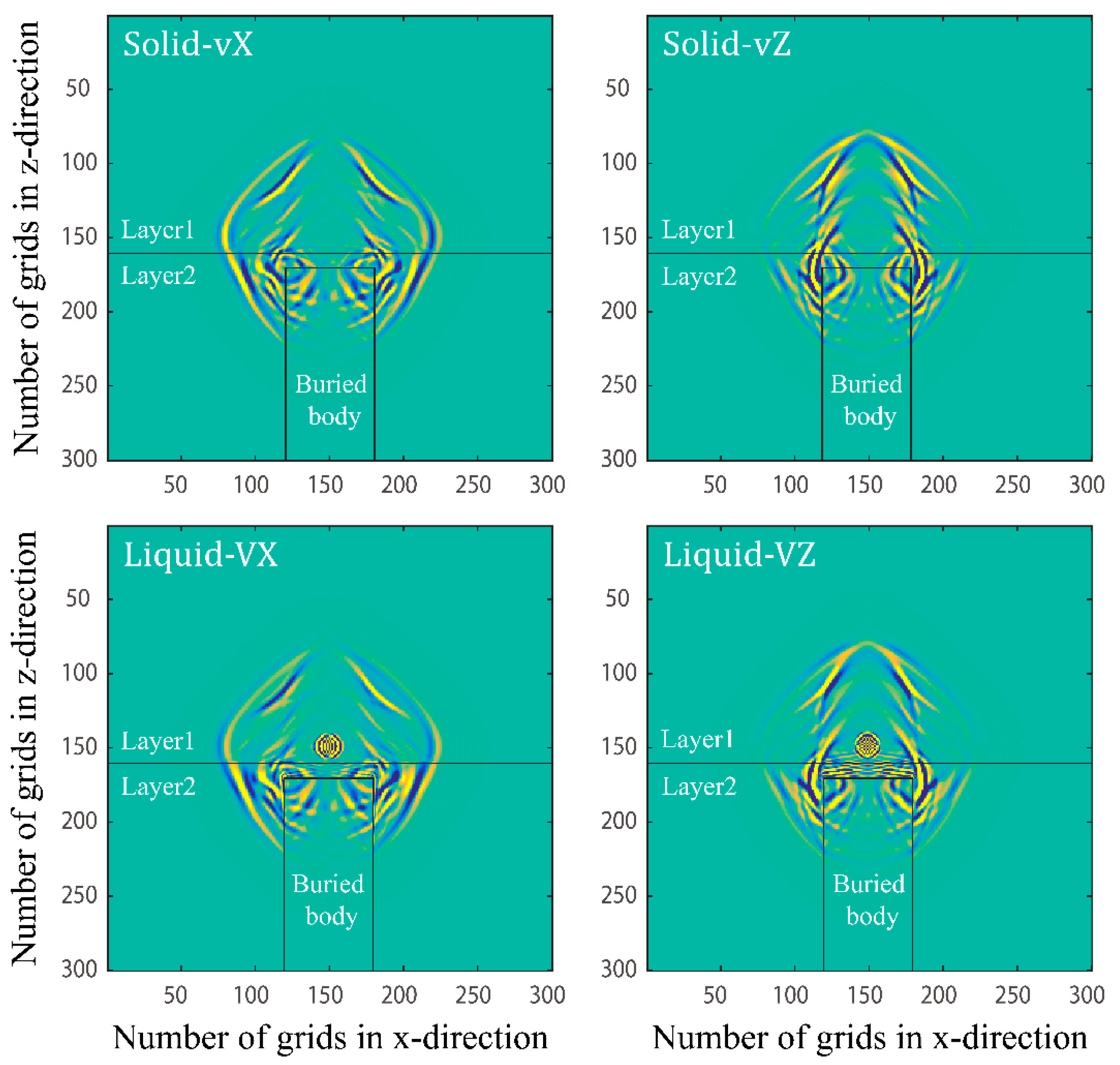
3.3. Double Layer Model with Buried Body
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiao, J.; Ghoreishi, S.M.; Moradi, Z.; Oslub, K. Coupled particle swarm optimization method with genetic algorithm for the static–dynamic performance of the magneto-electro-elastic nanosystem. Eng. Comput. 2021, 1–15. [Google Scholar] [CrossRef]
- Yu, X.M.; Allam, M.; Zohre, M. Electroelastic high-order computational continuum strategy for critical voltage and frequency of piezoelectric NEMS via modified multi-physical couple stress theory. Mech. Syst. Signal Process. 2022, 165, 1–18. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, Y.; Vafaei, P.; Moradi, Z.; Davoudi, M. An iterative simulation algorithm for large oscillation of the applicable 2d-electrical system on a complex nonlinear substrate. Eng. Comput. 2021, 1–13. [Google Scholar] [CrossRef]
- Abbas, E.; Alaa, H.A. Effect of Maximum Size of Aggregate on the Behavior of Reinforced Concrete Beams Analyzed using Meso Scale Modeling. J. Eng. 2020, 26, 143–155. [Google Scholar] [CrossRef]
- Picchi, D.; Battiato, I. The impact of pore-scale flow regimes on upscaling of immiscible two-phase flow in porous media. Water Resour. Res. 2018, 54, 6683–6707. [Google Scholar] [CrossRef]
- Bao, Z.; Niu, Z.; Jiao, K. Numerical simulation for metal foam two-phase flow field of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2019, 44, 6229–6244. [Google Scholar] [CrossRef]
- Garofalo, F.; Socco, L.V.; Foti, S. Joint inversion of seismic and electrical data in saturated porous media. Near Surf. Geophys. 2021, 20, 64–81. [Google Scholar] [CrossRef]
- Yang, S.; Bai, C.; Zhou, B. Wavefield modeling in two-phase media including undulated topography based on reformulated BISQ model by Curvilinear Grid FD method. Chin. J. Geophys. 2018, 61, 3356–3373. [Google Scholar]
- Kumar, D.; Singh, J.; Tanwar, K.; Baleanu, D. A new fractional exothermic reactions model having constant heat source in porous media with power, exponential and Mittag-Leffler laws. Int. J. Heat Mass Transf. 2019, 138, 1222–1227. [Google Scholar] [CrossRef]
- Xu, W.; Jiao, Y. Theoretical framework for percolation threshold, tortuosity and transport properties of porous materials containing 3D non-spherical pores. Int. J. Eng. Sci. 2019, 134, 31–46. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Depollier, C.; Ogam, E.; Mitri, F.G. Wave propagation in porous materials. Comput. Exp. Stud. Acoust. Waves 2018, 6, 99. [Google Scholar]
- Ni, J.; Gu, H.; Wang, Y. Seismic wave equation formulated by generalized viscoelasticity in fluid-saturated porous media. Geophysics 2021, 87, 1–37. [Google Scholar] [CrossRef]
- Christmann, J.; Mueller, R.; Humbert, A. On nonlinear strain theory for a viscoelastic material model and its implications for calving of ice shelves. J. Glaciol. 2019, 65, 212–224. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Xu, Z.; Ge, T.; Xu, C. Equivalent fractional order micro-structure standard linear solid model for viscoelastic materials. Chin. J. Theor. Appl. Mech. 2017, 49, 1059–1069. [Google Scholar]
- Liu, H.P.; Anderson, D.L.; Kanamori, H. Velocity dispersion due to anelasticity. Geophys. J. Int. 1976, 47, 41–58. [Google Scholar] [CrossRef] [Green Version]
- Nie, J.X.; Ba, J.; Yang, D.H.; Yan, X.F.; Yuan, Z.Y.; Qiao, H.P. BISQ model based on a Kelvin-Voigt viscoelastic frame in a partially saturated porous medium. Appl. Geophys. 2012, 9, 213–222. [Google Scholar] [CrossRef]
- Kjartansson, E. Constant Q-wave propagation and attenuation. J. Geophys. Res. Atmos. 1979, 84, 4737–4748. [Google Scholar] [CrossRef] [Green Version]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar]
- Emmerich, H.; Korn, M. Incorporation of attenuation into time-domain computations of seismic wave fields. Geophysics 1987, 52, 1252–1264. [Google Scholar] [CrossRef]
- Carcione, J.M.; Dan, K.; Kosloff, R. Wave propagation simulation in a linear viscoacoustic medium. Geophys. J. 1988, 93, 393–401. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; José, M.; Carcione, J.; Harris, M. Approximating constant-Q seismic propagation in the time domain. Geophys. Prospect. 2013, 61, 931–940. [Google Scholar] [CrossRef]
- Carcione, J.M.; Cavallin, F.; Mainardi, F.; Hanyga, A. Time-domain modeling of constant-Q elastic waves using fractional derivatives. Pure Appl. Geophys. 2002, 159, 1719–1736. [Google Scholar] [CrossRef]
- Carcione, J.M. Theory and modeling of constant-Q P- and S-waves using fractional time derivatives. Geophysics 2009, 74, 1JF–Z17. [Google Scholar] [CrossRef]
- Sene, N. Analytical solutions of Hristov diffusion equations with non-singular fractional derivatives. Choas 2019, 29, 023112. [Google Scholar] [CrossRef] [PubMed]
- Sene, N. Integral balance methods for stokes’ first, equation described by the left generalized fractional derivative. Physics 2019, 1, 154–166. [Google Scholar] [CrossRef] [Green Version]
- Sene, N. Second-grade fluid model with Caputo-Liouville generalized fractional derivative. Chaos Solitons Fractals 2020, 133, 109631. [Google Scholar] [CrossRef]
- Gulen, S.; Popescu, C.; Sari, M. A new approach for the blackscholes model with linear and nonlinear volatilities. Mathematics 2019, 7, 760. [Google Scholar] [CrossRef] [Green Version]
- Ozdemira, N.; Yavuz, M. Numerical solution of fractional blackscholes equation by using the multivariate padé approximation. Acta Phys. Polonica A 2017, 132, 1050–11053. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N. A different approach to the European option pricing model with new fractional operator. Math. Modell. Nat. Phenom. 2018, 13, 12. [Google Scholar] [CrossRef] [Green Version]
- Khader, M.M. On the numerical solutions for the fractional diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2535–2542. [Google Scholar] [CrossRef]
- Deng, W.; Morozov, L.B. Mechanical interpretation and generalization of the Cole-Cole model in viscoelasticity. Geophysics 2018, 6, 1ND–Z38. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acous. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Plona, T.J. Observation of a second bulk compressional wave in a porous at ultrasonic frequencies. Appl. Phys. Lett. 1980, 36, 259–261. [Google Scholar] [CrossRef] [Green Version]
- Kelder, O.; Smeulders, D.M.J. Observation of the BISQ slow wave in water-saturated Nivelsteiner sandstone. Geophysics 1997, 62, 1794–1796. [Google Scholar] [CrossRef]
- Dvorkin, J.; Nur, A. Dynamic poroelasticity: A unified model with the squirt and the BISQ mechanisms. Geophysics 1993, 58, 466–599. [Google Scholar] [CrossRef]
- Parra, J.O. Poroelastic model to relate seismic wave attenuation and dispersion to permeability anisotropy. Geophysics 2000, 65, 202–210. [Google Scholar] [CrossRef]
- Yang, D.H.; Zhang, Z.J. Poroelastic wave equation including the BISQ/Squirt mechanism and solid/fluid coupling anisotropy. Wave Motion 2002, 35, 223–245. [Google Scholar] [CrossRef]
- Christensen, R.M. Theory of Viscoelasticity, an Introduction; Academic Press: San Diego, CA, USA, 1982. [Google Scholar]
- Caputo, M.; Mainardi, F. Linear Models of Dissipation in Anelastic Solids. La Riv. Nuovo Cim. 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Zhu, Y.; Tsvankin, I. Plane-wave propagation in attenuative transversely isotropic. Geophysics 2006, 71, T17–T30. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Cerjan, C.; Kosloff, D.; Kosloff, R.; Reshef, M. A nonreflecting boundary condition for discrete acoustic and elastic wave equation. Geophysics 1985, 50, 705–708. [Google Scholar] [CrossRef]

| Solid Phase Parameters | Unit | Model 1 | Model 2 | Model 3 |
| 2050 | 2050 | 2050 | ||
| Gpa | 7.78 | 7.78 | 7.78 | |
| 0.3 | 0.3 | 0.3 | ||
| 30 | 30 | 30 | ||
| 15 | 15 | 15 | ||
| 3300 | 3300 | 3300 | ||
| 3167 | 3167 | 3167 | ||
| 1600 | 1600 | 1600 | ||
| Fluid Phase Parameters | Unit | Model 1 | Model 2 | Model 3 |
| 1040 | 1040 | 1040 | ||
| Gpa | 0.372 | 0.372 | 0.372 | |
| 420 | 420 | 420 | ||
| md | 20 | 20 | 20 | |
| cp | 0.001 | 0.05 | 0.09 |
| Solid Phase Parameters | Unit | Model 1 | Model 2 | Model 3 |
| 2050 | 2050 | 2050 | ||
| Gpa | 7.78 | 7.78 | 7.78 | |
| 0.3 | 0.3 | 0.3 | ||
| 10 | 30 | 60 | ||
| 5 | 15 | 30 | ||
| 3300 | 3300 | 3300 | ||
| 3167 | 3167 | 3167 | ||
| 1600 | 1600 | 1600 | ||
| Fluid Phase Parameters | Unit | Model 1 | Model 2 | Model 3 |
| 1040 | 1040 | 1040 | ||
| Gpa | 0.372 | 0.372 | 0.372 | |
| 420 | 420 | 420 | ||
| md | 20 | 20 | 20 | |
| cp | 0.001 | 0.001 | 0.001 |
| Solid Phase Parameters | Unit | Layer 1 | Layer 2 | Buried Body |
| 2050 | 2050 | 2050 | ||
| Gpa | 7.78 | 7.78 | 7.78 | |
| 0.3 | 0.3 | 0.3 | ||
| 20 | 30 | 40 | ||
| 10 | 15 | 20 | ||
| 3300 | 3300 | 3300 | ||
| 3167 | 3167 | 3167 | ||
| 1600 | 1600 | 1600 | ||
| Fluid Phase Parameters | Unit | Layer 1 | Layer 2 | Buried Body |
| 1040 | 1040 | 1040 | ||
| Gpa | 0.372 | 0.372 | 0.372 | |
| 420 | 420 | 420 | ||
| md | 20 | 20 | 20 | |
| cp | 0.01 | 0.01 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, N.; Wang, M.; Qiu, B.; Tao, Y. Numerical Simulation of Elastic Wave Field in Viscoelastic Two-Phasic Porous Materials Based on Constant Q Fractional-Order BISQ Model. Materials 2022, 15, 1020. https://doi.org/10.3390/ma15031020
Hu N, Wang M, Qiu B, Tao Y. Numerical Simulation of Elastic Wave Field in Viscoelastic Two-Phasic Porous Materials Based on Constant Q Fractional-Order BISQ Model. Materials. 2022; 15(3):1020. https://doi.org/10.3390/ma15031020
Chicago/Turabian StyleHu, Ning, Maofa Wang, Baochun Qiu, and Yuanhong Tao. 2022. "Numerical Simulation of Elastic Wave Field in Viscoelastic Two-Phasic Porous Materials Based on Constant Q Fractional-Order BISQ Model" Materials 15, no. 3: 1020. https://doi.org/10.3390/ma15031020
APA StyleHu, N., Wang, M., Qiu, B., & Tao, Y. (2022). Numerical Simulation of Elastic Wave Field in Viscoelastic Two-Phasic Porous Materials Based on Constant Q Fractional-Order BISQ Model. Materials, 15(3), 1020. https://doi.org/10.3390/ma15031020






