Crystal Plasticity Simulation of Yield Loci Evolution of SUS304 Foil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
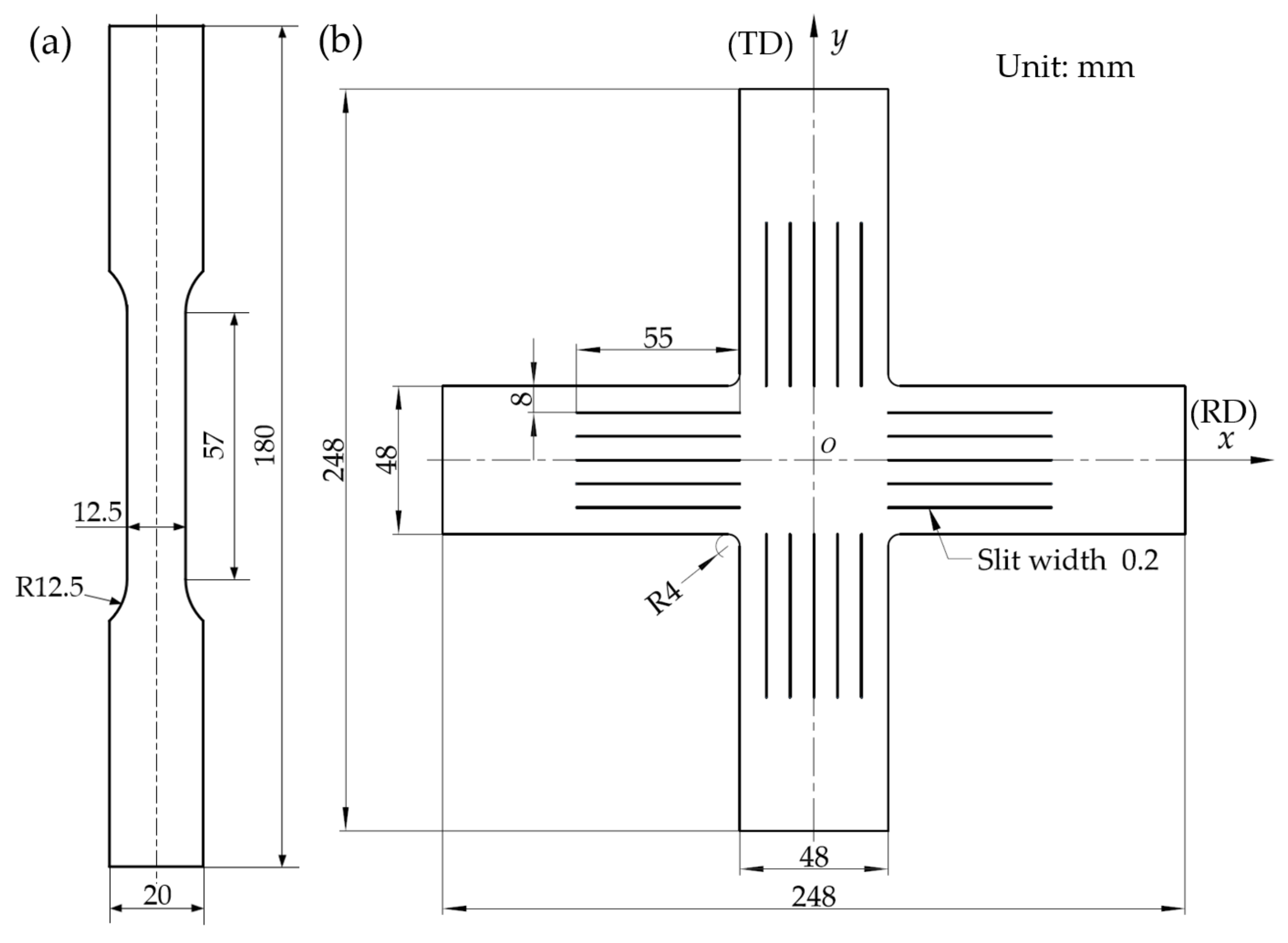
2.2. Experimental Process
2.3. Theory of Crystal Plasticity
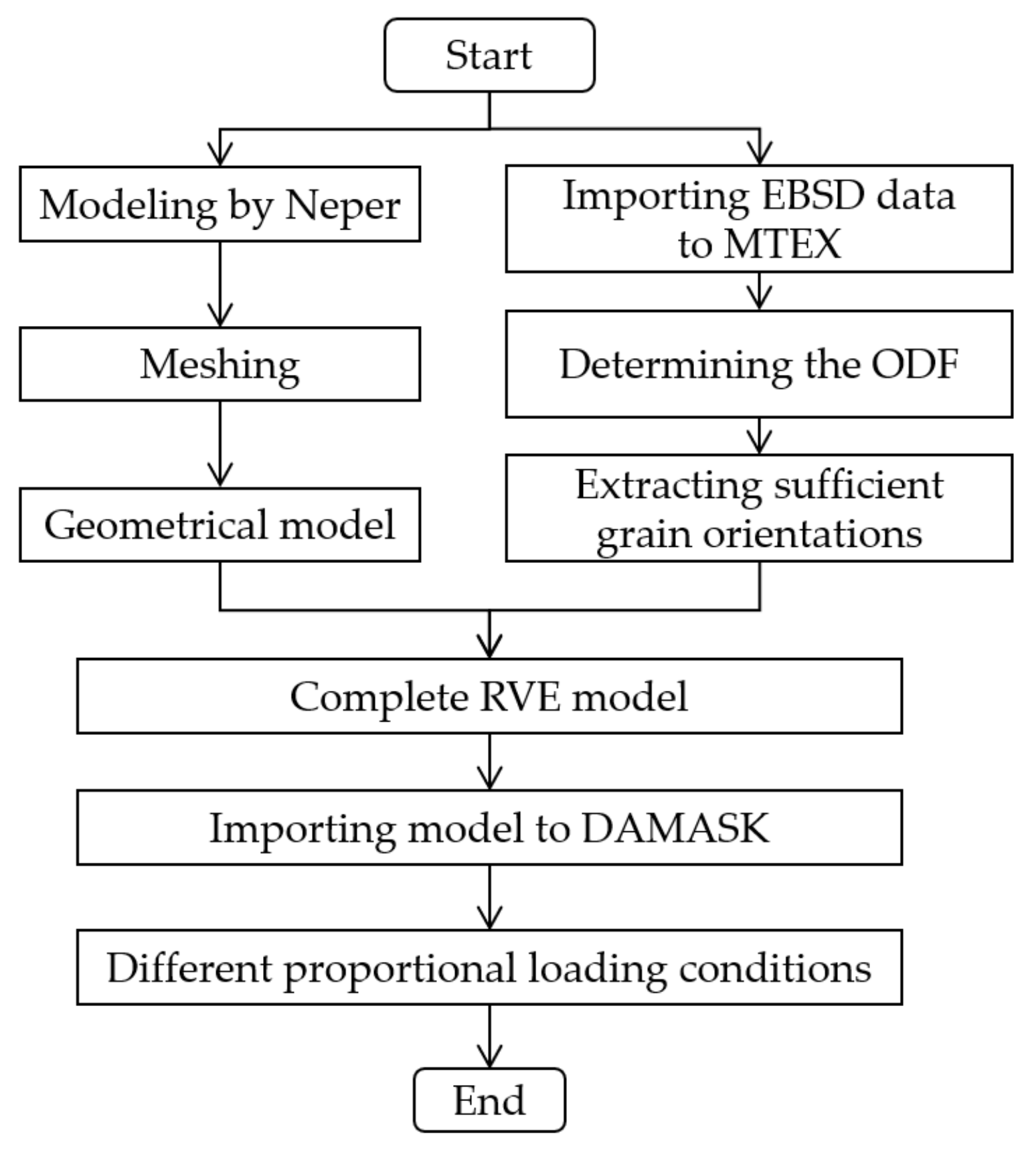
2.4. Crystal Plasticity Simulation
3. Results and Discussion
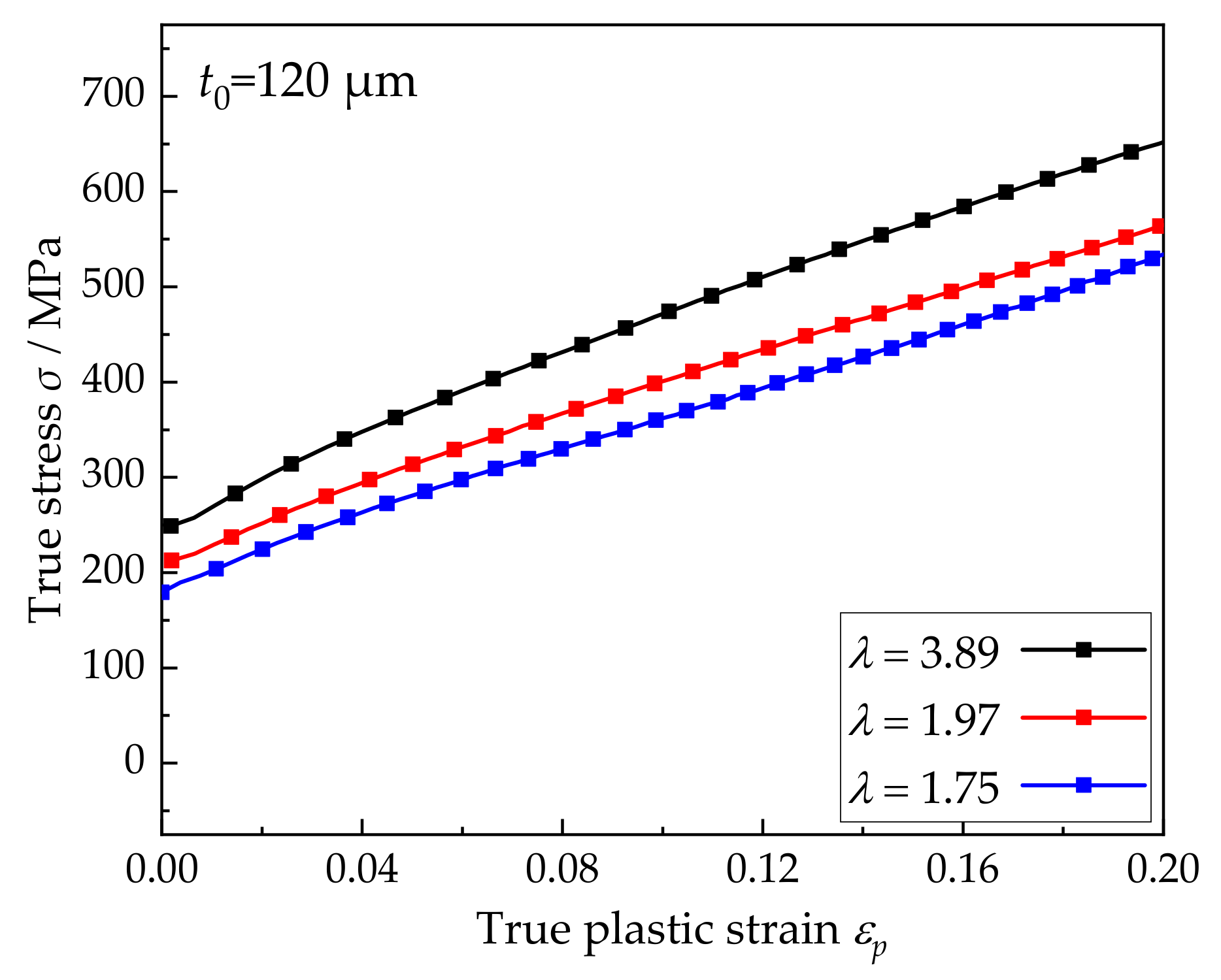
3.1. Experimantal Results
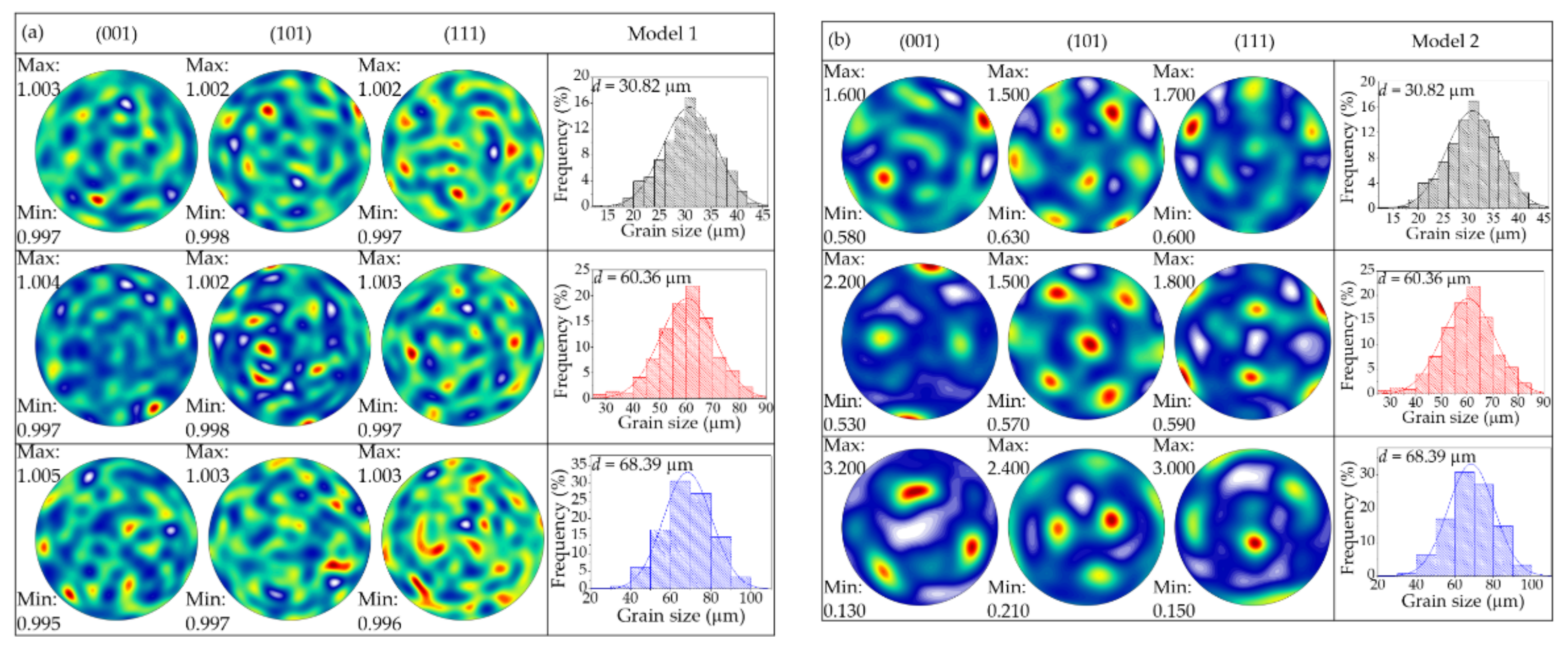
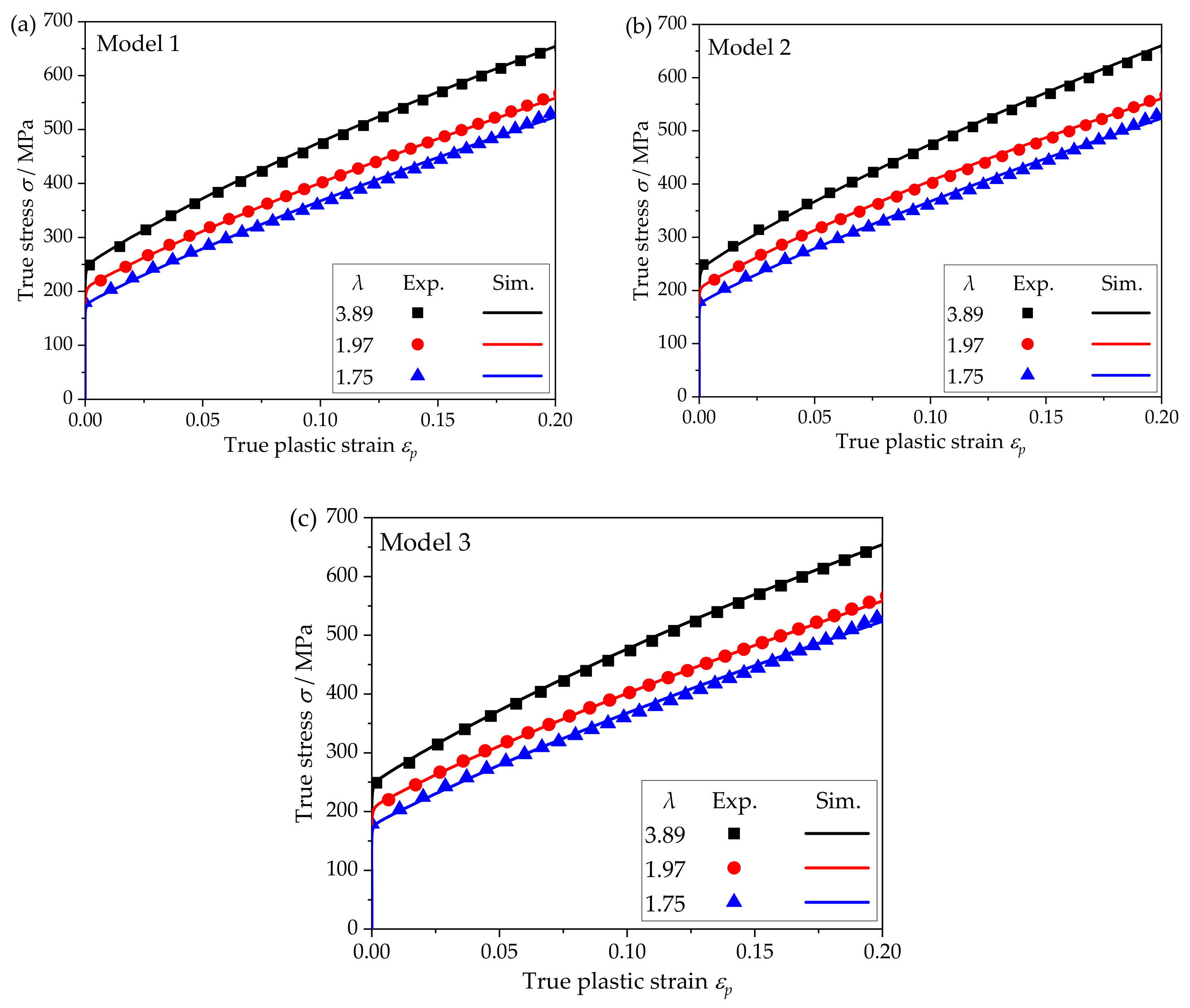
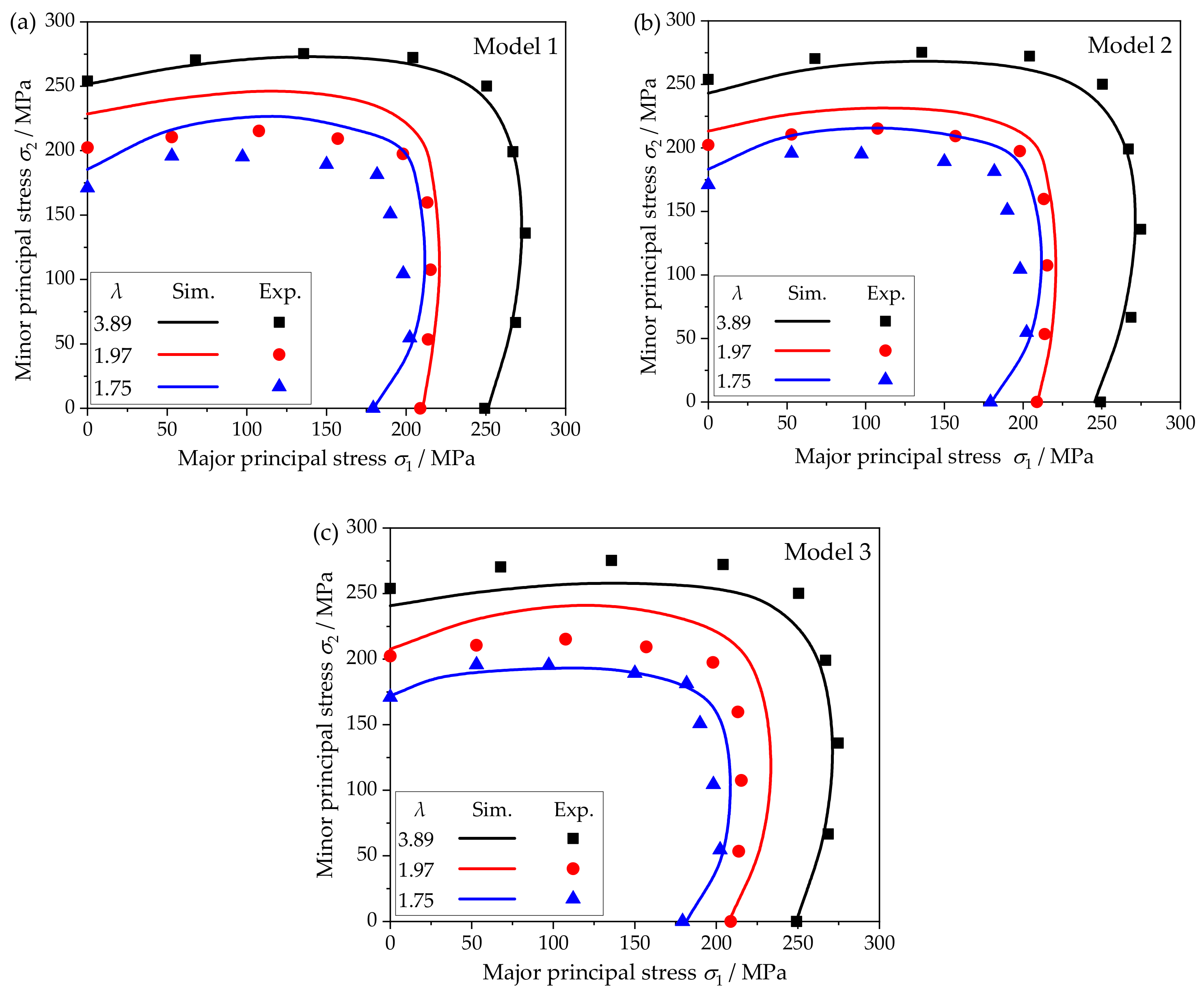
3.2. Simulation Results
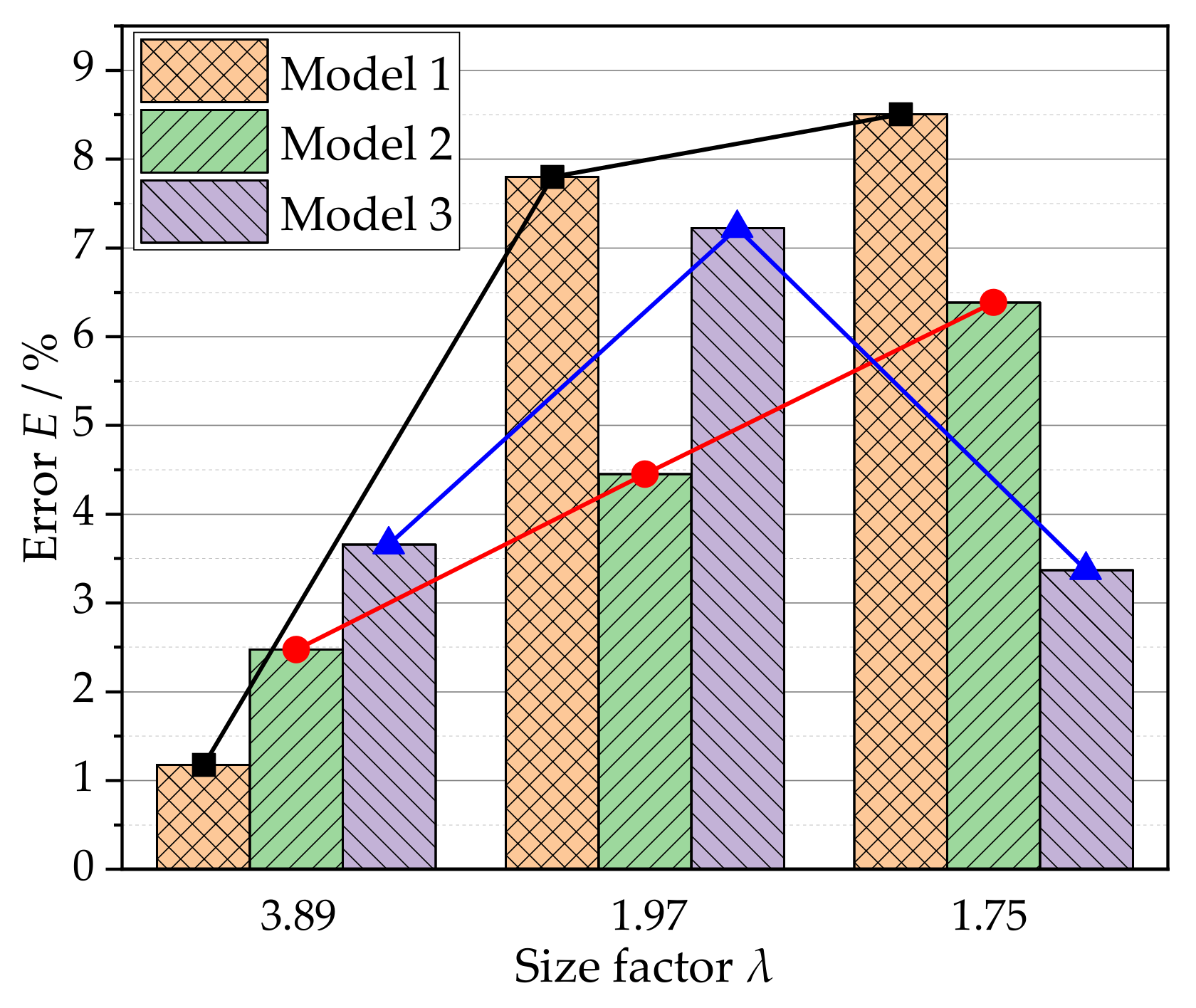
3.3. Discussion
4. Conclusions
- (1)
- With the decrease in the size factor, the yield locus shrinks inward and its shape changes. The size effect has a significant impact on both size and shape of the yield locus. This variation is mainly caused by the different texture characteristics of metal foils.
- (2)
- When the average grain size is the same, as the size factor decreases, the error shows an increasing trend. When the grain size distribution is more uniform, the enhancement of grain deformation coordination will weaken the influence of size effect on yield locus shape.
- (3)
- When the model is given the real orientation texture and normal grain size distributation, finite element simulation of crystal plasticity can better capture the change of yield locus shape and size.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, M.W.; Chan, W.L. A review on the state-of-the-art microforming technologies. Int. J. Adv. Manuf. Technol. 2013, 67, 2411–2437. [Google Scholar] [CrossRef]
- Meng, B.; Wan, M.; Zhao, R.; Zou, Z.; Liu, H. Micromanufacturing technologies of compact heat exchangers for hypersonic precooled airbreathing propulsion: A review. Chin. J. Aeronaut. 2021, 34, 79–103. [Google Scholar] [CrossRef]
- Pradeep Raja, C.; Ramesh, T. Influence of size effects and its key issues during microforming and its associated processes—A review. Eng. Sci. Technol. 2021, 24, 556–570. [Google Scholar] [CrossRef]
- Bodnariuk, M.; Melentiev, R. Bibliometric analysis of micro-nano manufacturing technologies. Nanotechnol. Precis. Eng. 2019, 2, 61–70. [Google Scholar] [CrossRef]
- Cheng, C.; Wan, M.; Meng, B.; Zhao, R.; Han, W. Size effect on the yield behavior of metal foil under multiaxial stress states: Experimental investigation and modelling. Int. J. Mech. Sci. 2019, 151, 760–771. [Google Scholar] [CrossRef]
- Meng, B.; Zhang, Y.; Cheng, C.; Han, J.; Wan, M. Effect of plastic anisotropy on microscale ductile fracture and microformability of stainless steel foil. Int. J. Mech. Sci. 2018, 148, 620–635. [Google Scholar] [CrossRef]
- Van Houtte, P.; Yerra, S.K.; Van Bael, A. The Facet method: A hierarchical multilevel modelling scheme for anisotropic convex plastic potentials. Int. J. Plast. 2009, 25, 332–360. [Google Scholar] [CrossRef]
- Shi, J.J.; Meng, B.; Cheng, C.; Wan, M. Size effect on the subsequent yield and hardening behavior of metal foil. Int. J. Mech. Sci. 2020, 180, 105686. [Google Scholar] [CrossRef]
- Zhang, H.M.; Diehl, M.; Roters, F.; Raabe, D. A virtual laboratory using high resolution crystal plasticity simulations to determine the initial yield surface for sheet metal forming operations. Int. J. Plast. 2016, 80, 111–138. [Google Scholar] [CrossRef]
- Zhang, H.M.; Xu, S.; Li, Q.; Liu, J.R.; Shang, X.Q.; Dong, X.H.; Cui, Z.S. Progress of crystal plasticity theory and simulations. J. Plast. Eng. 2020, 27, 12–32. [Google Scholar]
- Zhang, K.S.; Wu, M.S.; Feng, R. Simulation of microplasticity-induced deformation in uniaxially strained ceramics by 3-D Voronoi polycrystal modeling. Int. J. Plast. 2005, 21, 801–834. [Google Scholar] [CrossRef]
- Zhang, K.-S.; Shi, Y.-K.; Ju, J.W. Grain-level statistical plasticity analysis on strain cycle fatigue of a FCC metal. Mech. Mater. 2013, 64, 76–90. [Google Scholar] [CrossRef]
- Huang, Y. A User-Material Subroutine Incroporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Harvard University Cambridge: Cambridge, MA, USA, 1991. [Google Scholar]
- Zhang, K.-S.; Ju, J.W.; Li, Z.; Bai, Y.-L.; Brocks, W. Micromechanics based fatigue life prediction of a polycrystalline metal applying crystal plasticity. Mech. Mater. 2015, 85, 16–37. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.S.; Duokui, Y.U. Anisotropy of yielding/hardening and microinhomogeneity of deforming/rotating for a polycrystalline metal under cyclic tension–compression. Acta Met. Sin. 2011, 47, 1292–1300. [Google Scholar]
- Chen, J.Y.; Zhang, K.S.; Kuang, Z.; Hu, G.J.; Song, Q.; Chang, Y.J. The anisotropic distortional yield surface constitutive model based on the chaboche cyclic plastic model. Materials 2019, 12, 543. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.M.; Zhang, K.S.; Hu, G.J.; Lan, Y.T.; Chang, Y.J. Investigation of Yield Surfaces Evolution for Polycrystalline Aluminum after Pre-Cyclic Loading by Experiment and Crystal Plasticity Simulation. Materials 2020, 13, 3069. [Google Scholar] [CrossRef]
- Hu, G.; Huang, S.; Lu, D.; Zhong, X.; Li, Z.; Brocks, W.; Zhang, K. Subsequent yielding of polycrystalline aluminum after cyclic tension–compression analyzed by experiments and simulations. Int. J. Solids Struct. 2015, 56, 142–153. [Google Scholar] [CrossRef]
- Tóth, L.S.; Molinari, A.; Zouhal, N. Cyclic plasticity phenomena as predicted by polycrystal plasticity. Mech. Mater. 2000, 32, 99–113. [Google Scholar] [CrossRef]
- Han, F.; Diehl, M.; Roters, F.; Raabe, D. Using spectral-based representative volume element crystal plasticity simulations to predict yield surface evolution during large scale forming simulations. J. Mater. Process. Technol. 2020, 277, 116449. [Google Scholar] [CrossRef]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.O.; et al. DAMASK—The Düsseldorf Advanced Material Simulation Kit for modeling multi-physics crystal plasticity, thermal, and damage phenomena from the single crystal up to the component scale. Comp. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Meng, B.; Wan, M.; Wu, X.D.; Fu, M.W. A modified yield function for modeling of the evolving yielding behavior and micro-mechanism in biaxial deformation of sheet metals. Int. J. Plast. 2020, 129, 102707. [Google Scholar] [CrossRef]
- Liu, W.; Chen, B.K.; Pang, Y.; Najafzadeh, A. A 3D phenomenological yield function with both in and out-of-plane mechanical anisotropy using full-field crystal plasticity spectral method for modelling sheet metal forming of strong textured aluminum alloy. Int. J. Solids Struct. 2020, 193, 117–133. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Zhou, B.; Liu, C.; Zeng, X. Grain-scale deformation in a Mg−0.8 wt% Y alloy using crystal plasticity finite element method. J. Mater. Sci. Technol. 2019, 35, 2200–2206. [Google Scholar] [CrossRef]
- Quey, R.; Dawson, P.R.; Barbe, F. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing. Comput. Methods Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef] [Green Version]
- Hielscher, R.; Schaeben, H. A novel pole figure inversion method: Specification of the MTEX algorithm. J. Appl. Cryst. 2008, 41, 1024–1037. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with MTEX—Free and Open Source Software Toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef] [Green Version]
- Li, L.T.; Lin, Y.C.; Li, L.; Shen, L.M.; Wen, D.X. Three-Dimensional Crystal Plasticity Finite Element Simulation of Hot Compressive Deformation Behaviors of 7075 Al Alloy. J. Mater. Eng. Perform. 2015, 24, 1294–1304. [Google Scholar] [CrossRef]
- Ren, Z.; Fan, W.; Hou, J.; Wang, T. A Numerical Study of Slip System Evolution in Ultra-Thin Stainless Steel Foil. Materials 2019, 12, 1819. [Google Scholar] [CrossRef] [Green Version]
- Dubos, P.-A.; Hug, E.; Thibault, S.; Bettaieb, M.B.; Keller, C. Size effects in thin face-centered cubic metals for different complex forming loadings. Met. Mater. Trans. A 2013, 44, 5478–5487. [Google Scholar] [CrossRef]

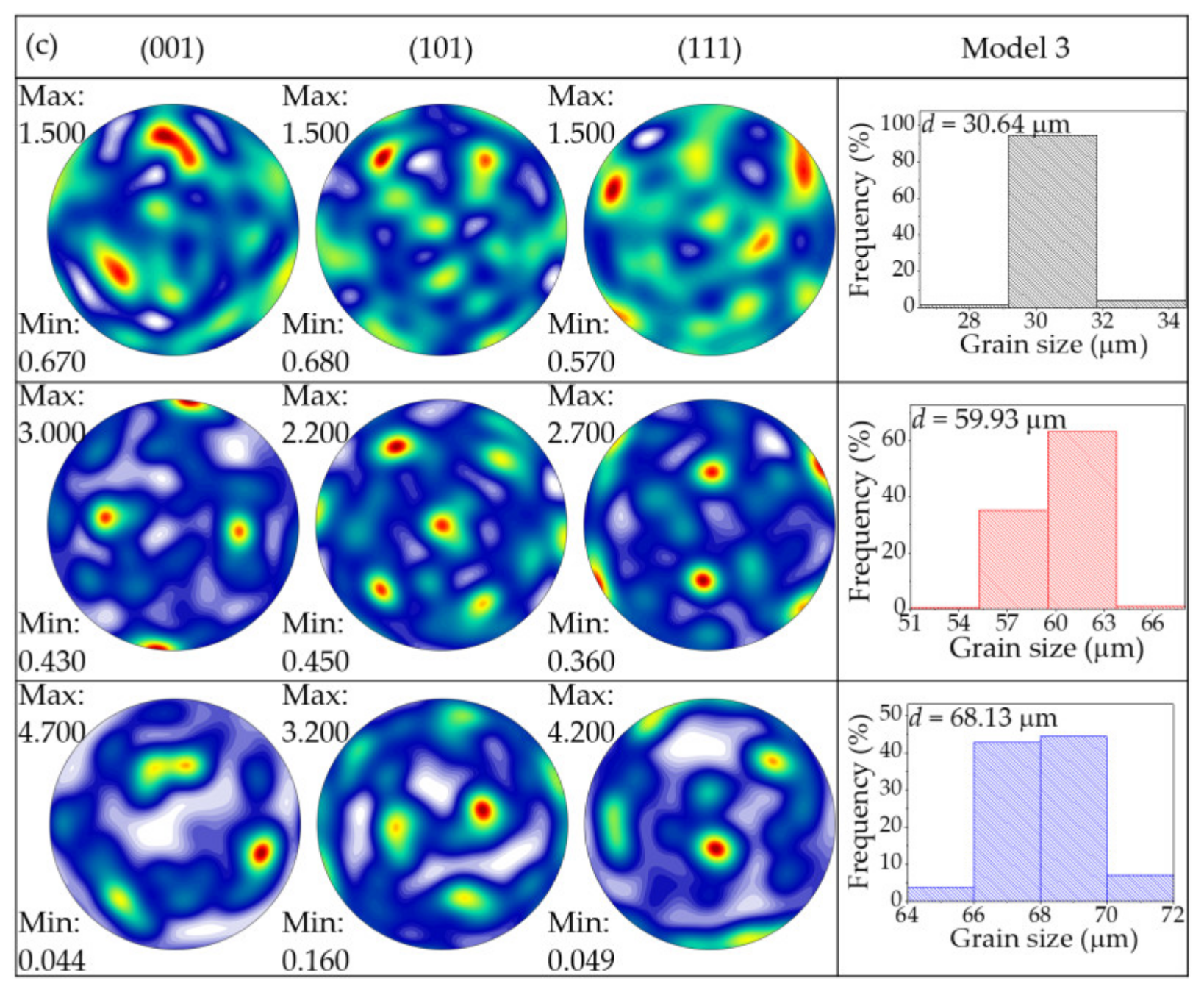

| Annealing Parameters | Average Grain Size d0 (μm) | Grain Size Deviation Δd0 (μm) | Size Factor λ = t0/d0 | ||
|---|---|---|---|---|---|
| No. | Annealing Temperature (°C) | Holding Time (min) | |||
| 1 | 1000 | 10 | 30.81 | 7.9 | 3.89 |
| 2 | 1050 | 30 | 60.87 | 10.1 | 1.97 |
| 3 | 1100 | 60 | 68.41 | 15.6 | 1.75 |
| Model | λ | |||
|---|---|---|---|---|
| 1 | 3.89 | 430 | 96 | 750 |
| 1.97 | 380 | 84 | 730 | |
| 1.75 | 325 | 72 | 900 | |
| 2 | 3.89 | 460 | 96 | 750 |
| 1.97 | 340 | 76 | 580 | |
| 1.75 | 325 | 69.5 | 880 | |
| 3 | 3.89 | 460 | 92 | 600 |
| 1.97 | 380 | 82 | 700 | |
| 1.75 | 290 | 65 | 610 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Men, M.; Meng, B. Crystal Plasticity Simulation of Yield Loci Evolution of SUS304 Foil. Materials 2022, 15, 1140. https://doi.org/10.3390/ma15031140
Men M, Meng B. Crystal Plasticity Simulation of Yield Loci Evolution of SUS304 Foil. Materials. 2022; 15(3):1140. https://doi.org/10.3390/ma15031140
Chicago/Turabian StyleMen, Mingliang, and Bao Meng. 2022. "Crystal Plasticity Simulation of Yield Loci Evolution of SUS304 Foil" Materials 15, no. 3: 1140. https://doi.org/10.3390/ma15031140
APA StyleMen, M., & Meng, B. (2022). Crystal Plasticity Simulation of Yield Loci Evolution of SUS304 Foil. Materials, 15(3), 1140. https://doi.org/10.3390/ma15031140







