TEM Microstructure, Mechanical Properties and Temperature Estimation in the 5XXX Series Al-Mg-Si Aluminum Alloy with W-Ni-Fe Tungsten Composite Friction-Welded Joints
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials Selection
2.2. Friction Welding Setup
2.3. Methods
2.3.1. Tensile Test
2.3.2. The Microhardness Test
2.3.3. The Temperature Measurements
2.3.4. TEM Preparation
3. Results
3.1. Effect of Plastic Deformation
3.2. Effect of Welding Parameters on Joint Efficiency
3.3. The Vickers Hardness Distributions
3.4. Estimation of Temperature Using an Analytical Model and an Experiment
3.5. Temperature Distributions
3.6. Mathematical Modelling of Temperature
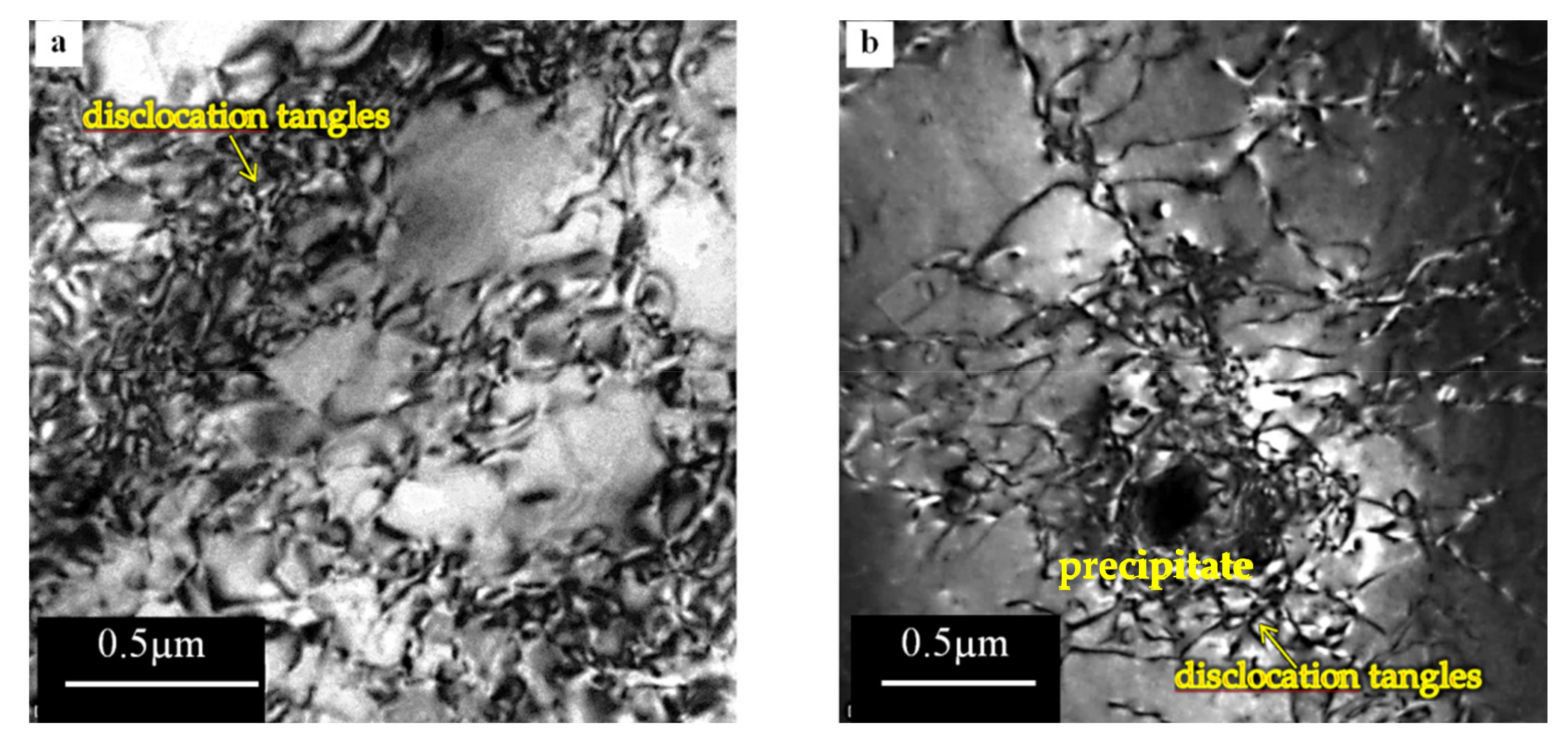
3.7. Microstructure Observation in TEM
4. Discussion
5. Conclusions
- (1)
- The ultimate tensile strength of the joint was comparable to the yield strength of the aluminum alloy, and it was approximately 85% at a friction force of 12.5 kN, friction time of 3.5 s, upsetting force of 50 kN, and upsetting time of 5 s.
- (2)
- Increasing the welding time resulted in a decrease of hardness, mainly when a greater friction force, equal to 22.5 kN, was applied. The local minimum and maximum values were observed as the effect of softening the material in the recrystallisation process. The recrystallisation was caused by maintaining a high temperature for a long time and strain hardening during the upsetting stage of the welding process, the effects of which were not removed by heat-affected processes, e.g., recrystallisation.
- (3)
- The peak temperatures measurements in the axis and at the half-radius of specimens were equal to 252 °C and 278 °C for a distance of 20 mm from the weld interface. The predicted maximum temperatures at the interface were close to 550 °C and 480 °C for the half-radius and at the axis of the aluminum specimens, respectively. The peak temperature was lower than the melting point of aluminum alloy. Moreover, empirical models and for estimation of peak temperature were formulated by the authors.
- (4)
- The friction welding process of tungsten composite to aluminum alloy leads to dynamic changes of the aluminum alloy microstructure due to strong plastic deformation. During friction welding of tungsten composite to aluminum alloy recovery and dynamic recrystallisation processes occur. The degree of these processes depends on the temperature and work hardening parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maalekian, M. Friction welding: Critical assessment of literature. Sci. Technol. Weld. Join. 2007, 12, 738–759. [Google Scholar] [CrossRef]
- Lee, W.B.; Yean, Y.M.; Kim, D.U.; Jung, S.B. Effect of friction welding parameters on mechanical and metallurgical properties of aluminium alloy 5052-A36 steel joint. Mater. Sci. Technol. 2003, 19, 773–778. [Google Scholar] [CrossRef]
- Olson, D.L.; Siewert, T.A.; Liu, S.; Edwards, G.R. ASM Handbook: Welding, Brazing and Soldering; ASM International: Phoenix, AZ, USA, 1993; Volume 6, pp. 150–154. [Google Scholar]
- Walter, S.A. Welding Handbook: Welding, Cutting and Related Processes, 6th ed.; AWS: Miami, FL, USA, 1970; p. 50.3. [Google Scholar]
- Zimmerman, J.; Włosiński, W.; Lindemann, Z.R. Thermo-mechanical and diffusion modelling in the process of ceramic-metal friction welding. J. Mater. Process. Technol. 2009, 209, 1644–1653. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, R.; Feo, L.; Fraternali, F. Friction welding of dissimilar plastic/polymer materials with metal powder reinforcement for engineering applications. Compos. Part B Eng. 2016, 101, 77–86. [Google Scholar] [CrossRef]
- Sharifitabar, M.; Nami, H. Microstructures of dissimilar friction stir welded joints between 2024-T4 aluminium alloy and Al/Mg2Si metal matrix cast composite. Compos. Part B Eng. 2011, 42, 2004–2012. [Google Scholar] [CrossRef]
- Kumar, R.; Sing, R.; Ahuja, I.P.S.; Amendola, A.; Penna, R. Friction welding for the manufacturing of PA6 and ABS structures reinforced with Fe particles. Compos. Part B Eng. 2018, 132, 244–257. [Google Scholar] [CrossRef]
- Domodaram, R.; Karthik, G.M.; Lalam, S.V. Microstructure and mechanical properties of a rotary friction welded tungsten heavy alloy. Mater. Test. 2019, 61, 209–212. [Google Scholar] [CrossRef]
- Winiczenko, R. Effect of friction welding parameters on the tensile strength and microstructural properties of dissimilar AISI 1020-ASTM A536 joints. Int. J. Adv. Manuf. Technol. 2016, 84, 941–955. [Google Scholar] [CrossRef] [Green Version]
- Winiczenko, R.; Kaczorowski, M. Friction welding of ductile cast iron using interlayers. Mater. Des. 2012, 34, 444–451. [Google Scholar] [CrossRef]
- Winiczenko, R.; Kaczorowski, M. Friction welding of ductile iron with stainless steel. J. Mater. Process. Technol. 2013, 213, 453–462. [Google Scholar] [CrossRef]
- Yu, Y.; Hu, H.; Zhang, W.; Xu, X. Microstructure evolution and recrystallisation after annealing of tungsten composite alloy subjected to severe plastic deformation. J. Alloys Compd. 2016, 685, 971–977. [Google Scholar] [CrossRef]
- Kiran, U.R.; Kumar, J.; Kumar, V.; Sankaranarayana, M.; Rao, G.V.S.N.; Nandy, T.K. Effect of cyclic heat treatment and swaging on mechanical properties of the tungsten heavy alloys. Mater. Sci. Eng. A 2016, 656, 256–265. [Google Scholar] [CrossRef]
- Lee, W.S.; Chiou, S.T. The influence of loading rate on shear deformation behaviour of tungsten composite. Compos. Part B Eng. 1996, 27, 193–200. [Google Scholar] [CrossRef]
- Nogami, S.; Noto, H.; Toyota, M.; Hattori, T.; Otomo, K.; Hasegawa, A. Solid state diffusion bonding of doped tungsten alloys with different thermomechanical properties. Fusion Eng. Des. 2018, 136, 76–81. [Google Scholar] [CrossRef]
- Wang, S.; Ling, Y.; Wang, J.; Xu, G. Microstructure and mechanical properties of W/Cu vacuum diffusion bonding joints using amorphous Fe-W alloy as interlayer. Vacuum 2015, 114, 58–65. [Google Scholar] [CrossRef]
- Cai, Q.; Liu, W.; Ma, Y.; Liu, H. Microstructure, residual stresses and mechanical properties of diffusion bonded tungsten-steel joint using a V/Cu composite barrier interlayer. Int. J. Refract. Met. Hard Mater. 2015, 48, 312–317. [Google Scholar] [CrossRef]
- Sánchez, M.; Garrido, M.A.; Múnez, C.J.; Rams, J.; Ureňa, A. Analysis of the brazeability of W-W joints using a high temperature Ni based alloy. Mater. Des. 2014, 54, 900–905. [Google Scholar] [CrossRef]
- Easton, D.; Zhang, Y.; Wood, J.; Galloway, A.; Robbie, M.O.; Hardie, C. Brazing development and interfacial metallurgy study of tungsten and copper joints with eutectic gold copper brazing alloy. Fusion Eng. Des. 2015, 98, 1956–1959. [Google Scholar] [CrossRef] [Green Version]
- Cole, N.C.; Gilli Land, R.G.; Slaughter, G.M. Weldability of tungsten and its alloys. Weld. J. Suppl. 1971, 9, 419–426. [Google Scholar]
- Farrell, K.; Houston, J.T.; Chumley, J.W. Hot Cracking in Fusion Welds in Tungsten. Weld. J. 1970, 49, 132–137. [Google Scholar]
- Das, J.; Appa Rao, G.; Pabi, S.K. Microstructure and mechanical properties of tungsten heavy alloys. Mater. Sci. Eng. A 2010, 527, 7841–7847. [Google Scholar] [CrossRef]
- Das, J.; Appa Rao, G.; Pabi, S.K.; Sankaranarayana, M.; Sarma, B. Deformation behaviour of a newer tungsten heavy alloy. Mater. Sci. Eng. A 2011, 528, 6235–6247. [Google Scholar] [CrossRef]
- Geng, P.-H.; Qin, G.-L.; Zhou, J.; Li, C.-A. Parametric optimization and microstructural characterization of friction welded aeronautic aluminum alloy 2024. Trans. Nonferrous Met. Soc. China 2019, 23, 2483–2495. [Google Scholar] [CrossRef]
- American Welding Society. Specifications and standards. In Recommended Practice for Friction Welding; American Welding Society: Miami, FL, USA, 1989. [Google Scholar]
- Winiczenko, R.; Goroch, O.; Krzyńska, A.; Kaczorowski, M. Friction welding of tungsten heavy alloy with aluminium alloy. J. Mater. Process. Technol. 2017, 246, 42–55. [Google Scholar] [CrossRef]
- Kimura, M.; Sakaguchi, H.; Kusaka, M.; Kaizu, K.; Takahashi, T. Joint properties of friction welded joint between 6061 Al alloy pipe and Al-Si12CuNi (AC8A) Al cast alloy pipe. Int. J. Adv. Manuf. 2016, 86, 2603–2614. [Google Scholar] [CrossRef]
- Winiczenko, R.; Kaczorowski, M.; Skibicki, A. The microstructures, mechanical properties, and temperature distributions in nodular cast iron friction-welded joint. J. Braz. Soc. Mech. Sci. 2018, 40, 1–15. [Google Scholar]
- Deb, K. Optimization for Engineering Design; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Design; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- MATLAB 7.6 R2008a. Documentation R, MathWorks, Inc.: Hoboken, NJ, USA, 2008.
- Mroczka, K.; Dutkiewicz, J.; Pietras, A. Microstructure of friction stir welded joints of 2017A aluminium alloy sheets. J. Microsc. 2010, 237, 521–525. [Google Scholar] [CrossRef]
- Wang, H.; Jing, H.; Zhao, L.; Han, Y.; Lv, X.; Xu, L. Dislocation structure evolution in 304L stainless steel and weld joint during cyclic plastic deformation. Mater. Sci. Eng. A 2017, 690, 16–31. [Google Scholar] [CrossRef]
- Kaczorowski, M.; Winiczenko, R. The microstructure and mass transport during friction welding of ductile cast iron. Ind. Lubr. Tribol. 2013, 65, 251–258. [Google Scholar] [CrossRef]
- Fukumoto, S.; Tsubakino, H.; Aritoshi, M.; Tomita, T.; Okita, K. Dynamic recrystallisation phenomena of commercial purity aluminium during friction welding. Mater. Sci. Technol. 2002, 18, 219–225. [Google Scholar]
- Wang, Y.; Pan, Q.; Song, Y.; Li, C.; Li, Z.; Chen, Q.; Yi, Z. Recrystallization of Al-5.8Mg-Mn-Sc-Zr alloy. Trans. Nonferrous Met. Soc. China 2013, 23, 3235–3241. [Google Scholar] [CrossRef]
- Bardel, D.; Fontaine, M.; Chaise, T.; Perez, M.; Nelias, D.; Bourlier, F.; Garnier, J. Integrated modelling of a 6061-T6 weld joint: From microstructure to mechanical properties. Acta Mater. 2016, 117, 81–90. [Google Scholar] [CrossRef]












| Material | Chemical Composition | Mechanical Properties | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Al | W | Fe | Ni | Mg | Mn | Si | TS | YS | EL | HB | |
| TC | - | Bal. | 2.25 | 5.25 | - | - | - | 960 | 680 | 27 | 285 |
| AA | Bal | - | 0.194 | 0.002 | 2.95 | 0.265 | 0.1 | 276 | 207 | 22 | 83 |
| Welding Parameters | Values |
|---|---|
| Friction force (kN) | 12.5, 15, 22.5, 25 |
| Friction time (s) | 0.5, 3.5, 4.5, 7.5, 9.5 |
| Upsetting force (kN) | 50 |
| Upsetting time (s) | 5 |
| Rotational speed (rpm) | 1450 |
| Heating Process | |||
|---|---|---|---|
| Thermocouple No. | Distance x | Mathematical model | R-squared |
| 1 | 20 mm | 0.9978 | |
| 2 | 25 mm | 0.9934 | |
| 3 | 30 mm | 0.9914 | |
| Cooling process | |||
| Thermocouple No. | Distance from x | Mathematical model | R-squared |
| 1 | 20 mm | 0.9997 | |
| 2 | 25 mm | 0.9974 | |
| 3 | 30 mm | 0.9984 |
| Heating Process | |||
|---|---|---|---|
| Thermocouple No. | Distance x | Mathematical model | R-squared |
| 1 | 20 mm | 0.9840 | |
| 2 | 25 mm | 0.9916 | |
| 3 | 30 mm | 0.9891 | |
| Cooling process | |||
| Thermocouple No. | Distance x | Mathematical model | R-squared |
| 1 | 20 mm | 0.9997 | |
| 2 | 25 mm | 0.9970 | |
| 3 | 30 mm | 0.9916 |
| Material | Position | Distance x (mm) | Mathematical Model | R-Squared R2 |
|---|---|---|---|---|
| AA | half-radius | 20, 25, 30 | 0.9989 | |
| AA | axial | 20, 25, 30 | 0.9962 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winiczenko, R.; Kaczorowski, M.; Krzyńska, A.; Goroch, O.; Skibicki, A.; Skoczylas, P. TEM Microstructure, Mechanical Properties and Temperature Estimation in the 5XXX Series Al-Mg-Si Aluminum Alloy with W-Ni-Fe Tungsten Composite Friction-Welded Joints. Materials 2022, 15, 1162. https://doi.org/10.3390/ma15031162
Winiczenko R, Kaczorowski M, Krzyńska A, Goroch O, Skibicki A, Skoczylas P. TEM Microstructure, Mechanical Properties and Temperature Estimation in the 5XXX Series Al-Mg-Si Aluminum Alloy with W-Ni-Fe Tungsten Composite Friction-Welded Joints. Materials. 2022; 15(3):1162. https://doi.org/10.3390/ma15031162
Chicago/Turabian StyleWiniczenko, Radosław, Mieczysław Kaczorowski, Anna Krzyńska, Olgierd Goroch, Andrzej Skibicki, and Paweł Skoczylas. 2022. "TEM Microstructure, Mechanical Properties and Temperature Estimation in the 5XXX Series Al-Mg-Si Aluminum Alloy with W-Ni-Fe Tungsten Composite Friction-Welded Joints" Materials 15, no. 3: 1162. https://doi.org/10.3390/ma15031162
APA StyleWiniczenko, R., Kaczorowski, M., Krzyńska, A., Goroch, O., Skibicki, A., & Skoczylas, P. (2022). TEM Microstructure, Mechanical Properties and Temperature Estimation in the 5XXX Series Al-Mg-Si Aluminum Alloy with W-Ni-Fe Tungsten Composite Friction-Welded Joints. Materials, 15(3), 1162. https://doi.org/10.3390/ma15031162







