Modelling and Characterisation of Residual Stress of SiC-Ti3C2Tx MXene Composites Sintered via Spark Plasma Sintering Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of the Composites
2.2. Characterisation of the Composites
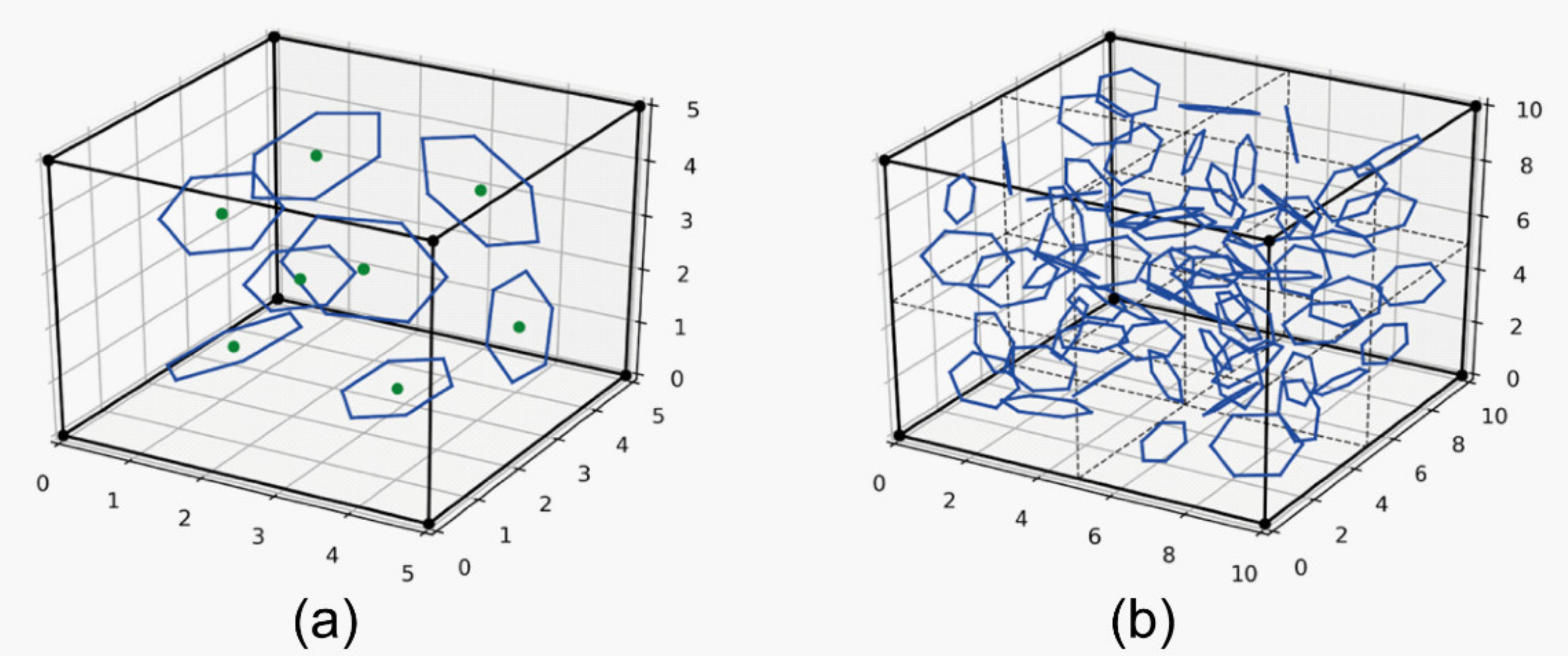
2.3. Modelling of Residual Stress in Composites
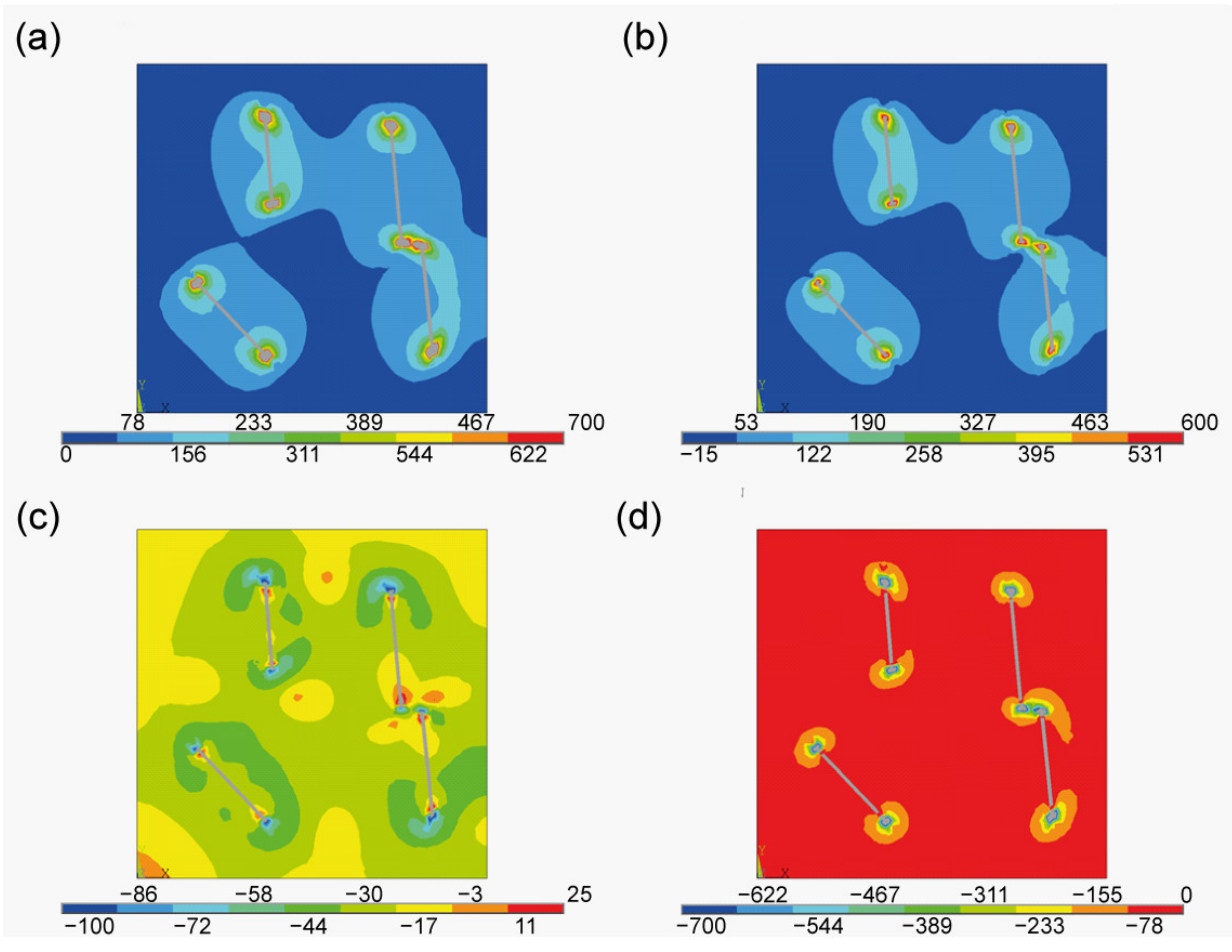
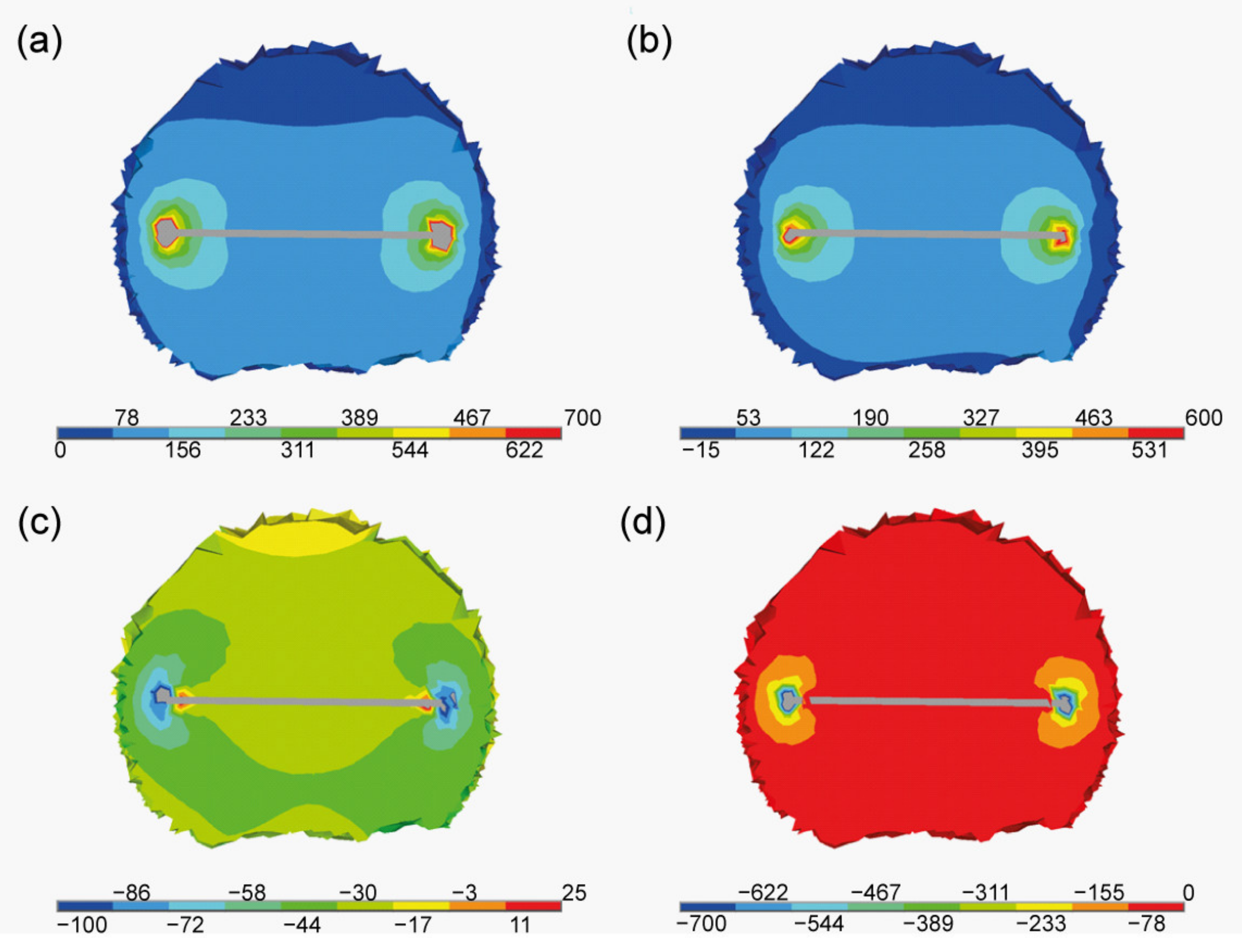
2.4. Residual Stress Analysis
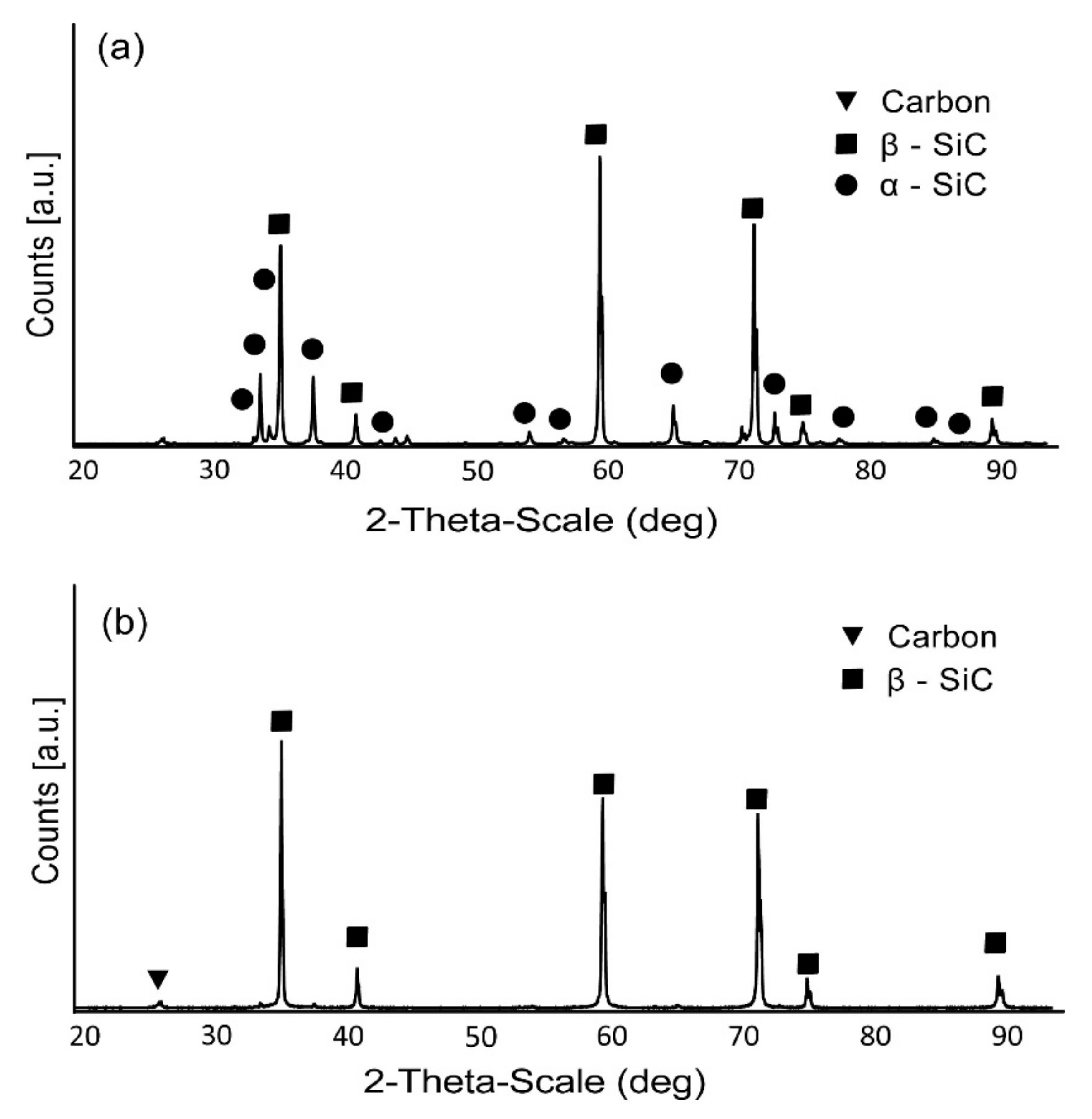
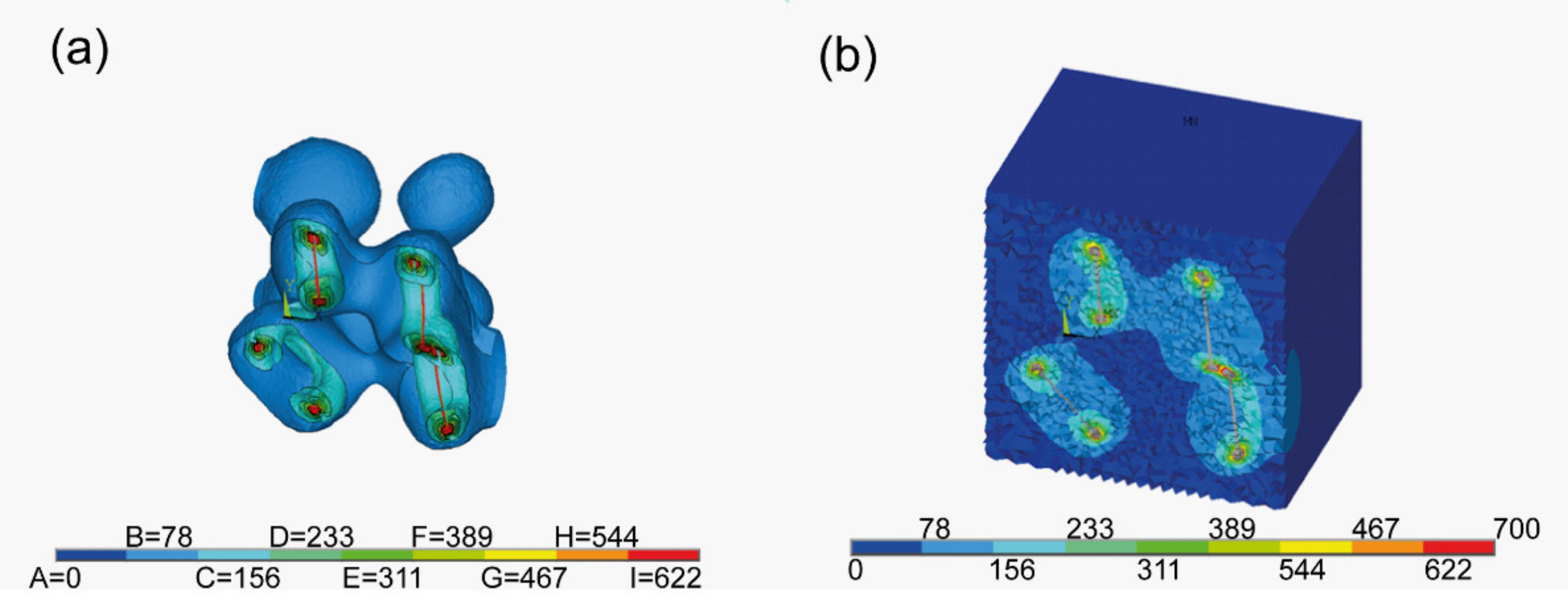
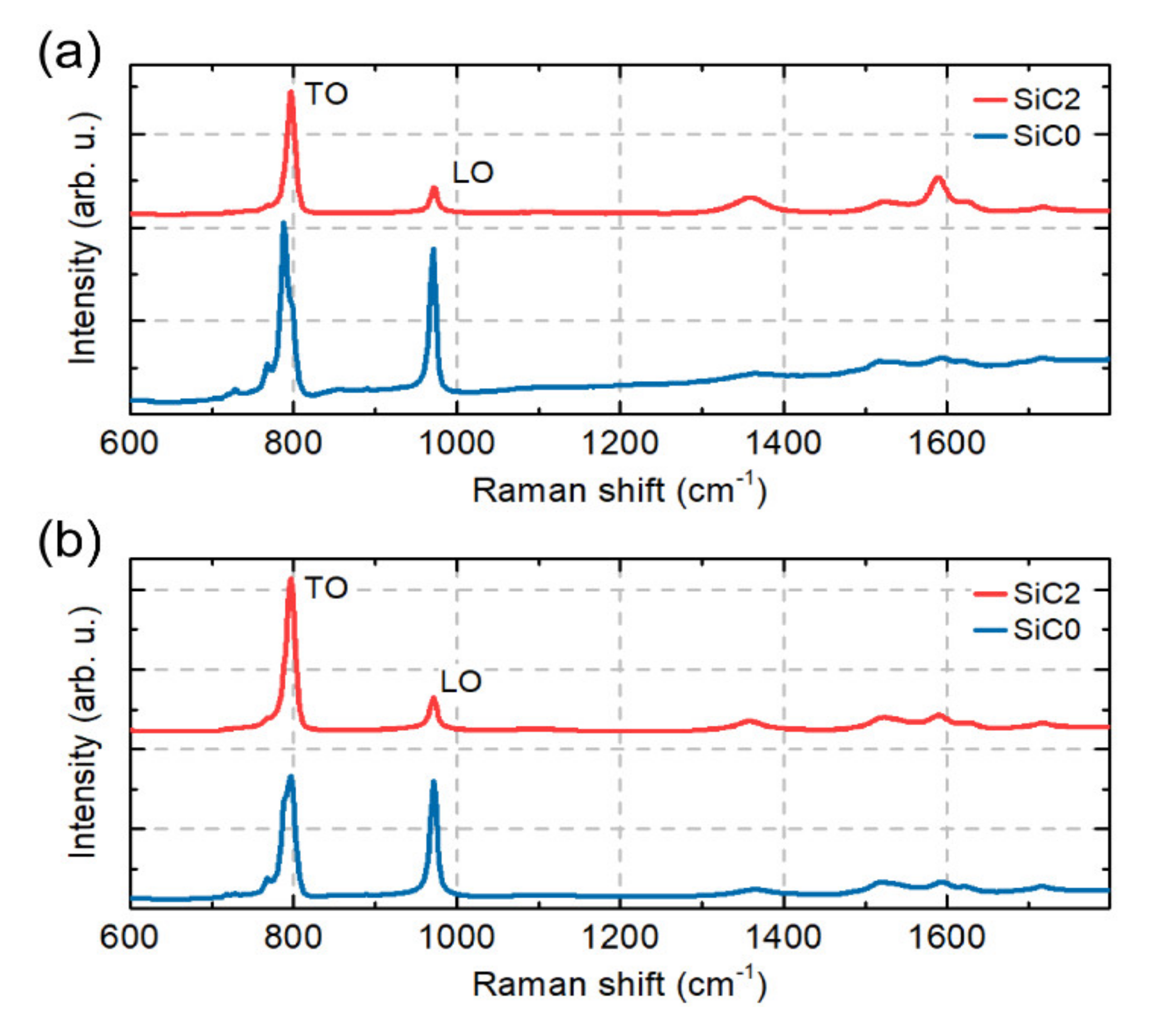
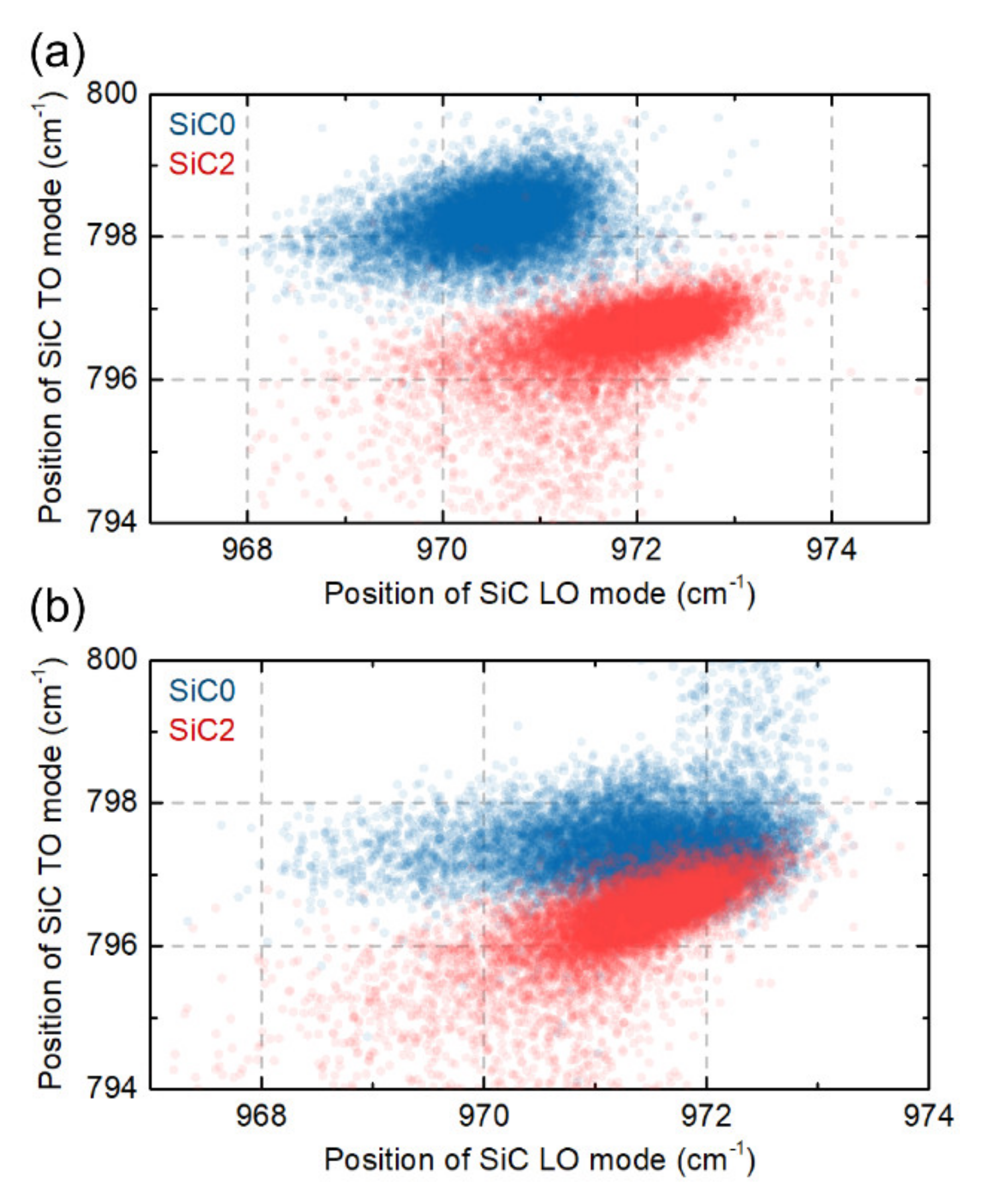
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gubernat, A.; Stobierski, L.; Łabaj, P. Microstructure and mechanical properties of silicon carbide pressureless sintered with oxide additives. J. Eur. Ceram. Soc. 2007, 27, 781–789. [Google Scholar] [CrossRef]
- Prochazka, S. Sintering of silicon carbide. Mater. Sci. Res. 1975, 9, 421–431. [Google Scholar]
- Lamon, J. Properties and characteristics of sic and sic/sic composites. In Comprehensive Nuclear Materials; Elsevier Ltd.: Amsterdam, The Netherlands, 2012; Volume 2, pp. 323–338. ISBN 9780080560335. [Google Scholar]
- DiCarlo, J.A.; Yun, H.M.; Morscher, G.N.; Bhatt, R.T. Progress in SiC/SiC ceramic composite development for gas turbine hot-section components under NASA EPM and UEET programs. In Proceedings of the 2002 ASME Turbo Expo, Amsterdam, The Netherlands, 3–6 June 2002; pp. 39–45. [Google Scholar] [CrossRef] [Green Version]
- Porwal, H.; Grasso, S.; Reece, M.J. Review of graphene–ceramic matrix composites. Adv. Appl. Ceram. 2013, 112, 443. [Google Scholar] [CrossRef]
- Sedlák, R.; Kovalčíková, A.; Girman, V.; Múdra, E.; Rutkowski, P.; Dubiel, A.; Dusza, J. Fracture characteristics of SiC/graphene platelet composites. J. Eur. Ceram. Soc. 2017, 37, 4307–4314. [Google Scholar] [CrossRef]
- Gutierrez-Gonzalez, C.F.; Smirnov, A.; Centeno, A.; Fernández, A.; Alonso, B.; Rocha, V.G.; Torrecillas, R.; Zurutuza, A.; Bartolome, J.F. Wear behavior of graphene/alumina composite. Ceram. Int. 2015, 41, 7434–7438. [Google Scholar] [CrossRef]
- Gutiérrez-Mora, F.; Cano-Crespo, R.; Rincón, A.; Moreno, R.; Domínguez-Rodríguez, A. Friction and wear behavior of alumina-based graphene and CNFs composites. J. Eur. Ceram. Soc. 2017, 37, 3805–3812. [Google Scholar] [CrossRef]
- Liu, J.; Yan, H.; Reece, M.J.; Jiang, K. Toughening of zirconia/alumina composites by the addition of graphene platelets. J. Eur. Ceram. Soc. 2012, 32, 4185–4193. [Google Scholar] [CrossRef]
- Liu, J.; Yan, H.; Jiang, K. Mechanical properties of graphene platelet-reinforced alumina ceramic composites. Ceram. Int. 2013, 39, 6215–6221. [Google Scholar] [CrossRef]
- Naguib, M.; Kurtoglu, M.; Presser, V.; Lu, J.; Niu, J.; Heon, M.; Hultman, L.; Gogotsi, Y.; Barsoum, M.W. Two-dimensional nanocrystals produced by exfoliation of Ti3AlC2. Adv. Mater. 2011, 23, 4248–4253. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wang, L.; Chen, Q.; Li, P.; Zhou, A.; Cao, X.; Hu, Q. Preparation, mechanical and anti-friction performance of MXene/polymer composites. Mater. Des. 2016, 92, 682–689. [Google Scholar] [CrossRef]
- Sheng, X.; Zhao, Y.; Zhang, L.; Lu, X. Properties of two-dimensional Ti3C2 MXene/thermoplastic polyurethane nanocomposites with effective reinforcement via melt blending. Compos. Sci. Technol. 2019, 181, 107710. [Google Scholar] [CrossRef]
- Lei, J.C.; Zhang, X.; Zhou, Z. Recent advances in MXene: Preparation, properties, and applications. Front. Phys. 2015, 10, 276–286. [Google Scholar] [CrossRef]
- Li, Z.; Wang, L.; Sun, D.; Zhang, Y.; Liu, B.; Hu, Q.; Zhou, A. Synthesis and thermal stability of two-dimensional carbide MXene Ti3C2. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 2015, 191, 33–40. [Google Scholar] [CrossRef]
- Li, J.; Du, Y.; Huo, C.; Wang, S.; Cui, C. Thermal stability of two-dimensional Ti2C nanosheets. Ceram. Int. 2015, 41, 2631–2635. [Google Scholar] [CrossRef]
- Guo, J.; Legum, B.; Anasori, B.; Wang, K.; Lelyukh, P.; Gogotsi, Y.; Randall, C.A. Cold Sintered Ceramic Nanocomposites of 2D MXene and Zinc Oxide. Adv. Mater. 2018, 30, 1801846. [Google Scholar] [CrossRef]
- Wozniak, J.; Petrus, M.; Cygan, T.; Lachowski, A.; Adamczyk-Cieślak, B.; Moszczyńska, D.; Jastrzębska, A.; Wojciechowski, T.; Ziemkowska, W.; Olszyna, A. Influence of mxene (Ti3C2) phase addition on the microstructure and mechanical properties of silicon nitride ceramics. Materials 2020, 13, 5221. [Google Scholar] [CrossRef]
- Cygan, T.; Wozniak, J.; Petrus, M.; Lachowski, A.; Pawlak, W.; Adamczyk-Cieślak, B.; Jastrzębska, A.; Rozmysłowska-Wojciechowska, A.; Wojciechowski, T.; Ziemkowska, W.; et al. Microstructure and Mechanical Properties of Alumina Composites with Addition of Structurally Modified 2D Ti3C2 (MXene) Phase. Materials 2021, 14, 829. [Google Scholar] [CrossRef]
- Petrus, M.; Woźniak, J.; Cygan, T.; Lachowski, A.; Rozmysłowska-Wojciechowska, A.; Wojciechowski, T.; Ziemkowska, W.; Chlubny, L.; Jastrzębska, A.; Adamczyk-Cieślak, B.; et al. Silicon carbide nanocomposites reinforced with disordered graphitic carbon formed in situ through oxidation of Ti3C2 MXene during sintering. Arch. Civ. Mech. Eng. 2021, 21, 87. [Google Scholar] [CrossRef]
- Petrus, M.; Woźniak, J.; Cygan, T.; Lachowski, A.; Moszczyńska, D.; Adamczyk-Cieślak, B.; Rozmysłowska-Wojciechowska, A.; Wojciechowski, T.; Ziemkowska, W.; Jastrzębska, A.; et al. Influence of Ti3C2Tx MXene and Surface-Modified Ti3C2Tx MXene Addition on Microstructure and Mechanical Properties of Silicon Carbide Composites Sintered via Spark Plasma Sintering Method. Materials 2021, 14, 3558. [Google Scholar] [CrossRef]
- Lanin, A.G. Effect of residual stresses on the strength of ceramic materials (Review). Russ. Metall. 2012, 2012, 307–322. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Mohammadi, A.R.G. The importance of measuring residual stresses in composite materials. In Residual Stresses in Composite Materials; Elsevier Ltd.: Amsterdam, The Netherlands, 2014; pp. 3–14. ISBN 9780857092700. [Google Scholar]
- Turan, M.E.; Aydin, F. Improved elevated temperature mechanical properties of graphene-reinforced pure aluminium matrix composites. Mater. Sci. Technol. 2020, 36, 1092–1103. [Google Scholar] [CrossRef]
- Totten, G.; Howes, M. Handbook of Residual Stress and Deformation of Steel; ASM International: Almere, The Netherlands, 2002. [Google Scholar]
- Turan, M.E.; Ozcelik, S.; Husem, F.; Ahlatci, H.; Sun, Y.; Tozlu, I. The effect of head hardening process on the residual stress of rails. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 589–595. [Google Scholar] [CrossRef]
- Craciun, E.M.; Soós, E. Anti-plane states in an anisotropic elastic body containing an elliptical hole. Math. Mech. Solids 2006, 11, 459–466. [Google Scholar] [CrossRef]
- Fan, K.; Jiang, W.; Ruiz-Hervias, J.; Baudín, C.; Feng, W.; Zhou, H.; Bueno, S.; Yao, P. Effect of Al2TiO5 Content and Sintering Temperature on the Microstructure and Residual Stress of Al2O3–Al2TiO5 Ceramic Composites. Materials 2021, 14, 7624. [Google Scholar] [CrossRef] [PubMed]
- Fan, K.; Pastor, J.Y.; Ruiz-Hervias, J.; Gurauskis, J.; Baudin, C. Determination of mechanical properties of Al2O3/Y-TZP ceramic composites: Influence of testing method and residual stresses. Ceram. Int. 2016, 42, 18700–18710. [Google Scholar] [CrossRef]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Ruoff, R.S.; Lorents, D.C. Mechanical and thermal properties of carbon nanotubes. Carbon N. Y. 1995, 33, 925–930. [Google Scholar] [CrossRef]
- McAllister, M.J.; Li, J.-L.; Adamson, D.H.; Schniepp, H.C.; Abdala, A.A.; Liu, J.; Herrera-Alonso, M.; Milius, D.L.; Car, R.; Prud’homme, R.K.; et al. Single Sheet Functionalized Graphene by Oxidation and Thermal Expansion of Graphite. Chem. Mater. 2007, 19, 4396–4404. [Google Scholar] [CrossRef]
- Mamedov, V. Spark plasma sintering as advanced PM sintering method. Powder Metall. 2002, 45, 322–328. [Google Scholar] [CrossRef]
- Tokita, M. Development of large-size ceramic/metal bulk FGM fabricated by spark plasma sintering. Mater. Sci. Forum 1999, 308–311, 83–88. [Google Scholar] [CrossRef]
- Anselmi-Tamburini, U.; Gennari, S.; Garay, J.E.; Munir, Z.A. Fundamental investigations on the spark plasma sintering/synthesis process: II. Modeling of current and temperature distributions. Mater. Sci. Eng. A 2005, 394, 139–148. [Google Scholar] [CrossRef]
- Guillon, O.; Gonzalez-Julian, J.; Dargatz, B.; Kessel, T.; Schierning, G.; Räthel, J.; Herrmann, M. Field-Assisted Sintering Technology/Spark Plasma Sintering: Mechanisms, Materials, and Technology Developments. Adv. Eng. Mater. 2014, 16, 830–849. [Google Scholar] [CrossRef]
- Wozniak, J.; Petrus, M.; Cygan, T.; Lachowski, A.; Kostecki, M.; Jastrzębska, A.; Wojciechowska, A.; Wojciechowski, T.; Olszyna, A. Investigation of MXenes Oxidation Process during SPS Method Annealing. Materials 2021, 14, 6011. [Google Scholar] [CrossRef] [PubMed]
- Farooqi, J.K.; Sheikh, M.A. Finite element modelling of thermal transport in ceramic matrix composites. Comput. Mater. Sci. 2006, 37, 361–373. [Google Scholar] [CrossRef]
- Jastrzębska, A.M.; Szuplewska, A.; Wojciechowski, T.; Chudy, M.; Ziemkowska, W.; Chlubny, L.; Rozmysłowska, A.; Olszyna, A. In vitro studies on cytotoxicity of delaminated Ti3C2 MXene. J. Hazard. Mater. 2017, 339, 1–8. [Google Scholar] [CrossRef]
- Basista, M.; Węglewski, W.; Bochenek, K.; Poniżnik, Z.; Nowak, Z. Micro-CT Finite Element Analysis of Thermal Residual Stresses and Fracture in Metal-Ceramic Composites. Adv. Eng. Mater. 2017, 19, 1600725. [Google Scholar] [CrossRef]
- Kilikevičius, S.; Kvietkaitė, S.; Žukienė, K.; Omastová, M.; Aniskevich, A.; Zeleniakienė, D. Numerical investigation of the mechanical properties of a novel hybrid polymer composite reinforced with graphene and MXene nanosheets. Comput. Mater. Sci. 2020, 174, 109497. [Google Scholar] [CrossRef]
- Ansys ®. Academic Research Mechanical, ANSYS, Inc., Release 19.2, USA. 2018. [Google Scholar]
- Monastyreckis, G.; Mishnaevsky, L.; Hatter, C.B.; Aniskevich, A.; Gogotsi, Y.; Zeleniakiene, D. Micromechanical modeling of MXene-polymer composites. Carbon N. Y. 2020, 162, 402–409. [Google Scholar] [CrossRef]
- Serbena, F.C.; Zanotto, E.D. Internal residual stresses in glass-ceramics: A review. J. Non. Cryst. Solids 2012, 358, 975–984. [Google Scholar] [CrossRef]
- Yoo, W.S.; Matsunami, H. Solid-state phase transformation in cubic silicon carbide. Jpn. J. Appl. Phys. 1991, 30, 545–553. [Google Scholar] [CrossRef]
- Rohmfeld, S.; Hundhausen, M.; Ley, L.; Zorman, C.A.; Mehregany, M. Quantitative evaluation of biaxial strain in epitaxial 3C-SiC layers on Si (100) substrates by Raman spectroscopy. J. Appl. Phys. 2002, 91, 1113–1117. [Google Scholar] [CrossRef]
- Nakashima, S.; Harima, H. Raman Investigation of SiC Polytypes. Phys. Status Solidi 1997, 162, 39–64. [Google Scholar] [CrossRef]
- Lei, L.; Li, Y.; Hong, L.; Ying, L.; Chun-Qiang, Z.; Long-Xing, Y.; Gui-Ping, L. First principles calculation of the nonhydrostatic effects on structure and Raman frequency of 3C-SiC. Sci. Rep. 2018, 8, 11279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.J.; Pezzotti, G.; Okui, Y.; Nishino, S. Raman microprobe mapping of residual microstresses in 3C-SiC film epitaxial lateral grown on patterned Si (1 1 1). Appl. Surf. Sci. 2004, 228, 10–16. [Google Scholar] [CrossRef]
- Naguib, M.; Mashtalir, O.; Lukatskaya, M.R.; Dyatkin, B.; Zhang, C.; Presser, V.; Gogotsi, Y.; Barsoum, M.W. One-step synthesis of nanocrystalline transition metal oxides on thin sheets of disordered graphitic carbon by oxidation of MXenes. Chem. Commun. 2014, 50, 7420–7423. [Google Scholar] [CrossRef] [Green Version]
- Nader, M.; Aldinger, F.; Hoffmann, M.J. Influence of the α/β-SiC phase transformation on microstructural development and mechanical properties of liquid phase sintered silicon carbide. J. Mater. Sci. 1999, 34, 1197–1204. [Google Scholar] [CrossRef]
- Petrus, M.; Wozniak, J.; Cygan, T.; Adamczyk-Cieslak, B.; Kostecki, M.; Olszyna, A. Sintering behaviour of silicon carbide matrix composites reinforced with multilayer graphene. Ceram. Int. 2017, 43, 5007–5013. [Google Scholar] [CrossRef]
- Wang, L.F.; Zheng, Q.S. Extreme anisotropy of graphite and single-walled carbon nanotube bundles. Appl. Phys. Lett. 2007, 90, 153113. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H.K.D.H. Residual stress part 2—Nature and origins. Mater. Sci. Technol. 2001, 17, 366–375. [Google Scholar] [CrossRef]
- Nienhaus, H.; Kampen, T.U.; Mönch, W. Phonons in 3C-, 4H-, and 6H-SiC. Surf. Sci. 1995, 324, L328–L332. [Google Scholar] [CrossRef]
- Jannotti, P.; Subhash, G.; Zheng, J.; Halls, V. Measurement of microscale residual stresses in multi-phase ceramic composites using Raman spectroscopy. Acta Mater. 2017, 129, 482–491. [Google Scholar] [CrossRef] [Green Version]
- Gao, L.; Yang, H.; Du, D.; Zhao, S.; Li, H.; Yuan, R. Effect of grinding and polishing on the residual stress and bending strength of a silicon nitride ceramic. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2005, 20, 46–48. [Google Scholar] [CrossRef]
- Johnson-Walls, D.; Evans, A.G.; Marshall, D.B.; James, M.R. Residual Stresses in Machined Ceramic Surfaces. J. Am. Ceram. Soc. 1986, 69, 44–47. [Google Scholar] [CrossRef]
- Everaerts, J.; Salvati, E.; Korsunsky, A.M. Nanoscale Depth Profiling of Residual Stresses Due to Fine Surface Finishing. Adv. Mater. Interfaces 2019, 6, 1900947. [Google Scholar] [CrossRef]
- Davidge, R.W.; Green, T.J. The strength of two-phase ceramic/glass materials. J. Mater. Sci. 1968, 3, 629–634. [Google Scholar] [CrossRef]


| Properties | Symbol | Temperature | ||
|---|---|---|---|---|
| 20 °C | 1900 °C | Unit | ||
| Young’s Modulus | E | 475 | 415 | GPa |
| Poisson’s Ratio | ν | 0.16 | 0.18 | - |
| Conductivity | k | 120 | 20 | W/(m·K) |
| Specific Heat | Cp | 0.829 | 1.4 | J (mol·K) |
| Thermal Expansion Coefficient | α | 4.4 × 10−6 | 4.9 × 10−6 | 1/K |
| Properties of Graphite | ||||||||
|---|---|---|---|---|---|---|---|---|
| Ex | 50 | Gpa | Gxy | 29,762 | Gpa | αx | 0.000025 | 1/K |
| Ey | 50 | GPa | Gyz | 28,274 | GPa | αy | 0.000025 | 1/K |
| Ez | 475 | GPa | Gxz | 28,274 | GPa | αz | 0.000002 | 1/K |
| νxy | 0.16 | - | kxy | 398 | W/(m·K) | Cp | 0.829 | J (mol·K) |
| νyz | 0.16 | - | kyz | 398 | W/(m·K) | |||
| νxz | 0.16 | - | kxz | 2.2 | W/(m·K) | |||
| Material | Designation | Relative Density [%] | Average Grain Size [µm] | Hardness [GPa] | VIF [MPa·m0.5] |
|---|---|---|---|---|---|
| SiC | SiC0 | 98.4 ± 0.15 | 0.98 ± 0.04 | 20.7 ± 0.50 | 3.1 ± 0.22 |
| SiC+2wt.% Ti3C2 | SiC2 | 98.4 ± 0.25 | 0.71 ± 0.05 | 23.0 ± 0.67 | 4.22 ± 0.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrus, M.; Woźniak, J.; Kostecki, M.; Cygan, T.; Jastrzębska, A.; Rozmysłowska-Wojciechowska, A.; Adamczyk-Cieślak, B.; Moszczyńska, D.; Sienkiewicz, M.; Marek, P.; et al. Modelling and Characterisation of Residual Stress of SiC-Ti3C2Tx MXene Composites Sintered via Spark Plasma Sintering Method. Materials 2022, 15, 1175. https://doi.org/10.3390/ma15031175
Petrus M, Woźniak J, Kostecki M, Cygan T, Jastrzębska A, Rozmysłowska-Wojciechowska A, Adamczyk-Cieślak B, Moszczyńska D, Sienkiewicz M, Marek P, et al. Modelling and Characterisation of Residual Stress of SiC-Ti3C2Tx MXene Composites Sintered via Spark Plasma Sintering Method. Materials. 2022; 15(3):1175. https://doi.org/10.3390/ma15031175
Chicago/Turabian StylePetrus, Mateusz, Jarosław Woźniak, Marek Kostecki, Tomasz Cygan, Agnieszka Jastrzębska, Anita Rozmysłowska-Wojciechowska, Bogusława Adamczyk-Cieślak, Dorota Moszczyńska, Maksymilian Sienkiewicz, Piotr Marek, and et al. 2022. "Modelling and Characterisation of Residual Stress of SiC-Ti3C2Tx MXene Composites Sintered via Spark Plasma Sintering Method" Materials 15, no. 3: 1175. https://doi.org/10.3390/ma15031175







