Some Slippage Issues in High-Pressure Torsion Using Cu and Ti Samples as an Example
Abstract
1. Introduction
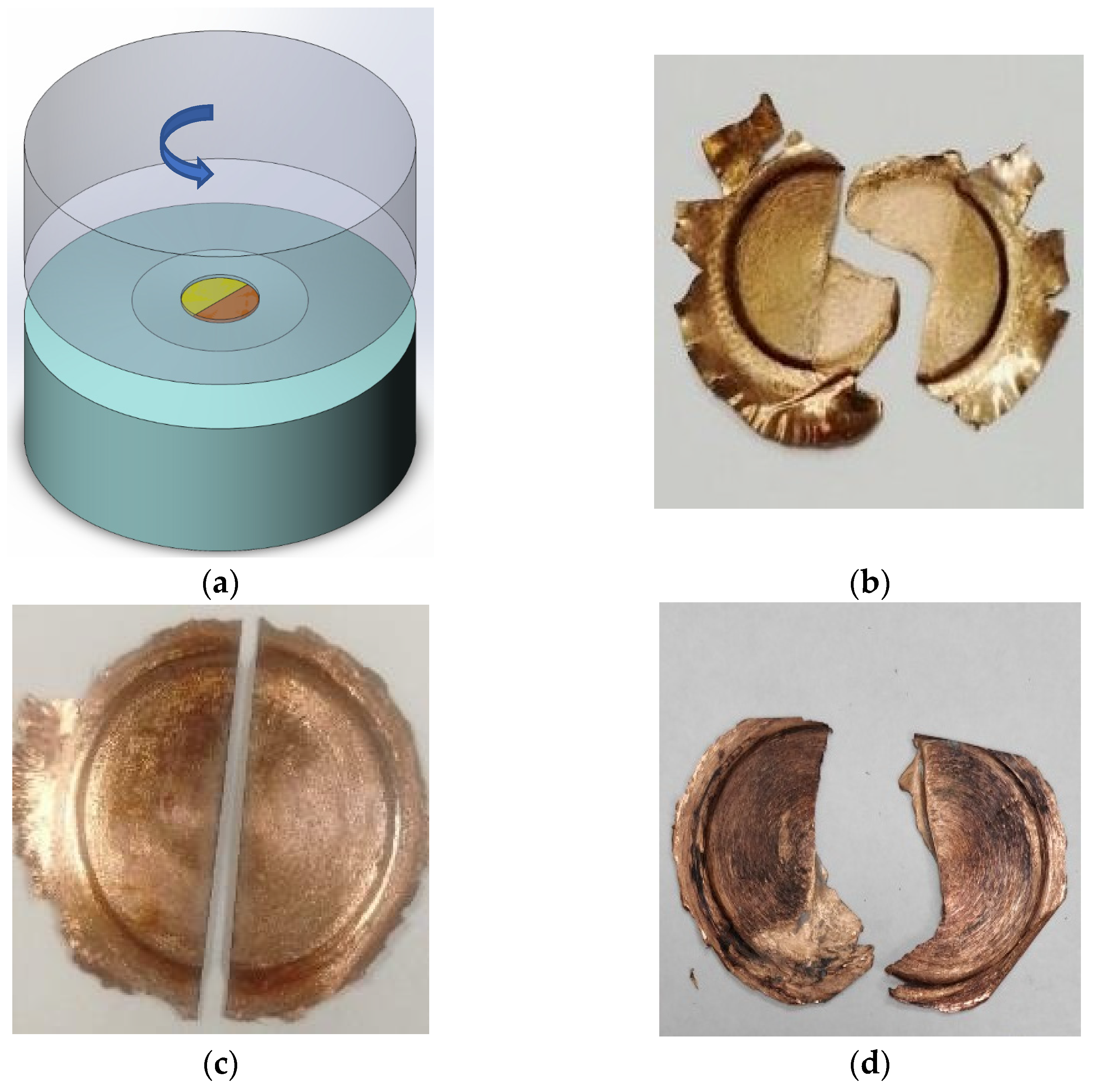
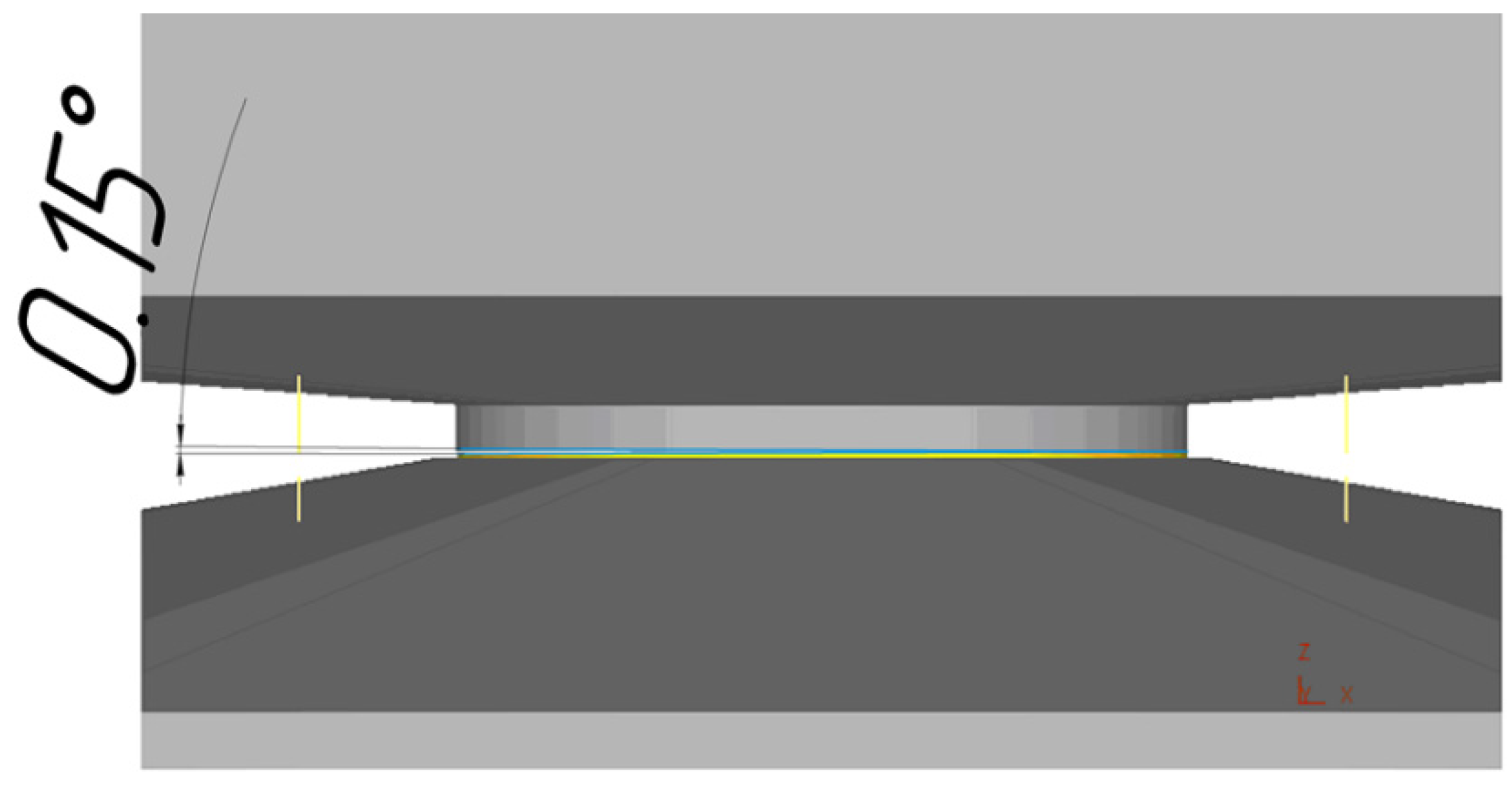
2. Materials and Methods
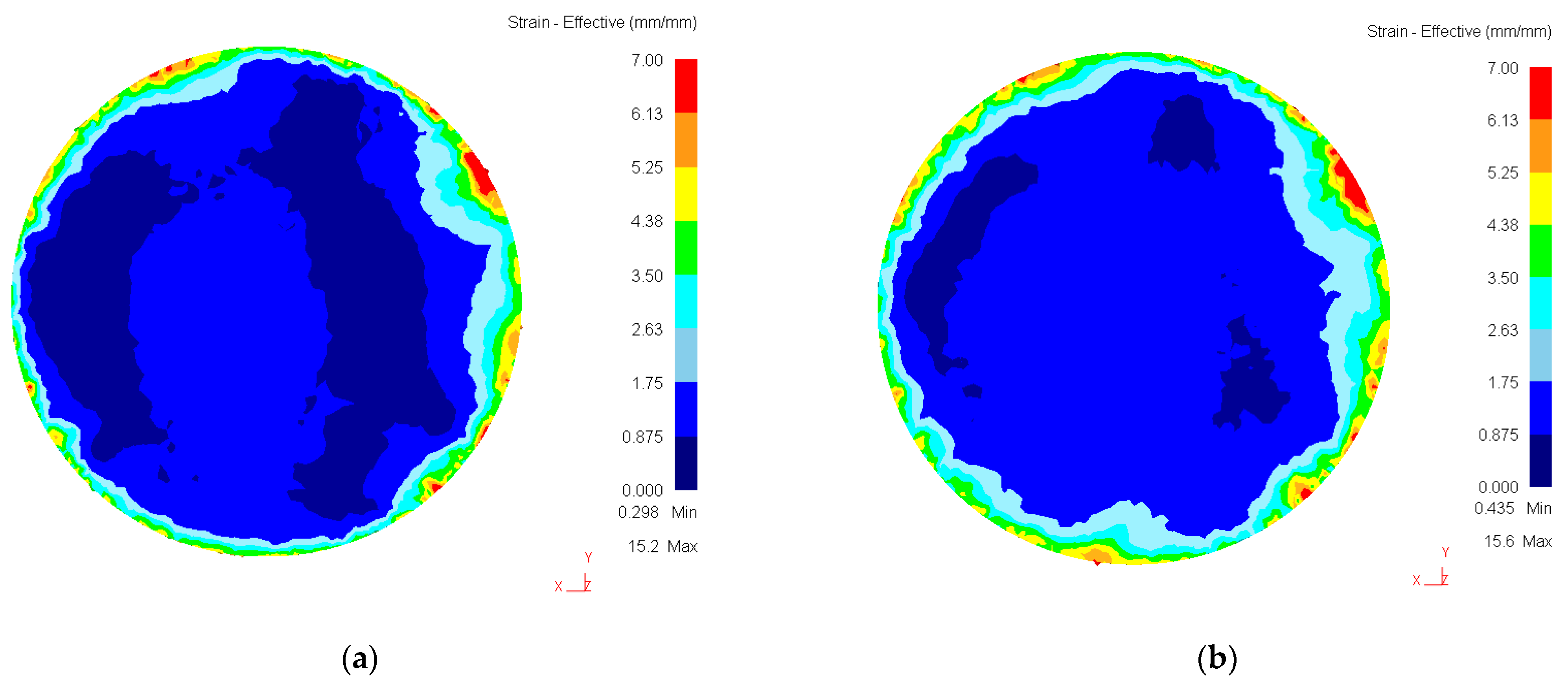
3. Results
3.1. Experiment I
3.2. Experiment II
3.3. Experiment III
3.4. Experiment IV
3.5. Experiment V
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhilyaev, A.P.; Langdon, T.G. Using high-pressure torsion for metal processing: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 893–979. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Zhilyaev, A.P.; Langdon, T.G. Bulk Nanostructured Materials: Fundamentals and Applications. In Bulk Nanostructured Materials; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Edalati, K.; Horita, Z. A review on high-pressure torsion (HPT) from 1935 to 1988. Mater. Sci. Eng. A 2016, 652, 325–352. [Google Scholar] [CrossRef]
- Bridgman, P.W. Effects of High Shearing Stress Combined with High Hydrostatic Pressure. Phys. Rev. 1935, 48, 825–847. [Google Scholar] [CrossRef]
- Stolyarov, V.V.; Gunderov, D.V.; Popov, A.G.; Gaviko, V.S.; Ermolenko, A.S. Structure evolution and changes in magnetic properties of strongly deformed Nd(Pr)-Fe-B alloys during annealing. J. Alloys Compd. 1998, 281, 69–71. [Google Scholar] [CrossRef]
- Popov, A.G.; Gaviko, V.S.; Shchegoleva, N.N.; Puzanova, T.Z.; Ermolenko, A.S. Severe plastic deformation of R-Fe-B (R= Pr or Nd) hard magnetic alloys. Phys. Met. Metallogr. 2002, 94, S75–S81. [Google Scholar]
- Gunderov, D.; Lukyanov, A.; Prokofiev, E.; Kilmametov, A.R.; Pushin, V.; Valiev, R. Mechanical properties and martensitic transformations in the nanocrystalline Ti49.4Ni50.6 alloy produced by high pressure torsion. Mater. Sci. Eng. A 2009, 503, 75–77. [Google Scholar] [CrossRef]
- Popov, A.; Pyshmintsev, I.; Demakov, S.; Illarionov, A.; Lowe, T.; Sergeyeva, A.; Valiev, R. Structural and mechanical properties of nanocrystalleve titanium processed by severe plastic deformation. Scr. Mater. 1997, 37, 1089–1094. [Google Scholar] [CrossRef]
- Islamgaliev, R.; Kazyhanov, V.; Shestakova, L.; Sharafutdinov, A.; Valiev, R. Microstructure and mechanical properties of titanium (Grade 4) processed by high-pressure torsion. Mater. Sci. Eng. A 2008, 493, 190–194. [Google Scholar] [CrossRef]
- Valiev, R.; Sergueeva, A.; Mukherjee, A. The effect of annealing on tensile deformation behavior of nanostructured SPD titanium. Scr. Mater. 2003, 49, 669–674. [Google Scholar] [CrossRef]
- Stolyarov, V.; Zhu, Y.; Lowe, T.; Islamgaliev, R.; Valiev, R. A two step SPD processing of ultrafine-grained titanium. Nanostructured Mater. 1999, 11, 947–954. [Google Scholar] [CrossRef]
- Kilmametov, A.R.; Khristoforov, A.V.; Wilde, G.; Valiev, R.Z. X-ray studies of nanostructured metals processed by severe plastic deformation. Z. Kristallogr. Suppl. 2007, 2007, 339–344. [Google Scholar] [CrossRef]
- Edalati, K.; Matsubara, E.; Horita, Z. Processing Pure Ti by High-Pressure Torsion in Wide Ranges of Pressures and Strain. Met. Mater. Trans. A 2009, 40, 2079–2086. [Google Scholar] [CrossRef]
- Shirooyeh, M.; Xu, J.; Langdon, T.G. Microhardness evolution and mechanical characteristics of commercial purity titanium processed by high-pressure torsion. Mater. Sci. Eng. A 2014, 614, 223–231. [Google Scholar] [CrossRef]
- Edalati, K.; Horita, Z.; Langdon, T.G. The significance of slippage in processing by high-pressure torsion. Scr. Mater. 2009, 60, 9–12. [Google Scholar] [CrossRef]
- Kuhlmann-Wilsdorf, D.; Cai, B.; Nelson, R. Plastic flow between Bridgman anvils under high pressures. J. Mater. Res. 1991, 6, 2547–2564. [Google Scholar] [CrossRef]
- Vorhauer, A.; Pippan, R. On the homogeneity of deformation by high pressure torsion. Scr. Mater. 2004, 51, 921–925. [Google Scholar] [CrossRef]
- Adachi, N.; Todaka, Y.; Yokoyama, Y.; Umemoto, M. Cause of hardening and softening in the bulk glassy alloy Zr50Cu40Al10 after high-pressure torsion. Mater. Sci. Eng. A 2015, 627, 171–181. [Google Scholar] [CrossRef]
- Gunderov, D.; Churakova, A.; Boltynjuk, E.; Ubyivovk, E.; Astanin, V.; Asfandiyarov, R.; Valiev, R.; Xioang, W.; Wang, J. Observation of shear bands in the Vitreloy metallic glass subjected to HPT processing. J. Alloys Compd. 2019, 800, 58–63. [Google Scholar] [CrossRef]
- Gunderov, D.; Churakova, A.; Astanin, V.; Asfandiyarov, R.; Hahn, H.; Valiev, R. Accumulative HPT of Zr-based bulk metallic glasses. Mater. Lett. 2019, 261, 127000. [Google Scholar] [CrossRef]
- Gunderov, D.; Stotskiy, A.; Lebedev, Y.; Mukaeva, V. Influence of HPT and Accumulative High-Pressure Torsion on the Structure and Hv of a Zirconium Alloy. Metals 2021, 11, 573. [Google Scholar] [CrossRef]
- Gunderov, D.; Asfandiyarov, R.; Raab, G.; Churakova, A.; Astanin, V. Method for slippage evaluation at various stages of high-pressure torsion and its application to Fe-0.1 %C. Lett. Mater. 2021, 11, 416–421. [Google Scholar] [CrossRef]
- Gunderov, D.; Prokoshkin, S.; Churakova, A.; Sheremetyev, V.; Ramazanov, I. Effect of HPT and accumulative HPT on structure formation and microhardness of the novel Ti18Zr15Nb alloy. Mater. Lett. 2020, 283, 128819. [Google Scholar] [CrossRef] [PubMed]
- Stembalski, M.; Preś, P.; Skoczyński, W. Determination of the friction coefficient as a function of sliding speed and normal pressure for steel C45 and steel 40HM. Arch. Civ. Mech. Eng. 2013, 13, 444–448. [Google Scholar] [CrossRef]
- Gunderov, D.; Polyakov, A.; Semenova, I.; Raab, G.; Churakova, A.; Gimaltdinova, E.; Sabirov, I.; Segurado, J.; Sitdikov, V.; Alexandrov, I.; et al. Evolution of microstructure, macrotexture and mechanical properties of commercially pure Ti during ECAP-conform processing and drawing. Mater. Sci. Eng. A 2012, 562, 128–136. [Google Scholar] [CrossRef]




| Ti | Al | Si | Fe | C | O | N | H | Remaining Impurities |
|---|---|---|---|---|---|---|---|---|
| Base | 0.010 | 0.002 | 0.120 | 0.004 | 0.143 | 0.003 | 0.0008 | 0.077 |
| Number of Revolutions, N | Measurement Region | HV0.1 | Lattice Distortion, % | CSR, * nm | ω-Phase Fraction, % |
|---|---|---|---|---|---|
| Initial | - | 210 | 0.17 | 72 | 0 |
| 5 | Center | 455 | 0.25 | 23 | 46 |
| 1/2 R | 475 | ||||
| 10 | Center | 440 | 0.34 | 16 | 20 |
| 1/2 R | 450 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunderov, D.; Asfandiyarov, R.; Titov, V.; Gunderova, S.; Astanin, V. Some Slippage Issues in High-Pressure Torsion Using Cu and Ti Samples as an Example. Materials 2023, 16, 162. https://doi.org/10.3390/ma16010162
Gunderov D, Asfandiyarov R, Titov V, Gunderova S, Astanin V. Some Slippage Issues in High-Pressure Torsion Using Cu and Ti Samples as an Example. Materials. 2023; 16(1):162. https://doi.org/10.3390/ma16010162
Chicago/Turabian StyleGunderov, Dmitriy, Rashid Asfandiyarov, Vyacheslav Titov, Sofia Gunderova, and Vasily Astanin. 2023. "Some Slippage Issues in High-Pressure Torsion Using Cu and Ti Samples as an Example" Materials 16, no. 1: 162. https://doi.org/10.3390/ma16010162
APA StyleGunderov, D., Asfandiyarov, R., Titov, V., Gunderova, S., & Astanin, V. (2023). Some Slippage Issues in High-Pressure Torsion Using Cu and Ti Samples as an Example. Materials, 16(1), 162. https://doi.org/10.3390/ma16010162






