Computational Study of the Influence of α/β-Phase Ratio and Porosity on the Elastic Modulus of Ti-Based Alloy Foams
Abstract
1. Introduction
2. Computational Modeling and Simulation
2.1. RVE-FEM Method
- (a)
- Microstructure Model Generation
- (i)
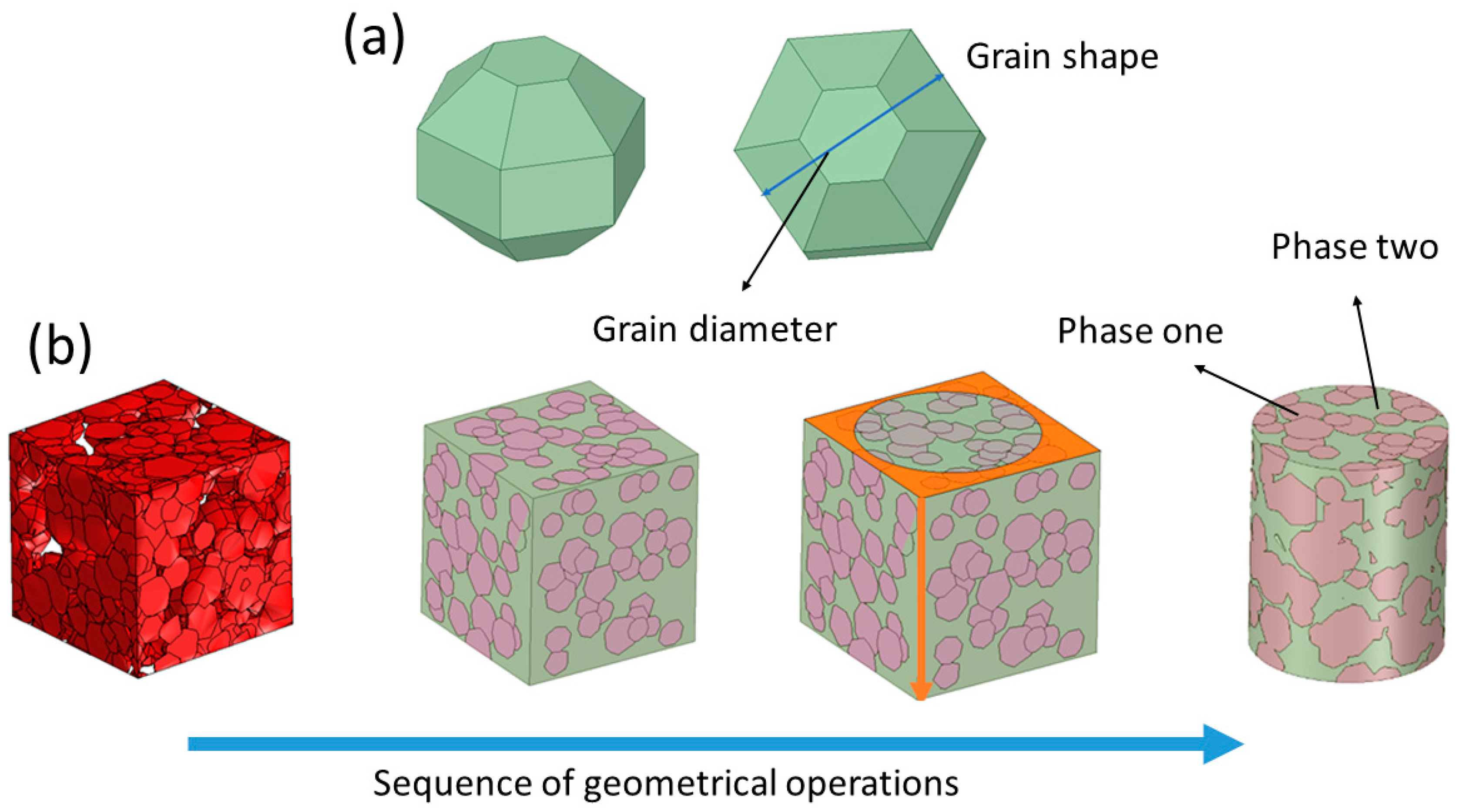
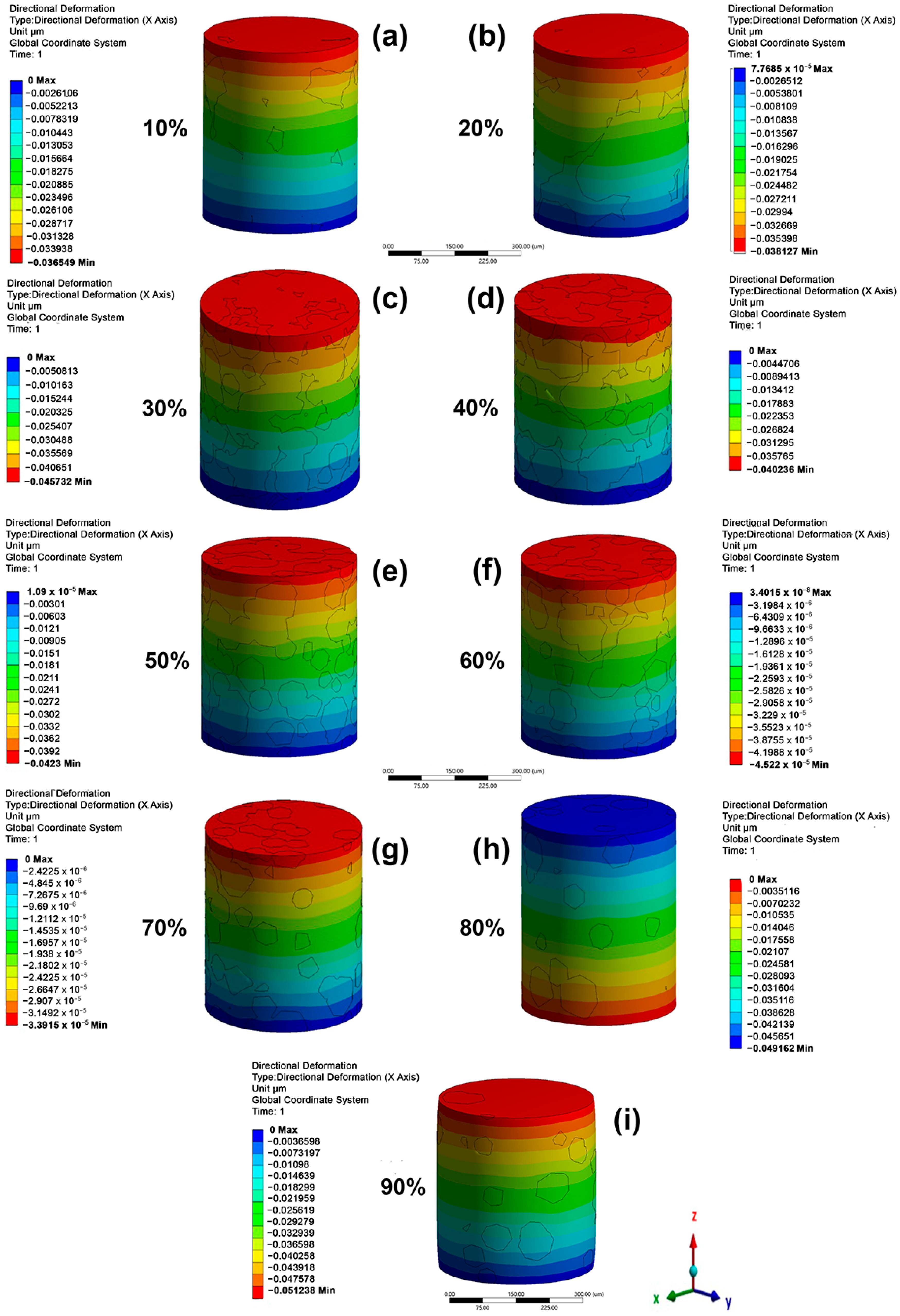
- First step, using the parameters listed in Table 1, the microstructures were generated. The β-phase amount was variated from 0 to 90.5%. Differences between designed and obtained β-phase were observed, with the highest difference being seen in the designed β-phase, showing 40%. The RVE model was designed to be at least five times larger than grain sizes. The computational procedure consisted of periodically and randomly inserting volumes of grains into a matrix cube until the desired volumetric fraction was achieved. Grains are considered as one type of phase, and the space between grains (grain boundary) is considered as a second type of phase (Figure 1a).
- (ii)
- Second step, the models were exported and loaded in the SpaceClaim CAD software (SpaceClaim Corporation, Version 2019 R3, Manufacturer, Ansys INC-SPACECLAIM CORP, Ciudad Concord, MA, USA).
- (iii)
- Third step, using the draw options, the cubic model was transformed into the cylinder model, where colors represented each phase, α or β (Figure 1b).
- (b)
- Porosity model generation
- (i)
- (ii)
- Second step, the models were exported and loaded in the SpaceClaim CAD software.
- (iii)
- Third step, using the draw options, the cubic model was transformed into cylinder models.
- (iv)
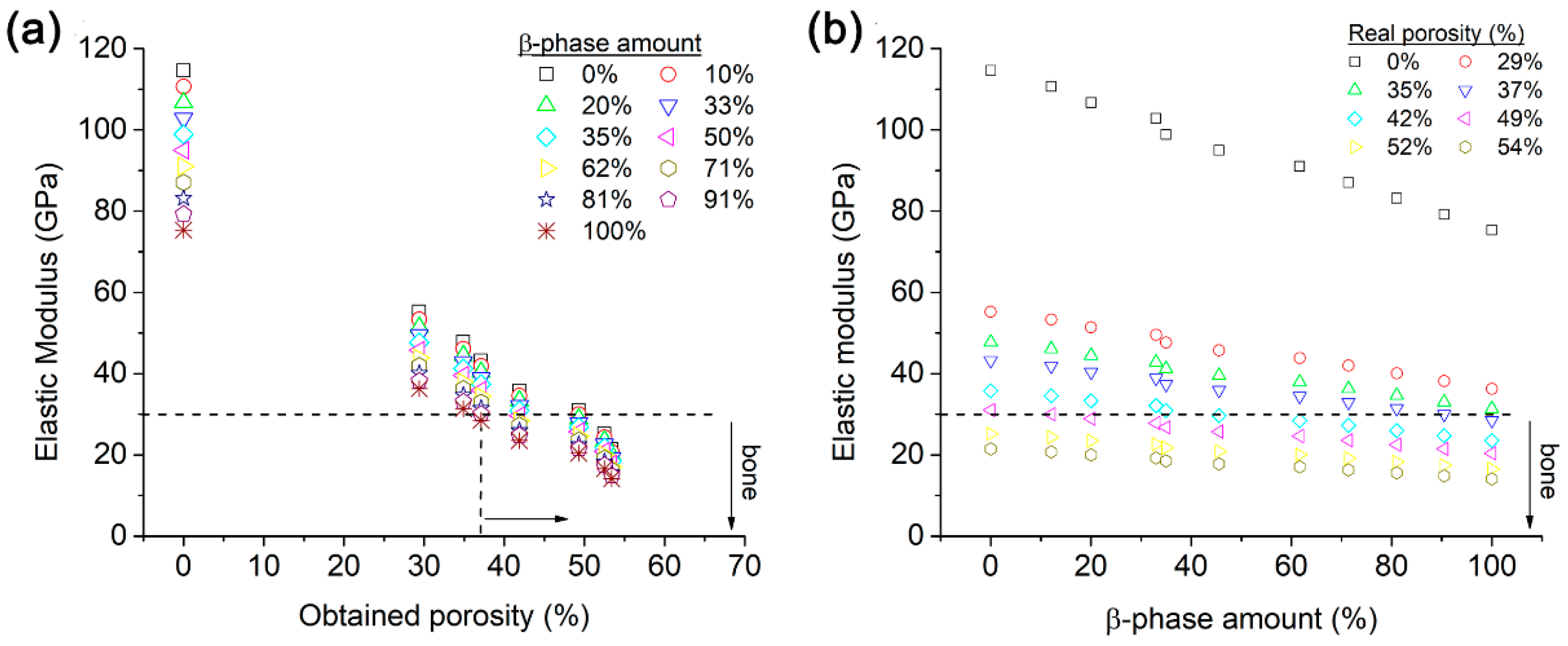
- For each of the seven porosity models, the α/β ratio phase was added (Table 3). There are 7 porosity models and 11 microstructure models, which gives 77 configurations to be simulated. Porosity values were taken from porosity reported for human bones [48,49,50,51]. The simulation parameters used in this study are listed in Table 4. The elastic modulus values for the α-phase and β-phase were obtained from first-principles calculations made for Ti-xTM (TM = V, Cr, Nb, Mo) and ternary Ti-15TM-yAl alloys [52]. The calculated alloy compositions are similar to that of the Ti-6Al-4V alloy; thus, the elastic modulus values for the α-phase and β-phase were considered.
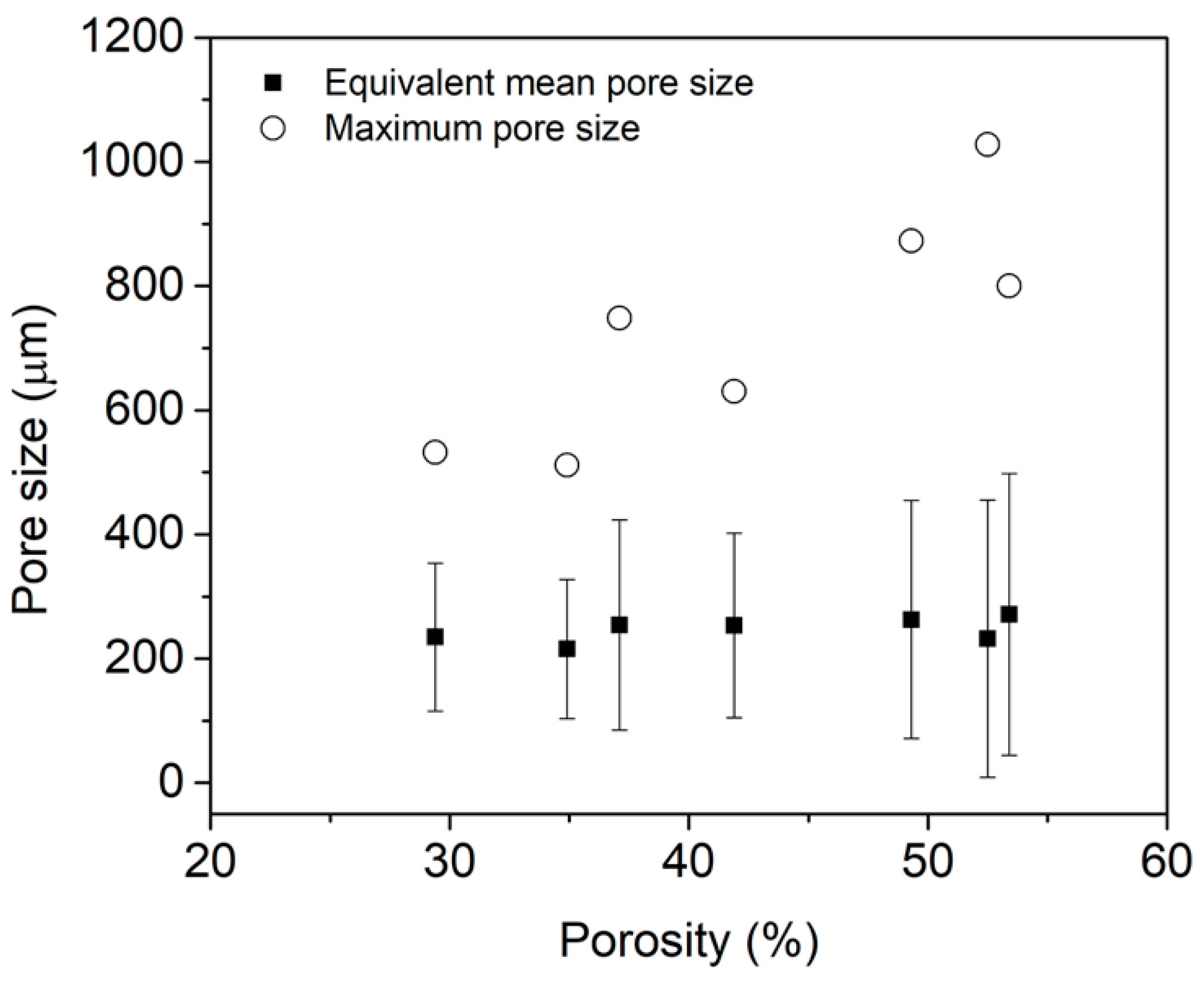
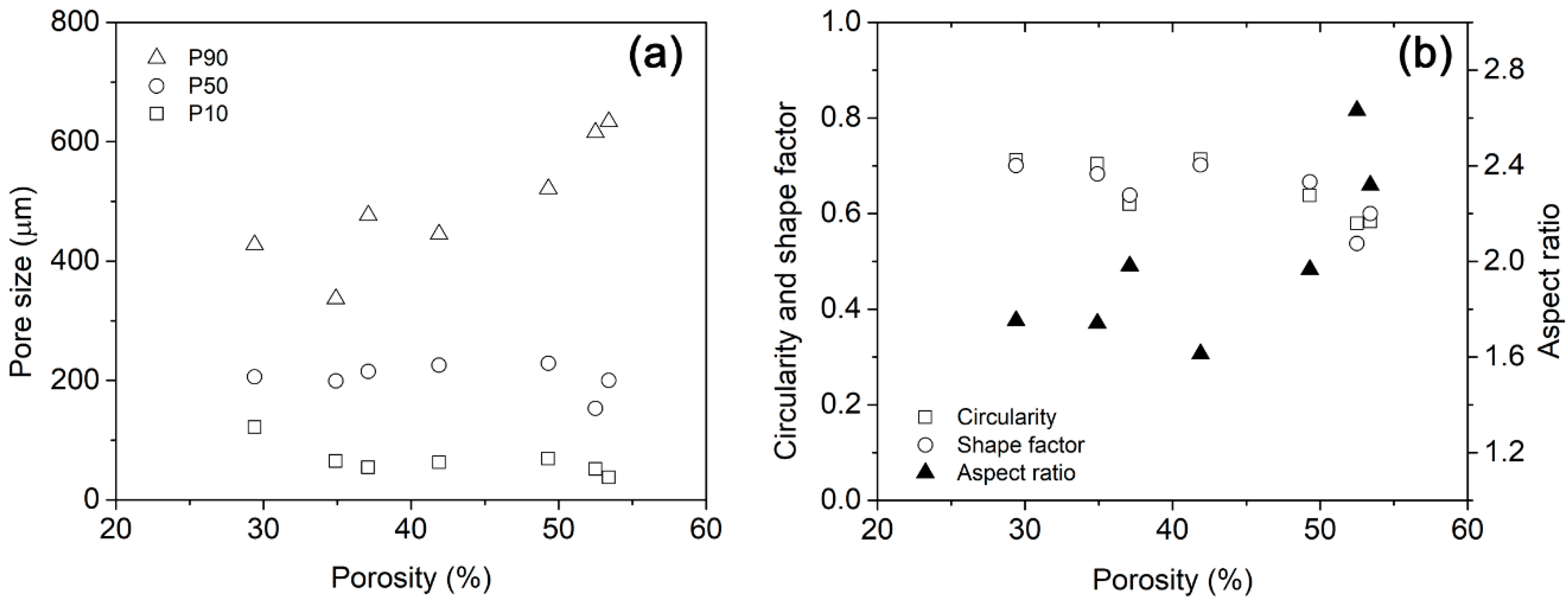
2.2. Image Analysis
2.3. Simulations
3. Results and Discussion
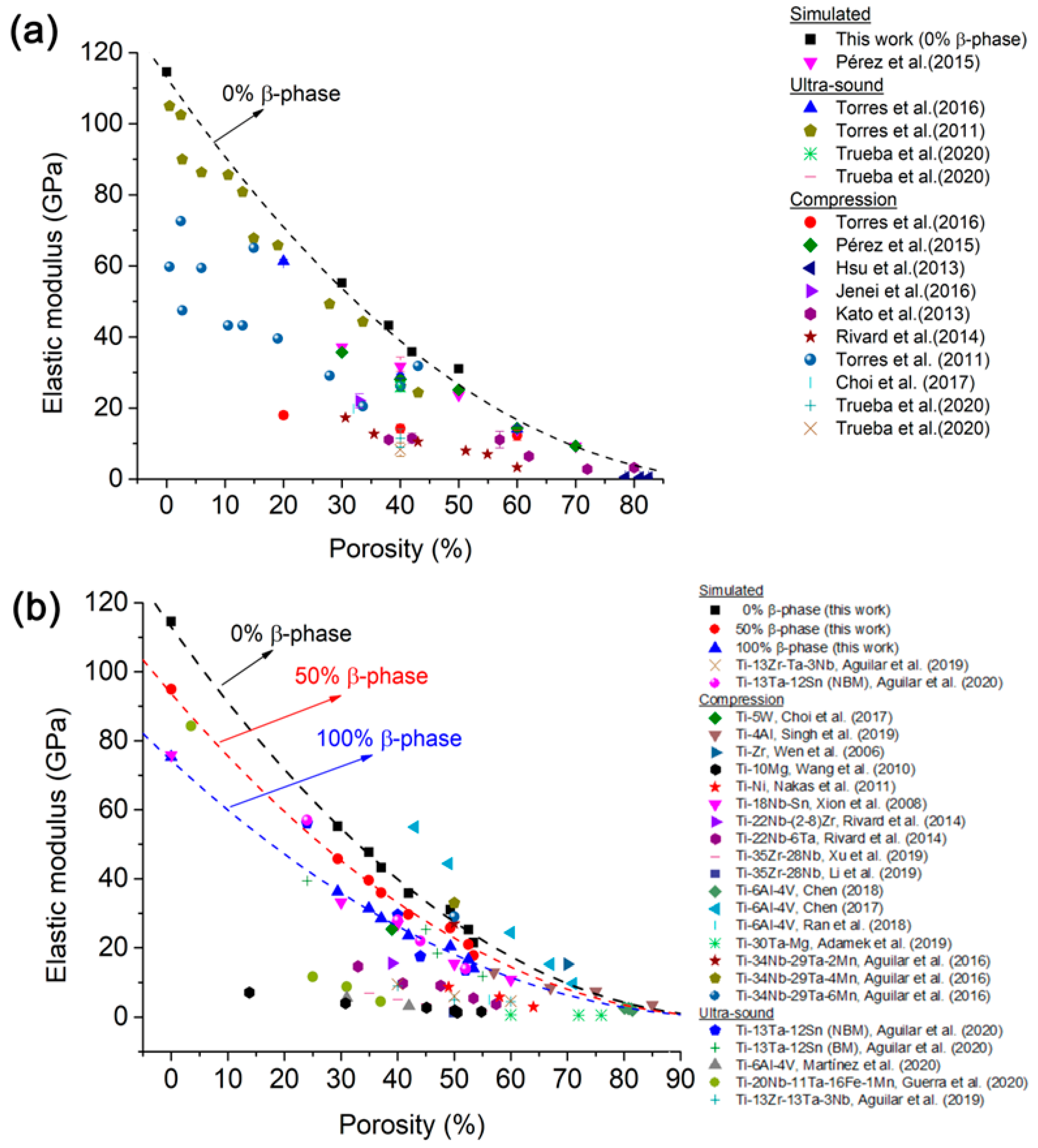
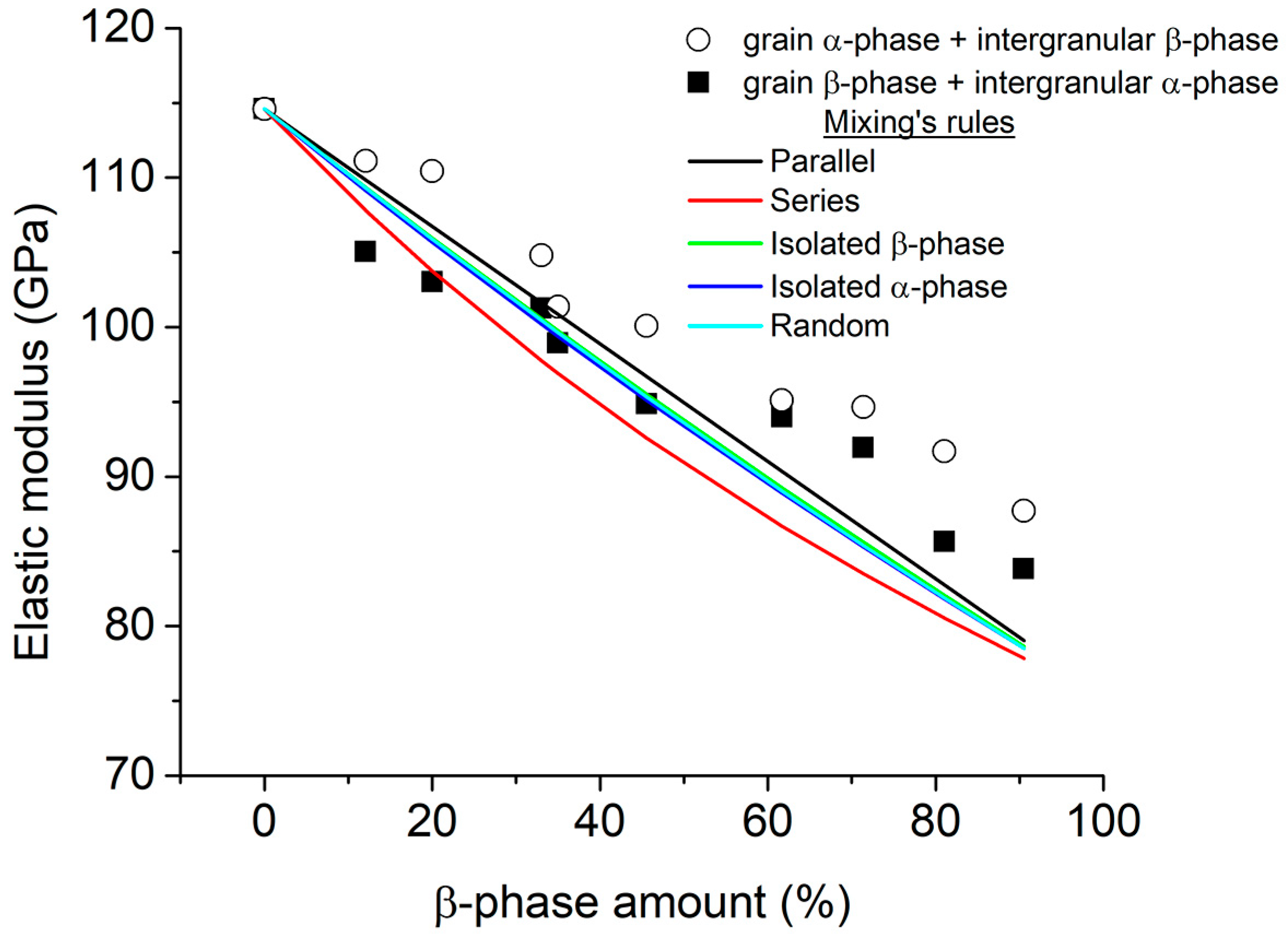
3.1. Effect of the Microstructure on E Values
3.2. Effect That Microstructure and Porosity Have on E Values
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Analytical Models to Determine E Values
References
- Li, P.; Ma, X.; Tong, T.; Wang, Y. Microstructural and mechanical properties of β-type Ti–Mo–Nb biomedical alloys with low elastic modulus. J. Alloys Compd. 2020, 815, 152412. [Google Scholar] [CrossRef]
- Rajabi, F.; Zarei Hanzaki, A.; Abedi, H.R.; Farghadany, E. Corrosion behavior of thermo-mechanically processed biomedical Ti-29Nb–13Ta–4.6Zr. J. Alloys Compd. 2017, 725, 23–31. [Google Scholar] [CrossRef]
- Yan, S.; Song, G.-L.; Li, Z.; Wang, H.; Zheng, D.; Cao, F.; Horynova, M.; Dargusch, M.S.; Zhou, L. A state-of-the-art review on passivation and biofouling of Ti and its alloys in marine environments. J. Mater. Sci. Technol. 2018, 34, 421–435. [Google Scholar] [CrossRef]
- Ivlev, I.; Vacek, J.; Kneppo, P. Multi-criteria decision analysis for supporting the selection of medical devices under uncertainty. Eur. J. Oper. Res. 2015, 247, 216–228. [Google Scholar] [CrossRef]
- Pruchova, E.; Kosova, M.; Fojt, J.; Jarolimova, P.; Jablonska, E.; Hybasek, V.; Joska, L. A two-phase gradual silver release mechanism from a nanostructured TiAlV surface as a possible antibacterial modification in implants. Bioelectrochemistry 2019, 127, 26–34. [Google Scholar] [CrossRef]
- Karacan, I.; Ben-Nissan, B.; Wang, H.A.; Juritza, A.; Swain, M.V.; Müller, W.H.; Chou, J.; Stamboulis, A.; Macha, I.J.; Taraschi, V. Mechanical testing of antimicrobial biocomposite coating on metallic medical implants as drug delivery system. Mater. Sci. Eng. C 2019, 104, 109757. [Google Scholar] [CrossRef]
- Ferraris, S.; Spriano, S. Antibacterial titanium surfaces for medical implants. Mater. Sci. Eng. C 2016, 61, 965–978. [Google Scholar] [CrossRef] [PubMed]
- Geetha, M.; Singh, A.K.K.; Asokamani, R.; Gogia, A.K.K. Ti based biomaterials, the ultimate choice for orthopaedic implants—A review. Prog. Mater. Sci. 2009, 54, 397–425. [Google Scholar] [CrossRef]
- Biesiekierski, A.; Wang, J.; Abdel-Hady Gepreel, M.; Wen, C. A new look at biomedical Ti-based shape memory alloys. Acta Biomater. 2012, 8, 1661–1669. [Google Scholar] [CrossRef]
- Ishida, T.; Wakai, E.; Hagiwara, M.; Makimura, S.; Tada, M.; Asner, D.M.; Casella, A.; Devaraj, A.; Edwards, D.; Prabhakaran, R.; et al. Study of the radiation damage effect on Titanium metastable beta alloy by high intensity proton beam. Nucl. Mater. Energy 2018, 15, 169–174. [Google Scholar] [CrossRef]
- Elias, C.N.; Lima, J.H.C.; Valiev, R.; Meyers, M.A. Biomedical applications of titanium and its alloys. Biol. Mater. Sci. 2008, 60, 46–49. [Google Scholar] [CrossRef]
- Abdel-Hady Gepreel, M.; Niinomi, M. Biocompatibility of Ti-alloys for long-term implantation. J. Mech. Behav. Biomed. Mater. 2013, 20, 407–415. [Google Scholar] [CrossRef] [PubMed]
- Leyens, C.; Peters, M. Titanium and Titanium Alloys; Leyens, C., Peters, M., Eds.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Long, M.; Rack, H. Titanium alloys in total joint replacement—A materials science perspective. Biomaterials 1998, 19, 1621–1639. [Google Scholar] [CrossRef] [PubMed]
- Peters, M.; Kumpfert, J.; Ward, C.H.; Leyens, C. Titanium Alloys for Aerospace Applications. Adv. Eng. Mater. 2003, 5, 419–427. [Google Scholar] [CrossRef]
- Singh, R.; Lee, P.D.; Dashwood, R.J.; Lindley, T.C. Titanium foams for biomedical applications: A review. Mater. Technol. 2010, 25, 127–136. [Google Scholar] [CrossRef]
- Aguilar, C.; Pio, E.; Medina, A.; Mangalaraja, R.V.; Salvo, C.; Alfonso, I.; Guzmán, D.; Bejar, L. Structural Study of Novel Nanocrystalline fcc Ti-Ta-Sn Alloy. Metall. Mater. Trans. A 2019, 50, 2061–2065. [Google Scholar] [CrossRef]
- Prasanthi, T.N.; Sudha, C.; Ravikirana; Saroja, S. Formation and reversion of metastable fcc phase in a Ti–5Ta–2Nb explosive clad. Mater. Charact. 2016, 116, 24–32. [Google Scholar] [CrossRef]
- Bolokang, A.S.; Phasha, M.J.; Motaung, D.E.; Cummings, F.R.; Muller, T.F.G.; Arendse, C.J. Microstructure and phase transformation on milled and unmilled Ti induced by water quenching. Mater. Lett. 2014, 132, 157–161. [Google Scholar] [CrossRef]
- Yu, Q.; Kacher, J.; Gammer, C.; Traylor, R.; Samanta, A.; Yang, Z.; Minor, A.M. In situ TEM observation of FCC Ti formation at elevated temperatures. Scr. Mater. 2017, 140, 9–12. [Google Scholar] [CrossRef]
- Van Heerden, D.; Josell, D.; Shechtman, D. The formation of f.c.c. titanium in titanium-aluminum multilayers. Acta Mater. 1996, 44, 297–306. [Google Scholar] [CrossRef]
- Zhang, D.; Ying, D. Formation of fcc titanium during heating high-energy, ball-milled Al–Ti powders. Mater. Lett. 2001, 50, 149–153. [Google Scholar] [CrossRef]
- Ahuja, R.; Fraser, H.L. Structure and mechanical properties of nanolaminated Ti-Al thin films. JOM 1994, 46, 35–39. [Google Scholar] [CrossRef]
- Ren, J.; Sun, Q.; Xiao, L.; Ding, X.; Sun, J. Size-dependent of compression yield strength and deformation mechanism in titanium single-crystal nanopillars orientated [0001] and [1120]. Mater. Sci. Eng. A 2014, 615, 22–28. [Google Scholar] [CrossRef]
- Lindemann, I.; Schmidt, R.; Pilz, S.; Gebel, B.; Teresiak, A.; Gebert, A. Ultrafine-grained Ti–40Nb prepared by reactive milling of the elements in hydrogen. J. Alloys Compd. 2017, 729, 1244–1249. [Google Scholar] [CrossRef]
- Aguilar, C.; Pio, E.; Medina, A.; Martínez, C.; Sancy, M.; Guzman, D. Evolution of synthesis of FCC nanocrystalline solid solution and amorphous phase in the Ti–Ta based alloy by high milling energy. J. Alloys Compd. 2021, 854, 155980. [Google Scholar] [CrossRef]
- Smith, D.; Joris, O.P.J.; Sankaran, A.; Weekes, H.E.; Bull, D.J.; Prior, T.J.; Dye, D.; Errandonea, D.; Proctor, J.E. On the high-pressure phase stability and elastic properties of β-titanium alloys. J. Phys. Condens. Matter 2017, 29, 155401. [Google Scholar] [CrossRef]
- Heiming, A.; Petry, W.; Trampenau, J.; Alba, M.; Herzig, C.; Schober, H.R.; Vogl, G. Phonon dispersion of the bcc phase of group-IV metals. II. bcc zirconium, a model case of dynamical precursors of martensitic transitions. Phys. Rev. B 1991, 43, 10948–10962. [Google Scholar] [CrossRef]
- Chinnappan, R.; Panigrahi, B.K.; van de Walle, A. First-principles study of phase equilibrium in Ti–V, Ti–Nb, and Ti–Ta alloys. Calphad 2016, 54, 125–133. [Google Scholar] [CrossRef]
- Sen, M.; Suman, S.; Mukherjee, S.; Banerjee, T.; Sivaprasad, S.; Tarafder, S.; Bhattacharjee, A.; Kumar Kar, S. Low cycle fatigue behavior and deformation mechanism of different microstructures in Ti–5Al–5Mo–5V–3Cr alloy. Int. J. Fatigue 2021, 148, 106238. [Google Scholar] [CrossRef]
- Lee, S.W.; Oh, J.M.; Kim, J.H.; Park, C.H.; Hong, J.-K.; Yeom, J.-T. Demonstration of martensite reorientation-induced plasticity by ultra-high strength titanium alloys. Mater. Sci. Eng. A 2021, 807, 140878. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, L.; Yang, H. Microstructure evolution of different loading zones during TA15 alloy multi-cycle isothermal local forging. Mater. Sci. Eng. A 2011, 528, 5112–5121. [Google Scholar] [CrossRef]
- Namus, R.; Nutter, J.; Qi, J.; Rainforth, W.M. Sliding speed influence on the tribo-corrosion behaviour of Ti6Al4V alloy in simulated body fluid. Tribol. Int. 2021, 160, 107023. [Google Scholar] [CrossRef]
- Aguilar, C.; Arancibia, M.; Alfonso, I.; Sancy, M.; Tello, K.; Salinas, V.; De Las Cuevas, F. Influence of Porosity on the Elastic Modulus of Ti-Zr-Ta-Nb Foams with a Low Nb Content. Metals 2019, 9, 176. [Google Scholar] [CrossRef]
- Egbo, M.K. A fundamental review on composite materials and some of their applications in biomedical engineering. J. King Saud Univ.-Eng. Sci. 2021, 33, 557–568. [Google Scholar] [CrossRef]
- Aguilar, C.; Guerra, C.; Lascano, S.; Guzman, D.; Rojas, P.A.; Thirumurugan, M.; Bejar, L.; Medina, A. Synthesis and characterization of Ti–Ta–Nb–Mn foams. Mater. Sci. Eng. C 2016, 58, 420–431. [Google Scholar] [CrossRef]
- Pérez, L.; Lascano, S.; Aguilar, C.; Domancic, D.; Alfonso, I. Simplified fractal FEA model for the estimation of the Young’s modulus of Ti foams obtained by powder metallurgy. Mater. Des. 2015, 83, 276–283. [Google Scholar] [CrossRef]
- Zhu, K.; Li, C.; Zhu, Z.; Liu, C.S. Measurement of the dynamic Young’s modulus of porous titanium and Ti6Al4V. J. Mater. Sci. 2007, 42, 7348–7353. [Google Scholar] [CrossRef]
- Ran, Q.; Yang, W.; Hu, Y.; Shen, X.; Yu, Y.; Xiang, Y.; Cai, K. Osteogenesis of 3D printed porous Ti6Al4V implants with different pore sizes. J. Mech. Behav. Biomed. Mater. 2018, 84, 1–11. [Google Scholar] [CrossRef]
- Martínez, C.; Guerra, C.; Silva, D.; Cubillos, M.; Briones, F.; Muñoz, L.; Páez, M.A.A.; Aguilar, C.; Sancy, M. Effect of porosity on mechanical and electrochemical properties of Ti-6Al-4V alloy. Electrochim. Acta 2020, 338, 135858. [Google Scholar] [CrossRef]
- Chen, S.Y.; Kuo, C.N.; Su, Y.L.; Huang, J.C.; Wu, Y.C.; Lin, Y.H.; Chung, Y.C.; Ng, C.H. Microstructure and fracture properties of open-cell porous Ti-6Al-4V with high porosity fabricated by electron beam melting. Mater. Charact. 2018, 138, 255–262. [Google Scholar] [CrossRef]
- Chen, S.Y.; Huang, J.C.; Pan, C.T.; Lin, C.H.; Yang, T.L.; Huang, Y.S.; Ou, C.H.; Chen, L.Y.; Lin, D.Y.; Lin, H.K.; et al. Microstructure and mechanical properties of open-cell porous Ti-6Al-4V fabricated by selective laser melting. J. Alloys Compd. 2017, 713, 248–254. [Google Scholar] [CrossRef]
- Martínez, C.; Briones, F.; Araya, N.; Aguilar, C.; Machado, I.; Guerra, C.; Medina, A.; Sancy, M. Influence of the synthesis technique on tribological behavior of a Ti-6Al-4V alloy. Mater. Lett. 2020, 281, 128627. [Google Scholar] [CrossRef]
- Silva, D.; Guerra, C.; Muñoz, H.; Aguilar, C.; Walter, M.; Azocar, M.; Muñoz, L.; Gürbüz, E.; Ringuedé, A.; Cassir, M.; et al. The effect of Staphylococcus aureus on the electrochemical behavior of porous Ti-6Al-4V alloy. Bioelectrochemistry 2020, 136, 107622. [Google Scholar] [CrossRef] [PubMed]
- Bolokang, A.S.; Mathabathe, M.N.; Motaung, D.E.; Arendse, C.J.; Swart, H.C. Grain structure orientational change in Ti6Al4V alloys induced by sea water quenching and novel stress relief annealing process. Mater. Chem. Phys. 2023, 297, 127328. [Google Scholar] [CrossRef]
- Öchsner, A.; Lamprecht, K. On the Uniaxial Compression Behavior of Regular Shaped Cellular Metals. Mech. Res. Commun. 2003, 30, 573–579. [Google Scholar] [CrossRef]
- Sebsadji, S.K.; Chouicha, K. Determining Periodic Representative Volumes of Concrete Mixtures Based on the Fractal Analysis. Int. J. Solids Struct. 2012, 49, 2941–2950. [Google Scholar] [CrossRef]
- Ibrahim, A.; Zhang, F.; Otterstein, E.; Burkel, E. Processing of porous Ti and Ti5Mn foams by spark plasma sintering. Mater. Des. 2011, 32, 146–153. [Google Scholar] [CrossRef]
- Zhang, L.; Tan, J.; Meng, Z.D.; He, Z.Y.; Zhang, Y.Q.; Jiang, Y.H.; Zhou, R. Low elastic modulus Ti-Ag/Ti radial gradient porous composite with high strength and large plasticity prepared by spark plasma sintering. Mater. Sci. Eng. A 2017, 688, 330–337. [Google Scholar] [CrossRef]
- Mansilla, J.; Moreno-Castilla, C.; Bosch, P.; Alemán, I.; Pijoan, C.; Botella, M. On porosity of archeological bones II. Textural characterization of Mesoamerican human bones. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2014, 414, 493–499. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, Z.; Zhang, B.; Kundu, T.; Sevostianov, I. The effect of porosity on the elastic properties of cortical bone and ultrasound propagation. Int. J. Eng. Sci. 2023, 182, 103772. [Google Scholar] [CrossRef]
- Zhang, S.-Z.; Cui, H.; Li, M.-M.; Yu, H.; Vitos, L.; Yang, R.; Hu, Q.-M. First-principles study of phase stability and elastic properties of binary Ti-xTM (TM = V,Cr,Nb,Mo) and ternary Ti-15TM-yAl alloys. Mater. Des. 2016, 110, 80–89. [Google Scholar] [CrossRef]
- Düster, A.; Sehlhorst, H.-G.; Rank, E. Numerical homogenization of heterogeneous and cellular materials utilizing the finite cell method. Comput. Mech. 2012, 50, 413–431. [Google Scholar] [CrossRef]
- Shen, H.; Brinson, L.C. Finite element modeling of porous titanium. Int. J. Solids Struct. 2007, 44, 320–335. [Google Scholar] [CrossRef]
- Hsu, H.-C.; Hsu, S.-K.; Wu, S.-C.; Wang, P.-H.; Ho, W.-F. Design and characterization of highly porous titanium foams with bioactive surface sintering in air. J. Alloys Compd. 2013, 575, 326–332. [Google Scholar] [CrossRef]
- Saeki, Y.; Yamada, Y.; Ishikawa, K. Relationship between Hydrogen Permeation and Microstructure in Nb–TiCo Two-Phase Alloys. J. Alloys Compd. 2015, 645, S32–S35. [Google Scholar] [CrossRef]
- Cho, J.Y.; Xu, W.; Brandt, M.; Qian, M. Selective laser melting-fabricated Ti-6Al-4V alloy: Microstructural inhomogeneity, consequent variations in elastic modulus and implications. Opt. Laser Technol. 2019, 111, 664–670. [Google Scholar] [CrossRef]
- Gain, A.K.; Zhang, L.; Lim, S. Tribological behavior of Ti-6Al-4V alloy: Subsurface structure, damage mechanism and mechanical properties. Wear 2021, 464–465, 203551. [Google Scholar] [CrossRef]
- Zhou, L.; Yuan, T.; Tang, J.; He, J.; Li, R. Mechanical and corrosion behavior of titanium alloys additively manufactured by selective laser melting—A comparison between nearly β titanium, α titanium and α + β titanium. Opt. Laser Technol. 2019, 119, 105625. [Google Scholar] [CrossRef]
- Torres, Y.; Pavón, J.J.; Nieto, I.; Rodríguez, J.A. Conventional Powder Metallurgy Process and Characterization of Porous Titanium for Biomedical Applications. Metall. Mater. Trans. B 2011, 42, 891–900. [Google Scholar] [CrossRef]
- Torres, Y.; Lascano, S.; Bris, J.; Pavón, J.; Rodriguez, J.A. Development of porous titanium for biomedical applications: A comparison between loose sintering and space-holder techniques. Mater. Sci. Eng. C 2014, 37, 148–155. [Google Scholar] [CrossRef]
- Jenei, P.; Choi, H.; Tóth, A.; Choe, H.; Gubicza, J. Mechanical behavior and microstructure of compressed Ti foams synthesized via freeze casting. J. Mech. Behav. Biomed. Mater. 2016, 63, 407–416. [Google Scholar] [CrossRef] [PubMed]
- Trueba, P.; Chicardi, E.; Rodríguez-Ortiz, J.A.; Torres, Y. Development and implementation of a sequential compaction device to obtain radial graded porosity cylinders. J. Manuf. Process. 2020, 50, 142–153. [Google Scholar] [CrossRef]
- Torres, Y.; Trueba, P.; Pavón, J.J.; Chicardi, E.; Kamm, P.; García-Moreno, F.; Rodríguez-Ortiz, J.A. Design, processing and characterization of titanium with radial graded porosity for bone implants. Mater. Des. 2016, 110, 179–187. [Google Scholar] [CrossRef]
- Banhart, J. Manufacture, Characterisation and Application of Cellular Metals and Metal Foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Ryan, G.; Pandit, A.; Apatsidis, D. Fabrication Methods of Porous Metals for Use in Orthopaedic Applications. Biomaterials 2006, 27, 2651–2670. [Google Scholar] [CrossRef]
- Manonukul, A.; Srikudvien, P.; Tange, M. Microstructure and Mechanical Properties of Commercially Pure Titanium Foam with Varied Cell Size Fabricated by Replica Impregnation Method. Mater. Sci. Eng. A 2016, 650, 432–437. [Google Scholar] [CrossRef]
- Rivard, J.; Brailovski, V.; Dubinskiy, S.; Prokoshkin, S. Fabrication, morphology and mechanical properties of Ti and metastable Ti-based alloy foams for biomedical applications. Mater. Sci. Eng. C 2014, 45, 421–433. [Google Scholar]
- Xiong, J.; Li, Y.; Wang, X.; Hodgson, P.; Wen, C. Mechanical Properties and Bioactive Surface Modification via Alkali-Heat Treatment of a Porous Ti–18Nb–4Sn Alloy for Biomedical Applications. Acta Biomater 2008, 4, 1963–1968. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, C.; Aguirre, T.; Martínez, C.; De Barbieri, F.; Martín, F.S.; Salinas, V.; Alfonso, I. Improving the Mechanical Strength of Ternary Beta Titanium Alloy (Ti-Ta-Sn) Foams, Using a Bimodal Microstructure. Mater. Des. 2020, 195, 108945. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties. Cambridge University Press: Cambridge, UK, 1997; ISBN 9780521499118. [Google Scholar]
- Spriggs, R.M. Expression for Effect of Porosity on Elastic Modulus of Polycrystalline Refractory Materials, Particularly Aluminum Oxide. J. Am. Ceram. Soc. 1961, 44, 628–629. [Google Scholar] [CrossRef]
- Warren, W.E.; Kraynik, A.M. The Linear Elastic Properties of Open-Cell Foams. J. Appl. Mech. 1988, 55, 341–346. [Google Scholar] [CrossRef]
- Nielsen, L.F. Elasticity and Damping of Porous Materials and Impregnated Materials. J. Am. Ceram. Soc. 1984, 67, 93–98. [Google Scholar] [CrossRef]
- Pabst, W.; Gregorová, E. New Relation for the Porosity Dependence of the Effective Tensile Modulus of Brittle Materials. J. Mater. Sci. 2004, 39, 3501–3503. [Google Scholar] [CrossRef]
- Zhu, H.X.; Mills, N.J.; Knott, J.F. Analysis of the high strain compression of open-cell foams. J. Mech. Phys. Solids 1997, 45, 1875–1904. [Google Scholar] [CrossRef]
- Knudsen, F.P. Dependence of Mechanical Strength of Brittle Polycrystalline Specimens on Porosity and Grain Size. J. Am. Ceram. Soc. 1959, 42, 376–387. [Google Scholar] [CrossRef]
- Phani, K.K.; Niyogi, S.K. Young’s modulus of porous brittle solids. J. Mater. Sci. 1987, 22, 257–263. [Google Scholar] [CrossRef]
- Kato, K.; Ochiai, S.; Yamamoto, A.; Daigo, Y.; Honma, K.; Matano, S.; Omori, K. Novel multilayer Ti foam with cortical bone strength and cytocompatibility. Acta Biomater. 2013, 9, 5802–5809. [Google Scholar] [CrossRef]
- Choi, H.; Shil’ko, S.; Gubicza, J.; Choe, H. Study of the compression and wear-resistance properties of freeze-cast Ti and Ti-5W alloy foams for biomedical applications. J. Mech. Behav. Biomed. Mater. 2017, 72, 66–73. [Google Scholar] [CrossRef]
- Singh, P.; Singh, I.B.; Mondal, D.P. A comparative study on compressive deformation and corrosion behaviour of heat treated Ti4wt%Al foam of different porosity made of milled and unmilled powders. Mater. Sci. Eng. C 2019, 98, 918–929. [Google Scholar] [CrossRef]
- Wen, C.E.; Yamada, Y.; Hodgson, P.D. Fabrication of novel TiZr alloy foams for biomedical applications. Mater. Sci. Eng. C 2006, 26, 1439–1444. [Google Scholar] [CrossRef]
- İpek Nakaş, G.; Dericioglu, A.F.; Bor, Ş. Fatigue behavior of TiNi foams processed by the magnesium space holder technique. J. Mech. Behav. Biomed. Mater. 2011, 4, 2017–2023. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Tian, J.; Liu, Z.; Lu, X.; Hayat, M.D.; Yan, Y.; Li, Z.; Qu, X.; Wen, C. Novel porous Ti35Zr28Nb scaffolds fabricated by powder metallurgy with excellent osteointegration ability for bone-tissue engineering applications. Mater. Sci. Eng. C 2019, 105, 110015. [Google Scholar] [CrossRef] [PubMed]
- Adamek, G.; Kozlowski, M.; Jurczyk, M.; Wirstlein, P.; Zurawski, J.; Jakubowicz, J. Formation and Properties of Biomedical Ti-Ta Foams Prepared from Nanoprecursors by Thermal Dealloying Process. Materials 2019, 12, 2668. [Google Scholar] [CrossRef] [PubMed]
- Guerra, C.; Sancy, M.; Walczak, M.; Martínez, C.; Ringuedé, A.; Cassir, M.; Han, J.; Ogle, K.; de Melo, H.G.; Salinas, V.; et al. Effect of added porosity on a novel porous Ti-Nb-Ta-Fe-Mn alloy exposed to simulated body fluid. Mater. Sci. Eng. C 2020, 111, 110758. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Q.; Tao, J.; Zhang, J.L.; Wang, T. Effects of Addition of NH4HCO3 on Pore Characteristics and Compressive Properties of Porous Ti-10%Mg Composites. Trans. Nonferrous Met. Soc. China (Engl. Ed.) 2011, 21, 1074–1079. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Y.; Munir, K.; Lin, J.; Brandt, M.; Atrens, A.; Xiao, Y.; Kanwar, J.R.; Wen, C. Novel β-Ti35Zr28Nb Alloy Scaffolds Manufactured Using Selective Laser Melting for Bone Implant Applications. Acta Biomater. 2019, 87, 273–284. [Google Scholar] [CrossRef]




| Designed β-Phase Amount (v/v%) | Obtained β-Phase Amount (v/v%) | Difference between Designed and Obtained β-Phase |
|---|---|---|
| 10 | 12.0 | 2.03 |
| 20 | 20.0 | 0. |
| 30 | 33.2 | 3.2 |
| 40 | 34.7 | −5.3 |
| 50 | 45.5 | −4.5 |
| 60 | 61.6 | 1.6 |
| 70 | 71.3 | 1.3 |
| 80 | 81.4 | 1.4 |
| 90 | 90.5 | 0.5 |
| Morphological Parameters | Characteristic of Porosity |
|---|---|
| Distribution of porosity | Homogenous |
| Shape pore | Sphere-cylinder |
| Aspect ratio | 1.1 |
| Distribution pore function | Normal distribution |
| Average pore size | 250 μm |
| Standard deviation | 50 μm |
| Designed Porosity (v/v%) | Obtained (Or Real) Porosity (v/v%) | Difference between Designed and Obtained Porosity |
|---|---|---|
| 29 | 29.4 | 0.4 |
| 34 | 34.8 | 0.8 |
| 38 | 37.0 | −1.0 |
| 43 | 41.8 | −1.2 |
| 47 | 49.2 | 2.2 |
| 52 | 52.5 | 0.5 |
| 56 | 53.4 | −2.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, C.; Henriquez, J.; Salvo, C.; Alfonso, I.; Araya, N.; Muñoz, L. Computational Study of the Influence of α/β-Phase Ratio and Porosity on the Elastic Modulus of Ti-Based Alloy Foams. Materials 2023, 16, 4064. https://doi.org/10.3390/ma16114064
Aguilar C, Henriquez J, Salvo C, Alfonso I, Araya N, Muñoz L. Computational Study of the Influence of α/β-Phase Ratio and Porosity on the Elastic Modulus of Ti-Based Alloy Foams. Materials. 2023; 16(11):4064. https://doi.org/10.3390/ma16114064
Chicago/Turabian StyleAguilar, Claudio, Javier Henriquez, Christopher Salvo, Ismelí Alfonso, Nicolas Araya, and Lisa Muñoz. 2023. "Computational Study of the Influence of α/β-Phase Ratio and Porosity on the Elastic Modulus of Ti-Based Alloy Foams" Materials 16, no. 11: 4064. https://doi.org/10.3390/ma16114064
APA StyleAguilar, C., Henriquez, J., Salvo, C., Alfonso, I., Araya, N., & Muñoz, L. (2023). Computational Study of the Influence of α/β-Phase Ratio and Porosity on the Elastic Modulus of Ti-Based Alloy Foams. Materials, 16(11), 4064. https://doi.org/10.3390/ma16114064