Failure Mechanism of Tensile CFRP Composite Plates with Variable Hole Diameter
Abstract
:1. Introduction
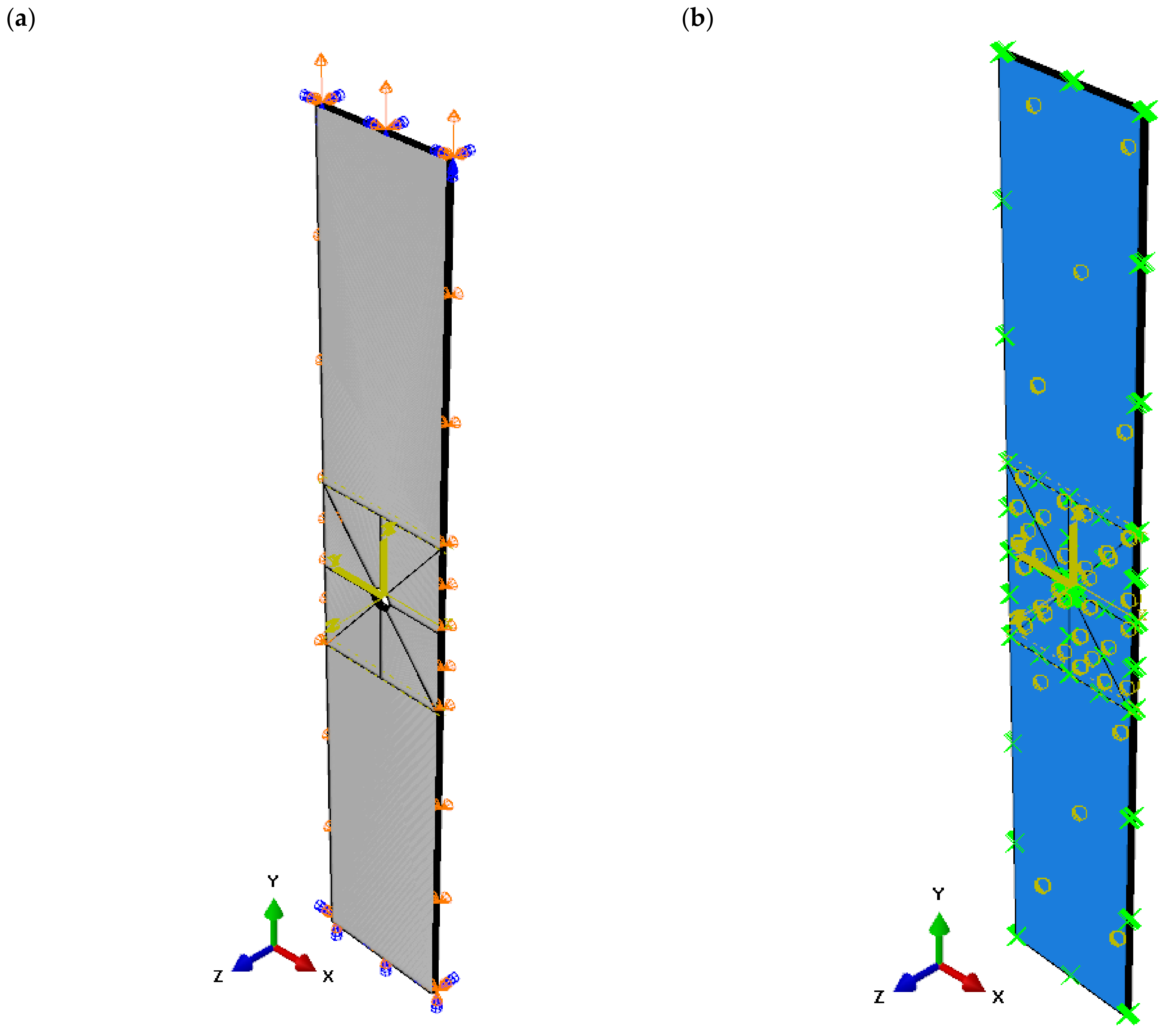
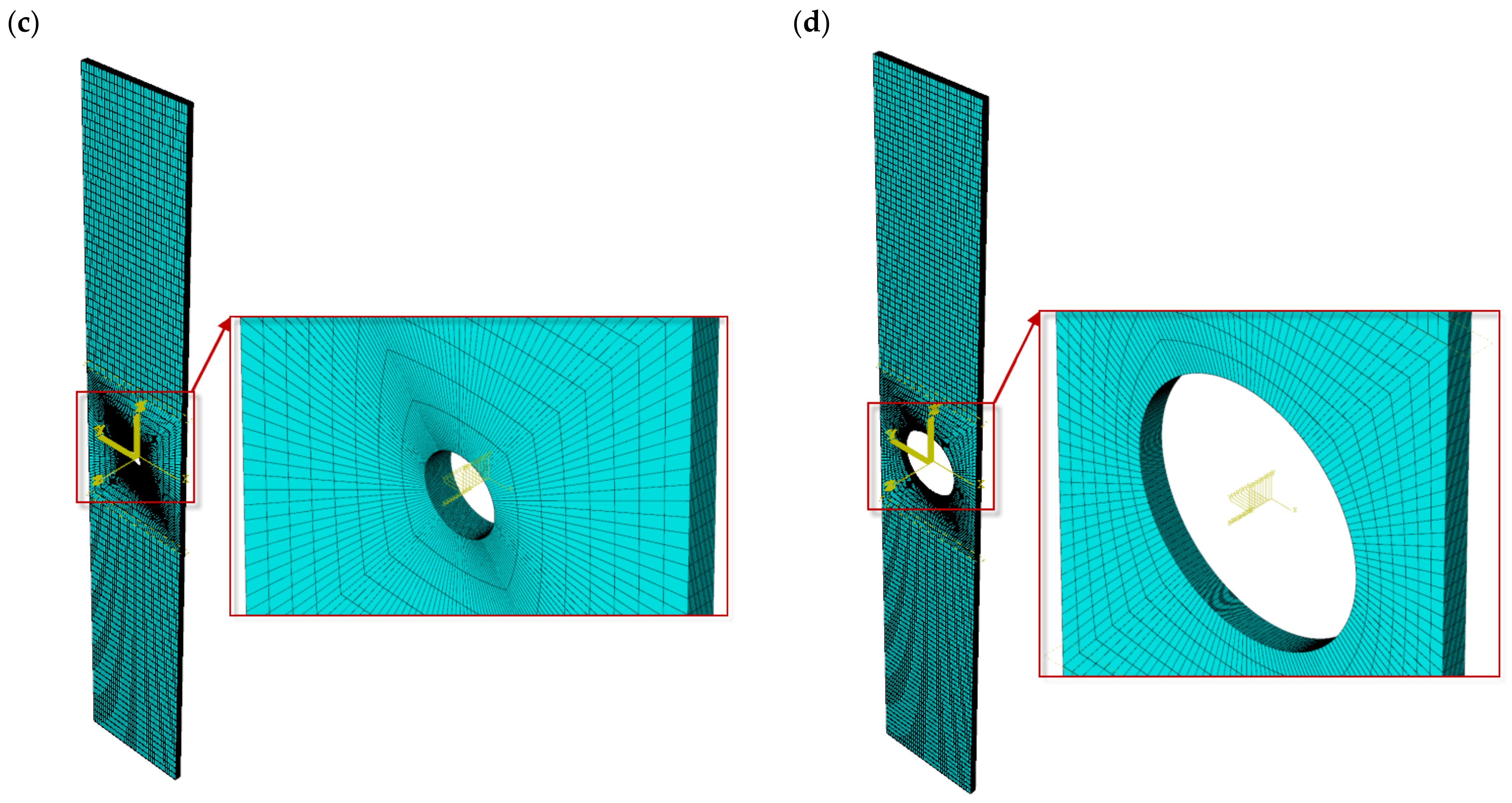
2. Object and Methodology
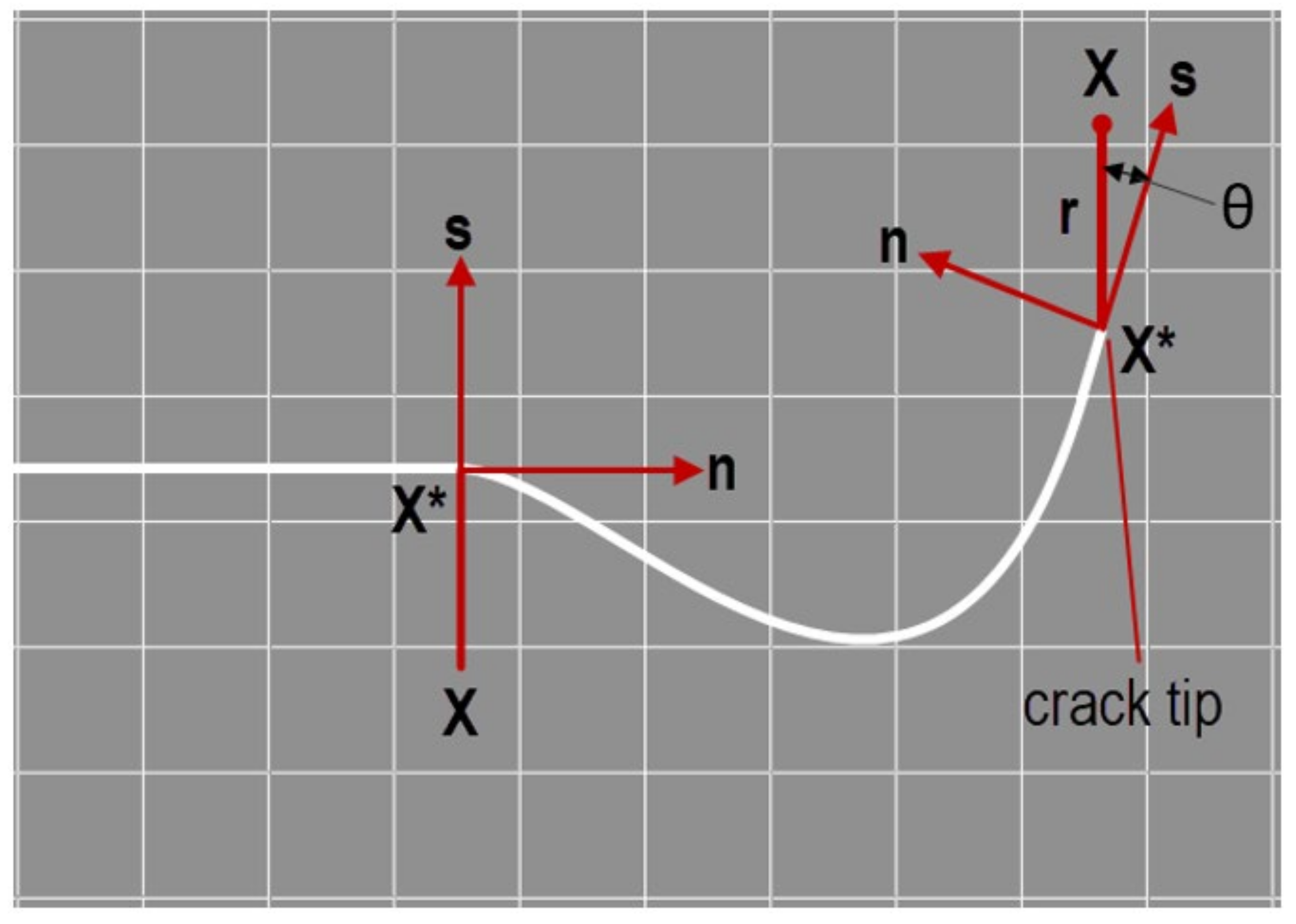
Theory of XFEM
3. Results and Discussion
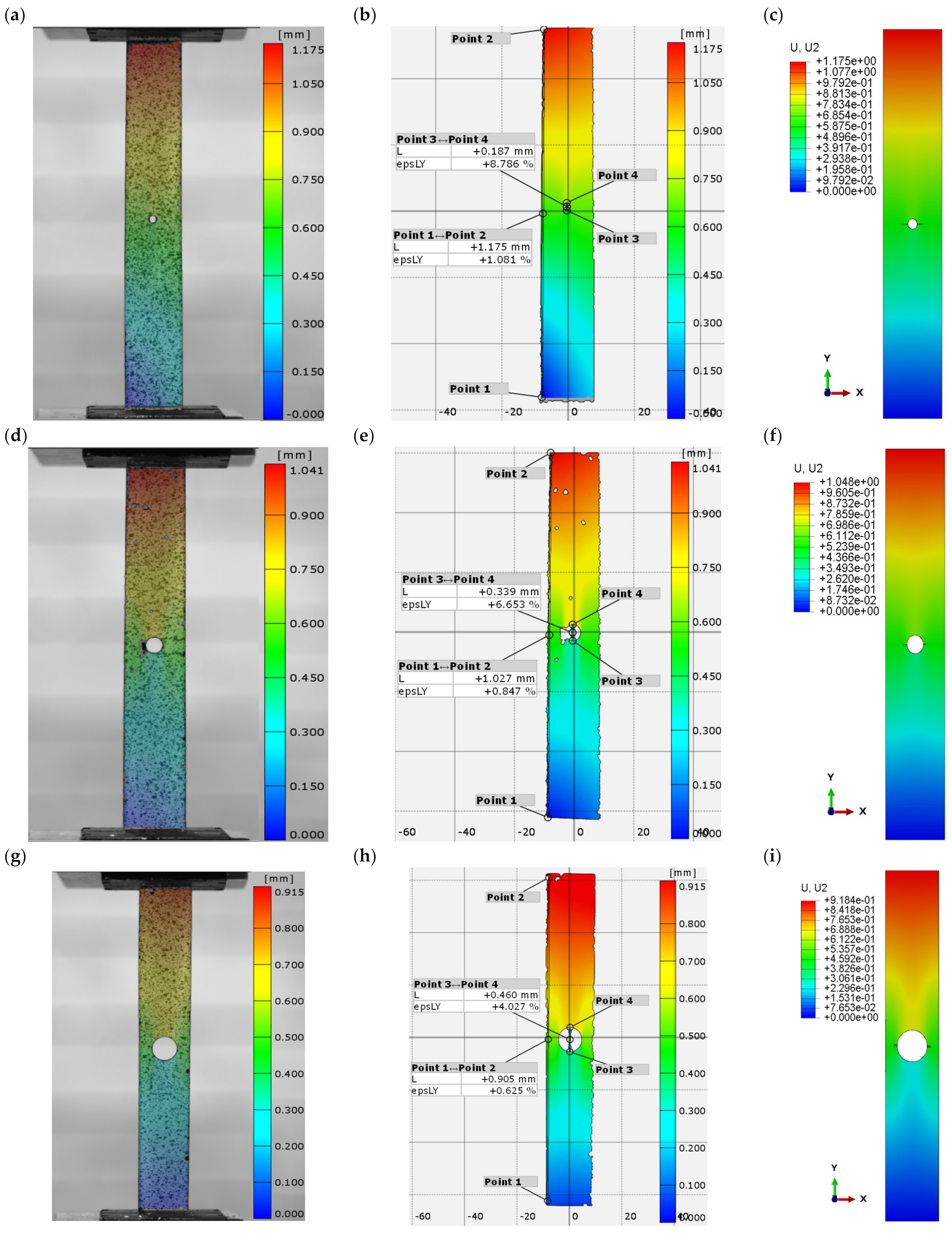
3.1. Plate Deformation
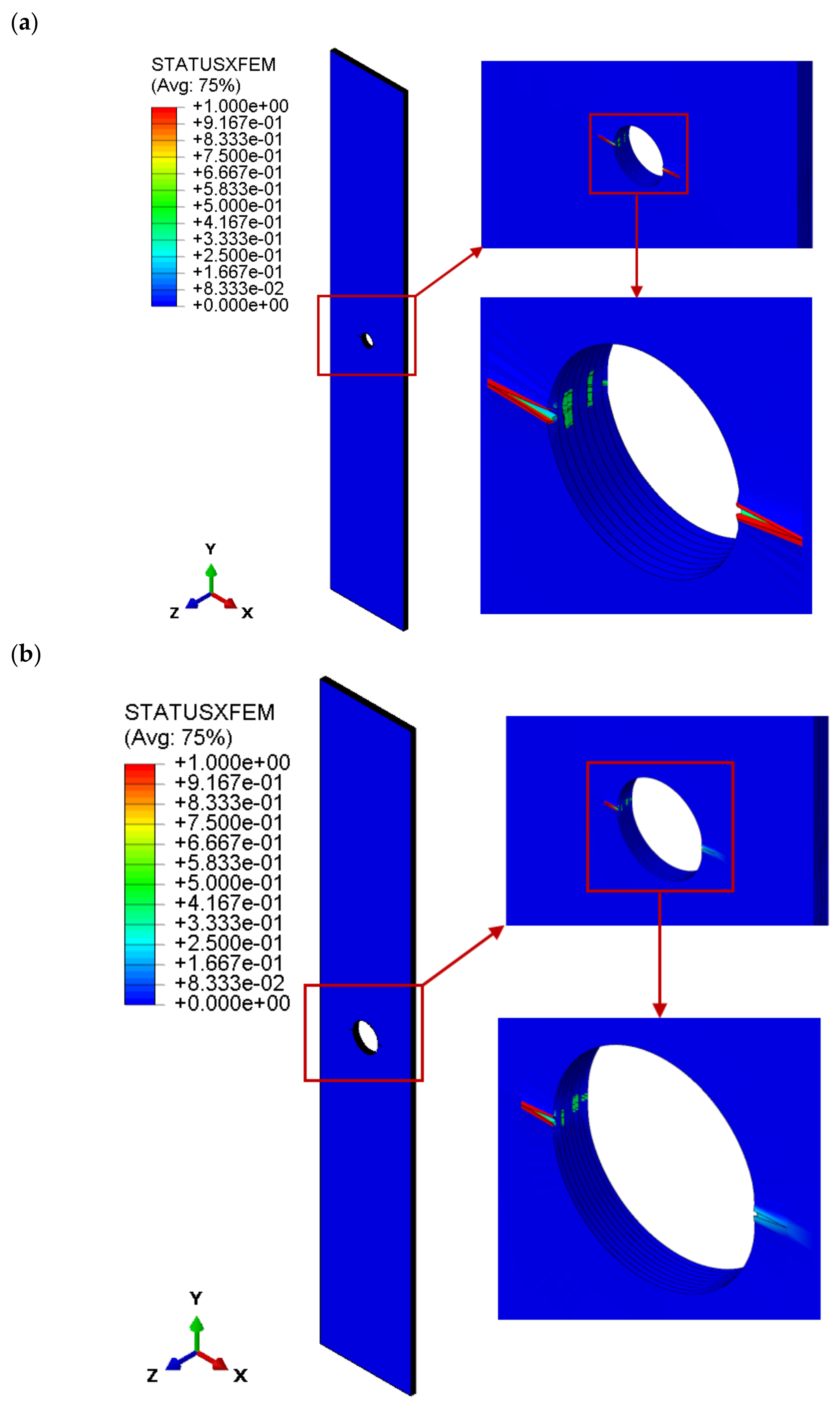
3.2. Crack Initiation
3.3. Failure of the Composite
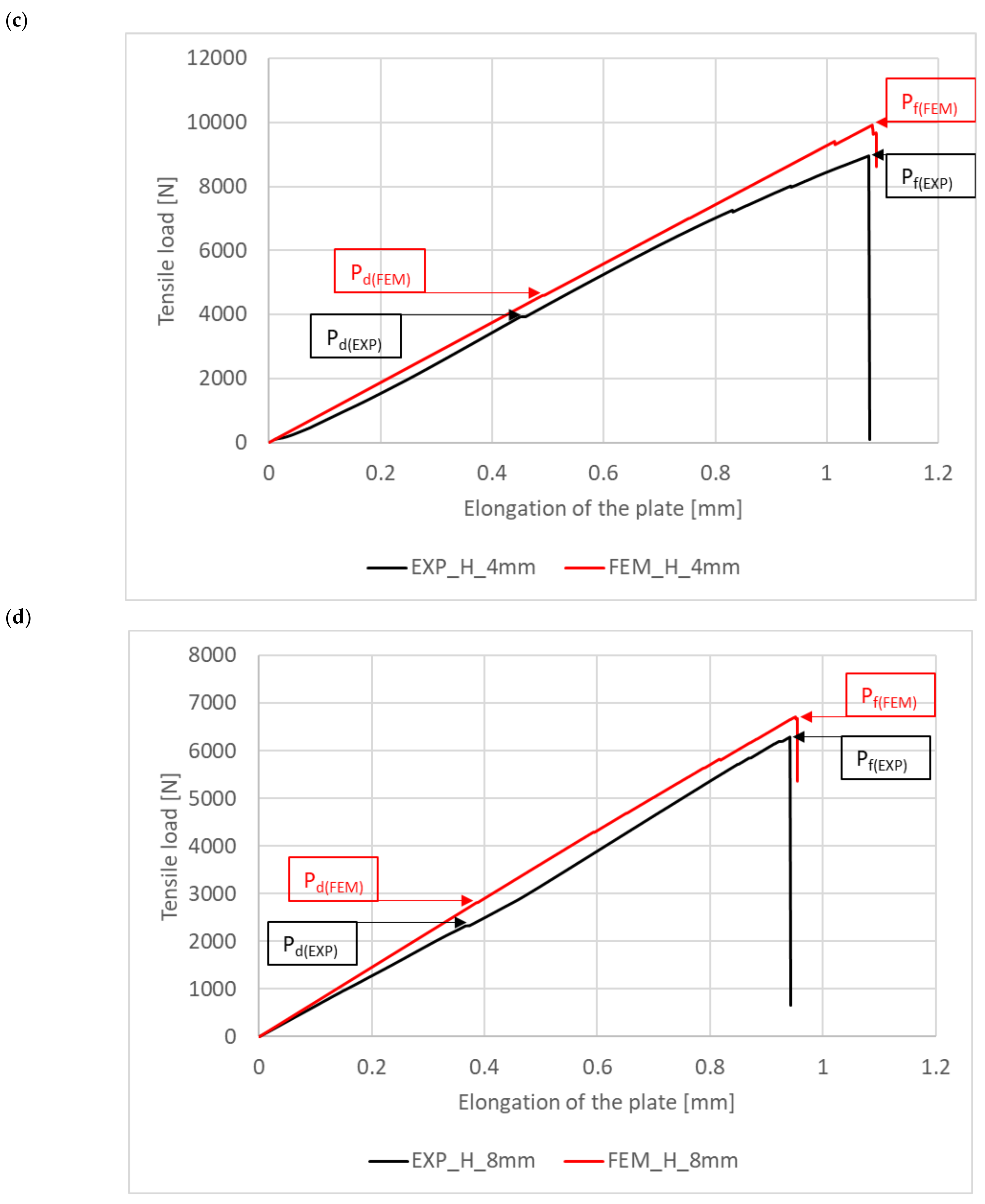
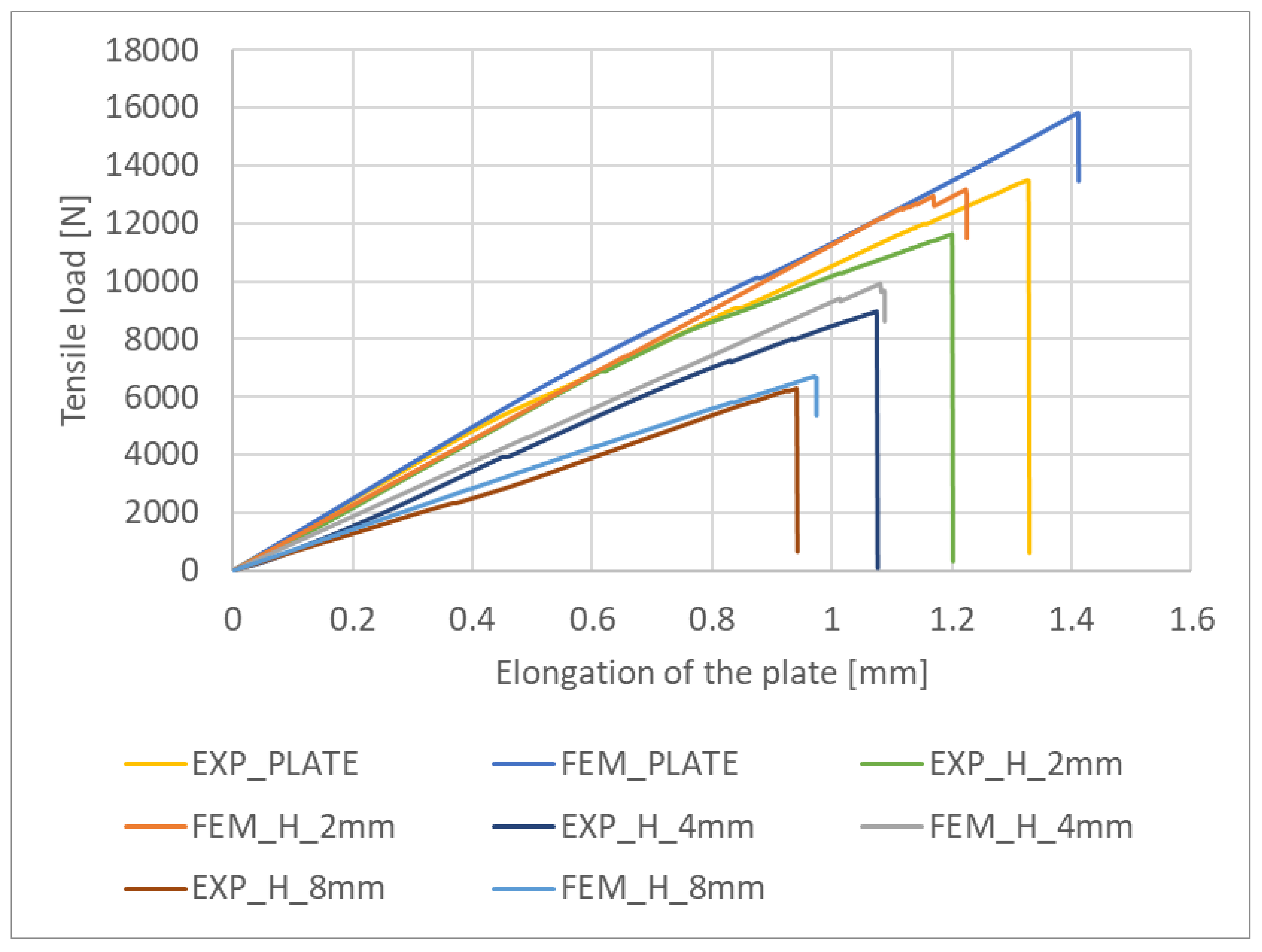
3.4. Damage and Failure Loads
4. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Campbell, F.C. Manufacturing Technology for Aerospace Structural Materials, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kassapoglou, C.; American Institute of Aeronautics and Astronautics. Design and Analysis of Composite Structures: With Applications to Aerospace Structures, 1st ed.; John Wiley & Sons: Reston, VA, USA, 2010. [Google Scholar]
- Mlýnek, J.; Petrů, M.; Martinec, T.; Koloor, S.S.R. Fabrication of High-Quality Polymer Composite Frame by a New Method of Fiber Winding Process. Polymers 2020, 12, 1037. [Google Scholar] [CrossRef]
- Jain, P.; Kumar, A. Postbuckling response of square laminates with a central circular/elliptical cutout. Compos. Struct. 2004, 65, 179–185. [Google Scholar] [CrossRef]
- Parlapalli, M.R.; Soh, K.C.; Shu, D.W.; Ma, G. Experimental investigation of delamination buckling of stitched composite laminates. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2024–2033. [Google Scholar] [CrossRef]
- Turvey, G.; Zhang, Y. A computational and experimental analysis of the buckling, postbuckling and initial failure of pultruded GRP columns. Comput. Struct. 2006, 84, 1527–1537. [Google Scholar] [CrossRef]
- Singer, J.; Arbocz, J.; Weller, T. Buckling Experiments. Experimental Methods in Buckling of Thin-walled Structure. In Basic Concepts, Columns, Beams, and Plates; John Wiley & Sons Inc.: New York, NY, USA, 1998. [Google Scholar]
- Teter, A.; Kołakowski, Z. Coupled dynamic buckling of thin-walled composite columns with open cross-sections. Compos. Struct. 2013, 95, 28–34. [Google Scholar] [CrossRef]
- Kubiak, T.; Mania, R.J. Hybrid versus FR laminate channel section columns—Buckling and postbuckling behaviour. Compos. Struct. 2016, 154, 142–149. [Google Scholar] [CrossRef]
- Gliszczynski, A.; Kubiak, T.; Wawer, K. Barely visible impact damages of GFRP laminate profiles—An experimental study. Compos. Part B Eng. 2019, 158, 10–17. [Google Scholar] [CrossRef]
- Gliszczynski, A.; Wiącek, N. Experimental and numerical benchmark study of mode II interlaminar fracture toughness of unidirectional GFRP laminates under shear loading using the end-notched flexure (ENF) test. Compos. Struct. 2021, 258, 113190. [Google Scholar] [CrossRef]
- Kolakowski, Z.; Kubiak, T. Interactive dynamic buckling of orthotropic thin-walled channels subjected to in-plane pulse loading. Compos. Struct. 2007, 81, 222–232. [Google Scholar] [CrossRef]
- Wong, P.; Wang, Y. An experimental study of pultruded glass fibre reinforced plastics channel columns at elevated temperatures. Compos. Struct. 2007, 81, 84–95. [Google Scholar] [CrossRef]
- Orifici, A.; Thomson, R.; Degenhardt, R.; Kling, A.; Rohwer, K.; Bayandor, J. Degradation investigation in a postbuckling composite stiffened fuselage panel. Compos. Struct. 2008, 82, 217–224. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-C.; Kim, J.S.; Yoon, H.-J. Experimental and numerical investigations of mode I delamination behaviors of woven fabric composites with carbon, Kevlar and their hybrid fibers. Int. J. Precis. Eng. Manuf. 2011, 12, 321–329. [Google Scholar] [CrossRef]
- Debski, H.; Kubiak, T.; Teter, A. Experimental investigation of channel-section composite profiles’ behavior with various sequences of plies subjected to static compression. Thin-Walled Struct. 2013, 71, 147–154. [Google Scholar] [CrossRef]
- Timoshenko, S.; Gere, J. Theory of Elastic Stability, International Student Edition, 2nd ed.; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Cheng, B.; Zhao, J. Strengthening of perforated plates under uniaxial compression: Buckling analysis. Thin-Walled Struct. 2010, 48, 905–914. [Google Scholar] [CrossRef]
- El-Sawy, K.M.; Martini, M.I. Elastic stability of bi-axially loaded rectangular plates with a single circular hole. Thin-Walled Struct. 2007, 45, 122–133. [Google Scholar] [CrossRef]
- Jayashankarbabu, B.S.; Karisiddappa. Stability of Square Plate with Concentric Cutout. Int. J. Civ. Environ. Eng. 2014, 8, 259–267. [Google Scholar] [CrossRef]
- Ghannadpour, S.; Najafi, A.; Mohammadi, B. On the buckling behavior of cross-ply laminated composite plates due to circular/elliptical cutouts. Compos. Struct. 2006, 75, 3–6. [Google Scholar] [CrossRef]
- Lorenzini, G.; Helbig, D.; Silva, C.; Real, M.; Santos, E.; Rocha, L. Numerical evaluation of the effect of type and shape of perforations on the buckling of thin steel plates by means of the constructal design method. Int. J. Heat Technol. 2016, 34, S9–S20. [Google Scholar] [CrossRef] [Green Version]
- Kaltakci, M. Stress concentrations and failure criteria in anisotropic plates with circular holes subjected to tension or compression. Comput. Struct. 1996, 61, 67–78. [Google Scholar] [CrossRef]
- Durão, L.M.P.; Matos, J.E.; Loureiro, N.C.; Esteves, J.L.; Fernandes, S.C.F. Damage Propagation by Cyclic Loading in Drilled Carbon/Epoxy Plates. Materials 2023, 16, 2688. [Google Scholar] [CrossRef]
- Mathavan, J.J.; Hassan, M.H.; Xu, J.; Franz, G. Hole Quality Observation in Single-Shot Drilling of CFRP/Al7075-T6 Composite Metal Stacks Using Customized Twist Drill Design. J. Compos. Sci. 2022, 6, 378. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Y.; Zhang, Y.; Zhang, X. Influence of the Temperature-Dependent Characteristics of CFRP Mechanical Properties on the Critical Axial Force of Drilling Delamination. Polymers 2023, 15, 680. [Google Scholar] [CrossRef] [PubMed]
- Elguedj, T.; Gravouil, A.; Combescure, A. Appropriate extended functions for X-FEM simulation of plastic fracture mechanics. Comput. Methods Appl. Mech. Eng. 2006, 195, 501–515. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Meth. Engng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Melenk, J.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Gu, Z.; Peng, X.; Zheng, J. Finite element analysis of the influence of cohesive law parameters on the multiple delamination behaviors of composites under compression. Compos. Struct. 2015, 131, 975–986. [Google Scholar] [CrossRef]
- Wong, K.J.; Johar, M.; Koloor, S.S.R.; Petrů, M.; Tamin, M.N. Moisture Absorption Effects on Mode II Delamination of Carbon/Epoxy Composites. Polymers 2020, 12, 2162. [Google Scholar] [CrossRef] [PubMed]
- Rozylo, P.; Falkowicz, K.; Wysmulski, P.; Debski, H.; Pasnik, J.; Kral, J. Experimental-Numerical Failure Analysis of Thin-Walled Composite Columns Using Advanced Damage Models. Materials 2021, 14, 1506. [Google Scholar] [CrossRef]
- Rozylo, P.; Wysmulski, P. Failure analysis of thin-walled composite profiles subjected to axial compression using progressive failure analysis (PFA) and cohesive zone model (CZM). Compos. Struct. 2021, 262, 113597. [Google Scholar] [CrossRef]
- Rozylo, P.; Falkowicz, K. Stability and failure analysis of compressed thin-walled composite structures with central cut-out, using three advanced independent damage models. Compos. Struct. 2021, 273, 114298. [Google Scholar] [CrossRef]
- Rozylo, P. Comparison of Failure for Thin-Walled Composite Columns. Materials 2021, 15, 167. [Google Scholar] [CrossRef] [PubMed]
- Rozylo, P. Failure phenomenon of compressed thin-walled composite columns with top-hat cross-section for three laminate lay-ups. Compos. Struct. 2023, 304, 116381. [Google Scholar] [CrossRef]
- Debski, H.; Samborski, S.; Rozylo, P.; Wysmulski, P. Stability and Load-Carrying Capacity of Thin-Walled FRP Composite Z-Profiles under Eccentric Compression. Materials 2020, 13, 2956. [Google Scholar] [CrossRef] [PubMed]
- Wysmulski, P. The effect of load eccentricity on the compressed CFRP Z-shaped columns in the weak post-critical state. Compos. Struct. 2022, 301, 116184. [Google Scholar] [CrossRef]
- Wysmulski, P.; Falkowicz, K.; Filipek, P. Buckling state analysis of compressed composite plates with cut-out. Compos. Struct. 2021, 274, 114345. [Google Scholar] [CrossRef]
- Wysmulski, P. Non-linear analysis of the postbuckling behaviour of eccentrically compressed composite channel-section columns. Compos. Struct. 2023, 305, 116446. [Google Scholar] [CrossRef]
- Shao, S.; Wu, Y.; Fu, H.; Feng, S.; Zhang, J. Numerical Investigation on the Mechanical Properties of Vault Void Lining and Steel Plate Strengthening. Materials 2023, 16, 789. [Google Scholar] [CrossRef]
- Hao, R.; Wen, Z.; Xin, H.; Lin, W. Fatigue Life Prediction of Notched Details Using SWT Model and LEFM-Based Approach. Materials 2023, 16, 1942. [Google Scholar] [CrossRef]
- Buccino, F.; Cervellera, F.; Ghidini, M.; Marini, R.; Bagherifard, S.; Vergani, L.M. Isolating the Role of Bone Lacunar Morphology on Static and Fatigue Fracture Progression through Numerical Simulations. Materials 2023, 16, 1931. [Google Scholar] [CrossRef]
- Wang, F.; Wei, Z.; Li, P.; Yu, L.; Huang, W. Initial Crack Propagation and the Influence Factors of Aircraft Pipe Pressure. Materials 2019, 12, 3098. [Google Scholar] [CrossRef] [Green Version]
- Rozylo, P. Experimental-numerical study into the stability and failure of compressed thin-walled composite profiles using progressive failure analysis and cohesive zone model. Compos. Struct. 2020, 257, 113303. [Google Scholar] [CrossRef]
- ASTM D5766/D5766M-11; Test Method for Open-Hole Tensile Strength of Polymer Matrix Composite Laminates. ASTM International: West Conshohocken, PA, USA, 2018. [CrossRef]
- Jonak, J.; Karpiński, R.; Wójcik, A.; Siegmund, M. The Effect of Undercut Anchor Diameter on the Rock Failure Cone Area in Pullout Tests. Adv. Sci. Technol. Res. J. 2022, 16, 261–270. [Google Scholar] [CrossRef]
- Koloor, S.; Ayatollahi, M.R.; Tamin, M. Elastic-damage deformation response of fiber-reinforced polymer composite laminates with lamina interfaces. J. Reinf. Plast. Compos. 2017, 36, 832–849. [Google Scholar] [CrossRef]
- Remmers, J.J.; Deborst, R.; Needleman, A. The simulation of dynamic crack propagation using the cohesive segments method. J. Mech. Phys. Solids 2008, 56, 70–92. [Google Scholar] [CrossRef]
- Ventura, G.; Benvenuti, E. Equivalent polynomials for quadrature in Heaviside function enriched elements. Int. J. Numer. Methods Eng. 2015, 102, 688–710. [Google Scholar] [CrossRef]







| Tensile Modulus | Shear Modulus | Poisson’s Ratio | Tensile Strength | Shear Strength | Compressive Strength | |||
|---|---|---|---|---|---|---|---|---|
| E1 | E2,3 | G12,13,23 | ν12,13,23 | FT1 | FT2 | FS | FC1 | FC2 |
| GPa | MPa | MPa | – | MPa | MPa | MPa | MPa | MPa |
| 130.71 | 6360 | 4180 | 0.32 | 1867.2 | 25.97 | 100.15 | 1531 | 214 |
| PLATE | H_2 mm | H_4 mm | H_8 mm | |
|---|---|---|---|---|
| Pd (EXP) [N] | 9031 | 6894 | 3938 | 2393 |
| Pd (FEM) [N] | 10,153 | 7430 | 4659 | 2801 |
| Pd (error in prediction) [%] | 11% | 7% | 15% | 15% |
| Pf (EXP) [N] | 13,484 | 11,635 | 8954 | 6299 |
| Pf (FEM) [N] | 15,672 | 13,179 | 9650 | 6683 |
| Pf (error in prediction) [%] | 14% | 12% | 7% | 6% |
| Pd (EXP) ÷ Pf (EXP)↑ [%] | 49.31% | 68.77% | 127.37% | 163.23% |
| Pd (FEM) ÷ Pf (FEM)↑ [%] | 54.36% | 77.38% | 107.13% | 138.59% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wysmulski, P. Failure Mechanism of Tensile CFRP Composite Plates with Variable Hole Diameter. Materials 2023, 16, 4714. https://doi.org/10.3390/ma16134714
Wysmulski P. Failure Mechanism of Tensile CFRP Composite Plates with Variable Hole Diameter. Materials. 2023; 16(13):4714. https://doi.org/10.3390/ma16134714
Chicago/Turabian StyleWysmulski, Pawel. 2023. "Failure Mechanism of Tensile CFRP Composite Plates with Variable Hole Diameter" Materials 16, no. 13: 4714. https://doi.org/10.3390/ma16134714
APA StyleWysmulski, P. (2023). Failure Mechanism of Tensile CFRP Composite Plates with Variable Hole Diameter. Materials, 16(13), 4714. https://doi.org/10.3390/ma16134714






