Genetic Algorithm Optimization of Beams in Terms of Maximizing Gaps between Adjacent Frequencies
Abstract
:1. Introduction
2. Fundamental Equations and Methods
2.1. Euler–Bernoulli Beam Theory
2.2. Dynamics in the Finite Element Method Approach
2.3. Genetic Algorithms
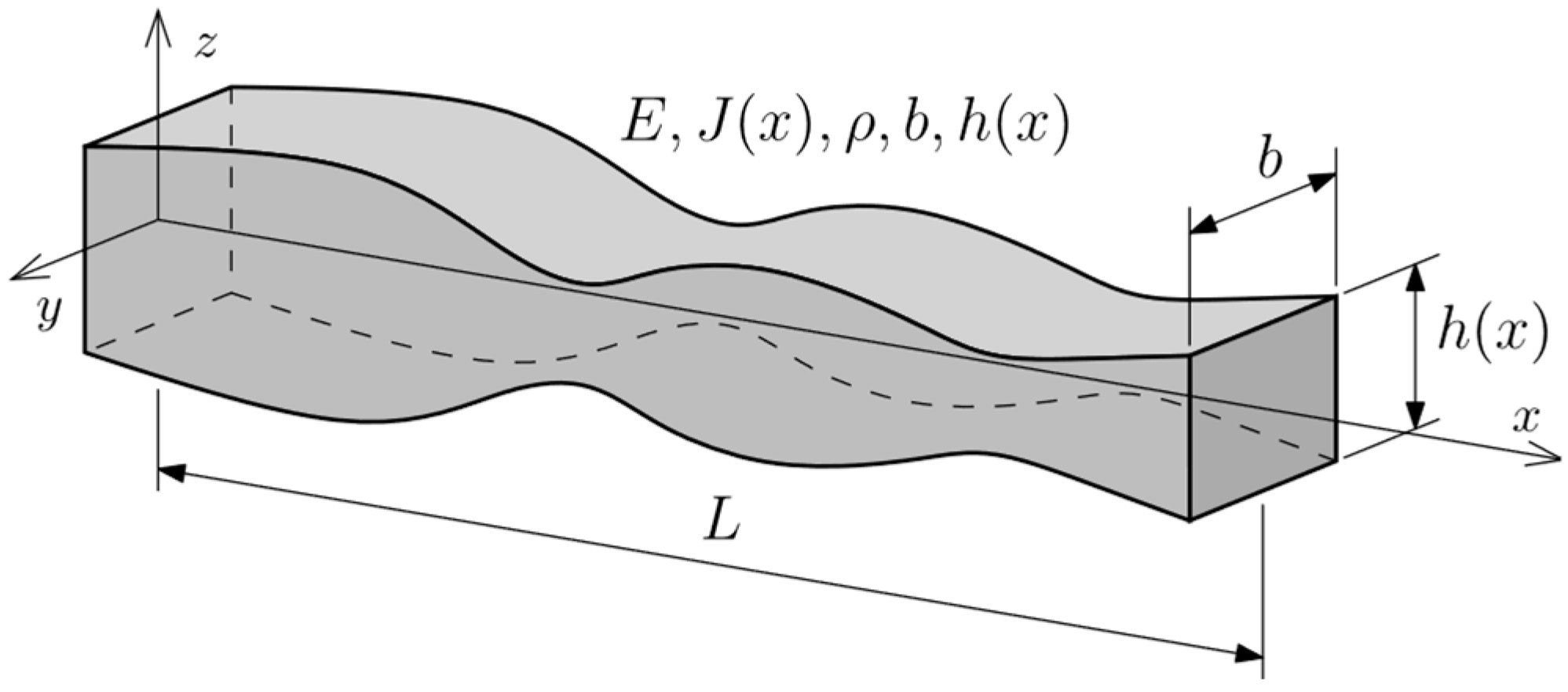
3. Problem Statement
4. Optimization Process Discussion
5. Results
5.1. Analysis in Terms of Eigenvalue Problems
5.2. Analysis in Terms of Forced Vibrations
6. Summary and Conclusions
- The application of GAs proved to be effective in optimizing the beams for maximizing the gaps between natural frequencies. Optimized beams exhibited increased gaps between adjacent natural frequencies, according to the defined fitness function.
- Based on the conducted analyses, it can be concluded that for relatively low natural frequencies (Δω1, Δω2), a division into larger elements can be successfully applied. This will result in shorter computational time while maintaining satisfying results.
- The randomness of parameters in the GA has a negligible influence on the final results. This was confirmed by the analysis of three independent approaches for each case. The ultimate results obtained from each approach for individual cases do not significantly differ.
- All optimized beams exhibit a periodic-like structure that is strongly correlated with the mode shape. Mass and stiffness reduction occurs at points where the lower mode shape of adjacent frequency k crosses the amplitude axis at 0 and the higher mode shape of frequency k + 1 reaches an extreme value.
- Both SS and CF optimized beams performed better than the reference beams at higher vibration frequencies.
- Optimization aimed at improving the properties of beams related to natural vibrations also resulted in a dynamic response. The optimization process had a complex impact on the resonance response, with no clear relationship identified.
- Although the adopted objective function is convenient to use due to limited numerical values, it may, however, lead to solutions in which the absolute value of the gap is not the maximum.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Warmuth, F.; Wormser, M.; Körner, C. Single Phase 3D Phononic Band Gap Material. Sci. Rep. 2017, 7, 3843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, J.; Yao, H.; Zhao, J.; Zhang, S.; He, Z.; Chen, X. Study on Band Gaps Characteristics of Local Resonance Phononic Crystal with Four-Core Structure. J. Phys. Conf. Ser. 2019, 1213, 042071. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Ma, F.; Shen, L.; Zhang, S. Application of Acoustic Metamaterials in Low-Frequency Vibration and Noise Reduction. J. Mech. Eng. 2016, 52, 68. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Olhoff, N. A Method of Design against Vibration Resonance of Beams and Shafts. Optim. Control Appl. Methods 1985, 6, 191–200. [Google Scholar] [CrossRef]
- Olhoff, N.; Parbery, R. Designing Vibrating Beams and Rotating Shafts for Maximum Difference between Adjacent Natural Frequencies. Int. J. Solids Struct. 1984, 20, 63–75. [Google Scholar] [CrossRef]
- Olhoff, N. Optimization of Vibrating Beams with Respect to Higher Order Natural Frequencies. J. Struct. Mech. 1976, 4, 87–122. [Google Scholar] [CrossRef]
- Olhoff, N.; Du, J. Topological Design for Minimum Dynamic Compliance of Structures under Forced Vibration. In CISM International Centre for Mechanical Sciences; Rozvany, G.I.N., Lewiński, T., Eds.; Springer: Vienna, Austria, 2014; Volume 549, pp. 325–339. [Google Scholar]
- Du, J.; Olhoff, N. Topological Design of Freely Vibrating Continuum Structures for Maximum Values of Simple and Multiple Eigenfrequencies and Frequency Gaps. Struct. Multidiscip. Optim. 2007, 34, 91–110. [Google Scholar] [CrossRef] [Green Version]
- Olhoff, N.; Niu, B.; Cheng, G. Optimum Design of Band-Gap Beam Structures. Int. J. Solids Struct. 2012, 49, 3158–3169. [Google Scholar] [CrossRef] [Green Version]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer: New York, NY, USA, 2003. [Google Scholar]
- Xiao, Y.; Wen, J.; Yu, D.; Wen, X. Flexural Wave Propagation in Beams with Periodically Attached Vibration Absorbers: Band-Gap Behavior and Band Formation Mechanisms. J. Sound Vib. 2013, 332, 867–893. [Google Scholar] [CrossRef]
- Gazonas, G.A.; Weile, D.S.; Wildman, R.; Mohan, A. Genetic Algorithm Optimization of Phononic Bandgap Structures. Int. J. Solids Struct. 2006, 43, 5851–5866. [Google Scholar] [CrossRef] [Green Version]
- Goh, J.; Fushman, I.; Englund, D.; Vučković, J. Genetic Optimization of Photonic Bandgap Structures. Opt. Express 2007, 15, 8218. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.-L.; Wu, F.-G.; Yao, L.-N. Application of Genetic Algorithm in Optimization of Band Gap of Two-Dimensional Phononic Crystals. Acta Phys. Sin. 2006, 55, 275. [Google Scholar] [CrossRef]
- Han, X.K.; Zhang, Z. Bandgap Design of Three-Phase Phononic Crystal by Topological Optimization. Wave Motion 2020, 93, 102496. [Google Scholar] [CrossRef]
- Dong, H.W.; Su, X.X.; Wang, Y.S.; Zhang, C. Topology Optimization of Two-Dimensional Asymmetrical Phononic Crystals. Phys. Lett. A 2014, 378, 434–441. [Google Scholar] [CrossRef]
- Halkjær, S.; Sigmund, O.; Jensen, J.S. Maximizing Band Gaps in Plate Structures. Struct. Multidiscip. Optim. 2006, 32, 263–275. [Google Scholar] [CrossRef]
- Kao, C.Y.; Osher, S.; Yablonovitch, E. Maximizing Band Gaps in Two-Dimensional Photonic Crystals by Using Level Set Methods. Appl. Phys. B 2005, 81, 235–244. [Google Scholar] [CrossRef]
- Shen, L.; Ye, Z.; He, S. Design of Two-Dimensional Photonic Crystals with Large Absolute Band Gaps Using a Genetic Algorithm. Phys. Rev. B 2003, 68, 035109. [Google Scholar] [CrossRef]
- Dong, H.-W.; Su, X.-X.; Wang, Y.-S.; Zhang, C. Topological Optimization of Two-Dimensional Phononic Crystals Based on the Finite Element Method and Genetic Algorithm. Struct. Multidiscip. Optim. 2014, 50, 593–604. [Google Scholar] [CrossRef]
- Han, X.K.; Zhang, Z. Topological Optimization of Phononic Crystal Thin Plate by a Genetic Algorithm. Sci. Rep. 2019, 9, 8331. [Google Scholar] [CrossRef] [Green Version]
- Biswal, A.R.; Roy, T.; Behera, R.K. Genetic Algorithm- and Finite Element-Based Design and Analysis of Nonprismatic Piezolaminated Beam for Optimal Vibration Energy Harvesting. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2016, 230, 2532–2548. [Google Scholar] [CrossRef]
- Shi, X.; Shu, H.; Dong, F.; Zhao, L. Inverse Problem of the Vibrational Band Gap of Periodically Supported Beam. In AIP Conference Proceedings; AIP Publishing: Busan, Republic of Korea, 2017; p. 030021. [Google Scholar]
- Fan, L.; He, Y.; Chen, X.; Zhao, X. A Frequency Response Function-Based Optimization for Metamaterial Beams Considering Both Location and Mass Distributions of Local Resonators. J. Appl. Phys. 2021, 130, 115101. [Google Scholar] [CrossRef]
- Alshabatat, N.T.; Naghshineh, K. Optimization of Natural Frequencies and Sound Power of Beams Using Functionally Graded Material. Adv. Acoust. Vib. 2014, 2014, 752361. [Google Scholar] [CrossRef]
- Mollik, T.; Geng, Y.; Shougat, M.R.E.U.; Fitzgerald, T.; Perkins, E. Genetic Algorithm Shape Optimization to Manipulate the Nonlinear Response of a Clamped-Clamped Beam. Heliyon 2022, 8, e11833. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Zhang, W.; Zhang, A.; Wu, N.; Liu, Z. Structural Damage Identification Based on Variable-Length Elements and an Improved Genetic Algorithm for Railway Bridges. Appl. Sci. 2022, 12, 5706. [Google Scholar] [CrossRef]
- Greco, A.; D’Urso, D.; Cannizzaro, F.; Pluchino, A. Damage Identification on Spatial Timoshenko Arches by Means of Genetic Algorithms. Mech. Syst. Signal Process. 2018, 105, 51–67. [Google Scholar] [CrossRef] [Green Version]
- Narques, T.V.N.; Carvalho, R.C.; Christoforo, A.L.; Mascarenhas, F.J.R.; Arroyo, F.N.; Bomfim Junior, F.C.; dos Santos, H.F. Use of Real Coded Genetic Algorithm as a Pre-Dimensioning Tool for Prestressed Concrete Beams. Buildings 2023, 13, 819. [Google Scholar] [CrossRef]
- Aydın, Z.; Ayvaz, Y. Overall Cost Optimization of Prestressed Concrete Bridge Using Genetic Algorithm. KSCE J. Civ. Eng. 2013, 17, 769–776. [Google Scholar] [CrossRef]
- Lu, M.; Ye, J. Guided Genetic Algorithm for Dome Optimization against Instability with Discrete Variables. J. Constr. Steel Res. 2017, 139, 149–156. [Google Scholar] [CrossRef]
- Lemonge, A.; Hallak, P.; Fonseca, L.; Barbosa, H. A Genetic Algorithm for Optimization of Spatial Trusses Considering Self-Weight Loads. In Engineering Optimization 2014; CRC Press: Boca Raton, FL, USA, 2014; pp. 175–180. [Google Scholar]
- Lemonge, A.C.C.; Silva, M.M.; Barbosa, H.J.C. Design Optimization of Geometrically Nonlinear Truss Structures Considering Cardinality Constraints. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 29–36. [Google Scholar]
- Woźniak, C.; Awrejcewicz, J.; Jemielita, G.; Kołakowski, Z.; Matysiak, S.; Nagórko, W.; Pietraszkiewicz, W.; Śniady, P.; Świtka, R.; Wągrowska, M.; et al. (Eds.) Mathematical Modelling and Analysis in Continuum Mechanics of Microstructured Media; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2010; ISBN 978-83-7335-752-5. [Google Scholar]
- Joseph Shibu, K.; Shankar, K.; Kanna Babu, C.; Degaonkar, G.K. Multi-Objective Optimum Design of an Aero Engine Rotor System Using Hybrid Genetic Algorithm. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Wuhan, China, 10–12 October 2019; Volume 624. [Google Scholar]
- Goldberg, D. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Gwiazda, T. Genetic Algorithms Reference. Volume I. Crossover for Single-Objective Numerical Optimization Problems; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2007; Volume I. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Whitley, D. A Genetic Algorithm Tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J.-Y. (Eds.) Handbook of Metaheuristics; Springer: Boston, MA, USA, 2010; Volume 146, ISBN 978-1-4419-1663-1. [Google Scholar]
























| k | ne | SS Beam | CF Beam | ||
|---|---|---|---|---|---|
| Δωk | Difference, % | Δωk | Difference, % | ||
| 1 | 32 | 0.91016 | 0.05 | 0.95414 | 0.03 |
| 64 | 0.90969 | 0.95385 | |||
| 2 | 32 | 0.83774 | 0.04 | 0.87324 | 0.21 |
| 64 | 0.83743 | 0.87512 | |||
| 3 | 32 | 0.79064 | 0.31 | 0.80859 | 1.13 |
| 64 | 0.79311 | 0.81783 | |||
| 4 | 32 | 0.75954 | 0.76 | 0.77534 | 0.81 |
| 64 | 0.76539 | 0.78164 | |||
| 5 | 32 | 0.74260 | 0.32 | 0.75772 | 0.41 |
| 64 | 0.74499 | 0.75460 | |||
| 6 | 32 | 0.72382 | 1.00 | 0.72113 | 1.02 |
| 64 | 0.71665 | 0.72857 | |||
| 7 | 32 | 0.68489 | 5.45 | 0.70526 | 2.23 |
| 64 | 0.72434 | 0.72138 | |||
| 8 | 32 | 0.64887 | 9.92 | 0.67391 | 6.15 |
| 64 | 0.72036 | 0.71808 | |||
| k | The Individual | SS Beam | CF Beam | ||
|---|---|---|---|---|---|
| Δf | Difference, % | Δf | Difference, % | ||
| 1 | reference | 128.41 | 12.89 | 76.86 | −11.10 * |
| optimized | 144.96 | 68.33 | |||
| 2 | reference | 207.57 | 33.69 | 165.10 | 30.82 |
| optimized | 277.51 | 215.99 | |||
| 3 | reference | 296.76 | 73.45 | 242.55 | 39.17 |
| optimized | 514.72 | 337.55 | |||
| 4 | reference | 371.75 | 93.85 | 324.18 | 101.80 |
| optimized | 720.62 | 654.18 | |||
| 5 | reference | 445.22 | 108.18 | 403.84 | 96.85 |
| optimized | 926.86 | 794.94 | |||
| 6 | reference | 510.52 | 119.02 | 472.00 | 108.36 |
| optimized | 1118.15 | 983.48 | |||
| 7 | reference | 570.74 | 123.02 | 533.87 | 119.57 |
| optimized | 1272.85 | 1172.22 | |||
| 8 | reference | 603.70 | 137.95 | 574.00 | 130.03 |
| optimized | 1436.51 | 1320.39 | |||
| k | The Individual | SS Beam | CF Beam | ||
|---|---|---|---|---|---|
| Δf | Difference, % | Δf | Difference, % | ||
| 1 | reference | 126.86 | 13.86 | 76.42 | −8.75 * |
| optimized | 144.44 | 69.73 | |||
| 2 | reference | 206.89 | 34.07 | 166.26 | 16.47 |
| optimized | 277.38 | 193.65 | |||
| 3 | reference | 285.49 | 62.88 | 247.30 | 47.54 |
| optimized | 465.01 | 364.87 | |||
| 4 | reference | 370.80 | 94.92 | 331.71 | 82.80 |
| optimized | 722.76 | 606.35 | |||
| 5 | reference | 442.63 | 118.23 | 405.86 | 101.58 |
| optimized | 965.96 | 818.15 | |||
| 6 | reference | 512.59 | 121.06 | 475.61 | 127.38 |
| optimized | 1133.13 | 1081.46 | |||
| 7 | reference | 622.68 | 254.00 | 565.22 | 176.29 |
| optimized | 1850.31 | 1561.67 | |||
| 8 | reference | 691.80 | 217.97 | 637.94 | 211.49 |
| optimized | 2199.70 | 1987.14 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domagalski, Ł.; Kowalczyk, I. Genetic Algorithm Optimization of Beams in Terms of Maximizing Gaps between Adjacent Frequencies. Materials 2023, 16, 4963. https://doi.org/10.3390/ma16144963
Domagalski Ł, Kowalczyk I. Genetic Algorithm Optimization of Beams in Terms of Maximizing Gaps between Adjacent Frequencies. Materials. 2023; 16(14):4963. https://doi.org/10.3390/ma16144963
Chicago/Turabian StyleDomagalski, Łukasz, and Izabela Kowalczyk. 2023. "Genetic Algorithm Optimization of Beams in Terms of Maximizing Gaps between Adjacent Frequencies" Materials 16, no. 14: 4963. https://doi.org/10.3390/ma16144963
APA StyleDomagalski, Ł., & Kowalczyk, I. (2023). Genetic Algorithm Optimization of Beams in Terms of Maximizing Gaps between Adjacent Frequencies. Materials, 16(14), 4963. https://doi.org/10.3390/ma16144963







