Optimization of Johnson–Cook Constitutive Model Parameters Using the Nesterov Gradient-Descent Method
Abstract
:1. Introduction
2. Formulation of the Problem
3. Modification of the JC Constitutive Model
4. Solution-Quality Function
5. Numerical Results and Discussion
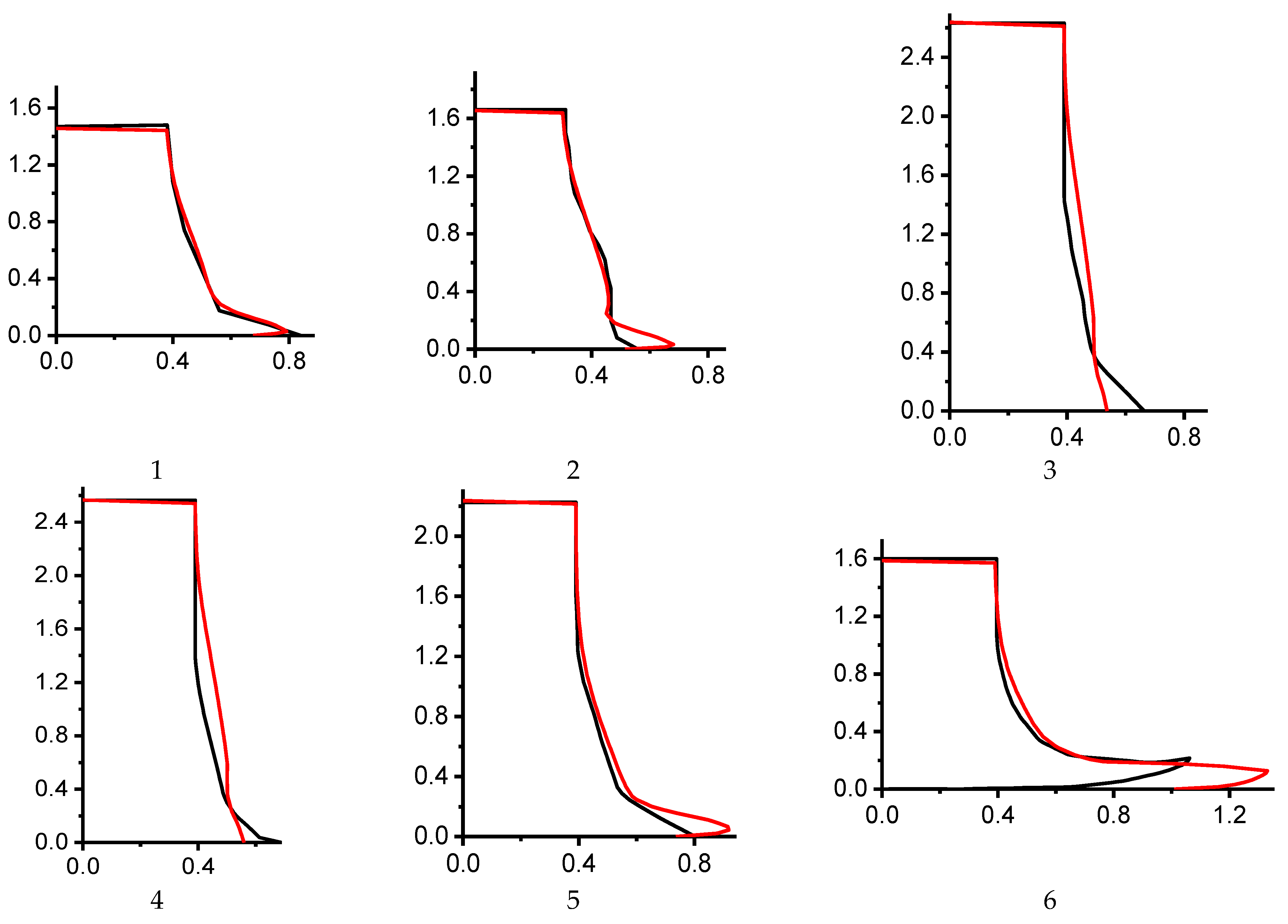
- Optimization of parameters for each of tests 1, 2, 3, 4, 5, and 6;
- Optimization of parameters for tests 1 and 2:
- 3.
- Optimization of parameters for tests 3–6:
- 4.
- Optimization of parameters for tests 1–6:
6. Conclusions
- The JC constitutive model was modified by introducing a material-hardening limit for plastic deformation, Bmax, at high strain-rates.
- A solution quality function, Qf, was proposed to estimate the deviation of calculations from the experimental data. The final length of the cylinder, the radius of the lateral surface of the cylinder at five points, and the maximum radius of the cylinder were taken as the function parameters, with weighting factors of 20, 2, and 1 according to the effect on the final quality of the solution and reliability of the parameter measurement.
- An optimization algorithm for selecting parameters B and C of the JC constitutive model and the limiter Bmax was developed to find the best agreement between the calculated and experimental data for the Taylor impact test using the Nesterov gradient-descent method.
- The optimal parameters, namely, B, Bmax, and C, of the modified JC constitutive model were calculated for nine sets of experimental data. The solution quality in some experiments increased by several times when using optimal parameters. For all experiments, the solution quality improved by 10% after optimization.
- The developed method for optimizing the selection of the constitutive model constants can be adapted for a wide range of problems (arbitrary set of optimized parameters, arbitrary material models, and software codes, including ANSYS/LS Dyna).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; American Defense Preparedness Association: Arlington, VA, USA, 1983; pp. 541–547. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Wu, J. Mechanical Properties of Fiber-Reinforced Polymer (FRP) Composites at Elevated Temperatures. Buildings 2023, 13, 67. [Google Scholar] [CrossRef]
- Xie, H.; Zhang, X.; Miao, F.; Jiang, T.; Zhu, Y.; Wu, X.; Zhou, L. Separate Calibration of Johnson–Cook Model for Static and Dynamic Compression of a DNAN-Based Melt-Cast Explosive. Materials 2022, 15, 5931. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Fu, X.; Xu, N.; Pan, Y.; Zhang, Y. Spatial Constitutive Modeling of AA7050-T7451 with Anisotropic Stress Transformation. Materials 2022, 15, 5998. [Google Scholar] [CrossRef]
- Zhang, F.; He, K.; Li, Z.; Huang, B. Strain-Rate Effect on Anisotropic Deformation Characterization and Material Modeling of High-Strength Aluminum Alloy Sheet. Metals 2022, 12, 1430. [Google Scholar] [CrossRef]
- Sun, X. Uncertainty Quantification of Material Properties in Ballistic Impact of Magnesium Alloys. Materials 2022, 15, 6961. [Google Scholar] [CrossRef]
- Yang, S.; Liang, P.; Gao, F.; Song, D.; Jiang, P.; Zhao, M.; Kong, N. The Comparation of Arrhenius-Type and Modified Johnson–Cook Constitutive Models at Elevated Temperature for Annealed TA31 Titanium Alloy. Materials 2023, 16, 280. [Google Scholar] [CrossRef]
- Yin, W.; Liu, Y.; He, X.; Li, H. Effects of Different Materials on Residual Stress Fields of Blade Damaged by Foreign Objects. Materials 2023, 16, 3662. [Google Scholar] [CrossRef]
- Liu, L.; Wu, W.; Zhao, Y.; Cheng, Y. Subroutine Embedding and Finite Element Simulation of the Improved Constitutive Equation for Ti6Al4V during High-Speed Machining. Materials 2023, 16, 3344. [Google Scholar] [CrossRef]
- Rodríguez Prieto, J.M.; Larsson, S.; Afrasiabi, M. Thermomechanical Simulation of Orthogonal Metal Cutting with PFEM and SPH Using a Temperature-Dependent Friction Coefficient: A Comparative Study. Materials 2023, 16, 3702. [Google Scholar] [CrossRef]
- Niu, W.; Wang, Y.; Li, X.; Guo, R. A Joint Johnson–Cook-TANH Constitutive Law for Modeling Saw-Tooth Chip Formation of Ti-6AL-4V Based on an Improved Smoothed Particle Hydrodynamics Method. Materials 2023, 16, 4465. [Google Scholar] [CrossRef]
- Ben Said, L.; Wali, M. Accuracy of Variational Formulation to Model the Thermomechanical Problem and to Predict Failure in Metallic Materials. Mathematics 2022, 10, 3555. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, Y.; Gorbachev, S.; Kuzin, V.; He, W.; Guo, J. Research on Conventional and High-Speed Machining Cutting Force of 7075-T6 Aluminum Alloy Based on Finite Element Modeling and Simulation. Metals 2022, 12, 1395. [Google Scholar] [CrossRef]
- Taylor, G.I. The use of flat ended projectiles for determining yield stress. 1: Theoretical considerations. Proc. R. Soc. Lond. A 1948, 194, 289–299. [Google Scholar] [CrossRef]
- Gust, W.H. High impact deformation of metal cylinders at elevated temperatures. J. Appl. Phys. 1982, 53, 3566–3575. [Google Scholar] [CrossRef]
- Bogomolov, A.N.; Gorel’skii, V.A.; Zelepugin, S.A.; Khorev, I.E. Behavior of bodies of revolution in dynamic contact with a rigid wall. J. Appl. Mech. Tech. Phys. 1986, 27, 149–152. [Google Scholar] [CrossRef]
- Pakhnutova, N.V.; Boyangin, E.N.; Shkoda, O.A.; Zelepugin, S.A. Microhardness and Dynamic Yield Strength of Copper Samples upon Impact on a Rigid Wall. Adv. Eng. Res. 2022, 22, 224–231. [Google Scholar] [CrossRef]
- Włodarczyk, E.; Sarzynski, M. Strain energy method for determining dynamic yield stress in Taylor’s test. Eng. Trans. 2017, 65, 499–511. [Google Scholar]
- Scott, N.R.; Nelms, M.D.; Barton, N.R. Assessment of reverse gun taylor cylinder experimental configuration. Int. J. Impact Eng. 2021, 149, 103772. [Google Scholar] [CrossRef]
- Bayandin, Y.V.; Ledon, D.R.; Uvarov, S.V. Verification of Wide-Range Constitutive Relations for Elastic-Viscoplastic Materials Using the Taylor–Hopkinson Test. J. Appl. Mech. Tech. Phys. 2021, 62, 1267–1276. [Google Scholar] [CrossRef]
- Volkov, G.A.; Bratov, V.A.; Borodin, E.N.; Evstifeev, A.D.; Mikhailova, N.V. Numerical simulations of impact Taylor tests. J. Phys. Conf. Ser. 2020, 1556, 012059. [Google Scholar] [CrossRef]
- Acosta, C.A.; Hernandez, C.; Maranon, A.; Casas-Rodriguez, J.P. Validation of material constitutive parameters for the AISI 1010 steel from Taylor impact tests. Mater. Des. 2016, 110, 324–331. [Google Scholar] [CrossRef]
- Revil-Baudard, B.; Cazacu, O.; Flater, P.; Kleiser, G. Plastic deformation of high-purity α-titanium: Model development and validation using the Taylor cylinder impact test. Mech. Mater. 2015, 80, 264–275. [Google Scholar] [CrossRef]
- Nguyen, T.; Fensin, S.J.; Luscher, D.J. Dynamic crystal plasticity modeling of single crystal tantalum and validation using Taylor cylinder impact tests. Int. J. Plast. 2021, 139, 102940. [Google Scholar] [CrossRef]
- Takagi, S.; Yoshida, S. Development of estimation method for material property under high strain rate condition utilizing experiment and analysis. Int. J. Press. Vessel. Pip. 2022, 199, 104771. [Google Scholar] [CrossRef]
- Ho, C.S.; Mohd Nor, M.K. An Experimental Investigation on the Deformation Behaviour of Recycled Aluminium Alloy AA6061 Undergoing Finite Strain Deformation. Met. Mater. Int. 2020, 27, 4967–4983. [Google Scholar] [CrossRef]
- Sen, S.; Banerjee, B.; Shaw, A. Taylor Impact Test Revisited: Determination of Plasticity Parameters for Metals at High Strain Rate. Int. J. Solids Struct. 2020, 193–194, 357–374. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for materials dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef] [Green Version]
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef] [Green Version]
- Preston, D.L.; Tonks, D.L.; Wallace, D.C. Model of plastic deformation for extreme loading conditions. J. Appl. Phys. 2003, 93, 211–220. [Google Scholar] [CrossRef]
- Lee, S.; Yu, K.; Huh, H.; Kolman, R.; Arnoult, X. Dynamic Hardening of AISI 304 Steel at a Wide Range of Strain Rates and Its Application to Shot Peening Simulation. Metals 2022, 12, 403. [Google Scholar] [CrossRef]
- Armstrong, R.W. Constitutive Relations for Slip and Twinning in High Rate Deformations: A Review and Update. J. Appl. Phys. 2021, 130, 245103. [Google Scholar] [CrossRef]
- Gao, C.; Iwamoto, T. Instrumented Taylor Impact Test for Measuring Stress-Strain Curve through Single Trial. Int. J. Impact Eng. 2021, 157, 103980. [Google Scholar] [CrossRef]
- Jia, B.; Rusinek, A.; Xiao, X.; Wood, P. Simple Shear Behavior of 2024-T351 Aluminum Alloy over a Wide Range of Strain Rates and Temperatures: Experiments and Constitutive Modeling. Int. J. Impact Eng. 2021, 156, 103972. [Google Scholar] [CrossRef]
- Li, J.-C.; Chen, G.; Huang, F.-L.; Lu, Y.-G. Load Characteristics in Taylor Impact Test on Projectiles with Various Nose Shapes. Metals 2021, 11, 713. [Google Scholar] [CrossRef]
- Li, J.-C.; Chen, G.; Lu, Y.-G.; Huang, F.-L. Investigation on the Application of Taylor Impact Test to High-G Loading. Front. Mater. 2021, 8, 717122. [Google Scholar] [CrossRef]
- Selyutina, N.S.; Petrov, Y.V. Prediction of the dynamic yield strength of metals using two structural-temporal parameters. Phys. Solid State 2018, 60, 244–249. [Google Scholar] [CrossRef]
- Pantalé, O.; Ming, L. An Optimized Dynamic Tensile Impact Test for Characterizing the Behavior of Materials. Appl. Mech. 2022, 3, 1107–1122. [Google Scholar] [CrossRef]
- Rodionov, E.S.; Lupanov, V.G.; Gracheva, N.A.; Mayer, P.N.; Mayer, A.E. Taylor Impact Tests with Copper Cylinders: Experiments, Microstructural Analysis and 3D SPH Modeling with Dislocation Plasticity and MD-Informed Artificial Neural Network as Equation of State. Metals 2022, 12, 264. [Google Scholar] [CrossRef]
- Zelepugin, S.A.; Pakhnutova, N.V.; Shkoda, O.A.; Boyangin, E.N. Experimental study of the microhardness and microstructure of a copper specimen using the Taylor impact test. Metals 2022, 12, 2186. [Google Scholar] [CrossRef]
- Nesterov, Y.E. A method of solving a convex programming problem with convergence rate O(1/k2). Soviet Math. Dokl. 1983, 27, 372–376. [Google Scholar]
- Wilkins, M.L.; Guinan, M.W. Impact of cylinders on a rigid boundary. J. Appl. Phys. 1973, 44, 1200–1206. [Google Scholar] [CrossRef]
- Johnson, G.R. Numerical algorithms and material models for high-velocity impact computations. Int. J. Impact Eng. 2011, 38, 456–472. [Google Scholar] [CrossRef]
- Gorel’skii, V.A.; Zelepugin, S.A.; Sidorov, V.N. Numerical solution of three-dimensional problem of high-speed interaction of a cylinder with a rigid barrier, taking into account thermal effects. Int. Appl. Mech. 1994, 30, 193–198. [Google Scholar] [CrossRef]
- Gorelski, V.A.; Zelepugin, S.A.; Smolin, A.Y. Effect of Discretization in Calculating Three-Dimensional Problems of High-Velocity Impact by the Finite-Element Method. Comput. Math. Math. Phys. 1997, 37, 722–730. [Google Scholar]
- Zelepugin, S.A.; Nikulichev, V.B. Numerical modeling of sulfur–aluminum interaction under shock-wave loading. Combust. Explos. Shock. Waves 2000, 36, 845–850. [Google Scholar] [CrossRef]
- Pashkov, S.V.; Zelepugin, S.A. Probabilistic approach in modelling dynamic fracture problems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 10681–10689. [Google Scholar] [CrossRef]
- Tolkachev, V.F.; Ivanova, O.V.; Zelepugin, S.A. Initiation and development of exothermic reactions during solid-phase synthesis under explosive loading. Therm. Sci. 2019, 23, S505–S511. [Google Scholar] [CrossRef]
- Banerjee, B. Validation of the material point method and plasticity with Taylor impact tests. Report no. C-SAFE-CD-IR-04-004. arXiv 2012, arXiv:1201.2476. [Google Scholar]
- Ojoc, G.G.; Totolici Rusu, V.; Pîrvu, C.; Deleanu, L. How friction could influence the shape and failure mechanism in impact, with the help of a finite element model. UPB Sci. Bull. Ser. D Mech. Eng. 2021, 83, 185–192. [Google Scholar]





| Test | Material | L0 (mm) | D0 (mm) | ʋ0 (m/s) | T0 (K) | Reference |
|---|---|---|---|---|---|---|
| 1 | OFHC Cu | 23.47 | 7.62 | 210 | 298 | [43] |
| 2 | ETP Cu | 30 | 6.0 | 188 | 718 | [16] |
| 3 | OFHC Cu M1 | 34.5 | 7.8 | 162 | 298 | [41] |
| 4 | OFHC Cu M1 | 34.5 | 7.8 | 167 | 298 | [41] |
| 5 | OFHC Cu M1 | 34.5 | 7.8 | 225 | 298 | [41] |
| 6 | OFHC Cu M1 | 34.5 | 7.8 | 316 | 298 | [41] |
| σ0 (MPa) | B (MPa) | C | n | m | Tm (K) |
|---|---|---|---|---|---|
| 89 | 292 | 0.025 | 0.31 | 1.09 | 1356 |
| Test | 1 | 2 | 3 | 4 | 5 | 6 | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|---|
| 0.149 | 0.292 | 0.099 | 0.143 | 0.162 | 0.311 | 0.193 | 0.07 |
| Test | B (GPa) | C | Bmax |
|---|---|---|---|
| 1 | 0.202 | 0.023 | 3.509 |
| 2 | 0.205 | 0.023 | 3.503 |
| 3 | 0.309 | 0.024 | 3.387 |
| 4 | 0.286 | 0.022 | 3.623 |
| 5 | 0.539 | 0.014 | 2.783 |
| 6 | 0.486 | 0.018 | 2.881 |
| 1 + 2 | 0.204 | 0.023 | 3.493 |
| 3 + 4 + 5 + 6 | 0.565 | 0.020 | 2.558 |
| 1 + 2 + 3 + 4 + 5 + 6 | 0.265 | 0.024 | 3.330 |
| Test | B/B0 | C/C0 | Bmax | Qf | Qf0 | Qf0/Qf |
|---|---|---|---|---|---|---|
| 1 | 0.692 | 0.919 | 3.509 | 0.011 | 0.149 | 13.6 |
| 2 | 0.702 | 0.907 | 3.503 | 0.046 | 0.292 | 6.4 |
| 3 | 1.059 | 0.948 | 3.387 | 0.098 | 0.099 | 1.0 |
| 4 | 0.981 | 0.865 | 3.623 | 0.143 | 0.143 | 1.0 |
| 5 | 1.846 | 0.566 | 2.783 | 0.041 | 0.162 | 3.9 |
| 6 | 1.663 | 0.725 | 2.881 | 0.088 | 0.311 | 3.5 |
| 1 + 2 | 0.697 | 0.910 | 3.493 | 0.028 | 0.221 | 7.8 |
| 3 + 4 + 5 + 6 | 1.936 | 0.820 | 2.558 | 0.063 | 0.179 | 2.8 |
| 1 + 2 + 3 + 4 + 5 + 6 | 0.908 | 0.965 | 3.330 | 0.177 | 0.193 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zelepugin, S.A.; Cherepanov, R.O.; Pakhnutova, N.V. Optimization of Johnson–Cook Constitutive Model Parameters Using the Nesterov Gradient-Descent Method. Materials 2023, 16, 5452. https://doi.org/10.3390/ma16155452
Zelepugin SA, Cherepanov RO, Pakhnutova NV. Optimization of Johnson–Cook Constitutive Model Parameters Using the Nesterov Gradient-Descent Method. Materials. 2023; 16(15):5452. https://doi.org/10.3390/ma16155452
Chicago/Turabian StyleZelepugin, Sergey A., Roman O. Cherepanov, and Nadezhda V. Pakhnutova. 2023. "Optimization of Johnson–Cook Constitutive Model Parameters Using the Nesterov Gradient-Descent Method" Materials 16, no. 15: 5452. https://doi.org/10.3390/ma16155452
APA StyleZelepugin, S. A., Cherepanov, R. O., & Pakhnutova, N. V. (2023). Optimization of Johnson–Cook Constitutive Model Parameters Using the Nesterov Gradient-Descent Method. Materials, 16(15), 5452. https://doi.org/10.3390/ma16155452






