Model of a 3D Magnetic Permeability Tensor Considering Rotation and Saturation States in Materials with Axial Anisotropy
Abstract
1. Introduction
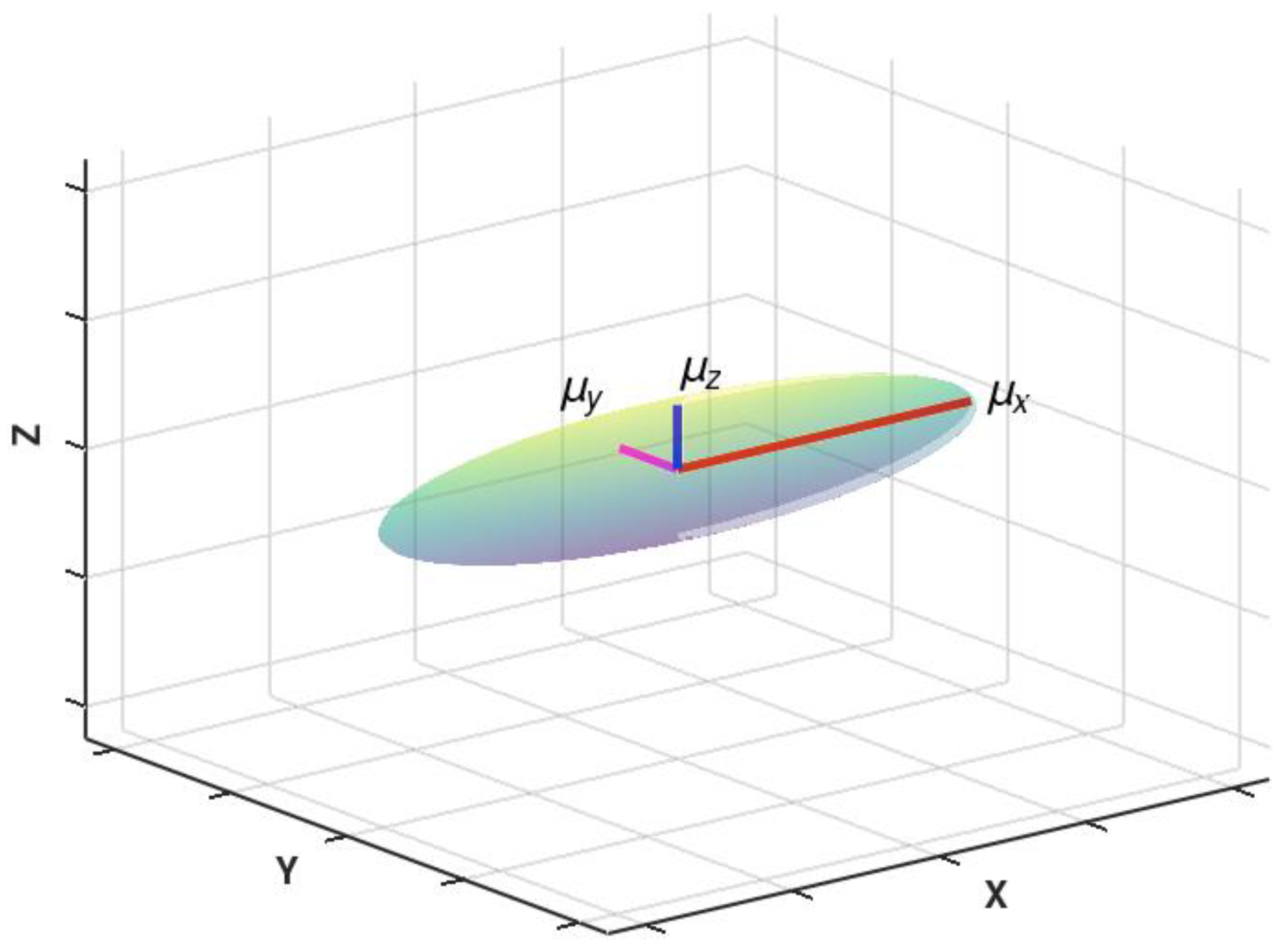
2. Axial Anisotropy of Relative Magnetic Permeability Tensor μ in 3D
3. The Proposed Linear–Rotation–Saturation (LRS) Model of Relative Magnetic Permeability for Materials with Axial Anisotropy
- The linear phase.
- The magnetization rotation phase, when the length of flux density vector B is equal to saturation flux density Bs; however, the magnetostatic energy is consumed for the rotation of flux density B vector towards the magnetizing field H.
- The magnetic saturation phase, in which when the length of flux density vector B is equal to saturation flux density Bs, it is parallel to the magnetizing field H, and saturation is modelled by shrinking the magnetic permeability tensor.
4. Modelling of Magnetization Curves
- Induced during the thermomagnetic annealing (Experiment in Ref. [38]).
5. Practical Implementation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zurek, S. Characterisation of Soft Magnetic Materials Under Rotational Magnetisation; CRC Press: New York, NY, USA, 2017; ISBN 9781138304369. [Google Scholar]
- Shiozaki, M.; Kurosaki, Y. Anisotropy of Magnetic Properties in Non-oriented Electrical Steel Sheets. Textures Microstruct. 1989, 11, 159–170. [Google Scholar] [CrossRef]
- Morita, H.; Fujimori, H.; Obi, Y. Magnetic anisotropy of amorphous (Fe1−x Co x)78Si10B12 alloys. Appl. Phys. 1979, 20, 125–127. [Google Scholar] [CrossRef]
- Silveyra, J.M.; Ferrara, E.; Huber, D.L.; Monson, T.D. Soft magnetic materials for a sustainable and electrified world. Science 2018, 362, aao0195. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Luo, Y.D.; Lin, Y.H.; Nan, C.W. Anisotropic ferromagnetic behaviors in highly oriented epitaxial NiO-based thin films. AIP Adv. 2015, 5, 077107. [Google Scholar] [CrossRef]
- Sasidharan, S.; Ghosh, S.; Sreedhar, R.; Kumari, K.; Thota, S.; Ramakrishnah, V. Anisotropic Ferromagnetic Organic Nanoflowers. J. Phys. Chem. C 2022, 126, 8511–8518. [Google Scholar] [CrossRef]
- Lόpez-Mir, L.; Frontera, C.; Aramberri, H.; Bouzehouane, K.; Cisneros-Fernández, J.; Bozzo, B.; Balcells, L.; Martínez, B. Anisotropic sensor and memory device with a ferromagnetic tunnel barrier as the only magnetic element. Sci. Rep. 2018, 8, 861. [Google Scholar] [CrossRef]
- Nowicki, M. Tensductor-Amorphous Alloy Based Magnetoelastic Tensile Force Sensor. Sensors 2018, 18, 4420. [Google Scholar] [CrossRef] [PubMed]
- Dahle, O. The pressductor and torductor—Two heavy-duty transducers based on magnetic stress sensitivity. IEEE Trans. Commun. Electron. 1964, 83, 752–758. [Google Scholar] [CrossRef]
- Legrand, B.; Genot, B.; Voyant, J.Y.; Yonnet, J.P. The use of local magnetic saturation for position sensor. J. Magn. Magn. Mater. 2002, 242, 1136–1138. [Google Scholar] [CrossRef]
- Jiles, D.C. Introduction to Magnetism and Magnetic Materials; CRC Press: New York, NY, USA, 2015; ISBN 978-1482238877. [Google Scholar]
- Available online: https://www.comsol.com (accessed on 20 March 2023).
- Zhang, H.; Titus, P. Modeling Magnetic Material Using Vector Potential-Based Elements in ANSYS and Comparing with Edge-Based Elements. Fusion Sci. Technol. 2021, 77, 687–691. [Google Scholar] [CrossRef]
- Available online: https://www.csc.fi/web/elmer (accessed on 20 March 2023).
- Appino, C.; Ragusa, C.; Fiorillo, F. Can rotational magnetisation be theoretically assessed? Int. J. Appl. Electromechanics Mech. 2014, 44, 355–370. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef]
- Szewczyk, R. Validation of the Anhysteretic magnetisation model for soft magnetic materials with perpendicular anisotropy. Materials 2014, 7, 5109–5116. [Google Scholar] [CrossRef] [PubMed]
- Frydrych, P.; Szewczyk, R.; Nowicki, M.; Charubin, T. Application of Anisotropic Vector Preisach Model for Bulk Materials. Acta Phys. Pol. A 2017, 131, 618–620. [Google Scholar] [CrossRef]
- Ramesh, A.; Jiles, D.C.; Roderik, J. A model of anisotropic anhysteretic magnetisation. IEEE Trans. Magn. 1996, 32, 4234–4236. [Google Scholar] [CrossRef]
- Keyhani, A.; Miri, S.M. Nonlinear modeling of magnetic saturation and hysteresis in an electromagnetic device. Electr. Power Syst. Res. 1988, 15, 15–23. [Google Scholar] [CrossRef]
- Bergqvist, A. Magnetic vector hysteresis model with dry friction-like pinning. Phys. B Condens. Matter 1997, 233, 342–347. [Google Scholar] [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A mechanism of magnetic hysteresis in heterogeneous alloys. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1948, 240, 599–601. [Google Scholar] [CrossRef]
- Henrotte, F.; Nicolet, A.; Hameyer, K. An energy-based vector hysteresis model for ferromagnetic materials. COMPEL Int. J. Comput. Math. Electr. 2006, 25, 71–80. [Google Scholar] [CrossRef]
- Hernotte, F.; Hameyer, K. A dynamical vector hysteresis model based on an energy approach. IEEE Trans. Magn. 2006, 42, 899–902. [Google Scholar] [CrossRef]
- Upadhaya, B.; Rasilo, P.; Perkkiö, L.; Handgruber, P.; Belahcen, A.; Arkkio, A. Comparison of Anisotropic Energy-Based and Jiles-Atherton Models of Ferromagnetic Hysteresis. IEEE Trans. Magn. 2020, 56, 7300307. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis. J. Appl. Phys. 1984, 55, 2115. [Google Scholar] [CrossRef]
- Daniel, L.; Hubert, O.; Buiron, N.; Billardon, R. Reversible magneto-elastic behavior: A multiscale approach. J. Mech. Phys. Solids 2008, 56, 1018–1042. [Google Scholar] [CrossRef]
- Szewczyk, R. Magnetic permeability tensor with saturation flux density description for 2D materials with uniaxial anisotropy. In Automation 2020; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; Volume 1140, pp. 300–308. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of the magnetisation process in ferromagnets and its application to the magnetomechanical effect. J. Phys. D Appl. Phys. 1984, 17, 2491. [Google Scholar] [CrossRef]
- Szewczyk, R. Generalization of the Model of Magnetoelastic Effect: 3D Mechanical Stress Dependence of Magnetic Permeability Tensor in Soft Magnetic Materials. Materials 2020, 13, 4070. [Google Scholar] [CrossRef]
- Nguyen-Schäfer, H.; Schmidt, J.P. Tensor Analysis and Elementary Differential Geometry for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-662-48495-1. [Google Scholar]
- Stuelpnagel, J. On the Parametrization of the Three-Dimensional Rotation Group. SIAM Rev. 1964, 6, 422–430. [Google Scholar] [CrossRef]
- O’Handley, R.C. Modern Magnetic Materials: Principles and Applications; Wiley: Hoboken, NJ, USA, 1999; ISBN 978-0-471-15566-9. [Google Scholar]
- Buschow KH, J.; de Boer, F.R. Physics of Magnetism and Magnetic Materials; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-0306474217. [Google Scholar]
- Bastos, J.P.A.; Sadowski, N. Magnetic Materials and 3D Finite Element Modeling; CRC Press: New York, NY, USA, 2013; ISBN 9781466592531. [Google Scholar]
- Available online: https://octave.org (accessed on 20 March 2023).
- Ripka, P. Magnetic Sensors and Magnetometers; Artech House INC: London, UK, 2001; ISBN 1-58053-057-5. [Google Scholar]
- Svec Sr, P.; Szewczyk, R.; Salach, J.; Jackiewicz, D.; Svec, P.; Bieńkowski, A.; Hosko, J. Magnetoelastic properties of selected amorphous systems tailored by thermomagnetic treatment. J. Electr. Eng. 2014, 65, 259–261. [Google Scholar] [CrossRef]
- Bieńkowski, A. Some effects of stresses in Ni-Zn ferrites containing cobalt. J. Magn. Magn. Mater. 1991, 101, 125–127. [Google Scholar] [CrossRef]
- Bieńkowski, A.; Rożniatowski, K.; Szewczyk, R. Effects of stress and its dependence on microstructure in Mn–Zn ferrite for power applications. J. Magn. Magn. Mater. 2003, 254–255, 547–549. [Google Scholar] [CrossRef]
- Råback, P.; Malinen, M.; Ruokolainen, J.; Pursula, A.; Zwinger, T. Elmer Models Manual; CSC—IT Center of Science: Espoo, Finland, 2022; Available online: http://www.nic.funet.fi/pub/sci/physics/elmer/doc/ElmerModelsManual.pdf (accessed on 20 March 2023).
- Feng, X.; Lewis, T.; Neilan, M. Discontinuous Galerkin finite element differential calculus and applications to numerical solutions of linear and nonlinear partial differential equations. J. Comput. Appl. Math. 2010, 299, 68–91. [Google Scholar] [CrossRef]
- Belytschko, T.; Moës, N.; Usui, S.; Parimi, C. Arbitrary discontinuities in finite elements. Int. J. Numer. Methods Eng. 2001, 50, 993–1013. [Google Scholar] [CrossRef]
- Moes, N.; Dolbow, J.; Belytschko, T. A Finite Element Method for Crack Growth without Remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Romkes, A.; Prudhomme, S.; Tinsley Oden, J. Convergence analysis of a discontinuous finite element formulation based on second order derivatives. Comput. Methods Appl. Mech. Eng. 2006, 195, 3461–3482. [Google Scholar] [CrossRef]
- Ahmed, U.; Blažević, D.; Mizukawa, Y.; Aydin, U.; Rasilo, P. Validation of Thermodynamic Magneto-Mechanical Finite-Element Model on Cantilever-Beam Type Magnetostrictive Energy Harvester. J. Magn. Magn. Mater. 2022, 564, 170098. [Google Scholar] [CrossRef]
- Ahmed, U.; Aydin, U.; Zucca, M.; Palumbo, S.; Kouhia, R.; Rasilo, P. Modeling a Fe-Ga Energy Harvester Fitted with Magnetic Closure Using 3D Magneto-Mechanical Finite Element Model. J. Magn. Magn. Mater. 2020, 500, 166390. [Google Scholar] [CrossRef]
- Szewczyk, R.; Nowicki, M.; Ostaszewska-Liżewska, A.; Bieńkowski, A.; Nowak, P.T.; Malinen, M. Accuracy of frame-shaped samples based measurements of magnetoelastic characteristics of soft magnetic materials. Measurements 2020, 162, 107899. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopala, D.; Ostaszewska-Liżewska, A.; Råback, P.; Szewczyk, R. Model of a 3D Magnetic Permeability Tensor Considering Rotation and Saturation States in Materials with Axial Anisotropy. Materials 2023, 16, 3477. https://doi.org/10.3390/ma16093477
Kopala D, Ostaszewska-Liżewska A, Råback P, Szewczyk R. Model of a 3D Magnetic Permeability Tensor Considering Rotation and Saturation States in Materials with Axial Anisotropy. Materials. 2023; 16(9):3477. https://doi.org/10.3390/ma16093477
Chicago/Turabian StyleKopala, Dominika, Anna Ostaszewska-Liżewska, Peter Råback, and Roman Szewczyk. 2023. "Model of a 3D Magnetic Permeability Tensor Considering Rotation and Saturation States in Materials with Axial Anisotropy" Materials 16, no. 9: 3477. https://doi.org/10.3390/ma16093477
APA StyleKopala, D., Ostaszewska-Liżewska, A., Råback, P., & Szewczyk, R. (2023). Model of a 3D Magnetic Permeability Tensor Considering Rotation and Saturation States in Materials with Axial Anisotropy. Materials, 16(9), 3477. https://doi.org/10.3390/ma16093477






