High Concentration Intrinsic Defects in MnSb2Te4
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
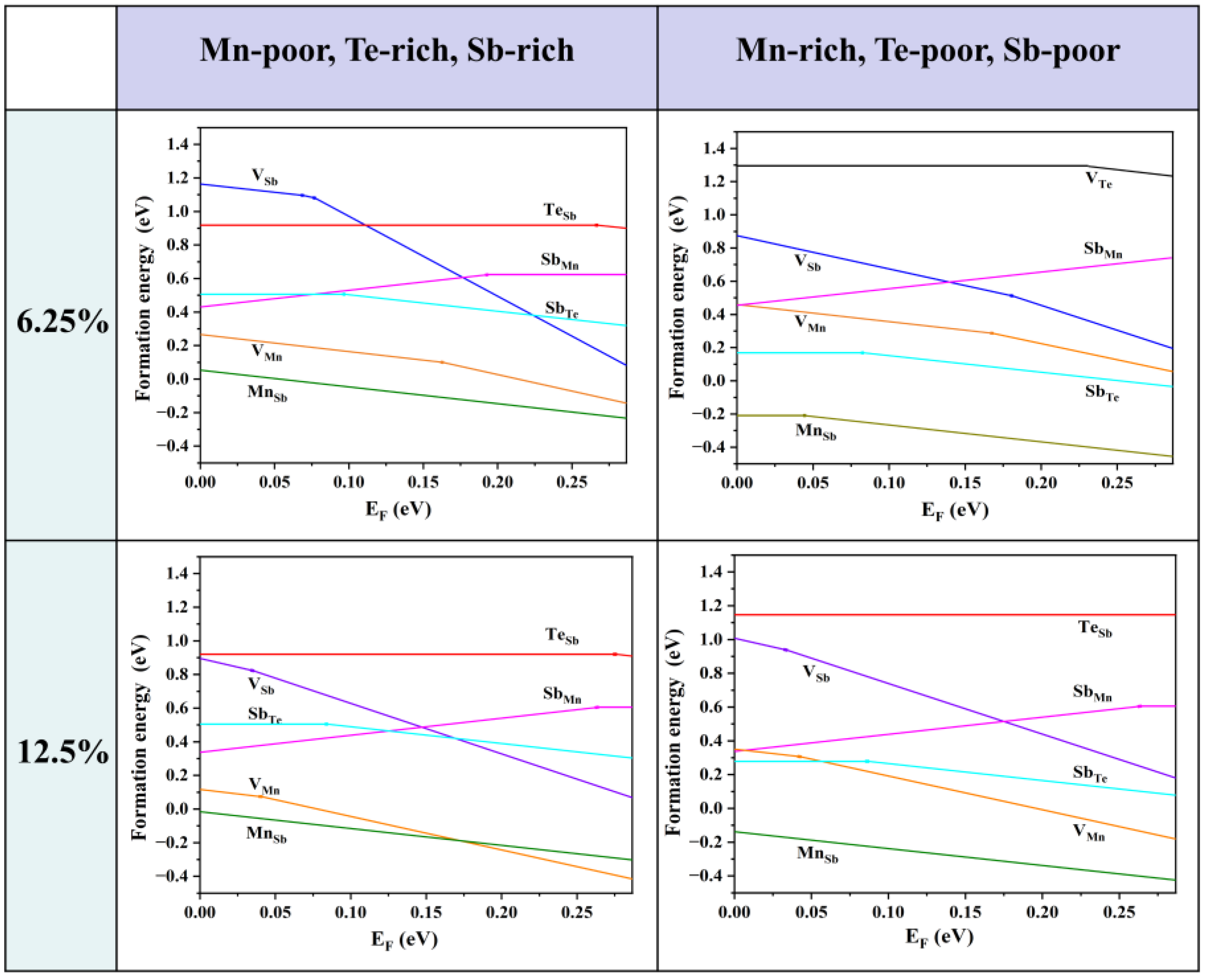
3.1. Intrinsic Defects of MnSb2Te4 at Low Concentrations
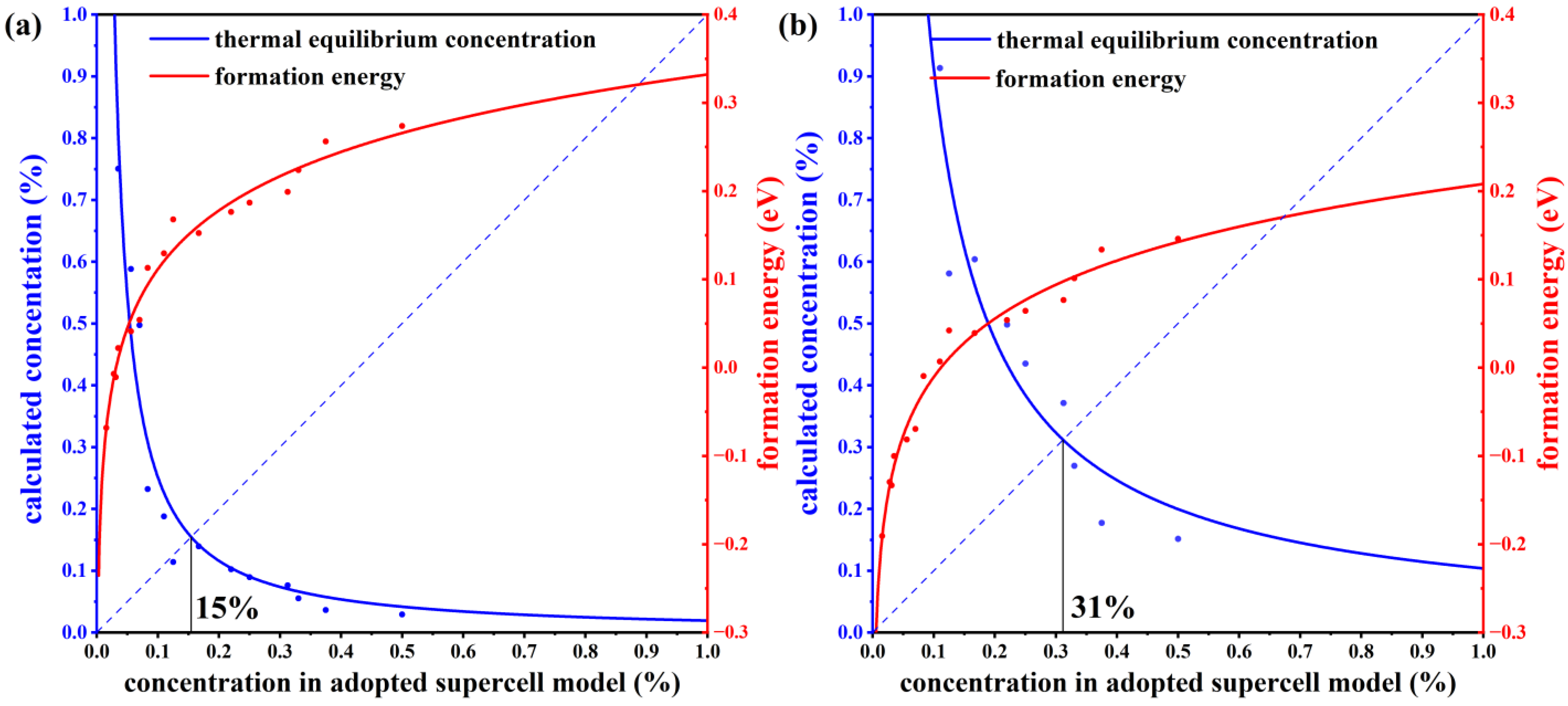
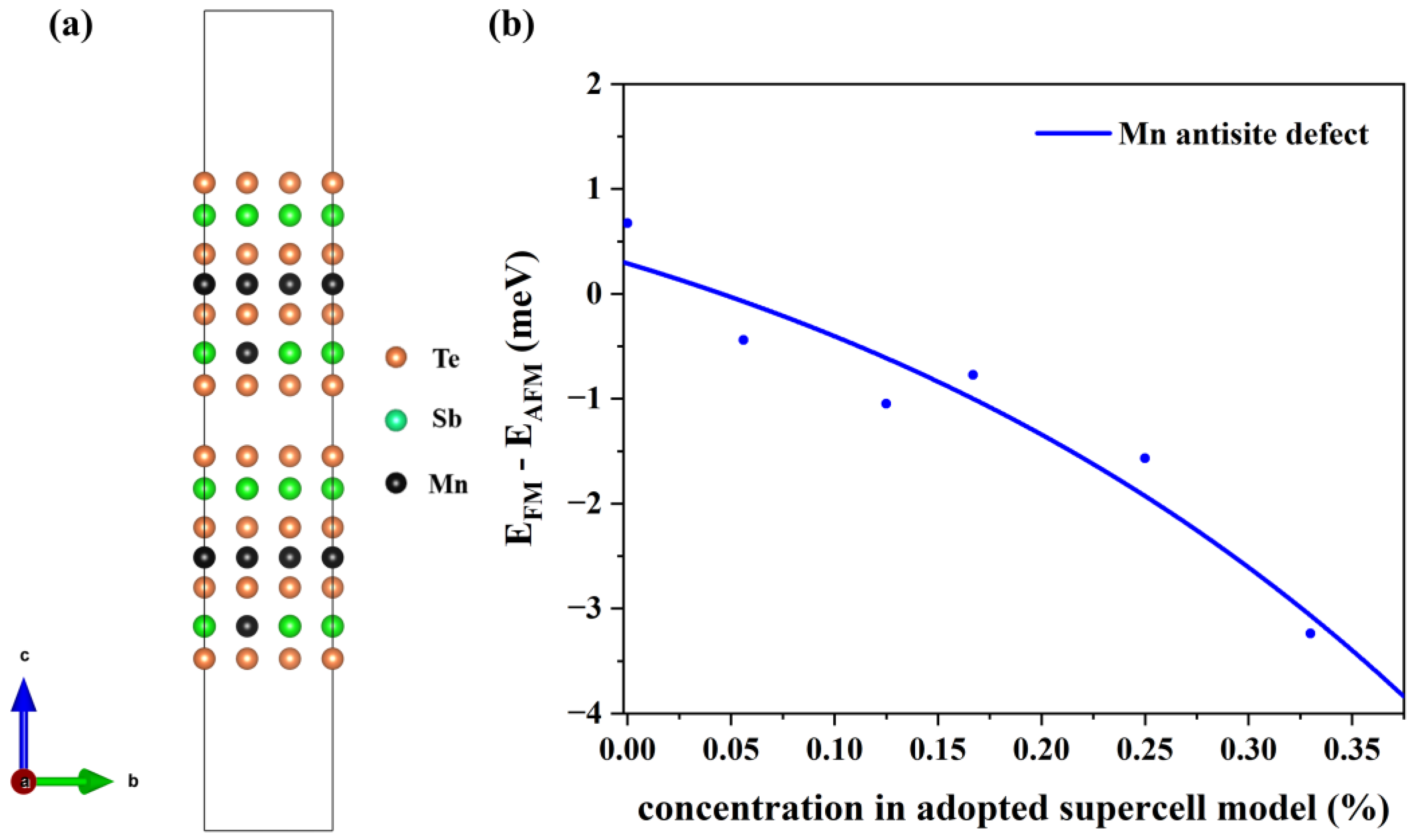
3.2. Defect Concentration of Mn Antisite Defect under a Thermal Equilibrium
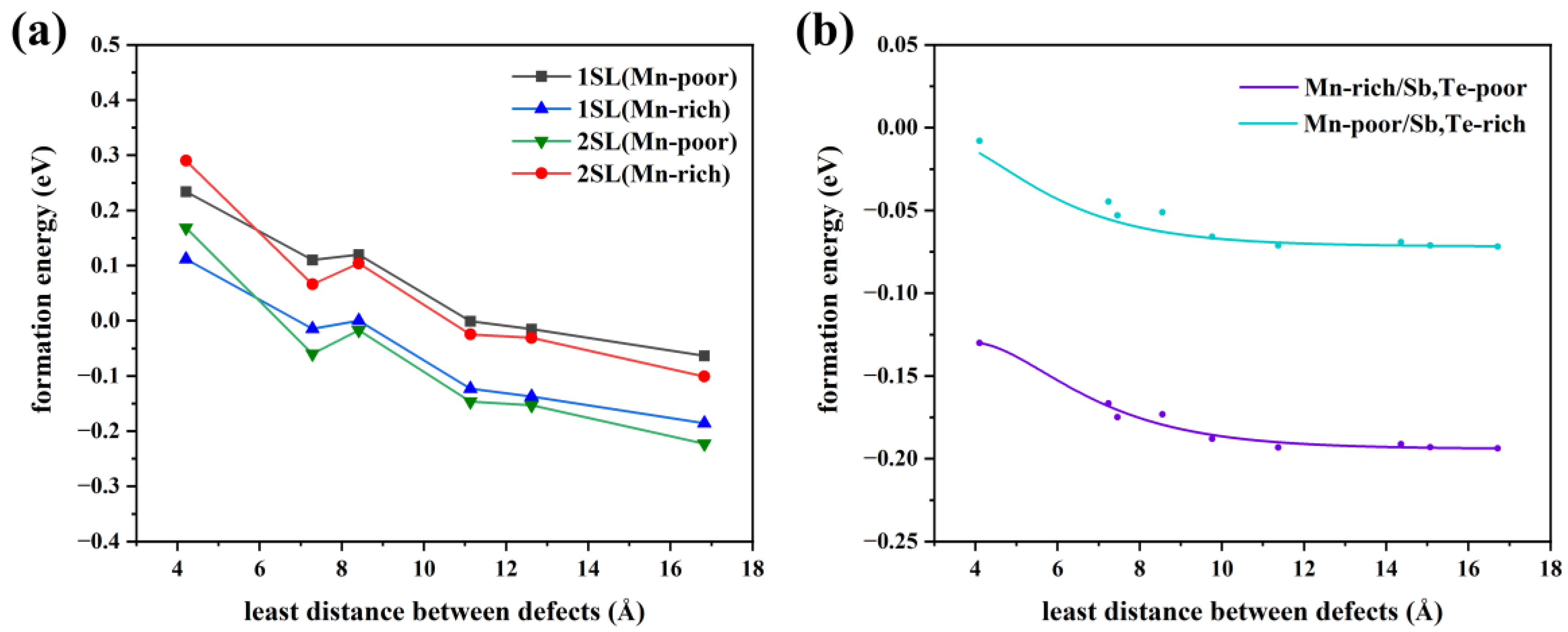
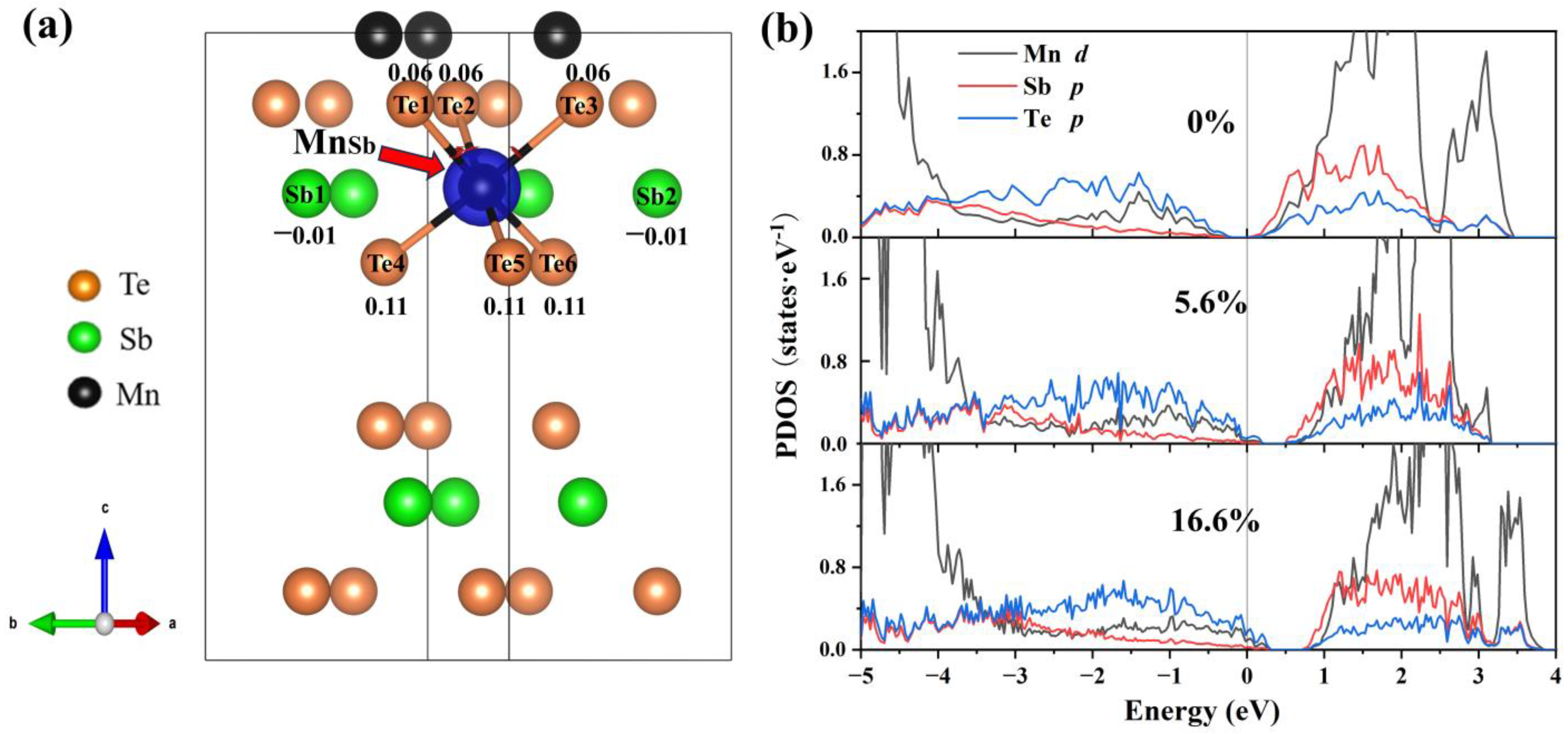
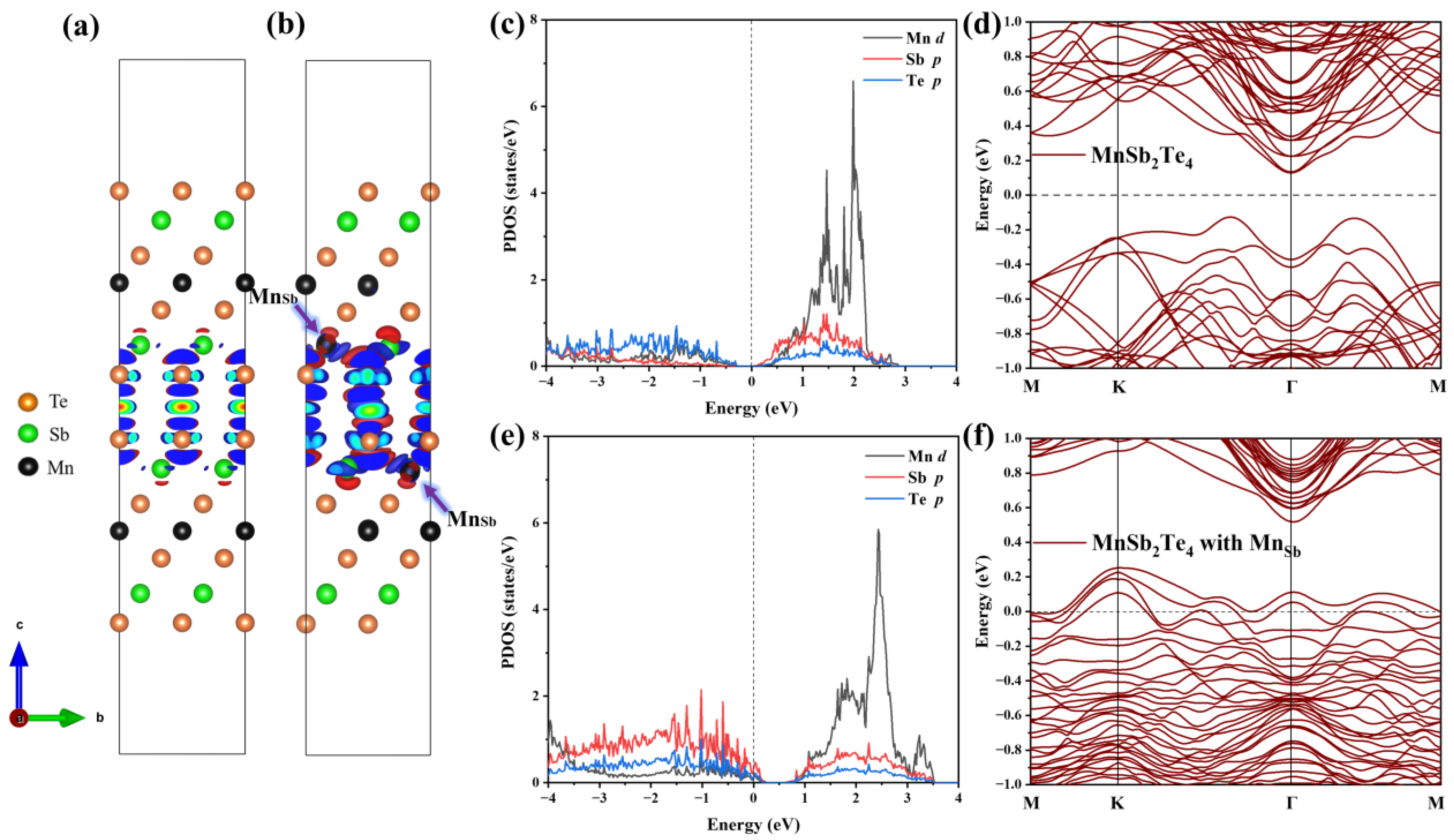
3.3. Magnetic Interlayer Coupling of MnSb2Te4 with Mn Antisite Defects
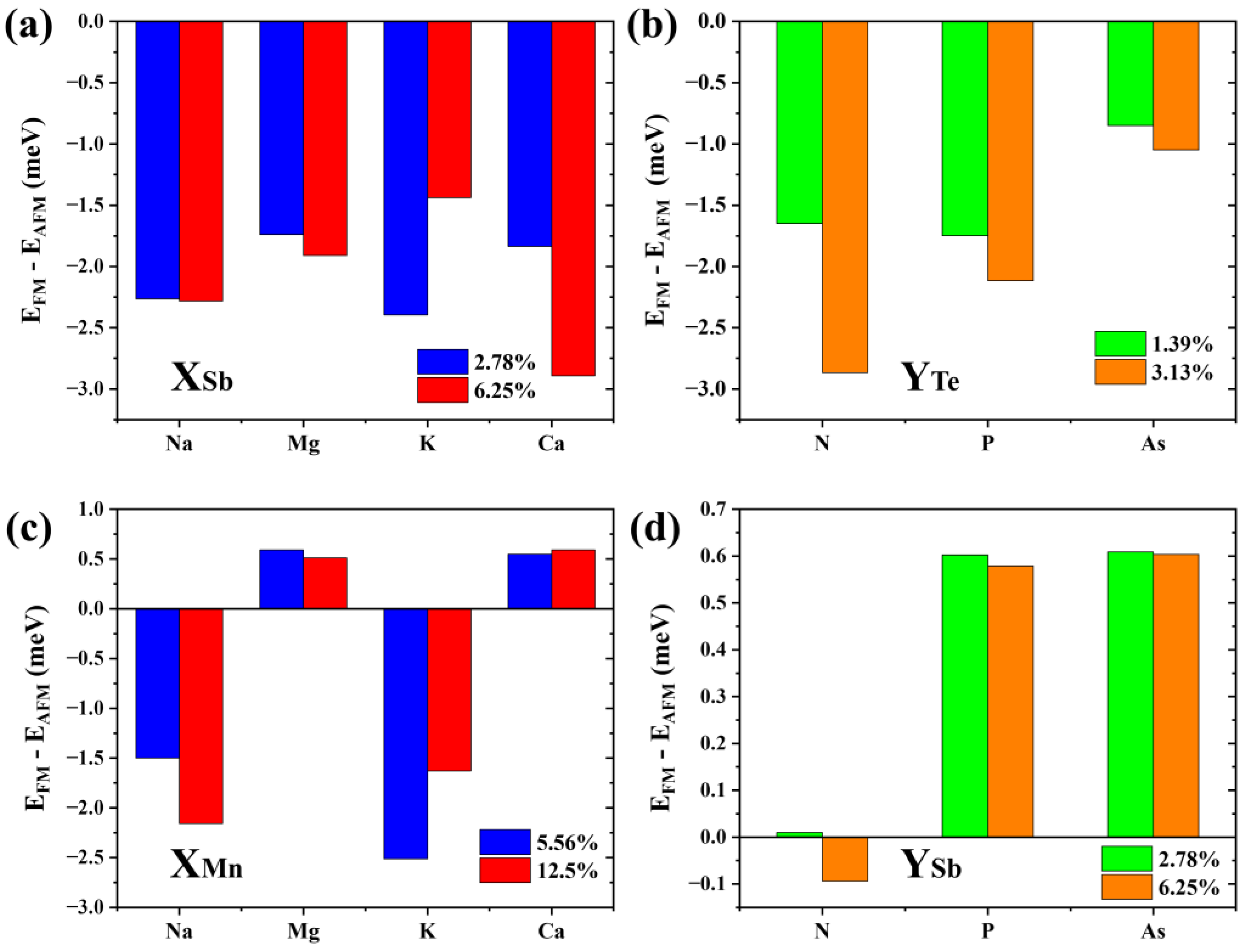
3.4. Magnetic Interlayer Coupling with Additional p-Type Doping
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, Y.; Guo, J.; Li, J.; Zhu, K.; Liao, M.; Liu, X.; Zhang, Q.; Gu, L.; Tang, L.; Feng, X. Experimental realization of an intrinsic magnetic topological insulator. Chin. Phys. Lett. 2019, 36, 076801. [Google Scholar] [CrossRef]
- Ovchinnikov, D.; Huang, X.; Lin, Z.; Fei, Z.; Cai, J.; Song, T.; He, M.; Jiang, Q.; Wang, C.; Li, H. Intertwined topological and magnetic orders in atomically thin Chern insulator MnBi2Te4. Nano Lett. 2021, 21, 2544–2550. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wang, Y.; Li, H.; Wu, Y.; Li, Y.; Li, J.; He, K.; Xu, Y.; Zhang, J.; Wang, Y. Robust axion insulator and Chern insulator phases in a two-dimensional antiferromagnetic topological insulator. Nat. Mater. 2020, 19, 522–527. [Google Scholar] [CrossRef] [PubMed]
- Otrokov, M.M.; Klimovskikh, I.I.; Bentmann, H.; Estyunin, D.; Zeugner, A.; Aliev, Z.S.; Gaß, S.; Wolter, A.U.B.; Koroleva, A.V.; Shikin, A.M. Prediction and observation of an antiferromagnetic topological insulator. Nature 2019, 576, 416–422. [Google Scholar] [CrossRef]
- Deng, Y.; Yu, Y.; Shi, M.Z.; Guo, Z.; Xu, Z.; Wang, J.; Chen, X.H.; Zhang, Y. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 2020, 367, 895–900. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, M.; Zhu, T.; Xing, D.; Zhang, H.; Wang, J. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys. Rev. Lett. 2019, 122, 206401. [Google Scholar] [CrossRef]
- Lian, B.; Liu, Z.; Zhang, Y.; Wang, J. Flat chern band from twisted bilayer MnBi2Te4. Phys. Rev. Lett. 2020, 124, 126402. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Du, S.; Wang, Z.; Gu, B.-L.; Zhang, S.-C.; He, K.; Duan, W.; Xu, Y. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Sci. Adv. 2019, 5, eaaw5685. [Google Scholar] [CrossRef]
- Zhou, L.; Tan, Z.; Yan, D.; Fang, Z.; Shi, Y.; Weng, H. Topological phase transition in the layered magnetic compound MnSb2Te4: Spin-orbit coupling and interlayer coupling dependence. Phys. Rev. B 2020, 102, 085114. [Google Scholar] [CrossRef]
- Eremeev, S.V.; Rusinov, I.P.; Koroteev, Y.M.; Vyazovskaya, A.Y.; Hoffmann, M.; Echenique, P.M.; Ernst, A.; Otrokov, M.M.; Chulkov, E.V. Topological magnetic materials of the (MnSb2Te4)·(Sb2Te3)n van der Waals compounds family. J. Phys. Chem. Lett. 2021, 12, 4268–4277. [Google Scholar] [CrossRef]
- Wimmer, S.; Sánchez-Barriga, J.; Küppers, P.; Ney, A.; Schierle, E.; Freyse, F.; Caha, O.; Michalička, J.; Liebmann, M.; Primetzhofer, D. Mn-Rich MnSb2Te4: A topological insulator with magnetic gap closing at high curie temperatures of 45–50 K. Adv. Mater. 2021, 33, 2102935. [Google Scholar] [CrossRef] [PubMed]
- Xi, M.; Chen, F.; Gong, C.; Tian, S.; Yin, Q.; Qian, T.; Lei, H. Relationship between antisite defects, magnetism, and band topology in MnSb2Te4 crystals with TC ≈ 40 K. J. Phys. Chem. Lett. 2022, 13, 10897–10904. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Du, M.-H.; Yan, J.; Wu, W. Native defects in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. Mater. 2020, 4, 121202. [Google Scholar] [CrossRef]
- Hou, F.; Yao, Q.; Zhou, C.-S.; Ma, X.-M.; Han, M.; Hao, Y.-J.; Wu, X.; Zhang, Y.; Sun, H.; Liu, C. Te-vacancy-induced surface collapse and reconstruction in antiferromagnetic topological insulator MnBi2Te4. ACS Nano 2020, 14, 11262–11272. [Google Scholar] [CrossRef]
- Du, M.H.; Yan, J.; Cooper, V.R.; Eisenbach, M. Tuning fermi levels in intrinsic antiferromagnetic topological insulators MnBi2Te4 and MnBi4Te7 by defect engineering and chemical doping. Adv. Funct. Mater. 2021, 31, 2006516. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.-L.; Zheng, Q.; Huang, Z.; Wang, X.; Chi, M.; Wu, Y.; Chakoumakos, B.C.; McGuire, M.A.; Sales, B.C. Site mixing for engineering magnetic topological insulators. Phys. Rev. X 2021, 11, 021033. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Lian, Y.; Xie, W.; Chen, L.; Zhang, J.; Wu, Y.; Fan, S. Glassy magnetic ground state in layered compound MnSb2Te4. Sci. China Mater. 2022, 65, 477–485. [Google Scholar] [CrossRef]
- Jiang, Y.; Sun, Y.Y.; Chen, M.; Wang, Y.; Li, Z.; Song, C.; He, K.; Wang, L.; Chen, X.; Xue, Q.-K. Fermi-level tuning of epitaxial Sb2Te3 thin films on graphene by regulating intrinsic defects and substrate transfer doping. Phys. Rev. Lett. 2012, 108, 066809. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Janesko, B.G. Replacing hybrid density functional theory: Motivation and recent advances. Chem. Soc. Rev. 2021, 50, 8470–8495. [Google Scholar] [CrossRef] [PubMed]
- Shinde, R.; Yamijala, S.S.; Wong, B.M. Improved band gaps and structural properties from Wannier–Fermi–Löwdin self-interaction corrections for periodic systems. J. Phys. Condens. Matter 2020, 33, 115501. [Google Scholar] [CrossRef]
- Petersilka, M.; Gossmann, U.J.; Gross, E.K.U. Excitation energies from time-dependent density-functional theory. Phys. Rev. Lett. 1996, 76, 1212. [Google Scholar] [CrossRef]
- Sham, L.J.; Schlüter, M. Density-functional theory of the band gap. Phys. Rev. B 1985, 32, 3883. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943. [Google Scholar] [CrossRef]
- Yin, Y.; Ma, X.; Yan, D.; Yi, C.; Yue, B.; Dai, J.; Zhao, L.; Yu, X.; Shi, Y.; Wang, J.-T. Pressure-driven electronic and structural phase transition in intrinsic magnetic topological insulator MnSb2Te4. Phys. Rev. B 2021, 104, 174114. [Google Scholar] [CrossRef]
- Zhang, S.B.; Wei, S.-H.; Zunger, A. Stabilization of ternary compounds via ordered arrays of defect pairs. Phys. Rev. Lett. 1997, 78, 4059. [Google Scholar] [CrossRef]
- Makov, G.; Payne, M.C. Periodic boundary conditions in ab initio calculations. Phys. Rev. B 1995, 51, 4014. [Google Scholar] [CrossRef] [PubMed]
- Murakami, T.; Nambu, Y.; Koretsune, T.; Xiangyu, G.; Yamamoto, T.; Brown, C.M.; Kageyama, H. Realization of interlayer ferromagnetic interaction in MnSb2Te4 toward the magnetic Weyl semimetal state. Phys. Rev. B 2019, 100, 195103. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Kanai, S.; Matsukura, F.; Ohno, H. Magnetic and transport properties of Sb2Te3 doped with high concentration of Cr. Appl. Phys. Express 2017, 10, 103001. [Google Scholar] [CrossRef]
- Han, Y.; Sun, S.; Qi, S.; Xu, X.; Qiao, Z. Interlayer ferromagnetism and high-temperature quantum anomalous Hall effect in p-doped MnBi2Te4 multilayers. Phys. Rev. B 2021, 103, 245403. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, J.; Peng, Y.-H.; Lin, J.-Y.; Cen, Y.-J.; Yang, X.-B.; Zhao, Y.-J. High Concentration Intrinsic Defects in MnSb2Te4. Materials 2023, 16, 5496. https://doi.org/10.3390/ma16155496
Xiong J, Peng Y-H, Lin J-Y, Cen Y-J, Yang X-B, Zhao Y-J. High Concentration Intrinsic Defects in MnSb2Te4. Materials. 2023; 16(15):5496. https://doi.org/10.3390/ma16155496
Chicago/Turabian StyleXiong, Jie, Yin-Hui Peng, Jia-Yi Lin, Yu-Jie Cen, Xiao-Bao Yang, and Yu-Jun Zhao. 2023. "High Concentration Intrinsic Defects in MnSb2Te4" Materials 16, no. 15: 5496. https://doi.org/10.3390/ma16155496
APA StyleXiong, J., Peng, Y.-H., Lin, J.-Y., Cen, Y.-J., Yang, X.-B., & Zhao, Y.-J. (2023). High Concentration Intrinsic Defects in MnSb2Te4. Materials, 16(15), 5496. https://doi.org/10.3390/ma16155496






